Precipitation governing vegetation patterns in an arid or semi-arid environment

Abstract

In an arid or semi-arid environment, precipitation plays a vital role in vegetation growth. Recent researches reveal that the response of vegetation growth to precipitation has a lag effect. To explore the mechanism behind the lag phenomenon, we propose and investigate a water-vegetation model with spatiotemporal nonlocal effects. It is shown that the temporal kernel function does not affect Turing bifurcation. For better understanding the influences of lag effect and nonlocal competition on the vegetation pattern formation, we choose some special kernel functions and obtain some insightful results: (i) Time delay does not trigger the vegetation pattern formation, but can postpone the evolution of vegetation. In addition, in the absence of diffusion, time delay can induce the occurrence of stability switches, while in the presence of diffusion, spatially nonhomogeneous time-periodic solutions may emerge, but there are no stability switches; (ii) The spatial nonlocal interaction may trigger the pattern onset for small diffusion ratio of water and vegetation, and can change the number and size of isolated vegetation patches for large diffusion ratio. (iii) The interaction between time delay and spatial nonlocal competition may induce the emergence of traveling wave patterns, so that the vegetation remains periodic in space, but is oscillating in time. These results demonstrate that precipitation can significantly affect the growth and spatial distribution of vegetation.

1 Introduction

In arid and semi-arid areas, precipitation is a dominant factor affecting the vegetation growth. For example, in the Xilingol grassland of northern China, vegetation biomass is higher in wet years and lower in dry years. Changes of precipitation may accelerate the emergence of spatial vegetation patterns, such as spots (Deblauwe et al. 2008), bands (Klausmeier 1999; Borgogno et al. 2009), fairy circles (Tlidi et al. 2008; Getzin et al. 2016; Tarnita et al. 2017), etc. The discovery of new spatial distribution structures and their formation mechanisms has always been one of the very important topics in vegetation research. Recent studies have suggested that these patterns are of great significance for understanding the structure of plant communities, and may even provide some information about future vegetation evolution (Getzin et al. 2016; Tarnita et al. 2017; Sherratt 2015; Kolokolnikov et al. 2018; Sherratt 2016; Gowda et al. 2014, 2016).

In arid environments, to cope with drought, plants tend to grow long and shallow root systems relative to the canopy size so that they can survive by maximizing the uptake of shallow soil moisture from small rainfall events. This is readily observed in arid areas and has been reported in many works (Schenk and Jackson 2002; Barbier et al. 2008; Meron 2015). For example, as a desert plant, a four-year-old salix plant is almost 3.5 ms tall, while the horizontal root system is more than 20 ms wide, more than five times as wide as the aboveground part. By parameterizing the root density data of Combretum micranthum G. Don as a kernel function describing interplant competition, Barbier et al. (2008) found that the extent of plant underground root system was greater than the canopy radius (125%). In addition, as drought intensifies, the root system tends to be shallower and wider, and the root-to-shoot ratio increases. Inspired by these characteristics of vegetation, Lefever and Lejeune (1997) originally proposed a kernel-based one-component (vegetation) model describing plant competition for water and found that interplant facilitation and competition could dominate the formation of vegetation stripes. The model in Lefever and Lejeune (1997) did not explicitly describe water dynamics and the interactions between water and plants. Actually, due to the well-developed lateral roots of plants, the plant will not only absorb water from where it is located, but also from where the root system can extend. Gilad et al. subsequently proposed models for vegetation growth by including explicitly the spatial nonlocality of water uptake, and they found that the feedbacks existing between vegetation and water significantly affect the spatial distribution of vegetation (Gilad et al. 2004, 2007; Meron et al. 2007).

It is worth mentioning that, in addition to these ’kernel-based’ models, models in the framework of the reaction-diffusion equations also play a very important role in understanding the formation mechanism of vegetation spatial structures (Klausmeier 1999; Borgogno et al. 2009; Tarnita et al. 2017; Rietkerk et al. 2000; HilleRisLambers et al. 2001; Meron 2015; Sun et al. 2018). A heuristic model is proposed by Klausmeier, which describes the interaction between water and vegetation in the form of a reaction-diffusion-advection equation (Klausmeier 1999); Rietkerk et al. (2000) further divided water resources into soil water and surface water and proposed a model in a three-component framework. These vegetation modeling efforts provide a solid foundation for studying the formation of vegetation patterns and uncovering the mechanisms behind some shapes. For example, by discussing a reduced Gilad et al. model (Gilad et al. 2007) with annual rainfall periodicity, Tzuk et al. (2019) found that seasonal changes in vegetation are influenced by the combination of precipitation and feedback between water and vegetation. Sun et al. (2022) also studied a simplified Gilad et al. model and found that the root and shoot characteristics of vegetation can induce a transition: spot pattern $\rightarrow$ labyrinth pattern $\rightarrow$ gap pattern. Eigentler and Sherratt (2019a) proposed a two-species reaction-diffusion model and found that different plant species can coexist in both spatially patterned and spatially uniform states if the difference of plant species’ average fitness is small. Pueyo et al. (2008) proposed a model incorporating seed dispersal traits and found that seed dispersal strategies that maintain high plant biomass are associated with spatial self-organization mechanisms that allow for the most effective soil water redistribution. Eigentler and Sherratt (2018) then found that widespread plant seed dispersal and increased dispersal rates have the potential to suppress vegetation patterns.

Notice that the models mentioned above are mainly limited to the consideration that the response of vegetation to soil moisture is rapid. Recently, some studies have indicated that the response of vegetation to soil water availability has a lag effect in arid and semi-arid environments (Rundquist and Harrington 2000; Wu et al. 2015; Tong et al. 2017; Bahram et al. 2019; Zhe and Zhang 2021; Harris et al. 2022). Tong et al. (2017) observed this lag phenomenon by comparing the standardized precipitation evapotranspiration index and normalized difference vegetation index (NDVI) in Xilingol grassland of northern China, and found that the responses of different types of vegetation to drought are different. Bahram et al. (2019) obtained similar results by investigating the Sari region in Northern Iran and further found that the lag period for vegetation response to drought is about one month. Wu et al. (2015) investigated the global vegetation response to different climate factors (temperature, precipitation, and solar radiation) and found that the average lag time of shrub response to precipitation was 1.14 months at high latitudes and 1.78 months at low latitudes. Harris et al. (2022) found that changes in water content within vegetation also tended to lag behind precipitation.

Although the lag phenomenon is common in vegetation response to climatic factors, to our knowledge, few studies have included this lag effect into the mathematical modeling for vegetation growth. Instead of just observing statistical data, in this paper, we explicitly introduce the lag period as a time delay into a modified Klausmeier model to explore how it affects the growth, evolution, and spatial distribution of vegetation. Also, considering the well-developed roots of plants, we follow the spatial nonlocal modeling technique in Gilad et al. (2004) and use mathematically a kernel function related to the root length to characterize the vegetation’s competition for water. These motivate us to model in the framework of delayed partial differential equations, so that the water-vegetation model proposed in this paper is a reaction-diffusion equations model with spatiotemporal nonlocal interactions. Our results show that the lag response of vegetation to soil water availability may make the vegetation remain periodic in space but be oscillating in time; Both the lag effect and the nonlocal competition for limited water resources can change the number and size of vegetation patches, and therefore significantly affect the dynamics of vegetation patterns.

The organization of this paper is as follows. We firstly perform a detailed derivation of the studied model based on the interaction mechanism between vegetation and water in Sect. 2. Then, in Sect. 3, we try to analyze the stability of positive uniform steady state under the framework of general kernel function. To further obtain the detailed information on stability, we turn our attention to some special kernel functions, which are shown in Sect. 4. In Sect. 5, some numerical simulations are presented to illustrate the influence of time delay and nonlocal interaction on vegetation pattern formation. Finally, some conclusions and important biological significance related to our results are given in Sect. 6.

2 Model formulation

In this section, we will derive a new water-vegetation model with lag effect and nonlocal interaction based on the well-known Klausmeier model in the flat environments (Klausmeier 1999). Assuming that the soil permeability is positively correlated with vegetation density, the model takes the form

$$\begin{aligned} \begin{aligned} \frac{\partial W(\vec {X},T)}{\partial T}&=D_1\varDelta W(\vec {X},T)+A-LW(\vec {X},T)-RW(\vec {X},T)P^{2}(\vec {X},T),\\ \frac{\partial P(\vec {X},T)}{\partial T}&=D_2\varDelta P(\vec {X},T)+RJW(\vec {X},T)P^{2}(\vec {X},T)-MP(\vec {X},T), \end{aligned} \end{aligned}$$

(1)

where $W(\vec {X},T)$ and $P(\vec {X},T)$ stand respectively for the water density and vegetation biomass at position $\vec {X}$ at time T. The term $-RW(\vec {X},T)P^{2}(\vec {X},T)$ in the first equation indicates the absorption of water by the vegetation roots, which causes a decrease in water density. The term $RJW(\vec {X},T)P^{2}(\vec {X},T)$ in the second equation means that the water absorbed by vegetation is converted into the vegetation biomass with rate J. $\varDelta$ is a Laplacian describing the diffusion (dispersal) rate of water (plant seeds).

Considering the lag effect between vegetation growth and precipitation and nonlocal interaction between vegetation and water in arid and semi-arid environments, we develop the following water-vegetation model with nonlocal interactions in time and space:

$$\begin{aligned} \frac{\partial W(\vec {X},T)}{\partial T}= & {} D_{1}\varDelta W(\vec {X},T)+A-LW(\vec {X},T)\nonumber \\{} & {} -RP(\vec {X},T)W(\vec {X},T)\int _{\varOmega }\varPhi _1(|\vec {X}-\vec {Y}|)P(\vec {Y},T)\textrm{d}\vec {Y},\nonumber \\ \frac{\partial P(\vec {X},T)}{\partial T}= & {} D_{2}\varDelta P(\vec {X},T)-MP(\vec {X},T)\nonumber \\{} & {} +RJ\int _{\varOmega }\int _{-\infty }^{T}\varPhi _2(|\vec {X}-\vec {Y}|,T-S)P(\vec {Y},S)W(\vec {Y},S)P(\vec {X},S)\textrm{d}S\textrm{d}\vec {Y},\nonumber \\ \end{aligned}$$

(2)

where $\varPhi _1(|\vec {X}-\vec {Y}|)$ and $\varPhi _2(|\vec {X}-\vec {Y}|,T-S)$ are kernel functions with $|\vec {X}-\vec {Y}|$ characterizing the lateral extension length of vegetation root zone, and $T-S$ being the response time of vegetation growth to precipitation, and $\varOmega$ is an infinite domain in $\mathbb {R}^N$ $(N=1$ or 2). Specially, $\varPhi _1(|\vec {X}|)$ and $\varPhi _2(|\vec {X}|,T-S)$ are nonnegative and satisfy

$$\begin{aligned} \int _{\varOmega }\varPhi _1(|\vec {X}-\vec {Y}|)\textrm{d}\vec {Y}=1,\ \int _{\varOmega }\int _{-\infty }^{t}\varPhi _2(|\vec {X}-\vec {Y}|,T-S)\textrm{d}S\textrm{d}\vec {Y}=1. \end{aligned}$$

(3)

The values, units and biological meanings of parameters in model (2) are listed in Table 1. These parameters are valid for grass and have been reported in Klausmeier (1999) and Siteur et al. (2014).

Table 1 List of parameters for model (2) and their biological meaning (Klausmeier 1999; Siteur et al. 2014)

The details for the derivation of the nonlocal terms appearing in model (2) are as follows.

• The consumption rate of water by vegetation For water, it will decrease due to the absorption by the vegetation roots. Through the well-developed root system, the water at position $\vec {X}$ can be absorbed by the plants at any position near $\vec {X}$. At position $\vec {X}$ at time T, the infiltration rate of water is assumed to be proportional to the vegetation biomass $P(\vec {X},T)$, i.e., $cP(\vec {X},T)$, where c is the infiltration rate coefficient. Thus the water infiltrated into the soil at position $\vec {X}$ at time T is

  $$\begin{aligned} cP(\vec {X},T)W(\vec {X},T). \end{aligned}$$

  Therefore the absorption rate of water by vegetation at a certain position $\vec {Y}$ around position $\vec {X}$ at time T is

  $$\begin{aligned} cP(\vec {X},T)W(\vec {X},T)\cdot qP(\vec {Y},T), \end{aligned}$$

  where q is the uptake rate coefficient. Integrating over $\vec {Y}$ in $\varOmega$, we can obtain that the consumption rate of the water at position $\vec {X}$ at time T by the vegetation in the overall region $\varOmega$ is

  $$\begin{aligned} RP(\vec {X},T)W(\vec {X},T)\int _{\varOmega }\varPhi _1(|\vec {X}-\vec {Y}|)P(\vec {Y},T)\textrm{d}\vec {Y}, \end{aligned}$$

  where $R=cq$, the kernel function $\varPhi _1(|\vec {X}-\vec {Y}|)$ describes the absorption to the water at position $\vec {X}$ by the vegetation at any position $\vec {Y}$ in $\varOmega$. Here we understand $\varPhi _1(|\vec {X}-\vec {Y}|)$ as a function of the distance between positions $\vec {X}$ and $\vec {Y}$.

• The growth rate of vegetation For vegetation, the lag effect indicates that the current vegetation growth can be affected by the precipitation at any time S before T. Through the well-developed root system, plant at position $\vec {X}$ can absorb water at any position $\vec {Y}$ near position $\vec {X}$. Arguing as above, for any fixed position $\vec {Y}$ near $\vec {X}$, the infiltration rate of the water at time S is proportional to the vegetation biomass $P(\vec {Y},S)$, i.e., $cP(\vec {Y},S)$. Thus the water infiltrated into the soil at position $\vec {Y}$ at time S is $cP(\vec {Y},S)W(\vec {Y},S),$ and therefore the absorption rate of water by vegetation at position $\vec {X}$ at time S is

  $$\begin{aligned} cP(\vec {Y},S)W(\vec {Y},S)\cdot qP(\vec {X},S). \end{aligned}$$

  Integrating over $\vec {Y}$ in $\varOmega$ and S in $(-\infty , T]$, we can obtain that the absorption of water in the overall region $\varOmega$ by vegetation at position $\vec {X}$ at time T is

  $$\begin{aligned} R\int _{\varOmega }\int _{-\infty }^{T}\varPhi _2(|\vec {X}-\vec {Y}|,T-S)P(\vec {Y},S)W(\vec {Y},S)P(\vec {X},S)\textrm{d}S\textrm{d}\vec {Y}, \end{aligned}$$

  where the kernel function $\varPhi _2(|\vec {X}-\vec {Y}|,T-S)$ describes the contribution of precipitation at position $\vec {Y}$ at time S to the vegetation growth at position $\vec {X}$ at time T. Thus the growth rate of vegetation at position $\vec {X}$ at time T is

  $$\begin{aligned} RJ\int _{\varOmega }\int _{-\infty }^{T}\varPhi _2(|\vec {X}-\vec {Y}|,T-S)P(\vec {Y},S)W(\vec {Y},S)P(\vec {X},S)\textrm{d}S\textrm{d}\vec {Y}. \end{aligned}$$

For model (2), we introduce the nondimensionalization:

$$\begin{aligned} \begin{aligned} w&=\frac{\sqrt{R}J}{\sqrt{L}}W,&p&=\frac{\sqrt{R}}{\sqrt{L}}P,\ \ m=\frac{M}{L}, \ \ t=LT,\ \ s=LS,\\ \vec {x}&=\frac{\sqrt{L}}{\sqrt{D_{1}}}\vec {X},&\vec {y}&=\frac{\sqrt{L}}{\sqrt{D_{1}}}\vec {Y}, \ \ a=\frac{\sqrt{R}J}{L\sqrt{L}}A, \ \ d=\frac{D_{1}}{D_{2}}, \end{aligned} \end{aligned}$$

(4)

which leads to

$$\begin{aligned} \frac{\partial w(\vec {x},t)}{\partial t}= & {} d\varDelta w(\vec {x},t)+a-w(\vec {x},t)\nonumber \\{} & {} -p(\vec {x},t)w(\vec {x},t)\int _{\varOmega }\phi _1(|\vec {x}-\vec {y}|)p(\vec {y},t)\textrm{d}\vec {y},\nonumber \\ \frac{\partial p(\vec {x},t)}{\partial t}= & {} \varDelta p(\vec {x},t)-mp(\vec {x},t)\nonumber \\{} & {} +\int _{\varOmega }\int _{-\infty }^{t}\phi _2(|\vec {x}-\vec {y}|,t-s)p(\vec {y},s)w(\vec {y},s)p(\vec {x},s)\textrm{d}s\textrm{d}\vec {y}, \end{aligned}$$

(5)

where

$$\begin{aligned} \phi _1(|\vec {x}-\vec {y}|)&=\varPhi _1\Big (\frac{\sqrt{D_{1}}}{\sqrt{L}}|\vec {X}-\vec {Y}|\Big ),\\ \phi _2(|\vec {x}-\vec {y}|,t-s)&=\varPhi _2\Big (\frac{\sqrt{D_{1}}}{\sqrt{L}}|\vec {X}-\vec {Y}|,\frac{1}{L}(T-S)\Big ). \end{aligned}$$

We take the initial functions in continuous function space $\textit{C}(\bar{\varOmega }\times (-\infty ,0],\mathbb {R}^+)$ as

$$\begin{aligned} w(\vec {x},t)=\varphi _{1}(\vec {x},t)>0, \quad p(\vec {x},t)=\varphi _{2}(\vec {x},t)>0 \quad \textrm{for} \quad \vec {x}\in \bar{\varOmega },\ \ t\in (-\infty ,0]. \end{aligned}$$

(6)

Model (5) with the initial condition (6) on an infinite domain $\varOmega$ in $\mathbb {R}^N(N=1,2)$ will be investigated in this paper. For the sake of mathematical analysis, we always assume that

$$\begin{aligned} \phi _2(|\vec {x}-\vec {y}|,t-s)=\phi _{21}(|\vec {x}-\vec {y}|)\phi _{22}(t-s), \end{aligned}$$

(7)

where $\phi _{21}(|\vec {x}-\vec {y}|)$ and $\phi _{22}(t-s)$ satisfy that

$$\begin{aligned} \int _{\varOmega }\phi _{21}(|\vec {x}-\vec {y}|)\textrm{d}\vec {y}=1,\ \int _{-\infty }^{t}\phi _{22}(t-s)\textrm{d}s=1. \end{aligned}$$

3 Stability of uniform steady states

In this section, we perform the linear stability analysis of the uniform steady state solutions of model (5). It follows from Klausmeier (1999) that the uniform steady state of (5) shows the following stability result with respect to spatially homogeneous perturbations.

Proposition 1

(Klausmeier (1999)) For model (5), the following conclusions are true under spatially homogeneous perturbations.

• (1) The ‘bare soil’ state (a, 0) always exists and is linearly stable.

• (2) If $a>2m$, there exist two uniform steady states: one is

  $$\begin{aligned} (w_{1},p_{1})=\Big (\frac{a-\sqrt{a^{2}-4m^{2}}}{2},\frac{2m}{a-\sqrt{a^{2}-4m^{2}}}\Big ), \end{aligned}$$

  which is linearly stable for $m<2$ or $m>2$ and $a>\frac{m^2}{\sqrt{m-1}}$, and the other is

  $$\begin{aligned} (w_{2},p_{2})=\Big (\frac{a+\sqrt{a^{2}-4m^{2}}}{2},\frac{2m}{a+\sqrt{a^{2}-4m^{2}}}\Big ), \end{aligned}$$

  which is an unstable saddle.

Notice that diffusion and spatiotemporal nonlocal interactions do not change the uniform steady states of the studied model, but may affect their linear stability. In the following, we focus on the linear stable equilibrium $(w_{1},p_{1})$ and discuss the influence of these two factors on the stability of $(w_{1},p_{1})$ for nonlocal model (5) with kernel function satisfying (7). To ensure that $(w_{1},p_{1})$ is linearly stable with respect to spatially homogeneous perturbations, in what follows, we always assume

$$\begin{aligned} m<1+p_1^2. \end{aligned}$$

(8)

Linearizing model (5) at $(w_{1},p_{1})$, we obtain

$$\begin{aligned} \begin{aligned} \frac{\partial w(\vec {x},t)}{\partial t}=&d\varDelta w(\vec {x},t)-\left( 1+p_{1}^{2}\right) w(\vec {x},t)-mp(\vec {x},t)\\&-m \int _{\varOmega }\phi _1(|\vec {x}-\vec {y}|)p(\vec {y},t)\textrm{d}\vec {y},\\ \frac{\partial p(\vec {x},t)}{\partial t}=&\varDelta p(\vec {x},t)-mp(\vec {x},t)+p_{1}^2\int _{\varOmega }\int _{-\infty }^{t}\phi _{21}(|\vec {x}-\vec {y}|)\phi _{22}(t-s)w(\vec {y},s)\textrm{d}s\textrm{d}\vec {y}\\&+m\int _{\varOmega }\int _{-\infty }^{t}\phi _{21}(|\vec {x}-\vec {y}|)\phi _{22}(t-s)\left( p(\vec {x},s)+p(\vec {y},s)\right) \textrm{d}s\textrm{d}\vec {y}, \end{aligned} \end{aligned}$$

(9)

where (7) has been used. We further assume that the solution of (9) has the form of

$$\begin{aligned} w(\vec {x},t)=w^0e^{\lambda t+i\vec {k}\cdot \vec {x}}, \ \ p(\vec {x},t)=p^0e^{\lambda t+i\vec {k}\cdot \vec {x}}, \end{aligned}$$

where i is the general imaginary unit with $i^2=-1$, $\vec {k}$ is the wave number vector with $|\vec {k}|=k$. Then the following characteristic equation of system (9) can be obtained

$$\begin{aligned} \begin{aligned} E_k(\lambda ;d,\tau ):=\,&\lambda ^2+A_k\lambda -m\widetilde{\phi _{22}}(\lambda )\Big (1+\widehat{\phi _{21}}(k)\Big ) \Big (\lambda +dk^2+1\Big )\\&+B_k -mp_{1}^2\widetilde{\phi _{22}}(\lambda )\Big (1-\widehat{\phi _{21}}(k)\widehat{\phi _{1}}(k)\Big )=0, \end{aligned} \end{aligned}$$

(10)

where

$$\begin{aligned} A_k=(d+1)k^2+1+p_{1}^{2}+m,\ \ B_k=(dk^2+1+p_{1}^2)(k^2+m), \end{aligned}$$

and

$$\begin{aligned} \widetilde{f}(\lambda ):=\int _{-\infty }^{t}f(t-s)e^{-\lambda (t-s)}\textrm{d}s=\int _{0}^{+\infty }f(t)e^{-\lambda t}\textrm{d}t \end{aligned}$$

is the Laplace transformation of function f(t), and

$$\begin{aligned} \widehat{g}(k):=\int _{\varOmega }g(|\vec {x}-\vec {y}|)e^{-i\vec {k}\cdot (\vec {x}-\vec {y})}\textrm{d}\vec {y}=\int _{\varOmega }g(|\vec {z}|)e^{i\vec {k}\cdot \vec {z}}\textrm{d}\vec {z} \end{aligned}$$

is the Fourier transformation of function $g(|\vec {z}|)$.

The stability of the equilibrium will change if there exists an eigenvalue that crosses the imaginary axis, which can be characterized by the existence of the eigenvalues with the form of $\lambda =i\omega , \ \omega \ge 0$ (notice that the complex roots always appear in pairs, we only need to discuss the situation when $\omega \ge 0$). Then the characteristic equation (10) becomes

$$\begin{aligned} \begin{aligned}&-\omega ^2+A_ki\omega -m\widetilde{\phi _{22}}(i\omega )\left( 1+\widehat{\phi _{21}}(k)\right) \left( i\omega +dk^2+1\right) +B_k\\ -&mp_{1}^2\widetilde{\phi _{22}}(i\omega )\left( 1-\widehat{\phi _{21}}(k)\widehat{\phi _{1}}(k)\right) =0. \end{aligned} \end{aligned}$$

(11)

It then follows that there may exist four bifurcating solutions: spatially homogeneous equilibrium, spatial patterns, spatially homogeneous oscillations and spatially nonhomogeneous oscillations. The first two are stationary bifurcations, and the latter two are induced by Hopf bifurcation. Note that the bifurcating solution of spatially homogeneous equilibrium will not emerge as pointed out in Proposition 1.

For spatially nonhomogeneous stationary bifurcation (Turing bifurcation), which occurs when $\omega =0$, $k\ne 0$, the bifurcation solutions are nonconstant steady state solutions (i.e., spatial patterns). The critical condition of Turing bifurcation can be determined by considering

$$\begin{aligned} \begin{aligned} h(k):=&\left( 1+dk^2+p_{1}^2\right) k^2-m(1+dk^2)\int _{\varOmega }\phi _{21}(|\vec {z}|) \cos (\vec {k}\cdot \vec {z})\textrm{d}\vec {z}\\&+mp_{1}^2\int _{\varOmega }\phi _{21}(|\vec {z}|)\cos (\vec {k}\cdot \vec {z})\textrm{d}\vec {z} \int _{\varOmega }\phi _{1}(|\vec {z}|)\cos (\vec {k}\cdot \vec {z})\textrm{d}\vec {z}=0, \end{aligned} \end{aligned}$$

(12)

where we have applied the properties that

$$\begin{aligned} \int _{\varOmega }\phi _{21}(|\vec {z}|)\sin (\vec {k}\cdot \vec {z})\textrm{d}\vec {z}=0\ \ \textrm{and} \ \ \int _{\varOmega }\phi _{1}(|\vec {z}|)\sin (\vec {k}\cdot \vec {z})\textrm{d}\vec {z}=0 \end{aligned}$$

by noting that $\phi _{21}(|\vec {z}|)$ and $\phi _{1}(|\vec {z}|)$ are both even functions. For large k, h(k) is dominated by the first term in (12), which implies that $h(k)\rightarrow \infty$ as $k\rightarrow \infty$. Notice that $h(0)=m\left( p_{1}^2-1\right) >0$. Then this bifurcation occurs only if there exists some k such that $h(k)\le 0$. The critical condition should satisfy

$$\begin{aligned} h(k)=0,\ \ h'(k)=0. \end{aligned}$$

(13)

For general kernel functions, it is difficult to obtain general results. Thus, we turn to consider some special kernel functions in the sequel. In addition, from (12), it is easy to see that Turing bifurcation is independent of the temporal kernel, which reveals that the form of the function $\phi _{22}(t)$ in (7) has no effect on Turing instability. Therefore, we take two special cases $\phi _{22}(t)=\delta (t-\tau )$, where $\tau$ is a fixed time delay, and $\phi _{22}(t)=\delta (t)$ in this paper.

For the remaining two bifurcations, it is nearly impossible to directly obtain some information from the related characteristic equations for general kernel functions. We will provide some relevant results for special kernel functions in the next section.

4 Some special kernels

In this section, we consider model (5) with several kernel functions $\phi _1(|\vec {x}|)$, $\phi _2(|\vec {x}|,t)$ for different specific biological situations. In each case, we study detailedly the linear stability of $(w_1,p_1)$ and some bifurcations.

4.1 With only time delay

By taking

$$\begin{aligned} \phi _1(|\vec {x}|)=\delta (|\vec {x}|),\ \phi _2(|\vec {x}|,t)=\delta (|\vec {x}|)\delta (t-\tau ), \end{aligned}$$

(14)

model (5) is reduced to the following local delayed reaction diffusion equations

$$\begin{aligned} \begin{aligned} \frac{\partial w(\vec {x},t)}{\partial t}&=d\varDelta w(\vec {x},t)+a-w(\vec {x},t)-p^2(\vec {x},t)w(\vec {x},t),\\ \frac{\partial p(\vec {x},t)}{\partial t}&=\varDelta p(\vec {x},t)-mp(\vec {x},t)+p^2(\vec {x},t-\tau )w(\vec {x},t-\tau ). \end{aligned} \end{aligned}$$

(15)

Here the kernel functions in (14) describe a limit scenario where the roots of plant are short and do not exceed its canopy radius, so that the plant can only absorb water from its location. In addition, the plant does not move, and also does the water absorbed into the body by the plant root system. Thus in this case, there exists a local delayed feedback between the vegetation growth and water, which makes the term $p^2(\vec {x},t-\tau )w(\vec {x},t-\tau )$ in the equation of plant growth of system (15) reasonable.

For system (15), the characteristic equation (11) becomes

$$\begin{aligned} \begin{aligned}&-\omega ^2+A_ki\omega -2m\left( i\omega +dk^2+1\right) e^{-i\omega \tau } +B_k=0. \end{aligned} \end{aligned}$$

(16)

We consider three forms of solutions of system (15) to explore the impact of lag period $\tau$ on the vegetation spatial distribution: non-constant steady state solution, spatially homogenous or nonhomogenous periodic solution.

4.1.1 Turing bifurcation

Non-constant steady state solution may occur when system (15) undergoes Turing bifurcation. Assuming $\omega =0,k\ne 0$ in (16), we obtain the following critical condition for the occurrence of Turing bifurcation:

$$\begin{aligned} B_k-2m(dk^2+1)=dk^4+(1+p_1^2-dm)k^2+m(p_1^2-1)=0. \end{aligned}$$

(17)

We choose the water diffusion coefficient d as the bifurcation parameter. For system (15), the water obviously diffuses faster than the seeds of vegetation, thus we assume that $d>1$ (the plant diffusion coefficient has been normalized to one).

Define

$$\begin{aligned} \mathbb {D}=\{d(k^2)|0<k^2<m,\ \textrm{and}\ a, m\ \textrm{satisfy}\ (8) \}. \end{aligned}$$

(18)

Lemma 1 below indicates that fast water diffusion can facilitate the occurrence of Turing instability.

Lemma 1

Assume that $a>2m$ and (8) hold. Then a simple zero eigenvalue appears if and only if $d\in \mathbb {D}$, where $\mathbb {D}$ is defined in (18). Moreover, there always exists a $k_T\in (0,\sqrt{m})$, which is defined in (21), such that $d_{*}=d(k_T^2)=\min d(k^2)$. If $d<d_{*}$, there is no Turing instability, while if $d>d_{*}$, there exist some k such that $B_k-2m(dk^2+1)<0$, i.e., Turing instability occurs.

Proof

Solving Eq. (17), we can obtain that

$$\begin{aligned} d(k^2)=\frac{m(1-p_{1}^2)-(1+p_{1}^2)k^2}{k^2(k^2-m)}. \end{aligned}$$

(19)

If (8) is satisfied, it then follows from $p_{1}^2>1$ that $d(k^2)>1$ for $k^2<m$. We now compute the extreme value of the function $d(k^2)$ in (19). By taking the derivative with respect to $k^2$, we can obtain

$$\begin{aligned} d'(k^2)=\frac{(1+p_{1}^2)k^4-2m(1-p_{1}^2)k^2+m^2(1-p_{1}^2)}{k^4(k^2-m)^2}. \end{aligned}$$

(20)

Then $d'(k^2)<0$ for $0<k<k_{T}$ and $d'(k^2)>0$ for $k>k_{T}$, where

$$\begin{aligned} k_{T}=\sqrt{\frac{m\left( 1-p_{1}^2\right) +mp_{1}\sqrt{2\left( p_{1}^2-1\right) }}{1+p_{1}^2}}. \end{aligned}$$

(21)

It is clear that $k_{T}<\sqrt{m}$ and the function $d(k^2)$ takes its minimum value at $k=k_T$, i.e.,

$$\begin{aligned} d(k_T^2)=\min d(k^2):=d_{*}. \end{aligned}$$

(22)

It then follows that when $d>d_{*}$, there is always some positive k such that $B_k-2m(dk^2+1)<0$; while when $d<d_{*}$, there is no positive k such that (17) is satisfied. In addition, a zero eigenvalue emerges if and only if $d\in \mathbb {D}$. Taking the derivative of $\lambda$ on both sides of Eq. (10) under the kernel function (14), we obtain that

$$\begin{aligned} \frac{\partial E_k(\lambda ;d,\tau )}{\partial \lambda }\Big |_{\lambda =0}=(d+1)k^2+1+p_1^2-m+2m(dk^2+1)\tau >0 \end{aligned}$$

(23)

for all $\tau \ge 0$, which indicates that $\lambda =0$ is a simple characteristic root. Moreover, we can obtain from (10) that

$$\begin{aligned} \frac{\partial \lambda }{\partial d}\Big |_{\lambda =0}=\frac{k^2(m-k^2)}{(d+1)k^2+1+p_1^2-m+2m(dk^2+1)\tau }, \end{aligned}$$

(24)

which is positive if $k<\sqrt{m}$. Therefore, the transversality condition holds. The proof is completed. $\square$

Remark 1

From the proof of Lemma 1, we know that

$$\begin{aligned} {B_k-2m(dk^2+1)} {\left\{ \begin{array}{ll}<0, &{}\textrm{if} \ 0<k<\sqrt{m}, d>d(k^2),\\ >0, &{}\textrm{if} \ k\ge \sqrt{m}, \ \textrm{or} \ 0\le k<\sqrt{m}, d<d(k^2). \end{array}\right. } \end{aligned}$$

Particularly, when $d<d_{*}$, $B_k-2m(dk^2+1)>0$ for all $k\ge 0$.

Lemma 1 indicates that Turing instability occurs when $d>d_{*}$. In what follows, we always assume that $d<d_{*}$, that is the constant steady state $(w_1,p_1)$ is stable for system (15) without delay, and consider the influence of delay on the stability.

4.1.2 Hopf bifurcation

Hopf bifurcation may occur when the following conditions are satisfied for $\omega >0$

$$\begin{aligned} \begin{aligned} -\omega ^{2}+B_k&=2m\omega \sin (\omega \tau )+2m(dk^2+1) \cos (\omega \tau ),\\ A_k\omega&=2m\omega \cos (\omega \tau )-2m(dk^2+1) \sin (\omega \tau ). \end{aligned} \end{aligned}$$

(26)

From (26), we know that

$$\begin{aligned} F(\omega ^2):=\omega ^{4}+\left( A_k^2-2B_k-4m^2\right) \omega ^{2}+B_k^2-4m^2(dk^2+1)^2=0, \end{aligned}$$

(27)

where

$$\begin{aligned} A_k^2-2B_k-4m^2=\left( d^2+1\right) k^4+2\left( d+dp_1^2+m\right) k^2 +\left( 1+p_1^2\right) ^2-3m^2. \nonumber \\ \end{aligned}$$

(28)

It follows from Remark 1 that when $d<d_*$, $B_k-2m(dk^2+1)>0$ for any $k\ge 0$. In addition, since $B_k+2m(dk^2+1)>0$, we have $B_k^2-4m^2(dk^2+1)^2>0$ for any $k\ge 0$, which indicates that (27) has positive roots only if

$$\begin{aligned} A_k^2-2B_k-4m^2<0, \ \ \triangle _k>0, \end{aligned}$$

(29)

where

$$\begin{aligned} \triangle _k=\left( A_k^2-2B_k-4m^2\right) ^2-4\left( B_k^2-4m^2(dk^2+1)^2\right) . \end{aligned}$$

(30)

Denote

$$\begin{aligned} \alpha =\left( 1+p_1^2\right) ^2-3m^2. \end{aligned}$$

(31)

We firstly look for the spatially nonhomogeneous Hopf bifurcation, i.e., when $k\ne 0$. There are two cases below.

Case 1. $\alpha >0$. In this case, $A_k^2-2B_k-4m^2>0$ for any $k\ge 0$, which violates the first condition in (29). Then, (27) has no positive roots and $(w_1,p_1)$ is stable for all $\tau \ge 0$.

Case 2. $\alpha <0$. In this case, $A_k^2-2B_k-4m^2>0$ for $k>k_1$ and $A_k^2-2B_k-4m^2<0$ for $0\le k<k_1$, where

$$\begin{aligned} k_1=\sqrt{\frac{-\left( d+dp_1^2+m\right) +\sqrt{\left( d+dp_1^2+m\right) ^2-(d^2+1)\alpha }}{d^2+1}}. \end{aligned}$$

(32)

Then if these exists a $k\in (0,k_1)$ such that $\triangle _k>0$, then (27) has two different positive roots $\omega _k^{\pm 2}$, where

$$\begin{aligned} \omega ^{\pm 2}(k)=\frac{-(A_k^2-2B_k-4m^2)\pm \sqrt{\triangle _k}}{2}. \end{aligned}$$

(33)

Moreover, from (26), we can know that

$$\begin{aligned} \sin (\omega \tau )=\frac{-\omega ^3+\left( -(dk^2+1)A_k+B_k\right) \omega }{2m\omega ^2+2m(dk^2+1)^2}. \end{aligned}$$

(34)

In particular, at $\omega =\omega _{k}^{+}$,

$$\begin{aligned} \sin (\omega _{k}^{+}\tau )=-\frac{(dk^2+\frac{1}{2})A_k+2m^2+\sqrt{\triangle _k}}{2m\omega _{k}^{+2}+ 2m(dk^2+1)^2}\omega _{k}^{+}<0. \end{aligned}$$

(35)

Then the corresponding critical values of $\tau$ are

$$\begin{aligned} \tau _{k}^{j+}=\frac{1}{\omega _{k}^{+}}\Big (2(j+1)\pi -\arccos S_k^+ \Big ), \end{aligned}$$

(36)

where

$$\begin{aligned} S_k^+=\frac{(A_k-(dk^2+1))\omega _k^{+2}+(dk^2+1)B_k}{2m\omega _{k}^{+2}+ 2m(dk^2+1)^2}. \end{aligned}$$

At $\omega =\omega _{k}^{-}$,

$$\begin{aligned} \begin{aligned} \tau _k^{j-}= \left\{ \begin{array}{l} \displaystyle {\frac{1}{\omega _k^{-}}\left( \arccos S_k^-+2j\pi \right) ,\ \textrm{if}\ \sin (\omega _k^{-}\tau )\ge 0,}\\ \displaystyle {\frac{1}{\omega _k^{-}}\left( 2(j+1)\pi -\arccos S_k^- \right) ,\ \textrm{if}\ \sin (\omega _k^{-}\tau )<0,} \end{array} \right. \end{aligned} \end{aligned}$$

(37)

where $j=0,1,2,\cdots$ and

$$\begin{aligned} S_k^-=\frac{(A_k-(dk^2+1))\omega _k^{-2}+(dk^2+1)B_k}{2m\omega _{k}^{-2}+ 2m(dk^2+1)^2}. \end{aligned}$$

Obviously, $\{\tau _{k}^{j+}\}_{j=0}^{\infty }$ and $\{\tau _{k}^{j-}\}_{j=0}^{\infty }$ ($k\in (0,\sqrt{m})$ and satisfies $\triangle _k>0$) are sequences of function. Their images are both a cluster of curves and the bottom curves corresponds respectively to the functions $\tau _{k}^{0+}$ and $\tau _{k}^{0-}$. Now we compute the crossing direction. It is easy to obtain that

$$\begin{aligned}&{\Re \left( \frac{d\lambda }{d\tau }\right) ^{-1}\bigg |_{\tau =\tau _{k}^{j-}}}<0, \end{aligned}$$

(38)

$$\begin{aligned}&{\Re \left( \frac{d\lambda }{d\tau }\right) ^{-1}\bigg |_{\tau =\tau _{k}^{j+}}}>0. \end{aligned}$$

(39)

Define

$$\begin{aligned} \tau ^*=\min _k \tau _{k}^{0+},\ \tau ^{**}=\min _k \tau _{k}^{0-}. \end{aligned}$$

(40)

If $\tau ^*>\tau ^{**}$, then $\tau ^{**}$ is the minimum critical value of delay $\tau$. It follows that $(w_1,p_1)$ is always asymptotically stable for all $\tau \ge 0$. If $\tau ^*<\tau ^{**}$, then $\tau ^{*}$ is the minimum critical value of delay $\tau$. Assume that $\tau ^{*}$ is taken at $k=k_2$. Since the function $\tau _{k}^{0+}$ is continuous in k, there is a neighborhood of $k_2$ such that the corresponding curve segment lies in the bottom of the whole curves. Therefore, no stability switches occur and when $\tau <\tau ^{*}$, all the eigenvalues has the negative real parts, when $\tau >\tau ^{*}$, the characteristic equation has at least a pair of conjugate complex roots with positive real parts.

As a summary, we have the following lemma.

Lemma 2

Assume that $a>2m$, $d<d_*$ and (8) hold. Then the following statements are true for system (15).

• (1) If $\alpha >0$, then $(w_1,p_1)$ is always asymptotically stable for all $\tau \ge 0$.

• (2) If $\alpha <0$ and these exists a $k\in (0,k_1)$ such that $\triangle _k>0$, then when $\tau ^*>\tau ^{**}$, $(w_1,p_1)$ is always asymptotically stable for all $\tau \ge 0$; when $\tau ^*<\tau ^{**}$, $(w_1,p_1)$ is asymptotically stable for $\tau <\tau ^*$ and unstable for $\tau >\tau ^*$, where $\tau ^*$ and $\tau ^{**}$ are defined in (40). When $\tau =\tau _k^{j\pm }\ (j=0,1,2,\cdots )$, a spatially nonhomogeneous Hopf bifurcation occurs at $(w_1,p_1)$.

Moreover, it is clear that $A_0^2-2B_0-4m^2=\alpha$. If $\alpha <0$ and $\triangle _0>0$, then (27) with $k=0$ has two different positive roots, which correspond to spatially homogeneous Hopf bifurcation. Arguing as above, we have the following lemma.

Lemma 3

Assume that $a>2m$ and (8) hold. Then for system (15) with $k=0$, the following statements are true.

• (1) If $\alpha >0$ or $\triangle _0<0$ then $(w_1,p_1)$ is always asymptotically stable for all $\tau \ge 0$.

• (2) If $\alpha <0$ and $\triangle _0>0$, then there is a $\kappa \ge 0$ such that $(w_1,p_1)$ is asymptotically stable for $\tau \in (0,\tau _0^{0+})\bigcup \cdots \bigcup (\tau _0^{(\kappa -1)-},\tau _0^{\kappa +})$ and unstable for $\tau \in (\tau _0^{0+},\tau _0^{0-})\bigcup \cdots \bigcup (\tau _0^{\kappa +},+\infty )$. When $\tau =\tau _0^{j\pm } (j=0,1,2,\cdots )$, a spatially homogeneous Hopf bifurcation occurs at $(w_1,p_1)$.

4.2 With only nonlocal spatial effect

In this section, we consider the following one-dimensional purely spatial kernels

$$\begin{aligned} \phi _1(|x|)=\phi (|x|),\ \phi _2(|x|,t)=\phi (|x|)\delta (t),\ x\in \mathbb {R} \end{aligned}$$

(41)

where

$$\begin{aligned} \begin{aligned} \phi (|x|)= \left\{ \begin{array}{l} \displaystyle {\frac{3(\rho ^2-|x|^2)}{4\rho ^{2}} \qquad |x|\le \rho ,}\\ \displaystyle {\ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \qquad \textrm{otherwise}.} \end{array} \right. \end{aligned} \end{aligned}$$

(42)

In this situation, model (5) becomes the following form

$$\begin{aligned} \begin{aligned} \frac{\partial w(x,t)}{\partial t}&=d\varDelta w(x,t)+a-w(x,t)-p(x,t)w(x,t)\int _{\mathbb {R}}\phi (|x-y|)p(y,t)\textrm{d}y,\\ \frac{\partial p(x,t)}{\partial t}&=\varDelta p(x,t)-mp(x,t)+p(x,t)\int _{\mathbb {R}}\phi (|x-y|)p(y,t)w(y,t)\textrm{d}y,\\ w(x,0)&=\varphi _{1}(x)>0, \ \ p(x,0)=\varphi _{2}(x)>0, \end{aligned} \end{aligned}$$

(43)

where the function $\phi (|x-y|)$ has the parabolic form (Segal et al. 2013) and describes the potential ability that the plant absorbs water from the position at distance $|x-y|$. Here the kernel functions (41) stand for a situation where the lateral roots of plants are very long, and the response of vegetation to water is rapid.

The characteristic equation (10) also becomes

$$\begin{aligned} \lambda ^{2}-\textrm{Tr}_{k}\lambda +{\varLambda }_{k}=0, \end{aligned}$$

(44)

where

$$\begin{aligned} \textrm{Tr}_{k}=&-(1+p_{1}^{2})+m\widehat{\phi }(k)-(1+d)k^{2}, \end{aligned}$$

(45)

$$\begin{aligned} {\varLambda }_{k}=&dk^{4}+\left( 1+p_{1}^{2}-dm\widehat{\phi }(k)\right) k^{2}-m\widehat{\phi }(k)\left( 1-p_{1}^{2}\widehat{\phi }(k) \right) , \end{aligned}$$

(46)

and

$$\begin{aligned} \widehat{\phi }(k)=\int _{\mathbb {R}}\phi (y)e^{iky}\textrm{d}y=\frac{3}{k^2\rho ^2} \Big (\frac{\sin (k\rho )}{k\rho }-\cos (k\rho )\Big ). \end{aligned}$$

(47)

We always assume that $d<d_{*}$ for which $(w_1,p_1)$ is asymptotically stable, and discuss the following two kinds of solutions of system (43): spatially nonhomogeneous periodic solution and nonconstant steady state solution.

4.2.1 Hopf bifurcation

System (43) may show a spatially nonhomogeneous periodic solution when a spatially nonhomogeneous Hopf bifurcation occurs. The critical condition is $\textrm{Tr}_{k}=0$ for a unique k and ${\varLambda }_{k}>0$ for all k. From $\textrm{Tr}_{k}=0$, we can directly obtain that

$$\begin{aligned} \widehat{\phi }(k)=\frac{(d+1)k^2+1+p_1^2}{m}. \end{aligned}$$

(48)

Then substituting (48) into (46), we have that

$$\begin{aligned} \begin{aligned} {\varLambda }_{k}=&\left( (d+1)^2p_1^4-md^2\right) k^4+\left( mp_1^2+2(1+p_1^2)((d+1)p_1^2-dm) \right) k^2\\&+\left( 1+p_1^2\right) \left( p_1^2(1+p_1^2)-m\right) . \end{aligned} \end{aligned}$$

(49)

It is easy to see that $\left( 1+p_1^2\right) \left( p_1^2(1+p_1^2)-m\right) >0$, then ${\varLambda }_{k}>0$ for all $k>0$ if

$$\begin{aligned} \begin{aligned}&\left( mp_1^2+2(1+p_1^2)((d+1)p_1^2-dm)\right) ^2\\ <&4\left( (d+1)^2p_1^4-md^2\right) \left( (1+p_1^2)(p_1^2(1+p_1^2)-m)\right) . \end{aligned} \end{aligned}$$

(50)

This indicates that a Hopf bifurcation may occur if (50) holds. In this situation, we choose d as the bifurcation parameter and then determine the critical value $d_{H}$ of Hopf bifurcation. For fixed $\rho$, it follows from (45) that $\textrm{Tr}_{k}<0$ for small k or large k. As discussed above, the critical condition of Hopf bifurcation is $\textrm{Tr}_{k}=0$ for a unique k, then only when zero is the maximum of the function $\textrm{Tr}_{k}$, Hopf bifurcation may occur. Denote this unique k as $k_{H}$, then a corresponding $d_{H}$ can be obtained and at $d=d_{H}$ and $k=k_{H}$, $\textrm{Tr}_{k}$ satisfies

$$\begin{aligned} \frac{\partial \textrm{Tr}_{k}}{\partial k}\Big |_{k=k_{H}}=0,\ \ \ \textrm{Tr}_{k_{H}}=0. \end{aligned}$$

(51)

Note that (51) is just a necessary condition of Hopf bifurcation and there may exist several pairs $k_{H}$ and $d_{H}$ satisfying (51). For ease of analysis, we might as well write them as $k_{cH}$ and $d_{cH}$.

From the first equation of (51), we have that

$$\begin{aligned} d_{cH}=\frac{m\widehat{\phi '}(k_{cH})}{2}-1, \end{aligned}$$

(52)

where

$$\begin{aligned} \widehat{\phi '}(k_{cH})=\frac{3(k_{cH}^2\rho ^2-3)\sin (k_{cH}\rho )+3(2k_{cH}\rho +2)\cos (k_{cH}\rho )}{k_{cH}^4\rho ^3}. \end{aligned}$$

The biological fact $d>1$ implies that $\widehat{\phi '}(k_{cH})>\frac{4}{m}$. Define

$$\begin{aligned} \mathscr {D}_1=\left\{ k_{cH}\Big | k_{cH} \ \textrm{satisfies} \ (52) \textrm{and}\ \widehat{\phi '}(k_{cH})>\frac{4}{m} \right\} . \end{aligned}$$

Substituting (52) into (45), we can obtain that

$$\begin{aligned} \textrm{Tr}_{k_{cH}}=-(1+p_1^2)+m\widehat{\phi }(k_{cH})-\frac{mk^2\widehat{\phi '}(k_{cH})}{2}, \end{aligned}$$

(53)

where $k_{cH}\in \mathscr {D}_1$. Then $k_{H}$ can be obtained by solving

$$\begin{aligned} 0=\max _{k_{cH}\in \mathscr {D}_1}\textrm{Tr}_{k_{cH}}:=\textrm{Tr}_{k_{H}}. \end{aligned}$$

(54)

Substituting the value of $k_{H}$ into (52), we can obtain the critical diffusion value $d_{H}$. It then follows that $\textrm{Tr}_{k}>0$ for some $k>0$ when $d<d_{H}$ and $\textrm{Tr}_{k}<0$ for all $k>0$ when $d>d_{H}$.

Moreover, the transversality condition is also satisfied. In fact,

$$\begin{aligned} \frac{\textrm{d}\Re (\lambda )}{\textrm{d}d}=\frac{\textrm{d}}{\textrm{d}d}\left( \frac{\textrm{Tr}_k}{2}\right) = -k^2<0. \end{aligned}$$

(55)

As a summary, we have the following lemma.

Lemma 4

Assume that $a>2m$ and (8) holds. For system (43), if (50) is satisfied, then when d passes across $d=d_H$, a spatially nonhomogeneous Hopf bifurcation occurs at $(w_1,p_1)$.

4.2.2 Turing bifurcation

System (43) may exist a nonconstant steady state solution when Turing bifurcation occurs. The critical condition is that the characteristic equation has a simple zero eigenvalue and all other eigenvalues have negative real parts, i.e., ${\varLambda }_{k}=0$ for a unique $k>0$ and $\textrm{Tr}_{k}<0$ for all $k>0$.

Obviously, if

$$\begin{aligned} m\widehat{\phi }(k)<1+p_1^2 \end{aligned}$$

(56)

holds for all $k>0$, then $\textrm{Tr}_{k}<0$ for all $k>0$. In this situation, we choose d as the bifurcation parameter and then determine the critical value $d_{T}$ of Turing bifurcation. From (46), it is easy to see that ${\varLambda }_{k}>0$ for small k or large k. The critical condition of Turing bifurcation is ${\varLambda }_{k}=0$ for a unique k, then zero must be the minimum of the function ${\varLambda }_{k}$. Denote this unique k as $k_{T}$. Then a corresponding $d_{T}$ can also be determined and at $d=d_{T}$ and $k=k_{T}$, ${\varLambda }_{k}$ satisfies

$$\begin{aligned} \frac{\partial {\varLambda }_{k}}{\partial k}=0,\ \ \ {\varLambda }_{k}=0. \end{aligned}$$

(57)

Note that (57) is just a necessary condition of Turing bifurcation and there may exist several pairs $k_{T}$ and $d_{T}$ satisfying (57). For ease of analysis, we might as well write them as $k_{cT}$ and $d_{cT}$.

From the first equation of (57), we have that

$$\begin{aligned} d_{cT}=\frac{m\widehat{\phi '}(k_{cT})-2(1+p_1^2)k_{cT}-2mp_1^2\widehat{\phi }(k_{cT})\widehat{\phi '}(k_{cT})}{4k_{cT}^3-mk_{cT}^2\widehat{\phi '}(k_{cT})-2mk_{cT}\widehat{\phi }(k_{cT})}. \end{aligned}$$

(58)

Define

$$\begin{aligned} \mathscr {D}_2=\left\{ k_{cT}\Big | k_{cT} \ \textrm{satisfies} \ (58) \textrm{and}\ d_{cT}>1 \right\} . \end{aligned}$$

Substituting (58) into (46), we can obtain that

$$\begin{aligned} {\varLambda }_{k_{cT}}=d_{cT}k_{cT}^{4}+\left( 1+p_{1}^{2}-d_{cT}m\widehat{\phi }(k_{cT})\right) k_{cT}^{2}-m\widehat{\phi }(k_{cT})\left( 1-p_{1}^{2}\widehat{\phi }(k_{cT}) \right) ,\nonumber \\ \end{aligned}$$

(59)

where $k_{cT}\in \mathscr {D}_2$. Then $k_{T}$ can be obtained by solving

$$\begin{aligned} 0=\min _{k_{cT}\in \mathscr {D}_2}{\varLambda }_{k_{cT}}:={\varLambda }_{k_{T}}. \end{aligned}$$

(60)

Substituting the value of $k_{T}$ into (58), we can obtain the critical diffusion value $d_{T}$. It then follows that ${\varLambda }_{k}<0$ for some $k>0$ when $d>d_{T}$ and ${\varLambda }_{k}>0$ for all $k>0$ when $d<d_{T}$.

As a summary, we show the following lemma.

Lemma 5

Assume that $a>2m$ and (56) holds. For system (43), then when $d=d_T$, at $(w_1,p_1)$, a Turing bifurcation occurs. Particularly, when $d<d_T$, there is no Turing instability, and when $d>d_T$, nonconstant steady state solutions emerge.

In the sequel of this section, we take the parameter values

$$\begin{aligned} a=1.8, \ m=0.45 \end{aligned}$$

(61)

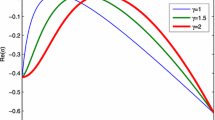
to show the influence of $\rho$ and d on the stability of $(w_{1},p_{1})$ by dispersal relation. By simple computations, we obtain that $(w_{1},p_{1})=(0.1206,3.732)$, $d_{*}=174.99$. Lemma 1 indicates that if spatial nonlocal interactions are ignored, $(w_{1},p_{1})$ is linearly stable for $d<d_{*}$ and unstable for $d>d_{*}$. Figures 1 and 2 shows the effects of nonlocal interaction and diffusion ratio of water and vegetation on the growth rate of perturbations. By investigating the impact of nonlocal interaction range on the growth rate of perturbations at different diffusion ratios of water and vegetation, we find that: (i) for small diffusion ratio of water and vegetation (for example, $d=150$), $(w_{1},p_{1})$ is linearly stable for small nonlocal range and unstable for large enough nonlocal range (see Fig. 1a). In this case, the spatial nonlocal interaction is the main possible driving factor of the emergence of Turing patterns. However, it holds only if there exists a very strong nonlocal interaction intensity, which is difficult to be observed in the real ecosystems; (ii) for large diffusion ratio of water and vegetation (for example, $d=500$), $(w_{1},p_{1})$ is unstable if the nonlocal interaction is not considered. When the nonlocal interaction is included, the growth rate of perturbations and the wavenumber range in which $\Re (\lambda )>0$ decreases as the nonlocal range increases (see Fig. 1b). In this case, the instability is induced by the diffusion ratio of water and vegetation. These findings reveal that the diffusion ratio of water and vegetation plays a vital role in the pattern onset.

Next, we explore the impact of nonlocal interaction on the critical diffusion ratio for pattern onset if we include the nonlocal interaction. As can be seen from Fig. 2, the relationship between the critical diffusion ratio and the range of nonlocal interactions is not linear. When the nonlocal range is small (for example, $\rho =0.01$ and $\rho =0.5$), the critical diffusion ratio is close to $d_{*}$; When the nonlocal range is large (for example, $\rho =5$ and $\rho =50$), the critical diffusion ratio increases. In particular, when $\rho =50$, the critical diffusion ratio is about $d\approx 420$, which is larger than that in the situation where the nonlocal interaction is ignored. This implies that the nonlocal interaction between vegetation and water resources seems to inhibit the occurrence of Turing pattern when the other factors are fixed.

Fig. 1

Dispersion relations of system (43) with different d. Other parameter values are set as $a=1.8$, $m=0.45$

Fig. 2

Dispersion relations of system (43) with different $\rho$. Other parameter values are set as $a=1.8$, $m=0.45$

It is worth mentioning that the phenomenon of multi-peaks in dispersion relationships appears for large $\rho$, and it is not common for general local reaction-diffusion equations model. It has been reported in the investigation about the pattern formation mechanism in drylands (Martínez-García et al. 2013), and they find that the long-range competition alone can induce the pattern onset. As we know, unimodal dispersion curve means that there is only one extreme point $k_c$ and it is concave $\left( i.e., \frac{\partial ^2 \Re (\lambda )}{\partial k^2}|_{k=k_c}<0\right)$. A curve with multiple peaks means that it has multiple extreme points and different convexities. In fact, $\Re (\lambda )=\frac{1}{2}\textrm{Tr}_k$. Taking the differential with respect to k, we can obtain

$$\begin{aligned} \frac{\textrm{d} \Re (\lambda )}{\textrm{d} k}=\frac{1}{2}m\widehat{\phi }'(k)-(1+d)k. \end{aligned}$$

Letting $\frac{\textrm{d }\Re (\lambda )}{\textrm{d} k}=0$, then

$$\begin{aligned} 3m\left( k\rho \cos (k\rho )-3\sin (k\rho )+k^2\rho ^2\sin (k\rho )\right) =2(1+d)k^5\rho ^3. \end{aligned}$$

(62)

For given parameter values m, d, $\rho$, the solution k of (62) can be ontained. Notice that (62) includes trigonometric functions. For given $\rho$, there may exist several k to satisfy Eq. (62), which indicates that the phenomenon with multi-peaks may emerge.

4.3 With both nonlocal spatial effect and time delay

In this section, we take the following kernels

$$\begin{aligned} \phi _1(x)=\phi (x),\ \phi _2(x,t)=\phi (x)\delta (t-\tau ), \end{aligned}$$

(63)

where $\phi (x)$ is given in (42). Then model (5) reduces to the following form:

$$\begin{aligned} \begin{aligned} \frac{\partial w(x,t)}{\partial t}=\,&d\varDelta w(x,t)+a-w(x,t)\\&-w(x,t)p(x,t)\int _{\mathbb {R}}\phi (x-y)p(y,t)dy,\\ \frac{\partial p(x,t)}{\partial t}=\,&\varDelta p(x,t)-mp(x,t)\\&+p(x,t-\tau )\int _{\mathbb {R}}\phi (x-y)p(y,t-\tau )w(y,t-\tau )dy. \end{aligned} \end{aligned}$$

(64)

The stability of positive equilibrium $(w_{1},p_{1})$ is determined by

$$\begin{aligned} \lambda ^{2}-\textrm{Tr}_{k}\lambda +\varLambda _{k}=0, \end{aligned}$$

(65)

where

$$\begin{aligned} \textrm{Tr}_{k}=\,&-(1+p_{1}^{2})-m+m\left( \widehat{\phi }(k)+1\right) e^{-\lambda \tau }-(1+d)k^{2}, \end{aligned}$$

(66)

$$\begin{aligned} \varLambda _{k}=\,&dk^{4}+\left( 1+p_{1}^{2}-dm\widehat{\phi }(k)e^{-\lambda \tau }\right) k^{2}-m\widehat{\phi }(k)\left( 1-p_{1}^{2}\widehat{\phi }(k) \right) e^{-\lambda \tau }. \end{aligned}$$

(67)

It is easy to know that $(w_{1},p_{1})$ is locally asymptotically stable if for all $k>0$,

$$\begin{aligned} \textrm{Tr}_{k}<0, \ \ \ \varLambda _{k}>0. \end{aligned}$$

(68)

If condition (68) is violated, the stability of $(w_{1},p_{1})$ will change. Due to the complexity of mathematical analysis, we employ numerical simulations to examine that how time delay $\tau$ and nonlocal distance $\rho$ affect the vegetation spatial distribution.

5 Numerical simulations

In this section, we present some numerical simulations to explore the impacts of time delay and nonlocal interactions on the growth and spatial distribution of vegetation in arid and semi-arid environments. We use a bounded domain that is large enough and has a periodic boundary to approximate the infinite domain $\varOmega$. Based on the parameter values in Table 1 and dimensionless transformations in (4), the parameter values can be converted into

$$\begin{aligned} m=0.45, \ \ a\in (0,3.56]. \end{aligned}$$

(69)

By Proposition 1, when $a>0.9$, the positive equilibrium $(w_{1},p_{1})$ exists and is stable to the spatially homogeneous perturbations. Unless specified, we will take the parameter values shown in (69) in this section.

5.1 The effect of time delay on vegetation evolution

In this section, we discuss model (5) with kernel function (14) (i.e., system (15)) to explore the effect of time delay on vegetation pattern. We take the precipitation level $a=1.8$, and the diffusion parameter $d=500$. Then the positive equilibrium $(w_{1},p_{1})=(0.1206,3.732)$, $\alpha =14.47>0$, $1+p_1^2-dm=-210.07<0$. The critical value of diffusion for Turing bifurcation is $d_{*}=174.99$. Our theoretical analyses suggest that if the perturbation is spatially homogeneous, $(w_{1},p_{1})$ is always stable (see Lemma 3(1)), and if the perturbation is spatially nonhomogeneous, $(w_{1},p_{1})$ is stable for $d<174.99$ and unstable for $d>174.99$ (see Lemma 2). It can be seen that the time delay in system (15) does not change the stability of $(w_{1},p_{1})$, and therefore does not affect the vegetation pattern onset. Interestingly, spot pattern structures appear when we simulate system (15) with $d=500$ and different time delays (see Fig. 3). In addition, the same or similar vegetation structure can be observed at different moments for different time delays. For example, the vegetation structures of $\tau =0.33$ and 1.5 are similar, respectively, at $t=150$ and $t=250$. This indicates that the time delay may not change the steady state distribution of vegetation but helps to postpone the vegetation evolution.

Fig. 3

Pattern formation of vegetation for system (15) with different time delays $\tau$ at different moments. The initial functions are taken as $w=w_{1}+ 0.2\cos (0.5x)$, $p=p_{1}+0.5\cos (0.5x)$ $\textrm{for}$ $t\in [-\tau ,0], x\in [0,100]$. The values of $\tau$ are set as $\tau =0$, $\tau =0.33$ and $\tau =1.5$. Other parameter values are set as $a=1.8$, $m=0.45$ and $d=500$

Notice that for the empirical parameters in (69), the time delay does not induce the occurrence of Hopf bifurcation as expected. From a biological perspective, this means that the lag response of vegetation to soil water availability is not the main factor responsible for temporal oscillations in vegetation. To further demonstrate the possible temporal oscillations in vegetation communities, we specifically take another different set of parameter values ($a=5.24$ and $m=2.5$) having not ever used in the previous relevant literature for numerical simulations. In this situation, $(w_{1},p_{1})=(1.836,1.362)$, $\alpha =-10.6<0$, $\triangle _0=8.885>0$. Here, we only show the case where the perturbation is spatially homogeneous. It follows from Lemma 3 (2) that there exist the following critical values of $\tau$

$$\begin{aligned} \{\tau _{j}\}_{j=1}^{\infty }=\{2.2795,3.1331,4.6901,6.3510,7.1001,\cdots \}, \end{aligned}$$

(70)

at which spatially homogeneous Hopf bifurcations occur. The stability of the equilibrium $(w_{1},p_{1})$ changes when the first five values of this sequence are taken for time delay $\tau$. In Fig. 4, we numerically show the stability switches of $(w_{1},p_{1})$ with respect to delay $\tau$. It can be clearly seen that $(w_{1},p_{1})$ is stable for $\tau \in [0,2.2795)\cup (3.1331,4.6901)\cup (6.3510,7.1001)$ and unstable for $\tau \in (2.2795,3.1331)\cup (4.6901, 6.3510)\cup (7.1001,\infty )$. Two specific time series diagrams for different $\tau$ are shown in Fig. 5. When $\tau =0.8\in [0,2.2795)$, $(w_{1},p_{1})$ is stable (see Fig. 5a) and when $\tau =2.6\in (2.2795,3.1331)$, $(w_{1},p_{1})$ is unstable and a periodic solution emerges (see Fig. 5b). If the perturbation is spatially nonhomogeneous, the stability switches disappear and spatially nonhomogeneous periodic solutions may emerge according to Lemma 2, and thus vegetation presents regular pattern structures.

Fig. 4

Bifurcation diagram of model (15) with respect to time delay $\tau$ under spatially homogeneous perturbation. The other parameter values are taken as $a=5.24$, $m=2.5$. The solid/dotted curves denote the stable/unstable steady state respectively

Fig. 5

The time series diagrams of model (15) with different time delays $\tau$ under spatially homogeneous perturbation. (15): a $\tau =0.8$ and b $\tau =2.6$. The other parameter values are the same as Fig. 4

5.2 The effect of spatial nonlocal interaction on vegetation evolution

In this section, we discuss model (5) with kernel function (41) (i.e., system (43)) to explore the effect of spatial nonlocal interaction on vegetation pattern formation. The dispersal relations in Fig. 1 shows that the diffusion ratio of water and vegetation is the main reason for the pattern onset, and long-range spatial nonlocal interaction may cause the occurrence of the pattern only when the diffusion ratio is relatively small. For given diffusion ratio, spatial nonlocal range will change the wavenumber of pattern. Notice that the kernel function (41) approaches a delta function as $\rho \rightarrow 0$, and in this case, system (43) degenerates into the corresponding local version. Based on the results in subsection 5.1 for the empirical parameters, in this subsection, we take $d=500$. Under this set of parameters, the vegetation pattern can appear even if the spatial nonlocal interactions are not considered. In view of the effect of spatial nonlocal interaction on wavenumber of patterns, we further vary $\rho$. The corresponding pattern results in one dimension space are shown in Fig. 6, which indicate that the spatial nonlocal interaction between vegetation and water can change significantly the spatial structure of vegetation. When $\rho$ is small, for example, $\rho =1.8$, vegetation follows a nonuniform steady state distribution with six spaced bumps that are distributed periodically in space (Fig. 6a). As $\rho$ increases, both the number of vegetation bumps and the density difference between adjacent bumps change. In particular, the vegetation does not show periodicity in space, and the density difference between adjacent bumps in the middle of the region is small (Fig. 6b and c). If $\rho$ is further increased, for example, $\rho =40$, it is surprised to find that the vegetation follows a spatial distribution curves with two peaks (Fig. 6d), that is, there only exist two vegetation bumps in the whole region. Moreover, by comparing the vegetation density at the peaks, it can be seen that with the increase of the nonlocal range, the vegetation density at the peak decreases first and then increases.

Fig. 6

Patterns in one dimensional space $\mathbb {R}^1$ of system (43) with different $\rho$. The initial functions are $w=w_{1}+ 0.005\cos (x)$ and $p=p_{1}+0.005\cos (x)$. The nonlocal distance is set as a $\rho =1.8$, b $\rho =2.5$, c $\rho =15$, d $\rho =40$. Other parameter values are set as $a=1.8$, $m=0.45$, $d=500$

5.3 Combined effect of time delay and spatial nonlocality on vegetation evolution

To further explore the combined effect when the lag effect and spatial nonlocal interaction are considered simultaneously, we perform a set of numerical simulations by varying $\tau$ on the basis of the parameters of Fig. 6a. The related results are shown in Figs. 7 and 8. In the absence of time delay (i.e., $\tau =0$, see Figs. 7a and 8a), the vegetation shows periodic spatial distribution, which is symmetrically distributed in space; while in the presence of time delay (see Figs. 7b and c, and 8b and c), vegetation tends to migrate to the right boundary of the region, and thus the spatial symmetry of vegetation distribution is broken. The migration rate seems to be positively related to the time delay. In addition, near both two boundaries of the region, the ’bare soil’ state appears, and the size of bare soil near the left boundary is obviously larger than that near the right boundary. Also, increasing the lag period will increase the size of vegetation patches, and thus the number of vegetation patches will decrease.

Fig. 7

Spatiotemporal patterns of system (64) with different $\tau$ in $\mathbb {R}^1$. The time delays are set as a $\tau =0$, b $\tau =0.01$, c $\tau =1.5$. The initial functions and other parameter values are the same as Fig. 6a

Fig. 8

Patterns of system (64) with different $\tau$ in $\mathbb {R}^1$. The time delays are set as a $\tau =0$, b $\tau =0.01$, c $\tau =1.5$. The initial functions and other parameter values are the same as Fig. 6a

6 Discussion

In this paper, we propose and analyze an extended Klausmeier model with lag effect and spatial nonlocal interaction in arid and semi-arid environments where water is the only nutrient element limiting the vegetation growth. Considering the lag response of vegetation to precipitation and the competition of vegetation roots for limited water resources, we innovatively introduce spatiotemporal nonlocal interactions into the classical Klausmeier model. The nonlocal interaction in space is used to describe long-range competition for water between plants, which has been confirmed by a large number of empirical studies as the basis for dryland vegetation patterns (Martínez-García et al. 2013, 2014). The lag feedback in time has not been included before in the modeling research related to the vegetation growth. Here, we treat the lag time as a growth delay. It is undeniable that growth delay and root length of vegetation will necessarily affect the response of vegetation to soil water availability, such as vegetation biomass and spatial distribution. Therefore, it is important to reveal the influence of these two factors on the vegetation growth and then to uncover possible mechanisms behind regular vegetation structures.

The lag feedback between vegetation growth and precipitation is common, especially in arid environments, which has rarely been considered in previous vegetation modeling. Field studies related to this lag feedback were mainly conducted by comparing the relationship between the NDVI datasets and key climate factors, and the results have shown that the explanation rate of vegetation growth variation will increase considerably if this lag feedback is taken into account (Zhao et al. 2020). For example, by conducting a research in the Jinghe River Basin (JRB) and the Beilo River Basin (BLRB), two typical ecologically vulnerable areas (arid regions) in the Loess Plateau of China, Zhao et al. (2020) found that when considering the lag feedbacks, the explanation rates of JRB and BLRB NDVI changes increased by 37.4% and 65.1%, respectively. For the main model (5) proposed in this paper, we first consider a limit case where the vegetation root is relatively short and does not exceed the canopy radius. In this situation, there only exists the lag feedback of vegetation to water, indicating that vegetation growth depends not only on the current time but also the past time. By performing the numerical simulations with the empirical parameters, we point out that the inclusion of time delay neither triggers the pattern onset nor changes the final pattern structure of vegetation (for different time delays, the final steady state distribution is spot patterns), but can postpone the vegetation evolution (see Fig. 3 for the details). This result implies that lag feedback present in vegetation to precipitation is not the main driver of interannual variation in vegetation biomass cycles, which have been observed in recent field observations, such as the interannual variation of the NDVI in the Great Mekong Subregion (Han and Song 2022) or that of monthly and seasonal NDVI in China from 1982 to 1999 (Piao et al. 2003). It is generally believed that this interannual variation in plants is mainly caused by temperature as well as seasonal precipitation (Wen et al. 2017; Piao et al. 2003; Han and Song 2022; Guttal and Jayaprakash 2007). Moreover, a pronounced spatial and seasonal variations in the interannual variation of vegetation activity can be observed (Chen et al. 2020; Wen et al. 2019, 2017). From a qualitative rather than quantitative perspective, our results are consistent with these observations to some extent. Specifically, for different time delays, vegetation will show different spatial distribution patterns at the same time before arriving at the steady state (see Fig. 3 for the details), which implies the temporal and spatial variations. Unfortunately, our study presents only a simple modeling framework for plant growth in arid regions and does not mathematically model plants for a specific arid region. If the plant species in a specific arid region are considered, the lag period of vegetation growth and precipitation can be roughly estimated by combining the actual relationship between NDVI and key climate factors. Further, if the data can be combined with a framework of mathematical models that conform to the laws of plant growth, the results will be more convincing.

Notice also that the diffusion ratio of water and vegetation has a great influence on the formation of Turing patterns when the lag feedback is considered. In particular, there exists a threshold of the diffusion ratio independent of time delay: when the diffusion ratio is larger than the threshold, vegetation shows nonconstant steady state distributions; while when the diffusion ratio is smaller than the threshold, vegetation follows a uniform distribution. Moreover, the system dynamics is sensitive to the perturbation form of initial values. If the perturbation is spatially homogeneous, large time delay can induce the stability switches, while if the perturbation is spatially nonhomogeneous, spatially nonhomogeneous time-periodic solutions may emerge, but stability switches do not occur.

The impacts of competition between vegetation for limited water resources on the spatial distribution of vegetation have been a key topic in arid regions. Numerous field studies have shown that this competition between plants is mainly achieved through their laterally extended and shallow root system (Getzin et al. 2022; Messaoudi et al. 2020; Schenk and Jackson 2002). In this paper, we use a kernel function (41) of the parabolic type to characterize this, and derive a modified Klausmeier model with nonlocal interactions. It is shown that the diffusion ratio of water and vegetation is responsible for the formation of vegetation patterns in most situations, and root length of vegetation may change the number and size of the vegetation bumps. The numerical results in Fig. 6 are based on the assumption that precipitation was fixed, which means that the soil water content is constant for different simulations in Fig. 6. Therefore, long root system allows the plant to access more water and increases the plant’s uptake of water and nutrients. The spatial nonlocal distance $\rho$ represents the length of the vegetation roots, which to some extent describes the ability of vegetation to absorb water and also measures the competitiveness of vegetation to limited water resources. Our results show that the vegetation with different root length will show different spatial distribution, and the longer the roots, the less fragmentation the vegetation patches exhibit. In fact, the existing results have confirmed that the structure of roots has a significant impact on the spatial distribution of plants, which is also consistent to the observations in Anderson and Hodgkinson (1997); Dong (2020) (For example, at the same site, two different pattern-formation species, A Aneura and Eucalyptus populea, show different spatial distributions due to their different root structures). Moreover, our results show that plants with shorter roots are more likely to cause spatial fragmentation of the landscape at the same precipitation level, which is consistent to the accepted statement that water scarcity causes hydraulic stress, which promotes nonuniform distribution of vegetation (vegetation patterns).

We further discuss the combined effects of lag effect and spatial nonlocal interaction on vegetation evolution. It can be seen that the inclusion of time delay may lead to the appearance of traveling wave patterns. That is, the vegetation migrates along a fixed direction, and the migration rate increases with the increase of time delay (see Fig. 7). In addition, near the boundaries of the region, the vegetation may die and then the bare soil may appear. The change of vegetation boundaries means that the original ecological balance is broken (Danz et al. 2013). It can be seen that the vegetation boundary corresponding to different lag periods is different, especially when considering lag periods and not considering lag periods. This reflects that the lag effect has a significant impact on the vegetation ecosystem. Therefore, in the actual prediction of vegetation evolution trend, ignoring the lag period may cause a unexpected deviation.

The above traveling wave patterns are simulated in a flat environment with no significant surface runoff, which is not very common in the literature. This phenomenon was reported mostly in sloped environments, which is either in field observations (Couteron et al. 2000; Deblauwe et al. 2012) or during the exploration of the formation mechanisms of vegetation patterns (Eigentler 2020; Eigentler and Sherratt 2018; Sherratt 2013; Eigentler and Sherratt 2019b; Kealy and Wollkind 2012). It is generally believed that the banded vegetation moves up the hillside, which is driven by the combination of precipitation and the slope of the terrain. We also notice a recent work by Sun et al. (2022) where the authors studied a Klausmeier model with water diffusion in a flat environment and found that vegetation shows the spatially nonhomogeneous periodic distribution for the appropriate parameter range but the vegetation does not move. This is clearly contrasted with our finding in this paper. We think that the reason leading to the migration of vegetation is mainly due to the lag response of vegetation to soil water availability and the competition of vegetation for limited water resources.

In this paper, we have discussed the influence of water, the most significant limiting factor of vegetation growth in arid environments, on the spatial distribution and temporal evolution of vegetation. As all known, many factors can affect the vegetation growth, such as minerals and light. To some extent, they can promote or inhibit the growth of plants, making the vegetation show a regular spatial distribution (Wu et al. 2015). How these key nutrients affect the growth of vegetation is also a topic worthy of consideration.