1 Introduction

The disappearance of vegetation, which is referred as desertification, has become a serious environmental problem, and the global ecosystems are threatened today more than ever before [1]. Various regular vegetation patterns have been observed in many semi-arid regions around the world, such as spot patterns, strip patterns, labyrinth patterns and gap patterns. The formation mechanism of vegetation patterns has been studied by many scholars from different perspectives, see [2,3,4,5,6,7,8,9,10,11,12] and references therein.

Mathematically, many scholars have also established a series of water-vegetation models to study the formation mechanism of various pattern structures [13,14,15,16]. Especially in 1999, based on ecological hypothesis, Klausmeier [13] proposed the first mathematical model to describe the relationship between vegetation biomass and water density. It captured the formation of striped vegetation patterns on hillslopes and explained the importance of nonlinear mechanisms in determining the vegetation pattern formation in semi-arid regions. Shortly thereafter, Rietkerk et al. [17] divided the water into surface water and underground water and constructed a spatial model to study the influence of spatial distribution of runoff water on the formation of vegetation patterns. Then in 2003, Shnerb et al. [18] considered that the competition of shrubs for a limited supply of water determined the spatial organization and presented a general model of the water-shrubs reaction. Based on the model in [18], Wang et al. [19] pointed out that the growth of vegetation can loosen the soil locally and the larger vegetation biomass density resulted in the higher infiltration, which can decrease the death rate of the vegetation due to more soil water available. Thus, they established a nondimensionalized water-vegetation model in the following form:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\frac{{\textrm{d} \omega }}{{\textrm{d} t}}} = R-p\omega b-\omega ,\\ \displaystyle {\frac{{\textrm{d} b}}{{\textrm{d} t}}}=\omega b-(\mu _{0}+\frac{\mu _{1}}{b +1})b,\\ \omega (0)\ge 0,\not \equiv 0,\quad b(0)\ge 0,\quad \not \equiv 0,\\ \end{array} \right. \end{aligned}$$
(1.1)

where \(\omega \) is the ground water density, b is the shrubs biomass density, \(R>0\) is the rainfall rate, \(p>0\) is the water consumption rate in the presence of vegetation, \(\mu _{0}>0\) indicates mortality due to human factors and \(\mu _{1}>0\) indicates the infiltration feedback parameter of vegetation. Wang et al. [19] showed that in the transition from global stability of bare-soil state for low rainfall to the global stability of high vegetation state for high rainfall rate, oscillatory states or multiple equilibrium states can occur.

Cross-diffusion is used to describe attraction/repulsion between species, which is another important diffusive process in the realistic diffusion and reaction models [20,21,22]. The concept of cross-diffusion was founded for the first time by Kerner [23] and then projected to water-vegetation models by von Hardenberg et al. [24]. It is well known that precipitation is the main source of water needed for vegetation growth, and vegetation can absorb this water through two ways. Firstly, it is directly absorbed by the leaves. Secondly, the vegetation absorbs the water that penetrates into the soil through the roots. Obviously, in the arid or semi-arid regions, the growth of vegetation depends mainly on the absorption of water by the roots. Because the water resources are limited, the vegetation competes with each other for water to survive. Accordingly, for the sake of modeling the competition of vegetation for water and water transport due to water-uptake by roots, von Hardenberg et al. introduced a new term \(\Delta ( \omega -\beta b)\) into water-vegetation models. Then, a large number of experimental results have demonstrated that the cross-diffusion is quite significant for the transition among different vegetation pattern structures [19, 22, 25]. Thus, following from [24, 26,27,28,29,30], we consider the following model:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{{\partial \omega }}{{\partial t}}=d_{1}\Delta ( \omega -\beta b)+R-p\omega b-\omega ,&{}\quad x \in \Omega ,\quad t> 0,\\ \frac{{\partial b}}{{\partial t}} = d_{2}\Delta b +\omega b-(\mu _{0}+\frac{\mu _{1}}{b+1})b,&{}\quad x \in \Omega ,\quad t>0,\\ \frac{{\partial \omega }}{{\partial \upsilon }} = \frac{{\partial b}}{{\partial \upsilon }} =0, &{}\quad x\in \partial {\Omega },\quad t>0, \\ \omega (x,0)=\omega _0(x)\ge 0,~b(x,0)=b_0(x)\ge 0, &{}\quad x\in {\bar{\Omega }},\\ \end{array} \right. \end{aligned}$$
(1.2)

where \(\Delta \) is Laplace operator, \(\Omega \) is a bounded planar domain with a smooth boundary \(\partial \Omega \), \(\upsilon \) is the outward unit normal vector of the boundary \(\partial \Omega \), \(d_{1}>0\) is the water diffusion coefficient, \(d_{2}>0\) is the diffusion coefficient of vegetation by clonal reproduction or seed dispersal. The cross-diffusion term \(\Delta ( \omega -\beta b)\) in the water equation describes the effect of vegetation by local uptake on the water transport, where \(\beta \) represents the hydraulic diffusivity due to the suction of roots in the vadose zone. Specifically speaking, the water-uptake by vegetation roots promotes the depletion of soil–water and forms the soil–water gradients between this vegetation patch and the surrounding patch. The soil–water gradient will give rise to the water transport toward the patch from the surrounding patch, and this effect can be called as soil–water diffusion feedback. The parameter \(\beta \) stands for the feedback intensity and reflects the water-uptake ability of vegetation roots. For system (1.2), Wang et al. [26] discussed the conditions of the diffusion-induced instability and the cross-diffusion-induced instability of a homogenous uniform steady state and found that either a fast diffusion speed of water or a great hydraulic diffusivity due to the suction of roots may drive the instability of the homogenous steady state. When \(\beta =0\), we carried out some qualitative analyses on the steady-state solutions to a diffusive water-vegetation model with the infiltration feedback, and the effects of the water diffusion coefficient, the water consumption rate, and the rainfall rate on the spatial distribution of vegetation were presented in [9].

The disappearance of vegetation may be a slow and gradual process in many forms, such as spotted vegetation patterns, fairy rings, and tiger bush strips [13, 31, 32]. Vegetation patterns can be used to describe the uneven distribution of vegetation in semi-arid areas and can serve as early warning signals for future ecosystem degradation. The amplitude equation is an effective tool, which can help us to give the specific parameter range affecting the change of vegetation patterns [14, 15, 33, 34].

Motivated by the above papers, we first consider the stability of positive equilibrium and the existence of Hopf bifurcation. Then taking the water-uptake ability of vegetation roots \(\beta \) as the Turing bifurcation parameter, Turing instability of the positive equilibrium is obtained when \(0<d_{1}\le d_{2}\), which is different from the case of self-diffusion. The amplitude equation analysis for Turing pattern is carried out, which can help us to derive parameter space more specific to confirm vegetation patterns such as spot patterns, strip patterns and the coexistence patterns. Then, we explore the relationship among parameter and pattern dynamics of the vegetation by numerical simulations and find that the small water-uptake ability of vegetation roots promotes the growth of vegetation and the vegetation pattern transitions: gap patterns \(\rightarrow \) strip patterns \(\rightarrow \) spot patterns. When the water-uptake ability of vegetation roots is much larger, the local vegetation biomass increases and the isolation between vegetation patches also increases, which can lead to desertification. Additionally, as water consumption rate p increases, the pattern transitions: strip patterns \(\rightarrow \) spot patterns \(\rightarrow \) uniform vegetation emerge and the vegetation biomass density decreases.

The rest of the paper is arranged as follows. In Sect. 2, the existence of Hopf bifurcation is given and the cross-diffusion-induced Turing instability is considered. In Sect. 3, we apply the multi-scale analysis method to derive the amplitude equations of system (1.2) near the critical value of Turing bifurcation. In Sect. 4, we verify theoretical results with numerical simulations and analyze the influences of p and \(\beta \) on the vegetation growth from the aspect of pattern structures and vegetation biomass density. In Sect. 5, we give some discussions and conclusions.

2 Bifurcation analysis

In this section, we first give the stability of positive equilibrium and the existence of Hopf bifurcation for system (1.1). Then, the conditions of Turing bifurcation for system (1.2) are obtained.

By simple calculations, we find that system (1.1) has a trivial (bare-soil) equilibrium \((\omega _{0}, b_{0}) = (R, 0)\) for all parameters. A positive equilibrium \((\omega , b)\) satisfies

$$\begin{aligned} \omega =\frac{R}{pb+1},\quad R=(pb+1)\left( \mu _{0}+\frac{\mu _{1}}{b+1}\right) . \end{aligned}$$

Thus, b is a positive root of the quadratic equation

$$\begin{aligned} p\mu _{0}b^{2}+(\mu _{0}+p\mu _{0}+p\mu _{1}-R)b+\mu _{0}+\mu _{1}-R=0. \end{aligned}$$
(2.1)

Define

$$\begin{aligned} \phi= & {} (\mu _{0}+p\mu _{0}+p\mu _{1}-R)^{2}+4p\mu _{0}(R-\mu _{0}-\mu _{1}), \\ R_{1}= & {} \mu _{0}+\mu _{1},\quad R_{2}=(\sqrt{p\mu _{1}}+\sqrt{(1-p)\mu _{0}})^{2}, \quad b_{\pm }=\frac{R-\mu _{0}-p\mu _{0}-p\mu _{1}\pm \sqrt{\phi }}{2p\mu _{0}}. \end{aligned}$$

We can obtain the following result about positive equilibria of system (1.1). See [19] for detailed calculations.

Theorem 2.1

Assume that parameters R,  p,  \(\mu _{0},\) \(\mu _{1}\) are all positive.

  1. (i)

    If either \(p\ge 1\) or \(0<p<1\) and \(\mu _{1}\le \displaystyle {\frac{p\mu _{0}}{1-p}},\) then system (1.1) has a unique positive equilibrium \((\omega _{+},b_{+})=({\frac{R}{pb_{+}+1}},b_{+})\) when \(R>R_{1}\) and has no positive equilibrium when \(R\le R_{1}.\)

  2. (ii)

    If \(0<p<1\) and \(\mu _{1}>\displaystyle {\frac{p\mu _{0}}{1-p}},\) then system (1.1) has a unique positive equilibrium \((\omega _{+},b_{+})=({\frac{R}{pb_{+}+1}},b_{+})\) when \(R\ge R_{1}\) or \(R=R_{2}\), has two positive equilibria \((\omega _{\pm },b_{\pm })=(\displaystyle {\frac{R}{pb_{\pm }+1}},b_{\pm })\) when \(R_{2}<R<R_{1}\) and has no positive equilibrium when \(R<R_{2}.\)

From the above discussion, it is easy to check that system (1.1) has a unique positive equilibrium \(E_{*}=(\omega _{*},b_{*})\) when

$$\begin{aligned} (H_{1}):R>R_{1}=\mu _{0}+\mu _{1} \end{aligned}$$

holds and

$$\begin{aligned} \omega _{*}=\frac{R}{pb_{*}+1},\quad b_{*}=\frac{R-\mu _{0}-p\mu _{0}-p\mu _{1}+\sqrt{\phi }}{2p\mu _{0}}. \end{aligned}$$

The linearization of system (1.2) in the neighborhood of \(E_{*}\) is given by:

$$\begin{aligned} {\left( \begin{array}{cc} \displaystyle {\frac{\partial \omega }{\partial t}}\\ \displaystyle {\frac{\partial b}{\partial t}} \end{array}\right) } =D\Delta {\left( \begin{array}{cc} \omega \\ b \end{array}\right) } +L{\left( \begin{array}{cc} \omega \\ b \end{array}\right) }, \end{aligned}$$
(2.2)

where

$$\begin{aligned} D\Delta =\left( \begin{array}{cc} d_{1}\Delta &{} -\beta d_{1}\Delta \\ 0 &{} d_{2}\Delta \\ \end{array}\right) ,\quad L=\left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \\ \end{array}\right) =\left( {\begin{array}{*{20}{c}} -pb_{*}-1 &{} -p\omega _{*}\\ b_{*} &{} \displaystyle \frac{\mu _{1}b_{*}}{(b_{*}+1)^{2}} \\ \end{array}}\right) . \end{aligned}$$

It is easy to see that \(a_{11}<0\), \(a_{12}<0\), \(a_{21}>0\), \(a_{22}>0\). Then, we suppose that

$$\begin{aligned} {\left( \begin{array}{cc} \omega \\ b \end{array}\right) } ={\left( \begin{array}{cc} \omega _{*}\\ b_{*} \end{array}\right) } +\varepsilon {\left( \begin{array}{cc} \omega _{n}\\ b_{n} \end{array}\right) } e^{\lambda t+i{\textbf {nr}}}+c.c.+o(\varepsilon ^{2}) \end{aligned}$$
(2.3)

represents the non-constant solution corresponding to system (1.2), where \({{\textbf {n}}}=(n_{\omega }, n_{b})\) is the wave number vector, \(n:=|{{\textbf {n}}}|=\sqrt{n_{\omega }^{2}+n_{b}^{2}}\) is the wave number, \({{\textbf {r}}}= (X,Y)\) represents the two-dimensional spatial vector, and c.c. is the complex conjugate term. Thus, by substituting (2.3) into (2.2), we obtain the characteristic equation

$$\begin{aligned} \lambda ^{2}-T_{n}\lambda +D_{n}=0,\quad n=0,1,2,\ldots , \end{aligned}$$
(2.4)

where

$$\begin{aligned} \begin{aligned} T_{n}&=T_{0}-(d_{1}+d_{2})n^{2},\\ D_{n}&=d_{1}d_{2}n^{4}-(a_{11}d_{2}+a_{22}d_{1}+a_{21}\beta d_{1})n^{2}+D_{0},\\ T_{0}&=a_{11}+a_{22}=\frac{\mu _{1}b_{*}}{(b_{*}+1)^{2}}-(pb_{*}+1),\\ D_{0}&=a_{11}a_{22}-a_{12}a_{21}=p\omega _{*}b_{*}-(pb_{*}+1)\frac{\mu _{1}b_{*}}{(b_{*}+1)^{2}}>0.\\ \end{aligned} \end{aligned}$$

In the following, choose the water consumption rate p and the water-uptake ability of vegetation roots \(\beta \) as controlled parameters, and consider the critical value of two bifurcations: Hopf and Turing bifurcations. For the spatially homogeneous Hopf bifurcation, if it occurs, it is required to satisfy the condition

$$\begin{aligned} \hbox {Im}(\lambda _{n}(p))\ne 0,\quad \hbox {Re}(\lambda _{n}(p))=0,\quad \text{ for }\quad n=0. \end{aligned}$$

When \(n=0,\) the characteristic Eq. (2.4) becomes

$$\begin{aligned} \lambda ^{2}-T_{0}\lambda +D_{0}=0, \end{aligned}$$
(2.5)

and so the Hopf condition is equivalent to the requirement \(T_{0}=0\) and \(D_{0}>0.\) In order to solve \(T_{0}=0,\) let

$$\begin{aligned} \Pi (p)=\frac{\mu _{1}}{(b_{*}+1)^{2}}-\frac{1}{b_{*}}=\frac{-b_{*}^{2}-(2-\mu _{1})b_{*}-1}{b_{*}(b_{*}+1)^{2}} \end{aligned}$$
(2.6)

so that \(T_{0}=b_{*}[\Pi (p)-p].\) Consider the polynomial

$$\begin{aligned} K(b_{*})=-b_{*}^{2}-(2-\mu _{1})b_{*}-1 \end{aligned}$$

with discriminant

$$\begin{aligned} \Delta _{1}=\mu _{1}^{2}-4\mu _{1}. \end{aligned}$$

When \(0<\mu _{1}\le 4\), we have \(\Delta _{1}\le 0\) and \(\Pi (p)\le 0\). Then \(T_{0}=b_{*}[\Pi (p)-p]<0\) holds for any p which means that the positive equilibrium \(E_{*}\) is always locally stable. System (1.1) cannot undergo Hopf bifurcation. Now we set

$$\begin{aligned} (H_{2}):\mu _{1}>4. \end{aligned}$$

Under the condition \((H_{2})\), it is not difficult to prove that when \(p>\Pi (p),\) we have \(T_{0}<0\) and \(E_{*}\) is locally asymptotically stable. When \(p<\Pi (p)\), the positive equilibrium \(E_{*}\) becomes unstable.

At \(p=\Pi (p)\), (2.5) has a pair of purely imaginary roots \(\pm \textrm{i}\sqrt{D_{0}}\). Then, we need to focus on the transversality condition. Suppose that \(p^{*}\) satisfies \(p^{*}=\Pi (p^{*})\) and

$$\begin{aligned} (H_{3}): R<\frac{1}{2}(p^{*}+1)(\mu _{0}+\mu _{1}). \end{aligned}$$

Let \(\lambda (p)\) be a root of (2.5) satisfying \(\lambda (p)= \textrm{i}\sqrt{D_{0}}\). Then, we have

$$\begin{aligned} \left. \dfrac{\partial }{\partial p}\hbox {Re}(\lambda (p))\right| _{p=p^{*}}=\frac{1}{2}\left[ \frac{1}{b_{*}(p^{*})}-\frac{2\mu _{1}b_{*}(p^{*})}{[b_{*}(p^{*})+1]^{3}}\right] \left. \frac{\partial b_{*}(p)}{\partial p}\right| _{p=p^{*}}-\frac{1}{2}b_{*}(p^{*}). \end{aligned}$$
(2.7)

By system (1.1), we know that \(b_{*}(p)\) satisfies

$$\begin{aligned} \frac{R}{pb_{*}(p)+1}-\mu _{0}-\frac{\mu _{1}}{b_{*}(p)+1}=0. \end{aligned}$$

Then, we have

$$\begin{aligned} \left. \frac{\partial b_{*}(p)}{\partial p}\right| _{p=p^{*}}=\frac{R [b_{*}(p^{*})]^{2}}{[p^{*} b_{*}(p^{*})+1]^{3}-R p^{*} b_{*}(p^{*})}. \end{aligned}$$
(2.8)

Substituting (2.8) into (2.7), we can get

$$\begin{aligned} \left. \dfrac{\partial }{\partial p}\hbox {Re}(\lambda (p))\right| _{p=p^{*}}=\frac{b_{*}(p^{*})[p^{*}b_{*}(p^{*})+1][R[1-b_{*}(p^{*})]-[b_{*}(p^{*})+1][p^{*}b_{*}(p^{*})+1]^{2}]}{2[b_{*}(p^{*})+1]\left[ [p^{*}b_{*}(p^{*})+1]^{3}-Rp^{*}b_{*}(p^{*})\right] }. \end{aligned}$$

Since \(D_{0}>0\), it’s easy to know that \([p^{*}b_{*}(p^{*})+1]^{3}-Rp^{*}b_{*}(p^{*})<0\). From the condition \((H_{3})\) and (2.1), it follows that \(b_{*}(p^{*})>1\). Thus, we have \(\left. \dfrac{\partial }{\partial p}\hbox {Re}(\lambda (p))\right| _{p=p^{*}}>0.\)

From the above discussion, we can state the following theorem.

Theorem 2.2

Suppose that the conditions \((H_{1})\) and \((H_{3})\) hold. Then for the positive equilibrium \(E_{*}\) of system (1.1), we have the following conclusions.

  1. (i)

    When \(\mu _{1}<4\), \(E_{*}\) is locally asymptotically stable for any p and consequently there is no Hopf bifurcation.

  2. (ii)

    When \((H_{2})\) holds, \(E_{*}\) is locally asymptotically stable if \(p >\Pi (p)\) and unstable if \(0< p < \Pi (p)\).

  3. (iii)

    When \((H_{2})\) holds, system (1.1) undergoes on Hopf bifurcation at \(E_{*}\) for \(p=\Pi (p)\).

Then we focus on the Turing instability for system (1.2) under the assumption that the positive equilibrium point \(E_{*}\) is asymptotically stable, i.e.,

$$\begin{aligned} (H_{4}): p>\Pi (p). \end{aligned}$$

As we all know, the Turing-driven bifurcation occurs if

$$\begin{aligned} \hbox {Im}(\lambda _{n}(p))=0,\quad \hbox {Re}(\lambda _{n}(p))=0,\quad \hbox {for} \quad n=n_{T}\ne 0, \end{aligned}$$

where

$$\begin{aligned} n_{T}=\root 4 \of {\displaystyle {\frac{a_{11}a_{22}-a_{12}a_{21}}{d_{1}d_{2}}}}. \end{aligned}$$
(2.9)

Rewrite

$$\begin{aligned} D_{n}=d_{1}d_{2}n^{4}-(a_{11}d_{2}+a_{22}d_{1}+a_{21}\beta d_{1})n^{2}+D_{0}. \end{aligned}$$
(2.10)

When \(\beta =0\) and \(0<d_{1} \le d_{2}\), we have

$$\begin{aligned} -(a_{11}d_{2}+a_{22}d_{1}+a_{21}\beta d_{1})>-T_{0}d_{1}>0, \end{aligned}$$

which, together with \(D_{0}>0\), implies that \(D_{n}> 0\). Thus, the self-diffusion does not induce the Turing instability when \(0<d_{1}\le d_{2}.\) Then, assume that \(\beta \ne 0\) and \(0<d_{1}\le d_{2}\). We can obtain the following results.

Lemma 2.1

Suppose that \(0<d_{1}\le d_{2}\), \((H_{1})\) and \((H_{4})\) hold. Define

$$\begin{aligned} C_{1}= & {} a_{11}d_{2}+a_{22}d_{1}+a_{21}\beta d_{1}, \end{aligned}$$
(2.11)
$$\begin{aligned} C_{2}= & {} (a_{11}d_{2}+a_{22}d_{1}+a_{21}\beta d_{1})^{2}-4d_{1}d_{2}D_{0}, \end{aligned}$$
(2.12)

and

$$\begin{aligned} n_{1}=\left[ \frac{C_{1}-\sqrt{C_{1}^{2}-4d_{1}d_{2}D_{0}}}{2d_{1}d_{2}}\right] ^{\frac{1}{2}},\quad n_{2}=\left[ \frac{C_{1}+\sqrt{C_{1}^{2}-4d_{1}d_{2}D_{0}}}{2d_{1}d_{2}}\right] ^{\frac{1}{2}}. \end{aligned}$$

If \(C_{1}>0\) and \(C_{2}>0\), then \(D_{n}<0\) for \(n_{1}<n<n_{2}\) and \(D_{n}>0\) for \(0<n<n_{1}\) or \(n>n_{2}.\)

By (2.10), the minimum of \(D_{n}\) is obtained, which is denoted by \(D_{n}^{min}=\displaystyle {\frac{-C_{2}}{4d_{1}d_{2}}}.\) If \(C_{1}>0\) and \(C_{2}=0\), we have \(D_{n}^{min}=D_{n_{T}}=0\). Thus, the critical value of Turing instability \(\beta ^{(T)}\) for system (1.2) is given by \(C_{2} = 0\) as follows

$$\begin{aligned} \beta ^{(T)}=\frac{-(a_{11}d_{2}+a_{22}d_{1})+2\sqrt{d_{1}d_{2}D_{0}}}{a_{21}d_{1}}. \end{aligned}$$
(2.13)

By Lemma 2.1, when \(\beta <\beta ^{(T)}\), if \(C_{1} > 0\), the two positive numbers \(n_{1}\) and \(n_{2}\) satisfy \(D_{n} < 0\) for \(n_{1}< n < n_{2}\) and \(D_{n}>0\) for \(0<n<n_{1}\) or \(n>n_{2}\). But when \(\beta >\beta ^{(T)}\), we have \(D_{n}>0\) for any \(n\ge 0\).

Thus, if the conditions \((H_{1})\) and \((H_{4})\) hold, all roots of (2.4) have negative real parts when \(\beta <\beta ^{(T)}\). Otherwise, when \(\beta >\beta ^{(T)}\), (2.4) has at least one positive real root. For \(\beta =\beta ^{(T)}\), (2.4) has one zero root and all other roots have negative real parts. Consequently, system (1.2) undergoes Turing bifurcation.

Summarizing the above discussion, we have the following results on cross-diffusion-driven Turing instability.

Theorem 2.3

Suppose that the conditions \(0<d_{1}\le d_{2}\), \((H_{1})\) and \((H_{4})\) hold.

  1. (i)

    When \(\beta =0,\) \(E_{*}\) is always locally asymptotically stable for system (1.2).

  2. (ii)

    When \(0<\beta <\beta ^{(T)},\) \(E_{*}\) is locally asymptotically stable for system (1.2) and when \(\beta >\beta ^{(T)},\) \(E_{*}\) is unstable for system (1.2). That is, the cross-diffusion-induced Turing instability occurs.

In Fig. 1, we set \(R=18\), \(\mu _{0}=6,\) \(\mu _{1}=8,\) \(d_{1}=0.9,\) \(d_{2}=1\). It follows from (2.6) that \(p^{*}=1.5.\) When \(p=p^{*}=1.5,\) by (2.13) that \(\beta ^{(T)}=12.7474.\) Then, we obtain the intersection between the Turing curve \(\beta \) and the Hopf curve p in the \(\beta -p\) plane. As seen in Fig. 1, the intersection between the blue straight line \(p=1.5\), which corresponds to \(T_{0} = 0\) and the red curve \(\beta \) divides the positive quadrant into four regions. \(E_{1}\) represents the stable region for the positive steady state \(E_{*}\), which coincides with \(p>\Pi (p)\) and \(\beta <\beta ^{(T)}\). \(E_{2}\) is the Turing region that corresponds to \(\beta >\beta ^{(T)}\). \(E_{3}\) is the Turing–Hopf region. \(E_{4}\) represents the Hopf region.

Fig. 1
figure 1

Bifurcation diagram of system (1.2) in the \(\beta -p\) plane carried out by setting \(R=18\), \(\mu _{0}=6,\) \(\mu _{1}=8,\) \(d_{1}=0.9,\) \(d_{2}=1\)

Full size image

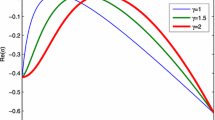
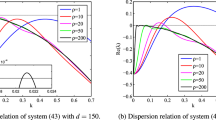
In Fig. 2, we investigate the effect of the water consumption rate p and the water-uptake ability of vegetation roots \(\beta \) on the real part of the eigenvalues \(\hbox {Re}(\lambda )\) in (2.4) for the linearized system (1.2). We fix \(R=18\), \(\mu _{0}=6,\) \(\mu _{1}=8,\) \(d_{1}=0.9\) and \(d_{2}=1\). In addition, take \(\beta =12.7474\) in Fig. 2a and take \(p=1.5\) in Fig. 2b. In Fig. 2a, we can see the impact of the parameter p on \(\hbox {Re}(\lambda _{n})\). It shows that the real part of eigenvalues \(\hbox {Re}(\lambda )\) decreases as p increases. The Turing pattern begins to rise when \(p<1.5\). From Fig. 2b, we can see that the real part of eigenvalues \(\hbox {Re}(\lambda )\) increases as \(\beta \) increases. When \(\beta >12.7474\), the real part of some eigenvalues are positive and Turing pattern emerges.

Fig. 2
figure 2

Impact of p and \(\beta \) on dispersion of \(\hbox {Re}(\lambda )\). a we plot \(\hbox {Re}(\lambda )\) with respect to n and different values of p where \(\beta =12.7474\). b we plot \(\hbox {Re}(\lambda )\) against n and different values of \(\beta \) where \(p=1.5\). Other parameters are \(R=18\), \(\mu _{0}=6,\) \(\mu _{1}=8,\) \(d_{1}=0.9,\) \(d_{2}=1\)

Full size image

Remark 2.1

Because of the great complexity in the formula (2.13), we cannot give an explicit relationship between \(\beta \) and p. But we can obtain numerically the expression of p with respect to \(\beta \) when other parameters are fixed.

3 Amplitude equations

In this section, we mainly focus on revealing the various kinds of spatiotemporal behavior near the critical value of Turing bifurcation \(\beta ^{(T)}\) by the method of multi-scale and weakly nonlinear analysis where the amplitude equations associated with system (1.2) are derived in order to obtain the different pattern formations generated by our model. Rewrite system (1.2) into the following form:

$$\begin{aligned} \frac{\partial }{\partial t}U=L_{1}U+N, \end{aligned}$$
(3.1)

where

$$\begin{aligned} U=\left( \begin{array}{cc} \omega \\ b \\ \end{array}\right) \quad L_{1}=\left( \begin{array}{cc} a_{11}+d_{1}\Delta &{} a_{12}-\beta d_{1}\Delta \\ a_{21} &{} a_{22}+d_{2}\Delta \\ \end{array}\right) ,\quad N=\left( \begin{array}{cc} f(\omega ,b)\\ g(\omega ,b) \\ \end{array}\right) \end{aligned}$$
(3.2)

with

$$\begin{aligned} f(\omega ,b)=-p\omega b,\quad g(\omega ,b)=\omega b+\mu _{1}(b_{*}+1)^{-3}b^{2}-\mu _{1}(b_{*}+1)^{-4}b^{3}+h.o.t. \end{aligned}$$

Since we consider the behavior close to \(\beta =\beta ^{(T)}\) in the following analysis, we expand the bifurcation parameter \(\beta ^{(T)}\) and the variable U with respect to a small parameter \(\varepsilon \) as

$$\begin{aligned} \beta -\beta ^{(T)}=\varepsilon \beta ^{(1)}+\varepsilon ^{2} \beta ^{(2)}+\varepsilon ^{3} \beta ^{(3)}+o(\varepsilon ^{4}) \end{aligned}$$
(3.3)

and

$$\begin{aligned} U=\varepsilon \left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) +\varepsilon ^{2}\left( \begin{array}{cc} \omega _{2}\\ b_{2}\\ \end{array}\right) +\varepsilon ^{3}\left( \begin{array}{cc} \omega _{3}\\ b_{3}\\ \end{array}\right) +o(\varepsilon ^{4}). \end{aligned}$$
(3.4)

Similarly, the nonlinear term N can be expanded to the different order of \(\varepsilon \) as

$$\begin{aligned} N=\varepsilon ^{2}h_{2}+\varepsilon ^{3}h_{3}+o(\varepsilon ^{4}) \end{aligned}$$
(3.5)

with

$$\begin{aligned} h_{2}= & {} \left( \begin{array}{cc} -p\omega _{1}b_{1}\\ \omega _{1}b_{1}+\mu _{1}(b_{*}+1)^{-3}b_{1}^{2}\\ \end{array}\right) , \\ h_{3}= & {} \left( \begin{array}{cc} -p(\omega _{1}b_{2}+\omega _{2}b_{1})\\ \omega _{1}b_{2}+\omega _{2}b_{1}+2\mu _{1}(b_{*}+1)^{-3}b_{1}b_{2}-\mu _{1}(b_{*}+1)^{-4}b_{1}^{3}\\ \end{array}\right) . \end{aligned}$$

Meanwhile, we can decompose the linear operator \(L_{1}\) into the following form:

$$\begin{aligned} L_{1}=L_{T}+(\beta -\beta ^{(T)})M, \end{aligned}$$
(3.6)

where

$$\begin{aligned} L_{T}=\left( \begin{array}{cc} a_{11}+d_{1}\Delta &{} a_{12}-\beta ^{(T)}d_{1}\Delta \\ a_{21} &{} a_{22}+d_{2}\Delta \\ \end{array}\right) ,\quad M=\left( \begin{array}{cc} b_{11} &{} b_{12} \\ b_{21} &{} b_{22} \\ \end{array}\right) =\left( \begin{array}{cc} 0 &{} -d_{1}\Delta \\ 0 &{} 0 \\ \end{array}\right) . \end{aligned}$$

For the method of multi-scale analysis, the most critical is to separate the dynamical behavior of (2.2) according to different time scale or spatial scale. Thus, we need to separate the timescale

$$\begin{aligned} T_{0}=t,\quad T_{1}=\varepsilon t,\quad T_{2}=\varepsilon ^{2} t,\ldots . \end{aligned}$$
(3.7)

Let us take \(w_{j}\), \(b_{j}\) to be variables that vary slowly over time, so that they are independent of the slow timescale \(T_{0}\). For a slow-varying amplitude A, we can get the derivative with respect to time t with

$$\begin{aligned} \frac{\partial A}{\partial t}=\varepsilon \frac{\partial A}{\partial T_{1}}+\varepsilon ^{2}\frac{\partial A}{\partial T_{2}}+\varepsilon ^{3}\frac{\partial A}{\partial T_{3}}+o(\varepsilon ^{4}). \end{aligned}$$
(3.8)

Substituting (3.3)–(3.7) into (3.1) and expanding (3.1) with respect to various orders of \(\varepsilon \), we have the following three equations:

$$\begin{aligned} \varepsilon : \quad L_{T}\left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right)&=0, \end{aligned}$$
(3.9)
$$\begin{aligned} \varepsilon ^{2}: \quad L_{T}\left( \begin{array}{cc} \omega _{2}\\ b_{2}\\ \end{array}\right)&=\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) -\beta ^{(1)}M\left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) -h_{2}, \end{aligned}$$
(3.10)
$$\begin{aligned} \varepsilon ^{3}:\quad L_{T}\left( \begin{array}{cc} \omega _{3}\\ b_{3}\\ \end{array}\right)&=\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} \omega _{2}\\ b_{2}\\ \end{array}\right) +\frac{\partial }{\partial T_{2}}\left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) -\beta ^{(1)}M\left( \begin{array}{cc} \omega _{2}\\ b_{2}\\ \end{array}\right) -\beta ^{(2)}M\left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) -h_{3}. \end{aligned}$$
(3.11)

For the order of \(\varepsilon \), by solving the (3.9), we get

$$\begin{aligned} \left( \begin{array}{cc} \omega _{1}\\ b_{1}\\ \end{array}\right) =\left( \begin{array}{cc} l_{1}\\ 1\\ \end{array}\right) (W_{1}e^{i{{\textbf {n}}}_{1}{{\textbf {r}}}}+W_{2}e^{i{{\textbf {n}}}_{2}{{\textbf {r}}}}+W_{3}e^{i{{\textbf {n}}}_{3}{{\textbf {r}}}})+c.c., \end{aligned}$$
(3.12)

where c.c. is the complex conjugate, \(|{{\textbf {n}}}_{j}|=n_{T}\), \(j=1,2,3,\)

$$\begin{aligned} l_{1}=\frac{a_{11}d_{2}+a_{21}\beta ^{(T)}d_{1}-a_{22}d_{1}}{2a_{21}d_{1}}, \end{aligned}$$

\(W_{j}\), \(j = 1, 2, 3\) is the amplitude of the pattern corresponding to the mode \(e^{i{{\textbf {n}}}_{j}{{\textbf {r}}}}\). Its form depends on the perturbational term of the higher order. In order to guarantee the existence of the nontrivial solution of (3.10), we use the Fredholm solubility condition, which implies the vector function of the right-hand side of (3.10) (i.e., \((F_{\omega }, F_{b})^{T}\)) must be orthogonal with the zero eigenvector of the adjoint operator \(L_{T}^{+}\) of the operator \(L_{T}\). By some calculations, we know

$$\begin{aligned} L_{T}^{+}=\left( \begin{array}{cc} a_{11}+d_{1}\Delta &{} a_{21} \\ a_{12}-\beta ^{(T)}d_{1}\Delta &{} a_{22}+d_{2}\Delta \\ \end{array}\right) . \end{aligned}$$

The zero eigenvectors of \(L_{T}^{+}\) are

$$\begin{aligned} \left( \begin{array}{cc} 1\\ l_{2}\\ \end{array}\right) e^{i{{\textbf {n}}}_{j}{{\textbf {r}}}},\quad l_{2}=\frac{(a_{21}\beta ^{(T)}+a_{22})d_{1}-a_{11}d_{2}}{2a_{21}d_{2}},\quad j=1,2,3. \end{aligned}$$
(3.13)

Let \(F_{\omega }^{j}\) and \(F_{b}^{j}\) represent the coefficients corresponding to \(e^{i{{\textbf {n}}}_{j}{{\textbf {r}}}}\) in \(F_{\omega }\) and \(F_{b}\). Then, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \left( \begin{array}{cc} F_{\omega }^{1}\\ F_{b}^{1}\\ \end{array}\right) =\left( \begin{array}{cc} l_{1}\displaystyle {\frac{\partial W_{1}}{\partial T_{1}}}\\[3mm] \displaystyle {\frac{\partial W_{1}}{\partial T_{1}}}\\[3mm] \end{array}\right) -\beta ^{(1)}\left( \begin{array}{cc} b_{12}W_{1}\\[3mm] 0\\[3mm] \end{array}\right) -\left( \begin{array}{cc} -2pl_{1}{\overline{W}}_{2}{\overline{W}}_{3}\\[3mm] \left[ 2l_{1}+2\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{2}{\overline{W}}_{3}\\[3mm] \end{array}\right) ,\\[3mm] \left( \begin{array}{cc} F_{\omega }^{2}\\[3mm] F_{b}^{2}\\[3mm] \end{array}\right) =\left( \begin{array}{cc} l_{1}\displaystyle {\frac{\partial W_{2}}{\partial T_{1}}}\\[3mm] \displaystyle {\frac{\partial W_{2}}{\partial T_{1}}}\\[3mm] \end{array}\right) -\beta ^{(1)}\left( \begin{array}{cc} b_{12}W_{2}\\[3mm] 0\\[3mm] \end{array}\right) -\left( \begin{array}{cc} -2pl_{1}{\overline{W}}_{1}{\overline{W}}_{3}\\[3mm] \left[ 2l_{1}+2\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{1}{\overline{W}}_{3}\\[3mm] \end{array} \right) ,\\[3mm] \left( \begin{array}{cc} F_{\omega }^{3}\\[3mm] F_{b}^{3}\\[3mm] \end{array}\right) =\left( \begin{array}{cc} l_{1}\displaystyle {\frac{\partial W_{3}}{\partial T_{1}}}\\[3mm] \displaystyle {\frac{\partial W_{3}}{\partial T_{1}}}\\[3mm] \end{array}\right) -\beta ^{(1)}\left( \begin{array}{cc} b_{12}W_{3}\\[3mm] 0\\[3mm] \end{array}\right) -\left( \begin{array}{cc} -2pl_{1}{\overline{W}}_{1}{\overline{W}}_{2}\\[3mm] \left[ 2l_{1}+2\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{1}{\overline{W}}_{2}\\[3mm] \end{array}\right) . \end{array} \right. \end{aligned}$$
(3.14)

From the orthogonal condition

$$\begin{aligned} (1,l_{2})\left( \begin{array}{cc} F_{\omega }^{j}\\ F_{b}^{j}\\ \end{array}\right) =0, \end{aligned}$$

we get

$$\begin{aligned} \left\{ \begin{array}{ll} (l_{1}+l_{2})\displaystyle {\frac{\partial W_{1}}{\partial T_{1}}}=\beta ^{(1)}b_{12}W_{1}-\left[ -2pl_{1}+2l_{1}l_{2}+2l_{2}\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{2}{\overline{W}}_{3},\\[3mm] (l_{1}+l_{2})\displaystyle {\frac{\partial W_{2}}{\partial T_{1}}}=\beta ^{(1)}b_{12}W_{2}-\left[ -2pl_{1}+2l_{1}l_{2}+2l_{2}\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{1}{\overline{W}}_{3},\\[3mm] (l_{1}+l_{2})\displaystyle {\frac{\partial W_{3}}{\partial T_{1}}}=\beta ^{(1)}b_{12}W_{3}-\left[ -2pl_{1}+2l_{1}l_{2}+2l_{2}\mu _{1}(b_{*}+1)^{-3}\right] {\overline{W}}_{1}{\overline{W}}_{2}. \end{array} \right. \end{aligned}$$
(3.15)

Next, assume that (3.10) has the following form

$$\begin{aligned} \begin{aligned} \left( \begin{array}{cc} \omega _{2}\\ b_{2}\\ \end{array}\right)&=\left( \begin{array}{cc} X_{0}\\ Y_{0}\\ \end{array}\right) +\sum _{j=1}^{3}\left( \begin{array}{cc} X_{j}\\ Y_{j}\\ \end{array}\right) e^{i{{\textbf {n}}}_{j}{{\textbf {r}}}}+\sum _{j=1}^{3}\left( \begin{array}{cc} X_{jj}\\ Y_{jj}\\ \end{array}\right) e^{2i{{\textbf {n}}}_{j}{{\textbf {r}}}}+\left( \begin{array}{cc} X_{12}\\ Y_{12}\\ \end{array}\right) e^{i({{\textbf {n}}}_{1}-{{\textbf {n}}}_{2}){{\textbf {r}}}}\\&\qquad +\left( \begin{array}{cc} X_{23}\\ Y_{23}\\ \end{array}\right) e^{i({{\textbf {n}}}_{2}-{{\textbf {n}}}_{3}){{\textbf {r}}}}+\left( \begin{array}{cc} X_{31}\\ Y_{31}\\ \end{array}\right) e^{i({{\textbf {n}}}_{3}-{{\textbf {n}}}_{1}){{\textbf {r}}}}+c.c.,\quad j=1,2,3. \end{aligned} \end{aligned}$$
(3.16)

Substituting (3.16) into (3.10) and collecting the coefficients of \(e^{0},\) \(e^{i{{\textbf {n}}}_{j}{{\textbf {r}}}}\), \(e^{2i{{\textbf {n}}}_{j}{{\textbf {r}}}}\) and \(e^{i({{\textbf {n}}}_{j}-{{\textbf {n}}}_{k}){{\textbf {r}}}}\), respectively, we obtain

$$\begin{aligned} \left( \begin{array}{cc} X_{0}\\ Y_{0}\\ \end{array}\right)&=\left( \begin{array}{cc} x_{0}\\ y_{0}\\ \end{array}\right) (|W_{1}|^{2}+|W_{2}|^{2}+|W_{3}|^{2}),\quad X_{j}=l_{1}Y_{j},\\ \left( \begin{array}{cc} X_{jj}\\ Y_{jj}\\ \end{array}\right)&=\left( \begin{array}{cc} x_{11}\\ y_{11}\\ \end{array}\right) W_{j}^{2},\quad \left( \begin{array}{cc} X_{jk}\\ Y_{jk}\\ \end{array}\right) =\left( \begin{array}{cc} x_{*}\\ y_{*}\\ \end{array}\right) W_{j}{\overline{W}}_{k},\quad j,k=1,2,3,\quad j\ne k, \end{aligned}$$

where

$$\begin{aligned} \left( \begin{array}{cc} x_{0}\\ y_{0}\\ \end{array}\right)&=\frac{2}{a_{11}a_{22}-a_{12}a_{21}}\left( \begin{array}{cc} a_{22}pl_{1}+a_{12}\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] \\ -a_{21}pl_{1}-a_{11}\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] \\ \end{array}\right) ,\\ \left( \begin{array}{cc} x_{11}\\ y_{11}\\ \end{array}\right)&=\left( \begin{array}{cc} \displaystyle {\frac{(a_{22}-4d_{2}n_{T}^{2})pl_{1}+(a_{12}+4\beta ^{(T)}d_{1}n_{T}^{2})\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] }{(a_{11}-4d_{1}n_{T}^{2}) (a_{22}-4d_{2}n_{T}^{2})-a_{21}(a_{12}+4\beta ^{(T)}d_{1}n_{T}^{2})}}\\[5mm] \displaystyle {\frac{-a_{21}pl_{1}-(a_{11}-4d_{1}n_{T}^{2})\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] }{(a_{11}-4d_{1}n_{T}^{2}) (a_{22}-4d_{2}n_{T}^{2})-a_{21}(a_{12}+4\beta ^{(T)}d_{1}n_{T}^{2})}}\\[5mm] \end{array}\right) ,\\ \left( \begin{array}{cc} x_{*}\\ y_{*}\\ \end{array}\right)&=\left( \begin{array}{cc} \displaystyle {\frac{(a_{22}-3d_{2}n_{T}^{2})pl_{1}+(a_{12}+3\beta ^{(T)}d_{1}n_{T}^{2})\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] }{(a_{11}-3d_{1}n_{T}^{2}) (a_{22}-3d_{2}n_{T}^{2})-a_{21}(a_{12}+3\beta ^{(T)}d_{1}n_{T}^{2})}}\\[5mm] \displaystyle {\frac{-a_{21}pl_{1}-(a_{11}-3d_{1}n_{T}^{2})\left[ l_{1}+\mu _{1}(b_{*}+1)^{-3}\right] }{(a_{11}-3d_{1}n_{T}^{2}) (a_{22}-3d_{2}n_{T}^{2})-a_{21}(a_{12}+3\beta ^{(T)}d_{1}n_{T}^{2})}}\\[5mm] \end{array}\right) . \end{aligned}$$

Similarly, substituting (3.12) and (3.16) into (3.11) and using the Fredholm solvability condition, we can get

$$\begin{aligned} (l_{1}+l_{2})\left( \frac{\partial Y_{1}}{\partial T_{1}}+\frac{\partial W_{1}}{\partial T_{2}}\right)&=(\beta ^{(1)}Y_{1}+\beta ^{(2)}W_{1})b_{12}+\left[ G_{1}|W_{1}|^{2}+G_{2}(|W_{2}|^{2}+|W_{3}|^{2})\right] W_{1}\\&\quad +2\left[ -pl_{1}+l_{1}l_{2}+\mu _{1}(b_{*}+1)^{-3}l_{2}\right] ({\overline{W}}_{2}{\overline{Y}}_{3}+{\overline{W}}_{3}{\overline{Y}}_{2}), \end{aligned}$$

where

$$\begin{aligned} G_{1}&=-pM_{1}+l_{2}(M_{1}+M_{3}),\quad G_{2}=-pM_{2}+l_{2}(M_{2}+M_{4}),\\ M_{1}&=l_{1}y_{0}+l_{1}y_{11}+x_{0}+x_{11},\quad M_{2}=l_{1}y_{0}+l_{1}y_{*}+x_{0}+x_{*},\\ M_{3}&=2\mu _{1}(b_{*}+1)^{-3}(y_{0}+y_{11})-3\mu _{1}(b_{*}+1)^{-4},\quad M_{4}=2\mu _{1}(b_{*}+1)^{-3}(y_{0}+y_{*})-6\mu _{1}(b_{*}+1)^{-4}. \end{aligned}$$

In addition, the remaining two equations can be obtained by changing the subscript.

Combining \(A_{j}=\varepsilon W_{j}+\varepsilon ^{2} Y_{j},\) \(j = 1, 2, 3\) and the above analysis, we get the following amplitude equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \tau _{0}\displaystyle {\frac{\partial A_{1}}{\partial t}}=\mu A_{1}+h{\overline{A}}_{2}{\overline{A}}_{3}-\left[ g_{1}|A_{1}|^{2}+g_{2}(|A_{2}|^{2}+|A_{3}|^{2})\right] A_{1},\\ \tau _{0}\displaystyle {\frac{\partial A_{2}}{\partial t}}=\mu A_{2}+h{\overline{A}}_{1}{\overline{A}}_{3}-\left[ g_{1}|A_{2}|^{2}+g_{2}(|A_{1}|^{2}+|A_{3}|^{2})\right] A_{2},\\ \tau _{0}\displaystyle {\frac{\partial A_{3}}{\partial t}}=\mu A_{3}+h{\overline{A}}_{1}{\overline{A}}_{2}-\left[ g_{1}|A_{3}|^{2}+g_{2}(|A_{1}|^{2}+|A_{2}|^{3})\right] A_{3},\\ \end{array} \right. \end{aligned}$$
(3.17)

where

$$\begin{aligned} g_{1}= & {} -\frac{G_{1}}{\beta ^{(T)}b_{12}},\quad g_{2}=-\frac{G_{2}}{\beta ^{(T)}b_{12}}, \\ \tau _{0}= & {} \frac{l_{1}+l_{2}}{\beta ^{(T)}b_{12}},\quad \mu =\frac{\beta -\beta ^{(T)}}{\beta ^{(T)}},\quad h= \frac{2\left[ pl_{1}-l_{1}l_{2}-\mu _{1}(b_{*}+1)^{-3}l_{2}\right] }{\beta ^{(T)}b_{12}}. \end{aligned}$$

Each amplitude can be decomposed into mode \(\rho _{i} = |A_{i}|\) and a corresponding phase angle \(\theta _{i}\). Then, substituting \(A_{i}= \rho _{i}e^{i \theta _{i}}\) into (3.17) and separating the real and imaginary parts give the following four different differential equations of the real variables

$$\begin{aligned} \left\{ \begin{array}{ll} \tau _{0}\displaystyle {\frac{\partial \theta }{\partial t}}=-h\displaystyle {\frac{\rho _{1}^{2}\rho _{2}^{2}+\rho _{1}^{2}\rho _{3}^{2}+\rho _{2}^{2}\rho _{3}^{2}}{\rho _{1}\rho _{2}\rho _{3}}}\sin \theta ,\\ \tau _{0}\displaystyle {\frac{\partial \rho _{1}}{\partial t}}=\mu \rho _{1}+h\rho _{2}\rho _{3}\cos \theta -g_{1}\rho _{1}^{3}-g_{2}(\rho _{2}^{2}+\rho _{3}^{2})\rho _{1},\\ \tau _{0}\displaystyle {\frac{\partial \rho _{2}}{\partial t}}=\mu \rho _{2}+h\rho _{1}\rho _{3}\cos \theta -g_{1}\rho _{2}^{3}-g_{2}(\rho _{1}^{2}+\rho _{3}^{2})\rho _{2},\\ \tau _{0}\displaystyle {\frac{\partial \rho _{3}}{\partial t}}=\mu \rho _{3}+h\rho _{1}\rho _{2}\cos \theta -g_{1}\rho _{3}^{3}-g_{2}(\rho _{1}^{2}+\rho _{2}^{2})\rho _{3}, \end{array} \right. \end{aligned}$$
(3.18)

where \(\theta =\theta _{1}+\theta _{2}+\theta _{3}.\)

The system (3.18) has four different kinds of pattern formations [14]:

  1. (i)

    The homogeneous stationary state is given by

    $$\begin{aligned} \rho _{1}=\rho _{2}=\rho _{3}=0. \end{aligned}$$

    When \(\mu <\mu ^{(2)}=0,\) this kind of pattern is stable. When \(\mu >\mu ^{(2)}=0,\) this kind of pattern is unstable.

  2. (ii)

    The strip pattern formation is produced if

    $$\begin{aligned} \rho _{1}=\sqrt{\frac{\mu }{g_{1}}}\ne 0,\quad \rho _{2}=\rho _{3}=0\quad \textrm{and}\quad g_{2}>0, \end{aligned}$$

    which is stable when \(\mu >\mu ^{(3)}=\displaystyle {\frac{g_{1}h^{2}}{(g_{2}-g_{1})^{2}}}\) and unstable when \(\mu <\mu _{(3)}.\)

  3. (iii)

    The Hexagonal pattern is represented as

    $$\begin{aligned} \rho _{1}=\rho _{2}=\rho _{3}=\rho _{\pm }^{*}=\frac{|h|\pm \sqrt{h^{2}+4(g_{1}+2g_{2})\mu }}{2(g_{1}+2g_{2})} \end{aligned}$$

    with \(\theta =0\) or \(\theta =\pi .\) When \(\mu >\mu ^{(1)}=\displaystyle {\frac{-h^{2}}{4(g_{1}+2g_{2})}},\) this kind of pattern exists and the solution \(\rho _{+}^{*}=\displaystyle {\frac{|h|+\sqrt{h^{2}+4(g_{1}+2g_{2})\mu }}{2(g_{1}+2g_{2})}}\) is stable if \(\mu <\mu ^{(4)}=\displaystyle {\frac{(2g_{1}+g_{2})h^{2}}{(g_{2}-g_{1})^{2}}}.\) But \(\rho _{-}^{*}=\displaystyle {\frac{|h|-\sqrt{h^{2}+4(g_{1}+2g_{2})\mu }}{2(g_{1}+2g_{2})}}\) is always unstable.

  4. (iv)

    The mixed structure state is given by:

    $$\begin{aligned} \rho _{1}=\frac{|h|}{g_{2}-g_{1}},\quad \rho _{2}=\rho _{3}=\sqrt{\frac{\mu -g_{1}\rho _{1}^{2}}{g_{1}+g_{2}}}, \end{aligned}$$

    which exists if \(g_{1}<g_{2}\) and \(\mu >\frac{g_{1}h^{2}}{(g_{2}-g_{1})^{2}},\) and is always unstable.

4 Numerical simulations

In this section, numerical simulations are carried out to support and supplement theoretical analyses above. Some rich and interesting phenomena are found. We know from Theorem 2.2 that the positive equilibrium \((\omega _{*}, b_{*})\) changes from stable to unstable for system (1.1). So we first simulate the Hopf bifurcation at \((\omega _{*}, b_{*})\) and obtain periodic solutions of (1.1) under certain parameter condition.

Next we mainly focus on the pattern formations of vegetation for system (1.2). The finite-difference methods are adopted, and we restrict \(\Omega \) in two-dimensional space. The boundary condition with a size of \(50\times 50\) is considered, and assume that the space step is \(\textrm{d}x = 1\). Choose the initial value as the random perturbation at \((\omega _{*}, b_{*})\) and assume the time step is \(\textrm{d}t = 0.001\). We run the simulations until each pattern reaches a stationary state or does not change its main characteristics any longer.

4.1 Hopf bifurcation

In Sect. 2, we establish the stability of positive equilibrium and the existence of Hopf bifurcation. In this subsection, we shall give some numerical examples to verify Theorem 2.2. Choose \(R=18\), \(\mu _{0}=6\), \(\mu _{1}=8\). It follows from (2.6) that \(p=\Pi (p)=1.5\). Take \(p=2>\Pi (p)\) and \((\omega _{*}, b_{*}) = (12.5830, 0.2153)\). By Theorem 2.2, \((\omega _{*}, b_{*})\) is locally asymptotically stable for system (1.1), see Fig. 3. Take \(p=1<\Pi (p)\) and \((\omega _{*}, b_{*}) = (10.8000, 0.6667)\). By Theorem 2.2, \((\omega _{*}, b_{*})\) loses its stability when p passes through the critical value \(p=1.5\) and a Hopf bifurcation occurs, see Fig. 4. This tells us that if the water consumption satisfies certain critical condition, system (1.1) will have time periodic solutions and the vegetation will change periodically.

Fig. 3
figure 3

The equilibrium \(E_{*}\) of system (1.1) is locally asymptotically stable for \(R=18\), \(p=2\), \(\mu _{0}=6\), \(\mu _{1}=8\). a Time diagram; b phase diagram

Full size image
Fig. 4
figure 4

System (1.1) produces the stable periodic orbits for \(R=18\), \(p=1\), \(\mu _{0}=6\), \(\mu _{1}=8\). a Time diagram; b phase diagram

Full size image

4.2 Pattern formation

If we choose suitable values of R,  p,  \(\mu _{0},\) \(\mu _{1},\) \(\beta ,\) \(d_{1}\) and \(d_{2}\), we shall obtain the values of parameters of h, \(g_{1}\), \(g_{2}\), \(\mu \), \(\mu ^{(1)}\), \(\mu ^{(2)}\), \(\mu ^{(3)}\) and \(\mu ^{(4)}\) according to the expressions of amplitude equation coefficients in Sect. 3.

In order to observe the pattern formation of vegetation, we select three sets of parameter values as in Table 1, and the corresponding pattern structures are shown in Fig. 5. Three typical pattern structures (spot, mixed and strip pattern) occur when the parameters are chosen for different values. When the first set of parameter values in Table 1 is taken, the controlled parameter \(\mu \) is between \(\mu ^{(2)}\) and \(\mu ^{(3)}\), and system (1.2) will present the spot patterns as in Fig. 5a, which shows that the uniform vegetation state begins to lose its stability and spot patterns emerge slowly. When the second set of parameter values in Table 1 is taken, the controlled parameter \(\mu \) is between \(\mu ^{(3)}\) and \(\mu ^{(4)}\), the spot patterns begin to lose stability and the strip patterns begin to appear. At this time, the mixed patterns occur as in Fig. 5b. When the third set of parameter values in Table 1 is taken, the controlled parameter \(\mu \) is greater than \(\mu ^{(4)}\) and the strip patterns emerge as in Fig. 5c. At this time, the spot patterns disappear and the strip patterns begin to hold for the entire region.

Table 1 The values of each parameter in Fig. 5
Full size table
Fig. 5
figure 5

Snapshots of contour pictures of different stationary-state pattern structures corresponding to the parameter values in Table 1. a Spot pattern; b mixed pattern; c strip pattern

Full size image

4.2.1 The effect of water consumption rate

Through numerical simulation, we explore the relation between water consumption rate p and vegetation patterns, as shown in Figs. 6 and 7. From the color scales of these simulation results, we conclude that vegetation biomass density gets smaller and smaller with p increasing, which is negatively correlated. The small p induces the pattern transitions, which follows the pattern sequence below: stripes \(\rightarrow \) spots \(\rightarrow \) bare soil, see Fig. 6. Many researchers have pointed out that spot patterns are the early warning of desertification, so we can get that the water consumption rate is of great significance in indicating desertification. Moreover, in general, the bigger vegetation density corresponds to a more robust ecosystem. From the tendency of pattern phase transition, it can be found that water consumption rate also has a vital influence on the ecosystem robustness.

Fig. 6
figure 6

Effects of the water consumption rate p on vegetation pattern structure. a \(p=0.6;\) b \(p=1;\) c \(p=1.2\). The other parameters are fixed at \(R=13,\) \(\mu _{0}=5\), \(\mu _{1}=5.2\), \(\beta =0.1\), \(d_{1}=10\) and \(d_{2}=0.9\)

Full size image
Fig. 7
figure 7

Effects of the water consumption rate p on vegetation biomass density. a \(p=1.2\); b \(p=2.2\); c \(p=3.2\). The other parameters are fixed at \(R=14\), \(\mu _{1}=5.2\), \(\mu _{0}=5\), \(\beta =0.2\), \(d_{1}=10\) and \(d_{2}=0.2\)

Full size image

4.2.2 The effect of water-uptake ability of vegetation roots

In order to explore the relation between water-uptake ability of vegetation roots and vegetation pattern transitions, some simulation results are shown as in Fig. 8. When \(\beta =0\), the gap patterns emerge, see Fig. 8a. When \(\beta \) increases slightly, the perfect gap patterns disappear and strip patterns begin to emerge, see Fig. 8b. As \(\beta \) continues to increase, the mixed patterns of strip and spot occur, see Fig. 8d and e. Finally, at even greater \(\beta \), the spot patterns occupy the whole space, see Fig. 8f. It can be seen that the pattern transitions occur as the water-uptake ability of vegetation roots increases and conforms to the following sequence: gap patterns \(\rightarrow \) strip patterns \(\rightarrow \) spot patterns, which is in complete agreement with the pattern transition presented in [10, 35].

Fig. 8
figure 8

Effects of the water-uptake ability of vegetation roots \(\beta \) on vegetation biomass density. a \(\beta =0\); b \(\beta =0.03\); c \(\beta =0.06\); d \(\beta =0.09\); e \(\beta =0.12\); f \(\beta =0.15\); the other parameters are fixed at \(R=20\), \(p=0.8\), \(\mu _{0}=5\), \(\mu _{1}=5.2\), \(d_{1}=10\) and \(d_{2}=0.2\)

Full size image

The parameter \(\beta \) refers to the water-uptake ability of vegetation roots. The vegetation absorbed water by roots reduces the water content, forms the water gradients and causes the water transport. When the soil–water content is abundant and constant, the vegetation absorbs water more easily as the parameter \(\beta \) increases. However, when we consider the water-uptake ability of vegetation roots in a water-limited environment, for example, in the arid and semi-arid environment, the vegetation with higher water-uptake ability of vegetation roots has greater potentiality to promote its own growth and inhibit the growth of surrounding vegetation. When the vegetation patterns exist, as the water-uptake ability of vegetation roots increases, different pattern forms emerge and ultimately induce the patch distribution.

4.2.3 The possible causes of desertification

In this subsection, define vegetation patch to be an area covered by vegetation and surrounded by bare soil. We refer to isolation degree as the average distance between vegetation patches, which can reveal the relationship between pattern structure and ecosystem collapse [36].

The relation between the water-uptake ability of vegetation roots and average biomass density of the vegetation is shown in Fig. 9. We find that the average density of vegetation is positively related to the parameter \(\beta \). That is, the water-uptake ability of vegetation roots is beneficial to increase the vegetation density. In fact, the parameter \(\beta \) indicates the competition of vegetation for water by root uptake. In the semi-arid region, the water is limited resource. When the rainfall capacity is a constant, the water-uptake ability of vegetation roots reflects the requirement of vegetation for water. The water in the soil is sufficient to sustain the survival of vegetation when \(\beta \) is small, thus the average density of vegetation increases. When \(\beta \) is large enough, the vegetation requires plenty of water to survive. The competition between vegetation is much stronger. The vegetation with higher water-uptake ability of vegetation roots promotes its own growth and inhibits the growth of surrounding vegetation. So it can be seen from Fig. 8 that, when \(\beta \) is larger, although the local vegetation density increases, the isolation between vegetation patches also increases, which is not beneficial to the ecological stability of vegetation, and desertification is prone to occur.

Fig. 9
figure 9

The relation between average density of the vegetation and water-uptake ability of vegetation roots. The curves with different colors stand for different water-uptake ability of vegetation roots from \(\beta = 0.03\) to \(\beta = 0.12\). The other parameters are fixed at \(R=20\), \(p=0.8\), \(\mu _{0}=5\), \(\mu _{1}=5.2\), \(d_{1}=10\) and \(d_{2}=0.2\)

Full size image

5 Discussion

In the natural world, two species are in relationships of both coexistence and competition. For a water-vegetation model, the specie water may be recognized as a restrained survival source by the other specie vegetation. Meanwhile, the diffusion of vegetation brings an influence on the water since the water is absorbed by the vegetation root. This phenomenon is caused by cross-diffusion. A great amount of works for semi-arid ecosystem models discuss the stability and bifurcation based on Lyapunov method, but some of the studiers don’t prefer to consider the diffusion effect, especially the cross-diffusion. So in this paper, we consider a semi-arid ecosystem on vegetation and water with cross-diffusion. The stability and Turing instability are first given. Then, a Hopf bifurcation to system (1.1) is obtained and the conditions for the existence of periodic solutions of (1.1) are established. Based on a nonlinear analysis, we also obtain the accurate parameters range of the model (1.2), which can produce the spatiotemporal patterns. Furthermore, we consider the effect of water-uptake ability of vegetation roots and water consumption rate on vegetation pattern formations. Note that the cross-diffusion coefficient \(\beta \) represents the water-uptake ability of vegetation roots. The results indicate that cross-diffusion is a critical term to the Turing spatial pattern formulation.

When \(\beta =0\), the Turing instability will not take place in system (1.2) when \(d_{1}\le d_{2}\), as discussed in Sect. 2. When \(\beta \) is small, the water-uptake ability of vegetation roots can promote the increase of vegetation biomass density and produce the transitions of vegetation patterns. However, when \(\beta \) is large, the water-uptake ability of vegetation roots is not beneficial to the ecological stability of vegetation. Thus, we put forward a conjecture with respect to the critical phenomenon: when the water-uptake ability of vegetation roots is smaller than a threshold, the feedback will accelerate the growth of vegetation. If the water-uptake ability of vegetation roots is larger than the threshold, it will lead to desertification.

At present, most of our models consider the influence of rainfall on vegetation patterns. Research on the influence of other factors on vegetation patterns is relatively scarce. In this work, we focus on the influence of water consumption rate on the dynamical behaviors for system (1.2). It is revealed that there is a negative correlation between water consumption rate and vegetation biomass density. That is to say, the vegetation biomass density decreases as the increase of p and water consumption rate can induce the transitions of vegetation patterns. The larger p is, the more unstable the system tends to be.

In this work, the results show that small change may induce the behavior shift between different dynamical regions. We investigate the influences of parameter \(\beta \) and p on the pattern formation. However, we all know that there are many factors affecting the structure of vegetation patterns, including natural factors and human factors. It is still worth exploring how to establish a model that considers various influencing factors. This will better protect our ecological environment.