Introduction

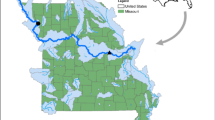
River water plays an important role in the supply of drinking water, and the quality of drinking water depends upon the quality of nearer river water. Yamuna is the largest tributary river of the Ganga in India. It originates from Yamunotri glacier at a height of 6,387 m on the southwestern slopes of Banderpooch peaks (38° 59′ N, 78° 27′ E) in the lower Himalayas in Uttarakhand. It travels a total length of 1,376 km by crossing several states, Uttarakhand, Haryana, Himachal Pradesh, Delhi, and Uttar Pradesh and has a mixing of drainage system of 366,233 km2 before merging with the Ganga at Allahabad, i.e., a total of 40.2 % of the entire Ganga basin. The river accounts for more than 70 % of Delhi’s water supplies and about 57 million people depend on river water for their daily usage (CPCB 2006).

Central Pollution Control Board (CPCB) monitors the water quality parameters at different sites of Yamuna River. Five sample sites are chosen according to utilization of river water, namely Hathnikund, Nizamuddin, Mazawali, Agra, and Juhikha. Hathnikund is approximately 157 km downstream from Yamunotri and 2 km upstream from Tajewala barrage. Nizamuddin is approximately 14 km downstream from Wazirabad barrage at Delhi. The distance from Hathnikund to Wazirabad is 224 km. The water quality at Hathnikund has the impact of industrial and sewerage discharge from Haryana and Delhi. Mazawali is about 84 km downstream from Wazirabad barrage and have the impact of wastewater discharge from Shahdara drain and Hindon river. Agra D/S at west Burzi of Taj Mahal monument is about 310 km downstream from Wazirabad barrage and depicts the impact of sewerage water discharge from Agra city and industrial waste from Mathura refinery. Juhikha is about 613 km downstream from Wazirabad barrage and assesses the impact of river Chambal confluence on river Yamuna (CPCB 2006).

Pollution in river water is continuously increasing due to urbanization, industrialization, etc., and most of the rivers are at dying position, which is an alarming signal (Parmar et al. 2009). Industrial wastes, municipal sewage, and agricultural runoff effect physicochemical parameters of river water (Akoto and Adiyiah 2007; Alam et al. 2007; Hermans et al. 2007; Shukla et al. 2008). Trihalomethane compounds were determined in the drinking water samples at consumption sites and treatment plants of Okinawa and Samoa Islands and observed that the chloroform, bromodichloromethane compound exceed the level of Japan water quality and WHO (World Health Organization) standards (APHA 1995; WHO 1971). Water quality modeling, using multiple linear regression, structural equation, trend and time series analysis are major tools for application in water quality management (Chenini and Khemiri 2009; Fang et al. 2010; Singh et al. 2004; Su et al. 2011; Vassilis et al. 2001; Bhardwaj and Parmar 2014; Panepinto and Genon 2010; Amiri and Nakane 2009; Boskidis et al. 2012).

Climatic dynamic plays an important role in determining the water quality. Using fractal dimensional analysis, trend and time series data of three major dynamic components temperature, pressure and precipitation of the climate analyzed (Dutta et al. 2013; Bhardwaj and Parmar (2013a); Rangarajan 1997). Regional climatic models would not be able to predict local climate as it deals, with averaged quantities and that precipitation during the southwest monsoon is affected by temperature and pressure variability during the preceding winter (Kahya and Kalayci 2004; McCleary and Hay 1980; Mousavi et al. 2008; Movahed and Hermanisc 2008; Park and Park 2009; Rangarajan and Ding 2000; Rangarajan and Sant 2004; Toprak 2009; Toprak et al. 2009; Calvo et al. 2012; Yarar 2014).

The quality of Yamuna River water depends upon quality of water parameters, potential of hydrogen (pH), chemical oxygen demand (COD), biochemical oxygen demand (BOD), dissolved oxygen (DO), water temperature (WT), free ammonia (AMM), and total Kjeldahl nitrogen (TKN). In this paper, statistical analysis, regression analysis, trend, time-series, autoregressive integrated moving average (ARIMA), residual autocorrelation function (ACF), residual partial autocorrelation function (PACF), lag, Hurst exponent, fractal dimension, and predictability index of these water parameters have been estimated at the five sample sites, Hathnikund (S1), Nizamuddin (S2), Mazawali (S3), Agra D/S (S4), and Juhikha (S5) of Yamuna River which crosses different states of India as shown in Fig. 1. Monthly average values of last 10 years of water quality parameters at these sites have been considered for study.

Fig. 1
figure 1

Flow of Yamuna River in India with five main stations, site1—Hathnikund (S1), site2—Nizamuddin (S2), site3—Mazawali (S3), site4—Agra D/S (S4), and site5—Juhikha (S5)

Full size image

Mathematical modeling

Statistical analysis

Measure of central tendency and dispersion are used to calculate mean, median, mode, standard deviation, kurtosis, skewness, and coefficient of variation. Mean explains average value. Median gives the middle values of an ordered sequence or positional average. Mode is defined as the value which occurs the maximum number of time that is having the maximum frequency. Standard deviation gives measure of spread of the sample. Kurtosis refers to the degree of flatness or peakedness in the region about the mode of a frequency curve. Skewness describes the symmetry of data. Coefficient of variation gives the relative measure of sample (Bhardwaj and Parmar (2013b) Box et al. 2008; Rangarajan and Ding 2000; Diodato et al. 2014).

R squared is an estimate of the proportion of the total variation in the series which is explained by the model and measure is useful when the series is stationary. Stationary R squared is a measure that compares the stationary part of the model to a simple mean model and is preferable to ordinary R squared when there is a trend or seasonal pattern. Stationary R squared can be negative with a range of negative infinity to 1. Negative values mean that the model under consideration is worse than the baseline model. Positive values mean that the model under consideration is better than the baseline model (Box et al. 2008; DeLurgio 1998; McCleary and Hay 1980).

In each of the forthcoming definitions, y t is the actual value, f t is the forecasted value, e t  = y t  − f t is the forecast error, and n is the size of the test set. Also, \( \overline{y}=\frac{1}{n}{\displaystyle \sum_{t=1}^n{y}_t} \) is the test mean and \( {\sigma}^2=\frac{1}{n-1}{\displaystyle \sum_{t=1}^n{\left({y}_t-\overline{y}\right)}^2} \) is the test variance.

The mean absolute error is defined as

$$ \mathrm{MAE}=\frac{1}{n}{\displaystyle \sum_{t=1}^n\left|{e}_t\right|} $$
(1)

Mean absolute percentage error, measure is given by

$$ \mathrm{MAPE}=\frac{1}{n}{\displaystyle \sum_{t=1}^n\left|\frac{e_t}{y_t}\right|}\times 100 $$
(2)

Mean percentage error, is defined as

$$ \mathrm{MPE}=\frac{1}{n}{\displaystyle \sum_{t=1}^n\left(\frac{e_t}{y_t}\right)}\times 100 $$
(3)

Mathematically, root mean square error is

$$ \mathrm{RMSE}=\sqrt{\mathrm{MSE}}=\sqrt{\frac{1}{n}{\displaystyle \sum_{t=1}^n{e}_t^2}} $$
(4)

Regression analysis

It is a technique used for modeling and analyzing the variables present in a sample. Regression analysis helps in understanding the variation in value of the dependent variable as independent variables is varied, while the other independent variables are held fixed. Regression line of Y (dependent variable) on X (independent variable) defined as (Chenini and Khemiri 2009)

$$ Y={b}_{yx} X+ C $$
(5)

where C is the intercept,

$$ \begin{array}{l}{b}_{y x}=\mathrm{regression}\;\mathrm{coefficient}= r\times \frac{\sigma_y}{\sigma_x}\hfill \\ {} r=\mathrm{Correlation}\kern0.5em \mathrm{coefficient}=\frac{E\left( X Y\right)- E(X) E(Y)}{\sqrt{\left( E\left({X}^2\right)- E{(X)}^2\right)\left( E\left({Y}^2\right)- E{(Y)}^2\right)}}=\frac{\operatorname{cov}\left( X, Y\right)}{\sigma_X{\sigma}_Y}\hfill \end{array} $$
(6)

σ Y , σ X are standard deviation of variables Y and X, respectively, and E(X), E(Y), E(XY) are expected value of variables X,Y and XY, respectively.

Time series analysis

Time series is a sequence of data points, measured at successive times spaced at uniform time intervals. Time series analysis comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data and to forecast future events based on known past events to predict data points before these are measured. Time series model will generally reflect the fact that observations close together in time will be more closely related than observations further apart (Weng, et al. 2008).

Autoregressive integrated moving average

Auto regressive integrated moving average (ARIMA) model of a time series is defined by three terms p, d, q. Identification of a time series is the process of finding integer values of p, d, and q. When the value is 0, the element is not needed in the model. The middle element, d, is investigated before p and q. The goal is to determine if the process is stationary and, if not, to make it stationary before determining the values of p and q. A stationary process has a constant mean and variance over the time period of the study. The representation of an autoregressive model in time series (Box et al. 2008; DeLurgio 1998; McCleary and Hay 1980), well-known as AR(p), is

$$ {Y}_t={\alpha}_0+{\alpha}_1{Y}_{t-1}+{\alpha}_1{Y}_{t-2}+....+{\alpha}_p{Y}_{t- p}+{\varepsilon}_t $$
(7)

where the term ε t is the source of randomness and is called white noise α i are constants.

In ARIMA models, a non-stationary time series is made stationary by applying finite differencing of the data points. The mathematical formulation of the ARIMA (p,d,q) model using lag polynomials is given below

$$ \begin{array}{l}\phi (L){\left(1- L\right)}^d{y}_t=\theta (L){\varepsilon}_t,\mathrm{i}.\mathrm{e}.\hfill \\ {}\left(1-{\displaystyle \sum_{i=1}^p{\phi}_i{L}^i}\right){\left(1- L\right)}^d{y}_t=\left(1+{\displaystyle \sum_{j=1}^q{\theta}_j{L}^j}\right){\varepsilon}_t\hfill \end{array} $$
(8)

Here, p, d, and q are integers greater than or equal to zero and refer to the order of the autoregressive, integrated, and moving average parts of the model, respectively. The integer d controls the level of differencing. Generally, d = 1 is enough in most cases. When d = 0, then it reduces to an ARMA(p,q) model. An ARIMA(p,0,0) is nothing but the AR(p) model and ARIMA(0,0,q) is the MA(q) model. ARIMA(0,1,0), i.e., y t  = y t − 1 + ε is a special one and called as the random walk model.

Autocorrelation functions and partial autocorrelation functions

To determine a proper model for a given time series data, it is necessary to carry out the autocorrelation functions (ACF) and partial autocorrelation functions (PACF) analysis. These statistical measures reflect how the observations in a time series are related to each other. For modeling and forecasting purpose, it is often useful to plot the ACF and PACF against consecutive time lags. These plots help in determining the order of AR and MA terms. Below, we give their mathematical definitions:

For a time series{x(t), t = 0,1, 2,…} the autocovariance at lag k is defined as

$$ {\gamma}_k=\mathrm{Cov}\left({x}_t,{x}_{t+ k}\right)= E\left[\left({x}_t-\mu \right)\left({x}_{t+ k}-\mu \right)\right] $$
(9)

The autocorrelation coefficient at lag k is defined as

$$ {\rho}_k=\frac{\gamma_k}{\gamma_0} $$
(10)

Here, μ is the mean of the time series, i.e., μ = E[x t ]. The autocovariance at lag zero, i.e., γ 0 is the variance of the time series. Autocorrelation coefficient ρ k is dimensionless and so is independent of the scale of measurement also, − 1 ≤ ρ k  ≤ 1. Statisticians Box and Jenkins termed γ k as the theoretical autocovariance function (ACVF) and ρ k as the theoretical autocorrelation function (ACF).

Partial autocorrelation function (PACF) is used to measure the correlation between an observation k period ago and the current observation, after controlling for observations at intermediate lags (i.e., at lags < k). At lag 1, PACF(1) is same as ACF(1).

Stochastic process governing a time series is unknown, and so, it is not possible to determine the actual or theoretical ACF and PACF values. Rather, these values are to be estimated from the training data, i.e., the known time series at hand. The estimated ACF and PACF values from the training data are respectively termed as sample ACF and PACF. The most appropriate sample estimate for the ACVF at lag k is

$$ {c}_k=\frac{1}{n}{\displaystyle \sum_{t=1}^{n- k}\left({x}_t-\mu \right)\left({x}_{t+ k}-\mu \right)} $$
(11)

Then the estimate for the sample ACF at lag k is given by

$$ {r}_k=\frac{c_k}{c_0} $$
(12)

Here, { x(t), t = 0,1,2,.......} is the training series of size n with mean μ.

Figure 2 explains Box and Jenkins methodology procedure; the sample ACF plot is useful in determining the type of model to fit to a time series of length N. Since ACF is symmetrical about lag zero, it is only required to plot the sample ACF for positive lags, from lag one onwards to a maximum lag of about N/4. The sample PACF plot helps in identifying the maximum order of an AR process.

Fig. 2
figure 2

Box-Jenkins methodology for optimal model selection

Full size image

Hurst exponent (H)

It refers the index of dependence. It quantifies the relative tendency of a time series either to regress strongly to the mean or to cluster in a direction. The value of the Hurst exponent ranges between 0 and 1. A value of 0.5 indicates a true random walk (a Brownian time series). In a random walk, there is no correlation between any element and a future element. A Hurst exponent value H, 0.5 < H < 1 indicates “persistent behavior” (a positive autocorrelation). If there is an increase from time step t i–1 to t i , there will probably be an increase from t i to t i+1. The same is true of decreases, where a decrease will tend to follow a decrease. A Hurst exponent value H, 0 < H < 0.5 will exist for a time series with “anti-persistent behavior” (or negative autocorrelation). Here, an increase will tend to be followed by a decrease or decrease will be followed by an increase. This behavior is sometimes called “mean reversion” (Rangarajan and Sant 2004).

$$ H=\left|\frac{b_{yx}-1}{2}\right| $$
(13)

Also, Hurst exponent can be calculated using power law decay (Rangarajan and Ding 2000)

$$ p(k)= C{k}^{-\alpha} $$
(14)

where C is a constant and p (k) is the autocorrelation function with lag k. The Hurst exponent is related to the exponent alpha in the equation by the relation

$$ H=1-\frac{\alpha}{2} $$
(15)

Fractal dimension (D)

It is a statistical quantity, which gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales.

$$ D=2- H $$
(16)

Also fractal dimension is calculated from the Hausdorff dimension. The Hausdorff dimension D H , in a metric space, is defined as (Rangarajan and Ding 2000; Rangarajan and Sant 2004)

$$ {D}_H=-\underset{\varepsilon \to 0}{ \lim}\;\frac{ \ln \left[ N\left(\varepsilon \right)\right]}{ \ln \varepsilon} $$
(17)

where N(ε) is the number of open balls of a radius ε needed to cover the entire set. An open ball with center P and radius ε in a metric space with metric d is defined as set of all points x such that d(P, x) < ε.

Predictability index

It describes the behavior of time series (Rangarajan 1997; Rangarajan and Ding 2000; Rangarajan and Sant 2004).

$$ PI=2\left| D-1.5\right| $$
(18)

Predictability index (PI) value increases when D value becomes less than or greater than 1.5. In the former case, persistence behavior is observed while in the later, an anti-persistence. If one of these indices comes close to 0, then the corresponding process approximates the Brownian motion and is therefore unpredictable.

Results and discussion

Using statistical, time series, and fractal analysis, the quality of water at different sites S1, S2, S3, S4, and S5 of full stretch river Yamuna has been discussed. Figure 3 depicts the average value, positional average, mode, standard deviation, skewness, kurtosis, and coefficient of variation for all parameters pH, COD, BOD, AMM, TKN, DO, and WT at sample sites S1, S2, S3, S4, and S5, respectively. Table 1 explains trend and time series analysis of ARIMA model, stationary R squared, R squared, RMSE, MAPE, MaxAPE, MAE, Ljung-Box, residual ACF, and residual PACF for all water quality parameters at all sample sites. Figure 4 shows the plot of ACF, PACF, time series, observed data, best fit, lower confidence limit (LCL), and upper confidence limit (UCL). Table 2 gives regression equation, coefficient of determination, Hurst exponent, fractal dimension, and predictability index, and Table 3 depicts fractal and predictability analysis behavior for S1–S2, S1–S3, S1–S4, S1–S5, S2–S3, S2–S4, S2–S5, S3–S4, S3–S5, and S4–S5. By using equations (1)–(18), the following are observed:

Fig. 3
figure 3

Graphical representation of statistical analysis of water quality parameters at sample sites of Yamuna River

Full size image
Table 1 Trend and time series analysis of water quality parameters
Full size table
Fig. 4
figure 4figure 4figure 4figure 4figure 4

Graphical representation of trend, time series analysis (ACF, PACF, observed, best fit, LCL, UCL) of water quality parameters

Full size image
Table 2 Fractal analysis of water quality parameters
Full size table
Table 3 Fractal Analysis of Water Quality Parameters for Different Sites of Yamuna River (AP- Anti persistence, P- Persistence, B- Brownian time series motion)
Full size table

  • pH: For all sites, the mean, median, and mode remain within prescribed limits of WHO/EPA and exhibit normal behavior, standard deviation, and skewness values that are close to zero, which show that curve is symmetrical and platykurtic. Prediction model is better than the baseline model as stationary R squared and R squared values exhibit the similar behavior. RMSE values are low, so dependent series is closed with its model-predicted level. Using Ljung-Box model, for all sites, value of statistics lies between 18 to 29, significance level varies from 0.03 to 0.39, and simple ARIMA model was used for prediction. It is observed that value of pH lies between 7 to 9, and quality of water remains same at all sites, which is calculated at 95 % confidence limits. Anti-persistence behavior exists at all sites except for S2–S5 which shows persistence behavior.

  • COD: For all sites, behavior is not normal, spread of data points is high, and curve is symmetrical and platykurtic, but for S1, it is nonsymmetrical and leptokurtic. COD crosses the prescribed limits of WHO/EPA at all sites with maximum at S2 and minimum at S1. Time series model is better than the baseline model as stationary R squared and R squared values exhibit the similar behavior. RMSE value is low so dependent series is closed with its model-predicted level. Using Ljung-Box model, for all sites, value of statistics lies from 11 to 25, significance level ranging from 0.17 to 0.85, and simple ARIMA model was used for prediction. Using plots of ACF, PACF, lag, and time series, it is observed that value of COD lies between 0 to 18 for S1, 0 to 120 for S2, 0 to 100 for S3, 0 to 150 for S4, and 0 to 60 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence interval. It is observed that persistence behavior exist for S1–S2, S1–S3, and S1–S4; anti-persistence for S2–S3, S2–S4, S2–S5, S3–S4, S3–S5, and S4–S5; and Brownian time series (true random walk) for S1–S5.

  • BOD: Behavior is not normal, spread of data points is high except for S1, and spread of data is low. BOD exhibits symmetrical behavior. Curve is platykurtic for all sites except for S1 and S5, which shows leptokurtic behavior. BOD remains within prescribed limits of WHO/EPA at S1 and S5, but for S2, S3, S4 crosses prescribed limits with maximum at S2. Model is better than the baseline model as stationary R squared and R squared value exhibit the similar behavior. RMSE value is low, so dependent series is closed with its model-predicted level for all sites. From Ljung-Box model, for all sites, statistics lies between 15 and 34, significance varies from 0.01 to 0.53, and simple ARIMA model was used for prediction. ACF, PACF, lag, and time series explains that value of BOD lies between 0 to 2 for S1, 0 to 50 for S2, 0 to 35 for S3, 0 to 40 for S4, and 0 to 6 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence limits. It is observed that anti-persistence behavior exist for S2–S3, S2–S4, S2–S5, S3–S4, S3–S5, and S4–S5 and Brownian time series (true random walk) for S1–S2, S1–S3, S1–S4, and S1–S5.

  • AMM: For all sites, behavior exhibits normal. Spread of data is high for all sites except for S1 and S5. Curve is symmetrical and platykurtic expect for S5; it is nonsymmetrical and leptokurtic. AMM crosses the prescribed limits of WHO/EPA at all sites except S1 and S5 with maximum at S2, S3. For all sites, stationary R squared and R squared value reveal the similar behavior so prediction model is better than the baseline model. RMSE value is low; thus, dependent series is closed with its model-predicted level except at S2, S3, and S4. Using Ljung-Box model, statistics lies between 13 and 37, significance level varies from 0.00 to 0.52, and simple ARIMA model was used for prediction. ACF, PACF, lag, and time series shows that value of AMM lies between 0 to 1 for S1, 0 to 30 for S2, 0 to 35 for S3,0 to 20 for S4, and 0 to 4 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence interval. It is observed that persistence behavior exist for S1–S5, S3–S5, and S4–S5; anti-persistence for S2–S3, S2–S4, S2–S5, and S3–S4; and Brownian time series (true random walk) for S1–S2, S1–S3, and S1–S4.

  • TKN: For all sites, curve is not normal. Data spread is high, symmetric, platykurtic for all sites except S1 and S5, which has spread low, nonsymmetrical, and leptokurtic. TKN crosses the prescribed limits of WHO/EPA at all sites except for S1 and S5 with maximum at S3. Prediction model is better than the baseline model as stationary R squared and R squared value reveal the similar behavior. RMSE values are low, so dependent series is closed with its model-predicted level except for S2, S3, and S4. Using Ljung-Box model, value of statistics ranges from 16 to 29, significance level lies from 0.03 to 0.52, and simple ARIMA model was used for prediction. ACF, PACF, lag, and time series shows that value of TKN lies between 0 to 3 for S1, 0 to 40 for S2, 0 to 40 for S3, 0 to 25 for S4, and 0 to 75 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence limits. It is observed that persistence behavior exist for S1–S5; anti-persistence for S2–S3, S2–S4, S2–S5, S3–S4, S3–S5, and S4–S5; and Brownian time series (true random walk) for S1–S2, S1–S3, and S1–S4.

  • DO: Mean, median, and mode are same and thus behaves normally for S1, S2 and S5. At all sites, data spread is low and symmetrical. Curve is platykurtic at all sites except for S2, which has leptokurtic. WHO/EPA standards are not satisfied by DO at S2, S3, and S4 except for S1 and S5. For all sites, time series model is better than the baseline model as stationary R squared and R squared value exhibit the similar behavior. RMSE values are low, so dependent series is closed with its model-predicted level except for S3, S4, and S5. From Ljung-Box model, for all sites, value of statistics lies between 12 and 40, significance level between 0.00 and 0.57, and simple ARIMA model was used for prediction. Using plots of ACF, PACF, lag, and time series, it is observed that value of DO lies between 7 to 13 for S1, 0 to 5 for S2, 0 to 14 for S3, 0 to 13 for S4, and 5 to 15 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence scale. It is observed that persistence behavior exist for S1–S2, S1–S3, S1–S4, S2–S5, and S3–S5 and anti-persistence for S1–S5, S2–S3, S2–S4, S3–S4, and S4–S5.

  • WT: For all sites, mean, median, and mode remains within the prescribed limits of WHO/EPA, exhibits normal behavior, standard deviation is high, and spread is same and symmetrical. Curve is platykurtic except for S2, which has leptokurtic. Model is better than the baseline model as stationary R squared and R squared value behave alike. RMSE values are low, so dependent series is closed with its model-predicted level. Using Ljung-Box model, value of statistics lies between 23 and 76, significance level between 0 and 0.07, and simple ARIMA model was used for prediction. Using plots of ACF, PACF, lag, and time series, it is observed that value of WT lies between 10 to 28 for S1, 15 to 35 for S2, 15 to 35 for S3, 13 to 35 for S4, and 18 to 30 for S5 and the quality of water gets effected at all sites, which is calculated at 95 % confidence limits. It is observed that anti-persistence behavior exist for S1–S2, S1–S3, S1–S4, S1–S5, S2–S3, S2–S4, S2–S5, S3–S4, S3–S5, and S4–S5.

Conclusion

River water quality management, using statistical, trend, and time series analysis has been studied for full stretch Yamuna River. It is observed that for most of the sites, RMSE value are comparatively very low which shows that dependent series is closed with the model predicted level; thus, predictive model is useful at 95 % confidence limits, and all water parameters exhibits platykurtic curve. For COD, BOD, AMM, and TKN parameters, the observed values are increasing from Hathnikund to Nizamuddin and almost remains constant between Nizamuddin to Mazawali and Agra D/S, but then it decreases again at Juhikha but not maintains the same water quality standard as at Hathnikund. ACF and PACF plots of original data indicates that the data is stationary and therefore does not require differencing (d = 0); thus, series is serially independent. Water quality does not remain same at all sites for all parameters except for pH. Brownian motion (true random walk) behavior exists at different sites for BOD, AMM, and TKN; therefore, water quality trend is unpredictable.

In comparison to all sites, quality of Yamuna River water at Hathnikund is good, declines at Nizamuddin, Mazawali, Agra D/S, and gain good quality again at Juhikha. The quality of water declines at Nizamuddin, Mazawali, Agra D/S because of the mixing of municipal, agricultural, drains and industrial waste in large scale at these sites, and as Yamuna River reaches at Juhikha after traveling a long distance, then most of the polluted river water parameters settled down or wash out; thus, water again gain good quality at Juhikha. For all sites, almost all parameters except pH and WT crosses the prescribed limits of WHO/EPA; thus, water is not fit for drinking, agriculture, and industrial use.