1 Introduction

Forecasting of river flows is very important part of water resources management as planning and operating the future water policy. There are a number of researchers investigating the streamflow forecast (Sanikhani and Kisi 2012; Kisi 2010; Shiri and Kisi 2010; Adamowski and Sun 2010). Forecasting with high accuracy is advantageous for water disciplines such as agriculture and hydropower generation.

Hydrological processes are under too many dynamic effects. It is hard, if not impossible, to consider all these dynamic effects in analytical studies. Sometimes, researchers use some black-box models to approach to hydrological problems. Data based modeling, for hydrological process, has been used widely in recent years because of its rapidity and less variation requirements. Artificial Intelligence was mostly considered for hydrological modeling of late years (Baratti et al. 2003; Chang and Chen 2001; Chang et al. 2004; Chen et al. 2006; Dawson and Wilby 1998; Dorum et al. 2010; El-Shafie et al. 2007; Grimes et al. 2003; Hasebe and Nagayama 2002; Kisi et al. 2006; Luk et al. 2000; Toprak and Cigizoglu 2008; Yarar et al. 2009). Chen et al. (2006) used the adaptive neuro-fuzzy inference system (ANFIS) for constructing a flood forecast model. The precipitation and flow data sets of the Choshui River in central Taiwan were analyzed to identify the useful input variables and then the forecasting model can be self-constructed through ANFIS. For the purpose of comparison, the commonly used back-propagation neural network (BPNN) was also examined. The forecast results demonstrate that ANFIS is superior to the BPNN, and ANFIS can effectively and reliably construct an accurate flood forecast model. El-Shafie et al. (2007) studied to forecast the inflow for the Nile River at Aswan High Dam (AHD) on monthly basis using ANFIS and compared to ANN. It was found that ANFIS model can be beneficial in water management of Lake Nasser reservoir at AHD. Kisi et al. (2006) studied to estimate suspended sediment concentration from streamflow with fuzzy logic model and they compared with rating-curve models. The results showed that the fuzzy model was able to produce much better results than rating-curve models. Toprak and Cigizoglu (2008) used three artificial neural network methods, i.e. feed forward back propagation, the radial basis function neural network, and the generalized regression neural network to compute the longitudinal dispersion coefficient for the evaluation of its behavior in predicting dispersion characteristics in natural streams. Yarar et al. (2009) studied to estimate level changes of Lake Beysehir using adaptive neuro-fuzzy inference system, artificial neural networks (ANN) and a seasonal autoregressive integrated moving average (SARIMA) models. They obtained the best results with ANFIS model by comparing the mean squared errors (MSE) and decisive coefficients (R2).

Wavelet Transform has become a useful tool for the analysis of the variations in time series. Especially, hybrid models have recently been applied to the hydrological modeling (Smith et al. 1998; Lane 2007; Adamowski and Sun 2010; Shiri and Kisi 2010; Kisi and Shiri 2011; Sang 2012; Wei et al. 2012). Smith et al. (1998) used wavelet transform for quantifying streamflow variability and their results suggest that river flows may be electively classified into distinct hydroclimatic categories using wavelet transform. Lane (2007) studied wavelet-based approaches to rainfall-runoff model. Wei et al. (2012) used a wavelet-neural network (WNN) hybrid modeling approach for the prediction of river discharge using monthly time series data. Comparison of results from the WNN models with ANN models indicated that WNN models performed a more accurate prediction.

In this study, it is aimed to investigate the accuracy performance of the combined wavelet-neuro fuzzy models for forecasting the streamflow data, and it is compared with the accuracy performance of a time series model which is called Auto Regressive Integrated Moving Average (ARIMA).

2 Model Description

2.1 Wavelet Analysis

The Wavelet Series is just a sampled version of Continuous Wavelet Transform (CWT) and its computation may consume significant amount of time and resources, depending on the resolution required. ψ(t) is the mother wavelet or the basis function (Eq. 1). The Continuous Wavelet Transform (CWT) is provided by Eq. (2), where f(t) is the signal to be analyzed. All the wavelet functions used in the transformation are derived from the mother wavelet through translation (shifting) and scaling (dilation or compression).

$$ {\psi}_{a,b}(t)=\frac{1}{\sqrt{\left|a\right|}}\psi \left(\frac{t-b}{a}\right) $$
(1)
$$ {X}_{WT}\left(a,b\right)=\frac{1}{\sqrt{\left|a\right|}}{\displaystyle \int }f(t).{\psi}^{*}\left(\frac{t-b}{a}\right) dt $$
(2)

where ψ a,b (t) is the successive wavelet, a is the frequence factor, b is the time factor and ψ* is the complex conjugate functions of ψ(t).

The Discrete Wavelet Transform (DWT), which is based on sub-band coding, is found to yield a fast computation of Wavelet Transform. It is easy to implement and reduces the computation time and resources required. Discrete wavelet transform of f(t) can be written as;

$$ {X}_{WT}\left(j,k\right)=\frac{1}{\sqrt[-j]{\left|{a}_0\right|}}{\displaystyle \int }f(t).{\psi}^{*}\left(\frac{t}{a_0^{-j}}-k{b}_0\right) dt $$
(3)

The most common choice for the parameters a 0 and b 0 is 2 and 1 time steps, respectively. This power of two logarithmic scaling of the time and scale is known as dyadic grid arrangement and is the simplest and the most efficient case for practical purposes (Mallat 1989).

DWT operates two sets of function viewed as high-pass and low-pass filters. The original time series is passed through high-pass and low-pass filters and separated at different scales. The time series is decomposed into one comprising its trend (the approximation) and one comprising the high frequencies and the fast events (the detail) (Kisi 2009).

2.2 Adaptive Neuro-Fuzzy Inference Systems (ANFIS)

Adaptive neuro-fuzzy inference system (ANFIS), first introduced by Jang (1993), is a universal approximation methodology and, as such, is capable of approximating any real continuous function on a compact set to any degree of accuracy (Jang et al. 1997). ANFIS is functionally equivalent to fuzzy inference systems. Specifically, the ANFIS system of interest here is functionally equivalent to the Sugeno first-order fuzzy model (Jang et al. 1997; Drake 2000). To explain the computations involved, we consider a simple fuzzy inference system with two inputs x and y, and one output z. A typical rule set for the first order Sugeno-fuzzy model that includes two fuzzy If-Then rules can be expressed as;

  1. Rule 1:

    If x is A 1 and y is B 1 , then

    $$ {f}_1={p}_1x+{q}_1y+{r}_1 $$
    (4)
  2. Rule 2:

    If x is A 2 and y is B 2 , then

    $$ {f}_2={p}_2x+{q}_2y+{r}_2 $$
    (5)

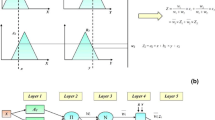
Figure 1 shows the Sugeno fuzzy reasoning system for this Sugeno-fuzzy model, while Fig. 2 shows the corresponding equivalent ANFIS architecture. Nodes at the same layer have similar function for this ANFIS structure. The output of the ith node in layer l is specified as O l,i . These 5 layers comprising the ANFIS structure are briefly described below:

  1. Layer 1:

    Every node i in this layer is an adaptive node, whose output is defined as follows;

    $$ \begin{array}{c}\hfill {O}_{l,i}=\mu {A}_i(x),\kern1em \mathrm{for}\;i=1,2\;\mathrm{or}\hfill \\ {}\hfill {O}_{l,i}=\mu {B}_{i-2}(x),\kern1em \mathrm{for}\;i=3,4\hfill \end{array} $$
    (6)

    Where x (or y) is the input to the ith node and A i (or B i_2 ) is a fuzzy label. The membership functions for A and B can be any membership functions parameterized appropriately; for instance:

    $$ {\mu}_A(x)=\frac{1}{1+{\left[{\left(\frac{x-{c}_i}{a_i}\right)}^2\right]}^{bi}} $$
    (7)

    where {a i , b i , c i } is the parameter set. As the values of these parameters change, the bell-shaped function varies accordingly, thus exhibiting various forms of membership functions on linguistic label A i . In fact, any continuous and piecewise differentiable functions, such as commonly used triangular-shaped membership functions, are also qualified candidates for node functions in this layer (Jang 1993). Parameters in this layer are referred to as premise parameters. The outputs of this layer are the membership values of the premise part.

  2. Layer 2:

    Each node in this layer, labeled Π, is a stable node which multiplies incoming signals and sends the product out. For example,

    $$ {O}_{2,i}={w}_i={\mu}_{Ai}(x)\times {\mu}_{Bi}(y),\kern0.5em i=1,2. $$
    (8)

    The output of each node represents the firing strength of a rule.

  3. Layer 3:

    Each node in layer 3, denoted as N, is a stable node. The ith node in this layer calculates the proportion of the ith rule’s firing strength to the sum of firing strength of all rules.

    $$ {O}_{3,i}={\overline{w}}_i=\frac{w_i}{w_1+{w}_2},i=1,2. $$
    (9)

    The outputs of this layer are called normalized firing strengths.

  4. Layer 4:

    Each node in this layer is an adaptive node, whose node function is defined as follows:

    $$ {O}_{4,i}={\overline{w}}_i{f}_i={\overline{w}}_i\left({p}_ix+{q}_iy+{r}_i\right) $$
    (10)

    where \( {\overline{w}}_i \) is the output of layer 3, and {p i ,q i ,r i } is the parameter set. Parameters of this layer are referred to as consequence or output parameters.

  5. Layer 5:

    As the last layer, layer 5 includes a stable and single node, labeled as Σ, which sums up all signals to calculate the total output:

    $$ {O}_{5,i}=\underset{i}{\varSigma }{\overline{w}}_i{f}_i=\frac{\underset{i}{\varSigma }{w}_i{f}_i}{\underset{i}{\varSigma }{w}_i} $$
    (11)
Fig. 1
figure 1

Two inputs of first-order Sugeno fuzzy model with two rules

Full size image
Fig. 2
figure 2

Equivalent ANFIS architecture

Full size image

The above equations describe an adaptive network which is functionally equivalent to a Sugeno first-order fuzzy inference system. The learning rule specifies how the premise parameters (layer 1) and consequent parameters (layer 4) should be updated to minimize a prescribed error measure, E. The error measure is a mathematical expression that measures the difference between the network’s actual output and the desired output, such as the squared error. The steepest descent method is used as the basic learning rule of the adaptive network. In this method, the gradient is derived by repeated application of the chain rule. Calculation of the gradient in a network structure requires use of the ordered derivative, denoted as ∂+, as opposed to the ordinary partial derivative ∂. This technique is called the back propagation rule (Jang 1993; Drake 2000). The core of this learning rule involves how recursively to obtain a gradient vector in which each element is defined as the derivative of an error measure with respect to a parameter (Haykin 1998). The update formula for the generic parameter α using the steepest descent method is:

$$ \varDelta \alpha =-\eta \frac{\partial E}{\partial \alpha } $$
(12)

where η is the learning rate.

While the back propagation learning rule can be used to identify the parameters in an adaptive network, this method is often slow to converge. The hybrid learning algorithm (Jang 1993), which combines back propagation and the least squares method, can be used to rapidly train and adapt the equivalent fuzzy inference system. It can be seen from Fig. 2 that if the premise parameters are fixed, the overall output can be given as a linear combination of the consequent parameters. The output f can be written as:

$$ f=\frac{w_1}{w_1+{w}_2}{f}_1+\frac{w_2}{w_1+{w}_2}{f}_2=\overline{w_1}\left({p}_1x+{q}_1y+{r}_1\right)+\overline{w_2}\left({p}_2x+{q}_2y+{r}_2\right)=\left(\overline{w_1}x\right){p}_1+\left(\overline{w_1}y\right){q}_1+\left(\overline{w_1}\right){r}_1+\left(\overline{w_2}x\right){p}_2+\left(\overline{w_2}y\right){q}_2+\left(\overline{w_2}\right){r}_2 $$
(13)

which is linear in the consequent parameters p 1 , q 1 , r 1 , p 2 , q 2 , and r 2 . Consequently, we define the following parameter sets:

S:

set of total parameters

S1 :

set of premise (nonlinear) parameters

S2 :

set of consequent (linear) parameters.

Given some values of S1, P training data are substituted into Eq. (13) leading to the matrix equation:

$$ A\theta =y $$
(14)

where θ is an unknown vector whose elements are parameters in S2, the set of consequent (linear) parameters.

The set S2 of consequent parameters can be identified with the standard least-squares estimator (LSE):

$$ {\theta}^{*}={\left({A}^TA\right)}^{-1}{A}^Ty $$
(15)

where A T is the transpose of A and (A T A) −1 A T is the pseudo-inverse of A if A T A is nonsingular. The recursive least-square estimator (RLS) could also be used to calculate θ * (Jang 1993).

3 Study Area and Model Application

3.1 Study Area

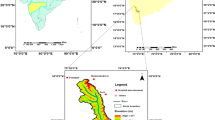
Turkey is separated into 25 river basins in terms of hydrological studies (Fig. 3). Sakarya Basin, numbered 12 (with coordinates 38° 38′–41° 09′ North, 29° 20′–33° 09″ East), is located in west of The Middle Anatolia and east of The Inner Aegean and The Marmara in Turkey (Fig. 4). Average temperature is 14.5 °C and average rainfall is 524.7 mm in the basin. The area covered by the basin is 58,160 km2 and about 2.88 % of it is agricultural land, 19.6 % is grassland, 28.7 % is forest, 2.0 % is wasteland, 1.6 % is settlement and 1.5 % is water surface. Main river of the basin is Sakarya River. And the main arms of the river are Porsuk, Ankara, Kirmir and Mudurnu Rivers. The biggest lake of the basin is Lake Sapanca. There are a number of dams and there are a lot of Flow Observation Stations (FOS), which are operated by General Directorate of Electrical Power Resources Survey and Development Administration (EIE), in the basin. 5 FOS were selected for modeling. Monthly streamflow data between 1964 and 2000 years (EIE, 2000), belonging to each FOS, were used. Selected FOSs and their data characterized are given in Table 1.

Fig. 3
figure 3

Basins of Turkey

Full size image
Fig. 4
figure 4

Sakarya basin

Full size image
Table 1 Characteristics of modeling data sets
Full size table

3.2 Model Application

3.2.1 Wavelet-Neuro Fuzzy (WNF) Model

Monthly mean streamflow data were used for modeling. Input data sets were obtained using DWT for ANFIS modeling. Original time series data was decomposed three level sub-time series by DWT and Approximation of the time series was also obtained. Their correlations with original time series were investigated. Therefore, data sets were selected for each FOS. Streamflow data was used for the output of the model. Table 1 shows the data characterization for each FOS. In this table Qt denotes streamflow at time t, D1, D2, and D3 denote sub-time series under each level (level 1, 2 and 3), A denotes approximation series, and t-1, t-2 denote previous month’s data. Hybrid modeling process consists of two parts. One of the parts is training and the other one is testing. The model was implemented by using MATLAB computer programming.

442 monthly data were used for modeling. 250 monthly data were selected for training process which consists of sub-time series D, and approximation series A as input layer and monthly streamflow data Q as output layer. Training process was performed with different epoch number.

In the testing procedure, the 192 monthly data which were having same character with the training process were utilized in the ANFIS models obtained from the training procedure. The best model depends on the epoch number which was determined by calculating the Root Mean Squared Errors (RMSE) of the models. The agreements between the observed streamflow values and the estimated values using the hybrid model WNF are shown in Fig. 5.

Fig. 5
figure 5

Observed and estimated Streamflow data for Wavelet Neuro Fuzzy model

Full size image

Further evaluation on the performance of the model can be done by comparing with a different model’s performance. A Time Series model Auto Regressive Integrated Moving Average (ARIMA) was selected for comparing the models’ performances.

3.2.2 Time Series Model

Inspection of the streamflow time series and its autocorrelation function (ACF) and partial autocorrelation function (PACF) indicates that the data is seasonal with a period of 12 months. Therefore, a seasonal autoregressive integrated moving average SARIMA (p, d, q) (P, D, Q)12 model may be used to analyze streamflow data. The parameters of the above model—p, d, and q—are non-negative integers that refer to the order of the autoregressive, integrated, and moving average parts of the model, respectively. The parameters of the model were determined from the ACF and PACF graphs and from the seasonal differences which were used to make the series steady. Using a Bayesian Information Criterion (BIC) and in conjunction with different values of q, Q, and D, best fitted SARIMA models were determined for each station. SARIMA models are given in Table 2, the parameters and the equations of SARIMA are given in Table 3. The estimated streamflow obtained with SARIMA models and the observed data which is the same with WNF model are presented in Fig. 6.

Table 2 Time series models
Full size table
Table 3 The parameters and the equations of SARIMA
Full size table
Fig. 6
figure 6

Observed and estimated Streamflow data for Seasonal ARIMA model

Full size image

The performances of two models may also be evaluated by comparing the correlation coefficients (R2) and the root mean squared error (RMSE) computed from the observed and estimated data. These two measures for each of the models are presented in Table 4. It is observed that WNF model gave low values of the RMSE and, according to the estimated and observed graphs, the WNF model shows more accurate values than the time series model.

Table 4 Model results
Full size table

4 Conclusion

The performance of Wavelet Neuro Fuzzy model for estimating the streamflow data was investigated in this study. For this aim, 5 flow observation stations’ data in Sakarya Basin, which is one of the most important basins of Turkey, were used. Monthly mean streamflow data were decomposed subseries and their correlations with following months’ data were analyzed. Subseries which have higher correlation value than the others were selected as the input data set for WNF model. Monthly streamflow data were used for the output data set. Using graphs, obtained from estimated and observed streamflow data, RMSE and R2 values, the best models were determined. To evaluate the performance of the WNF model, seasonal ARIMA model were set by using streamflow data. The best structure of the SARIMA models were determined from the autocorrelation and partial autocorrelation functions of the data and Bayesian Information Criterion.

Depending on the models results, while RMSE ranges between 0.89 and 5.58 in WNF model for the stations, it ranges between 1.93 and 10.08 in SARIMA model. R2 takes a value between 0.82 and 0.94 in WNF, on the other hand, its value is in range between 0.60 and 0.63 in SARIMA model.

According to the RMSE and R2 values and the graphs, it is obvious that WNF model is superior than SARIMA model, because SARIMA model estimated negative (−) data which is contrary to reality.

The WNF model, investigated in this study, provided us reliable results to estimate the streamflow data. This tool can be used to identify the optimal policies such as protection from floods, management of the available water resources.