1 Introduction

Hydrological processes are, by nature, nonlinear systems showing different behaviors at a different time and space scales (Shang and Kamae 2005). The statistical behavior of such systems may follow the scaling law with a fractional non-integer scaling exponent. Self-similarity and self-affinity are common terms to explain this behavior. By definition, self-affinity is a disordered type of self-similarity in which it comprises different scaled identical self-similar substructures (Kantelhardt 2008). For times series analysis, self-affinity is more applicable to specify the essential characteristics of time series (e.g., Malamud and Turcotte 1999; Kantelhardt 2008). For less complex systems, a single scaling exponent is capable of describing the fractal features, which are counted as monofractals, whereas in the more complex and most dynamic ones, multifractality demonstrates the requirements of numerous scaling exponents (Kantelhardt et al. 2002).

Fractal analysis has been employed as an appealing model in the recent decades (Blöschl and Sivapalan 1995; Kantelhardt 2008; Maskey et al. 2015; Fallico et al. 2020) to quantify the variability of soil parameters as a function of space (Ghanbarian-Alavijeh et al. 2010), assess variability in the stream network structure (De Bartolo et al. 2000), evaluate the fractal performance of precipitation as a function of time and space (e.g., Tessier et al. 1993; Over and Gupta 1994; Breslin and Belward 1999; Sivakumar 2000; García-Marín et al. 2008), evaluate fractal behavior of groundwater level fluctuations (e.g., Li and Zhang 2007; Rakhshandehroo and Amiri 2012; Joelson et al. 2016; Yu et al. 2016), and analyze the fractal scaling of groundwater dynamics in confined aquifers (Tu et al. 2017). Precipitation, surface water, and groundwater resources are vital parts of the hydrological cycle and together play an essential role in watershed management. Shang and Kamae (2005) confirmed the existence of multifractal behavior and long-range dependence on the sediment transportation process in the Yellow River basin in China using 31 years of data. Zhang et al. (2009a; b) identified the self-affinity of streamflow in the East River of China. They found climate change and precipitation variations to be the main factors contributing to multifractal behavior in river discharge. Li et al. (2015) studied fractal and statistical characteristics at four hydrological stations along the Yellow River in China. They showed long-range correlation and sensitivity of multifractal formation against a large magnitude of streamflow time series fluctuations.

Detrended fluctuation analysis (DFA) and multifractal detrended fluctuation analysis (MF-DFA) have been widely applied for assessment of fractal scaling properties of flow discharge and precipitation time series (e.g., Matsoukas et al. 2000; Kantelhardt et al. 2002; Livina et al. 2003; Kantelhardt et al. 2006; Koscielny-Bunde et al. 2006; Zhang et al. 2008, 2009a, b; Labat et al. 2011; Zhou et al. 2014; Maskey et al. 2016; Tan and Gan 2017). The MF-DFA can detect the linear–nonlinear long-term memory of the time series, such as precipitation and river runoffs (Bunde et al. 2012). Also, many researchers have recently employed these methods for assessing air quality (e.g., Xue et al. 2015; Carmona-Cabezas et al. 2019). Furthermore, MF-DFA is a somewhat practical method for evaluating multifractal exponent spectra (Koscielny-Bunde et al. 2006; Czarnecki and Grech 2009).

Statistical procedures such as the Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) test, besides the heteroscedasticity test and autocorrelation function, can help identify essential characteristics of various datasets (Shumway and Stoffer 2005). The KPSS test signifies the stationarity state commonly used to determine the variation of the mean value and variance of a time series, which can present underlying physical mechanisms in identifying the state of series (Kwiatkowski et al. 1992; Rakhshandehroo et al. 2018; Fooladi et al. 2021). Heteroscedasticity tests (Breusch–Pagan and White tests) have been used to determine the error variance state in the time series, which can be categorized into heteroscedastic or homoscedastic types (e.g., Breusch and Pagan 1979; White 1980; Koenker 1981). Subsequently, assessing self-affinity behavior in the time series can be delineated by applying the autocorrelation function. It has been widely employed to evaluate any heterogeneity among observations as a function of the lag time length to distinguish the existence of any probable correlation between time series (Kwiatkowski et al. 1992; Rakhshandehroo et al. 2018).

This study aims to examine the scaling behavior of time series incorporating fractal and statistical methods. Despite the high ability of fractal analysis in identifying the fluctuation features of time series, better clarification would be achieved by carrying out a complementary technique containing statistical tests (KPSS test, heteroscedasticity test, and autocorrelation function). As the concept of statistical techniques, these tests can describe the general properties of signals in general terms, whereas the fractal approaches are capable of obtaining more in-depth features of time series. To this end, four hydrological variables, including flow and suspended sediment discharge, precipitation, and groundwater level datasets of two stations on the Missouri River in the USA, were selected. The scaling exponent of three types of signals containing the original plus reversed and shuffled data of the time series has been calculated to investigate the effects of the fluctuation function on multifractal behaviors. Eventually, the results of multifractal besides statistical techniques were interpreted to assess the scaling behavior of mentioned time series at two Missouri River stations.

2 Materials and Methods

2.1 Data and Study Area

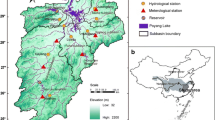
Two stream gauges were studied on the Missouri River Basin (MRB)—the upstream station at St. Joseph, located on the river where it enters Missouri, and the downstream station at Hermann, located close to the point where the Missouri River joins the Mississippi River (Fig. 1). The Missouri River is the longest river in the USA and is considered a permanent river due to several major tributaries in its basin (e.g., Galat et al. 2005; Mitsch and Day 2006; Ahiablame et al. 2017). Several dams have been built on the main river and its tributaries, which may result in meaningful changes in the basin (Rahmani et al. 2018). These constructed dams may have many varieties of influence on the hydrological behavior of Missouri River watersheds. The two study stations are located in an area with fewer dams and anthropogenic changes. Data were available for fractal and statistical analyses for all four parameters at the two stations.

Fig. 1
figure 1

Location of Hermann and St. Joseph stations in MRB

Full size image

Daily precipitation data were downloaded from the cli-MATE (https://mrcc.illinois.edu/CLIMATE), and daily groundwater level, flow discharge and suspended sediment discharge were downloaded from the United States Geological Survey (USGS; https://www.usgs.gov/mission-areas/water-resources). The St. Joseph station is located at 39°45′12″ latitude and 94°51′25″ longitude with an elevation of 241 m above mean sea level and has 1105 square kilometers of drainage area. It includes 3040 field measurement data per day (for 03/04/2009–06/29/2017). The Hermann station is located at 38°42′35″ latitude and 91°26′19″ longitude with an elevation of 147 m above mean sea level and has 1353 square kilometers of drainage area. It includes 3312 days of field measurement data (for 10/01/2008–10/25/2017). Each station has more than 3000 data points for the analysis. The time series of four datasets at both stations are shown in Fig. 2.

Fig. 2
figure 2

Time series of datasets in St. Joseph and Hermann stations of MRB

Full size image

2.2 Detrended and Multifractal Detrended Fluctuation Analysis (DFA and MF-DFA)

Based on the random walk theory, DFA was introduced to determine the fluctuation exponent of the time series and detect the reliability of long-range correlations in a non-stationary series (Peng et al. 1994). The DFA method is presented as (Kantelhardt et al. 2001; Matos et al. 2004; Kantelhardt 2008):

$$y(j) = \sum\limits_{i = 1}^{j} {\left[ {x(i) - \overline{x}} \right],\quad j = 1,\,2,\,3, \ldots ,N}$$
(1)

where \(x\left( i \right)\) is the data time series, \(\overline{x}\) is the average of the time series, and \(y\left( j \right)\) is the integrated time series. The integrated time series can be divided into \(N_{l} = N/l\) non-overlapping segments of length \(l\) where \(N\) and \(l\) are the total number of time series and length of each time segment, respectively. The length of each time segment, \(l\), is usually proposed to be between 10 and\(N/4\) (Kantelhardt et al. 2002). The least-square fit is made by determining the variance for each of the segments υ = 1, 2,…, N:

$$F^{2} (\upsilon ,l) = \frac{1}{l}\sum\limits_{j = 1}^{l} {[y((\upsilon - 1)l + j) - Y_{\upsilon }^{n} (j)]^{2} }$$
(2)

where \({Y}_{v}^{n}(j)\) is the fitting polynomial in the segment υ of the order n (\(n=\) 1, 2, … produce DFA1, DFA2, …). The second-order fluctuation function or concisely fluctuation function can be given by the square root of the average of all segments:

$$F_{2} (l) = \left\{ {\frac{1}{{N_{l} }}\mathop \sum \limits_{\upsilon = 1}^{{N_{l} }} \left[ {F^{2} (\upsilon ,l)} \right]} \right\}^{1/2}$$
(3)

Plotting \(log \left( {F_{2} \left( l \right)} \right)\) versus \(log\left( l \right)\) presents a straight line (for DFA1) whose slope, \(\lambda\), is the fluctuation exponent that revealed the seasonality of time series (e.g., Matos et al. 2004; Rakhshandehroo and Amiri 2012). Kantelhardt et al. (2002) developed MF-DFA as an extension of DFA. Equation (3) may be generalized as the qth-order fluctuation function:

$$F_{q} (l) = \left\{ {\frac{1}{{N_{l} }}\mathop \sum \limits_{\upsilon = 1}^{{N_{l} }} \left[ {F^{2} (\upsilon ,l)} \right]^{q/2} } \right\}^{1/q}$$
(4)

where \(q\) may take any real and nonzero value. Analyzing log–log plots of \(F_{q} \left( l \right)\) versus \(l\) for each \(q\) provides the scaling behavior of the \(q\)th-order fluctuation functions. If the series are long-range power-law correlated, then \(F_{q} \left( l \right)\) increases for large values of \(l\) as a power law \(u\):

$$F_{q} (l) \propto l^{h(q)}$$
(5)

Different orders of DFA, such as linear (DFA1), quadratic (DFA2), or higher-order polynomials, are known as scaling exponent \(h\left( q \right)\), presenting different detrending capabilities, which may be used for detecting trends of the time series. Thus, the standard DFA is retrieved for \(q = 2\), so, \(h\left( 2 \right) = \lambda\), also mentioned as Hurst exponent in the literature (Koscielny-Bunde et al. 2006). Most of the natural time series indicate complex behavior due to long-term instability, whose correlation attributes can be specified by the Hurst exponent (Dubuc et al. 1989; Breslin and Belward 1999; Morency and Chapleau 2003). In definition, the scaling exponent \(h\left( q \right)\) for \(q = 2\) is identical to the Hurst exponent, while \(h\left( q \right)\) for the whole acceptable value of \(q\) is called a generalized Hurst exponent (Kantelhardt et al. 2002). Also, time series can be established as long-range correlated (persistent) if \(h\left( 2 \right) > 0.5\), or long-range uncorrelated (anti-persistent) if \(h\left( 2 \right) < 0.5\) and \(h\left( 2 \right) = 0.5\) which depicts an uncorrelated time series. Furthermore, the value of \(h\left( 2 \right) < 1\) describes the fractional Gaussian noise process (fGn) (stationary signals) and \(h\left( 2 \right) \ge 1\) classifies the time series as a fractional Brownian motion process (fBm) (non-stationary signals) (Mandelbrot and Van Ness 1968; Kantelhardt et al. 2002, 2006; Movahed and Hermanis 2008; Yu et al. 2016). The dependency of \(h\left( q \right)\) on \(q\) implies multifractal behavior of the time series, while in monofractal behavior, \(h\left( q \right)\) is independent of various values of \(q\). In terms of positive \(q\), scaling exponent \(h\left( q \right)\) will represent the existence of large fluctuations in the scaling behavior of segments, while negative \(h\left( q \right)\) describes the scaling behavior of segments with mild fluctuations. The plots of \(h\left( q \right)\) versus \(q\) can be covered with a two-parameter equation (Kantelhardt 2006):

$$h(q) = \frac{{_{1} }}{{^{{^{q} }} }}{ - }\frac{{_{{\ln (a^{ q} + b^{q} )}} }}{{^{q \ln (2)} }}$$
(6)

Parameters \(a\) and \(b\) are responsible for multifractal model properties. For the monofractal time series, \(h\left( q \right)\) does not depend on \(q\). However, if different fluctuation exponents are required to represent different parts of a series fluctuation, then multifractal behavior exists and \(h\left( q \right)\) strongly depends on \(q\). The multifractality level can be introduced by the Holder exponent spectra (Feder 1988; Dimri 2005). Holder exponent (\(\alpha\)) and Holder spectrum (or singularity spectrum \(f\left( \alpha \right)\)) can be calculated as (Kantelhardt et al. 2002):

$$\alpha = h(q) + q\frac{d(h(q))}{{d(q)}}$$
(7)
$$f(\alpha ) = q[\alpha { - }h (q)] + 1$$
(8)

The form of the singularity spectrum in a multifractal dataset is similar to an inverted parabola. The opening width of the singularity spectrum can determine the multifractality level of the signal (Rak and Zięba 2015). The multifractality level of the time series can be defined by the difference between maximum and minimum values of \(\alpha\):

$$\Delta \alpha = \alpha_{\max } { - }\alpha_{\min }$$
(9)

where \(\alpha_{\max }\) is the maximum value of the Holder exponent and \(\alpha_{\min }\) is the minimum one. Considering the represented multifractal model in Eq. (6), Koscielny and Bunde (2006) expressed a formula for determining \(\Delta \alpha\) as a function of parameters a and b:

$$\Delta \alpha = \frac{{\ln a{ - }\ln b}}{\ln (2)}$$
(10)

Hence, in moving from monofractal to multifractal behavior, \(\Delta \alpha\) indicates continuous drops. In other words, in signals with a high level of multifractality, the \(f\left( \alpha \right)\) spectrum is extended (Czarnecki and Grech 2010).

2.3 Statistical Methods

2.3.1 Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) Test of Stationary

The KPSS test was presented by Kwiatkowski, Phillips, Schmidt, and Shin (Kwiatkowski et al. 1992). This test employs a null hypothesis to assess the stationary trend of a univariate time series against the alternative hypothesis of a non-stationary characteristic. This process signifies the nonstationary unit root based on linear regression. In other words, the series are stationary when statistical properties, such as the variance (\(\sigma^{2}\)) and mean, have no statistically significant change over time. In the null hypothesis, \(\sigma^{2} = 0\) implies a constant value for a random walk term and \(\sigma^{2} > 0\) is the alternative hypothesis that explains the unit root in the random walk. The KPSS test was conducted according to a p value with an alpha of 0.05.

2.3.2 Heteroscedasticity test

Heteroscedasticity was utilized to determine the variance of the residual errors with respect to a linear regression of the dataset, which was begun using a general, autoregressive integrated moving average (ARIMA) model. This technique often uses Breusch–Pagan and White tests for evaluating residual errors (e.g., Breusch and Pagan 1979; White 1980; Koenker 1981; Wooldridge 2009; Rakhshandehroo et al. 2018). Breusch and Pagan (1979) calculated the error variance as \(\sigma_{i}^{2} = \sigma^{2} h \left( {z_{i} \alpha } \right)\), where \(z_{i}\) is a vector of independent variables. If \(\alpha = 0\) (\(\alpha\) is significance level), the series has a homoscedasticity type, and for \(\alpha \ne 0\), the series has a heteroscedasticity type. White (1980) proposed a test similar to Breusch–Pagan, which considers the heteroscedasticity procedure to be a function of one or more independent variables and allows them to have a nonlinear and interactive effect on error variance. These two tests (Breusch–Pagan and White tests) are based on a p value with an alpha of 0.05.

2.3.3 Autocorrelation Function

The autocorrelation function can be used to determine the correlation coefficient over a time series, which is a mutual correlation of a signal in a time series with itself. Furthermore, it can detect non-randomness in the data and identify an appropriate time series model if the data are not random (Box et al. 2015). The autocorrelation coefficient, \(r_{k}\), of a time series with a specified lag time, \(k\), is defined as:

$$r_{k} = \frac{{\sum\nolimits_{t = 1}^{N - k} {\left( {x_{t} - \overline{x}} \right)\left( {x_{t + k} - \overline{x}} \right)} }}{{\sum\nolimits_{t = 1}^{N} {\left( {x_{t} - \overline{x}} \right)^{2} } }}$$
(11)

where \(\overline{x}\) is the average of the series and \(x_{t }\) is the observed value at time \(t = 1,{ }2,{ }3,{ } \ldots ,{ }N\). A flowchart is presented in Fig. 3, showing all steps followed in this study.

Fig. 3
figure 3

Flowchart of the conceptual model of steps followed for the study

Full size image

3 Interpretation of Results

3.1 Fractal Methods

3.1.1 Detrended Fluctuation Analysis (DFA) of Time Series

Flow discharge, suspended sediment discharge, precipitation, and groundwater level datasets were analyzed for more than 3000 field measurements of daily information for St. Joseph and Hermann gauging stations. As mentioned earlier, DFA is capable of distinguishing the effect of seasonal oscillatory trends (scaling behavior) from intrinsic fluctuations in the time series such that those were revealed for some other signals of natural oscillating phenomena, including temperature (Kantelhardt et al. 2001). In other words, DFA detects an oscillatory trend in the time series of datasets for \(l > x\), where x is the beginning day of starting perceptible oscillations. Accordingly, the DFA of the mentioned time series represents one scaling region (one slope), which delineates one seasonality time point (one point of change in the seasonality behavior). Having one scaling region in DFA plots of the time series can imply some notable characteristics of the study area, such as size of the river or the vastness of drainage area (Koscielny-Bunde et al. 2006; Hirpa et al. 2010). The scaling behavior of the four mentioned time series with the equation of the straight fitted line for the two stations is illustrated in Fig. 4, and the values of the seasonality time point (\(x\)) and fluctuation exponent (\(\lambda\)) are reported in Table 1. The log–log plot of \(F_{2} \left( l \right)\) versus \(l\) is divided into two seasonal regions by the seasonality time point. The approximate location of the seasonality time point is specified where the scattering of \(F_{2} \left( l \right)\) versus \(l\) is ended, converging to a regular pattern after this point (Fig. 4).

Fig. 4
figure 4

Results of detrended fluctuation analysis (DFA) for quantification of the fluctuation exponent (λ) of original datasets for a flow discharge and b suspended sediment discharge, c precipitation, and d groundwater levels at St. Joseph and Hermann stations in the MRB

Full size image
Table 1 Summarized results of fractal analysis, statistical analysis, and characteristics of time series in Herman and St. Joseph stations in the MRB
Full size table

Estimated values of the seasonality time point for flow discharge, suspended sediment discharge, precipitation, and groundwater level in St. Joseph are 165, 250, 250, and 160; and those in Hermann station are 220, 260, 290, and 260, respectively. Seasonality points patently indicate the seasonal cycle of intrinsic fluctuations in each time series. Describing differences and similarities of the seasonality time point of both stations can clarify the period of the seasonal oscillatory trend in the time series mentioned above. St. Joseph's flow discharge represents a shorter seasonal cycle period than at Hermann, suggesting that intrinsic fluctuations of the flow discharge time series at the St. Joseph station will be repeated every 165 days, which means large fluctuations will be occurring twice in a hydrological year. The suspended sediment discharge of the two stations represents similar periodicity properties. For the precipitation time series, the difference between the seasonality time point of both stations is around 30 days, which explains a similar perceptible behavior in the two stations. Furthermore, the DFA plots of the precipitation time series are more scattered than the other time series, demonstrating a randomness characteristic and probably its effectiveness from external factors such as climate change. The difference in seasonality points of the groundwater level time series at both stations is around 100 days, considerably more than the other cases.

In addition, the Hurst exponent can also be used to understand the fractal behavior of signals with the DFA method. The Hurst exponent \(\lambda\) (or \(h\left( 2 \right)\)) is the slope of the DFA plot (Fig. 4), and fractal dimension, \(D\), is defined as \(D = 3 {-}\lambda\). The Hurst exponent and fractal dimension describe the complexity and irregularity of signals in series, and above all, DFA has the capability to distinguish another attribute of the time series, such as types of signal probability (fGn of fBm) or stationarity state regarding the Hurst exponent (Hurst 1965; Mandelbrot and Van Ness 1968, Kantelhardt 2002). The Hurst exponent of the above ordered time series calculated for the St. Joseph station is 1.30, 0.97, 0.91, and 1.38; and for Hermann is 1.14, 0.99, 0.72, and 1.35, respectively (Table 1). It can be denoted that all of the time series at the two gauging stations indicate persistent long-range correlation (\(\lambda > 0.5\)). Furthermore, the flow discharge, suspended sediment discharge, and groundwater level time series can be classified as an fBm process with non-stationary behavior due to \(\lambda \ge 1\), whereas the minimum Hurst exponent values of the precipitation at both stations are regarded as an fGn process with stationary behavior because of \(\lambda < 1\). The characteristics of four mentioned hydrological signals have been reported in previous studies, such as flow discharge in Movehed and Hermanis (2007), multifractal assessment of the precipitation time series in Zhang et al. (2019), suspended sediment discharge fractal in Shang and Kamae (2005), and the groundwater level time series in Yu et al. (2016).

3.1.2 Multifractal Detrended Fluctuation Analysis (MF-DFA) of Time Series

MF-DFA was hired to specify monofractal or multifractal characteristics of the effects of various moments in the detrended fluctuation functions. The multifractal characteristics of the mentioned time series can be discussed using different parameters of the MF-DFA, i.e., fluctuation function, Hurst exponent, and singularity spectrum, as illustrated in Figs. 5, 6, and 7. The effects of fluctuation function were obtained using different values of \(q\) as the log–log plots of \(F_{q} \left( l \right)\) versus a specified timescale \(l\) (Fig. 5). The results present that different values of generalized Hurst exponent \(h\left( q \right)\) strongly depend on the values of \(q\), denoting the existence of multifractal sources in the time series (Fig. 6). Also, the variation of \(h\left( q \right)\) was much higher at smaller timescales, representing a higher degree of multifractality in smaller timescales of all the time series. The negative values of \(q\) indicate the existence of small fluctuations in the time series and led to a higher generalized Hurst exponent value (steeper slope). Hence, the positive values of \(q\) imply large fluctuations and smaller \(h\left( q \right)\) values (milder slope) as frequently observed in multifractal time series (Hekmatzadeh et al. 2020).

Fig. 5
figure 5

Results of logarithmic fluctuation function Fq versus logarithmic timescale l of original datasets for a flow discharge, b suspended sediment discharge, c precipitation, and d groundwater level time series at St. Joseph and Hermann stations in the MRB

Full size image
Fig. 6
figure 6

Results of scaling exponent h(q) versus different values of q on three types of original, reversed, and shuffled datasets for a flow discharge, b suspended sediment discharge, c precipitation, and d groundwater level time series at St. Joseph and Hermann stations in the MRB

Full size image
Fig. 7
figure 7

Singularity spectrum of original datasets for a flow discharge, b suspended sediment discharge, c precipitation, and d groundwater level time series at St. Joseph and Hermann stations in the MRB

Full size image

Comparing each of the mentioned time series of the two stations can help comprehend variations in each time series’s behavioral complexity. Consequently, different multifractal behaviors in all of the time series have been detected using MF-DFA. For the St. Joseph station, the fluctuation function with different values of \(q\) for various moments does not converge together in the large timescales, indicating the tendency of flow discharge time series toward the less multifractal behavior in large fluctuations. In contrast, the branches of detrended fluctuation functions of flow discharge in the Hermann station converge together in large timescales, which denotes the existence of multifractal sources in the large and small fluctuations and the following long-range correlation behavior. Also, the suspended sediment discharge of both stations exhibits the same pattern of converging in large fluctuations, indicating a long-range correlation. However, the pattern of small fluctuations is not similar in both stations that demonstrate different behavior in small fluctuations of the suspended sediment discharge time series at the upstream of each station.

A brief comparison between the flow discharge and suspended sediment discharge time series of both stations may reveal a relationship between the existence of two crossover points in the small fluctuations (negative \(q\)) of the flow discharge at St. Joseph and flow discharge along with suspended sediment discharge at Hermann. The first and second crossover points in the flow discharge time series at the St. Joseph station can be specified approximately at day 100 (\(\log 2\)) and 200 (\(\log 2.3\)), while those values at the Hermann station can be considered the same as the St. Joseph crossover point values with less precision. With the suspended sediment discharge, these points have been shifted forward and can almost be determined by days 158 (\(\log 2.2\)) and 316 (\(\log 2.5\)), respectively. So first, this means the same value for the crossover points of the flow discharge time series demonstrates the same pattern of small fluctuations in both stations. Secondly, the lag time between the crossover points of the time series can delineate the occurrence of some extreme hydrological events (such as flooding due to an increase in the flow discharge values) at the upstream station and then tracking its effects on the suspended sediment discharge along Missouri River to the downstream station. In the literature, similar results for flow discharge have been presented by Emadi et al. (2016). By applying DFA and MF-DFA on ten hydrometric stations at the Karkheh watershed in western Iran, the team investigated the multifractal behavior of a daily streamflow time series and found that streamflow follows multifractal behavior with an annual non-significance level, denoting a long-range correlation.

The precipitation time series at both stations show a slightly different fluctuation pattern. The branches of fluctuation functions in MF-DFA plots of both stations converge on a large timescale, indicating a long-range correlation. However, slight variations in the slope of the branches of the fluctuation functions related to small and large fluctuations (negative and positive values of \(q\)) may describe less strength of multifractality, particularly in the precipitation time series of Hermann station. This kind of fluctuation pattern has been reported through previous studies, probably due to the high randomness characteristics of the precipitation time series (Zhang et al. 2019).

The groundwater level at both stations exhibits the same fluctuation pattern regarding different negative and positive q-order moments. In this regard, the fluctuation patterns related to negative values of \(q\) are showing two crossover points approximately at days 100 (\(\log 2\)) and 158 (\(\log 2.2\)), which indicates the time period of alteration in the small fluctuation patterns. However, the groundwater time series shows a long-term persistence correlation due to the convergence of all branches of the fluctuation function at larger timescales, such as the flow discharge and suspended sediment discharge time series. It should be mentioned that previous studies, such as Rakhshandehroo and Amiri (2012), have reported the same fluctuation function pattern related to different q-order moments of groundwater level time series.

Another customary way to describe multifractality features of the time series is to assess variations of the generalized Hurst exponent \(h\left( q \right)\) as a function of different values of \(q\). In order to investigate sources of multifractality, the plots of \(h\left( q \right)\) versus \(q\) have been calculated for three types of sorting time series—original, reversed, and shuffled data. The sources of the multifractal behavior in most hydrological time series have been predominantly introduced in two types. The first is the broadness of the probability density function (PDF) of the time series known as the Noah phenomenon. The second is the long-range correlation of the Joseph phenomenon’s time series (Mandelbrot et al. 1968). The plots of original data in Fig. 6 confirm that in the time series, as mentioned earlier, \(h\left( q \right)\) decreases continuously as \(q\) increases, which can be considered an indication of nonlinear memory and existence of multifractality (Bunde et al. 2012). Comparing the original data with the reverse ordering of the time series data can also be pivotal in authenticating the existence of multifractality in the original data arrangement. Moreover, the shuffling time series has been introduced in the literature as a straightforward method to detect multifractal behavior. The shuffling process can remove multifractality caused by the long-range correlation. It can transform a multifractal time series into a monofractal signal without changing the broadness of the PDF. Of note in monofractal signals, \(h\left( q \right)\) is constantly equal to 0.5 as a horizontal line related to different values of \(q\), illustrating the self-affinity of the time series over different timescales (Wu et al. 2018; Czarnecki and Grech 2010). As can be seen in most of the time series mentioned earlier, the slope of the curves linked to the negative values of \(q\) is steeper than the slope of the curves obtained from the positive values of \(q\), describing that the smaller fluctuations may appear more often than large fluctuations. This behavior has been detected in the signals as mentioned above, which demonstrates the high value of \(R^{2}\) with the standard multifractal cascade model. It should be noted that segments of the time series with small variances will govern the fluctuation function when the \(q\) value is negative. Therefore, the calculated values of \(h\left( q \right)\) linked to negative \(q\) values magnify the scaling properties of the segments with small fluctuations, and the segments with large variances will govern the fluctuation function regarding the positive values of \(q\) (Katnelhardt et al. 2002).

The indispensable point that can illustrate the degree of multifractality is Eq. (6), similar to the well-known multifractal cascade model and appropriate for characterizing river runoff’s multifractality (Feder 1988; Dimri 2005; Koscielny-Bunde et al. 2006). Accordingly, the parameters \(a\), \(b\), and \(R^{2}\) values of each dataset at both gauging stations were determined by applying a curve-fitting procedure on \(h\left( q \right)\) spectra in the range \(- 5 \le q \le 5\), which can be specified as a multifractal fingerprint for the considered time series (see Fig. 6 and Table 1). The parameters of Eq. (6) are particularly essential for assessing the flow discharge, suspended sediment discharge, precipitation, and groundwater level models. For example, in the literature, a flow discharge artificial signal (as an input dataset) can be generated using those parameters, and it can be studied (output of model) on the basis of them. It should be noted that those parameters have been calculated from the asymptotic part of the generalized fluctuation function, denoting that they are not affected by seasonal dependencies (Kantelhardt 2006; Koscienly-Bunde 2006). In other words, conformity of the multifractal plot of \(h\left( q \right)\) versus \(q\) with the multifractal cascade model presented in Eq. (6) signifies the adequate ability of the model in explaining the multifractal behavior of the signal. In contrast, unconformity with this model can delineate a minor degree of multifractality, denoting influences of some external factors on signal records.

In moving from negative toward positive values of \(q\), more sensible fits of the original data with higher \(R^{2}\) values were carried out for flow discharge, suspended sediment discharge, and groundwater level time series of both stations, whereas the lower \(R^{2}\) values of the precipitation were obtained, especially at the Hermann station. As a consequence, the lesser \(R^{2}\) value of Hermann station’s precipitation can describe the more complex behavior of this time series and assure the influence of some external factors such as extreme weather events on this signal. The conformity of \(h\left( q \right)\) versus \(q\) plots of reversed data compared to the original data can indicate the degree of multifractality in signals. Stronger multifractality would be found in the time series showing similar variations between original and reversed data; however, they are not precisely the same in most of the \(h\left( q \right)\) versus \(q\) plots, indicating different patterns in small fluctuations (negative \(q\)) and the same pattern in large fluctuations (positive \(q\)). With reference to multifractal sources, the \(h\left( q \right)\) values of shuffled data related to different \(q\) are approximately equal to 0.5, which can delineate the self-affine characteristics of the mentioned time series, except the precipitation due to shuffled data \(h\left( q \right)\) variations, especially at Hermann station. Unlike the multifractal behavior of the mentioned time series of both stations, Hermann precipitation signal moves from monofractal behavior in small fluctuations to multifractal behavior in large fluctuations, which is entirely different from the precipitation at St. Joseph station. It shows that multifractal properties in the flow discharge, suspended sediment discharge, and groundwater level of both stations predominantly arise from different long-range correlations of the time series. In contrast, multifractality in the precipitation time series may be governed by other sources, such as the broadness of the PDF, which can originate from more complex behavior of this kind of signal.

The level or strength of the multifractality of the signals can be addressed using Holder exponent \(\left( \alpha \right)\) versus \(f\left( \alpha \right)\) called Holder spectrum, singularity spectrum, or multifractal spectrum. The asymmetric multifractal spectrums corresponding to the time series mentioned earlier at St. Joseph and Hermann gauging stations are illustrated in Fig. 7. Also, the multifractal characteristics of the mentioned time series are reported in Table 1. Considering Eq. (7), the term of \(d\left( {h\left( q \right)} \right)/{\text{d}}q\) experienced negative values due to the decrease in \(h\left( q \right)\) versus \(q\), and also the value of \(\alpha\) and \(f\left( \alpha \right)\) at \(q = 0\) are equal to \(h\left( 0 \right)\) and \(f\left( \alpha \right) = 1\) (see Eq. 8), respectively, which denotes that the left side of the Holder spectrum is related to the positive \(q\) values and the right side is associated with the negative values of \(q\).

In the flow discharge, suspended sediment discharge, and groundwater level diagrams, the Holder spectrums are truncated from the left side and have longer tails at the right, clarifying that they possess multifractal structures that are more sensitive to small fluctuations. In contrast, the singularity spectrum of the precipitation at St. Joseph is more associated with large fluctuations because it has a longer tail at the left side and is truncated from the right. At the same time, at Hermann station, it does not emerge as an inverted parabola. It only has the left-side tail, indicating a multifractal pattern in large fluctuations in addition to monofractal behavior in small fluctuations. Furthermore, Eqs. (9) and (10) can explain the multifractality richness of the time series by defining \(\Delta \alpha\) value as the opening of Holder diagrams. The Hermann station exhibits a higher degree of multifractality in the flow discharge, suspended sediment discharge, and groundwater level time series due to denoting larger \(\Delta \alpha\) values in comparison with St. Joseph station. In contrast, the precipitation at St. Joseph station displays more multifractality features than at Hermann (see Fig. 7 and Table 1).

3.2 Statistical Methods

3.2.1 Stationarity Test

Results of the KPSS test for determining the stationarity of the time series mentioned earlier at St. Joseph and Hermann gauging stations are given in Table 1. The stationarity test has been conducted the entire time series period, and asymptotic critical values and p values adapted to the size of the samples were computed utilizing Monte Carlo simulation with a 5% significance model. As reported, the computed p values for the flow discharge, suspended sediment discharge, and groundwater level are lower than the significance level, indicating that the stationarity null hypothesis should be rejected. The p value for the precipitation is larger than the significance level alpha = 0.05, which means that the stationarity null hypothesis cannot be refused. In other words, the precipitation shows stationary behavior, while the flow discharge, suspended sediment discharge, and groundwater level can be regarded as non-stationary signals.

3.2.2 Heteroscedasticity Test

The heteroscedasticity test for residual errors of the time series mentioned at both stations was employed to assess the error variance state (assessing equality of residual errors) using a general, autoregressive integrated moving average model (ARIMA). The computed p values related to Breusch–Pagan and White tests of all the time series are reported in Table 1. The p values of the precipitation time series are greater than the significance level alpha = 0.05, denoting homoscedasticity in residual errors. In contrast, the obtained p values of flow discharge, suspended sediment discharge, and groundwater level of the two gauging stations are lower than alpha = 0.05, which explains the heteroscedasticity in residual errors.

3.2.3 Autocorrelation analysis

The autocorrelation function of the mentioned time series was determined for a lag length of 100 days. As presented in Fig. 8, different autocorrelation functions can be distinguished. The autocorrelation function diagrams of flow discharge at both stations show a significant decreasing pattern (from 1 to 0.22 in both stations) as lag length increases, which is probably because of the non-stationary and heteroscedastic behavior of the signal. Also, the same decreasing pattern can be seen in the groundwater level time series of the two gauging stations (from 1 to 0.42 at St. Joseph and from 1 to 0.22 at Hermann), but the suspended sediment discharge can be regarded as semi-periodic (from 1 to 0.05 at St. Joseph and from 1 to -0.05 at Hermann) because it decreases first and then changes to the periodic situation in high lag length. Conversely, the autocorrelation functions of the two stations’ precipitation time series illustrate a thoroughly periodic function, probably due to the stationary and homoscedastic state of the signal. The autocorrelation function is not a sufficient indicator in determining the short-range or long-range correlation of the time series. However, it may be proper for initial recognition of the behavior of the time series, considering variation patterns of each autocorrelation function. At first glance, the precipitation may be regarded as a short-range correlated time series, while the flow discharge, suspended sediment discharge, and groundwater level may be considered as signals with long-range correlations.

Fig. 8
figure 8

Sample autocorrelation function as a function of lag time for original datasets in St. Joseph and Hermann stations for a flow discharge, b suspended sediment discharge, c precipitation, and d groundwater level time series in the MRB

Full size image

4 Discussion on Combining Fractal and Statistical Approaches

In general, the findings of statistical tests and multifractal analysis can authenticate or reject results of each other and demonstrate the necessity of doing further analysis. So, the interpretation of statistical results accompanied by multifractal outputs will lead to a more precise understanding of some signal specifications. Eventually, the findings of both methods can address two separate ways of recognizing the vital characteristics of the hydrological time series.

According to the outputs of the KPSS test of stationarity, the precipitation indicates stationary behavior, while the other three mentioned time series denote a non-stationary state. In the same way, the DFA can describe the stationarity of the time series by considering the fractal degree parameters, such as the Hurst exponent (\(h(2)=\lambda\)). As reported in Table 1, the Hurst exponent of precipitation in both stations is less than 1. In contrast, the Hurst exponent values of the three other mentioned time series are higher than or equal to 1, which can authenticate the stationarity results of the KPSS test. Furthermore, MF-DFA plots are another tool that can help recognize the stationarity of the time series. The convergence branches of the fluctuation function in the long term are the key to identifying the stationarity of the time series (see Fig. 5). Also, plots of the calculated \(h\left(q\right)\) related to different values of \(q\) of the shuffled data are another way to describe the stationarity of the time series (see Fig. 6). In this regard, MF-DFA plots of the flow discharge, suspended sediment discharge, and groundwater level illustrate the convergence branches for various moments of fluctuation function. Moreover, the \(h\left(q\right)\) versus \(q\) of the shuffled data is similar to a horizontal line equal to 0.5, while the fluctuation function plots of the precipitation could not demonstrate a precise convergency in the long term, and the plots of \(h\left(q\right)\) versus \(q\) of the shuffled data represent a decreasing pattern, which is not similar to a horizontal line (see Figs. 5 and 6).

In addition, interpreting the DFA and MF-DFA plots is a feasible way to confirm the results of the autocorrelation function. As shown in Fig. 8, the precipitation displays a fast decay in its autocorrelation function with periodic behavior denoting long-range uncorrelated (anti-persistent) characteristics. In contrast, the three other mentioned time series illustrate the same decreasing pattern that denotes long-range correlated (persistent) signals. The multifractal results of the flow discharge, suspended sediment discharge, and groundwater level time series demonstrate a perceptible level of consistency with the autocorrelation function spectrums, but the precipitation reveals a more complex behavior. Furthermore, the multifractal results of the precipitation time series are displaying long-range correlated (persistent) characteristics (\(h\left( 2 \right) > 0.5\)), while the autocorrelation plots are expressing long-range uncorrelated (anti-persistent) characteristics. So, the conclusion is that the homoscedastic characteristic of the precipitation time series resulting from the heteroscedasticity test can probably be the cause of the contradiction, while the existence of heteroscedastic behavior in the other three mentioned time series can be the reason for conformity between multifractal and statistical findings. Consequently, this kind of behavior denotes more random characteristics and effects of extreme events in the homoscedastic time series like precipitation, signifying the necessity of further analysis to understand the precipitation time series better.

Another finding of incorporating the multifractal and statistical results is the evaluation of the correlation between the flow discharge and suspended sediment discharge in each station. As mentioned in the section on multifractal properties of the time series, the pattern of fluctuation functions of \(h\left( q \right)\) linked to various values of \(q\) in the flow discharge and suspended sediment discharge of Hermann station demonstrated a higher level of conformity than St. Joseph gauging station, especially in the fluctuation functions related to small fluctuations. In this regard, the correlation between the flow discharge, and suspended sediment discharge time series of each station has been calculated (Fig. 9). As presented in Fig. 9, the coefficient of determination, \(R^{2}\) between flow discharge and suspended sediment discharge at St. Joseph station is 0.27, which is lower than 0.66 at Hermann station, authenticating the results of the MF-DFA plots. It can be inferred that having a similar pattern in fluctuation function plots resulting from the MF-DFA between two time series with mutual hydrological interactions can lead to obtaining a higher value of \(R^{2}\).

Fig. 9
figure 9

Correlation between flow discharge and suspended sediment discharge at a St. Joseph station and b Hermann station of the MRB

Full size image

5 Conclusion

This paper presents four hydrological time series—flow discharge, suspended sediment discharge, precipitation, and groundwater level at St. Joseph and Hermann stations in the USA—investigated by means of fractal methods and conventional statistical tests. By incorporation of multifractal and statistical analysis, flow discharge, suspended sediment discharge, and groundwater level time series of both stations can be regarded as self-affine plus non-stationary and heteroscedastic with fBm behavior, and only precipitation represents stationary, homoscedastic besides fGn characteristics and is not self-affine. Moreover, all the mentioned time series demonstrate the long-term correlation, except precipitation that displays a periodic behavior that should be considered as long-range uncorrelated due to the comparison of the autocorrelation function and multifractal analysis. Subsequently, the MF-DFA results indicated a high level of multifractality with complex behaviors in the flow discharge, suspended sediment discharge, and groundwater level at both stations. Also, the MF-DFA plots of the flow discharge and suspended sediment discharge at the Hermann station are more similar to each other than the St. Joseph station. Eventually, the calculated correlation between the flow discharge and suspended sediment discharge at both stations could authenticate the higher correlation value at Hermann station. In the end, assessing multifractality in addition to the statistical analysis of the hydrological time series in the short and long term is a competent tool to discuss contribution of different vital factors, such as extreme events (flood and drought) and anthropogenic impacts that have affected the natural condition of different rivers around the world, especially the Missouri River.