Background

Cycling exercise typically involves frequent changes in external power output and an associated metabolic power demand (MPD) that stresses various energy pathways for energy production [1]. The relative contribution of each key energy system primarily is dictated by the exercise intensity, by the responses of the systems involved in metabolic control [2], exercise duration and endogenous carbohydrate stores availability [3, 4].

Following a step change in power output in the moderate intensity domain, at steady state [5] a fully and evenly aerobic condition can be reached [6] after a brief transitory phase that relies on anaerobic pathways. Energy requirements are met through carbohydrate and lipid oxidation, without net accumulation of blood lactate [7] (e.g., easy riding in the peloton [8]). As the exercise intensity increases, the utilization of lipids is thought to be progressively reduced and the contribution of glycogen breakdown, that ends in lactate production [9], becomes more and more relevant. Above certain individualized intensities [10], the exercise becomes unevenly aerobic [6] and more carbohydrate-dependent [9] and the exercise cannot be maintained indefinitely (e.g., 40 km time trials and high mountain ascents [11]). This threshold is well-explained by studies [12] that used the maximal lactate steady state (MLSS) methodology (considered the gold standard for evaluating this threshold), but also other methods have been used to demarcate the boundary between sustainable-unsustainable exercises (e.g., the critical power CP [13]). At extreme intensities, which are characterised by a limited sustainability (e.g., sprints [14]), intramuscular high-energy phosphates (ATP and PCr) and the anaerobic glycogen breakdown provide the predominant energy required [15] while the contribution of the aerobic metabolism slowly rises over time and becomes essential in reconstituting the depleted energy stores, allowing the repetition of intermittent extreme exercise bouts [16].

A single exercise session triggers a specific acute physiological response that, if repeated, promotes a specific chronic adaptation [17]. Understanding how internal human energy is provisioned to create external power can assist us to understand topics as broad as performance analysis, exercise prescription and exercise physiology. Exercise intensity (i.e., the internal metabolic power demand), can be linked to an associated external power output (P) during cycling that is derived across a cadence (ω) distribution by means of the cycling efficiency [18]. The processes enabling this power output evokes an acute physiological response, typically measured by the oxygen consumption (\({\dot{\text{V}}}\)O2) and the lactate concentration [La], proxies of the oxidative and glycolytic components of the metabolic response, respectively. \({\dot{\text{V}}}\)O2 mirrors oxygen consumption at the level of the working muscles, considered as the aerobic contribution to the exercise [19], while [La] can be used to express the balance between the rate of lactate production and removal [6], and indirectly, the involvement of anaerobic metabolism [20]. The variation of muscular PCr concentrations, can only be assessed with expensive and invasive techniques like the standard biopsy or by 31P magnetic resonance spectroscopy [21].

At steady-state [5], the energy turn-over can be expressed by means of the formula [22]:

$${\text{MPD}} = a \cdot \frac{\text{d}}{{{\text{d}}t}}{\text{PCr}} + b \cdot \frac{\text{d}}{{{\text{d}}t}}\left[ {\text{La}} \right] + c \cdot {\dot{\text{V}}\text{O}}_{ 2}$$

where d/dt is the time derivative operator and the three constants (a, b and c) corresponds to the moles of ATP resynthesized by a mole PCr, lactate or oxygen respectively [5]. To use this equation in dynamic conditions (i.e., with a time-varying MPD) we need to include and solve the differential equations for the \({\dot{\text{V}}}\)O2, [La] and PCr responses in a single system of equations, i.e.; a dynamic model. This is made particularly challenging by the different time constants characterising these responses [23], especially in the recovery phase [24].

The goal of a dynamic model is, therefore, to mathematically describe the dynamic behaviour of \({\dot{\text{V}}}\)O2, [La] and PCr. Accurate and reliable models can be highly useful in a number of applications, especially when physiological data collection is problematic. Particularly, \({\dot{\text{V}}}\)O2 and [La] values are used in training prescription [25], to assess the aerobic performance [26] and the training status of endurance athletes [27]. The PCr response to exercise is often neglected mainly because: (1) direct information on PCr is expensive and invasive and (2) PCr contribution during prolonged activities is limited.

Existing models of cycling \({\dot{\text{V}}}\)O2 and [La] are all abstracted using mathematical “hand-written” formulations. The great advantage of this approach is that every equation of the model has a physical/physiological meaning: model developers try to incorporate all the relevant data, and include relationships between relevant variables [e.g., height, age, weight, gender, heart rate (HR) or arterial blood saturation (SaO2)] as a function of the exertion. However, with this approach, we only use few variables in our models because the more variables we add, the more difficult it becomes to make sense of the relationships between them and to express these relationships mathematically. Despite the great work done by sport scientists, exercise physiologists and model developers in the last decades, today there are no modelling solutions that can work for every exercising condition.

The purpose of this narrative review is to provide to model users (typically exercise physiologists or sport scientists) and model developers (typically engineers or mathematicians) a common ground to meet on. We everyday experience a lack of communication between these groups, which may be hindering the development of new and more sophisticated models. However, it would be impossible to extensively review both the entire exercise physiology literature and the different kind of mathematical tools that model developers have in their arsenal. We limit our review to linear dynamic models of \({\dot{\text{V}}}\)O2 and [La], i.e., models that account for time-dependent changes in the metabolic power requirements and that can be written with linear differential operators.

Having said this, first we briefly review the bioenergetic modelling literature; we highlight the limitations that exist, and ultimately the roadblock that has been reached in the area. Second, we introduce potential new solutions to existing limitations on a critical base. The review has been written and organised so to be understandable by both model users and developers: this first introductory section sets the scene on the physiological response to cycling exercise; the second section describes the main features of the \({\dot{\text{V}}}\)O2 and the [La] kinetics; the third section presents the currently available mathematical formulations, the techniques adopted to describe the \({\dot{\text{V}}}\)O2 and the [La] kinetics and the related limitations; the fourth section presents where and how new possible modelling solutions can evolve and how we can bridge the historical results with the modern techniques; the fifth and conclusive section sums up the implications of our arguments.

Bioenergetic modelling

Introduction

Bioenergetic models are used to estimate \({\dot{\text{V}}}\)O2 and [La] responses to cycling exercise. With such models, measurable mechanical variables (typically cadence and power output) represent the system’s input, allowing an estimation of the required metabolic power demand provided by the athlete. Measurable physiological variables (typically \({\dot{\text{V}}}\)O2 and [La]) are considered the system’s outputs that describe the metabolic control of the workload.

Within the realm of cycling science, estimations of the bioenergetic models are used for mainly two distinct purposes: performance analysis and data generation. Performance analysis is usually conducted in a post-process phase and is used, for example, to assess the effect of a treatment on a model parameter or to uncover the most influential parameter [28, 29]. Models adopted in performance analysis should always reflect the system’s physiological features and be consistent with the purpose intended for the model. The goal of data generation initiatives is to create simulated data in a pure predictive fashion. For optimizing pacing strategy, for example, quantities like anaerobic source depletion [30] are commonly adopted, with the goal of finding the best power distribution that minimizes the total race time. Alternatively, training design with bioenergetic modelling aims to find the ideal training intensity distribution that can trigger the optimal training-induced adaptation [31]. Data generation initiatives also include innovative studies attempting to predict physiological variables on a real-time basis using easy-to-obtain information [32]. Two major limitations to the development of accurate and reliable bioenergetic models include data quality and mathematical complexity. Both limitations are direct consequences of the variability of the measured physiological variables alongside an individual physiological response. While external mechanical variables (e.g., speed, power, and cadence) are easily collected in both indoor and outdoor conditions [33], internal physiological variables (e.g., \({\dot{\text{V}}}\)O2, [La]) are more difficult to measure. Experimental data collection of \({\dot{\text{V}}}\)O2 and [La] require highly sophisticated and expensive hardware [34] or invasive techniques [35]. Additionally, such data are always affected by biological noise that makes it harder to recognize distinct characteristics of the response, thereby impacting model parameter choice [36]. Acute physiological responses are highly complex and variable within and between individuals, due to a number of factors that include pedal frequency [37] and prior exercise intensity [38, 39].

Great contributions to our understanding of \({\dot{\text{V}}}\)O2 kinetics have been made by Wasserman and Whipp [40], Barstow [41], Poole and Jones (with a book entirely devoted to \({\dot{\text{V}}}\)O2 kinetics [42]). In the field of exercising [La], Stegmann [43], Brooks [44], Gladden [45] and Beneke [35] progressively refined our understanding of the area. In the field of the energetics of the muscular exercise and regulatory mechanisms at whole body level, fundamental contribution has been given by scientists of: the “school of Milan” (e.g., di Prampero and Margaria [22, 46] with a first systematic discussion on the oxygen deficit, Cerretelli [47] with the introduction of the early lactate concept, Lador [48] with the application of the double-exponential model to the study of the cardiac output kinetics and Ferretti [49] with a recent book summarizing the latest advances in the field); the “Canadian school” (e.g., Hughson [50] with the first studies investigating \({\dot{\text{V}}}\)O2 kinetics under lower body negative pressure, Faisal et al. [51] for their analyses on the role of the primary exercise on \({\dot{\text{V}}}\)O2 kinetics and lately Beltrame [52] for applying new AI technologies to the problem of modelling exercising \({\dot{\text{V}}}\)O2) and the “British School” (e.g., Rossiter et al. [53] for their research on PCr kinetics and Binzoni [54] for bridging with the “School of Milan”).

Exercising \({\dot{\text{V}}}\)O2 and [La] have been well characterized for on-set [55] and off-set [56] of step exercise, during recovery after exercise [57, 58], for impulsive/pseudo-random/sinusoidal force functions [59,60,61,62], for intermittent exercises [63, 64], for decremental [65] and incremental [66, 67] ramp and graded exercises [68, 69]. A mathematical abstraction of these complex behaviours requires a large number of “what if” scenarios, conditions and exceptions to be expressed in mathematical form. Typically, hand-written formulas are included and coded with the logic of Box 1.

Box 1 Representative example of a pseudo-code written to implement a bioenergetic model
Full size table

Mathematicians and model developers have the ability to use hand-written formula by choosing from a variety of functions (e.g., exponential functions [70], delayed functions [71] and sigmoidal functions [72]) that can lead to concise and informative mathematical forms. While bioenergetic models have grown in size and complexity over the last decades, solutions for the variety of potential exercising conditions encountered remains unavailable.

Important features of \({\dot{\text{V}}}\)O2 and [La] kinetics to be considered in the development of bioenergetic models are presented separately in the next sessions for an ideal fatigue-free state. This is because a multitude of models available in the literature only focus on one of these variables at time. However, in a model combining both the \({\dot{\text{V}}}\)O2 and [La] responses, the interplay between the aerobic and the anaerobic metabolism and the role of the early blood lactate or the lactate energy equivalent should be considered. The mechanical efficiency and the internal power contributions are also presented.

\({\dot{\text{V}}}\)O2 kinetics

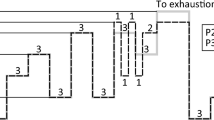
Schematic representations of \({\dot{\text{V}}}\)O2 kinetics have been reported for exercise intensity domains of relevance (Fig. 1) based on ventilatory thresholds VTI (or GET) and VTII (or RCP) [1] (i.e., the intensity thresholds that we can identify with breakpoints in the ventilatory variables during a cardiopulmonary exercising test). These include: moderate (power output lies below the first ventilatory threshold or GET, i.e., P < PVTI), heavy (power output lies between the first and the second ventilatory thresholds or RCP, i.e., PVTI < P < PVTII), severe (power output lies between the second ventilatory threshold or RCP and the minimal power eliciting the maximal oxygen consumption during a cardiopulmonary exercising test, i.e., PVTII < P < PVO2max) [73] and extreme (power output is greater than the minimal power eliciting the maximal oxygen consumption during a cardiopulmonary exercising test). In the case of moderate exercise, a steady state of \({\dot{\text{V}}}\)O2 is attained and is equal to the nominal one (Fig. 1a) as predicted from the MPD/P relationship (see “[La] kinetics” section). Even in the moderate domain, on- and off-kinetics depend on the power output baseline [74], and they show good symmetry (Fig. 1b) [75]. For heavy exercise, still a steady-state is attained and this “excess” \({\dot{\text{V}}}\)O2 (Fig. 1c) can be seen as a change in the MPD/P relationship (see “[La] kinetics” section). In this intensity domain, the on-kinetics is slower than the off-kinetics (Fig. 1d) [75]. For severe exercises, no steady state is shown (Fig. 1e), and the development of a slow component can raise \({\dot{\text{V}}}\)O2 towards \({\dot{\text{V}}}\)O2max [76] without exceeding it [77]. However, exhaustion might occur before \({\dot{\text{V}}}\)O2 could reach the maximal values [78]. \({\dot{\text{V}}}\)O2 can rise, although less significantly, during prolonged heavy exercise, and some authors prefer to refer to this as drift (Fig. 1i) [79]. In the severe intensity domain, the augmented \({\dot{\text{V}}}\)O2 at constant power output can be viewed as a lowered efficiency due to progressive fatigue development and decreased muscle efficiency [80]. When severe exercise ends, \({\dot{\text{V}}}\)O2 drops to a new steady state value dictated by the new reduced intensity with slower kinetics, determining the excess post-exercise oxygen consumption (EPOC) (Fig. 1f) [81]. If the on-kinetics of \({\dot{\text{V}}}\)O2 is dissected, two different phases that correspond to distinct physiological events are evident: the cardiopulmonary phase [or phase-I (Fig. 1g), evident from tON to TD1], and the dominant phase [or phase-II (Fig. 1h), evident after tON + TD1]. In the case of extreme exercise intensities, the \({\dot{\text{V}}}\)O2 response saturates at a maximal value defined by \({\dot{\text{V}}}\)O2max (Fig. 1k) in a time that decreases as the exercise intensity increases [82] (Fig. 1j). However, \({\dot{\text{V}}}\)O2max might not be reached for extreme exercise intensities, especially when power exceeds the ~ 130% of PVO2max [83].

Fig. 1
figure 1

Schematic representations of \({\dot{\mathbf{V}}}\)O2 behaviour in response to a single bout of constant work rate in different intensity domains. For moderate exercises, a steady state is attained and it equals the nominal one (a). The on- and off-kinetics are similar (b). For heavy exercises, a steady state is attained that is greater than the nominal one (c) and the off-kinetics appear to be faster than the on-kinetics, albeit \({\dot{\text{V}}}\)O2 does not return to basal values immediately (d). For severe exercise, no steady state is shown (e) and the off-kinetic is very slow (f) as determined by an additional oxygen consumption (i.e., EPOC). More detailed on-kinetics involves a first phase in which there is an abrupt rise in \({\dot{\mathbf{V}}}\)O2, called phase-I or the cardiopulmonary phase (g) and a phase-II, i.e., the dominant kinetics (h). A drift in the oxygen consumption is reported for prolonged submaximal exercises as a result of rising body temperature (i). In extreme exercise, the time to reach \({\dot{\mathbf{V}}}\)O2max decreases as the exercise intensity increases (j) and the value of \({\dot{\mathbf{V}}}\)O2max is attained and maintained (k) until exhaustion occurs or exercise workload drops

Full size image

[La] kinetics

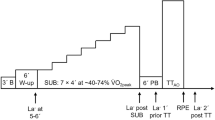
A schematic example of the behaviour of the [La] is reported in Fig. 2 for different exercise intensity domains of interest based on lactate thresholds LTI and LTII (or MLSS) [1] (i.e., the intensity thresholds that we can identify with variations in [La] during a cardiopulmonary exercising test). These include: moderate (below the first lactate threshold, i.e., P < PLTI), heavy (between the first and the second lactate thresholds or CP/MLSS, i.e., PLTI < P < PLTII) and severe (above the second lactate thresholds or CP/MLSS, i.e., P > PLTII). In the case of moderate exercise, lactate clearance exceeds lactate accumulation rate, so any change in lactate concentration is restored and [La] is kept constant at the basal value (Fig. 2a). In the case of heavy exercise intensities, lactate production equals lactate removal and [La] typically stabilises between the 2 and 4 mM [43]. Here, the upper boundary corresponds to the maximal lactate steady state (Fig. 2d). It should, however, be noted that maximal lactate steady state tests have great variability [43] in terms of [La] but they are very repeatable in terms of power output [84], meaning that any correspondence with fixed [La] values of 2 and 4 mM is a simplification of the likely response. In the case of severe exercise, the [La] continues increasing (Fig. 2e) and whole body energy turnover is considerably larger than that indicated by the \({\dot{\text{V}}}\)O2 by an amount that is proportional to the net rate of lactate turnover [6]. Generally, [La] shows a delayed response to the power output and this is particularly evident after severe exercise (Fig. 2f) [85], where a prominent fraction of the total power is in fact provided by the anaerobic metabolism [6]. At the onset of the exercise (tON), regardless of the workload, an increase in the lactate concentration is observed [47]: the early lactate response (Fig. 2a) that gives an overshoot at the start of heavy (Fig. 2c) or severe exercises. When the exercise ends (tOFF), the [La] slowly decreases to the basal value with exponential behaviour (Fig. 2b) [58] with a slow time constant ([La] returns to basal values after ~ 20 min).

Fig. 2
figure 2

Schematic representations of blood lactate concentration ([La]) behaviours in response to different exercise intensities, beginning in tON and ending in tOFF. At every exercise intensity, [La] shows a delayed response to the exercise. For moderate exercises, after a small peak due to early production (a), lactate returns to the basal value LB exponentially (b). For heavy exercise, after a brief overshoot due to early production (c), a steady state is attained above the basal value (d). For severe exercise, the lactate continues increasing (e) and a delayed peak is evident when exercise ends (f). Irrespective of the exercise intensity, lactate returns to its basal value in an exponential fashion (b)

Full size image

Including the ‘internal power’ and the mechanical efficiency

Internal power (IP) in cycling has three main contributors [86]—(1) the variation of the kinetic energy of the body, (2) the co-activation of agonist and antagonistic muscles and (3) the frictional/viscous resistance of joints. Observational [87] and theoretical [86] studies report that IP increases linearly with the mass (not the weight [88]) and the moment of inertia of the moving segments and as a power function of ω. However, if a higher ω requires an additional metabolic power, it can be assumed that the faster cadence is detrimental to efficiency, which is not necessarily the case [89]. This of course is a simplification of the issue, but there are different alternatives [90] and model developers should also consider that cadence selection has a large number of biomechanical [91] and metabolic determinants [37]. With the inclusion of the contribution of the internal power, the linear formula for the metabolic power demand becomes:

$${\text{MPD}} = G \cdot \left( {P + {\text{IP}}} \right) + {\text{MPD}}_{0} = G \cdot \left( {P + k \cdot \omega^{\gamma } } \right) + {\text{MPD}}_{0} ,$$

where k is a compound term for the inertial parameters and γ is a constant parameter (see, e.g., [87]) and MPD0 is the metabolic power demand at rest (i.e., generally assumed equal to the resting \({\dot{\text{V}}}\)O2 value, ≈ 3.5 ml kg−1 min−1 [92]). Typical values of 1/G (Δ efficiency) range from between 18 and 25% [18] (values are close to the efficiency of concentric muscle contraction). G is also known as the “gain” and is usually assumed to be ≈ 10  ml O2 min−1 W−1 for moderate exercise intensities and it gets progressively higher at heavy and severe intensities [75, 78] (≈ 13 ml O2 min−1 W−1). Here, the augmented gain can lead to a \({\dot{\text{V}}}\)O2 excess as high as 230 ml O2 min−1 dependent on the methodology adopted [93] for the calculation. However, it has been suggested that the value of the oxygen gain depends on the exercise intensity domain and the baseline exercise intensity and that it progressively changes with the power output [94].

Existing modelling solutions

\({\dot{\text{V}}}\)O2 models

Models for \({\dot{\text{V}}}\)O2 kinetics have been developed throughout a wide range of different formulations [42]. The simplest and most common form is the first-order form:

$$\tau \frac{\text{d}}{{{\text{d}}t}}{\dot{\text{V}}\text{O}}_{ 2} + {\dot{\text{V}}\text{O}}_{ 2} = G \cdot \left( {P + k \cdot \omega^{\gamma } } \right) + {\text{MPD}}_{ 0} = {\dot{\text{V}}\text{O}}_{2p} ,$$

where τ is the characteristic time of \({\dot{\text{V}}}\)O2 kinetics (is recognized as one key parameter of aerobic fitness) and \({\dot{\text{V}}}\)O2p is the value of the target \({\dot{\text{V}}}\)O2 (typically inferred from MPD). The solution of the first-order equation in response to a step-input is:

$${\dot{\text{V}}\text{O}}_{2} = A \cdot \left( {1 - e^{ - t/\tau } } \right) + {\dot{\text{V}}\text{O}}_{20}$$

This is why this model is often referred to as a single-phase or mono-exponential model. Where A is the steady state amplitude of the response, calculated as the difference between the target \({\dot{\text{V}}}\)O2p and the baseline \({\dot{\text{V}}}\)O20. First-order \({\dot{\text{V}}}\)O2 models can be used to assess the exercise-induced improvements [95], intermittent training [96], performance [82] and the oxygen debt [97].

A double-exponential (double-phase) model puts together the phase-I and phase-II of the \({\dot{\text{V}}}\)O2 response (Fig. 1g, h). The sum of the time constant of phase-II and the time delay of phase-I has been termed the “effective” time-characteristic or the “mean response time” [98]. However, the choice of a double-exponential model over a single-exponential model is not only mathematical, but it has to be underpinned by important conceptual assumptions made a priori [48]. Phase-I is often assumed to be exponential [99] but there is still a lack of evidence that can support this assumption likely because the asymptote of phase-I is not approached before phase-I/II transition. However, single and double-phase models cannot precisely describe overall \({\dot{\text{V}}}\)O2 kinetics in heavy and severe intensity domains, because the additional \({\dot{\text{V}}}\)O2 requirements (see how in Fig. 1c, e the \({\dot{\text{V}}}\)O2 response deviates from the mono-exponential response). To improve the descriptions, Scheuermann et al. [70] included an additional exponential function in a three-phase model. The slow component of \({\dot{\text{V}}}\)O2 is included as an additional exponential term that switches on after an independent time delay with the onset of the exercise. During heavy exercises, an exponential term with an asymptote of constant amplitude seems adequate [75], but it has to point towards \({\dot{\text{V}}}\)O2max (or above) to correctly represent the \({\dot{\text{V}}}\)O2 slow component mechanism (Fig. 2e). It must also be specified that multi-phase models must include a limit to the maximal values of \({\dot{\text{V}}}\)O2 (Fig. 1k) before they can be adopted to predict exercising \({\dot{\text{V}}}\)O2 values.

Variations in the oxygen gain, kinetics (τ) or time-delays relationships with the power output have been reported by researchers implementing linear \({\dot{\text{V}}}\)O2 models [74, 94]. However, it is important to realise that including these non-linear relationships can lead to non-linear dynamic models of \({\dot{\text{V}}}\)O2 that usually require more complex protocols for their calibration (see “Limitations of hand-written models” section) and additional computational efforts. There are a number of modelling solutions equally justifiable for these function [i.e., G(P) and τ(P)], e.g., a linear profile or an asymptote of increasing amplitude [100] (that could be also used to model the \({\dot{\text{V}}}\)O2 drift mechanism depicted in Fig. 1i), an intensity-dependent [74] or a time-varying τ [101] (that can also be used to describe the fast \({\dot{\text{V}}}\)O2 response to extreme exercises depicted in Fig. 1j), the inclusion of τ as a function of lactate concentration [6] (e.g., τ = λ[La] + τ0 where λ is a constant parameter and τ0 is the characteristic time of \({\dot{\text{V}}}\)O2 kinetics at rest [47]). As comprehensively reviewed in [6], this increase in \({\dot{\text{V}}}\)O2 kinetics (τ) is associated with a greater reliance on anaerobic sources for energy provision. In this last case both \({\dot{\text{V}}}\)O2 and [La] equations must be solved together.

However, model developers must be warned: even if we choose simple linear functions for G(P) and τ(P) (e.g., τ = m · P + q, with m the slope of the linear relationship and q the intercept), we introduce additional parameters (i.e., m and q) that need to be computed. Of course a model that includes these non-linear behaviours is likely to bee more generalizable (it can adapt to a wider range of exercising conditions), but it is usually more difficult to understand and analyse and poses computational issues, like numerical instability. This trade-off between simplicity and accuracy of the model is well-known in the field of mathematical modelling, where between two models with equal predictive power, the simplest one is the most desirable. These concepts are discussed in more depth in “Limitations of hand-written models” section.

Stirling et al. [102] mathematically formulated the multi-phase models of \({\dot{\text{V}}}\)O2 kinetics in the differential form suitable for numerical integrators. They used the model to assess the effects of exercise training on \({\dot{\text{V}}}\)O2 kinetics [103]. However, the original version of the model has been designed for running, and requires amendments to meet cycling activity requirements [104]. Gonzalez and collaborators [71] included a curvilinear characteristics of the P/MPD relationship and the slow component is included as a secondary state variable triggered after an independent time delay and constantly superimposed to the primary component.

While modelling has made physiological inferences drawn from studies that have measured \({\dot{\text{V}}}\)O2 during exercise, it is still not completely clear whether each of the parameters in the models are system descriptors. Further work is required to allow more parameters to offer a testable and justifiable physiological meaning [105].

[La] models

The classic oxygen-debt and anaerobic threshold theories have been formed on the basis that lactate produced during exercise is a dead-end metabolite that relates to the absence of oxygen or to the development of fatigue [106]. Historically, this has resulted in the development of the so-called threshold models, where [La] is linked to \({\dot{\text{V}}}\)O2 by means of static relationships [107]. The more recent lactate shuttle theories [44] suggest that increasing lactate production with increasing power output does not appear to be strictly the result of inadequate oxygen supply [45] and should not be considered a threshold phenomenon [108]. Skeletal muscles and organs like kidney, liver and brain, can be considered as compartments, with the circulating blood providing the route to link the compartments together. Lactate exchange rate correlates with circulating lactate and follows normal concentration gradients. With this in mind, Zouloumian and Freund [58, 109, 110] proposed a model consisting of two communicating compartments—the working muscle and a lactate space. The Freund’s model can be expressed by means of a second order ordinary differential equation that can resemble the delayed behaviour and the overshoot typical of the [La] response to P (Fig. 2) [68]. It is commonly represented in the bi-exponential solution for constant inputs:

$$\left[ {\text{La}} \right]_{b} = A_{1}^{{ - \lambda_{1} t}} + A_{2}^{{ - \lambda_{2} t}} + A_{3} \left[ {\text{La}} \right]_{bp}$$

Here, A1, A2, A3, λ1, and λ2 are constants that depend on the system characteristics and on their initial conditions, where [La]bp is the lactate production term. Freund’s model has been applied to assess the exercise-induced improvements elicited by intermittent and continuous exercise training [111], to assess [La] kinetics after maximal short term exercise in different populations [112], after high intensity exercises [39] with active/passive recovery [113], to assess training-induced improvements in blood lactate removal ability [114]. For a short-term working period, Freund’s model can accurately describe the time-evolution of [La], suggesting that the model is qualitatively and quantitatively accurate [115]. It may be worth noting, however, that the original model was designed for recovery phases. In fact, in the original formulation, the lactate production term is neglected and a physiological meaning is given to the constant parameters: λ1 represents the lactate production ability and λ2 the lactate clearance ability [116] that depend on intensity and exercise duration. As suggested in the “\({\dot{\text{V}}}\)O2 models” section, it would be appropriate to include power output dependencies in the parameters of the model. This for example would mean to specify equations for λ1(P) and λ2(P), but this would require additional parameters and then more complex protocols for parameter calibration, with all the complications that follow (see “Limitations of hand-written models” section). As previously mentioned, non-linear and explicit time-dependent functions should be included cautiously.

Neglecting the lactate production term has important mathematical and conceptual consequences. First of all, the model becomes a static non-linear function and it loses its mechanical meaning. Second, we cannot apply this equation to the prediction of [La] in response to varying power output. Possible modelling solutions for the lactate production term can be proposed by means of the lactate energy equivalent [117]. Provided that any increase 1 mM in [La] is equivalent to the energy released by the consumption of ~ 3 ml O2 per kg of body mass [6], and neglecting the PCr contribution, we could relate the lactate production term with the difference between the metabolic power demand and \({\dot{\text{V}}}\)O2. However, this would not be sufficient to explain constant [La] values during heavy exercises (Fig. 2d) and it would require an additional power output dependent term.

Introducing a parameter for the lactate energy equivalent, Moxnes and Sandbakk proposed a mathematical model [72] for the lactate production and removal during whole-body exercise that can be adapted for cycling [118] and that can be used to estimate both \({\dot{\text{V}}}\)O2 and [La] kinetics with the same system of equations. The peculiarity of this model resides within the use of a sigmoidal function (tanh) that can be used to model smooth transitions between exercise intensities [119] and to describe the lactic acid buffering capacity. This model can be adopted to predict [La] in response to varying power output, but the large number of parameters with questionable physiological meaning impairs its predictive ability.

Limitations of hand-written models

The development of new and accurate hand-written models is mainly limited by the mathematical complexity required to describe the physiological phenomena of interest. It is difficult even to fathom how one would “hand-write” models for \({\dot{\text{V}}}\)O2 or [La] that can include the complicated internal power contribution, along with time-varying and intensity-dependent gains, τs and λs. The complexity of a model then depends upon the extension of the underlying physiological mechanism of interest: complex models are made to cover a large number of different kinetics (therefore, require a large number of parameters), whereas simpler models can only cover limited aspects of the physiological response (therefore, require a limited number of parameters).

The main problem is that every parameter of the model must be estimated within an acceptable level of confidence and that the number of parameters widens the confidence interval (CI) of the estimates (usually computed with statistical techniques like the bootstrap method [120]) and reduces the number of degrees of freedom (i.e., the difference between the number of data points and the number of parameters). Usually parameters are estimated by a model fitting procedure, i.e., an  optimization problem consisting of minimizing an objective function by selecting the parameters from within an allowed set and computing the value of the objective function. The objective function typically consists in a sum of the squared differences between the simulated (the data generated with the model) and the experimental data points. The optimization problem is then solved by means of a nonlinear programming solver (e.g., implemented in the fminsearch [121] or particleswarm [122] functions in Matlab software). The higher the number of the parameters of the model, the less their effect on the fitting is discernible because the presence of local minima. In addition, if parameters are interdependent, the performances of the model (in terms of objective function) is poorly sensitive to variations in the parameters. In this case we say that the optimization problem is poorly conditioned and that the choice of the parameters is not making relevant difference on the value of the objective function [123]. As a consequence, the number of the parameters and the presence of interdependent parameters have a detrimental effect on the CI of the parameters. It can be assumed that, if the change in the error with experimental data is sufficient to offset the loss in degrees of freedom associated with the number of parameters, then the inclusion of a greater number of parameters is statistically justified [124]. However, if the CI of the estimates is larger than the smallest worthwhile changes [125] considered for those parameters, then the number of data points should be increased [126, 127]. Given that the testing protocols should elicit all the different behaviours that the model wants to describe, this requires long and articulated protocols for parameter estimation, so the number of individuals that can be tested is reduced if a more complex model is involved. Conversely, for simple models, a larger pool of individuals can be tested for different trials.

Besides mathematical complexity, data quality is also a limiting factor in the development of new bioenergetic models. High-quality data is characterized by a high signal to noise S/N ratio and by an adequate number of data points. Increasing the workload is the most straightforward method to increase the magnitude of the \({\dot{\text{V}}}\)O2 and [La] responses, but, as a consequence, the exercise becomes less sustainable. Noise reduction can be obtained by averaging over a different number of trials or by applying different smoothing techniques [128]. Most of the difficulties in modelling the different phases of \({\dot{\text{V}}}\)O2 kinetics lie behind the noise. In fact, the different phases of exercising \({\dot{\text{V}}}\)O2 only become discernible when they emerge from the noise of the background component of the fundamental profile. Noise affecting \({\dot{\text{V}}}\)O2 data can be approximated with a stochastic uncorrelated Gaussian noise of ≈ 120 ml O2 min−1 [13] (the assumption of normality has been questioned [129]) independent from the metabolic rate [36] while with respect to [La], uncertainty in measurements can range from ≈ 10 to ≈ 25% of the absolute value [130]. The number of data points is highly determined by the sampling rate (e.g., breath-to-breath for \({\dot{\text{V}}}\)O2 or blood sample time for [La]). The number of data points increases the number of degrees of freedom and narrows the CI of the parameter estimates. A possible strategy to increase \({\dot{\text{V}}}\)O2 data points and improve parameter estimation [131] is by interpolating at 1-s. This is reasonable for \({\dot{\text{V}}}\)O2 breath-to-breath signals, as the average respiratory frequency is ≈ 3.5 s for moderate exercises and the main dynamic of \({\dot{\text{V}}}\)O2 is ≈ 25–50 s [36]. In the case of [La], data points are typically spares (e.g., every minute [112], every 30 s [39], 10 s [58], up to real-time during bed rest [132]). During a classic Wingate test, [La] can rise as fast as ≈ 5 mM min−1 [133] indicating that exercising [La] could have surprisingly fast kinetics compatible to that of the \({\dot{\text{V}}}\)O2. This suggests that interpolation error may become relevant if sampling or interpolation time is not compatible with variations in the power output. Another method to improve the quality of the dataset is to exclude outliers or data points that are not likely to be part of the physiological response of interest and to avoid estimates influenced by unassociated portions of the response (e.g., see comparisons between [134, 38]).

To summarize: (1) simple models are best suited for performance analysis, as they have sufficient validity and sensitivity to identify worthwhile changes in the parameters characterizing the response, (2) complex models are best suited for data generation and simulations, as they cover a wide range of different scenarios, but the low confidence in parameter estimation impairs their predictive ability. The stages outlined in the conceptual scheme of Fig. 4 (left half) offer a structured format for the design of “hand-written” bioenergetic models.

Alternative approaches to bioenergetic modelling to predict cycling \({\dot{\text{V}}}\)O2 and [La]

If the understanding of the underlying physiological mechanism is not a priority, then we can rely on a different class of models, where a number of free-adjustable parameters without physiological meaning is included. With this approach, parameters are tuned until the model behaves with satisfactory accuracy like a specific instance of the real system. This is the approach of the Artificial Intelligence (AI) technologies, where the general goal is to recreate with computers the cognitive functions of the human mind, e.g., learning and problem solving [135]. AI algorithms, and in particular, machine learning and deep learning [136] have been adopted in vast and complicated conditions like health care [137], motor vehicle operations [138] and physical activity type classification [139]. In sports, machine learning have been used to treat cycle training data [140] or swimming performance data [141]. However, while AI is rapidly advancing forward in other fields, it is still in its infancy in cycling science [142].

In the realm of the AI-related technologies, neural networks are a biologically inspired programming paradigm which allows a computer to learn from experimental data through machine learning techniques [143]. At first, as with hand-written models, examples that specify the correct output (y) for a given set of inputs (x) are used to train the model, i.e., to adjust the parameters of the neural network. Second, the model is applied to process a data set where only the x variables are available to estimate the y. Training a neural network also involves an optimization problem that typically requires a high amount of numerical computation due to the great number of parameters. However, while in “hand-written” models it is often possible to retrieve an analytical formulation for the exact solution and speed up the optimization process with faster and robust solvers [123], machine learning algorithms usually refine the estimates of the solution via iterative processes. In fact, most learning algorithms are based on a class of optimization algorithms called stochastic gradient descent [144] that require massive amount of data and computational efforts [143].

Two common machine learning task are classification and regression. In a classifier, y variables take class labels, and the algorithm returns a membership identification probability. In a regressor, the y variables take continuous values and the program can learn to find the best relationship to represent the data. A classifier can be trained to provide the probability of \({\dot{\text{V}}}\)O2 and [La] across different training zones (Fig. 3a), whereas a regressor can be used to estimate exact values of \({\dot{\text{V}}}\)O2 and [La] (Fig. 3b) for a given power output.

Fig. 3
figure 3

Example of two different kinds of artificial neural networks that can be adopted in oxygen consumption \({\dot{\text{V}}}\)O2 and blood lactate concentration [La] prediction by means of easy-to-obtain inputs, such as: power (P), cadence (ω), heart rate (HR), respiratory frequency (RF), and oxygen saturation (SaO2). a A classifier is used to assign a label to the different data inputs. In the case of a classifier, the output variable takes a class label, such as the intensity domains (e.g., basal, moderate, hard, severe). b A regressor is used to estimate the exact value of \({\dot{\text{V}}}\)O2 and [La] from input data. Here, the output variables take continuous values

Full size image

With a neural network approach, adding more measurable variables means supplying useful information to learn input/output relationships. Particularly, additional inputs can be useful if they: (1) bear strong relationships with the output variables, (2) are independent of each other, and (3) are always available. A number of easy-to-obtain inputs can be used to predict exercising \({\dot{\text{V}}}\)O2 and [La] data on a real time basis. For example, x datasets can be formed by the concomitant collection of power output, cadence, heart rate (HR), respiratory frequency (RF) and blood arterial saturation (SaO2). Additional information is provided by the simultaneous collection of different physiological markers, and used to predict a more accurate response of the target outputs, i.e., the \({\dot{\text{V}}}\)O2 and [La], so that:

$${\mathbf{x}} = \left[ {P,\omega ,{\text{HR}},{\text{RF}},{\text{SaO}}_{2} } \right]\mathop \Rightarrow \limits^{?} {\mathbf{y}} = \left[ {{\dot{\text{V}}\text{O}}_{2} ,\left[ {\text{La}} \right]} \right]$$

Neural networks are made to create relationships between x and y, without a priori defined structures that automatically discern relevant and un-relevant correlations. The absence of these conditions makes neural networks more flexible than “hand-written” models and their application requires less knowledge about the system being modelled (i.e., in our case, \({\dot{\text{V}}}\)O2 and [La] kinetics). Furthermore, when a sufficient number of parameters are included, neural networks can approximate any function to the desired level of accuracy [145]. This allows the representation of very complex systems across a large variety of exercising conditions. If individual characteristics change, knowledge from historical data can be transferred and adapted to different individual characteristics (transfer learning) [146].

Particularly, among the many different classes of neural networks, great contribution can be provided by the so-called deep, convolutional and recurrent neural networks. Deep neural networks (as opposed to shallow neural networks) have multiple hidden layers of neurons between the input and output layers and have been used in the prediction of \({\dot{\text{V}}}\)O2 kinetics during treadmill walking [147], activities of daily living [139, 148] and cycling [149]. Convolutional neural networks are a special class of deep neural networks specifically designed for image recognition and classification [150]. They have been used to detect arrhythmias from ECG signals [151], but unfortunately they have not been already embedded in portable HR monitors that could be used in outdoor cycling [152]. Recurrent neural networks have the ability to include past values of the inputs and to keep memory of recent exercise history, thereby being particularly suited for time-series analysis [153]. Recurrent neural networks are currently applied in health care and diagnostics [154], in lactate threshold detection in running [155], in ventilatory thresholds estimation from cardiopulmonary exercising test data [156] and hold potential to be exploited for estimating cycling \({\dot{\text{V}}}\)O2.

AI techniques suffer from two major limitations, however. First, such models involve a “black box” approach [157] and the knowledge of the complex internal mathematical formulation is limited (the model is not self-explanatory, and hence the term “black box”). Second, the approach requires substantial training data to cover the variety of learnt processes, with sufficient data density needed for all exercising conditions (otherwise over-fitting may occur). To this extent, large datasets may be provided by the advent of the current and future wearable sensor industry, capable of non-invasively acquiring a large array of metabolic markers [158]. These large datasets, the high number of parameters, alongside the aforementioned condition-specific training process, will together require massive collaborative and computational efforts.

With AI, instead of writing a program by hand (Box 1) for each specific exercising condition (Figs. 1, 2), a computer program can be written so that the computer can determine by itself the relationships between parameters and inputs for different exercising conditions. When we compare against the complexity and work involved in writing out by hand all the possible combinations involved, AI solutions become extremely appealing and exciting. It should be clear, however, that with AI, we are replacing known knowledge and procedures with one single big one. Thus, it can become difficult if not impossible to elucidate underlying physiological mechanisms from a neural network, as relationships between variables may be hidden. We believe that a trade-off solution can be found in a hybrid approach (see, e.g., [159]), where physiology equations are combined together with neural networks. In these models it is possible to incorporate prior knowledge about the bioenergetics (e.g., the first-order model of \({\dot{\text{V}}}\)O2 kinetics) into a neural network that is used to estimate non-linear/time-dependent parameters [e.g., G(P), τ(P), λ1(P) or λ2(P) introduced in “\({\dot{\text{V}}}\)O2 models” and “[La] models” sections]. As a consequence, a hybrid model typically requires a significantly smaller number of experimental data and parameters than a pure neural network [160]. To the best of our knowledge, this promising approach has yet to be tested against \({\dot{\text{V}}}\)O2 and [La] data.

As it has been done for “hand-written” models, we offer the different critical stages in the creation of an AI-bioenergetic model in Fig. 4 (right side). It must, therefore, clear that there is not a superior approach, and that the best modelling solution depends on the purpose intended for the model. In an age where new communication devices are offering new ways to collect big amount of data [161], the collaborative work between sport scientists and mathematicians will be instrumental for enabling future solutions towards a more effective utilization of this data. Neural networks and machine learning [136], by their very nature of how they function, may in effect thrive on using a large volume of information in a productive and informative way: model developers have new and complementary tools in their toolboxes. Currently, however, extra work is needed to embed these innovative technologies and their hybrid combinations in portable devices and reach the athletes on the field.

Fig. 4
figure 4

Decision process and stages of the creation of a bioenergetic model following the “hand-written” model (left side) and the AI-model (e.g., neural network NN) (right-side) approaches. The best modelling solution depends on the purpose intended for the model and on data availability. In both cases, a trade-off exists between the mathematical complexity of the model and generalizability to a variety of exercising conditions

Full size image

Conclusions

In the field of modelling \({\dot{\text{V}}}\)O2 and [La] responses to cycling exercise, despite the great amount of synergistic work done by model developers and exercise physiologists together, a single model or approach that can fit all the possible exercising conditions is currently unavailable. Limits to current model development lie behind the mathematical complexity required to describe the physiological responses to the exercise and to the high variability of the data characterizing this response. Due to a reduced number of parameters, “hand-written” models typically show low flexibility to adapt to changes in exercise conditions. Among the AI-related technologies, neural networks fit well in a framework where many physiological variables that are easy-to-obtain can be used to generate predictions of cycling \({\dot{\text{V}}}\)O2 and [La] in a great variety of exercise conditions. However, in neural networks, models parameters do not have direct physiological meaning and require big datasets for calibration. We hope that this review might be the start of a conversation that brings together these exciting technologies into exercise physiology and sport science understanding and application.