1 Introduction

Graph is a ubiquitous structure for modeling networks in various areas including social networks [24, 40, 41, 43], P2P networks [7], biological networks [1], web networks [39], etc. In a graph, each vertex represents an entity, and each edge represents the relationship between two entities. To recognize groups of well-connected vertices, a variety of cohesive subgraph models are proposed such as clique [4], k-core [28], k-truss [10], and k-ecc [5]. The model of k-core is well-studied for its elegant structure and efficient algorithms to compute [31]. It is defined as a maximal subgraph in which every vertex has at least k neighbors (adjacent vertices) in the subgraph. There are various applications based on the model of k-core such as community discovery [24], network engagement analysis [22], finding influential spreaders [17], social contagion [34], finding molecular complexes [1], etc.

Assume each entity incurs a cost (e.g., k) to remain engaged in a network but receives a benefit proportional to (e.g., equal to) the number of engaged neighbors (adjacent vertices), the k-core corresponds to the natural equilibrium of this engagement model [3]. Thus, the size (the number of vertices) of k-core in a network well estimates the (structural) stability of this network. In order to improve the stability of a network, current studies focus on enlarging the size of k-core such that the vertices in the network are better connected [42]. Considering the linking of non-adjacent vertices, the edge k-core problem is studied recently [46]: given a graph G, an integer k and a budget b, add b edges to non-adjacent vertex pairs in G such that the size of k-core is maximized.

Example 1

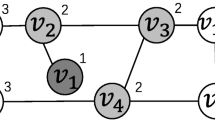
Consider a graph G in Figure 1(a), the coreness of each vertex is marked with a value. The whole graph G forms a 1-core because every vertex has at least one neighbor in G, and the subgraph induced by vertices v1, v2, v3 and v4 is a 3-core. Assume that k = 3 and b = 2, the edge k-core problem aims to maximize the 3-core by adding two new edges into graph G. One of the optimal results is to add (v5, v9) and (v7, v8). Figure 1(b) depicts the modified graph \(G^{\prime }\). By adding only two edges, we can get a larger 3-core induced by the vertices in G except v10 and v11.

Figure 1
figure 1

An example of Edge k-core problem. Here, k = 3 and b = 2. By adding two new edges (v5, v9) and (v7, v8), the new 3-core is maximized with five more vertices {v5, v6, v7, v8, v9}

Full size image

Applications

As a fundamental problem, the edge k-core can be used in many applications, e.g., connection construction in telecom networks, link recommendation for a group of webs, etc. Some examples are as follows.

  • Peer-to-Peer (P2P) Networks. For any machine (vertex) to steadily benefit from a P2P network, they should be connected to at least a certain number (e.g., k) of other machines for data exchange. The edge k-core problem can figure out which connections (edges) shall be established so that many devices can successfully retrieve the resources from others and share the data with others [7]. Besides, in mobile P2P network, the edge k-core problem may also benefit the users getting resources from surrounding users instead of accessing the central cloud for low-latency connection [45].

  • Social Networks. In current online social platforms, there are various user groups based on different themes, e.g., for organizing a hiking or an online game. To improve the engagement of users in a group, it is critical to promote the social connections of group members. The edge k-core problem can be used to recommend key connections such that user engagement of a group is largely improved.

  • Online Game. In multiplayer games such as “Death Stranding”, users share resources based on social connections. Due to the importance of connection in the game experience, every player must establish connections with enough players, i.e., a threshold of k players. In this regard, the edge k-core can be used to find key connections and enhance the player experience.

Challenges

The main challenge of edge k-core problem stems from the huge number of candidate edges (non-adjacent vertex pairs), because the real-life networks are usually quite sparse. Although the k-core can be computed in O(m) time by recursively removing the vertices with degree less than k, a straightforward exact solution has to exhaustively compute the size of k-core for every possible candidate edge set with size b. It is cost-prohibitive even if b is very small. From the theoretical side [46], the edge k-core problem is proven to be NP-hard when k ≥ 3. The problem is even hard to have an approximate solution, as it cannot be approximated in polynomial time within a ratio of (1 − 1/e + 𝜖) for k ≥ 3 and any 𝜖 > 0, unless P = NP.

The state-of-the-art algorithm (named EKC) for the edge k-core problem is proposed in [46]. In each of the b iterations, EKC greedily finds a best pair of vertices such that their connection leads to the largest k-core for current iteration. The result quality (the size of k-core with added edges) of the greedy solution (EKC) is much better than other heuristics, as evaluated in [46]. Although many unpromising candidates are pruned by the optimizations in EKC , the remaining candidate edges are still too many to enable an efficient solution on large graphs. For a graph with about 2 million edges, EKC costs more than 1000 seconds on a commercial machine when k = 20 and b = 5, as reported in [46]. Consequently, it is crucial to carefully design a novel heuristic with much less time cost while the result quality is basically not sacrificed.

Our solution

As the number of vertices is much fewer than the number of edges even for sparse graphs, a vertex-oriented approach can be much more efficient than the greedy EKC . That is, we consider to find the results (the edges to be inserted) based on the idea of preserving outside vertices (through edge additions) in k-core . We first precisely locate the candidate vertices outside of k-core which are worthwhile to be preserved (i.e., anchored). A well-designed scoring function is proposed to select most promising vertices such that the k-core is enlarged by a few new edges. In order to further reduce the addition cost (the number of edges need to be added for vertex anchoring), we design a budget rebate strategy to adjust the added edges incident to different anchored vertices. The k-core computation with added edges in [46] is improved by using better data structure. We also introduce an optimization to reuse intermediate results. Moreover, the VEK algorithm runs in O(b ⋅ n ⋅ m) time, which is superior to the state-of-the-art method EKC [46]. As verified in our experiments, our proposed VEK is much faster than EKC while their result qualities are similar.

Contributions

Our main contributions in this paper are as follows:

  • We analyze the limitations of the state-of-the-art algorithm EKC for the edge k-core problem, and propose a novel vertex-oriented approach VEK to achieve better performance.

  • Several optimization techniques are proposed to improve the result quality of VEK and the efficiency, including a well-designed scoring function for vertex selection, a budget rebate strategy, a result-reusing method, etc.

  • Our experiments on 9 real datasets demonstrate our proposed VEK is faster than the state-of-the-art EKC by 1-3 orders of magnitude, and the result qualities of them (the sizes of k-core with b inserted edges) are similar.

Roadmap

The rest of the paper is organized as follows. Section 2 formally defines the problem, and introduces the existing solution. We then propose our VEK algorithm in Section 3. The experiments are conducted in Section 4. Section 5 surveys the related works. Finally, Section 6 concludes the paper.

2 Preliminaries

2.1 Problem definition

Let G = (V,E) be an undirected graph, where V and E are the set of vertices and edges, respectively. We denote n = |V |, m = |E| and assume m > n. Given a subgraph S, the neighbor set of u is denoted by N(u,S). The degree of u in S, i.e., |N(u,S)|, is denoted by deg(u,S). We may omit the target graph in notations when the context is clear, e.g., we use deg(u) instead of deg(u,G). Table 1 summarizes the notations in this paper.

Table 1 Summary of Notations
Full size table

The k-core of a graph is the maximal subgraph where every vertex has at least k neighbors in the subgraph. We use Ck(G) (or Ck) to denote the k-core of the original graph G.

Definition 1 (k-Core)

Given a graph G, a subgraph S is the k-core of G, denoted by Ck, if (i) deg(u,S) ≥ k for every vertex u ∈ S; and (ii) S is maximal, i.e., any supergraph \(S^{\prime }\supset S\) is not a k-core .

The k-core can be obtained by recursively removing every vertex with degree less than k in the graph, with a time complexity of O(m) [2]. The coreness of a vertex u, denoted by cn(u), is the largest k such that u is in the k-core , i.e., \(\max_{k:u\in C_{k}} \{k\}\). We use Hk to denote the k-shell of G, which is the set of vertices with coreness equals to k, i.e., Hk = {u∣cn(u) = k}.

If we add an edge between a pair of vertices which are not adjacent, the k-core of the graph may be enlarged, which is named the edge k-core . The added new edge is called an an anchor or anchor edge. The set of added edges, i.e., the anchor set, is denoted by EA. We use GA to denote G with EA added, i.e., GA = (V,E ∪ EA). In this paper, we say anchor, add, or insert an edge interchangeably, e.g., an inserted edge is also called an anchored edge. The edges, which may be inserted into the graph, are called candidate anchor edges.

Definition 2 (Edge k-Core)

Given a graph G = (V,E) and a set of anchor edges EA, the edge k-core , denoted by Ck(GA), is the k-core of GA.

After adding the anchor edges EA, some vertices not in Ck(G) may follow the anchor edges to join the edge k-core . We use the followers of EA to denote these vertices.

Definition 3 (Follower Set)

Given a graph G = (V,E) and a set of anchor edges EA, the follower set of EA, denoted by \(\mathcal {F}(E_{A})\), is the set of vertices that are in the edge k-core but not in the k-core , i.e., \(\mathcal {F}(E_{A})\) is the vertex set of Ck(GA) − Ck(G).

The number of followers reflects the importance of the corresponding anchor edges. Given a graph G and a set EA, the vertex set of Ck(GA) is same to the vertex set of \(C_{k}(G) \cup \mathcal {F}(E_{A})\).

Problem statement

Given a graph G, a degree constraint k and an edge budget b, the edge k-core problem aims to find a set EA of b edges in \({\binom {V}{2}}\setminus E\) such that the number of followers of EA is maximized, i.e., \(|\mathcal {F}(E_{A})|\) is maximized.

Problem hardness

Given a set of anchor edges EA, the edge k-core Ck(GA) can be obtained in O(m) time by computing the k-core of GA. However, it is challenging to find the optimal EA, due to the large volume of candidate edges. Chitnis and Talmon [7] show that the edge k-core problem is polynomial-time solvable for k ≤ 2 and W[1]-hard. They also propose an algorithm for graphs with bounded tree-width. In [46], the problem is proved to be NP-hard for k ≥ 3. Besides, the problem cannot be approximated in polynomial time within a ratio of (1 − 1/e + 𝜖) for k ≥ 3 and any 𝜖 > 0, unless P = NP.

2.2 EKC algorithm: state-of-the-art

EKC [46] is the state-of-the-art approach for the edge k-core problem on general graphs, and Algorithm 1 outlines its pseudo-code. EA is the result set of anchor edges, while Ecand is a set of candidate anchor edges. We use \(\mathcal {F}(e,G_{A})\) to denote the followers of e, after adding it to EA.

Algorithm 1 iteratively finds the anchor edge with the most followers until EA contains b edges. Line 1–1 selects a new anchor edge in each round. Specifically, we first compute the candidate edges Ecand (Line 1), then we find the followers of each candidate edge (Line 1) while pruning the candidate edge set (Line 1), and finally insert into EA the edge e∗ that incurs the most followers (Line 1). The time complexity of EKC is O(b ⋅ n2 ⋅ m) and it cannot scale to large graphs.

figure a

The techniques in EKC are summarized as follows. GetCandidates(GA, k) returns the candidate edges Ecand base on the (k − 1)-shell structure and a onion-layer based pruning, to reduce the size of Ecand. FindFollower(e,GA) returns the followers incurred by adding e to EA, using an onion-layer based follower computation optimization proposed in [42]. PruneCandidates(Ecand) prunes the candidate edge set according to the followers of e. Throughout the iterations, the algorithm reuses the intermediate results of connected components.

3 Vertex-oriented solution

In this section, we present our proposed vertex-oriented algorithm VEK . Section 3.1 introduces our basic idea of VEK . Section 3.2 prunes the search space of candidate pivots. Section 3.3 presents a scoring function that can choose a promising pivot vertex, and Section 3.4 enhances this scoring function by two edge budget saving strategies. Finally, Section 3.5 combines all the techniques of VEK together.

3.1 Basic ideas

Despite adopting several optimization techniques, EKC runs in O(b ⋅ n2 ⋅ m) time, which cannot scale to large graphs. The time cost comes from an enormous set of candidate edges whose worst-case size is n2. Motivated by this, we develop a vertex-oriented heuristic that considers the potential of each vertex rather than that of each edge. We evaluate the potential of a vertex by anchor score (Section 3.3), which aims to introduce more vertices into the k-core at a lower cost. In each iteration, we select a pivot with the highest anchor score from the pruned search space (Section 3.2), and find the anchor edges that can bring the pivot into the k-core . These anchor edges are returned as an approximation solution of the edge k-core problem. Section 3.4 further designs two strategies that optimize the quality of anchor score.

Definition 4 (Pivot)

Given a graph G = (V,E) and a set of anchor edges EA, the pivot vertex is the vertex with highest anchor score in \(G^{\prime }=(V, E+E_{A})\).

3.2 Candidate pivot pruning

By connecting the anchor edges between a pivot and the k-core , we add the pivot into the edge k-core along with its followers. To select a pivot that brings in followers and enlarges the edge k-core , we derive the necessary conditions for a vertex to be the follower of a pivot.

In the following theorem, u is a pivot and EA is an anchor edge set that (i) bridges u and the k-core EA = {(v,u)∣v ∈ Ck}, and (ii) brings u into the edge k-core u ∈ Ck(GA). We have that u’s follower set \(\mathcal {F}(u)=C_{k}(G_{A})\setminus C_{k}\) is contained in the (k − 1)-shell .

Theorem 1

Given a graph G, a vertex u, and a set of anchor edges EA = {(v,u)∣v ∈ Ck} such that u ∈ Ck(GA), the followers of u are all from the (k − 1)-shell , i.e., \(\mathcal {F}(u)\subseteq H_{k-1}\).

Proof

Proof by contradiction. Assume there is a follower v of u that is not in the (k − 1)-shell . We have cn(v) < k − 1, because a follower must have coreness less than k and cn(v)≠k − 1 (v∉Hk− 1).

According to the definition of k-core , for each x ∈ Ck(GA), we have deg(x,Ck(GA)) ≥ k.

After removing u and EA from Ck(GA), we have deg(x,Ck(GA) ∖ u) ≥ k − 1 for each vertex x ∈ Ck(GA) ∖ u, because all edges in EA are incident to u, and the degree of x decreases by at most 1. So, Ck(GA) ∖ u is a (k − 1)-core according to the definition. We have cn(v) ≥ k − 1 since v ∈ Ck(GA) ∖ u, which contradicts cn(v) < k − 1. □

Let u ∈ V ∖ Ck be a pivot we select. Theorem 1 states that u can bring in new followers only if its neighbors are from the (k − 1)-shell . Thus, we select the candidate pivots from the neighbors of the (k − 1)-shell , namely N(Hk− 1).

Assume we have already selected EA as anchor edges, the theorem can also be applied. The candidate pivot set would be N(Hk− 1(GA)), by regarding GA as the original graph in Theorem 1.

3.3 Anchor score evaluation

In this section, we introduce anchor score that evaluates the potential of a vertex to be a pivot. Intuitively, we aim to add more followers using as few anchor edges as possible. The anchor score of a vertex u is proportional to the number of u′s followers \(|\mathcal {F}(u)|\) (the vertices added to the edge k-core) and in inverse proportion to the anchor cost of u, i.e., how many anchor edges we must use.

The anchor cost of a vertex u measures how many anchor edges are needed to bring u into the edge k-core . The following theorem not only gives the minimum value for the anchor cost of a pivot u, but also ensures there is always a set of anchor edges satisfying this lower bound.

Theorem 2

Given a graph G, a vertex u, for a set of anchor edges EA = {(v,u)∣v ∈ Ck} such that u ∈ Ck(GA), the size of EA is at least \(\varphi (u)=k - |N(u)\cap C_{k}| - |N(u)\cap \mathcal {F}(u))|\) and there is always a EA satisfying |EA| = φ(u).

Proof

Assume we select u as a pivot. According to the definition of follower , the followers of u will not leave the edge k-core unless u leaves. Initially, u has |N(u) ∩ Ck| edges to the k-core . Then u′s followers contribute \(|N(u) \cap \mathcal {F}(u, G)|\) degrees to u. If we anchor \(k-|N(u)\cap C_{k}|-|N(u) \cap \mathcal {F}(u, G)|\) more edges between the k-core and u, we have deg(u,Ck(GA)) = k. We can always construct such an EA.□

Theorem 2 shows the cost (the number of required anchor edges) of adding a pivot into the edge k-core . On the other hand, the number of followers measures the gains of adding a pivot into the edge k-core . The anchor score ϕ(u) is defined as the number of followers divided by the anchor cost.

$$ \phi(u) = \frac{|\mathcal{F}(u)|}{\varphi(u)}=\frac{|\mathcal{F}(u)|}{k - |N(u)\cap C_{k}| - |N(u)\cap \mathcal{F}(u)|} $$

A pivot with a higher anchor score can bring in more edges at a lower cost. Similar to Theorem 1, Theorem 2 can also applied to GA with EA added, by considering GA as the original graph.

$$ \begin{array}{ll} \phi(u,G_{A}) = \frac{|\mathcal{F}(u,G_{A})|}{\varphi(u,G_{A})}=\frac{|\mathcal{F}(u,G_{A})|}{k - |N(u)\cap C_{k}(G_{A})| - |N(u)\cap \mathcal{F}(u,G_{A})|} \end{array} $$
(1)

Compute \(\mathcal {F}(u)\): the followers of a vertex

We adopt the onion-layer based follower computation in [42], which explores candidate followers layer by layer, with a heap to maintain the traversal order. The heap can be replaced by multiple queues. When generating a candidate follower, instead of inserting it into a heap keyed by the layer number, we push it into the queue of the corresponding layer, so that the maintenance cost decreases from \(O(\log n)\) to O(1).

Compute anchor cost φ(u)

We conduct a core decomposition [16] before each iteration, so that |N(u) ∩ Ck(GA)| for any vertex u can be pre-computed in O(m) time. We also maintain a hash table that answers if a vertex pair is adjacent. After that, \(|N(u)\cap \mathcal {F}(u,G_{A}))|\) for a given u can be answered in \(O(|\mathcal {F}(u,G_{A})|)\) time, by traversing the followers of u and check if it is a neighbor of u.

3.4 Optimized anchor score

In Section 3.3, we select a pivot u with the highest anchor score in each iteration. The scoring function can be further optimized by looking back. Specifically, we can replace or delete some selected anchor edges, such that we use fewer anchor edges to retain the vertices in the edge k-core . This saves the edge budget for further pivot selections.

Example 2 (Look-Back Ability)

Figure 2 can illustrate the need for look-back ability. In this example, we seek to maximize the size of the edge 5-core. The edges between the 5-core and the outside are highlighted in bold. Using the anchor score in Section 3.3, we first select v1 using 2 anchor edges, then select v2 with two edge budgets, which results in a follower v3. The total edge budget is 4. However, we can anchor (v1, v3) and an edge from v3 to the 5-core, to bring all three vertices into the 5-core. By looking back and removing the redundant edges, we can save 2 edge budgets in this example.

Figure 2
figure 2

Maximize the Size of the Edge 5-Core. The edges between the 5-core and {v1, v2, v3} are bold

Full size image

In the following, we discuss two strategies that optimize the effectiveness of anchor score. The optimized anchor score uses (i) Budget Return: deletes redundant anchor edges and return its budget; (ii) Edge Reconnection: reconnects anchor edges to save budget without losing the vertices in the edge k-core.

Budget return (Line 2-2)

Assume we bring v into the k-core using anchor edges EA, and then we want to bring in another pivot u. The followers of u are \(\mathcal {F}(u, G_{A})\). Let \(C=E_{A}\cap \{(v, v^{\prime })\mid v^{\prime }\in C_{k}\}\) and \(D= N(v)\cap \mathcal {F}(u, G_{A})\).

Here, C is a set of selected anchor edges between the original k-core and v, while D is the set of u’s followers that are adjacent to v. The followers of u can add |D| degrees to v. On the other hand, the anchor edges in C, which are previously used to increase the degree of v, can be removed due to u’s followers. To sum up, we can safely delete \(\min \limits (|C|,|D|)\) edges in C from the anchor edge set.

Example 3 (Budget Return)

In Figure 2, assume we first (Step.A) anchor pivot v1 into the 5-core with 2 anchor edges, then (Step.B) bring pivot v2 into the 5-core using two anchor edges, and result in a follower v3. The degree of v1 increase by 1 due to the (v1, v3), so we can return one edge budge that is used to increse the degree of v1 in Step.A, while all vertices still exist in the k-core.

Edge reconnection (Line 2-2)

Suppose a pivot v has been inserted into the k-core using anchor edges EA, and then another pivot u is to be selected. Let \(C= E_{A}\cap \{(v, v^{\prime })\mid v^{\prime }\in C_{k}\}\), which is the anchor edges between the original k-core and v. The new pivot u needs φ(u) additional degrees to engage in the edge k-core . Connecting u to the k-core can increase u′s degree by one. However, connecting (u,v) can contribute to the degree of both v and u, so that one anchor edge in C can be removed without affecting the edge k-core .

Example 4 (Edge Reconnection)

In Figure 2, assume v1 has been inserted in the edge 5-core, and v1 and v3 is not adjacent. When selecting v3 as a pivot, we can connect (v1, v3) and remove an anchor edge from v1 to k-core (no edge budget is used). Then, rather than two edges, we only need to add one edge from the 5-core to v3 to insert v3 into the edge 5-core.

Algorithm 2 illustrates how to compute the optimized anchor score for a given vertex u. VP is the set of selected pivot vertices, EA is the set of anchor edges we select. We use Enext to maintain the set of anchor edges, and initialize it with EA. Cost is the anchor cost of u, i.e., how many edges we need to connect between u and the original k-core , while Score is the anchor score u.

figure b

The initial anchor cost of u is computed in Line 2. Line 2–2 apply the budget return strategy discribed above, where we compute C,D and remove \(\min \limits (|C|,|D|)\) redundant edges in C from Enext. Line 2-2 conduct the edge reconnection strategy. For each selected pivot v that is not adjacent to u, we use (u,v) to replace an anchor edge e ∈ C. Line 2 decreases Cost by (|EA|−|Enext|) the number of anchor edges we removed from EA. In Line 2, Cost is the number of anchor edges to connect between the original k-core and u, so Line 2 divides the number of followers by the cost to get the optimized anchor score. In case Cost ≤ 0, Line 2 sets Score to \(\infty \), because the edge budget would not decrease after selecting u as a pivot, i.e., we should choose u anyway. Finally, Line 2 returns the results.

3.5 VEK Algorithm

Algorithm 3 organizes the techniques in the previous sections into our proposed VEK algorithm, which implements the ideas in Section 3.1. The algorithm keeps picking a pivot vertex from the pruned candidates (Section 3.2) whose optimized anchor score (Section 3.4) is the highest, until the edge budget is used up.

figure c

VP is the set of pivot vertices we have selected, EA is the set of anchor edges attached to the pivots. The arrays in Line 3 exactly match the return value of Algorithm 2, that is, Score[u] stores the optimized anchor score of u, and Enext[u] stores the set of anchor edges after selecting u as a pivot.

Line 3 initializes the pivot vertex set VP and the anchor edge set EA. Line 3-3 selects a pivot u∗ and updates EA using the selected pivot, until the number of anchor edges |EA| reaches the edge budget b. Line 3–3 chooses from the pruned candidate set (Section 3.2) a pivot u∗ such that (i) the optimized anchor score Score[u∗] (Section 3.4) is the highest, and (ii) after choosing u∗, the number of anchor edges |Enext[u∗]| are within the budget b. Line 3 terminates the loop if there is no valid pivot to select. Otherwise, Line 3 adds u∗ to the pivot set VP, and Line 3 updates EA to Enext which is the set of anchor edges after selecting u∗ as a pivot. Line 3 returns the result anchor edges EA.

Reuse intermediate results

The intermediate results of Algorithm 3 can be reused. In each round of Line 3–3, only one vertex u∗ is selected as a pivot. For a vertex v that is not connected to u∗ in the original graph G, the selected pivot u∗ will not affect v, so we can reuse the optimized anchor score and the follower set of v in the next round. By pre-computing the connectivity of the graph, we can efficiently skip those vertices and reuse the results.

Algorithm complexity

We analyze the time and space complexity of VEK . VEK iteratively introduces a most promising vertex into k-core in each round until the budget is exhausted. Although two strategies Budget Return and Edge Reconnection are adopted to maximize the effectiveness of the budget, the vertex selected by the algorithm has to be linked to at least one addition edge finally. Considering that the budget is b, VEK runs at most 2b rounds. In one iteration, VEK evaluates the advanced anchor score for each candidate pivot. VEK takes O(m) time at most for the evaluation of one candidate pivot. The size of candidate pivot set |N(Hk− 1(GA))|≤ n. Then VEK can update the graph in O(1) time. As a result, the overall time complexity is O(b ⋅ n ⋅ m). It costs O(m) to store the graph and O(n) space to maintain the candidate pivot. Anchor score and corresponding anchor edge set also takes O(n) space to keep in record. Thus, the space complexity of VEK is O(m).

4 Experiment evaluation

4.1 Experimental setting

Datasets

Flickr dataset is from Network RepositoryFootnote 1, and the others are from SNAPFootnote 2. Table 2 shows the statistics of the datasets deployed in the experiments.

Table 2 Statistics of datasets
Full size table

Algorithms.

Our proposed algorithm VEK is described in Section 3.5. We compare VEK with existing solutions including EKC and other heuristics as introduced in [46]. The onion layers \({\mathscr{L}}\) in [42] is an auxiliary structure to facilitate the follower computation and candidate pruning for EKC. Table 3 shows the summary of algorithms.

Table 3 Summary of algorithms
Full size table

Parameters

All programs are implemented in C++. All experiments are performed on Intel Xeon 2.20GHz CPU and Linux system. We vary the parameters k and b. The effectiveness is evaluated by the number of the followers produced. The efficiency is measured by running time.

4.2 Effectiveness

Figure 3 compares the number of followers w.r.t. b anchor edges produced by all the algorithms in Table 3, when k = 10 and b = 20. In Figure 3, Layer or Degree fail to get any followers in several datasets, because a vertex in higher onion layer or with a larger degree does not necessarily have a follower . For Rand, we report the average number of followers for 200 independent tests. Given the inputs of k and b, the resulting number of followers is fixed for any of the other four approaches. If we randomly anchor (insert) edges in the whole graph, it is common to get no follower after 20 random insertions. It is because the candidate edges with more than 1 follower are quite rare in the graph, while the number of candidate edges is large. Thus, in Rand, we only choose the edges from the set \(E^{\prime }\) where each edge has at least one follower if inserted. Note that the computation of \(E^{\prime }\) costs more time than VEK , as it requires to compute the follower set of each candidate vertex pair (candidate anchor edge).

Figure 3
figure 3

Effectiveness of different heuristics, k = 10, b = 20

Full size image

Although the majority of the candidate edges does not have any followers , the state-of-the-art EKC produces many followers in the experiments, which shows the greedy heuristic is effective. For our proposed VEK , with the help of promising pivot vertices, we can easily identify a small part of candidate edges with lots of followers . Thus, though VEK is much faster than EKC as shown in latter experimental results, the number of followers produced by VEK is similar to that of EKC . As reported in Figure 3, the margins between the results of VEK and EKC are very small. In some cases, the followers from VEK can be even more than that from EKC , e.g., for Enron and Twitter. It is because VEK considers the addition of edges in a batch manner based on the pivot vertices. Figure 4 shows the number of followers for other settings by varying the value of k or b, the results are similar to that in Figure 3. As EKC focuses on finding a best anchor edge which is always from (k-1)-core in one iteration, there may be no single anchor edge with any followers . Thus, the performance of EKC may degenerate in some settings, e.g., k = 25 and b = 10 on Twitter. However, as our VEK aims to preserve a good pivot vertex which adds a batch of edges at the same time, the performance of VEK is more robust than EKC . Besides, since VEK is always faster than EKC by at least 1 order of magnitude, it is often worthwhile to use VEK instead of EKC in real applications.

Figure 4
figure 4

EKC vs VEK on the number of follower

Full size image

4.3 Efficiency

Figure 5 reports the time cost of EKC and VEK on all the datasets with k = 10 and b = 20. If the running time exceeds 48 hours, we set it to timeout. Figure 5 shows that the time cost of VEK is smaller than EKC by 3 orders of magnitude on most datasets. Our VEK can return in 100 seconds on most settings while the time cost of EKC is larger than 10000 seconds on many settings. We observe that the runtime among different datasets is largely influenced by the size of the dataset, the average degree, and the onion layer structures [42], while none of the characteristics is deterministic on time cost. The outperformance of VEK is more obvious when the dataset is larger, because the number of candidate edges in EKC are much larger than candidate pivots used in VEK on larger real-life datasets.

Figure 5
figure 5

Running time on different datasets

Full size image

Figure 6 shows the impact of different k and b on the two algorithms. Figure 6(a) reports that the runtime decreases with a larger input of k. This is because the number of candidate edges becomes fewer as k increases. When k is relatively large, there is no anchor in one iteration with any follower for EKC , then the set of candidate edges for EKC is empty. In this case, the margin between EKC and VEK becomes smaller because EKC is basically a random method. Figure 6(b) reports that the runtime is basically proportional to the input of b for both EKC and VEK . The outperformance of VEK against EKC is clear on every setting. As the result quality (the number of produced followers) of VEK is similar to EKC , our proposed VEK becomes the state-of-the-art solution for the edge k-core problem.

Figure 6
figure 6

Effect of k and b

Full size image

5 Related work

The concept of k-core and the computing algorithm are first introduced in [28, 31]. Core decomposition finds the k-core for any k value, which costs O(m) time by recursively removing each vertex with degree less than k [2]. The computation of k-core is also studied in other environments, including multi-core platform [11, 14], distributed environment [29], and I/O efficient configuration [38] where the space complexity is bounded by O(n). [23] studies the core decomposition in multilayer graphs, and an in-depth discussion of core decomposition is conducted by [25]. The hierarchical core maintenance on dynamic graphs is studied by [21]. The best k in a k-core decomposition can be found by [8].

The mode of k-core is widely applied in different areas, e.g., community discovery [13, 36, 37], anomaly detection [32], influential spreader identification [12, 26], and user engagement study [3, 9, 43]. The variants of k-core combine the degree constraint with auxiliary informations, such as influential community [20], skyline community [19], and spatial-aware community [13]. Besides k-core , many other models detect cohesive subgraphs using different structural property, e.g., k-truss [10, 35], clique [4, 6], quasi-clique [30], and k-ecc [5].

As the computation of k-core precisely captures the decaying dynamic of a network, the size of k-core is often used to evaluate the structural stability of a network [3, 27, 44]. To improve the stability of a network, some models are proposed to maximize the k-core through different operations, e.g., the anchored k-core by enhancing vertices [3], the collapsed k-core by defending key vertices [43], and the edge k-core by adding critical edges [7]. Edge addition methods are also applied in other topics, e.g., modifying graph diameter [33], enlarging graph bandwidth [18] and anonymizing a set of vertices [15]. As most of the stability problems are NP-hard, different heuristics are evaluated in existing studies and the greedy solution is shown to be effective in many datasets, including the EKC algorithm [46] for the edge k-core problem. However, due to the huge number of candidates, EKC still cannot efficiently handle large graphs. Thus, a faster vertex-oriented approach is proposed in this paper.

6 Conclusion

In this paper, we propose a novel vertex-oriented solution for the edge k-core problem : given a graph G, an integer k, and a budget b, it aims to connect b non-adjacent vertex pairs s.t. the number of vertices in the k-core is maximized. Due to the huge number of candidate vertex pairs to connect, the state-of-the-art algorithm EKC is not efficient enough for real-life large graphs. Our proposed VEK algorithm iteratively chooses a pivot vertex by a scoring function, and carefully adds the edges to the pivot s.t. it is preserved in the k-core . We design a budegt return strategy and an edge re-connection method to optimize the scoring function and ensure the quality of our pivot selection. Effective optimization techniques are proposed to prune unpromising pivots and reuse the intermediate results. Extensive experiments demonstrate that VEK outperforms EKC in efficiency by 1-3 orders of magnitude while the result is still of high quality.