1 Introduction

Complex networks are often modeled as graphs to process the entities/users and their relations. The structural stability of a graph is critical for maintaining the functionality of the graph, e.g, the running of a social network. In the dynamic of a network, some users may leave the network due to particular defects and/or attacks (e.g., user attraction strategies) from the competitor networks. The leave of key users will affect the engagement of their neighbors and the others s.t. the whole network becomes unstable. For instance, Friendster was a popular social network with more than 115 million users while it is collapsed due to the contagious user leave [20, 38].

As the departure of users may greatly break overall user engagement, i.e., the network stability, it is critical to discover these key users and conduct wise actions accordingly. We can motivate the key users to continuously engage in the network by proper actions, e.g., providing incentives for user engagement. The model of k-core is often utilized in the study of network stability for its effectiveness, e.g., [36]. It is defined as a maximal subgraph where each vertex has at least k neighbors in the subgraph [34, 37]. As the size of k-core can be used to estimate the (structural) stability of a network, the collapsed k-core problem is proposed to find b vertices (users) s.t. the deletion of these vertices leads to the smallest k-core. Nevertheless, this problem only extracts the key users from a partial group of users, i.e., the users related to the k-core with the input k. The result of the problem becomes different when a different k is given, and the best k is hard to be determined.

To address the above defects, we propose and study the collapsed coreness problem: finding b vertices s.t. the deletion of these vertices leads to the largest coreness loss (the total decrease of coreness from every vertex. The coreness of a vertex is validated as the “best practice” for measuring the engagement of the vertex [33]. Clearly, there is no input of k required for the collapsed coreness problem, and the only input is the budget b for the number of collapsers. The collapsed coreness problem essentially considers the k-core of every input k to find the key users, while its result is not a trivial aggregation. Since the collapsed coreness problem considers the coreness dynamic of each vertex, it is more promising in finding the key users regarding the stability of a network. The following example illustrates the difference between the collapsed k-core and collapsed coreness problems.

Example 1

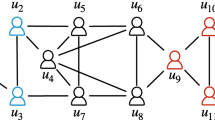
Figure 1 shows a graph G with 12 vertices and their connections. The coreness of each vertex is marked near the vertex, e.g., the coreness of v4 is 2. The k-core of G is induced by all the vertices with coreness of at least k, e.g., the 2-core is induced by v2, v3 and v4.

Fig. 1
figure 1

A Toy Graph (The coreness of each vertex is marked near the vertex)

Full size image

Table 1 shows the results of the collapsed k-core problem (CKP) and the collapsed coreness problem (CCP) when b = 1. If k = 2, the result of CKP may be v3. The deletion of v3 will decrease the coreness of v2 which is named the follower of v3. If k = 3, the result of CKP may be v6 and the followers are v5,v7 and v8. As k is not an input for CCP, its result is just v5 and the followers are v2,v6,v7 and v8. It is more important to protect v5 compared with v3 or v6, because the leave of v5 may affect more users.

Table 1 Collapsed k-core v.s. collapsed coreness in Figure 1
Full size table

From theoretical perspective, we prove the collapsed coreness problem is NP-hard and hard to approximate. It is essentially more challenging than the collapsed k-core problem, because there are more candidates and the computation of coreness loss is more costly (core decomposition v.s. k-core computation). We first analyze the problem in the case of one collapsed vertex, and prove several effective theorems. The lower and upper bounds are proposed to fast estimate the coreness loss of deleting a vertex, based on the core forest structure. An efficient way to compute the exact coreness loss for a collapser is introduced. With the integration of all the proposed techniques, a novel greedy algorithm is proposed to efficiently address the collapsed coreness problem. The algorithm is adapted to fast find the collapsers within a given time limit.

Contributions

Our major contributions in this paper are as follows:

  • Considering the coreness loss of each vertex, we propose the collapsed coreness problem to support the structural stability of a network.

  • We prove the collapsed coreness problem is NP-hard, and APX-hard unless P=NP. The function of coreness loss is shown to be monotone but not submodular.

  • An efficient greedy algorithm GCC is proposed with novel pruning techniques based on the theorems of one collapsed vertex, the upper/lower bounds of coreness loss, and the efficient computation of coreness loss.

  • Our experiments on 12 real datasets show that the greedy GCC is more effective than other heuristics, and GCC outperforms the baseline algorithm on runtime by up to 3 orders of magnitude.

Roadmap

The rest of the paper is organized as follows. Section 2 formally defines the problem. Section 3 analyzes the hardness of the problem. Section 4 proposes the techniques and the GCC algorithm. The experiments are conducted in Section 5. More related works are surveyed in Section 6. Finally, Section 7 concludes the paper.

2 Preliminaries

We consider an undirected and unweighted simple graph G = (V,E), with n = |V | vertices and m = |E| edges (assume m > n). Given a vertex v in a subgraph S of G, N(v,S) denotes the neighbor set of v in S, i.e., N(v,S) = {u∣(u,v) ∈ E(S)}. The degree of v in subgraph S, i.e., |N(v,S)|, is denoted by d(v,S). Table 2 summarizes the notations.

Table 2 Summary of Notations (We may omit the target graph in notations when the context is clear, e.g., we may abbreviate N(v,S) to N(v))
Full size table

The model of k-core [34, 37] is defined as follows.

Definition 1 (k-core C k(⋅))

Given a graph G and an integer k, a subgraph S is a k-core of G, if (i) each vertex v ∈ S has at least k neighbors in S, i.e., d(v,S) ≥ k; (ii) S is connected; and (iii) S is maximal, i.e., any supergraph of S is not a k-core except S itself.

The computation of k-core is to recursively delete each vertex with degree less than k in the graph. According to the definition of k-core, every vertex has a coreness value.

Definition 2 (coreness c(⋅))

Given a graph G, the coreness of a vertex u ∈ V (G), denoted by c(u,G), is the largest k such that Ck(G) contains u, i.e., \(c(u,G)=\arg \max \limits _{k} u\in C_{k}(G)\).

A graph can be decomposed in a hierarchy where the vertices are distinguished by their coreness values.

Definition 3 (core decomposition)

Given a graph G, core decomposition of G is to compute the coreness of every vertex in V (G).

Core decomposition can be computed in O(m) time by recursively removing each vertex with the smallest degree in the graph, and update the degrees of its neighbors by bin sort [4].

Though the coreness of a user (vertex) in a network well estimates the engagement of the user [28, 33], the users with any coreness values may leave the network by outside forces, e.g, the user attraction strategy of a competing network. In this paper, such a leaved user (vertex) is named as a collapser, and we say they are collapsed or we collapse them.

Definition 4 (collapsers D)

Given a graph G, the set D of collapsers (i.e., collapsed vertices), are removed from the G regardless of their coreness values.

The collapsed (removed) vertices may change the corenesses of other vertices in G, i.e., the coreness values of some vertices will decrease. These vertices are called the followers of the collapsers in this paper. For each follower v, the coreness of v is changed (certainly decreased) by deleting D in G.

Definition 5 (followers F(⋅))

Given a graph G and the collapser set D, the follower set of D in G is denoted by F(D,G). As the followers do not contain the collapsers, we have F(D,G) = {v∣v ∈ V (G − D) ∧ c(v,G)≠c(v,G −{D + E(D)}).

We use cD(u,G) (resp. cx(u,G)) to denote the coreness of u in G with D collapsed (resp. the vertex x collapsed). The loss of coreness by the collapsers is the sum of coreness decrease from each follower.

Definition 6 (coreness loss l(⋅))

Given a graph G and the collapser set D, the coreness loss of G regarding D, denoted by l(D,G), is the total decrease of coreness for every vertex in V (G) ∖ D, i.e., \(l(D,G)={\sum }_{v\in V(G) \setminus D}(c(v)-c^{D}(v))\).

For a graph with collapsers, the computation of core decomposition is to first delete the collapsers and then recursively remove each vertex with the smallest degree in the graph. The time complexity is still O(m), because the only difference to core decomposition without collapsers is that we delete the collapsers first. The pseudo-code is given in Algorithm 1.

figure a

As the coreness loss is promising for evaluating the leave effect of the key users (e.g., the collapsers), we propose and study the collapsed coreness problem to find these important users according to the coreness loss.

Problem definition

Given a graph G and a budget b, the collapsed coreness problem aims to find a set D of b vertices in G such that the coreness loss regarding D is maximized, i.e., l(D,G) is maximized.

3 Problem analysis

In this section, we analyze the hardness of the collapsed coreness problem.

Theorem 1

Given a graph G, the collapsed coreness problem is NP-hard.

Proof

We reduce the maximum coverage (MC) problem, which is NP-hard, to the collapsed coreness problem. Given an integer b and a collection of sets where each set contains some elements, the MC problem is to find at most b sets to cover the largest number of elements.

Consider an arbitrary instance H of MC with c sets T1,⋯,Tc and d elements {e1,⋯,ed} = ∪1≤i≤cTi, we construct a corresponding instance of the collapsed coreness problem on a graph G. W.l.o.g., we assume b < c < d, Figure 2 shows an example of the construction from 3 sets and 4 elements.

Fig. 2
figure 2

Construction example for hardness proofs

Full size image

The graph G contains three parts: W, P, and some 4-cliques. The part W contains c cliques of size 4, i.e., W = ∪1≤i≤cWi where each Wi corresponds to Ti of instance H. The part P contains d cliques of size 3, i.e., P = ∪1≤i≤dPi where each Pi corresponds to ei of instance H.

For each set Ti(1 ≤ i ≤ c) and each elements ej(1 ≤ j ≤ d),if ej ∈ Ti, we add an edge \((w_{i},{p_{i}^{j}})\) in G where wi ∈ Wi and \({p_{i}^{j}}\in P_{j}\). Then, we attach a 4-clique for each vertex with degree 2 in current G. The construction of G is completed.

The degree of each vertex in G is at least 3. Recall that core decomposition iteratively deletes the vertices with degree less than k and assigns them the coreness of k − 1 in current iteration, from k = 1,2,⋯ to \(k=k_{\max \limits }\). Thus, the coreness of each vertex in G is 3.

For each wi ∈ W, if wi is collapsed (deleted), the 4-clique containing wi becomes a 3-clique, and the coreness of each vertex in Pj decreases by 1 if ej ∈ Ti. Similarly, the coreness loss of collapsing any vertex v ∈ Wi ∖{wi} is same as the coreness loss of collapsing wi. Note that it is not worthwhile to collapse more than 1 vertex in the 4-clique, because the coreness loss is less than collapsing the vertices in different 4-cliques. Besides, the coreness loss of collapsing the vertices in the 4-cliques attached to P is less than collapsing the same number of vertices in W where each 4-clique has one collapsed vertex.

Consequently, the optimal collapser set D for the collapsed coreness problem corresponds to the optimal collection I for the MC problem, where each vertex wi ∈ D corresponds to the set Ti ∈ I. Since the MC problem is NP-hard, we have the collapsed coreness problem is NP-hard. □

Then, we prove that the collapsed coreness problem is hard to approximate.

Theorem 2

Given a graph G, the collapsed coreness problem is APX-hard, unless P=NP.

Proof

We use the reduction from the MC problem same to the proof of Theorem 1. For any 𝜖 > 0, the MC problem cannot be approximated in polynomial time within a ratio of (1 − 1/e + 𝜖), unless P=NP. If there is a solution with γ-approximation on the coreness loss for the collapsed coreness problem, there will be a λ-approximate solution on optimal element number for the MC problem. Thus, there is no PTAS for the collapsed coreness problem and it is APX-hard unless P=NP. □

Besides, the function of coreness loss is monotone but not submodular.

Theorem 3

The coreness loss function l(⋅) is monotone but not submodular.

Proof

As vertex deletion will not increase the coreness of any vertex, l(⋅) is monotone. For two arbitrary collapser sets A and B, if l(⋅) is submodular, it must hold that l(A) + l(B) ≥ l(A ∪ B) + l(A ∩ B). We consider a graph G where the vertex set V = ∪1≤i≤ 5vi, as shown in Figure 3. Suppose A = {v1} and B={v2}, we have l(A ∪ B) = 3, l(A ∩ B) = l(A) = l(B) = 0, and l(A) + l(B) = 0 < l(A ∪ B) + l(A ∩ B) = 3. □

Fig. 3
figure 3

Example for non-submodularity

Full size image

4 Our approach

As the collapsed coreness problem is NP-hard, we aim to design an effective heuristic algorithm that can return high-quality results efficiently. Although it is not promising to have an approximation guarantee on the heuristics, we find that the computation cost is relatively restricted when the target is to find one best collapser. Besides, our preliminary experiments find that the result quality of a greedy heuristic is close to that of the optimal solution.

In this section, we first present the theoretical properties for one collapsed vertex, and the bounds to restrict the computation cost. Then, we introduce the algorithm for computing the followers, and the efficient GCC algorithm to greedily find promising collapsers.

4.1 Theorems for one collapser

For the deletion of one vertex, the coreness change of the affected vertices is limited as shown by the following theorem.

Theorem 4

If a vertex x is collapsed (i.e., deleted) in G, any vertex u ∈ V (G) ∖{x} may reduce its coreness by at most 1.

Proof

Suppose there is a vertex u ∈ V (G) ∖{x} with coreness decreasing from k to \(k^{\prime }\) after deleting x and \(k > k^{\prime }+1\). Let M be the k-core before x is deleted, we have u ∈ M and d(v,M) ≥ k for every vertex v ∈ M. If we delete x and its corresponding edges from M, we have d(v,M ∖{x ∪ E(x)}) ≥ k − 1 for every vertex v ∈ M due to at most one edge is removed for each vertex v ∈ M. Thus, \(M \setminus \{x\cup E(x)\} \subseteq C_{k-1}(G)\). As u ∈ M and u≠x, we have u ∈ Ck− 1(G) and thus \(k^{\prime }\ge k-1\) which causes a contradiction. □

According to the theorem, the coreness of each follower of x decreases by exactly 1 for collapsing (only) x. Thus, for the collapse of one vertex, the number of followers is equal to the coreness loss.

Then, we show that the followers of a collapser always have a smaller coreness than the coreness of the collapser.

Theorem 5

If a vertex x is collapsed in G and the vertex u is a follower of vertex x (i.e., u ∈ F(x,G)), we have c(u) ≤ c(x).

Proof

For any integer k > c(x), the k-core of G is same to the k-core of G −{x ∪ E(x)} according to the computation of k-core, i.e., recursively deleting each vertex with degree less than k. Thus, any vertex v with c(v) > c(x) is not a follower of x. □

Note that every vertex u with the same coreness to x may have its coreness decreased by collapsing x, despite the deletion sequence of u and x in core decomposition.

For the collapse of one vertex, to find out the effective candidate collapsers, we define the pivot set as follows.

Definition 7 (pivot set PS)

For each k-core, the pivots are the vertices with degree equal to coreness in the k-core. The pivot set of the graph G, denoted by PS, is the union of all the pivots for each k-core and each integer k, i.e., PS = {u∣d(u,Cc(u)(G)) = c(u,G) ∧ u ∈ V (G)}.

The coreness of a pivot u is relatively unstable because it will decrease if any neighbor of u in c(u)-core is collapsed. Thus, we can find the set of candidate collapsers based on the pivot set for the collapse of one vertex.

Theorem 6

Given a graph G, if a vertex x is collapsed and it has at least one followers, x is from X where X = {u∣u ∈ N(v,G) ∧ v ∈ PS ∧ c(u) ≥ c(v)}; that is |F(x,G)| > 0 implies x ∈ X.

Proof

For any vertex u ∈ V (G) ∖ X and any vertex v ∈ N(u,G), we have v is not a pivot, and c(v,G) > d(v,C) where C is any k-core containing v. Thus, the collapse of u will not decrease the coreness of any neighbor of u, i.e., there is no follower for collapsing u. □

Example 2

In Figure 1, the coreness of each vertex is attached to the vertex. For 1-core, the pivot is v1 as c(v1) = d(v1,C1(G)) = 1. For 2-core, the pivot is v2 as c(v2) = d(v2,C2(G)) = 2. For 3-core, the pivot set is ∪5≤i≤ 12{vi}. Thus, we have X = V (G) ∖{v1,v4}, i.e., each of {v1,v4} has no follower while any other vertex has at least one follower.

The theorems in this section indicate that computing the collapse of one vertex can be largely optimized to reduce the time cost, because the cost of follower computation is limited (Theorem 4 and 5) and the candidate collapsers are restricted (Theorem 6). Naturally, a greedy algorithm to find one good collapser in each iteration may be promising.

4.2 Core forest structure

Here we introduce the core forest structure of core decomposition which can be used to design effective optimizations (e.g., the bounding techniques in next subsection).

For every integer k, we have (i) a k-core is contained in exactly one (k − 1)-core, and (ii) each k-core is disjoint from each other. Thus, all the k-cores in the graph (for every possible k) can be organized into a forest structure, i.e., the core forest, where each connected component of the graph corresponds to a tree in the core forest.

Tree nodes in core forest

For every k-core C in G, if there is at least one vertex in C with coreness k, the k-core C is associated with a tree node N. The node N stores all the the vertices in C with coreness k (i.e., {u∣u ∈ C ∧ c(u,G) = k}). A tree node can only have one associated k-core. Let T denote the core forest. We use T[v] to denote the tree node containing v, and Ti.V to denote the vertex set in node Ti.

Tree edges in core forest

Given a k1-core C1 associated with tree node N1, and a k2-core C2 associated with tree node N2, the node N1 is the parent node of N2, if (i) k1 < k2; (ii) \(C_{1}\supset C_{2}\); and (iii) any tree node associated with a \(k^{\prime }\)-core is not the parent of N2, where \(k_{1}<k^{\prime }<k_{2}\).

Example 3

Figure 4 depicts the core forest of the graph G in Figure 1, where G is shown at the left and the corresponding T is at the right. As there is only one 1-core (resp. 2-core), we have T[v1] = v1 and T[v2] = {v2,v3,v4}. As there are two (connected) 3-cores, we have T[v5] = {v5,v6,v7,v8} and T[v9] = {v9,v10,v11,v12}.

Fig. 4
figure 4

Core component tree

Full size image

Constructing the core forest

The state-of-the art algorithm for constructing the forest of k-core is LCPS (Level Component Priority Search) [34] with time complexity of O(m). The algorithm pushes every vertex and its unvisited neighbors into queues (according to a priority function) s.t. the subtree containing the vertex is built.

4.3 Bounds of follower number

In a greedy algorithm, we need to compute the coreness loss for each vertex s.t. the best collapser can be found for the collapse of one vertex, in each iteration. However, it is costly to compute such coreness loss. In this subsection, we aim to fast estimate the lower/upper bounds of coreness loss for each vertex (if it is collapsed). Note that the number of followers is equal to the coreness loss for one collapsed vertex.

Lower bound of follower number

For a vertex x, we get the lower bound of followers from its neighbors which are pivots.

Theorem 7

Given a graph G, if a vertex x is collapsed, we have |F(x,G)|≥ lb(x), where

$$lb(x)= | \{u\mid u\in N(x,G)\cap PS \land c(u)\le c(x)\}|$$

Proof

For each vertex u ∈ N(x,G) ∩ PS with c(u) ≤ c(x), we have d(u,Cc(u)(G)) = c(u,G), and its degree in c(u)-core will decrease by 1 after deleting x, i.e., d(u,Cc(u)(G ∖{x ∪ E(x)})) ≥ c(u,G) − 1. Thus, the coreness of u decreases by 1 after deleting x, and u is a follower of x. □

The lower bound can be more accurate if we consider h-hop neighbors of x, i.e., the vertices affected by the neighbors of x with coreness decreased. The most accurate version becomes the exact computation of the follower number. Our preliminary experiments find that the additional cost of bound computation is not worthwhile, and the proposed lower bound well balances the computation cost and the bound accuracy.

Upper bound of follower number

For a vertex x, we can get the upper bound of follower number from its own tree node T[x] and the tree nodes containing its neighbors which are pivots. Specifically, the upper bound of follower number for a collapser x, denoted by ub(x), is the number of vertices in the tree nodes where each node has at least one pivot which is a neighbor of x.

Theorem 8

Given a graph G, if a vertex x is collapsed, we have |F(x,G)|≤ ub(x), where

$$ ub(x)=|\mathcal{T}|\text{,~~and~~} \mathcal{T}=\bigcup_{v\in N(x,G) \cap PS \land c(v)\le c(x)} T[v].V\setminus \{x\} $$

Proof

Let \(T^{\prime }\) be any tree node NOT in \(\mathcal {T}\), and u be any vertex in \(T^{\prime }.V\). (i) If c(u) > c(x), the coreness of u keeps same on G and G −{x ∪ E(x)} by Theorem 5. (ii) If c(u) ≤ c(x), every vertex \(v\in T^{\prime }.V\) is a non-pivot neighbor of x or is not a neighbor of x, i.e., v∉N(x,G) ∩ PS. So, we have Cc(v)(G −{x ∪ E(x)}) = Cc(v)(G) −{x ∪ E(x)} by Theorem 4: [ii.a] for v ∈ N(x,G) and v∉PS, we have d(v,Cc(v)(G)) > c(v,G) and the degree of v in c(v)-core decreases by 1 after the deletion of x. So, the coreness of v is same in G and G −{x ∪ E(x)}; [ii.b] for v∉N(x,G), the degree of v is same in c(v)-core of G and G −{x ∪ E(x)}. Thus, c(v,G) = c(v,G −{x ∪ E(x)}) for every vertex \(v\in T^{\prime }.V\), and there is no follower of x in \(T^{\prime }\). Since each vertex in V (G) exists in one and only one tree node of T, and x is not a follower of itself, ub(x) is a correct upper bound of |F(x,G)|. □

figure b

Example 4

For the graph in Figure 4, we have PS = V (G) ∖{v3,v4}. If v5 is collapsed (the others are not collapsed), the set {u∣u ∈ N(v5,G) ∩ PS ∧ c(u) ≤ c(v5)} = {v2,v6,v7,v8}. Therefore, we have lb(v5) = 4, ub(v5) = |T[v2].V ∪ T[v6].V ∖{v5}| = |{v2,v3,v4,v6,v7,v8}| = 6, and 4 ≤|F(v5,G)|≤ 6. If v6 is collapsed (the others are not collapsed), we have {u∣u ∈ N(v6,G) ∧ u ∈ PS ∧ c(u) ≤ c(v6)} = {v5,v7,v8}. So, lb(v5) = 3, ub(v6) = |T[v5].V ∖{v6}| = 3, and |F(v6,G)| = 3. Similarly, we have lb(v1) = ub(v1) = lb(v4) = ub(v4) = 0, lb(v2) = ub(v2) = 1, lb(v3) = 1 < ub(v3) = 2, and ub(u) = lb(u) = 3 for any other vertex u.

Algorithm 2 shows the pseudo-code for computing the upper bound and lower bound of follower number for each vertex. For each x ∈ V (G) (Line 1), we initialize the upper bound ub(x) and lower bound lb(x) at Line 2. The tree nodes are set to unvisited or updated to unvisited (for latter iterations). Then for each non-pivot neighbor u of x with c(u) ≤ c(x) (Line 4), we count the lower bound (Line 5) and upper bound (Line 6-8) of x. At Line 9, the algorithm returns the bounds for each vertex.

The time complexity of Algorithm 2 is O(m), because each edge is visited by at most twice for neighbor query (Line 4), each vertex is visited by at most twice (Line 1 and 4) for enumeration, and the tree nodes are visited along with the edge visit within O(m) times.

4.4 Computation of followers

As there are still many candidates collapsers for a greedy solution, it is cost-prohibitive to compute the followers by core decomposition from scratch. The algorithm for core maintenance can be used to compute (update) the follower set efficiently, which is to update the coreness of each vertex against edge insertion or deletion. The state-of-the-art algorithm for core maintenance is proposed in [49]. The deletion of a vertex can be regarded as the deletion of its incident edges.

figure c

Algorithm 3 shows the pseudo-code for computing the follower set if x is collapsed. For each x’s neighbor u with c(u) ≤ c(x) (Line 1), we delete the edge (u,x) from G and update the coreness of each vertex by core maintenance [49] (Line 2). Note that a neighbor u with c(u) > c(x) is not visited at Line 1, because it cannot be a follower of x by Theorem 5. Since the coreness of each vertex may decrease by at most 1 for the collapse of x (Theorem 4), we simply record the vertices with coreness changed after running Line 2 and accumulate it to the set F (Line 3 and 4).

According to the time cost of core maintenance [49], the time complexity of Algorithm 3 is \(O({\sum }_{u\in N(x,G)} {\sum }_{w\in F_{(x,u)}} d(w))\) where F(x,u) is the set of vertices with coreness decreased after the deletion of (x,u).

Although the average time cost of Algorithm 3 is not large for one collapsed vertex, considering the large number of candidate collapsers to compute, it is necessary to apply the lower/upper bounds in Section 4.3 s.t. unpromising candidates can be immediately pruned (i.e., unnecessary follower computations are skipped).

4.5 The greedy algorithm (GCC)

In this subsection, we introduce the final GCC algorithm which integrates all the proposed techniques. The aforementioned theorems and techniques naturally suggest a greedy algorithm as the computation for one collapsed vertex can be significantly optimized by them. In each of the b iteration, GCC greedily finds a best collapser by computing/estimating the follower number of each candidate collapser.

Algorithm 4 shows the detail of our GCC algorithm. We use cmin to record the smallest coreness of the vertices with coreness decreased in last iteration, and use D to denote the set of collapsers (Line 1). We firstly apply core decomposition (Algorithm 1) to get the initial coreness of each vertex (Line 2). The pivot set PS can be retrieved along with the core decomposition when the degree threshold k increases (from the computation of k-core to (k + 1)-core). Then, we apply LCPS [34] to build the core forest T (Line 3). The upper bound ub(⋅) and lower bound lb(⋅) of follower number are computed by Algorithm 2 (Line 4).

figure d

In each of the b iterations (Line 5), we use x to record the best collapser found so far, and use lmax to record the follower number (i.e. coreness loss) of the best collapser (Line 6). Then, we enumerate each vertex with non-zero follower and not in D in decreasing order of their upper bounds based on Theorem 6 (Line 7). A vertex with larger upper bound often has more followers in our experiments, and the computation of such vertex at an early stage may speed up the algorithm because it fast produces a large lmax.

Only when the upper bound of a vertex u is larger than lmax (Line 8), it is worthwhile to compute the follower set of x, i.e., lmax and x may be updated. If the lower bound and upper bound of u are the same, then the coreness loss of u is simply lb(u) (Line 9-10); Otherwise, we compute the follower set of u and retrieve its coreness loss by Algorithm 3 (Line 11-12). If l(u) is larger than lmax, u becomes the current best collapser (Line 13-14).

After we determine the best collapser x in current iteration, we will update the set D (Line 15) and delete x with its incident edges from G (Line 16). The coreness c(⋅) of each vertex is updated by core maintenance [49] where PS is updated together, and the core forest T is updated by hierarchical core maintenance [27] (Line 17). After b iterations, Algorithm 4 returns the set D of b collapsed vertices (Line 18).

The time complexity of Algorithm 4 is \(O({\sum }_{i=1}^{b} {\sum }_{x\in CV_{i}} Time_{f}(x))\) where CVi is the candidate vertices in ith iteration for finding a best collapser and Timef(x) is the time cost of Algorithm 3 with the input of x. Note that the overall time cost of core decomposition, core forest construction, and hierarchical core maintenance is not dominated for Algorithm 4.

To find high-quality collapsers within a time limit, we may first choose b collapsers with the largest vertex degrees, and then replace each collapser (with the smallest coreness loss for one collapsed vertex) by the collapsers produced by Algorithm 4 if the total coreness loss can be larger.

5 Experiments

In this section, we conduct extensive experiments to verify the effectiveness of the collapsed coreness model and the efficiency of our proposed algorithms.

5.1 Experimental setting

Datasets

The experiments are conducted on 12 real-life datasets. Table 3 shows the statistics of the datasets, ordered by the number of edges in each dataset, where davg is the average vertex degree, dmax is the largest vertex degree and kmax is the largest vertex coreness. The datasets are obtained from SNAPFootnote 1 and Network Repository.Footnote 2

Table 3 Statistics of datasets
Full size table

Algorithms

For effectiveness, we mainly compare 7 algorithms with our GCC algorithm, including 4 heuristics, the exact solution, the algorithm for collapsed k-core problem, and the GCC-T algorithm. For efficiency, we incrementally equip the baseline with our proposed techniques to evaluate the performance. Table 4 lists all the evaluated algorithms.

Table 4 Summary of algorithms
Full size table

Parameters

We perform our experiments on a CentOS Linux serve (Release 7.5.1804) with Quad-Core Intel Xeon CPU (E5-2640 v4 @ 2.20GHz) and 128G memory. All the algorithms are implemented in C++. The source code is complied by GCC(7.3.0) under -O3 optimization.

5.2 Performance evaluation

Comparison with exact solution

We first compare the result of GCC with the Exact algorithm which identifies the optimal b collapses by enumerating all possible combinations of b vertices. Due to the huge time cost of Exact, we build small datasets by iteratively extracting a vertex and all its neighbours from Brightkite or Arxiv, until the number of extracted vertices reaches 20. We randomly extract 100 subgraphs, and then calculate the average coreness loss of them. Figure 5 shows that the coreness loss of GCC is at least 94.7% (resp. 96.2%) of the optimal value in Brightkite (resp. Arxiv). In addition, GCC is faster than Exact by up to 6 orders of magnitude, as shown by the time in the figures.

Fig. 5
figure 5

Exact v.s. GCC on small graphs

Full size image

Comparison with CKC

Table 5 shows that the largest coreness loss (denoted by maxCKC) that CKC can achieve on all the datasets, which is computed by running CKC with every possible input of k. Specifically, for the collapser set C computed by CKC, we compute the total sum of coreness loss for every coreness value if C is collapsed. It is reported that the largest coreness loss by CKC is only 36% − 98% of the coreness loss by GCC). Table 5 also shows that the average coreness loss of CKC (denoted by avgCKC) for an input of k, which is 19% − 82% of the coreness loss by GCC. Besides, Figure 6 shows the coreness loss of different k for CKC on different datasets, which indicates that CKC is infeasible to solve the collapsed coreness problem.

Table 5 Coreness loss from CKC and GCC
Full size table
Fig. 6
figure 6

Coreness Loss on Different k

Full size image

We also investigate the distribution of collapsers and followers regarding their coreness values, from GCC and CKC, respectively. Let CKCnum denote CKC with k = num, e.g., CKC10 is CKC with k = 10. We observe that the distribution of CKC highly depends on the choice of k value. In Figure 7a, the collapsers from CKC10 have small coreness values while the collapsers from GCC have a relatively uniform distribution on coreness. In Figure 7b, for the distribution of followers, the margin is smaller while GCC has more followers than CKC on almost every coreness value.

Fig. 7
figure 7

Distributions of collapsers and followers on Stanford

Full size image

Comparison with other heuristics

In Figure 8, we compare the coreness loss from GCC with other heuristics (Rand, Deg, Deg-c, and Core). The details of these heuristics are introduced in Table 4. In Figure 8a, the performance of Rand is the worst as it chooses random vertices to collapse, where the results are omitted if the values are too small. The performance of Core is better than Rand as they choose vertices with large coreness to collapse, which may affect many vertices. Deg often has a larger coreness loss than Core. It indicates that the degree of a vertex is more relevant to the power of collapse for the collapsed coreness problem, compared with the coreness of the vertex. Deg-C represents the redundancy of a vertex on its coreness value towards its degree, which performs almost the same to Deg (better on Facebook). Compared with the above heuristics, GCC always has the largest coreness loss. In Figure 8b and c, we can see the result of Deg is similar to GCC when b is very small, but the margin becomes much larger with the increase of b.

Fig. 8
figure 8

Coreness loss from different heuristics

Full size image

Case study on DBLP

We evaluate the effectiveness of our model on a graph which is built on DBLP, where each vertex is an author and two authors are linked if they have more than 5 co-authored papers in top Database conferences including SIGMOD, VLDB, and ICDE. Figure 9 depicts the collapser identified by GCC with b = 1 as well as the corresponding followers. The collapser is the author “Hector Garcia-Molina” who has 66 followers. Here 24 of the followers are not the 1-hop neighbors of “Hector” which means a large amount of followers does not have direct relations to the collapser. It implies that Deg is not a good choice for the problem. Besides, we observe that the followers include many computer scientists, and many of them are ACM fellows, e.g., “Magdalena Balazinska”, “Stanley B. Zdonik”, and so on. The followers are also from different universities and institutions in different countries. The above finding indicates that the engagement of many users may be affected if the collapser left a network.

Fig. 9
figure 9

Case study on DBLP, b = 1

Full size image

Performance of time-dependent GCC

As shown in Figure 8, the algorithm Deg performs well when b is small. This motivates us to design a time-dependent algorithm GCC-T which first uses Deg to choose b collpasers, and then applies GCC to replace the collapsers s.t. the coreness loss can be larger, within a given time limit. Figure 10 shows the performance of GCC-T, GCC, and Deg on facebook (b = 3000) and Socfb-Northeastern19 (b = 1000), we can see that the coreness loss of GCC-T fast approaches that of GCC when the algorithm costs more time. Regarding a given time limit, a relatively effective result can be retrieved by GCC-T.

Fig. 10
figure 10

Performance of time-depend GCC slgorithm

Full size image

Evaluating optimization techniques

Figure 11a shows the total running time of GCC-O-P-B, GCC-P-B, GCC-B, and GCC on all the 12 datasets when b = 100. The results show that GCC-P-B is much faster than GCC-O-P-B by applying core maintenance as introduced in Section 4.4, and GCC is faster than GCC-P-B and GCC-B by at least 2 times because of the optimization by Theorem 5 and Theorem 6. Figure 11b and c study the impact b on four algorithms DBLP and Stanford. We can see that GCC is scalable with the growth of b and it is always faster than the other algorithms.

Fig. 11
figure 11

Time cost of different algorithms

Full size image

6 Related work

Identifying cohesive subgraphs is an important problem in graph analytics. In the literature, many cohesive subgraph models have been proposed, e.g., k-core [4, 7, 22, 30, 34, 37, 45], k-truss [15, 23, 31, 39, 41], clique [1, 8, 12], k-plex [43] and k-ECC [10, 51]. Among them, k-core is a well-studied model, due to its effectiveness in various applications including community discovery [11, 17, 19, 25], influential spreader identification [18, 24, 26, 32], network structure analysis [3, 6, 9, 13, 16], predicting structural collapse [36], and graph visualization [2, 50].

The concept of k-core and the computing algorithm are first introduced in [34, 37]. An O(m)-time in-memory algorithm for core decomposition is proposed in [4]. The core forest can also be computed in O(m) time as studied in [34]. Additionally, the core decomposition algorithms under different environments are also studied including I/O efficient core decomposition [44] and distributed core decomposition [35]. Besides, various variants of k-core are explored, e.g., (α,β)-core [29, 42], (k,r)-core [48], (k,s)-core [21, 46], radius-bounded k-core [40] and skyline k-core [25].

The engagement dynamics in social networks has attracted significant focus, e.g., [5, 14, 28, 33, 47]. In these works, the k-core model is widely adopted, due to its degeneration property that can be used to quantify engagement dynamics in real social networks [34]. In the view of enhancing the engagement of some users, the anchored k-core problem [5] and the anchored coreness problem [28] are studied, where the degrees of the anchored (enhanced) users are regarded as positive infinity. The collapsed k-core problem [47] considers a different view where some key users should be protected against the attacks from the competing networks. Thus, it investigates the effect of user departure while the anchor problems focus on user enhancement. However, the collapsed k-core problem only considers the key users regarding a given k-core. The collapsed coreness problem studied in this paper finds the key users regarding the stability of the whole network.

7 Conclusion and future work

The coreness sum of all the vertices in a network is regarded as a major indicator for the stability of the network. In this paper, we propose and study the collapsed coreness problem to find the key users for network structural stability. Given a graph G and a budget b, the problem aims to find b vertices in G such that the deletion of the b vertices leads to the largest coreness loss on all the vertices. We prove the problem is NP-hard and APX-hard unless P=NP. An efficient greedy heuristic is proposed with effective optimization techniques. The algorithm is also extended to return a set of key users within a given time limit. Extensive experiments on 12 real-life graphs verify that the collapsed coreness model is effective and the proposed algorithm is efficient.

The proposed GCC algorithm may inspire efficient parallel and distributed solutions, as the data locality and independence derived from the heuristic can ensure a sound strategy for task allocation. We may assign the candidate vertices according to the sub-trees containing the vertices in the forest, restrict the computation in each computing node by carefully partitioning the graph with tree nodes, and thus reduce the communication cost between different computing nodes. Besides, it is also interesting to explore a faster variant of the greedy heuristic with acceptable sacrifice on result quality.