Generalized core maintenance of dynamic bipartite graphs

Abstract

k-core is important in many graph mining applications, such as community detection and clique finding. As one generalized concept of k-core, (i, j)-core is more suited for bipartite graph analysis since it can identify the functions of two different types of vertices. Because (i, j)-cores evolve as edges are inserted into (removed from) a dynamic bipartite graph, it is more economical to maintain them rather than decompose the graph recursively when only a few edges change. Moreover, many applications (e.g., graph visualization) only focus on some dense (i, j)-cores. Existing solutions are simply insufficiently adaptable. They must maintain all (i, j)-cores rather than just a subset of them, which requires more effort. To solve this issue, we propose novel maintenance methods for updating expected (i, j)-cores. To estimate the influence scope of inserted (removed) edges, we first construct quasi-(i, j)-cores, which loosen the constraint of (i, j)-cores but have similar properties. Second, we present a bottom-up approach for efficiently maintaining all (i, j)-cores, from sparse to dense. Thirdly, because certain applications only focus on dense (i, j)-cores of top-n layers, we also propose a top-down approach to maintain (i, j)-cores from dense to sparse. Finally, we conduct extensive experiments to validate the efficiency of proposed approaches. Experimental results show that our maintenance solutions outperform existing approaches by one order of magnitude.

1 Introduction

In numerous graph mining applications, one key goal is to discover the k-core (Cheng et al. 2011; Khaouid et al. 2015; Montresor et al. 2011) of a given graph, which is the largest subgraph such that every vertex has at least degree k within the subgraph. The k-core is widely used in a variety of applications, including community evaluation (Giatsidis et al. 2012), clique finding (Lu et al. 2017), and graph clusters (Cheng et al. 2013).

Unfortunately, k-core has certain limitations because it ignores the extra edge information (e.g., direction, time, probability) in other types of graphs, such as direct graphs, temporal graphs and uncertain graphs. As a result, several generalized concepts of k-core such as D-core (Giatsidis et al. 2012), $(k,\eta )$-core (Bonchi et al. 2014) and (k, h)-core (Wu et al. 2015) are presented, to deal with these types of graphs.

As one generalized concept of k-core, the (i, j)-core (Ahmed et al. 2007; Liu et al. 2020) is proposed to handle bipartite graph analysis, which is the largest subgraph in which a vertex in one set has at least degree i and its neighbor in the other set has at least degree j within the subgraph. It allows a vertex and its neighbors to have varying degrees. Clearly, k-core is a subset of (i, j)-core satisfying $i=j$. Because (i, j)-core can reveal the roles of two different kinds of vertices, it is more suited to bipartite graph mining tasks. Related studies indicate that (i, j)-cores can be employed in graph visualization and analysis (Ahmed et al. 2007) as well as fault-tolerant group recommendation (Ding et al. 2017). Given the strong relation between k-core and (i, j)-core, our research may benefit certain traditional bipartite graph issues, such as biclique finding (Mukherjee and Tirthapura 2017), vertex ranking (He et al. 2017) and community detection (Wang and Liu 2018).

Consider an application assignment in which we intend to locate high-value consumers and popular goods from Taobao,¹ which is the largest online shopping website in China, to demonstrate the importance of (i, j)-cores. We can observe from modeling these users and goods on a bipartite graph that one user only purchases a tiny number of goods, while many users buy the same items. This bipartite graph is imbalanced. As a result, the outcomes of obtaining k-cores from such a network are unreasonable because users and goods have different weights in our objective. We could use the (i, j)-core to allow users and items to have various neighbors to solve this issue. Then, we will create a high-quality community and provide superior recommendation services for these people who have comparable preferences.

Edges are inserted into (removed from) a dynamic bipartite graph over time in real-world applications, resulting in the evolution of (i, j)-cores. To trace (i, j)-cores in such a bipartite graph, a decomposition method must recalculate all (i, j)-cores even if the network only changes one edge. In contrast, the maintenance method updates the affected (i, j)-cores, making it more efficient.

Despite the fact that k-core maintenance (Saríyüce et al. 2013; Li et al. 2014; Wen et al. 2016) is widely explored, it can not be utilized to address the (i, j)-core due to the unique structure. Furthermore, Liu et al. (2020) provided an index-based (i, j)-core computation method. Unfortunately, their approach must update (i, j)-cores, otherwise bipartite core indexes will be wrong. As a result, they are unsuitable for some applications, such as community detection and graph visualization, which need just a few dense (i, j)-cores.

We investigate the (i, j)-core maintenance of a dynamic graph to solve the issues mentioned above. In this paper, we extend our earlier work (Bai et al. 2020) to a bipartite graph, with an emphasis on (k, h)-cores of temporal graphs. Due to differing structural definitions, there are two significant differences between (k, h)-cores and (i, j)-cores.

• (1) The number of (i, j)-cores of a bipartite graph is considerably more than the number of (k, h)-cores in an almost equal-size temporal graph, since the maximum k is substantially less than the maximal degree of vertices in a temporal graph. So, (i, j)-core maintenance needs greater processing time and memory space.

• (2) Because the initial stage does not create unsatisfied edges, (k, h)-core decomposition methods eliminate unsatisfied edges before invalid vertices. However, the procedure of eliminating invalid left and right vertices should alternate in (i, j)-core decomposition. As a result, we need to redesign the appropriate algorithm.

This work presents a bottom-up approach using bipartite core indexes to effectively maintain all (i, j)-cores from sparse to dense while keeping a low memory cost. Furthermore, because some applications (e.g., graph visualization) primarily focus on dense (i, j)-cores of top-n layers, we propose a top-down maintenance approach to maintain (i, j)-cores from dense to sparse, which has not been reported in any studies. It is worth noting that our top-down maintenance method can also update all (i, j)-cores, although it is less efficient than the bottom approach. Finally, we conduct comprehensive tests to validate the effectiveness of proposed solutions. Experimental results indicate that when only a few edges change, our maintenance methods outperform baselines by one order of magnitude.

The main contributions of our paper are listed below:

• We present a bottom-up approach for rapidly updating all (i, j)-cores from sparse to dense.

• To handle applications that need dense (i, j)-cores of top-n layers, we devise a top-down method.

• We validate the effectiveness of our proposed methods by conducting comprehensive experiments.

The rest of this paper is structured as follows: Sect. 2 introduces some preliminaries of bipartite graph and (i, j)-core; Sect. 3 describes the specifics of quasi-(i, j)-core; Sects. 4 and 5 illustrate the proposed maintenance approaches; experimental results are reported in Sect. 6; the related studies are discussed in Sect. 7, and the paper is concluded in Sect. 8.

2 Preliminaries

This section will review the fundamentals of bipartite graphs and (i, j)-cores. Table 1 lists several standard notations, which are used in the rest of this paper frequently.

Table 1 Frequently used notations

2.1 Bipartite graph

$G = (L(G),R(G),E(G))$ is a simple bipartite graph with two disjoint vertices sets L(G) and R(G), called the left and right vertex sets respectively, and an edge set $E(G) \subseteq L(G) \times R(G)$. If $|E(G) |=0$, we regard G as an empty graph, denoted by $\emptyset$. Furthermore, assuming the context is clear, we use $l \in G\ (r \in G)$ to substitute $l \in L(G)\ (r \in R(G))$ and $(l,r) \in G$ to replace $(l,r) \in E(G)$. Additionally, the size of G is represented by $|G |$.

For convenience, we generalize four set notations $\subseteq , \cup ,\cap ,\setminus$ for graph operations. Let $G_{1}, G_{2}$ be two arbitrary bipartite graphs, we get the following notations: $G_1 \subseteq G_2$ means that $G_1$ is a subgraph of $G_2$; $G_1 \cup G_2$ is the union graph of $G_1$ and $G_2$, containing all edges of $G_1$ and $G_2$; $G_1 \cap G_2$ is the intersection graph of $G_1$ and $G_2$, including common edges of $G_1$ and $G_2$; $G_1 \setminus G_2$ is the difference graph of $G_{1}$ and $G_{2}$, such that $E(G_1\setminus G_2) = E(G_1)\setminus E(G_2)$. In above operations, edges are automatically linked if they share the same vertices.

Given $G = (L(G),R(G),E(G))$ and a vertex $l \in L(G)\ (r \in R(G))$, $N(G,l)\ (N(G,r))$ is defined as the set of all neighbors of $l\ (r)$ in G. And $|N(G,l) |$ is defined as the degree of the vertex $l \in G$, denoted by d(G, l). Similarly, d(G, r) is defined for $r \in G$. Furthermore, $d(G,L(G))\ (d(G,R(G)))$ indicates the maximum degree of vertices in $L(G)\ (R(G))$.

2.2 Bipartite core

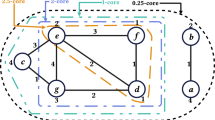
A (i, j)-core is a type of cohesive subgraphs of the given bipartite graph $G = (L(G), R(G),E(G))$, denoted by C(G, i, j) , which represents the dense area of G. In general, $(i,j) \succcurlyeq (1,1)$ holds for every (i, j)-core, where $\succcurlyeq$ is a vector comparative notation used to compare each component of two vectors. We also use $C(G,i,j) = \emptyset$ to indicate that C(G, i, j) is an empty graph. Furthermore, we can observe that the (i, j)-core (see Fig. 1) cannot expand according to Definition 1, which is frequently utilized in subsequent proofs.

Definition 1

A (i, j)-core of G, denoted by C(G, i, j), is the largest subgraph of G such that $d(G, l) \ge i$ and $d(G, r) \ge j$ for $l,r \in C(G,i,j)$.

Fig. 1

A bipartite graph and its two (i, j)-cores, where circles and squares indicate the left and right vertices, respectively, and the dashed lines represent the (2, 2)-core and the (3, 2)-core. In general, the (3, 2)-core has a greater density than (2, 2)-core, which can be computed by $|E(G) |/(|L(G) |\cdot |R(G) |)$. The density of a complete bipartite graph should be 1

The (i, j)-core of a bipartite graph G is unique and partially nested. It is worth noting that the inclusion relation is non-linear, which is clearly distinct from that of k-cores (Saríyüce et al. 2013). Based on partially nested property of (i, j)-cores, we can create a direct relation graph without loop (see Fig. 2), denoted by D(G), in which each vertex represents a (i, j)-core and each edge corresponds to the inclusion relation between two adjacent (i, j)-cores. Because (i, j)-cores are arranged in layers, we define the layer height of C(G, i, j) in D(G) to differentiate them, denoted by h(C(G, i, j)) (see Definition 2).

Definition 2

Given an arbitrary (i, j)-core of G, the layer height of C(G, i, j) in D(G) is defined as $h(C(G,i,j)) = i+j-1$. Specially, $h(C(G,1,1)) = 1$.

(i, j)-cores in higher layers are often denser than those in the lower layers. Given an arbitrary (i, j)-core of G, its layer height $h(C(G,i,j)) = i+j-1$ holds, which can be verified by mathematical induction.

Fig. 2

The direct relation graph of (i, j)-cores in a complete graph with 3 left vertices and 3 right vertices

2.3 Core decomposition

The main idea behind generating (i, j)-cores of a given graph is to delete the left vertices with degrees less than i and the right vertices with degrees less than j repeatedly. The issue of identifying all (i, j) pairs of vertices in a graph is known as (i, j)-core decomposition.

We can define the core number (Cheng et al. 2013) of a vertex in k-core decomposition to indicate which k-cores contain it. However, this concept is inapplicable to (i, j)-core since their inclusion relations are partially nested. In other words, a vertex may be located in two (i, j)-cores that are not overlapping. A vertex, for example, can be located in both (2, 3)-core and (3, 2)-core. We know that they have different structures based on Definition 1. Storing all (i, j) pairs of a vertex will use a large amount of memory space. For example, in a complete bipartite graph $G = (L(G),R(G),E(G))$, it takes $O((|L(G) |+ |R(G)|)\cdot |E(G) |)$to store all (i, j) pairs. The major benefit of this technique is that it can obtain the vertices of any (i, j)-core without traversing the entire graph. For simplicity, this technique is referred to as (i, j)-pair sets.

Wu et al. (2015) developed the core number of k-cores to the core number set for (k, h)-cores of temporal graphs, which only stores pairs without partial inclusion relation, to save memory usage. If a vertex is located in (1, 1)-core, (2, 1)-core, (1, 2)-core and (2, 2)-core, then its core number set is $\{(2, 2)\}$. Obviously, this approach may also be used in (i, j)-cores and is known as (i, j)-core number sets.

Although storing the core number set of all vertices can save a significant amount of memory, it has certain disadvantages. Given an arbitrary vertex, it is difficult to determine if it can be included in a (i, j)-core with a single query. To solve this issue, Liu et al. (2020) created bipartite core indexes, which can assure that the space usage is proportional to the graph size. Based on this index, Liu et al. (2020) presented an effective core decomposition algorithm with a time complexity of $O(\delta \cdot |E(G) |)$, where $\delta$ is bounded by $\sqrt{|E(G) |}$ but is considerably smaller in practice. This approach, however, has a disadvantage in that it must conserve the bipartite core index of vertices in all (i, j)-cores. This technique is ineffective if we require a subset of (i, j)-cores.

We primarily employ bipartite core indexes and (i, j)-pair sets in this paper for our bottom-up and top-down methods, respectively. Because most real graphs are sparse, the memory usage of these methods is substantially lower than the theoretical bound.

3 Quasi core

When edges are inserted into (removed from) a dynamic bipartite graph, we explore how to locate and update impacted (i, j)-cores. In a recent study (Bai et al. 2020), we use quasi-(k, h)-core to estimate affected (k, h)-cores of temporal graph (Wu et al. 2014). Similarly, we can define quasi-(i, j)-core for bipartite graphs. By decomposing the insertion (removal) graph (consisting of inserted (removed) edges) to a collection of quasi-(i, j)-cores, we estimate influenced (i, j)-cores, and then update anticipated (i, j)-cores rather than all of them.

Let $G_p$ and $G_c$ be previous and current bipartite graphs, respectively, and define the insertion (removal) graph $S_{+}=G_{c} \setminus G_p\ (S_{-}=G_p \setminus G_{c})$. It should be noted that immediately decomposing $S_{+}\ (S_{-})$ will yield the incorrect bipartite core index of vertices in $S_{+}\ (S_{-})$ since some of them link additional edges in $G_{c}\ (G_p)$. Instead, we decompose $S_{+}\ (S_{-})$ into a set of quasi-(i, j)-cores. Because the insertion and removal procedures are the same, we use S to represent $S_{+}\ (S_{-})$ and G to indicate $G_{c}\ (G_p)$.

Definition 3

Let $S = (L(S),R(S),E(S))$ and $G = (L(G),R(G),E(G))$ be two bipartite graphs, $S(G)=(L(S(G)),R(S(G)),E(S(G)))$ is an extended graph of S on G, such that $L(S(G))=L(S) \cup \{l: l \in N(G,r) \wedge r \in S \}$, $R(S(G))=R(S) \cup \{r: r \in N(G,l) \wedge l \in S \}$ and $E(S(G)) = E(S) \cup \{(l,r): l \in L(S) \wedge r \in N(G,l) \} \cup \{(l,r):r \in R(S) \wedge l \in N(G, r)\}$. Additionally, if $S \cap G = \emptyset$, then $S(G) = S$.

In Definition 3, S(G) simply expands S by one step on G, ensuring $d(S(G),l) = d(S \cup G,l)$ and $d(S(G),r) = d(S \cup G,r)$ for every $l,r \in S$. If $S \subseteq G$, then $d(S(G),l) = d(G,l)$ and $d(S(G),r) = d(G,r)$ both true. In other words, vertices in S will have the same degree in both S(G) and G. If $|S |\ll |G |$, the size of S(G) is significantly smaller than $S \cup G$.

Definition 4, based on the extended graph, gives formal details of the quasi-(i, j)-core, which loosens the restrictions of the (i, j)-core on the extended graph. Nonetheless, quasi-(i, j)-core is unique and somewhat nested.

Definition 4

A quasi-(i, j)-core is the largest subgraph of S, denoted by ${\hat{C}}(S,$ G, i, j), such that $d({\hat{C}}(G),l) \ge i$ and $d({\hat{C}}(G),r) \ge j$ for an arbitrary $l,r \in {\hat{C}}(S,G,i,j)$, where ${\hat{C}}(G)$ is the extended graph of ${\hat{C}}(S,G,i,j)$ on G.

In contrast to (i, j)-core, quasi-(i, j)-core only demands that its vertices fulfill constraints on its extended graph rather than itself. If the extended graph is unique, so is quasi-(i, j)-core.

A decomposition approach may use to obtain quasi-(i, j)-cores, which are similar to (i, j)-cores. Other operations are identical to those of (i, j)-core decomposition, except that the quasi-(i, j)-core decomposition calculates the degree of vertices of S on S(G) rather than itself.

4 Bottom-up core maintenance

This section provides a bottom-up approach for fast maintaining affected (i, j)-cores with a set of inserted (removed) edges from sparse to dense. The core idea behind our algorithms is to locate all impacted (i, j)-cores and update them one by one. Because the operations for insertion and removal situations differ, we will explain them independently.

For the insertion case, we estimate affected (i, j)-cores using quasi-(i, j)-cores and then update each of them in turn. Edges of a quasi-(i, j)-core, in particular, impact adjacent vertices and spread their effects through linked edges for each affected (i, j)-core, but the quasi-(i, j)-core does not include all influenced vertices and edges. As a result, the quasi-(i, j)-core is extended to a candidate graph. To avoid changing the union graph of the candidate graph and the previous (i, j)-core, we extract the partial-(i, j)-core from the candidate graph, which is the difference graph of the current (i, j)-core and the previous (i, j)-core.

We still discover affected (i, j)-cores for the removal case by utilizing quasi-(i, j)-cores and then updating them from sparse to dense. For each affected (i, j)-core, we simply concentrate on the common edges of the quasi-(i, j)-core and the previous (i, j)-core. We obtain the current (i, j)-core by recursively eliminating unsatisfied vertices and edges from the previous (i, j)-core at the lowest cost.

4.1 Insertion case

As previously stated, our maintenance procedure for the insertion case consists of four phases. Firstly, we decompose $S_{+}$ to get a collection of quasi-(i, j)-cores, which utilizes to locate affected (i, j)-cores. Secondly, we find a candidate graph including all potential vertices and edges for each impacted (i, j)-core. Thirdly, we extract a partial-(i, j)-core from the candidate graph and update the associated (i, j)-core. Finally, we proceed to the following layer of (i, j)-cores until all affected (i, j)-cores have been updated.

After obtaining a set of quasi-(i, j)-cores, we explore how to use the quasi-(i, j)-core to discover a candidate graph. Vertices and edges that are accessible from edges in ${\hat{C}}(S_{+},G_c,i,j)$ through a path are clearly impacted. We skip edges in the previous (i, j)-core since they do not propagate their impacts. Because we can get the candidate graph from either $C(G_c,i-1,j)$ or $C(G_c,i,j-1)$, $C^{*}$ is used to represent either of them. If not specified, $i> 1 \ (j > 1)$ always holds for $i-1\ (j-1)$.

Definition 5

$F_{b}(i,j)$ is a bottom-up candidate graph, whose edge $(l,r) \in C^{*}$ is reachable from edges in ${\hat{C}}(S_+,G_c,i,j)$ via a path, such that $d(C^{*},l) \ge i$, $d(C^{*},r) \ge j$ and $(l,r) \notin C(G_p,i,j)$.

To avoid having to recalculate the (i, j)-core of $C(G_p,i,j) \cup F_{b}(i,j)$, we obtain the partial-(i, j)-core from $F_{b}(i,j)$, denoted by P(i, j). It should be noted that P(i, j) cannot grow, otherwise $C(G_c,i,j)$ will also increase, which contradicts Definition 1.

Definition 6

A partial-(i, j)-core, denoted by P(i, j), is the difference graph of $C(G_c,i,j)$ and $C(G_p,i,j)$ such that $P(i,j) = C(G_c,i,j) \setminus C(G_p,i,j)$.

According to Definition 6, given $l,r \in P(i,j)$, we get $d(P(C),l) \ge i$ and $d(P(C),r) \ge j$, where P(C) is the extended graph of P(i, j) on $C(G_p,i,j)$. Moreover, the partial-(i, j)-core has an important property, the quasi-(i, j)-core of itself on the previous (i, j)-core is identical to itself. As a result, we can establish a connection between quasi-(i, j)-core and partial-(i, j)-core.

Lemma 1

$P(i,j) = {\hat{C}}(P(i,j),C(G_p,i,j),i,j)$ holds.

It should be emphasized that Definition 6 cannot be used to obtain P(i, j) since it needs the knowledge of $C(G_c,i,j)$, which is unavailable in our methods. According to Definition 5, we know that $C(G_c,i,j) \subseteq F_b(i,j)$, otherwise, $F_b(i,j)$ will continue to expand. Therefore, we can derive the partial-(i, j)-core from $F_{b}(i,j)$. Two scenarios must be considered in light of the existence of C(Gp, i, j): (1) if $C(G_p,i,j) \ne \emptyset$, then $P(i,j)= {\hat{C}}(F_t(i,j),C(G_p,i,j),i,j)$; (2) if $C(G_p,i,j) = \emptyset$, then $P(i,j) = C(F_t(i,j),i,j)$. Theorems 1 and 2 give thorough proofs for two situations (See Appendix). They verify the correctness of our bottom-up insertion algorithm.

Theorem 1

If $C(G_p,i,j) \ne \emptyset$, then $P(i,j) = {\hat{C}}(F_{b}(i,j),C(G_p,i,j),i,j)$.

Theorem 2

If $C(G_p,i,j)=\emptyset$, then $P(i,j) = C(F_b(i,j),i,j)$.

Theorem 1 states that we can get P(i, j) from $F_{b}(i,j)$ by obtaining the quasi-(i, j)-core of $F_{b}(i,j)$ on $C(G_p,i,j)$. Actually, Theorem 2 is a special case of Theorem 1. When $C(G_p,i,j) = \emptyset$, there is no available information of $C(G_p,i,j)$. According to Definition 5, $P(i,j) \subseteq F_b(i,j)$ holds. Thus, we can drive P(i, j) by decomposing $F_b(i,j)$.

Algorithm 1 first decomposes $S_{+}$ to get a set of quasi-(i, j)-cores using $G_{c}$. It only conserves a map of (i, j)-pairs and related edge sets for convenience, e.g., $\varvec{{\hat{\Psi }}}_{+}(i,j)$ is an edge set containing edges in the quasi-(i, j)-core. Updating $C(G_p,1,1)$ is a trivial case, it revises bipartite core indexes of vertices in $S_+$ directly. In the main loop, if $\varvec{{\hat{\Psi }}}_+(i+1,j) \ne \emptyset$, it gets $P(i+1,j)$ from $F_b(i+1,j)$ and updates the bipartite core indexes of vertices. Similarly, the operations for $\varvec{{\hat{\Psi }}}_+(i,j+1)$ are identical. It returns updated $\varvec{\Phi }_{L}$ and $\varvec{\Phi }_{R}$ until the algorithm ends.

To conserve the updated index of vertices in Algorithm 1, additional bipartite indexes $\varvec{\Phi }'_{L}$ and $\varvec{\Phi }'_{R}$ are required. If we directly update $\varvec{\Phi }_{L}$ and $\varvec{\Phi }_{R}$, the process of identifying a candidate graph may get an erroneous result since it depends on $\varvec{\Phi }_{L}$ and $\varvec{\Phi }_{R}$ to determine whether a vertex can be located in $C(G_p,i,j)$. Besides, we also provide an extra algorithm for updating each affected (i, j)-core (see Appendix).

Algorithm 1 has a time complexity of $O(|\varvec{C} ||G_c |)$, where $|\varvec{C}|$ is the number of (i, j)-cores and $O(|G_c |)$ is the cost to update each influenced (i, j)-core. When $G_c$ is a complete graph, then $|\varvec{C}|= d(G_c,L(G_c)) \cdot d(G_c,R(G_c))$. Because most graphs are sparse, $|\varvec{C} |$ is significantly smaller than its theoretical bound. In most cases, the size of a candidate graph is typically less than $G_c$. In terms of space complexity, because the method just saves the entire graph $G_c$, the space required is $O(|G_c|)$.

Fig. 3

The steps for updating (2, 2)-core with two inserted edges are as follows: a the previous (2, 2)-core is marked by a black dashed line and two inserted edges are specified by a green dotted line; b the quasi-(2, 2)-core is shown by a purple half-dashed line; c the candidate graph is indicated by a blue half-dashed line; d the partial-(2, 2)-core is indicated by a red half-dash line; e the current (2, 2)-core is indicated by a dashed line (Color figure online)

Example 1

We give a simple example (see Fig. 3) to illustrate the process of Algorithm 1. When two edges are added to the graph, we focus on updating (2, 2)-core. Other (i, j)-cores can be updated similarly. Firstly, we visit the quasi-(2, 2)-core by using $\varvec{{\hat{\Psi }}}_+$, $\varvec{{\hat{\Psi }}}_+(2,2)$ only has one edge, which is highlighted in purple. Secondly, we use traversal to discover a candidate graph marked in blue and has six vertices. It is worth noting that the candidate graph has no edges from the previous (2, 2)-core, which can be ruled out by visiting $\varvec{\Phi }_L$ and $\varvec{\Phi }_R$. Thirdly, we get the partial-(i, j)-core from this candidate graph, which is highlighted in red and has 4 vertices, and we update the maximal i and j of these vertices in $\varvec{\Phi }'_L$ and $\varvec{\Phi }'_R$. Fourthly, we continue to visit the next layer of (i, j)-cores, such as (2, 3)-core and (3, 2)-core, until all affected (i, j)-cores are updated. Finally, the algorithm swaps $\varvec{\Phi }_L$ and $\varvec{\Phi }_R$ with $\varvec{\Phi }'_L$ and $\varvec{\Phi }'_R$.

4.2 Removal case

We have three stages of updating influenced (i, j)-cores in the removal case. Firstly, we decompose $S_{-}$ to get a set of quasi-(i, j)-cores. Secondly, we recursively eliminate unsatisfied vertices and edges impacted by the quasi-(i, j)-core for each affected (i, j)-core. We adjust $C(G_p,i,j)$ to get $C(G_c,i,j)$ at the lower possible cost. Lastly, we proceed to the following layer of (i, j)-cores until all relevant (i, j)-cores have been updated.

In Algorithm 2, it first obtains a set of quasi-(i, j)-cores from $S_-$. Similar to the insertion case, the algorithm only conserves a map $\varvec{{\hat{\Psi }}}_-$ of (i, j)-pairs and corresponding edge sets. The main loop traverses (i, j)-cores in each layer. If $\varvec{{\hat{\Psi }}}_-(i,j) \ne \emptyset$, then it computes the degree of vertices in $C(G_p,i,j)$ and inserts unsatisfied vertices into corresponding vertex sets. Next, it recursively removes influenced vertices in two sets (auxiliary procedures are presented in Appendix). When the algorithm terminates, all bipartite core indexes of affected vertices are updated, and the algorithm returns $\varvec{\Phi }_{L}$ and $\varvec{\Phi }_{R}$.

For the removal algorithm, we do not need to calculate all degrees of vertices in $C(G_p, i,j)$ beforehand, and the value can be computed when a vertex is visiting.

Algorithm 2 detects impacted vertices of $C(G_p,i,j)$ for each $(l,r) \in \varvec{{\hat{\Psi }}}_{-}(i,j)\ne \emptyset$. In the worst case, it may traverse all vertices and edges in $C(G_p,i,j)$, therefore its time complexity is $O(|\varvec{C} ||G_p |)$, where $\varvec{C}$ is the number of (i, j)-cores in $G_p$. The space complexity is $O(|G_p |)$ because Algorithm 2 requires $O(|G_p |)$ to store the whole graph.

Example 2

We present a simple example (see Fig. 4) to demonstrate the process of Algorithm 2. We are still considering how to update (2, 2)-core with two removed edges because other (i, j)-cores can be changed in the same way. Firstly, we visit the quasi-(2, 2)-core using $\varvec{{\hat{\Psi }}}_-$, $\varvec{{\hat{\Psi }}}_-(2,2)$ only has one edge, which is highlighted in purple. Secondly, we get the partial-(2, 2)-core in $C(G_p,2,2)$, which is indicated in red and has 4 vertices. In contrast to the insertion case, we can search for influenced vertices directly in $C(G_p,2,2)$. Thirdly, we reduce the maximum i and j of these vertices in $\varvec{\Phi }'_L$ and $\varvec{\Phi }'_R$. Lastly, we continue to visit the next layer of (i, j)-cores, such as (2, 3)-core and (3, 2)-core, until all affected (i, j)-cores are updated. The algorithm uses $\varvec{\Phi }'_L$ and $\varvec{\Phi }'_R$ to update $\varvec{\Phi }_L$ and $\varvec{\Phi }_R$.

Fig. 4

The steps of updating (2, 2)-core with two removed edges are as follows: a the previous (2, 2)-core is indicated by a black dashed line, and two removed edges are noted by a green dotted line; b the quasi-(2, 2)-core is demonstrated by a purple half-dashed line; c the affected vertices and edges are implied by a red half-dashed line; d the current (2, 2)-core is stated by a black dashed line (Color figure online)

5 Top-down core maintenance

This section proposes a top-down approach for maintaining (i, j)-cores from dense to sparse. In many applications, such as recommendation system or vertex ranking, dense (i, j)-cores are more critical than sparse (i, j)-cores. For example, many people enjoy sharing their posts on Weibo,² the most popular social platform in China. We are especially interested in the evolution of high-impact users and associated posts by modeling the network to a bipartite graph since they determine information flow across the whole graph. Analyzing these users can have a substantial business impact (e.g., advertising and attracting activity users). However, these users only employ a subset of dense (i, j)-cores. Tracing the evolution of all (i, j)-cores is impractical.

To satisfy this demand, a top-down approach that can update expected (i, j)-cores of top-n layers with less time is present. Supergraphs (e.g., $(i-1,j)$-core and $(i,j-1)$-core) cannot not be used to reduce costs, unlike the bottom-up approach. We use current $(i+1,j)$-core and $(i,j+1)$-core instead to reduce cost while maintaining the previous (i, j)-core.

The essential processes of maintaining (i, j)-cores in the top-down approach are identical to those in the bottom-up solution but implement details differ significantly. For the insertion case, we redefine a candidate graph using the current $(i+1,j)$-core and the current $(i,j+1)$-core, and then extract the quasi-(i, j)-core from this candidate graph. Because the top-down method explores the whole graph, the candidate graph is larger than in the bottom-up condition. In the removal case, we ignore any vertex that is located in the current $(i+1,j)$-core or the current $(i,j+1)$-core because they must belong to the current (i, j)-core.

Because we maintain the (i, j)-cores from dense to sparse, the key issue for the top-down approach is to locate the highest layer of the direct relation graph $D(G_{c})$, denoted by $h(D(G_{c}))$ (see Sect. 2). When a bipartite graph is a complete graph, then $h(D(G_c)) = d(L(G_c)) + d(R(G_c)) -1$. Otherwise, $h(D(G_c)) < d(L(G_c)) + d(R(G_c)) -1$. Therefore, we identify the existing (i, j)-cores in order to reset the highest layer and then update expected (i, j)-cores in turn.

5.1 Insertion case

Except the candidate graph, the processes for maintaining (i, j)-cores are similar to the bottom-up approach. We first decompose the insertion graph into a set of quasi-(i, j)-cores; then, using quasi-(i, j)-core, $(i+1,j)$-core and $(i,j+1)$-core, we find a candidate graph for each influenced (i, j)-core; following that, we get the quasi-(i, j)-core from this candidate graph, and update (i, j)-pairs of vertices; lastly, we repeat the loop until all top-n layers of (i, j)-cores are updated.

After decomposing $S_{+}$, we investigate how to construct a top-down candidate graph on the entire graph using ${\hat{C}}(S_+,G_c,i,j)$, $C(G_c,i+1,j)$ and $C(G_c,i,j+1)$. The top-down candidate graph, unlike the bottom-up case, does not include the current (i, j)-core. More importantly, the impacts of a quasi-(i, j)-core will not spread across edges in the previous (i, j)-core, but may spread over edges in $C(G_c,i+1,j)$ and $C(G_c,i,j+1)$. In other words, we simply can not stop the search path when edges are located in $(C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$.

Definition 7

$F_t(i,j)$ is a top-down candidate graph, whose edge $(l,r) \in G_{c}$ is reachable from edges in ${\hat{C}}(S_+,G_c,i,j)$ via a path, such that $d(G_c,l) \ge i$, $d(G_{c},r) \ge j$ and $(l,r) \notin C(G_p,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)$.

Then, we consider getting P(i, j) from $F_t(i,j)$. Because we utilize the available information of $C(G_c,i+1,j)$ and $C(G_c,i,j+1)$, corresponding cases are more complicated than those of the bottom-up approach. In summary, four cases must be addressed: (1) if $C(G_c,i+1,j) \cup C(G_c,i,j+1) \ne \emptyset$, $C(G_p,i,j) \ne \emptyset$, and $C = C(G_p,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)$, then $P(i,j)= ({\hat{C}}(F_t(i,j),C, i,j)$ $\cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$; (2) if $C(G_c,i+1,j) \cup C(G_c,i,j+1)= \emptyset$, $C(G_p,i,j) \ne \emptyset$, and $C = C(G_p,i,j)$, then $P(i,j)= {\hat{C}}(F_t(i,j),C,i,j)$; (3) if $C(G_c,i+1,j) \cup C(G_c,i,j+1) \ne \emptyset$, $C(G_p,i,j) = \emptyset$, and $C = C(G_c,i+1,j) \cup C(G_c,i,j+1)$, then $P(i,j)= C \cup {\hat{C}}(F_t(i,j),C,i,j)$; (4) if $C = C(G_p,i,j) \cup C(G_c,i+1,j)\cup C(G_c,i,j+1) = \emptyset$, then $P(i,j) = C(F_t(i,j),i,j)$.

Although cases (1), (2) and (3) are similar, the associated solutions for getting partial-(i, j)-cores differ dramatically. Case (2) and (4) are identical to those of the bottom-up approach when $C(G_c,i+1,j) \cup C(G_c,i,j+1) = \emptyset$. Theorem 3 and 4 verify the correctness of two cases, we present detailed proofs in Appendix.

Theorem 3

If $C(G_c,i+1,j) \cup C(G_c,i,j+1) \ne \emptyset$, $C(G_p,i,j) \ne \emptyset$, and $C = C(G_p,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)$, then $P(i,j)= ({\hat{C}}(F_t(i,j),C, i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$.

Theorem 4

If $C(G_c,i+1,j) \cup C(G_c,i,j+1) \ne \emptyset$, $C(G_p,i,j) = \emptyset$, and $C = C(G_c,i+1,j) \cup C(G_c,i,j+1)$, then $P(i,j) = C \cup {\hat{C}}(F_t(i,j),C,i,j)$.

Algorithm 3 first decomposes $S_+$ to produce a map of quasi-(i, j)-pairs and edge sets, then copies $\varvec{\Psi }_L, \varvec{\Psi }_R$ to $\varvec{\Psi }_L^n, \varvec{\Psi }_R^n$. In the main loop, it gets $C(G_c,i,j)$ according to two cases. If $C(G_c,i,j) = \emptyset$ and $C(G_c,i-1,j) \ne \emptyset \vee C(G_c,i,j-1) \ne \emptyset$, it directly decomposes the candidate graph to get $(i',j')$-cores ($i' \ge i$ and $j' \ge j$) because no previous (i, j)-cores are accessible. Otherwise, it gets the quasi-(i, j)-core of $F_t(i,j)$ on C. Next, it adjusts $\varvec{\Psi }_L^n, \varvec{\Psi }_R^n$ based on preceding situations. Lastly, it inserts valid pairs $(i-1,j)$ and $(i,j-1)$ into $\mathcal {Q}'$ and continues the next loop. The algorithm returns $\varvec{\Psi }_L^n$ and $\varvec{\Psi }_R^n$ until it terminates.

Fig. 5

The following are the processes involved in updating the (2, 2)-core utilizing the current (3, 2)-core and two inserted edges: a the previous (2, 2)-core equals to the current (3, 2)-core, and they are both marked by a black dash-dotted line, with two inserted edges marked by a green dotted line; b the quasi-(2, 2)-core is indicated by a purple half-dashed line; c the candidate graph is highlighted by a blue half-dashed line; d the quasi-(2, 2)-core is depicted by a red half-dashed line; e the current (2, 2)-core is shown by a black dashed line and a dash-dotted line (Color figure online)

Example 3

We present a simple example (see Fig. 5) to illustrate the procedure of Algorithm 3. When two edges are inserted into the graph, we focus on updating the (2,2)-core. We emphasize the distinctions between bottom-up and top-down cases. When searching for a candidate graph, the method skips edges located in the previous (2,2)-core, and the current (3,2)-core, which can be omitted by visiting $\varvec{\Psi }_L$ and $\varvec{\Psi }_R$. Thirdly, the algorithm gets the quasi-(2, 2)-core of the candidate graph on C, which is highlighted in red and contains four vertices, and the algorithm revises $\varvec{\Psi }_L$ and $\varvec{\Psi }_R$ for vertices in the quasi-(2,2)-core. Lastly, the algorithm visits the following layer of (i, j)-cores, such as (1,2)-core and (2, 1)-core, until all expected (i, j)-cores have been updated. The algorithm returns $\varvec{\Psi }_L^n$ and $\varvec{\Psi }_R^n$.

The time complexity of Algorithm 3 is similar to Algorithm 1, except some operations on $F_t(i,j)$. Because the method searches for $F_t(i,j)$ on $G_{c}$, the size of $F_t(i,j)$ may be larger than that of $F_b(i,j)$. Thus, the overall time complexity is $O(|\varvec{{\hat{\Psi }}}_n ||G_c |) \ll O(|\varvec{C}||G_c |)$, where $|\varvec{{\hat{\Psi }}}_n |$ is the number of quasi-(i, j)-cores of top-n layers. In terms of the space complexity, it merely stores the entire graph $G_c$, hence it is $O(|G_c|)$.

It is worth mentioning that we do not apply bipartite core indexes of vertices in Algorithm 3. Because we only update top-n layers of (i, j)-cores, the bipartite core indexes of vertices are incorrect. Instead, we just save each (i, j)-pair and its associated vertices. Because the top-down approach can maintain expected (i, j)-cores, the inputs do not need to contain all (i, j)-pairs of vertices.

5.2 Removal case

Related operations for the remove case are comparable to those of the bottom-up approach. Because we update the $(i+1,j)$-core and the $(i,j+1)$-core before the (i, j)-core, we can skip vertices located in $(i+1,j)$-core and $(i,j+1)$-core. We are only interested in (i, j)-cores of top-n layers, therefore we maintain (i, j)-cores from dense to sparse.

Algorithm 4 decomposes $S_-$ into a map of quasi-(i, j)-pairs and edge sets, and then copies $\varvec{\Psi }_L, \varvec{\Psi }_R$ to $\varvec{\Psi }_L^n, \varvec{\Psi }_R^n$. In the main loop, it first scans edges in $\varvec{{\hat{\Psi }}}_{-}(i,j)$, and inserts unsatisfied vertices into $\mathcal {Q}_L$ and $\mathcal {Q}_R$ respectively; next, it modifies $C(G_p,i,j)$ to get $C(G_c,i,j)$, and updates $\varvec{\Psi }_L^n, \varvec{\Psi }_R^n$ by recursively removing unsatisfied vertices; at last, it inserts valid pairs $(i-1,j), (i,j-1)$ into $\mathcal {Q}'$ and continues the next loop. Until the algorithm terminates, it returns $\varvec{\Psi }_L^n$ and $\varvec{\Psi }_R^n$.

The time complexity of Algorithm 4 is $O(|\varvec{{\hat{\Psi }}}_n |\cdot |G_p |) \ll O(|\varvec{C} |\cdot |G_p |)$, where $|\varvec{{\hat{\Psi }}}_n |$ is the number of quasi-(i, j)-cores of top-n layers. In terms of the space complexity, storing the entire graph still takes $O(|G_p |)$.

6 Experiments

In this section, we conduct extensive experiments to evaluate the performance of our proposed algorithms. Experimental results show that our maintenance approaches outperform baselines.

All algorithms are written in C++ and compiled using GCC 9.3 with -O3 optimization setting. Experiments are carried out on a workstation with two Xeon E5-2630v3@2.4GHz CPUs (16 cores and 128GB RAM) running Linux operating system Ubuntu 20.04.

6.1 Dataset

Real graphs are downloaded from KONECT,³ including: actor2 (Actor2), actor-movie (AM), dbpedia-location (DL), dbpedia-producer (DP), dbpedia-starring (DS), dbpedia-writer (DW), komatrix-imdb (KI), dbpedia-recordlabel (DR), komatrix-citeseer (KC), opsahl-collaboration (OC). The details of them can be seen in Table 2, and none of them have isolated vertices.

Table 2 The details of real graphs: $|L(G) |$, $|R(G) |$ and $|E(G) |$ denote the size of left vertices, right vertices and edges, respectively

We can observe from Table 2 that most real graphs are sparse, with significantly less (i, j)-cores than $d(G,L(G)) \cdot d(G,R(G))$, implying that the maintenance solution is more effective than the decomposition method on most of them.

6.2 Metric and baseline

Because the (i, j)-core is a well-defined graph with a distinct structure, we do not require any additional metric to evaluate it. Previous studies (Cheng et al. 2011; Saríyüce et al. 2013; Li et al. 2014; Liu et al. 2020) have shown that running time is a significant criterion for assessing the efficiency of core decomposition and maintenance algorithms. Most methods have low dependence on memory size as they just traverse the graph. Moreover, some studies (Cheng et al. 2011; Wen et al. 2019) investigated I/O efficiency strategies for big size graphs that cannot be fitted into memory. Since we are primarily concerned with in-memory algorithms, running time is appropriate for assessing our algorithms. Mathematical proofs confirm the validity of our methods. In addition, we check the results of maintenance approaches to guarantee that all algorithms are correctly executed.

In comparison, we present three baselines algorithms (Liu et al. 2020). The first is the decomposition method, called ComShrDecom, denoted by Dec., which directly decomposes the entire bipartite graph to get its (i, j)-cores. Its basic idea is to investigate computation sharing opportunities while processing left and right vertices consistently. The number of iterations of Dec. is $2 \delta$, where $2\delta$ refers to the maximum value such that $(\delta , \delta )$-core is not empty. The remainder algorithms are two enhanced edge-based maintenance methods for insertion and removal cases, named BiCore-Index-Ins$^{*}$ and BiCore-Index-Rem$^{*}$, denoted by II and IR, respectively. BiCore-Index-Ins$^{*}$ (BiCore-Index-Rem$^{*}$) updates the maximal $i\ (j)$ for left (right) vertices by visiting a local subgraph rather than the entire graph, and then the algorithms revise bipartite core indexes of the corresponding vertices.

6.3 Running time

To simulate the edges are inserted into (removed from) a dynamic graph, we shuffle the edge set and randomly select the last $0.1\%$ from each graph as inserted edges. At the same time, the remainder is regarded as the previous graph. In the removal case, we shuffle the edge set and randomly choose the top $0.1\%$ from the graph as removed edges, while the previous graph has all edges. We do not seek the best outcomes for all graphs evaluated because edges can have various effects on (i, j)-cores. Since the running time of our maintenance algorithms depends on the local structure of a graph, optimizing these approaches for real applications with numerous inserted (removed) edges is rugged.

Table 3 The running time of core maintenance under the insertion case (second): our BUI obtains the best performance on all graphs except DL, DP and DR

Table 2 demonstrates that DL and DR are dense. The primary benefit of maintenance algorithms is that they can avoid recalculating unaffected (i, j)-cores. Maintenance methods are not appropriate for a dense or a sparse graph with many inserted (removed) edges (see Table 3), in which case most (i, j)-cores are affected. The performance of II is superior to ours while dealing with an imbalanced graph because II can only update the maximal $i\ (j)$ of corresponding vertices. In contrast, our methods must update all affected (i, j)-cores. Moreover, because TDI incurs a higher cost when searching the candidate graph, its performance is worse than BUI.

In contrast to the insertion case, Table 4 demonstrates that removal maintenance algorithms outperform the decomposition method. Although inserted and removed edges both disseminate their impact through nearby paths, there are apparent differences. The insertion algorithms refer to search and evict operations, whereas the removal case concerns the evict process. TDR, unlike BUR, can utilize the information of updated (i, j)-cores to avoid calculating the core degree of affected vertices. As a result, it is inexpensive. In comparison to our approaches, IR performs relatively poorly. The gap in some graphs, such as AM, reaches one order of multitude. It also does well on DW and OC.

Table 4 The running time of core maintenance under removal case (second): all maintenance algorithms outperform the decomposition method

6.4 Ratio test

To track the running time evolution of our algorithms, we run all methods with varying values of r and n on these graphs, where r and n denote the edge ratio and the number of layers, respectively. Apart from these factors, the rest of the settings are comparable to our performance evaluation. Because of the randomization of inserted (removed) edges, the running time for the identical settings varies for each graph experiment.

Table 5 The running time of core maintenance with different values of r under insertion case (second): Dec. performs best on DL and DR, whereas our BUI obtains the best performance on DS, DW, OC

Table 5 illustrates that when r increases, the performance of all insertion maintenance algorithms decreases since inserted edges influence more (i, j)-cores. Because decomposition approaches always decompose entire graphs, their running time is rather stable. Similar to the insertion case, when the number of edges triples, BUI and TDI take 1.5x time. But the consuming time of II is proportional to the edge growth ratio.

Table 6 illustrates that the performance of all removal maintenance algorithms degrades when removed edges influence more (i, j)-cores. Because removed edges take up a small proportion of the total edges, the running time of the decomposition remains consistent, although with a slight fluctuation. When the number of removed edges triples, the running time of all maintenance algorithms becomes proportional to the edge increase ratio.

Table 6 The running time of core maintenance with various r values under remove case (second): IR achieves the best results on DL and DR while our TDR obtains the best effect on DS and DW

Lastly, we study the impact of maintaining (i, j)-cores of top-n layers with $r = 0.1\%$, where n is the number of layers of (i, j)-cores and varies from 1 to 20. Other settings are analogous to those used in the above experiments.

Table 7 The running time of maintaining (i, j)-cores of top-n layers under insertion case (second): our TDI outperforms all other algorithms

Table 8 The running time of maintaining (i, j)-cores of top-n layers under removal case (second): our TDR performs best on AM, Actor2 and KI, and our BUR achieves the best performance on KC

We realize that the performance of TDI and TDR (see Tables 7 and 8) is more stable when compared with different values of r. On the one hand, the number of (i, j)-cores in top-n layers is minimal; on the other hand, dense (i, j)-cores are hardly affected by inserted (removed) edges due to its high density.

As previously stated, the maintenance cost of removal algorithms is lower than that of insertion methods. As a result, the cost of estimating the maximal layer of the current graph will be a significant fraction under the top-down approach. If removed edges only influence a few (i, j)-cores, the cost of our top-down approach may outweigh the bottom-up method.

6.5 Discussion

Finally, we provide a summary of (i, j)-core maintenance. In detail, we first analyze the benefits and drawbacks of baselines. Then, we discuss the advantages and disadvantages of our approaches. Lastly, we address the distinction between bottom-up and top-down approaches.

Through our experiments, we observe that Dec. outperforms other approaches in dense graphs. The basic principle behind maintenance algorithms is to find increment (decrement) of the previous (i, j)-core. A few inserted (removed) edges in a dense graph will affect most (i, j)-cores. As a result, the expense of maintenance is high. Meanwhile, most inserted (removal) edges in a sparse graph do not affect dense (i, j)-cores, but Dec. must recalculate them. This is why maintenance algorithms are developed. II and IR only update the maximal bipartite core indexes of vertices for each edge. It does not recalculate all (i, j)-cores, so it is appropriate for dealing with extremely unbalanced graphs. However, the cost of II and IR are proportion to the edge increase ratio, implying that they are not fit for other types of graphs with numerous inserted (removed) edges.

When compared to II and IR, our methods reduce the cost of seeking increment (decrement) of the previous (i, j)-core since it deals with several edges at the same time. Similarly, our methods suffer from the same disadvantages, making them unsuitable for dense graphs. Furthermore, our approaches perform worse when tackling extremely imbalanced graphs because our methods must calculate all affected (i, j)-cores. However, there is no such restriction in II and IR, which offers the possibility of combining two strategies to take advantage of both approaches.

Bottom-up and top-down approaches are generally intended for different purposes. The former is used to handle cases when all (i, j)-cores are required, while the latter is used to take (i, j)-cores of top-n layers. Although the top-down approach can also maintain all (i, j)-cores, it will cost more than the bottom-up approach for the insertion case. A bottom-up approach, for example, can be employed as filter stages for some complicated subgraphs, e.g., bicliques (Mukherjee and Tirthapura 2017). On the other hand, the top-down approach can be used in the community detection of some recommendation systems. Our methods are currently not adequately parallelized. Hence, they are unsuitable for dealing with large graphs. In future work, we will utilize the possibility of concurrently updating (i, j)-cores, improving resource utilization.

7 Related work

Numerous works on cohesive subgraphs (Semertzidis et al. 2019) have been published in recent years, including maximal cliques (Akkoyunlu 1973; Jiang et al. 2017), quasi-cliques (Yang et al. 2016), k-plexes (Berlowitz et al. 2015), k-cores (Saríyüce et al. 2013; Montresor et al. 2011; Wu et al. 2015), k-trusses (Huang et al. 2014). We will look into cohesive subgraphs of unipartite and bipartite graphs.

Some studies concentrate on k-core decomposition in various scenarios. Cheng et al. (2011) presented the external-memory approach in massive graphs, and their algorithms achieved comparable performance with the in-memory algorithm. Montresor et al. (2011) demonstrated new distributed algorithms in large networks, allowing the decomposition over a set of connected machines and analyzing the low bound of the complexity. Wu et al. (2015) developed efficient distributed algorithms to compute (k, h)-cores in a temporal graph. Khaouid et al. (2015) implemented an algorithm that can calculate the k-core decomposition for massive networks in a consumer-grade PC.

Some other works are concerned with k-core maintenance. Saríyüce et al. (2013) introduced incremental k-core decomposition algorithms for the streaming graph data based on the edge inserted (removed). Li et al. (2014) suggested an efficiency approach for updating a certain number of nodes after inserting (deleting) an edge. To further improve the performance, they also provided two pruning strategies by exploiting the lower and upper bounds of the core number. Zhang et al. (2017) proposed a fast order-based approach for the core maintenance that outperformed the state-of-the-art algorithms. Bai et al. (2020) presented an efficient method to handle core maintenance of enormous temporal graphs, which served as the idea for our research.

Researchers are interested in bipartite graphs because they may readily model the collaborative relationship between two different entities. Zou (2016) exploited the bitruss problem in a bipartite graph to find the largest edge-induced subgraph in which every edge is included in at least k rectangles within the subgraph. Wang et al. (2018) proposed a novel local search framework with four heuristics algorithms to improve the performance of the maximum balanced biclique issue. Wang and Liu (2018) evaluated the performance of community detection on bipartite graphs. Liu et al. (2020) proposed efficient (i, j)-core decomposition and maintenance methods based on bipartite core indexes, whose space complexity is proportional to the graph size. However, their approaches must compute all bipartite core indexes, which is inefficient for applications that focus on a few dense (i, j)-cores.

8 Conclusions

(i, j)-core, as a general concept of k-core, can distinguish various roles of two types of vertices in bipartite graph analysis. (i, j)-cores maintenance is more challenging due to its unique structure. To further decrease the cost of finding (i, j)-cores of a dynamic bipartite graph when a few edges change, we provide a bottom-up approach to update all (i, j)-cores quickly and a top-down approach to get the expected (i, j)-cores of top-n layers. Experimental results show that our maintenance approaches achieve better performance than baselines on most graphs.

We will continue to parallelize our algorithms to deal with (i, j)-core maintenance of massive graphs that may fully utilize hardware resources in future work.

Appendix A Proofs and Algorithms

Proof for Lemma 1

Let $C = C(G_p,i,j)$ and $P = P(i,j)$, ${\hat{C}}(P,C,i,j) \subseteq P$ holds by Definition 4. Thus, we just prove $P \subseteq {\hat{C}}(P,C,i,j)$. Suppose there is a nonempty graph $A = P \setminus {\hat{C}}(P,C,i,j)$, there must be a vertex $l\ (r) \in A$ such that $d(P(C),l)<i\ (d(P(C),r)<j)$, where P(C) is the extended graph of A on C, and this vertex leads to the recursive deletion on P. Otherwise, ${\hat{C}}(P,C,i,j)$ can expand via $l\ (r)$. Since $P = C(G_c,i,j) \setminus C$, $d(P(C),l) \ge i\ (d(P(C),r) \ge j)$ always holds for $l\ (r) \in P$, which makes a contradiction. Thus, $P \subseteq {\hat{C}}(P,C,i,j)$.

In summary, $P = {\hat{C}}(P,C,i,j)$. $\square$

Proof for Theorem 1

Let $C = C(G_p,i,j)$, $F = F_b(i,j)$ and $P = P(i,j)$. Firstly, we prove ${\hat{C}}(F,C,i,j) \subseteq P$. Suppose there is a nonempty graph $A = {\hat{C}}(F,C,i,j) \setminus P$, there must be a vertex $l\ (r) \in A$ such that $d(F(C),l)<i\$ $(d(F(C),r)<j)$ and this vertex leads to recursive deletion on A, where F(C) is the extended graph of F on C. Otherwise, P can expand via $l\ (r)$, which contradicts Definition 6. According to Definition 5, $d(F(C),l) \ge i\$ $(d(F(C),r) \ge j)$ holds for an arbitrary $l\ (r) \in F$ unless there is a vertex $l'\ (r') \in C$ such that $d(C,l')< i\ (d(C,r') <j)$. Since C is the previous (i, j)-core, this makes a contradiction. As for an edge $(l,r) \in A$, since $l,r \in P$, P can expand via adding (l, r), which contradicts Definition 6. Thus, ${\hat{C}}(F,C,i,j) \subseteq P$.

Secondly, we prove $P \subseteq {\hat{C}}(F,C,i,j)$. Since $P\subseteq F$, ${\hat{C}}(P,C,i,j) \subseteq {\hat{C}}(F,C,i,$ j) holds. By Lemma 1, $P(i,j) = {\hat{C}}(P,C,i,j) \subseteq {\hat{C}}(F,C,i,j)$.

In summary, $P = {\hat{C}}(P,F,i,j)$. $\square$

Proof for Theorem 2

Since $C(G_p,i,j)=\emptyset$, we have $C(G_c,i,j) = P(i,j) \subseteq F_b(i,j)$. Since $F_b(i,j) \subseteq G_{c}$, $C(F_b(i,j),i,j) \subseteq C(G_c,i,j)$ holds. Due to $C(G_c,i,j) \subseteq F_b(i,j)$, we have $C(G_c,i,j) \subseteq C(F_b(i,j),i,j)$.

In summary, $C(F_b(i,j),i,j)=C(G_c,i,j) = P(i,j)$. $\square$

Proof for Theorem 3

Let $F = F_t(i,j)$, $P = P(i,j)$ and $C = C(G_c,i+1,j) \cup C(G_c,i,j+1) \cup C(G_p,i,j)$. Firstly, we prove $({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j) \subseteq P$. Since $C(G_c,i+1,j) \cup C(G_c,i,j+1) \subseteq C(G_c,i,j)$, $(C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j) \subseteq P$ holds. Since ${\hat{C}}(F,C,i,j) \setminus C(G_p,i,j) = \emptyset$, we just need to prove ${\hat{C}}(F,C,i,j) \subseteq P$. Suppose there is a nonempty graph $A ={\hat{C}}(F,C,i,j)\setminus P$, we have $d(F(C), l) \ge i$ or $d(F(C),r) \ge j$ for arbitrary $l,r \in A$, where F(C) is the extended graph of F on C. If $l \notin P$, there must be a vertex $l' \in C \ (r' \in C)$ such that $d(C,l')<i\ (d(C, r') < j)$, which makes a contradiction. Since $l,r \in P$, if $(l,r) \notin P$, then we have $P \subseteq P \cup (l,r)$, which contradicts Definition 6. Thus, $({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1) ) \setminus C(G_p,i,j) \subseteq P$.

Secondly, we prove $P \subseteq ({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$. Suppose there is a nonempty graph $A = P \setminus (({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j))$. Since $(C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j) \subseteq P$ and ${\hat{C}}(F,C,i,j) \setminus C(G_p,i,j) = {\hat{C}}(F,C,i,j)$, $A \subseteq P \setminus {\hat{C}}(F,C,i,j)$ holds. Clearly, $A \subseteq F$. Since $A \ne \emptyset$, there must be a vertex $l\ (r) \in A$ such that $d(F(C),l)<i\ (d(F(C),r)<j)$, where F(C) is the extended graph of F on C. By Definition 7 and C is the union graph of previous (i, j)-core, $(i+1,j)$-core and $(i,j+1)$-core, $d(F(C),l) \ge i\ (F(C),r) \ge j)$ holds for $l\ (r) \in A$. Again, this is contradiction. Hence, $P \subseteq ({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$.

In summary, $P = ({\hat{C}}(F,C,i,j) \cup C(G_c,i+1,j) \cup C(G_c,i,j+1)) \setminus C(G_p,i,j)$. $\square$

Proof for Theorem 4

Let $F = F_t(i,j)$, $P = P(i,j)$ and $C = C(G_c,i+1,j) \cup C(G_c,i,j+1)$. Firstly, we prove ${\hat{C}}(F,C,i,j) \cup C \subseteq P$. Since $C(G_p,i,j) = \emptyset$, we have $P= C(G_c,i,j)$. By Definition 6, we have $C \subseteq C(G_c,i,j) = P$. Thus, we just need to prove ${\hat{C}}(F,C,i,j) \subseteq P$. Suppose there is a nonempty graph $A = {\hat{C}}(F,C,i,j)\setminus P$, we have $d(F(C),l) \ge i\ (d(F(C), r) \ge j)$ for arbitrary $l \in A\ (r \in F)$, where F(C) is the extended graph of F on C. If $l \notin P$, there must be a vertex $l' \in C\ (r' \in C)$ such that $d(C,l')< i\ (d(C,r') < j)$, which makes a contradiction because C is the union graph of $(i+1,j)$-core and $(i,j+1)$-core. Since $l,r \in P$, if $(l,r) \notin P$, then we have $P \subseteq P \cup (l,r)$, which contradicts Definition 6. Thus, ${\hat{C}}(F,C,i,j) \cup C \subseteq P$.

Secondly, we prove $P\subseteq {\hat{C}}(F,C,i,j) \cup C$. Suppose there is a nonempty graph $A = P \setminus ({\hat{C}}(F,C,i,j) \cup C)$, since $C \subseteq P$, we have $A \subseteq P \setminus {\hat{C}}(F,C,i,j)$. Clearly, $A \subseteq F$, otherwise it contradicts our assumption. Since $A \ne \emptyset$, there must be a vertex $l\ (r) \in A$ such that $d(F(C),l)<i\ (d(F(C),r)<j)$, where F(C) is the extended graph of F on C. By Definition 7 and C is the union graph of $(i+1,j)$-core and $(i,j+1)$-core, $d(F(C),l) \ge i\ (d(F(C),r) \ge j)$ holds for $l\ (r) \in A$. Again, this is a contradiction. Hence, $P \subseteq {\hat{C}}(F,C,i,j) \cup C$.

In summary, $P = {\hat{C}}(F,C,i,j) \cup C$. $\square$