Core decomposition and maintenance in weighted graph

Abstract

Coreness is an important index to reflect the cohesiveness of a graph. The problems of core computation in static graphs and core update in dynamic graphs, known as the core decomposition and core maintenance problems respectively, have been extensively studied in previous work. However, most of these work focus on unweighted graphs. Considering that graphs are weighted in a lot of realistic applications, it is indispensable to extend the coreness to weighted graphs and devise efficient algorithms for weighted core decomposition and weighted core maintenance. In this work, we present a new definition of weighted coreness for vertices in a weighted graph, by taking into account the weights of vertices, which makes the coreness in unweighted graph be a special case. We propose efficient algorithms for both weighted core decomposition and weighted core maintenance problems. The coreness of vertices can be computed in linear time by the proposed decomposition algorithm, while the proposed core maintenance algorithm can process multiple-edge insertions/deletions simultaneously, which greatly reduces the core update time. Comprehensive experiments on both realistic networks and temporal graphs exhibit our algorithms are efficient and scalable.

1 Introduction

Benefiting from the efficient computation and effectiveness, coreness has been recognized as one of the most helpful and efficient index among a variety of indexes that depicts cohesiveness of vertices in graphs, such as clique, k-truss [7] and k-shell. Coreness has been broadly used to detect community [10], as well as biological studies [22] and large-scale network visualization [2, 4]. In unweighted graphs, a maximal connected subgraph is called a k-core only if it satisfies that each vertex’s degree is larger than or equal to k in the subgraph, as a vertex v existing in different k-core, the core number of v is actually equal to the maximum k of k-core. The computation of coreness, known as core decomposition, has been extensively studied, and an O(m) algorithm was given in [5], m stands for the quantity of edges in the graph. Furthermore, considering that the graphs will be continuously changing as long as vertices and edges are inserted or deleted, the core maintenance problem which is to renew vertices’ core number and avoid coreness recomputation, were presented [19] and extensively studied [23].

Previous work mostly focus on handling unweighted graphs, and the proposed algorithms cannot be adapted to weighted graphs, which is commonly seen in realistic. For instance, in a social network, different vertices have different influence in the network, such as the number of followers in twitter, which can be seen as the weight of vertices. Obviously, connecting to a vertex with large weight can impact the network more significantly. Hence, it is important and necessary to consider the weights of vertices in the coreness, rather than just counting the number of connected vertices as in the unweighted scenario.

In this work, we present a new definition of weighted coreness for vertices in a weighted graph, by taking into account the weights of vertices. The coreness in the unweighted graph can be considered as a particular example of our definition when the weight of each vertex is one. Hence, our definition well unifies the definitions of coreness in both weighted and unweighted graphs, which can greatly facilitate the studies of coreness. In [27], k-core decomposition is applied to analyze the large-scale software system, where relationships have all been treated equally and have the same importance for structural analysis in [27]. With the definition we proposed, the influence of each component of a software system can be considered in the analysis of large-scale software system. Clearly, in this case, the result will be closer to the real scene. k-core decomposition is also widely used in the identification of influential spreaders [13, 16],but only the degree of nodes in social networks cannot offer exact influence of users. In [1], Mohammed studied that weighted k-core decomposition (link-weighted) can be applied to identify the influential spreaders.

In the social network like Instagram and Twitter, some indicators cannot be represented by the link of users, such as the official certification of the platform and the popularity of user outside the platform, while the indicators can be represented by the weight of users itself. There are also a number of different groups in social networks, while a user may belong to several different groups. The influence of a user differs in the different groups and it is difficult to distinguish the influence by the link of users for the reason that the links of users will not change in different groups. It should also be noticed that in the social network like Twitter, some people may possess many followers by registering a number of account maliciously, the normal k-core cannot find the user with these low-quality followers. When we use weighted k-core to analyze the cohesive subgraph and reduce the weight of these users, we can moderate the impact of these malicious accounts and mine more accurate results.

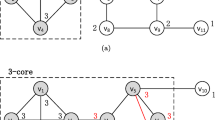
Under the proposed weighted coreness, we study both the core decomposition and core maintenance problems. For the weighted core decomposition problem, we show that we can compute the weighted core numbers of vertices in linear time. Then we pay our attention to maintain the weighted core number in the single-edge insertion/deletion scenario. We present an efficient core maintenance algorithm on the basis of a key observation that when a single edge is inserted/deleted, only a few vertices may update its core numbers. The observation helps greatly reduce the searching range of potential update vertices, and hence significantly improve the maintenance efficiency. We finally consider the more realistic scenario, say multiple edges insertion and deletion. Multiple-edge insertion/deletion incurs many difficulties that do not exist in single-edge cases. For example, if we insert multiple edges into the graph, it is hard to know the cumulative increase on each vertex’s core number, as shown in Figure 1. To overcome the difficulties, we first show that when a k-edge set and a k-favorable edge set are inserted/deleted, the range of vertices whose core number may alter can be bounded. Based on it we proposed our multiple-edge core maintenance algorithms, by splitting inserted/deleted edges into multiple k-edge sets and k-favorable edge sets and handling these sets one by one, instead of handling the inserted/deleted edges one by one, such that the processing time can be greatly reduced. Experiments on realistic graphs and temporal networks prove that the proposed multiple-edge maintenance algorithm can remarkably make the maintenance more efficient.

Fig. 1

Assume < v₂, v₃ >,< v₂, v₉ > will be inserted into the graph(a), after the insertion, the core number of v₂ will be updated from 6 to 10, the core number of v₃ will be updated from 9 to 10. Assume < v₂, v₃ >,< v₂, v₆ > will be inserted into the graph(b), the core number of v₂ will be updated from 6 to 11, and the core number of v₃ will be updated from 9 to 11, the core number of v₄, v₅, v₆ will be updated from 10 to 11

Contributions

Our contributions are multi-folded:

• We present a new definition of weighted coreness for vertices in a weighted graph, by taking into account the weights of vertices. Our definition well unifies the definitions of coreness in both weighted and unweighted graphs.

• We propose efficient algorithms for both weighted core decomposition and weighted core maintenance problems. The coreness of vertices can be computed in linear time by the proposed decomposition algorithm, while the proposed core maintenance algorithm can process multiple-edge insertions / deletions simultaneously, which greatly reduces the core update time.

• Extensive experiments on both realistic networks and temporal graphs show that our algorithms are efficient and scalable.

Organizations

The remainder of this paper is organized as follows. In Section 2, some closely related works are reviewed. In Section 3, we give some definitions that will be used in the following paper. The weighted core decomposition algorithms in static graphs is in Section 4. Theoretical bases that can support the algorithm are presented in Section 5. We present incremental core maintenance algorithm and decremental core maintenance algorithm in Section 5. In Section 6, we maintain the weighted core number for multiple edge insertion or deletion instead of single edge. In Section 7, there are illustration and analysis for the experiments. At last, this work is concluded in Section 8.

2 Related works

In unweighted graph, the core decomposition and maintenance problems have been well studied. An O(m) algorithm for cores decomposition was given in [5], m stands for the quantity of edges. In [6], an external-memory algorithm was given to solve the problem that the memory cannot hold a very large graph. Core decomposition in the distributed setting was studied in [21]. In [15], the above-mentioned three k-core-decomposition algorithms were compared using the WebGraph and GraphChi model. A parallel core decomposition algorithm was given in [8]. For core maintenance, in unweighted graphs, efficient algorithms was proposed in [19, 23], it focus on single edge to maintain the core number of each vertex. In [28], an order-based approach was proposed to reduce the time cost by maintaining a k-order. The scenario of core maintenance with multiple edge insertion/deletion was studied in [14, 24]. It shows that when a k-superior edge set is inserted into or deleted from the graph, only the vertex whose core number equals to k may update its core number and the change is at most 1. In [12], a joint edge set was proposed to optimize the algorithm in [14, 24]. Core maintenance in distributed systems was considered in [3].

There have been some works studying core decomposition in weighted graphs. In [9], Eidsaa puts forward the s-core in weighted graphs with weights on edges. The s-core is defined by replacing the vertex degree with node strength which is the sum of edge weights connected to a vertex. A s-core decomposition algorithm was proposed in [9]. In [11] and [25], both edge’s weight and node degree were considered in the core definition. Wu [26] presented a unified framework to generalize the established k-core decomposition algorithm for both weighted and unweighted graphs with edge weights. The core maintenance problem on edge-weighted graph was studied in [20], the definition of weighted subcore and purecore were introduced, the time cost can be reduced by operating the weighted subcore and purecore. Unlike our work, all above results considered the weight on edges.

In [18], a new community model called k-influential community was proposed, which can capture the influence of a community in a weighted graph with weights on vertex. This model is based on normal k-core and the minimal node weight in a community. Li et al. [18] studied the community search problem. Given two parameters r and k, it can find the top-r-no-contained-k-influential community with the highest influence value. The difference between our work and [18] is that we consider the node weight while we find the subgraphs, but [18] do the normal k-core decomposition first to find the subgraphs, and node weight is just a parameter that used to measure the influence of each k-core.

3 Problem definition

Let G be a undirected and weighted graph G = (V, E, W), where V is the vertex set, E is the edge set and W is the set of weight on each vertex. For a vertex v ∈ G, let N(v) be the neighborhood of v. Denote by d(v) = |N(v)|. Let W_v be the weight of v. The current weighted degree of v is determined as the sum of v’s neighbors’ weights, i.e., cd[v] =_u∈N(v)W(u).

Based on the weighted degree of vertices, we define the weighted core below.

Definition 1 (k-Weighted Core)

A graph H is named a k-weighted core, only if H meets the conditions below: (1) H is connected; (2) The weighted degree of each vertex is larger than or equal to k; (3) H is the maximal substructure satisfying (1) and (2).

Now we can give the definition for the weighted core number of vertices. In particular, the definition of weighted core number is similar with unweighted scenario, as a vertex v existing in different k-weighted cores, the weighted core number of v is actually equal to the maximum k of k-weighted-core. The weighted degree is the sum of v’s neighbors’ weights whose core number is at least core_w(v), denoted as d_w(v).

We study the weighted core decomposition and the weighted core maintenance problems. Specifically, the weighted core decomposition problem is computing the weighted core number of each vertex in graphs, while the weighted core maintenance problem is renewing the weighted core numbers of vertices avoiding recomputation. The core maintenance problem can be further classified into two cases: incremental core maintenance and decremental core maintenance, which corresponds to the cases that edges are inserted and deleted respectively.

4 Weighted core decomposition

In this section, we present a weighted core decomposition algorithm as shown in Algorithm 1.

The basic strategy of the algorithm is deleting a vertex with the minimum weighted degree recursively. In each iteration, the vertex v with the minimum weighted degree is found, whose weighted core number is then determined. The principle is that if its current weighted degree is larger than the weighted core number determined in the last iteration, this means that v can be in a weighted core with larger weighted core number, and so v’s weighted core number is set to its current weighted degree; otherwise, v’s weighted core number is set to be the weighted core number determined in the last iteration. At the end of the iteration, v and its connected edges are deleted. We show an example using the graph given in Figure 1. In the first iteration, the vertex with the minimum weighted degree is v₂, and the weighted degree of v₂ is 6. By this algorithm, the weighted core number of v₂ equals to 6, v₂ and its connected edges will be deleted. In the second iteration, the vertex with the minimum weighted degree is v₃ and its weighted degree is 9. Then the weighted core number of v₃ is 9 by the principle given in the algorithm, v₃ and its connected edges will be deleted. In the third iteration, the vertex v₆ has the minimum weighted degree 10. This means v₆’s weighted core number is 10, and then v₆ and its connected edges will be deleted. In the fourth iteration, the vertex v₄ has the minimum weighted degree 5, then the weighted core number of v₄ is 10 by the given principle. Similarly, we can finally get the weighted core numbers of every vertex (Fig. 2).

Fig. 2

An example for weighted core decomposition. The red numbers represent the weighted core numbers of vertices

5 Core maintenance with single-edge insertion/deletion

In this section, we consider the core maintenance problem with single-edge insertion and deletion. Specifically, we will first present some theoretical results that can help reduce searching range of vertices that their weighted core number may be updated, on the basis of which we give our algorithms for both single-edge incremental and decremental core maintenance.

5.1 Theoretical basis

In this section, we first show that when an edge is inserted or deleted, only vertices whose weighted core numbers are in a specified range may update their weighted core numbers. These results can greatly reduce the search range in the graph.

We first consider the insertion case. let G be a graph and an insert a edge (u₁, u₂) into G, the weighted core numbers of u₁ and u₂ are k₁ and k₂ respectively. Assume that k₁ ≤ k₂. w₁ is the weight of vertex u₁ and w₂ is the weight of vertex u₂.

By the definition of the weighted core number, we get the following result.

Lemma 1

The weighted core number of u₁ can be at most k₁ + w₁ after an insertion.

We next show that only vertices satisfying a specified condition may update the weighted core number.

Lemma 2

When an edge (u₁, u₂)(k₁ ≤ k₂) is inserted into the graph, only vertices whose weighted core numbers are in the range [k₁, k₁ + w₂) and can connect to (u₁, u₂) may update their weighted core numbers after the edge insertion.

Proof

If a vertex v is not connected to the insert edge u₁, u₂, the cd of every vertex in its subgraph will not be updated after the insertion, hence the weighted core number of v will not be updated. We first prove the upper bound. It is known that the weighted core number of u₁ after edge insertion is at most k₁ + w₂ by Lemma 1. Consider a vertex v with weighted core number k₃ not smaller than k₁ + w₂ which updates its weighted core number after the insertion, and the new weighted core number is $k_{3}^{\prime }$. Let H_v and $H_{v}^{+}$ denote the max-weighted cores for vertex v before and after the insertion, respectively. It must have that $(u_{1}, u_{2}) \in H_{v}^{+}$, as otherwise H_v has been a $k_{3}^{\prime }$-core including v, the contradiction occurs. Let $Z=H_{v}^{+}\setminus \{e\}$. It is easy to see that Z is a $k_{3}^{\prime }-w_{2}>k_{1}$ weighted core, which is a contradiction.

Using a similar approach, we can show the lower bound. □

Similarly with the insertion case, we can show that when an edge is deleted, only vertices whose weighted core numbers are in a specified range can change their weighted core number.

Lemma 3

When an edge (u₁, u₂)(k₁ ≤ k₂) is deleted from the graph, only those vertices whose weighted core numbers are in the range (k₁ − w₂, k₁] and can connect to (u₁, u₂) may update their core numbers after the deletion.

Proof

The weighted core number k₂ may update to is [k₁ − w₂, k₁], the neighbor of u₂ whose weighted core number is in (k₁ − w₂, k₁] may update its weighted core number then. The rage of the weighted core number will decrease for the neighbor’s neighbor. So only vertex whose weighted core number is in (k₁ − w₂, k₁] may update its weighted core number. □

The above results can help reducing the searching range of update vertices greatly. Based on these results, we then present our weighted core maintenance algorithm.

5.2 Incremental core maintenance algorithm

The incremental algorithm for single-edge insertion is given in Algorithm 2, Algorithm 3 and Algorithm 4. In particular, the main algorithm is given in Algorithm 3, which shows how to update the current degree of vertices that may update their weighted core numbers, such that the real value of the weighted core number of vertices can be obtained; Algorithm 2 shows how to find the vertices which may update the weighted core number, and we try to find the fewest vertices, based on the theoretical results given in the last section; In Algorithm 2, it is shown how to update the current degree of vertices when a vertex is determined not to update the weighted core number. We next introduce the algorithms in more detail.

5.3 Insertion algorithm

In this section, we present our weighted core maintenance algorithm as shown in Algorithm 2

In the algorithm, the endpoint of the inserted edge that has smaller weighted core number is recognized as the root vertex. Then a DFS traversal is executed to find the vertices that may update the weighted core number. This process is given in Algorithm 3. Only vertices that are reachable from the root (vertex r) and whose weighted core numbers are not smaller than that of the root should be checked by Lemma 2 (those in subgraph P). During the process, a cd value, which is recording the weighted degree of a vertex caused by neighbors whose weighted core numbers are at least k(the weighted core number of the root), is computed for each vertex. This value indicates whether the vertex is potential to increase the weighted core number. After all vertices are found (those in P), the vertices with the smallest core numbers are iteratively processed to determine whether there are still update vertices. In particular, when a vertex’s weighted core number is confirmed, as shown in Algorithm 4, a DFS process is executed to update the current degree cd of vertices that will be used in the remaining computation. Finally, when the core numbers of vertices in H are all at least K(r) + W[l], then by Lemma 2, all remaining vertices will not change their weighted core number, and hence, the algorithm halts.

5.4 Decremental core maintenance algorithm

We give the weighted core maintenance algorithm for single-edge deletion in Algorithm 6 and Algorithm 5. Here the algorithm uses the bound given in Lemma 3 to determine the potential vertices.

6 Core maintenance with multiple-edge insertion/deletion

We turn our attention to the scenario of multiple edge insertion and deletion. A naive approach is to handle the inserted/deleted edges one by one using the algorithms given in the last section. However, this approach is clearly very inefficient. We investigate the approaches which can handle multiple edges at one time.

To solve the problem of multiple edges insertion and deletion, it is hard to determine the cumulative increase/decrease on the weighted core number of vertices, we instead think the problem that what kind of edges are inserted/deleted will make the weighted core number of vertices change in the same boundary. In this case, after the insertion and deletion of multiple edges, edges can be handled at the same time.

In subsequence, we find the set of edges that can make coreness of vertices change in a same boundary, based on which we present our algorithms.

6.1 Incremental algorithm

6.1.1 Theoretical basis

We first give some notations. Let graph G = (V, E, W) be a graph, an edge e =< u, v > is called a favorable edge for u if core_w(v) ≥ core_w(u). The weighted core value of an edge is the smaller one of its endpoints’ core value, i.e., core_w(e) = min{core_w(u),core_w(v)}.

Definition 2 (k-Edge Set)

E_k = {e₁, e₂,...,e_m} is a k-edge set, if it satisfies:

• (i) The weighted core number of e_i is k, for 1 ≤ i ≤ m.

• (ii) if e_a and e_b (1 ≤ a, b ≤ m, a ≠ b) have the same endpoints q, core_w(q) > k.

Given a k-edge set E_k = {e₁, e₂,...,e_m}, without loss of generality, for each edge e_i =< u_i, v_i >,1 ≤ i ≤ m, we assume core_w(v_i) ≥ core_w(u_i). Furthermore, let l ∈{v₁, v₂,...,v_m} be the vertex with the maximum weight. Then we have the following result.

Lemma 4

After inserting E_k into graph G, for every vertex v in G, it satisfies that:

• (i) if k ≤ core_w(v) < k + W(l), after insertion, core_w(v) will not exceed k + W(l);

• (ii) if core_w(v) ≥ k + W(l) or core_w(v) < k, core_w(v) will not change.

Proof

For (i), we assume the vertex v with k ≤ core_w(v) < k + W(l) can increase its weighted core number to k + x (x > W(l)). Let H_v and $H_{v}^{+}$ be the max-k-core of v before edge insertion and the max-(k + x)-core of v after the insertion respectively. It can be known that one of the edges in E_k must belong to $H_{v}^{+}$, if not, core_w(v) = k + x before the insertion, and a contradiction occurs. Let Z = $H_{v}^{+}\backslash E_{k}$. For a vertex u ∈ Z, if core_w(u) < k, the weighted degree of u does not change when the edges in E_k are deleted from $H_{v}^{+}$, so d_w(u) ≥ k + x in Z. If core_w(u) = k, u can lose at most one neighbor j that is connected by a favorable edge for it in E_k. Because W(j) ≤ W(l)and x > W(l), we can conclude d_w(u) ≥ k + x − W(j) > k in Z. If core_w(u) > k, u would not lose any neighbor that will influence its weighted degree after the deletion, and hence d_w(u) > k. Then it can be concluded that each vertex in Z has a weighted degree that is larger than k. This contradicts with our assumption.

For (ii), we assume core_w(v) = y increases by x to y + x, where x ≥ 1. Let H_v and $H_{v}^{+}$ be the max-y-core of v before edge insertion and the max-(y + x)-core after edge insertion respectively.

We first consider the case that core_w(v) > k + W(l). It must hold that at least one of the edges e_i in E_k belongs to $H_{v}^{+}$, if not, y = core_w(v) ≥ y + x before the insertion. For edge e_i, there is at least one of its endpoints has a weighted core number k as it is in a k-edge set. Denote the vertex as $v^{\prime }$. as proved in (i), $core_{w}(v^{\prime })$ can increase at most to k + W(l). Hence, after the insertion, $core_{w}(v^{\prime }) \leq k+W(l) < y+x$. It means $v^{\prime }$ is not in $H_{v}^{+}$, which is a contradiction. So, if core_w(v) > k + W(l), core_w(v) will not increase after the insertion.

We then consider the case core_w(v) < k. Similar with above, it can obtained that there must be at least one of the edges e_i in E_k belonging to $H_{v}^{+}$. Let $Z = H_{v}^{+}\backslash E_{k}$. Let u be a vertex in Z. We need to consider three cases. If core_w(u) = k in graph G , core_w(u) = k in Z can be obtained as proved before. If core_w(u) > k in G, the weighted core number of u will not be affected by the insertion. If core_w(u) < k in G, the vertex in $H_{v}^{+}$ has a weighted degree which is larger than y + x, and u does not connect to any edges in E_k due to the definition. Then we can get that d_w(u) ≥ y + x. Hence, Z is a s-core. It can be concluded that core_w(v) ≥ y + x in Z. But on the hand, the weighted core number of v in Z is not larger that that in G, and we know that core_w(v) = y < y + x. This contradiction completes the proof. □

As defined before, for an edge set E_m = {e₁, e₂,...,e_p}, where e_i =< u_i, v_i >, we let l denote the vertex that has the largest weighted core number among endpoints of edges in E_m.

Definition 3 (k-Favorable Insertion Edge Set)

An edge set E_m is a k-favorable insertion edge set, if it satisfies:

• (i) k < core_w(e_i) < k + W(l) for each edge in E_m;

• (ii) d_w(u_i) + W(v_i) ≤ k + W(l) for each edge e_i in E_m;

• (iii) Each vertex u has only one favorable edge.

Using a similar analysis as in Lemma 4, we then can bound the weighted core number change after we insert a k-favorable insertion edge set,

Lemma 5

Let graph G = (V, E, W), if a k-favorable insertion edge set is inserted to G after the insertion of a k-edge set, where k > 0, for each vertex v in G, it holds that:

• (i) if k ≤ core_w(v) < k + W(l), after insertion core_w(v) will not exceed k + W(l);

• (ii) if core_w(v) ≥ k + W(l) or core_w(v) < k, core_w(v) will not change.

Claim

Given an edge (u, v) of the k-favorable insertion edge set, (u, v) is inserted to G after the insertion of k-edge set, if k ≤ core_w(v) < k + W(l), the weighted core number of vertex in G after insertion will not exceed k + W(l).

Proof

For (i), The insertion of the k-favorable insertion edge set can be seen as insert the edge one by one, we assume a vertex v whose weighted core number core_w(v) ∈ (k, k + W(l)), the weighted degree of v is d_w(v). Based on Lemma 4, after the insertion of k-edge set, the vertices’ weighted core number in graph will not exceed k + W(l), the sum weight of v’s neighbor whose weighted core number is larger than k + W(l) denoted as S_v, hence, S_v ≤ d_w(v). If an edge (u, v) which satisfies d_w(v) + W(u) ≤ k + W(l) is inserted, as d_w(v) + W(u) ≤ k + W(l), then we get W(u) < k + W(l), and S_v ≤ d_w(v) ≤ k + W(l) can be concluded, hence, the weighted core number of v is maximally not exceeding k + W(l), the weighted core number of vertex in graph G is no more than k + W(l), (i) is done. (ii) can be proved as Lemma 4. □

6.1.2 Algorithm

As shown above, if a k-edge set and a k-favorable edge set have been inserted to the graph, the weighted core value change of every vertex can be bounded. Using these properties we can greatly reduce the searching range of potential vertices that may update its weighted core number, and hence we can get an efficient algorithm.

Our algorithm is shown in Algorithm 7 and Algorithm 8. The algorithm split the inserted edges into several sets, each of which consists of a k-edge sets and a k-favorable insertion edge set for some k > 0. Algorithm 11 get a subgraph H of G that the weighted core number of every vertex in H is at least k. With the k-edge set, the searching range of potential vertices and the change range of weighted core numbers of vertices can be determined. More specifically, in each iteration of the algorithm execution, a set of insertion edges is first elected from remaining uninserted edges, by finding a k-edge set and a k-favorable edge set. After inserting the edges, a similar approach as that for the single-edge insertion is adopted to update the current degree value of vertices and determine the final weighted core number.

6.2 Deletion algorithm

We then consider the deletion case. Similarly, we can show that if we delete a k-edge set from the graph, the weighted core number change can be bounded as follows.

Lemma 6

Given a graph G, if a k-edge set E_k is deleted from G, for each vertex v, it satisfies that:

• (i) if k − W(l) ≤ core_w(v) ≤ k, after deletion, core_w(v) will not be less than k − W(l);

• (ii) if core_w(v) > k or core_w(v) < k − W(l), core_w(v) will not change.

We then define the k-favorable deletion edge set for the deletion case. We use the same notations as those in the incremental section.

Definition 4 (k-Favorable Deletion Edge Set)

An edge set E_m is called a k-favorable deletion edge set if it satisfies:

• (i) k − W(l) ≤ core_w(e_i) < k

• (ii) d_w(u_i) − W(v_i) ≥ k − W(l)

• (iii) Each vertex u has only one favorable edge.

For k-favorable deletion edge set, we can get the following result similarly.

Lemma 7

Given a graph G, if a k-favorable deletion edge set is deleted from G after the deletion of a k-edge set, where k > 0, for each vertex v, it holds that:

• (i) if k − W(l) < core_w(v) ≤ k, after deletion, core_w(v) will not be less than k − W(l);

• (ii) if core_w(v) > k or core_w(v) ≤ k − W(l), core_w(v) will not change.

With the above properties, we then present our decremental algorithm, as shown in Algorithm 9 and Algorithm 10.

7 Comparision between weighted k-core maintenance and unweighted k-core maintenance

Our algorithm can also be applied to unweighted k-core maintenance for the reason that the weight of each node in unweighted graph can be seen as 1. But the algorithms that have been proposed in [19, 23] perform better than our algorithm in unweighted graphs. This is because in unweighted graphs, when an edge is inserted into or deleted from the graph, the core number of a vertex can change at most 1, but this principle is not applied for weighted graphs. Using the principle proposed in the weighted graph, the range of vertices that may update the core number may be larger than the proposed core maintenance algorithm for unweighted graph.

8 Experiments

We evaluate how efficient and scalable our algorithms are by experiments conducted on realistic networks and temporal graphs.

We first evaluate the efficiency and scalability of the algorithms on realistic networks, by changing the quantity of the edges in insertion/deletion. To further show our algorithms’ performance in reality, we also implement our algorithms on temporal graphs. Finally, we compare our multi-edge weighted core maintenance algorithms(MEIA, MEDA) with single-edge ones (SEIA, SEDA), to evaluate the improvement by simultaneously handling multiple edges.

All experiments are conducted on a Mac OS machine with Intel CPU Core i7@2.2GHz and 16GB main memory implemented in Java.

Datasets

Six realistic networks and three temporal graphs are used in experiments, which can be downloaded from SNAP [17]. Among the six real-world graphs, Facebook and Wiki-vote are social networks, Email is a communication network, Ca-Hepth is a collaboration network, Berstan and Google are Weblink networks. Among the three temporal graphs, CM (CollegeMSG), Mo (sx-matheoverflow) and CQ (sx-mathoverflow-c2q), CM is an interaction network similar to Facebook platform, Mo is a complete interaction network on the mathoverflow platform, and CQ is a temporal network of interactions on the stack exchange Web site Stack Overflow.

We use the PageRank value of each vertex as its weight, to simulate a weighted graph. We measure the efficiency of our algorithms by comparing the processing time per edge.

8.1 Performance comparison

We compare the proposed MEIA and MEDA with the SEIA and SEDA on real-word graphs (Table 1). The performance comparisons for the insertion and the deletion cases are illustrated in Figure 3a and b. From the figures, it shows that using the proposed multi-edge maintenance algorithms, the processing time per edge can be significantly reduced. Hence, we then turn our attention to evaluate how efficient and scalable the multiple-edge maintenance algorithms are.

Table 1 Realistic DataSets

Fig. 3

Contrast between the single-edge core maintenance algorithm and the multiple-edge core maintenance algorithm, x-axis stands for the graphs, y-axis stands for the processing time per edge

8.2 Performance evaluation

The performance of MEIA and MEDA are evaluated in both realistic networks and temporal graphs. In the experiments, number of inserted/deleted edges are changed to show the efficiency and scalability of the algorithms.

The results of the experiments on realistic networks are presented in Figure 4a and b. We insert/delete 1%, 3%, 5%, 7% edges of the original graphs. From the figures, it can be observed that if we increase the number of inserted or deleted edges, the average processing time for single edge will decreases. This is because the more edges are inserted or deleted, the more edges will be processed simultaneously in each iteration, such that the average processing time is reduced. Hence, our algorithms have good scalability, which perform better when larger number of edges inserted/deleted.

Fig. 4

Effect of the quantity of inserted or deleted edges on realistic graphs, x-axis stands for different datasets, and the y-axis stands for the processing time per edge

The experimental results on temporal networks are presented in Figures 5 and 6. The algorithms are implemented on four selected time points. The results showed in figures are similar to realistic graph scenario. The process time per edges will be reduced if the number of inserted or deleted edges increases.

Fig. 5

Effect of the quantity of inserted or deleted edges in temporal networks, x-axis stands for the various time points, y-axis stands for the processing time per edge

Fig. 6

Case study: results when a vertex update its weight

8.3 Case study

A case is illustrated in Figure 6. The weight of vertex represents the followers of the user in a social network. In Figure 6a, the weighted core number of Ben is 16, and the weighted core number of Lisa, Lili, Joe and Anne is 26, The weighted-26-core consisits of Lisa, Lili, Joe and Anne. If Lisa update its weight to 21 as [b] showed, the weighted core number of Ben, Lisa, Lili, Joe and Anne will update to 30. All users in the social network form a weighted-30-core.

9 Conclusion

We studied the core decomposition and maintenance problem in weighted graphs. By considering the weight of vertices, we gave a new definition of coreness for weighted graphs, which extends the coreness of unweighted graphs. We presented efficient algorithms for both weighted core decomposition and maintenance problems, such that the vertices’ weighted core number can be computed and update efficiently. Importantly, by deeply investigating the graph structure, our weighted core maintenance algorithm can process multiple edge insertions/deletions simultaneously, such that the efficiency of core maintenance is significantly improved. Extensive experiments show that our algorithms works well in real scenarios.

Our work extend the coreness studies to weighted graphs. Proper definitions would be further considered about both vertex and edge weights.