Secure Relay Selection of Cognitive Two-Way Denoise-and-Forward Relaying Networks

Abstract

In this paper, secrecy performance of a cognitive two-way denoise-and-forward relaying network consisting of two primary user (PT and PD) nodes, two secondary source (SA and SB) nodes, multiple secondary relay (${\textit{SR}}_i$) nodes and an eavesdropper (E) node is considered, where SA and SB exchange their messages with the help of one of the relays using a two-way relaying scheme. The eavesdropper tries to wiretap the information transmitted between SA and SB. To improve secrecy performance of the network, two relay selection schemes called maximum sum rate and maximum secrecy capacity based relay selection (MSRRS and MSCRS) are proposed and analyzed in terms of intercept probability. It is proved that the MSRRS and MSCRS schemes have the same secrecy performance. Two parameters called average number gain and average cost gain are proposed to show the performance of the proposed relay selection schemes. Numerical results demonstrated that with 10 relay nodes, the proposed relay selection schemes can achieve, respectively, 3.7 dB and 1.9 dB’s improvements in terms of the reduced intercept probability and the enhanced secrecy capacity compared to the traditional round-robin scheme.

1 Introduction

Cognitive radio (CR) has received much attention from the research community due to its improvement of spectrum utilization efficiency of wireless networks [1,2,3]. Generally, for a CR network, there exists two classes of users, namely, licensed and unlicensed (also called primary and secondary) users using two types of spectrum sharing methods: overlay and underlay approaches. For the overlay approach, secondary users directly access the primary users’ spectrum when the primary users are in the idle status. For the underlay approach, however, secondary users can utilize the primary users’ spectrum without deteriorating the quality of service of the primary users. On the other hand, cooperative relay technologies can resist fading and path loss effects and have received much attention as well.

Physical-layer security is an emerging technique being able to secure the open communication environment against eavesdropping attacks at the physical layer [4]. Wyner proposed the wiretap channel model and studied its information-theoretic security in [5]. Leung-Yan-Cheong and Hellman [6] extended Wyner’s work to the Guassian wiretap channel. Dong et al. [7] addressed the secure transmission issues by using cooperative relaying techniques, where different cooperative relaying protocols are considered, i.e., decode-and-forward (DF), amplify-and-forward (AF), and cooperative jamming (CJ). By using AF and DF relaying, Zou et al. [8] proposed an optimal relay selection scheme for physical-layer security. Chen et al. [9] and Zhao et al. [10] investigated the physical-layer security problem in the two-way relaying systems and proposed an effective relaying technology that can improve both the spectrum efficiency and the throughput simultaneously. Wang et al. [11] proposed a jammer selection scheme to enhance the secrecy performance of an DF two-way relaying network. Ding et al. [12] studied opportunistic relay selection scheme for the physical-layer security of artificial noise aided DF two-way relaying network.

However, most of the existing works regarding physical-layer security of two-way relaying do not consider cognitive radio settings. It is worth-mentioning that due to the interference between primary and secondary users, investigating secure techniques at the physical layer for a CR network becomes much more difficult. Zhang and Gursoy [13] studied secure communication in cognitive two-way relaying networks by using multi-relays beamforming designs. The authors of [14] investigated a new cooperative paradigm to provide information security for the primary network in cognitive two-way relaying networks. In [15], a joint resource allocation and relay selection scheme is proposed to secure the communication of CR networks via DF relays. Zhao et al. [16] investigated the physical-layer security problem of cognitive DF relay networks over Nakagami-m fading channels. Different from [13,14,15,16], we investigate secure techniques of secondary users for a two-way CR network by using denoise-and forward (DNF) relaying. It should be noted that, unlike DF relay, the DNF relay only detects and re-modulates the XOR of the two sources transmitted bits [17,18,19], and can result in more throughput than that of AF and DF relaying under low signal-noise-ratio (SNR) regime [20]. Table 1 gives a summarized comparison between the existing works and our work.

Table 1 Existing works regarding physical-layer security of two-way relaying networks

The network considered in this paper consists of two primary users (PT and PD), two secondary sources (SA and SB) and multiple secondary relays (${\textit{SR}}_i$) in the present of an eavesdropper (E). In the network, the secondary users transmit only when they detect a spectrum hole. First, we propose two relay selection schemes called maximum secrecy capacity relay selection (MSCRS) and maximum sum rate relay selection (MSRRS) schemes. Second, closed-form expressions of intercept probability of the two proposed relay selection schemes are derived, where the missed detection of spectrum hole is considered. Moreover, we propose two parameters called ANG and ACG to show the performance of the proposed relay selection schemes. Our simulation results confirmed the efficiency of our propositions.

This paper is organized as follows. The system model under investigation is presented in Sect. 2. In Sect. 3, the intercept probabilities of the proposed MSCRS and MSRRS schemes as well as the traditional round-robin scheme are derived. ANG and ACG parameters are introduced in Sect. 4. The numerical results are presented in Sect. 5. Section 6 concludes the paper.

2 System Model

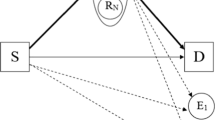
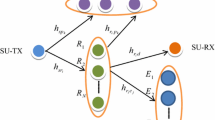
As shown in Fig. 1, the considered CTWDNFR network consists of two primary users PT and PD, two secondary users SA and SB, N relay nodes ${\textit{SR}}_i$, $i \in \left\{ {1,2, \ldots ,N} \right\}$, and one eavesdropper E. For spectrum sharing, the overlay approach is employed. The two secondary users SA and SB use the two-way relaying scheme to exchange messages with each other. There are two time-slots in one round of transmission between SA and SB. In the first time-slot, SA and SB transmit their messages ${x_A}$ and ${x_B}$ to N relays, and then the selected relay uses the DNF protocol to decode the message into ${x_R}$, which is combined with ${x_A}$ and ${x_B}$. In the second time-slot, the relay forwards ${x_R}$ to SA and SB. During the first and the second time-slots, E aims to wiretap SA, SB and the relay’s signals. Let ${x_P}$ denote the signal transmitted by primary user PT. Without loss of generality, $E\left[ {{{\left| {{x_A}} \right| }^2}} \right] = E\left[ {{{\left| {{x_B}} \right| }^2}} \right] = E\left[ {{{\left| {{x_P}} \right| }^2}} \right] = 1$ is assumed.

Fig. 1

System model

Suppose that there is no direct link between SA and SB because of deep channel fading. Furthermore, all the relays cannot communicate with each other. We use “$H{-}L$” to denote channel link from node H to L, where $H,L \in \left\{ {{\textit{SA}}, {\textit{SB}}, {\textit{SR}}_i,{\textit{PT}},E} \right\}$. The instantaneous channel gain of link $H{-}L$ is denoted by ${h_{HL}}$ and assumed to be zero mean complex Gaussian random variables with variance $\sigma _{HL}^2$. All the channels are assumed to undergo Rayleigh fading and to be independent and reciprocal. Thus, we have ${h_{HL}} = {h_{LH}}$. Let ${P_S}$ denote the transmit power of SA, SB and ${SR}_i$, and ${P_P}$ denote the transmit power of PT. Meanwhile, let ${N_0}$ denote the variance of the zero mean additive white Gaussian noise at all the receiving nodes. Furthermore, $E\left[ {{{{P_S}{{\left| {{h_{{SBSR}_i}}} \right| }^2}} / {{N_0}}}} \right] = E\left[ {{{{P_S}{{\left| {{h_{{SASR}_i}}} \right| }^2}} / {{N_0}}}} \right] = {1 / {{\lambda _S}}}$, $E\left[ {{{{P_P}{{\left| {{h_{{PTSR}_i}}} \right| }^2}} / {{N_0}}}} \right] = E\left[ {{{{P_P}{{\left| {{h_{PTSA}}} \right| }^2}} / {{N_0}}}} \right] = E\left[ {{{{P_P}{{\left| {{h_{PTSB}}} \right| }^2}} / {{N_0}}}} \right] = E\left[ {{{{P_P}{{\left| {{h_{PTE}}} \right| }^2}} / {{N_0}}}} \right] = {1 / {{\lambda _P}}}$ and $E\left[ {{{{P_S}{{\left| {{h_{SAE}}} \right| }^2}} / {{N_0}}}} \right] = E\left[ {{{{P_S}{{\left| {{h_{SBE}}} \right| }^2}} / {{N_0}}}} \right] = {1 / {{\lambda _E}}}$ are assumed. Let ${R_A}$ and ${R_B}$ denote the transmission rate of source SA and SB, respectively, and ${R_A} = {R_B} = R$ is assumed.

In this paper, SA and SB exchange their messages only when they detect a spectrum hole. Let $\hat{H}$ denote the result of spectrum detection, where $\hat{H} = {H_0}$ indicates that the licensed spectrum is unoccupied, while $\hat{H} = {H_1}$ represents the case that licensed spectrum is used. Moreover, ${P_d} = \Pr \left( {\hat{H} = {H_0}\left| {{H_0}} \right. } \right)$ and ${P_f} = \Pr \left( {\hat{H} = {H_0}\left| {{H_1}} \right. } \right)$ are used to denote the probabilities of correct detection and missed detection, respectively.

For the case of $\hat{H} = {H_0}$, SA and SB exchange messages via the selected relay ${SR}_i$. Thus, at the end of the first time-slot, the signal received at ${SR}_i$ can be expressed as:

$$\begin{aligned} y_{{SR}_i}^{1{\text {st}}} = \sqrt{{P_S}} {h_{{SASR}_i}}{x_A} + \sqrt{{P_S}} {h_{{SBSR}_i}}{x_B} + \sqrt{\alpha {P_P}} {h_{{PTSR}_i}}{x_P} + {n_{{R_i}}} \end{aligned}$$

(1)

where $\alpha = \left\{ \begin{array}{ll} 0, &{}\quad {H_0} \\ 1, &{}\quad {H_1} \\ \end{array} \right.$, ${n_{{R_i}}}$ is the additive white Gaussian noise at the relay ${SR}_i$.

Here, the two sources’ transmission rate R should follow the bellowing constraints.

$$\begin{aligned} R\leqslant & {} Ca\left( {{SNR}_{{SASR}_i}^{1{\text {st}}}} \right) \nonumber \\ R\leqslant & {} Ca\left( {SNR_{SBS{R_i}}^{1{\text {st}}}} \right) \nonumber \\ R\leqslant & {} \frac{1}{2}Ca\left( {SNR_{S{R_i}}^{1{\text {st}}}} \right) \end{aligned}$$

(2)

where $Ca\left( x \right) = \frac{1}{2}{\log _2}\left( {1 + x} \right)$, $SNR_{SAS{R_i}}^{1{\text {st}}} = \frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{\alpha {\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}$, $SNR_{SBS{R_i}}^{1{\text {st}}} = \frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{\alpha {\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}$, $SNR_{S{R_i}}^{1{\text {st}}} = \frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2} + {\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{\alpha {\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}$, ${\gamma _S} = \frac{{{P_S}}}{{{N_0}}}$, ${\gamma _P} = \frac{{{P_P}}}{{{N_0}}}$.

At the end of the first time-slot, the signal received at E can be expressed as:

$$\begin{aligned} y_E^{1{\text {st}}} = \sqrt{{P_S}} {h_{SAE}}{x_A} + \sqrt{{P_S}} {h_{SBE}}{x_B} + \sqrt{\alpha {P_P}} {h_{PTE}}{x_P} + {n_E} \end{aligned}$$

(3)

Thus, the maximum information that E obtains can be expressed as

$$\begin{aligned} I_{E - i}^{1{\text {st}}} = \max \left( {Ca\left( {SN{R_{SAE}}} \right) ,Ca\left( {SN{R_{SBE}}} \right) } \right) \end{aligned}$$

(4)

where $SN{R_{SAE}} = \frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2} + \alpha {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2} + 1}}$, and $SN{R_{SBE}} = \frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2} + \alpha {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2} + 1}}$.

In the second time-slot, $S{R_i}$ forwards ${x_R}$ to SA and SB, and the signal received at SA, SB and E can be, respectively, expressed as:

$$\begin{aligned} y_A^{2{\text {nd}}}= & {} \sqrt{{P_S}} {h_{SAS{R_i}}}{x_R} + \sqrt{\alpha {P_P}} {h_{PTSA}}{x_P} + {n_A} \end{aligned}$$

(5)

$$\begin{aligned} y_B^{2{\text {nd}}}= & {} \sqrt{{P_S}} {h_{SBS{R_i}}}{x_R} + \sqrt{\alpha {P_P}} {h_{PTSB}}{x_P} + {n_B} \end{aligned}$$

(6)

$$\begin{aligned} y_E^{2{\text {nd}}}= & {} \sqrt{{P_S}} {h_{ES{R_i}}}{x_R} + \sqrt{\alpha {P_P}} {h_{PTE}}{x_P} + {n_E} \end{aligned}$$

(7)

From (5) and (6), SA and SB use their self-information being transmitted to the relay in the first time-slot to decode ${x_R}$. Thus, R should follow the bellowing constraints.

$$\begin{aligned} R\leqslant & {} Ca\left( {SNR_{S{R_i}SA}^{2{\text {nd}}}} \right) \nonumber \\ R\leqslant & {} Ca\left( {SNR_{S{R_i}SB}^{2{\text {nd}}}} \right) \end{aligned}$$

(8)

where $SNR_{S{R_i}SA}^{2{\text {nd}}} = \frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{\alpha {\gamma _P}{{\left| {{h_{PTSA}}} \right| }^2} + 1}}$, $SNR_{S{R_i}SB}^{2{\text {nd}}} = \frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{\alpha {\gamma _P}{{\left| {{h_{PTSB}}} \right| }^2} + 1}}$.

From (2) and (8), the maximum value of R is given by.

$$\begin{aligned}&{R_{DNF - i}} = \min \left( Ca\left( SNR_{SAS{R_i}}^{1{\text {st}}}\right) ,Ca\left( SNR_{SBS{R_i}}^{1{\text {st}}}\right) ,\frac{1}{2}Ca\left( SNR_{S{R_i}}^{1{\text {st}}}\right) ,\nonumber \right. \\&\quad \left. Ca\left( SNR_{S{R_i}SA}^{2{\text {nd}}}\right) ,Ca\left( SNR_{S{R_i}SB}^{2{\text {nd}}}\right) \right) \end{aligned}$$

(9)

It is worth-mentioning that, the eavesdropper E can decode ${x_A}$ or ${x_B}$ from ${x_R}$ only when E has intercepted ${x_A}$ or ${x_B}$ in the first time-slot, meaning that E cannot intercept any information from the signal ${x_R}$ if the $SA - S{R_i}$ and $SB - S{R_i}$ transmission in the first time-slot are kept secrecy.

3 Relay Selection Schemes and Intercept Probability Analysis

Here, we study two relay selection schemes called MSRRS and MSCRS schemes in addition to the traditional round-robin scheme.

3.1 MSCRS Scheme

For the MSCRS scheme, the relay having the maximum instantaneous secrecy capacity is selected as the optimal relay. Thus, the MSCRS criterion can be expressed as

$$\begin{aligned} o = \arg \left\{ \begin{array}{ll} \mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } C_{S - i}^{proposed},&{}\quad if\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } C_{S - i}^{proposed} > 0 \\ \mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}},&{}\quad if\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } C_{S - i}^{proposed} = 0 \\ \end{array}\right. \end{aligned}$$

(10)

where o denotes the subscript of the selected optimal relay. $C_{S - i}^{proposed}$ is the system secrecy capacity of relay $S{R_i}$, and can be expressed as

$$\begin{aligned} C_{S - i}^{proposed} = {\left[ {{R_{DNF - i}} - I_{E - i}^{1st}} \right] ^ + } \end{aligned}$$

(11)

where ${\left[ a \right] ^ + } = \left\{ \begin{array}{ll} a,&{}\quad if\;a > 0 \\ 0,&{}\quad if\;a \leqslant 0 \\ \end{array} \right.$.

It should be note that in the case of $C_{S-i}^{proposed} = 0$, $i \in \left\{ {1,2, \ldots ,N} \right\}$, we will choose the optimal relay which can provide the maximum sum rate. Here, the global CSIs of all the channels are assumed to be available, which is a common assumption in the literature. However, CSIs of the wiretap channels, i.e., $SA - E$, $SB - E$, $S{R_i} - E$, $PT - E$ links, are not always easy to be estimated because the eavesdroppers are passive. Thus, we should consider a more practical scheme without requirement of CSI of the wiretap channel, which will be described in the next section.

3.2 MSRRS Scheme

For the MSRRS scheme, the relay having the maximum instantaneous sum rate is selected as the optimal relay. Thus, the MSRRS criterion can be expressed as

$$\begin{aligned} l = \arg \mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \end{aligned}$$

(12)

where l denotes the subscript of the selected optimal relay.

According to (10) and (12), we have the following Proposition.

Proposition 1

For a CTWDNFR network, the MSCRS scheme equals to the MSRRS scheme. In other words, the CSI of wiretap channels has no effect on the MSCRS scheme.

Proof

From (10) and (11), the MSCRS scheme equals to the MSRRS scheme if $\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } C_{S - i}^{proposed}= 0$. In the case of $\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } C_{S - i}^{proposed}> 0$, the MSCRS scheme can be rewritten as $o = \arg \mathop { \max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} }(R_{DNF - i} - I_{E - i}^{1st})$. From (4), $I_{E - i}^{1{\text {st}}}$ is always independent from the selected relay $S{R_i}$. Then MSCRS scheme can be rewritten as $o = \arg \mathop { \max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}}$, which equals to the MSRRS scheme. This completes the proof.

Thus, we only analyze the MSRRS scheme in the rest of this paper. The intercept event is defined as that the eavesdropper can successfully decode ${x_A}$ or ${x_B}$ during the two transmission time-slots. However, E can decode ${x_A}$ or ${x_B}$ from ${x_R}$ only when E has intercepted ${x_B}$ or ${x_A}$ in the first time-slot. With (12), the intercept probability of the network can be expressed as

$$\begin{aligned} P_{in - l}^{MSRRS} = \Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {\hat{H} = {H_0}} \right. } \right) \end{aligned}$$

(13)

Considering that the primary network still occupies the licensed spectrum while the secondary network detects a spectrum hole, which is a missed detection case, and by using the total probability law, (13) can be rewritten as

$$\begin{aligned} P_{in - l}^{MSRRS}= & {} \underbrace{\Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_0},\hat{H} = {H_0}} \right. } \right) }_{{Q_1}}\Pr \left( {\hat{H} = {H_0}\left| {{H_0}} \right. } \right) \nonumber \\&\quad + \underbrace{\Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_1},\hat{H} = {H_0}} \right. } \right) }_{{Q_2}}\Pr \left( {\hat{H} = {H_0}\left| {{H_1}} \right. } \right) \end{aligned}$$

(14)

where ${Q_1} = \Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_0},\hat{H} = {H_0}} \right. } \right)$,

${Q_2} = \Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } {R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_1},\hat{H} = {H_0}} \right. } \right)$.

Here, ${1 / {{\lambda _S}}} \gg 1$ and ${1 / {{\lambda _E}}} \gg 1$ are assumed to simplify the derivation of (14). In the case of ${H_0}$ occurring, ${Q_1}$ can be rewritten as

$$\begin{aligned} {Q_1}&= {} \Pr \left( \mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } \min \left( Ca\left( {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}\right) ,Ca\left( {\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}\right) ,\frac{1}{2}Ca\left( {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}{\text { + }}{\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}\right) \right) \right. \nonumber \\&\leqslant \left. \max \left( Ca(\frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}),Ca(\frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}})\right) \right) \end{aligned}$$

(15)

According to “Appendix A”, we can obtain

$$\begin{aligned} {Q_1} &=1 + \sum \limits _{m = 0}^{N - 1} {\sum \limits _{n = 0}^{N - m} {\sum \limits _{k = 0}^{2\left( {N - m - n} \right) } {} } } C_N^mC_{N - m}^nC_{2\left( {N - m - n} \right) }^k{\left( { - 1} \right) ^{3N - 3m - 2n - k}}\lambda _S^{N - m - n - {{\left( {k - 1} \right) } / 2}} z \\&\times {\left( {N - m} \right) ^{{{ - \left( {k - 1} \right) } / 2}}}{e^{{\lambda _S}\left( {N - m} \right) }}\int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {{u^{\frac{{\left( {k - 1} \right) }}{2} - 1}}{e^{ - u}}du} \end{aligned}$$

(16)

where$\int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {{u^{\frac{{\left( {k - 1} \right) }}{2} - 1}}{e^{ - u}}du} = \left\{ \begin{array}{ll} \Gamma \left( {\frac{{k - 1}}{2},4{\lambda _S}\left( {N - m} \right) } \right) ,&{}\quad k > 1 \\ {\text {Ei}}\left( {1,4{\lambda _S}\left( {N - m} \right) } \right) ,&{}\quad k = 1 \\ 2\sqrt{\pi }\left( {{\text {erf}}\left( {\sqrt{4{\lambda _S}\left( {N - m} \right) } } \right) - 1} \right) &{}\\ + 2{e^{ - 4{\lambda _S}\left( {N - m} \right) }}{\left( {4{\lambda _S}\left( {N - m} \right) } \right) ^{ - {1 / 2}}},&{}\quad k = 0 \\ \end{array} \right.$

In the case of ${H_1}$ occurring, ${Q_2}$ can be rewritten as

$$\begin{aligned} {Q_2} = \Pr \left( \begin{array}{l} \mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } \min \left( \begin{array}{l} Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) , \\ \frac{1}{2}Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2} + {\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) , \\ Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTSA}}} \right| }^2} + 1}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTSB}}} \right| }^2} + 1}}} \right) \\ \end{array} \right) \\ \leqslant \max \left( {Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2} + {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2}}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2} + {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2}}}} \right) } \right) \\ \end{array}\right) \end{aligned}$$

(17)

However, it is difficult to obtain a closed form solution to ${Q_2}$. Although finding a general closed-form expression for $P_{in - l}^{MSRRS}$ is challenging, we can obtain the numerical results by computer simulations. $\square$

3.3 Round-Robin Transmission Scheme

For the round-robin transmission scheme, N relays act as a DNF two-way relay to help the sources’ transmission in turn [21]. The intercept event is defined as that the eavesdropper can successfully decode ${x_A}$ or ${x_B}$ during the two transmission time-slots. However, E can decode ${x_A}$ or ${x_B}$ from ${x_R}$ only when E has intercepted ${x_B}$ or ${x_A}$ in the first time-slot. Thus, an intercept even in the first time-slot results in a system interception, giving

$$\begin{aligned} P_{in - i}^{round} = \Pr \left( {{R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {\hat{H} = {H_0}} \right. } \right) \end{aligned}$$

(18)

Considering the missed probability of the spectrum detection and by using the total probability law, (18) can be rewritten as

$$\begin{aligned} P_{in - i}^{round}&= {} \underbrace{\Pr \left( {{R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_0},\hat{H} = {H_0}} \right. } \right) }_{{G_1}}\Pr \left( {\hat{H} = {H_0}\left| {{H_0}} \right. } \right) \nonumber \\&\quad + \underbrace{\Pr \left( {{R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_1},\hat{H} = {H_0}} \right. } \right) }_{{G_2}}\Pr \left( {\hat{H} = {H_0}\left| {{H_1}} \right. } \right) \end{aligned}$$

(19)

where ${G_1} = \Pr \left( {{R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_0},\hat{H} = {H_0}} \right. } \right)$, ${G_2} = \Pr \left( {{R_{DNF - i}} \leqslant I_{E - i}^{1{\text {st}}}\left| {{H_1},\hat{H} = {H_0}} \right. } \right)$.

To simplify the derivation, ${1 / {{\lambda _S}}} \gg 1$ and ${1 / {{\lambda _E}}} \gg 1$ are assumed. By substituting $\alpha = 0$ to (2) and (8), ${G_1}$ can be rewritten as

$$\begin{aligned} {G_1} = \Pr \left( \begin{array}{l} \min \left( {Ca\left( {{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}} \right) ,Ca\left( {{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}} \right) ,\frac{1}{2}Ca\left( {{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2} + {\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}} \right) } \right) \\ \leqslant \max \left( {Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}} \right) } \right) \\ \end{array} \right) \end{aligned}$$

(20)

Substituting $\alpha = 1$ to (2) and (8), ${G_2}$ can be rewritten as

$$\begin{aligned} {G_2} = \Pr \left( \begin{array}{l} \min \left( \begin{array}{l} Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) ,\\ \frac{1}{2}Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2} + {\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTS{R_i}}}} \right| }^2} + 1}}} \right) , \\ Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTSA}}} \right| }^2} + 1}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}}}{{{\gamma _P}{{\left| {{h_{PTSB}}} \right| }^2} + 1}}} \right) \\ \end{array} \right) \\ \leqslant \max \left( {Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2} + {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2}}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2} + {\gamma _P}{{\left| {{h_{PTE}}} \right| }^2}}}} \right) } \right) \\ \end{array} \right) \end{aligned}$$

(21)

According to “Appendix B”, we have

$$\begin{aligned}{G_1} = 1 - {e^{ - 3{\lambda _S}}}\left( {\left( {2\sqrt{\pi }{e^{4{\lambda _S}}}\lambda _S^{{3 / 2}} + \sqrt{\pi }{e^{4{\lambda _S}}}\lambda _S^{{1 / 2}}} \right) \left( {{\text {erf}}(2\sqrt{{\lambda _S}} ) - 1} \right) - 2{\lambda _S}{e^{4{\lambda _S}}}{\text {Ei}}\left( {1,4{\lambda _S}} \right) + {\lambda _S} + 1} \right) \end{aligned}$$

(22)

However, it is quite difficult to obtain a closed-form solution to ${G_2}$. Although finding a general closed-form expression for $P_{in - i}^{round}$ is challenging, we can obtain the numerical results by computer simulations. As aforementioned, N relays act in turn as a DNF two-way relay in the round-robin transmission scheme. Thus, the intercept probability of the round-robin transmission scheme is the average intercept probability of N relays, given by.

$$\begin{aligned}P_{in}^{round} = \frac{1}{N}\sum \limits _{i = 1}^N {P_{in - i}^{round}} \end{aligned}$$

(23)

4 Tradeoff Between Performance and Relay Numbers Analysis

It is well known that with increasing the number of relay nodes, more performance gain can be achieved. However, with the increment of relay numbers, the cost of relay deployment will also increase. Thus, it must exist a tradeoff between performance gain and relay numbers. Two parameters called ANG and ACG to study the performance improvement from the increment of the relay numbers. Here, ANG is defined as the ratio of intercept probability improvement to the relay numbers, which can be written as the following.

$$\begin{aligned} ANG\left( n \right) = \frac{{{1 / {P_{in - l}^{MSRRS}\left( n \right) }} - {1 / {P_{in - l}^{MSRRS}\left( 1 \right) }}}}{n} \end{aligned}$$

(24)

where n is the number of the relays, and $P_{in - l}^{MSRRS}\left( n \right)$ is the intercept probability of the network with n participated relays, which is given by (13). Here, we use ${1 / {P_{in - l}^{MSRRS}\left( n \right) }} - {1 / {P_{in - l}^{MSRRS}\left( 1 \right) }}$ to show the improvement of the intercept probability.

ACG is defined as the ratio of intercept probability decrement to relay cost, which can be written as.

$$\begin{aligned} ACG\left( n \right) = \frac{{{1 / {P_{in - l}^{MSRRS}\left( n \right) }} - {1 / {P_{in - l}^{MSRRS}\left( 1 \right) }}}}{{1 + \varpi \left( {n - 1} \right) }} \end{aligned}$$

(25)

where $\varpi$ is coefficient indicating the cost of the relays taking part in the cooperating but not being selected. The cost of the selected relay is assumed to be 1. Because the unselected relay nodes keep silence during the relaying phase, its cost will be smaller than the selected relay, thus we have $\varpi \in \left( {0,1} \right)$.

From (13)–(17), we find it is difficult to obtain a closed-form solution for ANG and ACG, computer simulations will be conducted to analyze the tradeoff between the system security performance and the relay numbers.

5 Numerical Results

In this section, numerical results are presented to demonstrate the performance of the proposed schemes. According to the IEEE 802.22 standard, ${P_d} \geqslant 0.9$, indicates ${P_f} \leqslant 0.1$. Here, we assume ${P_d} = 0.9$ and ${P_f} = 0.1$. Moreover, ${1 / {{\lambda _E}}} = 10\,{\text {dB}}$ is assumed. Figure 2 plots the intercept probabilities of the MSCRS, MSRRS and round-robin schemes as a function of the number of the available relay nodes. Here, we consider two cases, namely, the missed detection probability is zero and nonzero. ${1 / {{\lambda _P}}} = 0\,{\text {dB}}$ and ${1 / {{\lambda _S}}} = 20\,{\text {dB}}$ are assumed. Figure 2 shows that MSRRS scheme has the same performance as the MSCRS scheme which has been proved in Proposition 1 . It can be observed that as the relay number increases, the intercept probability of the MSCRS and MSRRS schemes decrease, meaning that the system secrecy performance can be improved by increasing the number of relays. Figure 2 also shows that with 10 relay nodes, the intercept probability of our proposed MSCRS and MSRRS schemes can be reduced by 3.7 dB compared to the traditional round-robin scheme. In addition, it can be seen that the simulation results of ${G_1}$ and ${Q_1}$ are extremely close to the theoretical values, confirming the correctness of our derived expressions. It should be pointed out that the intercept probability of the round-robin scheme stays unchanged when the number of relays increases. This is because that all the relay nodes serve as a DNF two-way relay to help the sources’ transmission in turn and all relay-to-source links follow the same distribution. For the round-robin scheme, no diversity gain is achieved.

Fig. 2

Intercept probability verse N of ${G_1}$ and ${Q_1}$, round-robin and MSCRS schemes where ${P_d} = 0.9$, ${P_f} = 0.1$, $1/{\lambda _S}=20$ dB, $1/{\lambda _E}=10$ dB and $1/{\lambda _P}=0$ dB

Figure 3 depicts the intercept probability against ${1 / {{\lambda _S}}}$ of the round-robin, MSCRS and MSRRS schemes, where ${1 / {{\lambda _S}}}$ is the exception of ${{{P_S}{{\left| {{h_{SBS{R_i}}}} \right| }^2}} / {{N_0}}}$ and ${{{P_S}{{\left| {{h_{SAS{R_i}}}} \right| }^2}} / {{N_0}}}$. $N = 4$ and ${1 / {{\lambda _E}}} = 10{\text { dB}}$ are assumed. Here, the following two cases are considered, i.e. (1) ${1 / {{\lambda _P}}} = 0{\text { dB}}$; (2) ${1 / {{\lambda _P}}} = 10{\text { dB}}$. Figure 3 shows that the intercept probabilities of the round-robin, MSCRS and MSRRS schemes decrease when ${1 / {{\lambda _S}}}$ increases. Moreover, it shows that as ${1 / {{\lambda _P}}}$ grows, the intercept probabilities of the three compared schemes increase simultaneously. It can be observed that the intercept probability of our proposed MSCRS and MSRRS schemes can be reduced by 2.6 dB compared to the traditional round-robin scheme when $1/{\lambda _S}=5$ dB and $1/{\lambda _P}=10$ dB. However, the performance of the considered two cases is very close because the primary user’s interference only exists in the case that the licensed spectrum has been occupied, i.e., ${P_f} = 0.1$. Figure 3 also shows that the proposed MSCRS and MSRRS schemes have the similar performance.

Fig. 3

Intercept probability verse $1/{\lambda _S}$ with round-robin and MSCRS schemes where $N=4$, ${P_d} = 0.9$, ${P_f} = 0.1$ and $1/{\lambda _E}=10$ dB

In Figure 4, we plot the average secrecy capacity against the relay numbers. The secrecy capacity is defined as the gap between the main channel capacity and the wiretap channel capacity, giving in (11). Here, ${1 / {{\lambda _S}}} = 20{\text { dB}}$, ${1 / {{\lambda _E}}} = 10{\text { dB}}$ and ${1 / {{\lambda _P}}} = 0{\text { dB}}$ are assumed. From Fig. 4, it can be seen that the system gains more secrecy capacity with increasing the relay numbers. The proposed MSCRS and MSRRS schemes are shown to have the same performance, and they outperform the traditional round-robin scheme, achieving 1.9 dB secrecy capacity when the relay number is 10. However, the increment of the achieved secrecy capacity decreases when the relay numbers increase.

Fig. 4

Average secrecy capacity verse relay numbers of round-robin and MSCRS schemes where ${P_d} = 0.9$, ${P_f} = 0.1$, $1/{\lambda _S}=20$ dB, $1/{\lambda _E}=10$ dB and $1/{\lambda _P}=0$ dB

Figure 5 illustrates the average secrecy capacity against ${1 / {{\lambda _S}}}$ of the round-robin, MSCRS and MSRRS schemes, where $N=4$ and ${1 / {{\lambda _E}}} = 10{\text { dB}}$ are assumed. The following two cases are considered, i.e., (1) ${1 / {{\lambda _P}}} = 0{\text { dB}}$; (2) ${1 / {{\lambda _P}}} = 10{\text { dB}}$. From Fig. 5, it can be seen that the average secrecy capacity of the round-robin, MSCRS and MSRRS schemes grow when ${1 / {{\lambda _S}}}$ increases. Figure 5 also shows that the MSCRS and MSRRS schemes can gain 1.8 dB secrecy capacity than the traditional round-robin scheme when $1/{\lambda _S}=5$ dB and $1/{\lambda _P}=10$ dB. Compared with Fig. 3, the better channel state of the secondary users, the higher secrecy performance will be achieved.

Fig. 5

Average secrecy capacity verse $1/{\lambda _S}$ of the round-robin and MSCRS schemes where $N=4$, ${P_d} = 0.9$, ${P_f} = 0.1$ and $1/{\lambda _E}=10$ dB

To further show the secrecy performance of the system, we plot ANG and ACG verse relay numbers in Figs. 6 and 7, respectively. In Fig. 6, ANG against relay numbers of the round-robin, MSCRS and MSRRS schemes are plotted. Two cases are considered, i.e. (1) ${1 / {{\lambda _S}}} = 10{\text { dB}}$; (2) ${1 / {{\lambda _S}}} = 20{\text { dB}}$. In addition, ${P_d} = 0.9$, ${P_f} = 0.1$, ${1 / {{\lambda _E}}} = 10{\text { dB}}$ and ${1 / {{\lambda _P}}} = 0{\text { dB}}$ are assumed. Both the MSCRS and MSRRS schemes are shown to have the same performance in Fig. 6. It can be seen that for the MSCRS and MSRRS schemes, ANG grows first with the increment of relay numbers, then it drops down after the highest ANG point, indicating that we should consider both the relay numbers deployed and the system secrecy performance achieved in practical. It shows that the highest value where the ANG achieves of the MSCRS and MSRRS schemes are different in the two cases, which means that the highest ANG is achieved when the relay numbers is 2 in case (1) while it is achieved when the relay numbers is 3 in case (2). However, the ANG always stays zero in the round-robin scheme of both two cases. This is because that there is no system security performance improvement achieved by increasing the relay numbers.

Fig. 6

ANG verse relay numbers of the round-robin and MSCRS schemes where ${P_d} = 0.9$, ${P_f} = 0.1$, $1/{\lambda _E}=10$ dB and $1/{\lambda _P}=0$ dB

Figure 7 plots the ACG against the relay numbers of the round-robin, MSCRS and MSRRS schemes. ${P_d} = 0.9$, ${P_f} = 0.1$, ${1 / {{\lambda _S}}} = { {2}}0{\text { dB}}$, ${1 / {{\lambda _E}}} = 10{\text { dB}}$ and ${1 / {{\lambda _P}}} = 0\,{\text { dB}}$ are assumed, and three cases are considered, i.e. (1) $\varpi = 0.1$; (2) $\varpi = 0.3$; (3) $\varpi = 0.5$. Figure 7 shows that ACG increases first, then decreases with the increment of relay numbers in the MSCRS and MSRRS schemes. Different values of $\varpi$ indicate different costs of the unselected relays. With the higher $\varpi$, the lower ACG will be achieved, and the less relay numbers where the best ACG achieves. We can also obtain that the ACG always stays zero in the round-robin scheme of both two cases, which is also shown in Fig. 6.

Fig. 7

ACG verse relay numbers of the round-robin and MSCRS schemes where ${P_d} = 0.9$, ${P_f} = 0.1$, $1/{\lambda _S}=20$ dB, $1/{\lambda _E}=10$ dB and $1/{\lambda _P}=0$ dB

6 Conclusions

In this paper, we studied the secrecy performance of a DNF protocol based two-way relaying in the cognitive radio network settings, where two secondary users try to communicate with each other when detecting a spectrum hole. Both the correct and missed detection events are considered. In order to improve the system secrecy performance, two relay selection schemes called MSRRS and MSCRS schemes are proposed. We proved that the MSRRS and MSCRS schemes have the same secrecy performance. Intercept probability of the proposed MSCRS scheme as well as the round-robin scheme were analyzed over Rayleigh fading channels, giving closed-form expressions in the correct detection event. We propose ANG and ACG to analyze the performance improvement from the increment of the relay numbers. Our simulation results show that the proposed schemes can significantly improve the secrecy performance and the network will become more secure either when the numbers of the relay increases or when the channel of the secondary users become better. Furthermore, the MSCRS and MSRRS schemes are shown to have the same performance, confirming the correctness of Proposition 1. It also shows that the ANG and the ACG not always grow with the increasing of the participated relay numbers, which indicates that we should consider both the relay numbers deployed and the system secrecy performance achieved in practical.

Appendices

Appendix A

1.1 Derivation of ${Q_1}$

Let ${K_{21}} = \mathop {\max }\limits _i \min \left( Ca\left( {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}\right) ,Ca\left( {\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}\right) ,\frac{1}{2}Ca\left( {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}{ { + }}{\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}\right) \right)$, $i \in \left\{ {1,2, \ldots ,N} \right\}$, ${K_{22}} = \max \left( Ca\left( \frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}\right) ,Ca\left( \frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}\right) \right)$. Because all the CSIs are mutual independent, thus ${Q_1}$ can be rewritten as (26).

$$\begin{aligned} {Q_1} = \Pr \left( {{K_{21}} \leqslant {K_{22}}} \right) = \oint {\Pr \left( {{K_{21}} \leqslant x} \right) {f_{{K_{22}}}}\left( x \right) dx} \end{aligned}$$

(26)

We first derive $\Pr \left( {{K_{21}} \leqslant x} \right)$ . Let ${a_1} = {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}$ and ${a_2} = {\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}$, we have (27).

$$\begin{aligned} \Pr \left( {{K_{21}} \leqslant x} \right)&= \Pr \left( {\mathop {\max }\limits _{i \in \left\{ {1,2, \ldots ,N} \right\} } \min \left( {Ca\left( {{a_1}} \right) ,Ca\left( {{a_2}} \right) ,\frac{1}{2}Ca\left( {{a_1}{ { + }}{a_2}} \right) } \right) \leqslant x} \right) \\&= {\left( {1 - \Pr \left( {\min \left( {Ca\left( {{a_1}} \right) ,Ca\left( {{a_2}} \right) ,\frac{1}{2}Ca\left( {{a_1} + {a_2}} \right) } \right)> x} \right) } \right) ^N} \\&= {\left( {{ {1}} - \Pr \left( {{a_1}> \underbrace{{2^{2x}} - 1}_z,{a_1}> {2^{2x}} - 1,{a_1} + {a_2} > \left( {{2^{4x}} - 1} \right) } \right) } \right) ^N} \\&= {\left( {1 - \left( {1 + {\lambda _S}{z^2}} \right) {e^{ - {\lambda _S}z\left( {z + 2} \right) }}} \right) ^N} \\&= \sum \limits _{m = 0}^N {\sum \limits _{n = 0}^{N - m} {C_N^m{{\left( { - 1} \right) }^{N - m}}C_{N - m}^n\lambda _S^{N - m - n}{z^{2\left( {N - m - n} \right) }}} {e^{ - {\lambda _S}z\left( {z + 2} \right) \left( {N - m} \right) }}} \\ \end{aligned}$$

(27)

The cumulative density function of ${K_{22}}$ can be obtained from (28).

$$\begin{aligned} {F_{{K_{22}}}}\left( x \right)&= \Pr \left( {{K_{12}}< x} \right) \\&= \Pr \left( {\max \left( {Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}} \right) ,Ca\left( {\frac{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}} \right) } \right)< x} \right) \\&= \Pr \left( {\max \left( {\frac{{{P_S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{P_S}{{\left| {{h_{SBE}}} \right| }^2}}},\frac{{{P_S}{{\left| {{h_{SBE}}} \right| }^2}}}{{{P_S}{{\left| {{h_{SAE}}} \right| }^2}}}} \right)< {2^{2x}} - 1} \right) \\&= \left\{ \begin{array}{ll} \frac{{{2^{2x}} - 2}}{{{2^{2x}}}}&{}\quad x \geqslant 0.5 \\ 0&{}\quad x < 0.5 \\ \end{array} \right. \end{aligned}$$

(28)

Thus, the probability density function of ${K_{22}}$ can be expressed as (29).

$$\begin{aligned} {f_{{K_{22}}}}\left( x \right) = \frac{{\partial {F_{{K_{22}}}}\left( x \right) }}{{\partial x}} = \left\{ \begin{array}{ll} \frac{{\ln \left( 2 \right) }}{{{2^{2x - 2}}}}&{}\quad x \geqslant 0.5 \\ 0&{}\quad x < 0.5 \\ \end{array} \right. \end{aligned}$$

(29)

Thus, we have (30).

$$\begin{aligned} {Q_1}&= \int _{0.5}^{ + \infty } {} \sum \limits _{m = 0}^N {\sum \limits _{n = 0}^{N - m} {} } C_N^m{\left( { - 1} \right) ^{N - m}}C_{N - m}^n\lambda _S^{N - m - n}{\left( {{2^{2x}} - 1} \right) ^{2\left( {N - m - n} \right) }} \\ &\quad\times {e^{ - {\lambda _S}\left( {{2^{2x}} - 1} \right) \left( {{2^{2x}} - 1 + 2} \right) \left( {N - m} \right) }}\frac{{\ln \left( 2 \right) }}{{{2^{2x - 2}}}}dx \\ \end{aligned}$$

(30)

Let $y = {2^{2x}} - 1$, (30) can be rewritten as (31).

$$\begin{aligned}{Q_1} = 2\sum \limits _{m = 0}^N {\sum \limits _{j = 0}^{N - m} {C_N^mC_{N - m}^n{{\left( { - 1} \right) }^{N - m}}\int _1^{ + \infty } {\lambda _S^{N - m - n}{y^{2\left( {N - m - n} \right) }}\frac{{{e^{ - {\lambda _S}y\left( {y + 2} \right) \left( {N - m} \right) }}}}{{{{\left( {y + 1} \right) }^2}}}dy} } } \end{aligned}$$

(31)

Let $u = {\lambda _S}{\left( {y + 1} \right) ^2}\left( {N - m} \right)$, (31) can be rewritten as (32).

$$\begin{aligned} {Q_1}&= 1 + 2\sum \limits _{m = 0}^{N - 1} {\sum \limits _{n = 0}^{N - m} {C_N^mC_{N - m}^n{{\left( { - 1} \right) }^{N - m}}\lambda _S^{N - m - n}{e^{{\lambda _S}\left( {N - m} \right) }}} } \\&\quad\times \int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {} {\left( {\sqrt{\frac{u}{{{\lambda _S}\left( {N - m} \right) }}} - 1} \right) ^{2\left( {N - m - n} \right) }}\frac{{{e^{ - u}}}}{{\frac{u}{{{\lambda _S}\left( {N - m} \right) }}}}d\left( {\sqrt{\frac{u}{{{\lambda _S}\left( {N - m} \right) }}} - 1} \right) \\&= { {1}} + { {2}}\sum \limits _{m = 0}^{N - 1} {\sum \limits _{n = 0}^{N - m} {C_N^mC_{N - m}^n{{\left( { - 1} \right) }^{N - m}}\lambda _S^{N - m - n}{e^{{\lambda _S}\left( {N - m} \right) }}} } \\&\quad\times \int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {\sum \limits _{k = 0}^{2\left( {N - m - n} \right) } {C_{2\left( {N - m - n} \right) }^k} {{\left( {\frac{u}{{{\lambda _S}\left( {N - m} \right) }}} \right) }^{{k / 2}}}{{\left( { - 1} \right) }^{2\left( {N - m - n} \right) - k}}\frac{{{e^{ - u}}}}{{\frac{{{u^{{3 / 2}}}}}{{\sqrt{{\lambda _S}\left( {N - m} \right) } }}}}\frac{1}{2}du} \\&= 1 + \sum \limits _{m = 0}^{N - 1} {\sum \limits _{n = 0}^{N - m} {\sum \limits _{k = 0}^{2\left( {N - m - n} \right) } {C_{2\left( {N - m - n} \right) }^k} C_N^mC_{N - m}^n{{\left( { - 1} \right) }^{3N - 3m - 2n - k}}} } \lambda _S^{N - m - n} \\&\quad\times {\left( {\frac{1}{{{\lambda _S}\left( {N - m} \right) }}} \right) ^{{{\left( {k - 1} \right) } / 2}}}{e^{{\lambda _S}\left( {N - m} \right) }}\int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {{u^{\frac{{\left( {k - 1} \right) }}{2} - 1}}{e^{ - u}}du} \\&= 1 + \sum \limits _{m = 0}^{N - 1} {\sum \limits _{n = 0}^{N - m} {\sum \limits _{k = 0}^{2\left( {N - m - n} \right) } {C_N^mC_{N - m}^nC_{2\left( {N - m - n} \right) }^k{{\left( { - 1} \right) }^{3N - 3m - 2n - k}}\lambda _S^{N - m - n - {{\left( {k - 1} \right) } / 2}}} } } \\&\quad\times {\left( {N - m} \right) ^{{{ - \left( {k - 1} \right) } / 2}}}{e^{{\lambda _S}\left( {N - m} \right) }}\int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {{u^{\frac{{\left( {k - 1} \right) }}{2} - 1}}{e^{ - u}}du} \end{aligned}$$

(32)

where

$$\begin{aligned} \begin{array}{l} \int _{4{\lambda _S}\left( {N - m} \right) }^{ + \infty } {{u^{\frac{{\left( {k - 1} \right) }}{2} - 1}}{e^{ - u}}du} \\ \qquad = \left\{ \begin{array}{ll} \Gamma \left( {\frac{{k - 1}}{2},4{\lambda _S}\left( {N - m} \right) } \right) ,&{}\quad k > 1 \\ {\text {Ei}}\left( {1,4{\lambda _S}\left( {N - m} \right) } \right) ,&{}\quad k = 1 \\ 2\sqrt{\pi }\left( {{\text {erf}}\left( {\sqrt{4{\lambda _S}\left( {N - m} \right) } } \right) - 1} \right) + 2{e^{ - 4{\lambda _S}\left( {N - m} \right) }}{\left( {4{\lambda _S}\left( {N - m} \right) } \right) ^{ - {1 / 2}}},&{}\quad k = 0 \\ \end{array} \right. \\ \end{array} \end{aligned}$$

Appendix B

1.1 Derivation of ${G_1}$

Let ${K_{11}} = \min \left( {Ca\left( {{a_1}} \right) ,Ca\left( {{a_2}} \right) ,\frac{1}{2}Ca\left( {{a_1}{ { + }}{a_2}} \right) } \right)$ and ${K_{12}} = \max \left( {Ca\left( b \right) ,Ca\left( {\frac{1}{b}} \right) } \right)$, where ${a_1} = {\gamma _S}{\left| {{h_{SAS{R_i}}}} \right| ^2}$, ${a_2} = {\gamma _S}{\left| {{h_{SBS{R_i}}}} \right| ^2}$ and $b = \frac{{{\gamma _S}{{\left| {{h_{SAE}}} \right| }^2}}}{{{\gamma _S}{{\left| {{h_{SBE}}} \right| }^2}}}$. Because all the CSIs are mutual independent, thus ${G_1}$ can be rewritten as (33).

$$\begin{aligned} {G_1} = \Pr \left( {{K_{11}} \leqslant {K_{12}}} \right) = \oint {\Pr \left( {{K_{11}} \leqslant x} \right) {f_{{K_{12}}}}\left( x \right) dx} \end{aligned}$$

(33)

We first drive $\Pr \left( {{K_{11}} \leqslant x} \right)$, given by (34).

$$\begin{aligned} \Pr \left( {{K_{11}} \leqslant x} \right)&= \Pr \left( {\min \left( {Ca\left( {{a_1}} \right) ,Ca\left( {{a_2}} \right) ,\frac{1}{2}Ca\left( {{a_1}{ { + }}{a_2}} \right) } \right) \leqslant x} \right) \\&= 1 - \Pr \left( {\min \left( {Ca\left( {{a_1}} \right) ,Ca\left( {{a_2}} \right) ,\frac{1}{2}Ca\left( {{a_1}{ { + }}{a_2}} \right) } \right) \leqslant x} \right) \\&= 1 - \Pr \left( {{a_1}> \underbrace{{2^{2x}} - 1}_z,{a_2}> {2^{2x}} - 1,{a_1}{ { + }}{a_2} > \left( {{2^{4x}} - 1} \right) } \right) \\&= 1 - \int _z^{z\left( {z + 1} \right) } {\int _{z\left( {z{ { + }}2} \right) - v}^{ + \infty } {{\lambda _S}{e^{ - {\lambda _S}u}}{\lambda _S}{e^{ - {\lambda _S}v}}du} dv} \\&\qquad - \int _{z\left( {z + 1} \right) }^{ + \infty } {\int _z^{ + \infty } {{\lambda _S}{e^{ - {\lambda _S}u}}{\lambda _S}{e^{ - {\lambda _S}v}}du} dv} \\&= 1 - \left( {1 + {\lambda _S}{{\left( {{2^{2x}} - 1} \right) }^2}} \right) {e^{ - {\lambda _S}\left( {{2^{4x}} - 1} \right) }} \\ \end{aligned}$$

(34)

The cumulative density function of ${K_{12}}$ can be obtained from (35).

$$\begin{aligned} {F_{{K_{12}}}}\left( x \right)&= \Pr \left( {{K_{12}}< x} \right) \\&= \Pr \left( {\max \left( {Ca\left( b \right) ,Ca\left( {\frac{1}{b}} \right) } \right)< x} \right) \\&= \Pr \left( {\max \left( {b,\frac{1}{b}} \right)< {2^{2x}} - 1} \right) \\&= \left\{ \begin{array}{ll} \frac{{{2^{2x}} - 2}}{{{2^{2x}}}}&{}\quad x \geqslant 0.5 \\ 0&{}\quad x < 0.5 \\ \end{array} \right. \\ \end{aligned}$$

(35)

Thus, the probability density function of ${K_{12}}$ can be expressed as (36).

$$\begin{aligned} {f_{{K_{12}}}}\left( x \right) = \frac{{\partial {F_{{K_{12}}}}\left( x \right) }}{{\partial x}} = \left\{ \begin{array}{ll} \frac{{\ln \left( 2 \right) }}{{{2^{2x - 2}}}}&{}\quad x \geqslant 0.5 \\ 0&{}\quad x < 0.5 \\ \end{array} \right. \end{aligned}$$

(36)

Let $y = {2^{2x}} - 1$, (34) can be rewritten as (37).

$$\begin{aligned} {G_1}&= \Pr \left( {{K_{11}} \leqslant {K_{12}}} \right) \\&= \int _{0.5}^{ + \infty } {1 - \left( {1 + {\lambda _S}{{\left( {{2^{2x}} - 1} \right) }^2}} \right) {e^{ - {\lambda _S}\left( {{2^{2x}} - 1} \right) \left( {\left( {{2^{2x}} - 1} \right) + 2} \right) }}\frac{{\ln \left( 2 \right) }}{{{2^{2x - 2}}}}dx} \\&= 2\int _1^{ + \infty } {\left( {1 - \left( {1 + {\lambda _S}{y^2}} \right) {e^{ - {\lambda _S}y\left( {y + 2} \right) }}} \right) \frac{1}{{{{\left( {y + 1} \right) }^2}}}dy} \\&= 2\int _1^{ + \infty } {\frac{1}{{{{\left( {y + 1} \right) }^2}}}dy} - 2\int _1^{ + \infty } {\frac{{\left( {1 + {\lambda _S}{y^2}} \right) {e^{ - {\lambda _S}y\left( {y + 2} \right) }}}}{{{{\left( {y + 1} \right) }^2}}}dy} \\&= 1 - {e^{ - 3{\lambda _S}}}\left( {2\sqrt{\pi }{e^{4{\lambda _S}}}\lambda _S^{{3 / 2}} + \sqrt{\pi }{e^{4{\lambda _S}}}\lambda _S^{{1 / 2}}} \right) \left( {{\text {erf}}(2\sqrt{{\lambda _S}} ) - 1} \right) \\&\quad - {e^{ - 3{\lambda _S}}}\left( { - 2{\lambda _S}{e^{4{\lambda _S}}}{\text {Ei}}\left( {1,4{\lambda _S}} \right) + {\lambda _S} + 1} \right) \\ \end{aligned}$$

(37)