A Physical Layer Network Coding Based Modify-and-Forward with Opportunistic Secure Cooperative Transmission Protocol

Abstract

This paper investigates a new secure relaying scheme, namely physical layer network coding based modify-and-forward (PMF), in which a relay node linearly combines the decoded data sent by a source node with an encrypted key before conveying the mixed data to a destination node. We first derive the general expression for the generalized secrecy outage probability (GSOP) of the PMF scheme and then use it to analyse the GSOP performance of various relaying and direct transmission strategies. The GSOP performance comparison indicates that these transmission strategies offer different advantages depending on the channel conditions and target secrecy rates, and relaying is not always desirable in terms of secrecy. Subsequently, we develop an opportunistic secure transmission protocol for cooperative wireless relay networks and formulate an optimisation problem to determine secrecy rate thresholds (SRTs) to dynamically select the optimal transmission strategy for achieving the lowest GSOP. The conditions for the existence of the SRTs are derived for various channel scenarios.

1 Introduction

Physical-layer security has recently attracted the interest of broader communications societies [1], especially in cooperative wireless relay networks (CWRNs) [2,3,4,5,6] where user cooperation has been identified as an innovative change enabling multi-hop communications [7]. The connection between a subscriber and a legitimate transmitter can be realised with the assistance of a relay node employing either amplify-and-forward (AF) or decode-and-forward (DF) protocols [8]. Over the wireless media, the eavesdropper and/or attacker can overhear the message from both the transmitter and the relay nodes. Therefore, in order to protect data from vulnerable attacks in the CWRNs, the security of both the direct and relaying links needs to be investigated.

From the physical-layer perspective, information-theoretic approach has been shown to be able to provide secure communications between legitimate users by using jamming signals and appropriate channel coding [2]. A basic approach was originally proposed in [9] for a noiseless cipher system where the data is encrypted by simply XORing with a shared secret key. The noisy channel was then investigated in [10] where Wyner first introduced the concept of wiretap channel. It is shown that the innate irregularity and diversity of the message can confuse the eavesdropper, and thus strengthen the legitimate communications. Specifically, independent transmitters can help in transmitting jamming signals to enhance the secrecy rate of the legitimate users [11,12,13]. However, such cooperative jamming (CJ) can cause interferences that reduce the decoding rate at the legitimate receivers [14,15,16]. Another approach of the CJ is noise forwarding [17] where a relay node sends extra irregularity to direct as haphazardly chosen codewords from codebook known to both the legitimate sender and the beneficiary [18].

Motivated by the concept of network coding (NC) for improving the throughput of lossless networks [19, 20], a vast number of works have investigated the performance of physical-layer NC (PNC) in CWRNs, e.g. in [21,22,23,24,25], and secure NC has also been proposed in [26, 27] to improve the security of wiretap channels. The principle of the PNC is that the relays perform algebraic linear/logic operations on received packets from multiple transmission source nodes and then forward the combined packets to the destination nodes in the subsequent transmissions.

Focusing on secure communications in CWRNs, various relaying strategies were investigated in [28,29,30]. Specifically, secure AF and DF schemes were analysed in [28, 29]. Modify-and-forward (MF) cooperation scheme was proposed in [30] where the relay first modifies the message received from the source in the first time slot and then forwards the modified message to the destination in the second time slot. In the MF scheme, the modification process at the relay is assumed to be inherently shared between legitimate users, and thus only the interested destination can recover the original message. This MF approach yields an enhanced secrecy performance in comparison with other relaying techniques. However, the work in [30] assumed that the eavesdropper can only decode the message from the source in the first time slot, which limits its application in practice since the eavesdropper could also overhear and decode a part of the message from the relay in the second time slot. Additionally, over the wireless media, the channel dedicated for sharing knowledge between the relay and the destination suffers from fading and background noise, which may cause a considerable performance degradation. Furthermore, it can be noticed that the relaying schemes do not always provide the best performance as they depend on the channel quality of various links and target secrecy rate. Therefore, it is crucial to address these practical issues as well as providing a numerical approach in finding the optimal scheme among the direct and relaying schemes with respect to the channel environment and the QoS requirement of secrecy rate.

In this paper, inspired by the principle of PNC, we first propose a new secure relaying scheme, namely secure PNC-based MF (PMF), to cope with the practical security issue of the imperfectly shared knowledge of the message modification between relay and destination in the conventional MF scheme, i.e. [30]. Furthermore, the proposed scheme takes into account a practical scenario that the eavesdropper can overhear and attempt to decode the message from both the source and the relay in CWRNs. By deriving the generalized secrecy outage probability (GSOP) of the PMF scheme with respect to other direct and relaying schemes,¹ the usage of the relay is shown not to be always beneficial, especially when the link between the source and the relay and (or) the link between the relay and the destination suffer(s) from severe fading and noise. This fact, however, is brought into question when the relay should be exploited to provide a higher secure communication, and thus motivates us to propose an opportunistic secure transmission protocol for the CWRNs. The main contributions of this paper can be summarised as follows:

• A novel PMF scheme for legitimate users: In the proposed PMF scheme, the PNC operation at the relay can restrict the eavesdropper to receiving only part of information from the relay rather than overhearing the full message. This PNC operation also differentiates the proposed scheme from the cryptographic techniques with only encrypted key. Furthermore, the assumption of perfectly shared information of PNC coefficients and encrypted key² between the relay and destination is relaxed, while only channel statistics are assumed to be known at the destination.

• Derivation of GSOP: GSOP is considered to link the concept of physical layer security and eavesdropper decodability [34, 35]. The derived GSOP for the proposed PMF scheme reveals not only its effectiveness in relation to the conventional direct transmission (DT) [36] and other relaying transmission (RT) schemes, such as DF [28], CJ [11] and MF [30], but also the level of secrecy requirements from the cryptographic perspective. In particular, this derived GSOP is shown to be a general expression also for the DF and MF schemes. It indicates that the DF scheme is a special case of the PMF scheme when neither encryption nor PNC operation is performed at the relay and the MF scheme can be regarded as an ideal case of the PMF scheme with no PNC operation and when the link between the relay and eavesdropper is neglected.

• GSOP comparison of different schemes: The proposed PMF scheme is shown to provide an enhanced security with a lower GSOP under certain channel link quality, channel knowledge and target secrecy rate when compared to DT, DF and CJ schemes. Moreover, the GSOP of the PMF scheme approaches that of the MF scheme which is regarded as a lower bound of the PMF scheme in an ideal scenario. It is further noticed that the DT scheme without the assistance of the relay can achieve a higher secrecy performance over all RT schemes at a high target secrecy rate, especially when the direct link is of very high quality. These remarkable facts accordingly mean that none of these schemes are able to ensure the highest secrecy at all times given variant channel conditions and secrecy rate requirements.

• A new opportunistic secure transmission protocol for CWRNs: The proposed protocol aims at finding an optimal protocol among DT and RT schemes that achieves the best secrecy performance with the lowest GSOP. It is shown that there exist secrecy rate thresholds (SRTs) which are the crossing points between the GSOPs of various schemes. The optimisation problem is thus turned into finding the SRTs with respect to channel conditions and secrecy rate requirements. Furthermore, the conditions of the channel quality are derived for the existence of the SRTs. The derived SRTs are shown to not only facilitate the finding of the optimal scheme for a secure CWRN, but also help in determining if the relay could be relied on in the practical CWRNs.

The rest of this paper is organised as follows: Section 2 describes the system model of a typical CWRN in the presence of an eavesdropper. Section 3 presents the proposed PMF scheme. The GSOP analysis of the PMF scheme is presented in Section 4 in comparison with DT, DF, CJ and MF schemes. The opportunistic secure transmission protocol for the CWRN is developed in Section 5 where the SRTs are determined. Numerical and simulation results are presented in Section 6 to validate the concepts. Finally, Section 7 draws the main conclusions from this paper.

2 System model

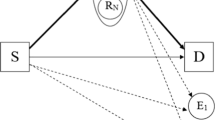
Figure 1 illustrates the system model of a CWRN under investigation consisting of a source node $\mathcal {S}$, a destination node $\mathcal {D}$ and a relay node $\mathcal {R}$ in the presence of an eavesdropper node $\mathcal {E}$. It is assumed that there exists a direct link $\mathcal {S}\to \mathcal {D}$ and thus $\mathcal {S}$ may transmit a data packet to $\mathcal {D}$ either with or without the assistance of $\mathcal {R}$. In Fig. 1, $\mathcal {E}$ is assumed to be located between $\mathcal {S}$ and $\mathcal {D}$ and in the vicinity of $\mathcal {R}$. Therefore, there exist two wiretap links from both $\mathcal {S}$ and $\mathcal {R}$ to $\mathcal {E}$.

Fig. 1

System model of a CWRN in the presence of an eavesdropper

The communication channel between nodes $\mathcal {A}$ and $\mathcal {B}$, $\mathcal {A},\mathcal {B} \in \{\mathcal {S},\mathcal {R},\mathcal {E},\mathcal {D}\}$, $\mathcal {A}\neq \mathcal {B}$, is assumed to experience identical and independently distributed quasi-static Rayleigh flat fading where all channel gains are time-invariant over the whole transmission of a data packet and vary independently in the next data packet. The instantaneous and average signal-to-noise ratio (SNR) or signal-to-interference-plus-noise ratio (SINR) of the link $\mathcal {A} \to \mathcal {B}$ are denoted by $\gamma _{\mathcal {AB}}$ and $\bar {\gamma }_{\mathcal {AB}}$, respectively. The probability density function (pdf) and cumulative distribution function (cdf) of a random variable X are denoted by f_X(⋅) and F_X(⋅), respectively.

In the DT scheme, $\mathcal {S}$ transmits data directly to $\mathcal {D}$, while in the RT scheme, the cooperative data transmission from $\mathcal {S}$ to $\mathcal {D}$ is realised via two time slots as follows:

• i) Time slot 1: $\mathcal {S}$ transmits the data packet to both $\mathcal {R}$ and $\mathcal {D}$;

• ii) Time slot 2: $\mathcal {R}$ processes the data packet received from $\mathcal {S}$ prior to forwarding the processed data to $\mathcal {D}$.

3 Proposed PMF scheme

In this section, we introduce the data transmission, decoding and encryption process in our proposed PMF scheme for enhancing the security of a CWRN as shown in Fig. 1.

In the first time slot, $\mathcal {S}$ transmits a data packet x to both $\mathcal {R}$ and $\mathcal {D}$. Over the eavesdropping channel, $\mathcal {E}$ also receives the data packet from $\mathcal {S}$. The received signal at node $\mathcal {X}$, $\mathcal {X}\in \{\mathcal {R},\mathcal {D},\mathcal {E}\}$, is given by

$$ {\textbf{r}}^{(1)}_{\mathcal{X}}=\sqrt{{\Lambda}_{\mathcal{S}}}h_{\mathcal{SX}}{\textbf{x}}+{\textbf{n}}^{(1)}_{\mathcal{X}}, $$

(1)

where ${\Lambda }_{\mathcal {S}}$ is the power of the source $\mathcal {S}$, $h_{\mathcal {SX}}$ is the channel gain between $\mathcal {S}$ and $\mathcal {X}$, and ${\textbf {n}}^{(1)}_{\mathcal {X}}$ is an independent circularly symmetric complex Gaussian (CSCG) noise vector at node $\mathcal {X}$ with each entry having zero mean and variance of ${\sigma ^{2}_{0}}$. Then, $\mathcal {X}$ decodes the data from $\mathcal {S}$, which is denoted by $\bar {{\textbf {x}}}^{(1)}_{\mathcal {X}}$.

In the second time slot, after decoding the data packet received from $\mathcal {S}$,³ the relay node $\mathcal {R}$ randomly and linearly combines the decoded data, i.e. $\bar {{\textbf {x}}}^{(1)}_{\mathcal {R}}$, with the encrypted key (denoted by k) using randomised PNC approach as follows:

$$ {\textbf{x}}^{(2)}_{\mathcal{R}}=\alpha \bar{{\textbf{x}}}^{(1)}_{\mathcal{R}} + \beta {\textbf{k}}, $$

(2)

where α and β are random PNC coefficients satisfying α² + β² = 1 and α≠ 0.

Through the second hop, $\mathcal {D}$ is expected to receive the data from $\mathcal {R}$, while $\mathcal {E}$ could overhear the same information. The received signal at node $\mathcal {Y}$, $\mathcal {Y}\in \{\mathcal {D},\mathcal {E}\}$, is given by

$$ {\textbf{r}}^{(2)}_{\mathcal{Y}}=\sqrt{{\Lambda}_{R}}h_{\mathcal{RY}}{\textbf{x}}^{(2)}_{\mathcal{R}}+{\textbf{n}}^{(2)}_{\mathcal{Y}}, $$

(3)

where ${\Lambda }_{\mathcal {R}}$ is the power of the relay $\mathcal {R}$, $h_{\mathcal {RY}}$ is the channel gain between $\mathcal {R}$ and $\mathcal {Y}$, and ${\textbf {n}}^{(2)}_{\mathcal {Y}}$ is a CSCG noise vector at node $\mathcal {Y}$ with each entry having zero mean and variance of ${\sigma ^{2}_{0}}$. Substituting Eq. 2 into Eq. 3, we obtain

$$ {\textbf{r}}^{(2)}_{\mathcal{Y}}=\sqrt{{\Lambda}_{\mathcal{R}}}h_{\mathcal{RY}}\alpha \bar{{\textbf{x}}}^{(1)}_{\mathcal{R}} + \sqrt{{\Lambda}_{\mathcal{R}}}h_{\mathcal{RY}}\beta {\textbf{k}}+{\textbf{n}}^{(2)}_{\mathcal{Y}}. $$

(4)

Although the PNC coefficients and encrypted key are only shared between the legitimate users, $\mathcal {E}$ can still decode the data sent from $\mathcal {R}$ by treating these unknowns as interference and performing maximum ratio combining (MRC) of the signals received in both time slots from $\mathcal {S}$ and $\mathcal {R}$. On the other hand, it is likely that $\mathcal {D}$ can decode the interested data given the shared information between $\mathcal {S}$, $\mathcal {R}$ and $\mathcal {D}$. However, at $\mathcal {D}$, imperfectly shared knowledge of the PNC coefficients and encrypted key can also take place due to the inherent fading and noises of the wireless channels. In other words, we need to consider the following two cases:

• i) PMF-perfect: With perfectly shared knowledge of α, β and k, $\mathcal {D}$ is able to decode the data from $\mathcal {R}$ in the second time slot by eliminating α, β and k in Eq. 4.

• ii) PMF-imperfect: This case implies that $\mathcal {D}$ may only obtain partial knowledge of α, β and k (either of them but not all). $\mathcal {D}$ can employ maximum likelihood detection to recover the data in the second time slot given the known channel statistics of the link $\mathcal {R}\to \mathcal {D}$.

Remark 1 (Improved Security With the Proposed PMF)

As shown in Eq. 4, in order to encrypt the data packet forwarded from the relay node $\mathcal {R}$, two layers of security are integrated into the PMF scheme including the PNC coefficients, i.e. α and β, and the encrypted key, i.e. k. Such modification process at $\mathcal {R}$ can thus confuse the eavesdropper $\mathcal {E}$ from overhearing the full message from $\mathcal {R}$, which accordingly results in a more secure relay communications between legitimate users. It can also be noticed that the cryptographic techniques correspond to the scenario when the PNC is not employed at $\mathcal {R}$, and thus only the encrypted key is required at the eavesdropper to decode the overheard packet.

Remark 2 (DF & MF - Special Cases of the Proposed PMF)

It can be seen in Eq. 4 that the conventional DF scheme can be deduced from the PMF scheme by setting α = 1 and β = 0, which means there is no encrypted key and no PNC operation at $\mathcal {R}$. In relation to the work in [30], the MF scheme assumes that $\mathcal {E}$ omits the message from $\mathcal {R}$ due to the unavailability of the modification process performed at $\mathcal {R}$, and thus can be regarded as a special case of the PMF when the link $\mathcal {R}\to \mathcal {E}$ does not exist. However, it is worth mentioning that such assumption of no decoding process performed at $\mathcal {E}$ in the second time slot may restrict the application of the MF scheme in practice. Instead, our work considers a general scenario dealing with the issue when $\mathcal {E}$ can partially decodes the message from $\mathcal {R}$ by treating the encrypted key as interference.

Regarding the complexity of the proposed PMF scheme at the relay, only arithmetic functions are required to combine the data packet and the encrypted key. From Eq. 2, it can be seen that there are a total of M additions and 2M multiplications where M is the data packet length. In other words, as compared to the conventional DF scheme (which simply decodes and amplifies the data packet received from the source), the security of the proposed scheme comes at the cost of an increase in computational complexity. Modulo addition (instead of linear addition) can be used with lattice code (as in [37]) in the scenario of untrusted relay channels for energy savings.

4 Generalized secrecy outage probability analysis

In this section, we first derive the GSOP of the proposed PMF scheme for a CWRN considering the general scenario of imperfectly shared information of message modification between relay and destination, i.e. PMF-imperfect scheme. For comparison, the GSOP of DT scheme [36] and other RT schemes, including DF [28], CJ [11] and MF [30], are also provided to verify the effectiveness of the PMF scheme as well as motivating us to propose an opportunistic secure transmission protocol which will be presented in the following section.

The GSOP is defined as the probability that the wireless system fails to achieve a target secrecy rate subject to secrecy requirements [34], i.e.

$$ P_{out}\triangleq \Pr\left\{\frac{C_{s}}{R_{s}}<\theta\right\}, $$

(5)

where R_s is the target secrecy rate, C_s is the instantaneous secrecy capacity and 𝜃, 0 < 𝜃 ≤ 1, is the minimum acceptable value of the fractional equivocation, i.e. the ratio of C_s to R_s. Here, 𝜃 represents the level of secrecy requirements. A particular case is when 𝜃 = 1, then the GSOP turns into the classical SOP. In Eq. 5, C_s can be computed by

$$ C_{s}=\max\{C_{d}-C_{e},0\}=\left[C_{d}-C_{e}\right]^{+}, $$

(6)

where C_d is the instantaneous channel capacity of the legitimate links, C_e is the instantaneous channel capacity of the eavesdropper links, and $[x]^{+}\triangleq \max \{x,0\}$. Intuitively, it can be observed in Eq. 6 that, to have a secure communication with a positive secrecy capacity, the legitimate links must be dominant over the eavesdropper links.

4.1 PMF scheme

We now proceed to derive C_d and C_e of the PMF scheme. Taking into account both direct and relaying links with decoding and PNC operation at $\mathcal {R}$, the maximum rate for reliable data communications between $\mathcal {S}$ and $\mathcal {D}$ can be expressed by

$$ C_{d}= \min\left\{\frac{1}{2}\log_{2}(1+\gamma_{\mathcal{SR}}),\frac{1}{2}\log_{2}(1+\gamma_{\mathcal{SD}}+\gamma_{\mathcal{RD}})\right\}, $$

(7)

where $\gamma _{\mathcal {SR}}$ and $\gamma _{\mathcal {SD}}$ denote the instantaneous SNR of the link $\mathcal {S}\to \mathcal {R}$ and $\mathcal {S}\to \mathcal {D}$, respectively, in the first time slot, and $\gamma _{\mathcal {RD}}$ denotes the instantaneous SINR of the link $\mathcal {R}\to \mathcal {D}$ in the second time slot. Here, the instantaneous SNR $\gamma _{\mathcal {SR}}$ and $\gamma _{\mathcal {SD}}$ can be respectively computed from Eq. 1 as

$$ \gamma_{\mathcal{SR}}=\frac{{\Lambda}_{\mathcal{S}}|h_{\mathcal{SR}}|^{2}}{{\sigma^{2}_{0}}}, $$

(8)

$$ \gamma_{\mathcal{SD}}=\frac{{\Lambda}_{\mathcal{S}}|h_{\mathcal{SD}}|^{2}}{{\sigma^{2}_{0}}}. $$

(9)

In the second time slot, $\mathcal {D}$ receives the combined data from $\mathcal {R}$ consisting of both the interested information and encrypted key. From Eq. 4, $\gamma _{\mathcal {RD}}$ can be determined by

$$ \gamma_{\mathcal{RD}}=\frac{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RD}}|^{2}\alpha^{2}}{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RD}}|^{2}\beta^{2}+{\sigma^{2}_{0}}}. $$

(10)

Due to the broadcast nature of the wireless channels, $\mathcal {E}$ can eavesdrop the data from $\mathcal {S}$ and $\mathcal {R}$ in both time slots. Such information leakage can be intuitively measured by comparing the uncertainty about the message before and after $\mathcal {E}$ receives it [38]. From an information theoretical point of view, this leakage is the mutual information and the maximum rate for reliable eavesdropping or the maximum leakage rate is the channel capacity of the eavesdropper link. Taking the advantage of both diversity branches with MRC approach, the maximum leakage rate at $\mathcal {E}$ is given by

$$ C_{e}= \frac{1}{2}\log_{2}(1+\gamma_{\mathcal{SE}}+\gamma_{\mathcal{RE}}), $$

(11)

where $\gamma _{\mathcal {SE}}$ and $\gamma _{\mathcal {RE}}$ are respectively given by

$$ \gamma_{\mathcal{SE}}=\frac{{\Lambda}_{\mathcal{S}}|h_{\mathcal{SE}}|^{2}}{{\sigma^{2}_{0}}}, $$

(12)

$$ \gamma_{\mathcal{RE}}=\frac{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RE}}|^{2}\alpha^{2}}{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RE}}|^{2}\beta^{2}+{\sigma^{2}_{0}}}. $$

(13)

Remark 3 (Impact of PNC Coefficients on GSOP Performance)

It can be seen in Eqs. 10 and 13 that the PNC coefficients affect both the SINR of both legitimate link $\mathcal {R}\to \mathcal {D}$ and eavesdropping link $\mathcal {R}\to \mathcal {E}$ in the second time slot. In order to validate their impacts on the GSOP performance, for instance, let us consider a specific scenario when $\gamma _{\mathcal {SR}}>\gamma _{\mathcal {SD}}+\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {SD}}\approx \gamma _{\mathcal {SE}}$. It can be shown that, as α increases (or β decreases), $(\gamma _{\mathcal {RD}}-\gamma _{\mathcal {RE}})$ increases if $|h_{\mathcal {RD}}|^{2}\geq |h_{\mathcal {RE}}|^{2}$; otherwise, $(\gamma _{\mathcal {RD}}-\gamma _{\mathcal {RE}})$ decreases. This accordingly results in the change of the GSOP. The finding of the optimal PNC coefficients at $\mathcal {R}$ is worth to investigate taking into account all channel gains. In the general case, the knowledge of all these gains is required to be either perfectly known or estimated at $\mathcal {R}$. This is however beyond the scope of this work where $\mathcal {R}$ is only required to know the channel from $\mathcal {S}$ to decode the data packet prior to employing the random PNC.

Substituting Eqs. 7 and 11 into Eq. 6, the secrecy capacity, i.e. C_S, can be obtained and the GSOP of the PMF can be thus derived from Eq. 5 as

$$ P^{(PMF)}_{out} \!\! = \Pr\left\{\!\left[\!\log_{2}\!\left( \!\frac{1 + \min\{\gamma_{\mathcal{SR}},\gamma_{\mathcal{SD}} + \gamma_{\mathcal{RD}}\}}{1+\gamma_{\mathcal{SE}}+\gamma_{\mathcal{RE}}}\!\right)\!\right]^{+}\!\!\!\!<\!\! 2\theta R_{s}\!\!\right\}. $$

(14)

In order to analyse (14), let us firstly find the pdf of $\gamma _{\mathcal {SR}}$, $\gamma _{\mathcal {SD}}$, $\gamma _{\mathcal {RD}}$, $\gamma _{\mathcal {SE}}$ and $\gamma _{\mathcal {RE}}$ defined in Eqs. 8, 9, 10, 12 and 13, respectively. Since the links between nodes are assumed to experience Rayleigh flat fading, the pdf of the SNR $\gamma _{\mathcal {AB}}$, $\mathcal {AB}\in \{\mathcal {SR},\mathcal {SD},\mathcal {SE}\}$ is given by [39]

$$ f_{\gamma_{\mathcal{AB}}}(\gamma_{\mathcal{AB}})=\frac{1}{\bar{\gamma}_{\mathcal{AB}}}\exp\left( -\frac{\gamma_{\mathcal{AB}}}{\bar{\gamma}_{\mathcal{AB}}}\right), $$

(15)

while the pdf of the SINRs $\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {RE}}$ can be obtained using the following Lemma 1.

Lemma 1

IfX = c|Z|²,where c is a positive constant, Z is a zero-mean complex Gaussian random variable with variance of 1,and$Y=\frac {a^{2} X}{b^{2} X + 1}$,wherea² + b² = 1 anda≠ 0,then the pdf of Y is given by

$$ f_{Y}(y)=\frac{a^{2}}{c(a^{2}-b^{2}y)^{2}}\exp\left[-{\frac{y}{c(a^{2}-b^{2}y)}}\right]. $$

(16)

Proof

See Appendix A. □

From the above Lemma 1, the pdf of the SINR $\gamma _{\mathcal {A^{\prime }B^{\prime }}}$, $\mathcal {A^{\prime }B^{\prime }}\in \{\mathcal {RD},\mathcal {RE}\}$, can be expressed by

$$\begin{array}{@{}rcl@{}} f_{\gamma_{\mathcal{A^{\prime}B^{\prime}}}}(\gamma_{\mathcal{A^{\prime}B^{\prime}}})&=& \frac{\alpha^{2}}{\bar{\gamma}_{\mathcal{A^{\prime}B^{\prime}}}(\alpha^{2}-\beta^{2} \gamma_{\mathcal{A^{\prime}B^{\prime}}})^{2}}\\ &&\times \exp\left[{\frac{-{\gamma}_{\mathcal{A^{\prime}B^{\prime}}}}{\bar{\gamma}_{\mathcal{A^{\prime}B^{\prime}}}(\alpha^{2}-\beta^{2} \gamma_{\mathcal{A^{\prime}B^{\prime}}})}}\right]. \end{array} $$

(17)

Remark 4 (General pdf of SINR $\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {RE}}$)

It can be observed that the pdf of the SNR in Eq. 15 is a special form of the pdf of the SINR in Eq. 17 when α = 1 and β = 0. In the scenario that the encrypted key and PNC operation at $\mathcal {R}$ are known at $\mathcal {D}$, the proposed PMF is regarded as PMF-perfect scheme when $\gamma _{\mathcal {RD}}$ is given by Eq. 15. In case that such modification process at $\mathcal {R}$ is known at both $\mathcal {D}$ and $\mathcal {E}$, then both $\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {RE}}$ are computed by Eq. 15. We then have a more special case of the PMF scheme which is indeed the conventional DF scheme as also noticed in Remark 2. However, it is worth noting that the eavesdropper in our work can overhear the message in both time slots but only a partial information can be recovered in the second time slot given imperfect knowledge of the modification process at $\mathcal {R}$. This accordingly reflects the novelty of our work in the GSOP analysis of the PMF scheme for CWRNs.

Given the pdf of all channel links in Eqs. 15 and 17, further derivation of Eq. 14 leads to the following finding:

Theorem 1

The GSOP of the proposed PMF scheme is obtained by Eq. 18, where

$$\begin{array}{@{}rcl@{}} P^{(PMF)}_{out} &=& {\int}_{2^{2\theta R_{s}}-1}^{\infty}f_{Y}(y){\int}_{y}^{\infty}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z) I_{1}(x) dz dx dy \\ &&+ {\int}_{2^{2\theta R_{s}}-1}^{\infty}f_{X}(x){\int}_{x}^{\infty}f_{Y}(y) I_{1}(x) dy dx \\ &&+ {\int}_{0}^{2^{2 \theta R_{s}}-1}f_{Y}(y){\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z)I_{1}(x) dz dx dy \\ &&+ {\int}_{0}^{2^{2 \theta R_{s}}-1}f_{Y}(y){\int}_{y}^{2^{2 \theta R_{s}}-1}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z) I_{2}(x) dz dx dy \\ &&+{\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{X}(x) {\int}_{2^{2 \theta R_{s}}-1}^{x}f_{Y}(y) {\int}_{2^{2 \theta R_{s}}-1-y}^{x-y}f_{Z}(z) I_{1}(y+z) dz dy dx \end{array} $$

(18)

$$ I_{1}(x)\triangleq {{\int}_{0}^{x}}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+x)-1-u}^{x-u}f_{V}(v) dv du, $$

(19)

$$ I_{2}(x)\triangleq {{\int}_{0}^{x}}f_{U}(u){\int}_{0}^{x-u}f_{V}(v) dv du, $$

(20)

$$ f_{X}(x)=\frac{1}{\bar{\gamma}_{\mathcal{SR}}}\exp\left( -\frac{x}{\bar{\gamma}_{\mathcal{SR}}}\right), $$

(21)

$$ f_{Y}(y)=\frac{1}{\bar{\gamma}_{\mathcal{SD}}}\exp\left( -\frac{y}{\bar{\gamma}_{\mathcal{SD}}}\right), $$

(22)

$$ f_{Z}(z)=\frac{\alpha^{2}}{\bar{\gamma}_{\mathcal{RD}}(\alpha^{2}-\beta^{2} z)^{2}}\exp\left( -{\frac{z}{\bar{\gamma}_{\mathcal{RD}}(\alpha^{2}-\beta^{2} z)}}\right), $$

(23)

$$ f_{U}(u)=\frac{1}{\bar{\gamma}_{\mathcal{SE}}}\exp\left( -\frac{u}{\bar{\gamma}_{\mathcal{SE}}}\right). $$

(24)

$$ f_{V}(z)=\frac{\alpha^{2}}{\bar{\gamma}_{\mathcal{RE}}(\alpha^{2}-\beta^{2} v)^{2}}\exp\left( -{\frac{v}{\bar{\gamma}_{\mathcal{RE}}(\alpha^{2}-\beta^{2} v)}}\right), $$

(25)

Proof

See Appendix B. □

It is noted that the derivation of the closed-form expression for the GSOP of the proposed PMF in Theorem 1 is challenging. Nevertheless, the GSOP of the conventional DF and MF schemes in the following subsection can be derived from Eq. 18 as special cases of the PMF scheme.

4.2 DT scheme

In DT scheme, the relay is assumed to be unavailable and thus, for fair comparison, $\mathcal {S}$ sends the encoded data to $\mathcal {D}$ using the power of $2{\Lambda }_{\mathcal {S}}$. The GSOP of the DT is given by [36]

$$\begin{array}{@{}rcl@{}} P^{(DT)}_{out}&=&\Pr\left\{\left[\log_{2}\left( \frac{1 + 2\gamma_{\mathcal{SD}}}{1 + 2\gamma_{\mathcal{SE}}}\right) \right]^{+}< \theta R_{s}\right\}\\ &=&1-\frac{\bar{\gamma}_{\mathcal{SD}}}{\bar{\gamma}_{\mathcal{SD}}+ 2^{\theta R_{s}}\bar{\gamma}_{\mathcal{SE}}}\exp\left( \frac{1 - 2^{\theta R_{s}}}{2\bar{\gamma}_{\mathcal{SD}}}\right). \end{array} $$

(26)

4.3 CJ scheme

Let us consider a typical CJ scheme in [11]. The principle of the CJ is that different transmitters transmit jamming signals with the aim of interfering the illegitimate receiver. In the context of the considered CWRN, $\mathcal {R}$ transmits jamming signals while $\mathcal {S}$ transmits the data to $\mathcal {D}$. Due to the autonomous property of the jamming signals, they may confuse $\mathcal {E}$ from eavesdropping the data; however, it can be noticed that such jamming signals could also harm $\mathcal {D}$. The GSOP of the CJ scheme can be computed by

$$ P^{(CJ)}_{out} = \Pr\left\{\left[\log_{2}\left( \frac{1+\frac{\gamma_{\mathcal{SD}}}{\gamma_{\mathcal{RD}}+ 1}}{1+\frac{\gamma_{\mathcal{SE}}}{\gamma_{\mathcal{RE}}+ 1}}\right) \right]^{+}<2 \theta R_{s}\right\}, $$

(27)

where

$$ \gamma_{\mathcal{RD}}=\frac{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RD}}|^{2}}{{\sigma^{2}_{0}}}. $$

(28)

$$ \gamma_{\mathcal{RE}}=\frac{{\Lambda}_{\mathcal{R}} |h_{\mathcal{RE}}|^{2}}{{\sigma^{2}_{0}}}. $$

(29)

Following [11], $P^{(CJ)}_{out}$ can be derived in closed form as

$$\begin{array}{@{}rcl@{}} P^{(CJ)}_{out} &=& 1 - \frac{2^{-\delta}}{\bar{\gamma}_{\mathcal{RD}}\zeta}\\ &&+ \frac{2^{-\delta}}{\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{RE}}\zeta^{2}}\left[\frac{2^{2 \theta R_{s}} \bar{\gamma}_{\mathcal{SE}}(\zeta+ 1)}{\bar{\gamma}_{\mathcal{SD}}} {\Xi}\left( \frac{1+\vartheta}{\bar{\gamma}_{\mathcal{RE}}}\right)\right.\\ && \left. + (\zeta-\vartheta){\Xi}\left( \frac{1+\vartheta}{\vartheta}(\delta+\bar{\gamma}^{-1}_{\mathcal{RD}})\right)\right], \end{array} $$

(30)

where $\delta \triangleq (2^{2 \theta R_{s}}-1)\bar {\gamma }^{-1}_{\mathcal {SD}}$, $\vartheta \triangleq 2^{2 \theta R_{s}}\bar {\gamma }_{\mathcal {SE}}\bar {\gamma }^{-1}_{\mathcal {SD}}$, $\zeta \triangleq \delta +\bar {\gamma }^{-1}_{\mathcal {RD}}-\vartheta \bar {\gamma }^{-1}_{\mathcal {RE}}$ and ${\Xi }(x)\triangleq e^{x} E_{1}(x)$. Here, $E_{1}(x)\triangleq \displaystyle {\int }_{x}^{\infty } e^{-t}t^{-1} dt$ is the exponential integral [40].

4.4 DF scheme

In this scheme, $\mathcal {R}$ follows the conventional DF relaying scheme [8]. That is, $\mathcal {R}$ decodes the data from $\mathcal {S}$, re-encodes the decoded data and then forwards the encoded data to $\mathcal {D}$. The GSOP of the DF scheme is given by

$$ P^{(DF)}_{out} = \Pr\!\left\{\!\left[\log_{2}\!\left( \frac{1 + \min\{\gamma_{\mathcal{SR}},\gamma_{\mathcal{SD}} + \gamma_{\mathcal{RD}}\}}{1+\gamma_{\mathcal{SE}}+\gamma_{\mathcal{RE}}}\!\right) \!\right]^{+}\!\!\!\!<\! 2 \theta R_{s}\!\right\}\!, $$

(31)

where $\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {RE}}$ are given by Eqs. 28 and 29, respectively.⁴ According to [28], $P^{(DF)}_{out}$ can be derived as

$$\begin{array}{@{}rcl@{}} P^{(DF)}_{out}& = &\frac{2^{-2 \theta R_{s}}\bar{\gamma}_{\mathcal{SR}}\left[ {\Theta}(\bar{\gamma}_{\mathcal{SE}}) {\Psi}(\bar{\gamma}_{\mathcal{SE}}) - {\Theta}(\bar{\gamma}_{\mathcal{RE}}) {\Psi}(\bar{\gamma}_{\mathcal{RE}})\right]} {(\bar{\gamma}_{\mathcal{RE}}-\bar{\gamma}_{\mathcal{SE}})(\bar{\gamma}_{\mathcal{RD}}-\bar{\gamma}_{\mathcal{SD}})}\\ &&+\frac{{\Theta}(\bar{\gamma}_{\mathcal{RE}})-{\Theta}(\bar{\gamma}_{\mathcal{SE}})}{\bar{\gamma}_{\mathcal{RE}}-\bar{\gamma}_{\mathcal{SE}}}, \end{array} $$

(32)

where

$$ {\Theta}(x)\triangleq\frac{x^{2}}{2^{-2 \theta R_{s}}\bar{\gamma}_{\mathcal{SR}}+x}\exp\left( \frac{1-2^{-2 \theta R_{s}}}{x}\right), $$

(33)

$$\begin{array}{@{}rcl@{}} &&{\Psi}(x)\triangleq \frac{\bar{\gamma}_{\mathcal{SR}}}{x(1+\bar{\gamma}_{\mathcal{SR}}/\bar{\gamma}_{\mathcal{SD}}) + 2^{-2 \theta R_{s}}\bar{\gamma}_{\mathcal{SR}}}\\ &&- \frac{\bar{\gamma}_{\mathcal{SR}}}{x(1 + \bar{\gamma}_{\mathcal{SR}}/\bar{\gamma}_{\mathcal{RD}}) + 2^{-2 \theta R_{s}}\bar{\gamma}_{\mathcal{SR}}}. \end{array} $$

(34)

Remark 5 (GSOP of DF Scheme)

As noticed in Remark 4, the DF scheme is a special case of the PMF scheme when the SINRs of the links $\mathcal {R}\to \mathcal {D}$ and $\mathcal {R}\to \mathcal {E}$ are replaced by the SNRs of those links with no encryption and PNC operation. Indeed, the GSOP of the DF scheme in Eq. 32 can be derived from that of the PMF scheme in Theorem 1 by setting α = 1 and β = 0 for the pdf of both $\gamma _{\mathcal {RD}}$ and $\gamma _{\mathcal {RE}}$ in Eq. 18.

Remark 6 (Lower GSOP With PMF-Perfect Over DF Scheme)

In the PMF-perfect scheme, given the fact that the message modification at $\mathcal {R}$ is perfectly shared between legitimate users, the SINR of the link $\mathcal {R}\to \mathcal {D}$ can be simplified to be the SNR of that link (see Remark 4), while the SINR of the link $\mathcal {R}\to \mathcal {E}$ is unchanged since $\mathcal {E}$ does not know the modification process at $\mathcal {R}$. Furthermore, it can be easily shown that ${\Lambda }_{R}|h_{\mathcal {RE}}|^{2}/\sigma ^{2}>{\Lambda } _{R}|h_{\mathcal {RE}}|^{2}\alpha ^{2}/({\Lambda }_{R}|h_{\mathcal {RE}}|^{2}\beta ^{2}+\sigma ^{2})$, ∀0 ≤ α, β ≤ 1. Therefore, from Eqs. 14 and 31, it can be concluded that the PMF-perfect scheme achieves a lower GSOP for an enhanced security compared to the DF scheme, which verifies the statement in Remark 1.⁵

4.5 MF scheme

In MF scheme [30], $\mathcal {R}$ decodes the source message, modifies the message and then forwards the modified message to $\mathcal {D}$ with the assumption that the knowledge of the message modification process at $\mathcal {R}$ is perfectly shared between $\mathcal {R}$ and $\mathcal {D}$, and $\mathcal {E}$ is not able to utilise the modified message from $\mathcal {R}$. The GSOP of the MF scheme is thus given by

$$\begin{array}{@{}rcl@{}} P^{(MF)}_{out} = \Pr\left\{\!\left[\log_{2}\left( \frac{1 + \min\{\gamma_{\mathcal{SR}},\gamma_{\mathcal{SD}} + \gamma_{\mathcal{RD}}\}}{1+\gamma_{\mathcal{SE}}}\right) \right]^{+}\!\!\!\!<\! 2 \theta R_{s}\!\right\}. \end{array} $$

(35)

Following [30], $P^{(MF)}_{out}$ can be derived as

$$ P^{(MF)}_{out}= 1-\frac{{\Phi}(\bar{\gamma}_{\mathcal{RD}})-{\Phi}(\bar{\gamma}_{\mathcal{SD}})} {\bar{\gamma}_{\mathcal{RD}}-\bar{\gamma}_{\mathcal{SD}}}, $$

(36)

where

$$\begin{array}{@{}rcl@{}} {\Phi}(x) & \triangleq& \left( 1+\frac{x}{\bar{\gamma}_{\mathcal{SR}}}\right)e^{(1-2^{2 \theta R_{s}})(\bar{\gamma}^{-1}_{\mathcal{SR}}+x^{-1})}\\ & &\times \!\left( \!\frac{1}{\bar{\gamma}^{-1}_{\mathcal{SR}} + x^{-1}} - \frac{1}{2^{-2 \theta R_{s}}\bar{\gamma}^{-1}_{\mathcal{SE}} + \bar{\gamma}^{-1}_{\mathcal{SR}} + x^{-1}}\!\right). \end{array} $$

(37)

Remark 7 (GSOP of MF Scheme)

From Eqs. 31 and 35, it can be observed that the GSOP of the MF scheme can be deduced from that of the DF scheme given $\gamma _{\mathcal {RE}}= 0$. In fact, in the MF scheme, it is assumed that $\mathcal {E}$ can only decode the message from $\mathcal {S}$ in the first time slot, which implies that $\gamma _{\mathcal {RE}}= 0$. The MF scheme can be referred to as an ‘ideal’ DF scheme with $\gamma _{\mathcal {RE}}= 0$, and consequently a special case of our proposed PMF scheme (see Remark 2). The GSOP of the MF scheme in Eq. 36 can be therefore derived from that of the PMF scheme in Eq. 18 in Theorem 1 when α = 1, β = 0 and $\gamma _{\mathcal {RE}}= 0$.

Remark 8 (Much Lower GSOP With MF Scheme for an Ideal Case)

From Eqs. 14, 31 and 35, it can be easily seen that the MF scheme with the absence of the link $\mathcal {R}\to \mathcal {E}$ achieves the lowest GSOP compared to the PMF and DF schemes. Although such assumption in the MF scheme does not sound naturally in practice when the eavesdropper can overhear the message from all nodes, the GSOP of the MF scheme can be regarded as a performance benchmark providing the lower bound of the proposed PMF scheme.

Remark 9 (Lower and Upper Bounds of the PMF Scheme)

It can be seen that $\gamma _{\mathcal {RE}}^{(PMF)}\geq \gamma _{\mathcal {RE}}^{(MF)}= 0$ and $\gamma _{\mathcal {RE}}^{(PMF)}=\frac {\lambda _{\mathcal {R}}|h_{\mathcal {RE}}|^{2}\alpha ^{2}}{\lambda _{\mathcal {R}}|h_{\mathcal {RE}}|^{2}\beta ^{2}+{\sigma ^{2}_{0}}} \leq \gamma _{\mathcal {RE}}^{(DF)}=\frac {\lambda _{\mathcal {R}}|h_{\mathcal {RE}}|^{2}}{{\sigma ^{2}_{0}}}$ when α² ≤ 1, and thus $C_{e}^{(MF)}\leq C_{e}^{(PMF)}\leq C_{e}^{(DF)}$. From Eqs. 5 and 6, we have $P_{out}^{(MF)}\leq P_{out}^{(PMF)}\leq P_{out}^{(DF)}$. This means that the GSOP of the PMF scheme is lower and upper bounded by that of the MF and DF schemes, respectively.

5 Opportunistic secure transmission protocol for CWRNs

In a practical CWRN, it can be intuitively seen that the usage of relay node may be unnecessary if the link between source and relay and/or the link between relay and destination suffer(s) from severe fading and noise. In other words, DT scheme could be favourable over RT schemes given a dominant direct link of very high quality compared to relaying links. This accordingly raises a research problem in our considered system model to find out when the relay should be used to provide a higher secure communication over the DT scheme.

For clarity, let us consider the following example:

Example 1

The SNRs of the links in a CWRN (see Fig. 1) are set as $\bar {\gamma }_{\mathcal {SR}}= 12$ dB, $\bar {\gamma }_{\mathcal {RD}}= 10$ dB, $\bar {\gamma }_{\mathcal {SE}}= 5$ dB and $\bar {\gamma }_{\mathcal {RE}}= 7$ dB. Figure 2 plots the GSOP of DT, DF, CJ, MF, PMF-perfect and PMF-imperfect schemes versus the target secrecy rate, i.e. R_s [b/s/Hz], with PNC coefficients {α² = 0.7,β² = 0.3}, level of secrecy requirement 𝜃 = 1 and with respect to two values of $\bar {\gamma }_{\mathcal {SD}}=\{0,12\}$ dB. It can be seen that the GSOP of the DT scheme achieves the best performance when $\bar {\gamma }_{\mathcal {SD}}= 12$ dB, while there exists a crossing point between the GSOPs of the DT, DF, MF, PMF-perfect and PMF-imperfect schemes when $\bar {\gamma }_{\mathcal {SD}}= 0$ dB. For instance, the GSOP of the DT scheme intersects with that of the PMF-imperfect, DF, PMF-perfect, and MF schemes when R_s = R_s,1 = 0.07 b/s/Hz, R_s = R_s,2 = 0.66 b/s/Hz, R_s = R_s,3 = 1.2 b/s/Hz and R_s = R_s,4 = 1.8 b/s/Hz, respectively. We have the following observations when $\bar {\gamma }_{\mathcal {SD}}= 0$ dB:

• i) If R_s < R_s,1, then $P_{out}^{(DT)}>P_{out}^{(PMF-imperfect)}>P_{out}^{(DF)}>P_{out}^{(PMF-perfect)}>P_{out}^{(MF)}$;

• ii) If R_s,1 ≤ R_s < R_s,2, then $P_{out}^{(PMF-imperfect)}>P_{out}^{(DT)}>P_{out}^{(DF)}>P_{out}^{(PMF-perfect)}>P_{out}^{(MF)}$;

• iii) If R_s,2 ≤ R_s < R_s,3, then $P_{out}^{(PMF-imperfect)}>P_{out}^{(DF)}>P_{out}^{(DT)}>P_{out}^{(PMF-perfect)}>P_{out}^{(MF)}$;

• iv) If R_s,3 ≤ R_s < R_s,4, then $P_{out}^{(PMF-imperfect)}>P_{out}^{(DF)}>P_{out}^{(PMF-perfect)}>P_{out}^{(DT)}>P_{out}^{(MF)}$;

• iv) If $R_{s}\geqslant R_{s,4}$, then $P_{out}^{(PMF-imperfect)}>P_{out}^{(DF)}>P_{out}^{(PMF-perfect)}>P_{out}^{(MF)}>P_{out}^{(DT)}$.

This accordingly reflects that the relay may be helpful in providing a lower GSOP at a specific range of the target secrecy rate, while the DT scheme could provide a better secrecy performance without any support of the relay.

Fig. 2

Illustration of threshold of R_s for selecting appropriate schemes for secure communications

Inspired from the above observations in Example 1, we introduce an optimisation problem as follows

$$ \min_{X\in\{DT,RT\}} P^{(X)}_{out}, $$

(38)

where $P^{(X)}_{out}$ of various schemes is derived in Section 3.

The optimisation problem in Eq. 38 aims to find the best transmission strategies, in terms of lowest GSOP, amongst the DT scheme and various RT schemes, i.e. DF, MF and PMF. Considering the GSOP as a function of the target secrecy rate, i.e. R_s, Example 1 suggests that there may exist crossing points or intersections between the GSOP curves. Having in mind that an intersection between two GSOP curves identifies their different trends, one can easily find the lower GSOP curve at a given R_s. Therefore, in order to avoid an exhaustive search when solving Eq. 38, it is crucial to find the existence conditions of these crossing points. Let us first introduce the following propositions:

Proposition 1

Given two non-negative increasing functionsf(x) andg(x) with$\frac {d f(x)}{d x}>\frac {d g(x)}{d x}>0$,then ∃!x^′ > 0 : f(x^′) = g(x^′) if and only iff(0) < g(0).

Proof

See Appendix C. □

Proposition 2

Given three non-negative increasing functionsf(x),g(x) andh(x) having$\frac {d f(x)}{d x}>\frac {d g(x)}{d x}>\frac {d h(x)}{d x}>0$,iff(0) > g(0) and ∃!x₁ > 0 : f(x₁) = h(x₁),then ∃!x₂ > 0 : g(x₂) = h(x₂).

Proof

From Proposition 1, given $\frac {d f(x)}{d x}>\frac {d h(x)}{d x}>0$, if ∃!x₁ > 0 : f(x₁) = h(x₁), then we have f(0) < h(0), and thus h(0) > g(0). Accordingly, it can be deduced that ∃!x₂ > 0 : g(x₂) = h(x₂) since $\frac {d g(x)}{d x}>\frac {d h(x)}{d x}>0$ and g(0) < h(0). □

The findings in Propositions 1 and 2 verify the crossing points of the GSOP curves of the DT, DF, MF and the proposed PMF in Fig. 2 at different values of R_s. For simplicity, let us consider DT and MF scheme as an exemplary RT scheme due to its tractability with the GSOP derived in the previous section, while the other RT schemes will be validated through numerical results in Section V. The conditions of the intersection between two GSOP curves of the DT and RT schemes are determined as in the following Theorem 2.

Theorem 2

On the subject of target secrecy rate, i.e. R _s , there exists a single crossing point of two GSOP curves for the DT and RT schemes if $\bar {\gamma }_{\mathcal {SD}}\bar {\gamma }_{\mathcal {SE}}<\bar {\gamma }^{2}_{\mathcal {SR}}$ , $\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {SE}}/2}$ and $\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {RD}}/2}$ . That is $\exists ! R^{\prime }_{s}>0: P^{(DT)}_{out}(R^{\prime }_{s})=P^{(RT)}_{out}(R^{\prime }_{s})$

Proof

See Appendix D. □

For convenience, let Ω_cross denote the set of conditions for the crossover of DT and RT schemes in Theorem 2, i.e.

$$\begin{array}{@{}rcl@{}} {\Omega}_{cross}&= & \{(\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}<\bar{\gamma}^{2}_{\mathcal{SR}}) \wedge (\bar{\gamma}_{\mathcal{SD}}<\sqrt{\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}/2})\\ &&\wedge (\bar{\gamma}_{\mathcal{SD}}<\sqrt{\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{RD}}/2})\}. \end{array} $$

(39)

We have the following observation:

Remark 10 (Existence of a Secrecy Rate Threshold (SRT) for Opportunistic Secure RT Protocol)

From Theorem 2, if the channel quality satisfies the condition set Ω_cross in Eq. 39, then there exists a SRT, i.e. R_th, which is the crossing point between the GSOPs of DT and RT schemes. Specifically, it can be deduced that

$$ \left\{\begin{array}{lllll} P^{(DT)}_{out}(R_{s})>P^{(RT)}_{out}(R_{s}) & \text{ if } R_{s}<R_{th}\\ P^{(DT)}_{out}(R_{s})\leq P^{(RT)}_{out}(R_{s}) & \text{ if } R_{s}\geq R_{th} \end{array}\right. $$

(40)

This accordingly means that we should select the RT scheme for a lower GSOP if the target secrecy rate is smaller than the SRT, while the DT scheme is preferable to achieve a higher target secrecy rate. Also, notice that if the SRT does not exist, i.e. the condition set Ω_cross is not satisfied, then the DT scheme should be selected as $P^{(DT)}_{out}(R_{s})<P^{(RT)}_{out}(R_{s})$, e.g. see Fig. 2 in Example 1 when $\gamma _{\mathcal {SD}}= 12$ dB.

Therefore, given Ω_cross, solving the optimisation problem (38) is turned into finding SRT between DT and each of RT schemes, i.e. DF, MF and PMF, as follows:

$$ R_{th}=\left\{R_{s} \left\vert P^{(DT)}_{out}(R_{s})=P^{(RT)}_{out}(R_{s}) \cap {\Omega}_{cross}\right\}\right. . $$

(41)

Using the derived GSOPs of various schemes in Section IV, R_th can be found via a simple numerical method and the optimal scheme can be opportunistically determined as in Remark 10.

6 Numerical results

In this section, we first illustrate the GSOP achieved with the proposed PMF scheme in CWRNs. In order to verify the effectiveness of the proposed PMF, the performance of DT [36], DF [28], CJ [11] and MF [30] are provided for comparison. The results are obtained with MATLAB under different scenarios of the wireless channel quality and the target secrecy rate. We then present the findings of SRTs for opportunistic secure RT protocol with respect to the quality of various links.

6.1 GSOP of DT & various RT schemes

6.1.1 GSOP versus Target Secrecy Rate

Figure 3 plots the GSOP of various schemes as a function of the target secrecy rate, i.e. R_s. The SNRs of all links are set as $\bar {\gamma }_{\mathcal {SR}}= 12$ dB, $\bar {\gamma }_{\mathcal {RD}}= 10$ dB, $\bar {\gamma }_{\mathcal {SD}}= 5$ dB, $\bar {\gamma }_{\mathcal {RE}}= 7$ dB and $\bar {\gamma }_{\mathcal {SE}}= 5$ dB. Note that the eavesdropper can be a neighbouring node of the relay and destination nodes, and thus the eavesdropping links can have approximately the same SNR values as those of the direct and relaying links. The PNC coefficients and the level of secrecy requirement are set as {α² = 0.7,β² = 0.3} and 𝜃 = 1, respectively. In Fig. 3, as noticed in the proof of Theorem 2, it can be seen that the GSOP increases over R_s and the gradient of the GSOP of the RT schemes is higher than that of the DT scheme. The PMF-perfect scheme is shown to achieve an improved GSOP performance over the DF, CJ and PMF-imperfect scheme, while the DT scheme achieves a better performance at high R_s. This accordingly verifies the statement in Remark 6 regarding the lower GSOP achieved with the PMF-perfect over the DF scheme, and also confirms the existence of the SRTs as stated in Remark 10. Additionally, it can be observed that the MF scheme achieves a lower GSOP compared to the proposed PMF-perfect scheme due to the neglect of the link $\mathcal {R}\to \mathcal {E}$. This is indeed regarded as the lower bound of the proposed PMF scheme, which according to Remark 8 the MF scheme is an ideal case though unnatural.⁶ Moreover, the numerical and analytical results in Section 3 are shown to be consistent with the simulation results.

Fig. 3

GSOP versus target secrecy rate

Considering different secrecy requirements, Fig. 4 illustrates the GSOP versus target secrecy rate, i.e. R_s, with respect to different levels of secrecy requirement, i.e. 𝜃. Specifically, two scenarios of 𝜃 = 1 and 𝜃 = 0.4 are considered, while the other parameters are similarly set as in Fig. 3. It can be observed in Fig. 4 that a relaxed secrecy requirement with a lower 𝜃 results in a lower secrecy outage and the GSOP is also shown to increase for all cases as the target secrecy rate increases. For simplicity, in the rest of this section, let us consider the scenario when 𝜃 = 1.

Fig. 4

GSOP versus target secrecy rate with respect to different secrecy requirements

6.1.2 Impacts of eavesdropper links

Figures 5 and 6 sequentially plot the GSOP of various schemes for secure CWRN as a function of the average SNRs of the links $\mathcal {S}\to \mathcal {E}$, i.e. $\bar {\gamma }_{\mathcal {SE}}$, and $\mathcal {R}\to \mathcal {E}$, i.e. $\bar {\gamma }_{\mathcal {RE}}$, respectively. In Fig. 5, the range of $\bar {\gamma }_{\mathcal {SE}}$ is selected to cover − 10 dB to 12 dB and $\bar {\gamma }_{\mathcal {RE}}= 7$ dB, while $\bar {\gamma }_{\mathcal {RE}}$ is in the range from − 10 to 10 dB in Fig. 6 and $\bar {\gamma }_{\mathcal {SE}}= 5$ dB. In both figures, the SNRs of other channels are set as $\bar {\gamma }_{\mathcal {SR}}= 12$ dB, $\bar {\gamma }_{\mathcal {SD}}= 5$ dB, $\bar {\gamma }_{\mathcal {RD}}= 10$ dB, the target secrecy rate is R_s = 0.1 b/s/Hz and the PNC coefficients are {α² = 0.7,β² = 0.3}.

Fig. 5

GSOP versus SNR of the link $\mathcal {S}\to \mathcal {E}$

Fig. 6

GSOP versus SNR of the link $\mathcal {R}\to \mathcal {E}$

As shown in Fig. 5, a higher $\bar {\gamma }_{\mathcal {SE}}$ causes a higher GSOP as the eavesdropper can more reliably decode the source message. It can be observed that the proposed PMF scheme achieves a lower GSOP compared to the DF and CJ schemes over the whole range of $\bar {\gamma }_{\mathcal {SE}}$ and performs better than the DT scheme at high $\bar {\gamma }_{\mathcal {SE}}$, while the DT scheme achieves a better performance at low $\bar {\gamma }_{\mathcal {SE}}$ which is corresponding to the scenario when $\mathcal {E}$ can not reliably decode the message from $\mathcal {S}$. This again verifies our statements in Remarks 1 and 6 regarding the improved security with the proposed PMF scheme as well as confirming Remark 10 in respect of the SRTs between the DT and RT schemes. A similar observation can be made in Fig. 6 where the proposed PMF is shown to achieve a better performance compared to the DT, DF and CJ schemes.

6.1.3 Impacts of relaying links

In CWRN, both links $\mathcal {S}\to \mathcal {R}$ and $\mathcal {R}\to \mathcal {D}$ need to be considered for reliable relaying. Figures. 7 and 8 plot GSOP of DT and various RT schemes including DF, CJ, MF, PMF-imperfect and PMF-perfect schemes versus $\bar {\gamma }_{\mathcal {SR}}$ and $\bar {\gamma }_{\mathcal {RD}}$, respectively. It is assumed that $\bar {\gamma }_{\mathcal {RD}}= 10$ dB in Fig. 7 and $\bar {\gamma }_{\mathcal {SR}}= 12$ dB in Fig. 8. In both figures, the SNRs of other channels are set as $\bar {\gamma }_{\mathcal {SD}}= 5$ dB, $\bar {\gamma }_{\mathcal {RE}}= 7$ dB and $\bar {\gamma }_{\mathcal {SE}}= 5$ dB. Similarly, the target secrecy rate is R_s = 0.1 b/s/Hz and the PNC coefficients are {α² = 0.7,β² = 0.3}. It can be observed in both Figs. 7 and 8 that a lower GSOP is achieved with the proposed PMF scheme compared to the DF scheme and also shown to be better than the DT scheme at high $\bar {\gamma }_{\mathcal {SR}}$. In fact, the high-quality link $\mathcal {S}\to \mathcal {R}$ provides a reliable relaying, and thus $\mathcal {R}$ can help to enhance the security in CWRN. At low $\bar {\gamma }_{\mathcal {SR}}$, e.g. $\bar {\gamma }_{\mathcal {SR}}<6$ dB, $\mathcal {R}$ may not be able to reliably decode the data message from $\mathcal {S}$ and thus the DT scheme is beneficial in this case. Additionally, in Fig. 7, the performance of the DT and CJ schemes is shown to be independent of $\bar {\gamma }_{\mathcal {SR}}$ as there is no relay involved in the DT scheme and the jamming process at $\mathcal {R}$ in the CJ scheme does not rely on the reliability of the link $\mathcal {S}\to \mathcal {R}$. It can also be noticed in Fig. 8 that the CJ scheme even has a poorer GSOP performance when $\bar {\gamma }_{\mathcal {RD}}$ increases since the jamming signals at $\mathcal {R}$ also causes a considerable harm on the message decoding at $\mathcal {D}$, especially in a very good channel condition.

Fig. 7

GSOP versus SNR of the link $\mathcal {S}\to \mathcal {R}$

Fig. 8

GSOP versus SNR of the link $\mathcal {R}\to \mathcal {D}$

6.1.4 Impacts of direct link

Taking into account the direct link $\mathcal {S}\to \mathcal {D}$ in CWRN, Fig. 9 plots the GSOP of various schemes as a function of $\bar {\gamma }_{\mathcal {SD}}$. The SNRs of other links are $\bar {\gamma }_{\mathcal {SR}}= 12$ dB, $\bar {\gamma }_{\mathcal {RD}}= 10$ dB, $\bar {\gamma }_{\mathcal {RE}}= 7$ dB and $\bar {\gamma }_{\mathcal {SE}}= 5$ dB. Similarly, the target secrecy rate and the PNC coefficients are R_s = 0.1 b/s/Hz and {α² = 0.7,β² = 0.3}. It can be observed in Fig. 9 that the proposed PMF scheme achieves a lower GSOP than the DF scheme. The PMF is also shown to be better than the DT and CJ schemes at low $\bar {\gamma }_{\mathcal {SD}}$. However, at high $\bar {\gamma }_{\mathcal {SD}}$, the DT scheme is shown to be the best scheme as the usage of $\mathcal {R}$ is not necessary in this case, even degrading the performance. This again verifies the statement in Remark 10 regarding the necessity of determining the SRT for opportunistic secure transmission scheme in the CWRN.

Fig. 9

GSOP versus SNR of the link $\mathcal {S}\to \mathcal {D}$

6.2 SRTs for opportunistic secure RT protocol

6.2.1 SRTs w.r.t. quality of relaying links

Considering the impacts of the links $\mathcal {S}\to \mathcal {R}$ and $\mathcal {R}\to \mathcal {D}$ on determining SRT for opportunistic secure communication protocol, Figs. 10 and 11 plot the SRT, i.e. R_th, of DF, MF and the proposed PMF schemes as a function of $\bar {\gamma }_{\mathcal {SR}}$ and $\bar {\gamma }_{\mathcal {RD}}$, respectively. The SNRs of other channel links are similarly set as in Figs. 7 and 8. It can be observed in both figures that R_th = 0 at low $\bar {\gamma }_{\mathcal {SR}}$. In fact, when $\bar {\gamma }_{\mathcal {SR}}$ is low, the condition set in Theorem 2, i.e. Ω_cross in Eq. 39, is not satisfied, and thus there do not exist any crossing points between the GSOP curves of the DT scheme and other schemes. This means that the DT scheme is optimal in the low-SNR regime of the link $\mathcal {S}\to \mathcal {R}$ (see Remark 10). It can also be observed that R_th increases as either $\bar {\gamma }_{\mathcal {SR}}$ or $\bar {\gamma }_{\mathcal {RD}}$ increases. This is due to the fact that a higher SNR of the relaying links results in a better GSOP performance of the RT schemes, and thus, as shown in Proposition 2, a higher R_th is obtained.

Fig. 10

SRT of various RT schemes versus $\bar {\gamma }_{\mathcal {SR}}$

Fig. 11

SRT of various RT schemes versus $\bar {\gamma }_{\mathcal {RD}}$

6.2.2 SRTs w.r.t. quality of direct link

Taking into account the direct link $\mathcal {S}\to \mathcal {D}$, Fig. 12 plots R_th of various RT schemes as a function of $\bar {\gamma }_{\mathcal {SD}}$. The range of $\bar {\gamma }_{\mathcal {SD}}$ is assumed to vary from 0 to 10 dB and the SNRs of other channel links are set as in Fig. 9. Different from Figs. 10 and 11, it can be observed in Fig. 12 that the increase of $\bar {\gamma }_{\mathcal {SD}}$ results in a lower R_th and such decrease approaches 0 as $\bar {\gamma }_{\mathcal {SD}}\geq 10$ dB. This accordingly means that if the direct link is of high quality, then the DT scheme is more beneficial than the RT schemes with a lower GSOP and also a lower R_th. In fact, at high $\bar {\gamma }_{\mathcal {SD}}$ dB, the condition set Ω_cross is not satisfied (see Eq. 39), and hence, as noticed in Remark 10 with an illustration in Example 1, the DT scheme is optimal in the high-SNR regime of the direct link.

Fig. 12

SRT of various RT schemes versus $\bar {\gamma }_{\mathcal {SD}}$

7 Conclusions

In this paper, an efficient PMF scheme has been proposed for secure CWRNs to cope with the scenario when the eavesdropper can overhear the message from both the source and the relay, and also the imperfectly shared knowledge between the relay and destination as in the conventional MF scheme. By employing PNC at the relay with encrypted key, the proposed scheme has been shown to provide a higher security compared to the conventional DF and CJ schemes with respect to various channel conditions and target secrecy rates. Additionally, the GSOP of the PMF scheme has been derived, which is a general form of the DF and MF schemes. The PMF scheme is shown to provide higher security compared to the DF scheme while approaching the MF scheme of which the GSOP is a lower bound in an ideal case of no communication link between the relay and the eavesdropper. Furthermore, we have proposed an opportunistic secure transmission protocol by finding the SRTs for determining the optimal scheme with or without the assistance of the relay. Depending on the quality of channel links, the conditions for the existence of the SRTs have been derived. It is shown that the SRTs increase as the SNR of either source-relay or relay-destination link increases, while the increase of the SNR of source-destination link results in lower SRTs. For future work, we will investigate the design of the PNC coefficients at the relay with respect to the channel gains of different links. Untrusted relay channels will be also taken into account for the scenario when the relay as a third party is not allowed to decode the confidential message.

Appendices

Appendix A: Proof of Lemma 1

Given $Y=\frac {a^{2}X}{b^{2}X + 1}$ and X = c|Z|² where c is a positive constant, it can be deduced that a² ≥ b²Y. The cdf of Y can be computed by [41]

$$ F_{Y}(y)=\Pr\{Y\leqslant y\}=\Pr\left\{X\leqslant\frac{y}{a^{2}-b^{2}y}\right\}. $$

(42)

Note that the pdf and cdf of X are given by

$$ f_{X}(x)=\frac{1}{c}\exp\left( -\frac{x}{c}\right), $$

(43)

$$ F_{X}(x) = Pr\{X\leqslant x\}={{\int}_{0}^{x}}f_{X}(t)dt= 1-\exp\left( -\frac{x}{c}\right), $$

(44)

respectively. Substituting Eq. 44 into Eq. 42, we have

$$ F_{Y}(y)=F_{X}\left( \frac{y}{a^{2}-b^{2}y}\right)= 1-\exp\left( -\frac{y}{c(a^{2}-b^{2}y)}\right) $$

(45)

The pdf of Y can be therefore obtained by

$$ f_{Y}(y)=\frac{dF_{Y}(y)}{dy}=\frac{a^{2}}{c(a^{2}-b^{2}y)^{2}}\exp\left[-{\frac{y}{c(a^{2}-b^{2}y)}}\right]. $$

(46)

Appendix B: Proof of Theorem 1

For brevity, let $X=\gamma _{\mathcal {SR}}$, $Y=\gamma _{\mathcal {SD}}$, $Z=\gamma _{\mathcal {RD}}$, $U=\gamma _{\mathcal {SE}}$ and $V=\gamma _{\mathcal {RE}}$. We can rewrite Eq. 14 as

$$ P^{(PMF)}_{out} = \Pr\left\{\left[\log_{2}\left( \frac{1+\min\{X,Y + Z\}}{1+U+V}\right)\right]^{+}\!<2 \theta R_{s}\right\}. $$

(47)

Note that the secure communication is possible with a positive secrecy capacity if the legitimate links, including the direct and/or relaying links, have higher channel gains over the eavesdropper links. In order to prevent the secrecy outage from always happening, it is assumed that min{X, Y + Z} > U + V. From Eq. 47, we have

$$\begin{array}{@{}rcl@{}} P_{out}^{(PMF)}&=&\Pr\!\left\{\log_{2}\left( \frac{1+\min\{X,Y + Z\}}{1+U+V}\right)<2 \theta R_{s}\right\}\\ & =&\Pr\!\left\{2^{-2R_{s}}(1 + \min\{X,Y + Z\}) - 1\!<\!U+V \right\},\\ \end{array} $$

(48)

Considering two scenarios of X ≤ Y + Z and X > Y + Z, Eq. 48 can be rewritten by Eq. 49 (see the top of next page).

$$\begin{array}{@{}rcl@{}} P_{out}^{(PMF)}\!\!&=&\!\underbrace{\Pr\{2^{-2 \theta R_{s}}(1 + X) - 1\!<\!U + V\!<\!X\}\Pr\{X\!\leqslant\! Y + Z\}}_{\displaystyle \triangleq P_{1}} \\ &&\!+\underbrace{\Pr\{2^{-2 \theta R_{s}}(1 + Y + Z) - 1\!<\!U + V\!<\!Y + Z\}\Pr\{X\!>\! Y + Z\}}_{\displaystyle \triangleq P_{2}}.\\ \end{array} $$

(49)

Deriving P₁ and P₂ in Eq. 49, it can be observed that, if $X\leqslant \min \{Y,2^{2 \theta R_{s}}-1\}$, then $\Pr \{2^{-2 \theta R_{s}}(1+X)-1<U+V<X\}= 1$ and Pr{X ≤ Y + Z} = 1 since $U+V\geqslant 0$ and $Z\geqslant 0$. This means P₁ = 1 and P₂ = 0, i. e. $P_{out}^{(PMF)}= 1$ (outage occurs). Similarly, if $Y+Z\leqslant \min \{X,2^{2 \theta R_{s}}-1\}$, then $\Pr \{2^{-2 \theta R_{s}}(1+Y+Z)-1<U+V<Y+Z\}= 1$ and Pr{X > Y + Z} = 1 since $U+V\geqslant 0$, and thus outage happens. Therefore, in order to avoid the outage, by considering all these above conditions, we can arrive at Eqs. 50 and 51 (see the top of next page).

$$\begin{array}{@{}rcl@{}} P_{1} &=& {\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{Y}(y){\int}_{y}^{\infty}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z){{\int}_{0}^{x}}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+x)-1-u}^{x-u}f_{V}(v) dv du dz dx dy \\ &&+ {\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{X}(x){\int}_{x}^{\infty}f_{Y}(y){{\int}_{0}^{x}}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+x)-1-u}^{x-u}f_{V}(v) dv du dy dx \\ &&+ {\int}_{0}^{2^{2 \theta R_{s}}-1}f_{Y}(y){\int}_{y}^{2^{2 \theta R_{s}}-1}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z){{\int}_{0}^{x}}f_{U}(u){\int}_{0}^{x-u}f_{V}(v) dv du dz dx dy \\ &&+ {\int}_{0}^{2^{2 \theta R_{s}}-1}f_{Y}(y){\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{X}(x){\int}_{x-y}^{\infty}f_{Z}(z){{\int}_{0}^{x}}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+x)-1-u}^{x-u}f_{V}(v) dv du dz dx dy, \end{array} $$

(50)

$$ P_{2}={\int}_{2^{2 \theta R_{s}}-1}^{\infty}f_{X}(x) {\int}_{2^{2 \theta R_{s}}-1}^{x}f_{Y}(y) {\int}_{2^{2 \theta R_{s}}-1-y}^{x-y}f_{Z}(z) {\int}_{0}^{y+z}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+y+z)-1-u}^{y+z-u}f_{V}(v) dv du dz dy dx. $$

(51)

For simplicity, let us define

$$ I_{1}(x)\triangleq {{\int}_{0}^{x}}f_{U}(u){\int}_{2^{-2 \theta R_{s}}(1+x)-1-u}^{x-u}f_{V}(v) dv du, $$

(52)

$$ I_{2}(x)\triangleq {{\int}_{0}^{x}}f_{U}(u){\int}_{0}^{x-u}f_{V}(v) dv du. $$

(53)

Substituting Eqs. 50 and 51 into Eq. 49 with I₁(x) and I₂(x), the theorem is proved.

Appendix C: Proof of Proposition 1

From $\frac {d f(x)}{d x}>\frac {d g(x)}{d x}>0$, there exist x₁ > 0 and x₂ > 0 such that

$$ \frac{f(x_{1})-f(0)}{x_{1}}>\frac{g(x_{2})-g(0)}{x_{2}}. $$

(54)

If f(0) < g(0), then there exists a crossing point x^′ = x₁ = x₂ > 0 such that f(x^′) = g(x^′) and thus (f(x^′) − f(0))/x^′ > (g(x^′) − g(0))/x^′ satisfying Eq. 54. Conversely, if there exists a crossing point x^′ = x₁ = x₂ > 0 satisfying Eq. 54, then we can easily deduce that f(0) < g(0).

Proof of uniqueness: Let us assume that there exists 0 < x^″ ≠ x^′ satisfying f(x^″) = g(x^″) and f(x^′) = g(x^′). We have

$$ \frac{f(x^{\prime\prime})-f(x^{\prime})}{x^{\prime\prime}-x^{\prime}}=\frac{g(x^{\prime\prime})-g(x^{\prime})}{x^{\prime\prime}-x^{\prime}}, $$

(55)

which contradicts the fact that $\frac {d f(x)}{d x}>\frac {d g(x)}{d x}$.

Therefore, we can conclude that ∃!x^′ > 0 : f(x^′) = g(x^′) if and only if f(0) < g(0).

Appendix D: Proof of Theorem 2

In the DT protocol, as R_s → 0, it can be observed from Eq. 26 that

$$ P^{(DT)}_{out}\to \frac{\bar{\gamma}_{\mathcal{SE}}}{\bar{\gamma}_{\mathcal{SD}}+\bar{\gamma}_{\mathcal{SE}}}\triangleq P^{(DT)}_{0}. $$

(56)

In the RT protocol, as R_s → 0, Φ(x) in Eq. 37 approaches

$$\begin{array}{@{}rcl@{}} {\Phi}(x) \!&\to&\! \left( \!1 + \frac{x}{\bar{\gamma}_{\mathcal{SR}}}\right) \!\left( \frac{1}{\bar{\gamma}^{-1}_{\mathcal{SR}} + x^{-1}} - \frac{1}{\bar{\gamma}^{-1}_{\mathcal{SE}} + \bar{\gamma}^{-1}_{\mathcal{SR}} + x^{-1}}\right)\\ &&=\frac{x^{2}\bar{\gamma}_{\mathcal{SR}}}{x\bar{\gamma}_{\mathcal{SR}} + x\bar{\gamma}_{\mathcal{SE}} + \bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}}. \end{array} $$

(57)

Substituting Eq. 57 into Eq. 36, the limit of $P^{(RT)}_{out}$ can be obtained by Eq. 58.

$$\begin{array}{@{}rcl@{}} P^{(RT)}_{out}&\to& 1-\frac{\frac{\bar{\gamma}_{\mathcal{RD}}^{2}\bar{\gamma}_{\mathcal{SR}}}{\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SR}}+\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}}-\frac{\bar{\gamma}_{\mathcal{SD}}^{2}\bar{\gamma}_{\mathcal{SR}}}{\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SR}}+\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}}}{\bar{\gamma}_{\mathcal{RD}}-\bar{\gamma}_{\mathcal{SD}}} \\ &=& \frac{\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SE}}(\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SR}}+\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}})+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}^{2}_{\mathcal{SE}}(\bar{\gamma}_{\mathcal{SD}}+\bar{\gamma}_{\mathcal{SR}})}{(\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SR}}+\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}})(\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SR}}+\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}})} \\ &\triangleq& P^{(RT)}_{0}. \end{array} $$

(58)

Denote ${\Delta }=P^{(RT)}_{0}-P^{(DT)}_{0}$. Solving Δ < 0, after some mathematical manipulations, we obtain the condition of the channel quality of various links as in Eq. 59.

$$\begin{array}{@{}rcl@{}} {\Delta} <0 &\Leftrightarrow& \bar{\gamma}_{\mathcal{SR}}\bar{\gamma}^{2}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{RD}}+\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}^{2}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}^{2}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SE}}<\bar{\gamma}^{2}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{RD}}+\bar{\gamma}^{2}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SE}} \\&\Leftrightarrow&\bar{\gamma}_{\mathcal{SR}}(\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}^{2}_{\mathcal{SD}}-\bar{\gamma}_{\mathcal{RD}}\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}+\bar{\gamma}^{2}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}})+\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{RD}}(\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}-\bar{\gamma}^{2}_{\mathcal{SR}})<0 \\&\Leftrightarrow& \bar{\gamma}_{\mathcal{SR}}[\bar{\gamma}_{\mathcal{RD}}(\bar{\gamma}^{2}_{\mathcal{SD}}-\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{SE}}/2)+\bar{\gamma}_{\mathcal{SE}} (\bar{\gamma}^{2}_{\mathcal{SD}}-\bar{\gamma}_{\mathcal{SR}}\bar{\gamma}_{\mathcal{RD}}/2)]+\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{RD}}(\bar{\gamma}_{\mathcal{SD}}\bar{\gamma}_{\mathcal{SE}}-\bar{\gamma}^{2}_{\mathcal{SR}})<0. \end{array} $$

(59)

It can be seen that, if $\bar {\gamma }_{\mathcal {SD}}\bar {\gamma }_{\mathcal {SE}}<\bar {\gamma }^{2}_{\mathcal {SR}}$, $\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {SE}}/2}$ and $\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {RD}}/2}$, then Δ < 0, i.e. $P^{(RT)}_{0}<P^{(DT)}_{0}$. Additionally, as in the conventional relaying scheme, the gradient of the GSOP performance of the RT scheme is higher than that of the DT scheme and the GSOP of both schemes increases as a function of the target secrecy rate, i.e. $\frac {dP^{(RT)}_{out}}{dR_{s}}>\frac {dP^{(DT)}_{out}}{dR_{s}}>0$. Therefore, from Proposition 1, we can conclude that $\exists ! R^{\prime }_{s}>0: P^{(DT)}_{out}(R^{\prime }_{s})=P^{(RT)}_{out}(R^{\prime }_{s})$.