Lubricated Sliding of a Rigid Cylinder on a Viscoelastic Half Space

Abstract

We study the lubricated sliding of a rigid cylinder on a viscoelastic half space with a single characteristic retardation time. Besides the generalized inverse Hersey number $\beta$, which is the sole parameter governing elastic lubrication, the viscoelastic lubrication solution depends on two additional dimensionless parameters: $\alpha$ and $f$. $\alpha$ is the characteristic retardation time divided by the time for the rigid cylinder to move one contact width and f determines the strength of viscoelasticity. We have developed a numerical scheme to solve this viscoelastic lubrication problem. Our numerical results show that the total friction force can be decomposed into viscoelastic and hydrodynamic components. The viscoelastic component of the friction is well approximated by the dry limit in which the liquid layer is all squeezed out and the resistance to sliding is due entirely to viscoelastic dissipation. The hydrodynamic limit is well approximated by a modification of the elastic limit in which friction is due entirely to hydrodynamics. We also study the dependence of the hydrodynamic pressure, film thickness and the friction coefficient on these parameters.

1 Introduction

Lubricated sliding, in which a thin liquid film separates two solids in relative motion, is ubiquitous, e.g., in the smooth operation of gears and pistons in machines and joints in our bodies. In the past decade or so, applications of lubricated sliding has expanded from stiff–stiff contact, such as in bearings [1, 2] and pistons [3, 4], to applications that involve stiff–soft or soft–soft contact, such as in rubber bearings and seals [5,6,7,8] and rubber tires to road contact [9, 10]. Many studies also have examined lubricated sliding of elastic contact with a sphere-on-fat or cylinder-on-fat contact geometry to investigate the effects of properties such as material modulus, lubricant viscosity and surface roughness [11,12,13,14,15,16,17,18,19].

As one of the intense research subject, elasto-hydrodynamic lubrication (EHL) has been studied for a long-time. In EHL, the materials are assumed to be elastic. However, most soft materials such as elastomers, gels or cartilage are viscoelastic. Viscoelasticity cause energy dissipation which significantly increases friction during lubricated sliding. Compared to EHL, viscoelastic–hydrodynamic lubrication (VEHL) has received much less attention, partly because of the difficulty of simultaneously solving the nonlinear Reynolds equation for the fluid phase and the history-dependent equations of viscoelasticity for the solid. Because of this difficulty, literature on this subject is scant, as noted by Putignano [20], who recently developed a numerical method to solve this class of problems.

A special case of VEHL is “dry” sliding, where the fluid layer is absent (or completely squeezed out) and solid–solid contact is itself frictionless. Thus, in “dry” sliding, the sliding resistance is due entirely to viscoelastic dissipation. Hunter [21] studied the sliding contact of a rigid cylinder with viscoelastic half space and obtained an exact formula for the contact pressure and contact width. Carbone and Putignano [22] extended Hunter’s result to address a similar sliding problem on a finite viscoelastic layer using a more realistic viscoelastic model. Additional numerical and experimental research on this topic can be found in [7, 23, 24].

The problem of a lubricated rigid cylinder sliding on a viscoelastic substrate have been studied by Herrebrugh [25], Dowson et al. [26], Hooke and Huang [27], Elsharkawy [28], Scaraggi and Persson [29], Putignano et al. [20, 23, 30, 31] and others [13, 18, 32]. These works have focused on issues such as the general effect of material viscoelasticity on the lubrication process and the analytical solution of some simplified viscoelastic lubrication geometries. However, previous work has not addressed the relationship between the mechanics of viscoelastic hydrodynamic lubrication and simpler cases of E and the pure dry sliding contact. Hui et al. [33] recently showed that the full VEHL solution of a cylinder sliding on a thin viscoelastic foundation can be decomposed, to a good approximation, into a combination of the corresponding dry sliding and the EHL solutions. Whether this decomposition is obtained in the more general VEHL problem of lubricated sliding on a viscoelastic half space remains an open question, and this is the main focus of the work presented here.

Specifically, we study the problem of lubricated sliding of a rigid cylinder on a soft viscoelastic half space. As pressure-sensitivity of viscosity is negligible for typical soft lubrication conditions [34], we assume lubricant to be iso-viscous, i.e., Newtonian with constant viscosity. In our previous works [35, 36], we have found that with appropriate normalization the EHL problem is governed by a single parameter $\beta$ which is a generalized version of the inverse Hersey number [11]. For soft contacts $\beta$ is typically much larger than 1. Including the viscoelasticity of the substrate introduces two additional dimensionless parameters $\alpha ,\;f$, which are the normalized loading rate and the normalized strength of the retardation spectrum. We study the nature of the solution over large ranges of these parameters to investigate how they affect features of the solution such as hydrodynamic pressure, liquid film thickness, and the friction force.

The plan for the remainder of this paper is as follows: Sect. 2 summarizes the formulation of the VEHL problem. In this section, two special cases are studied in detail. One is the dry sliding case where the liquid layer is absent, and second one is the EHL problem where viscoelasticity is not considered. We show that these two cases approximately constitute two important components of the full problem. Section 3 presents the detailed numerical recipes to solve the full VEHL problem. We highlight some findings that cause numerical difficulties especially for the cylinder problem where the displacement is not well-defined. Section 4 presents the numerical results and comparison with the existing theory. Results are presented in the form of a generalized Stribeck surface. We conclude with a summary and discussion in Sect. 5.

2 Theoretical Methods

2.1 Problem Statement and Theoretical Formulation

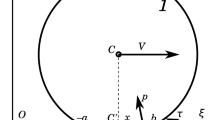
A schematic of lubricated sliding of a rigid circular cylinder on viscoelastic half space is shown in Fig. 1. The rigid cylinder is assumed to be infinitely long in the out-of-plane direction. The radius of the cylinder is R. Between the rigid cylinder and the viscoelastic half space, there exists a thin liquid layer of constant viscosity $\eta$. The cylinder is moving with a constant velocity V to the right under the application of a horizontal line force F. A constant vertical line force N is imposed on the cylinder. A coordinate system $\left( {x,\;y} \right)$ is attached to the moving cylinder. In this moving coordinate frame, the vertical position of the cylinder is $h\left( x \right)$ and at $x = 0$, $h_{0} \equiv h\left( 0 \right)$. The substrate is deformed under the hydrodynamic pressure and the deformed surface is denoted by $w\left( x \right)$. The liquid film thickness is $u\left( x \right) = h\left( x \right) - w\left( x \right)$.

Fig. 1

A schematic of lubricated sliding of a rigid cylinder on a viscoelastic half space

The deformation in the half space is under plane strain, where the out-of-plane displacement is zero and the in-plane stress and strain fields are independent of the out-of-plane coordinate. As is well-known, in-plane strain, the displacement field has a logarithmic singularity at infinity. As a result, the surface displacement w and $h_{0}$ are only defined to within an arbitrary constant. Here we follow the standard procedure to determine this constant: we chose a point on the surface at distance r₀ far from the cylinder as a datum for normal displacement w and $h_{0}$. Details are given below.

In steady sliding, all the fields are independent of time $t$ in the moving frame (x, y) even though the material is rate-dependent. Specifically, the material time derivative of field quantities in a stationary frame can be converted to spatial derivative in the moving frame, both in the fluid or in the viscoelastic solid. For details, please see Supporting Information (SI). The Reynolds equation for the lubrication layer is [37]:

$$ \left( {\frac{{p,_{x} \left( {h - w} \right)^{3} }}{12\eta }} \right),_{x} = - \left( \frac{V}{2} \right)\left( {h,_{x} - w,_{x} } \right), $$

(1)

where $p$ is the hydrodynamic pressure and a comma denotes differentiation. Since the “effective contact region” is usually much smaller than the cylinder radius, the circular profile of cylinder is approximated as a parabola, i.e.,

$$ h = h_{0} + \frac{{x^{2} }}{2R}. $$

(2)

The substrate is assumed to be a standard viscoelastic solid where there is a single characteristic retardation time $\tau$. Specifically, the creep function C(t) in simple tension is

$$ C\left( t \right) = E_{0}^{ - 1} \left[ {1 + f\left( {1 - {\text{e}}^{ - t/\tau } } \right)} \right], $$

(3)

where $E_{0}$ is the instantaneous Young’s modulus and $f$ is the strength of retardation spectrum; $f$ is related to the long and short time Young’s modulus $E_{\infty } ,\;E_{0}$ by

$$ f = \frac{{E_{0} }}{{E_{\infty } }} - 1. $$

(4)

For highly viscoelastic solids such as rubber, $f \approx 10^{3}$ [38]. For a purely elastic solid, f = 0. We assume that the Poisson ratio of the half space, $\nu$, is a constant independent of time, which is a good approximation for soft solids which are almost incompressible;$\nu \approx 1/2.$

The vertical surface displacement $w\left( x \right)$ due to a normal pressure distribution $p\left( x \right)$ was given by Hunter [21]:

$$ w\left( x \right) = \frac{2}{{\pi E_{0}^{*} }}\left[ {\int_{ - \infty }^{ + \infty } {p\left( {x^{\prime}} \right)\ln \left| {x - x^{\prime}} \right|{\text{d}}x^{\prime}} + f\int_{0}^{\infty } {{\text{e}}^{ - \xi } {\text{d}}\xi \int_{ - \infty }^{ + \infty } {p\left( {x^{\prime}} \right)\ln \left| {x + V\tau \xi - x^{\prime}} \right|{\text{d}}x^{\prime}} } } \right] + {\text{const}}, $$

(5)

where $E_{0}^{*} = \frac{{E_{0} }}{{1 - v^{2} }}$ is the instantaneous plane strain modulus. Note that $p\left( x \right)$ is the hydrodynamic fluid pressure acting on the substrate surface. It is positive when the fluid is in compression. The term $\left. w \right|_{x = 0}$ is always negative in the coordinate frame shown in Fig. 1. The first integral in Eq. (5) is the elastic displacement (for an elastic substrate with $E_{0}$ and v). The double integral in Eq. (5) accounts for viscoelasticity. When $f = 0$ ($E_{0} = E_{\infty }$), we recover the elastic solution. As noted above, the constant in Eq. 3 indicates that w cannot be determined uniquely. Force balance indicates that the overall hydrodynamic pressure should balance the normal applied line load, i.e.,

$$ \int_{ - \infty }^{ + \infty } {p\left( x \right){\text{d}}} x = N. $$

(6)

Finally, we note that the stress and strain must vanish at infinity; in particular, the material far away from the cylinder is elastic with relaxed modulus $E_{\infty }$.

2.1.1 Normalization

We normalize location of material point, $x$, by the “Hertz contact length” $a_{0}$, which is the half contact width of a cylinder on an elastic solid without sliding, subjected to a line force N. The Young’s modulus and Poisson’s ratio of this reference elastic solid are denoted by $E_{\infty } ,\;v$, respectively. The half contact length $a_{0}$ and the pressure distribution of the classical elastic “Hertz contact” are given by Eqs. (7) and (8) [39].

$$ {\text{a}}_{0} \equiv \left( {\frac{4NR}{{\pi E_{\infty }^{*} }}} \right)^{1/2} ,\quad E_{\infty }^{*} = \frac{{E_{\infty } }}{{1 - v^{2} }}, $$

(7)

$$ p_{{{\text{Hertz}}}} = \left\{ {\begin{array}{*{20}c} {\frac{2N}{{\pi a_{0} }}\sqrt {1 - \left( {\frac{x}{{a_{0} }}} \right)^{2} } ,} & {\left| x \right| < a_{0} ,} \\ {0,} & {\left| x \right| \ge a_{0} .} \\ \end{array} } \right. $$

(8)

We normalize the hydrodynamic pressure $p$ by $\max \left( {p_{{{\text{Hertz}}}} } \right)$.The normalization of each variable is:

$$ \overline{x} = \frac{x}{{a_{0} }},\quad \overline{h} = \frac{Rh}{{a_{0}^{2} }} = \overline{h}_{0} + \frac{1}{2}\overline{x}^{2} ,\quad \overline{w} = \frac{Rw}{{a_{0}^{2} }},\quad \overline{p} = \frac{{\pi a_{0} }}{2N}p. $$

(9)

The normalized form of Eqs. (1), (5) and (6) are:

$$ \beta \left[ {\overline{p},_{{\overline{x}}} \left( {\overline{h} - \overline{w}} \right)^{3} } \right],_{{\overline{x}}} = - \left( {\overline{h},_{{\overline{x}}} - \overline{w},_{{\overline{x}}} } \right), $$

(10)

$$ \overline{w}\left( {\overline{x}} \right) = \frac{1}{{\pi \left( {1 + f} \right)}}\left[ {\int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}^{\prime}} \right)\ln \left| {\overline{x} - \overline{x}^{\prime}} \right|{\text{d}}\overline{x}^{\prime}} + f\int_{0}^{\infty } {{\text{e}}^{ - \xi } {\text{d}}\xi \int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}^{\prime}} \right)\ln \left| {\overline{x} + \frac{1}{\alpha }\xi - \overline{x}^{\prime}} \right|{\text{d}}\overline{x}^{\prime}} } } \right] + {\text{const}}, $$

(11)

$$ \int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}} \right){\text{d}}} \overline{x} = \frac{\pi }{2}, $$

(12)

$$ \alpha = \frac{{a_{0} }}{V\tau }, $$

(13)

$$ \beta = \frac{{E_{\infty }^{*} a_{0}^{4} }}{{12\eta VR^{3} }} = \frac{{4N^{2} }}{{3\pi^{2} \eta VE_{\infty }^{*} R}}. $$

(14)

Note $\beta$ in Eq. (10) is the inverse generalized Hersey number. Large $\beta$ indicates either larger normal force or smaller sliding velocity. $\alpha$ is the ratio of the time to slide a Hertz contact length to the retardation time of the viscoelastic substrate. When $\alpha \to 0$, the viscoelastic material behaves elastically with modulus $E_{0}$ as the material is fully unrelaxed, while for $\alpha \to \infty$ the material is fully relaxed and behaves as an elastic solid with Young’s modulus $E_{\infty }$. For intermediate values of $\alpha$, the substrate dissipates energy. Here we note that $\beta$ is typically very large for soft material sliding. As an example, in an experiment of recent study [35] where $R = 2mm$, $E_{\infty }^{*} = 10^{5} Pa$, $\eta = 5.1Pa \cdot s$, $N = 119mN/mm$, $V = 1mm/s$, $\beta \approx 1.8 \times 10^{3} > > 1$.

2.1.2 Substrate Deformation

For most electrohydrodynamic lubrication simulations, the evaluation of the substrate deformation ranks as the most computationally demanding part of the entire simulation process [40,41,42], followed by the process of solving of the Reynolds equation and checking the force balance condition. For VEHL, the evaluation of substrate deformation is even more difficult since the deformation depends on the loading history. This difficulty is reflected by the double integral in Eq. (11). Therefore, it is important to find an efficient way to evaluate the viscoelastic deformation of substrate. By changing the integration order of $\overline{x}$ (space) and $\xi$ (time) in the 2nd part of RHS of Eq. (6b), we convert the double integral in Eq. (11) into a single integral Eq. (15), which can be evaluated much more efficiently:

$$ \overline{w}\left( {\overline{x}} \right) = \frac{1}{\pi }\int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}^{\prime}} \right)\ln \left| {\overline{x} - \overline{x}^{\prime}} \right|{\text{d}}\overline{x}^{\prime}} - \frac{f}{{\pi \left( {1 + f} \right)}}\int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}^{\prime}} \right)} {\text{e}}^{{\alpha \left( {\overline{x} - \overline{x}^{\prime}} \right)}} {\text{Ei}}\left( { - \alpha \left( {\overline{x} - \overline{x}^{\prime}} \right)} \right){\text{d}}\overline{x}^{\prime} + {\text{const}}, $$

(15)

where ${\text{Ei}}\left( x \right)$ is the exponential integral function, ${\text{Ei}}\left( x \right) = \int_{ - \infty }^{x} {\frac{{{\text{e}}^{t} }}{t}{\text{d}}t}$. Details on the derivation of Eq. (15) is given in the SI. The constant in Eq. (15) is determined by selecting a datum at $\overline{x} = \overline{r}_{0}$ where $\overline{w}\left( {\overline{r}_{0} } \right) = 0$ for $f = 0$. Physically, it corresponds to the case that when the substrate is fully relaxed, the vertical displacement is zero at $\overline{x} = \overline{r}_{0}$. The constant in Eq. (15) is:

$$ {\text{const}} = - \frac{1}{\pi }\int_{ - \infty }^{ + \infty } {\overline{p}\left( {\overline{x}^{\prime}} \right)\ln \left| {\overline{r}_{0} - \overline{x}^{\prime}} \right|{\text{d}}\overline{x}^{\prime}} . $$

(16)

In our problem, $\overline{r}_{0}$ is selected to be large enough so it lies in the relaxed region. The final expression for the vertical displacement is:

$$ \overline{w}\left( {\overline{x}} \right) = \frac{1}{\pi }\int_{ - \infty }^{ + \infty } {\overline{P}\left( {\overline{s}} \right)\ln \left| {\frac{{\overline{x} - \overline{s}}}{{\overline{r}_{0} - \overline{s}}}} \right|{\text{d}}\overline{s}} - \frac{f}{{\pi \left( {1 + f} \right)}}\int_{ - \infty }^{ + \infty } {P\left( {\overline{s}} \right)} {\text{e}}^{{\alpha \left( {\overline{x} - \overline{s}} \right)}} {\text{Ei}}\left( { - \alpha \left( {\overline{x} - \overline{s}} \right)} \right){\text{d}}\overline{s}. $$

(17)

2.1.3 Friction Force due to Hydrodynamics and Viscoelasticity

Friction during lubricated sliding results from two sources. The first is due to shear flow of the liquid layer while the second is due to viscoelastic dissipation which causes the hydrodynamic pressure to be skewed.

The friction $F_{\rm{h}}$ due to hydrodynamics can be obtained by integrating the shear traction $\tau_{yx}$ in the fluid layer. For a Newtonian fluid, $\tau_{yx}$ is related with the strain rate $\partial v_{x} /\partial y$ by:

$$ \tau_{yx} = \eta \frac{{\partial v_{x} }}{\partial y}, $$

(18)

where $v_{x} \left( x \right)$ is the component of the fluid velocity in the horizontal direction. Following [36]:

$$ v_{x} \left( {x,\;y} \right) = \left[ {\frac{{p,_{x} }}{2\eta }\left( {y - h} \right){ + }\frac{v}{h - w}} \right]\left( {y - w} \right). $$

(19)

Integrating the shear traction $\left. {\tau_{xy} } \right|_{y = h}$ over the entire domain gives

$$ F_{{\text{h}}} = \int_{ - \infty }^{\infty } {\left. {\tau_{yx} } \right|_{y = h} {\text{d}}x} = \frac{{Na_{0} }}{R}\int_{ - \infty }^{\infty } {\left[ {\frac{{\overline{p},_{{\overline{x}}} \overline{u}}}{\pi } + \frac{1}{{3\pi \beta \overline{u}}}} \right]{\text{d}}\overline{x}} \equiv \frac{{Na_{0} }}{R}\overline{F}_{{\text{h}}} . $$

(20)

The friction coefficient $\mu_{h}$ that corresponds to $F_{h}$ is defined as $\mu_{\rm{h}} \equiv F_{\rm{h}} /N$ and is given by

$$ \mu_{\rm{h}} = \frac{{a_{0} }}{R}\int_{ - \infty }^{\infty } {\left[ {\frac{{\overline{p},_{{\overline{x}}} \overline{u}}}{\pi } + \frac{1}{{3\pi \beta \overline{u}}}} \right]\rm{d}\overline{x}} . $$

(21)

Next, we consider the friction force $F_{\rm{v}}$ due to viscoelastic dissipation. When the substrate is viscoelastic, the hydrodynamic pressure is generally skewed. This skewed pressure distribution gives rise to a net horizontal force which results in a friction force $F_{\rm{v}}$. A schematic figure illustrating this mechanism is in Fig. 2.

Fig. 2

Schematic figure showing how viscoelasticity causes a skewed hydrodynamic pressure, which leads to friction force $F_{\rm{v}}$

Figure 2 shows the free body diagram of the cylinder and the viscoelastic half space. The friction force is the integral of $\rm{d}F_{\rm{v}} = - p\left( x \right)\sin \theta \rm{d}x$ over the entire domain, where the negative sign represents the direction of $F_{\rm{v}}$ pointing to the right and $\sin \theta \simeq \rm{d}w/\rm{d}x$. Therefore,

$$ F_{\rm{v}} = - \int_{ - \infty }^{ + \infty } {p\left( x \right)\sin \theta \rm{d}x} = - \int_{ - \infty }^{ + \infty } {p\left( x \right)\frac{{\rm{d}w}}{{\rm{d}x}}\rm{d}x} = - \int_{ - \infty }^{ + \infty } {p\left( x \right)\rm{d}w} = - \frac{{Na_{0} }}{R}\frac{2}{\pi }\int_{ - \infty }^{ + \infty } {\overline{p}\left( x \right)\rm{d}\overline{w}} \equiv \frac{{Na_{0} }}{R}\overline{F}_{\rm{v}} . $$

(22)

The friction coefficient $\mu_{\rm{v}}$ is

$$ \mu_{\rm{v}} \equiv \frac{{F_{\rm{v}} }}{N} = - \frac{{2a_{0} }}{\pi R}\int_{ - \infty }^{ + \infty } {\overline{p}\left( x \right)\rm{d}\overline{w}} . $$

(23)

2.2 Two Limiting Cases: Drying Sliding and EHL

A recent study by Hui et al. [33] has shown that the friction force during viscoelasto-hydrodynamic lubrication can be well approximated as a combination of two simpler cases: the dry sliding case where the liquid is absent and the lubricated sliding case where the substrate is elastic. However, the substrate in that work was modeled as a viscoelastic spring foundation in which mechanical interactions are purely local, in the sense that the displacement of the substrate at a point is affected by the pressure only at that point. This is in general not a good assumption for a substrate that is large in extent compared with all relevant dimensions. Here we study the feasibility of a similar decomposition for lubricated sliding of a rigid cylinder on a viscoelastic half space. These two limiting cases are considered in the next two Sects. 2.2.1 and 2.2.2.

2.2.1 Dry Sliding

In the absence of a liquid film, the cylinder slides on the viscoelastic half space with solid-to-solid contact. We call this case dry sliding. A schematic of dry sliding is shown in Fig. 3. In it, the liquid film thickness $u\left( x \right) \equiv h\left( x \right) - w\left( x \right) = 0$ so $h\left( x \right) = w\left( x \right)$ everywhere. In particular, the pressure must vanish at the leading and trailing contact edges, which we denote by $x_{1}$ and $x_{2}$, respectively. That is, $p\left( {x_{1} } \right) = p\left( {x_{2} } \right) = 0$. In Fig. 3, $a$ is the semi-contact width and $b$ is the x coordinate of the contact midpoint. The solution of this problem was obtained by Bongaerts et al. [11]. Here we adopt his solution to study the relevant mechanics. It must be noted that, because by supposition physical contact between the surfaces bears no shear traction, the friction force in dry sliding is due entirely to viscoelastic dissipation [11].

Fig. 3

A schematic of dry sliding of a rigid cylinder on a viscoelastic half space

The pressure distribution is given by Bongaerts et al. [11]. Using our normalization, it is

$$ \overline{p}\left( {\overline{x}} \right) = \left\{ {\begin{array}{*{20}l} {k\overline{a} \cdot {\text{e}}^{{\frac{{k\left( {\overline{x} - \overline{b}} \right)}}{{\overline{a}}}\int_{{\left( {\overline{x} - \overline{b}} \right)/\overline{a}}}^{1} {{\text{e}}^{ - k\xi } \left\{ {\sqrt {1 - \xi^{2} } + \frac{{\left( {\overline{\Gamma }_{2} - \overline{\Gamma }_{1} \xi } \right)}}{{\sqrt {1 - \xi^{2} } }}} \right\}{\text{d}}\xi ,} }} } & {\overline{x}_{2} \le \overline{x} \le \overline{x}_{1} ,} \\ {0,} & {{\text{elsewhere}},} \\ \end{array} } \right. $$

(24)

where:

$$ k = \left( {1 + f} \right)\alpha \overline{a}, $$

(25)

$$ \overline{a}^{2} \equiv \left( {\frac{a}{{a_{0} }}} \right)^{2} = \frac{{K_{0} \left( {\alpha \overline{a}} \right)/K_{1} \left( {\alpha \overline{a}} \right) + I_{0} \left( k \right)/I_{1} \left( k \right)}}{{K_{0} \left( {\alpha \overline{a}} \right)/K_{1} \left( {\alpha \overline{a}} \right) + I_{0} \left( k \right)/I_{1} \left( k \right) + 2f/k}}, $$

(26)

$$ \overline{\Gamma }_{1} = - \frac{1}{k} - \frac{1}{2}\left( {\frac{1}{{\overline{a}^{2} }} - 1} \right)\frac{{I_{0} \left( k \right)}}{{I_{1} \left( k \right)}}, $$

(27)

$$ \overline{\Gamma }_{2} = \frac{1}{2}\left( {\frac{1}{{\overline{a}^{2} }} - 1} \right), $$

(28)

$$ \overline{b} \equiv \frac{b}{{a_{0} }} = \overline{\Gamma }_{1} + \frac{1}{{\alpha \overline{a}}}, $$

(29)

$$ \overline{x}_{1} = \overline{a} + \overline{b},\quad \overline{x}_{2} = \overline{b} - \overline{a}. $$

(30)

In Eq. (26) $I_{0}$, $I_{1}$ and $K_{0}$, $K_{1}$ are the modified Bessel function of the first and second kind, respectively. The normalized semi-contact width $\overline{a}$ is determined by the numerical solution of the transcendental Eq. (26). Once $\overline{a}$ is determined, Eqs. (27)–(29) can be used to determine $\overline{\Gamma }_{1} ,\;\overline{\Gamma }_{2}$ and $\overline{b}$. In the SI, we show that for the special cases where $\alpha \to 0$ or $\alpha \to \infty$, one recovers the classical elastic Hertz solution.

We use Eqs. (23) and (24) to determine the dry friction force F_v. Since in dry sliding the deformed surface’s curvature is the same as the cylinder’s surface curvature, $\sin \theta \approx \frac{{\rm{d}w}}{{\rm{d}x}} = \frac{x}{R}$ for $x_{2} \le x \le x_{1}$. The dry sliding friction $F_{\rm{v}}$ and the friction coefficient $\mu_{\rm{v}}$ are:

$$ F_{\rm{v}} = - \int_{{x_{2} }}^{{x_{1} }} {p\left( x \right)\frac{x}{R}\rm{d}x} = \frac{{Na_{0} }}{R}\left[ {\overline{b} - \frac{1}{{\alpha \left( {1 + f} \right)}} - \overline{a}^{3} \overline{\Gamma }_{1} } \right] \equiv \frac{{Na_{0} }}{R}\overline{F}_{\rm{v}} , $$

(31)

$$ \mu_{\rm{v}} = \frac{{F_{\rm{v}} }}{N} = \frac{{a_{0} }}{R}\left[ {\overline{b} - \frac{1}{{\alpha \left( {1 + f} \right)}} - \overline{a}^{3} \overline{\Gamma }_{1} } \right]. $$

(32)

2.2.2 Lubricated Sliding with an Elastic Substrate (Special Case, $f = 0$ or $\alpha = \infty$)

Next, we consider the special case of an elastic substrate. For this case, $f = 0$ or $\alpha = \infty$, and the solution depends on a single parameter $\beta$. Integrating both sides of the Reynolds equation, Eq. (10), gives:

$$ \beta \overline{p},_{{\overline{x}}} \overline{u}^{3} = - \overline{u} + c. $$

(33)

The constant of integration c depends only on $\beta$ and is the normalized thickness where the pressure gradient is exactly zero. A scaling analysis (see the SI) shows that for $\beta > > 1$, Eq. (13) holds when $c = O\left( {1/\sqrt \beta } \right)$ and $\overline{u} = O\left( {1/\sqrt \beta } \right)$. To validate this scaling analysis, we numerically solved Eq. (33) together with (Eq. 15 with $f = 0$) to determine c and the pressure distribution. Details of these calculations are given in SI. We found

$$ c = \frac{0.197}{{\sqrt \beta }} + \frac{0.951}{\beta }. $$

(34)

Figure 4 shows that Eq. (34) agrees very well with the numerical values of $c$ for $\beta \ge 50$. The error is less than 20% even at $\beta = 10$.

Fig. 4

Comparison of $c\left( \beta \right)$. Numerical result are symbols (the line is to guide the eyes) and the scaling result of Eq. (34)

To obtain the hydrodynamic friction (see Eq. 20), we need both the pressure and film thickness distribution. As expected, the pressure distribution for large $\beta$ is almost identical to the Hertz pressure (see SI), which is

$$ \overline{p}\left( {\overline{x}} \right) = \left\{ {\begin{array}{*{20}c} {\sqrt {1 - \overline{x}^{2} } ,} & { - 1 < \overline{x} < 1,} \\ {0,} & {{\text{elsewhere}}{.}} \\ \end{array} } \right. $$

(35)

The fact that normalized pressure distribution vanishes rapidly outside $\left[ { - 1,\;1} \right]$ allows us to replace the integration limits in Eq. (20) from − 1 to 1. An approximate expression for the liquid film thickness $\overline{u}$ in the interval $\left| {\overline{x}} \right| < 1$ can be obtained using Eqs. (33) and (34), this results in (for details, see SI):

$$ \overline{u} \approx c\left( \beta \right)\left( {1 + a_{1} \overline{x} + a_{2} \overline{x}^{2} } \right) = \left( {\frac{0.197}{{\sqrt \beta }} + \frac{0.951}{\beta }} \right)\left( {1 + \left( {0.197} \right)^{2} \cdot \overline{x} + 3 \times \left( {0.197} \right)^{4} \cdot \overline{x}^{2} } \right)\quad \left| {\overline{x}} \right| < 1. $$

(36)

Figure 5 shows that the numerical film thickness profiles for $\beta = 1000$ and $\beta = 2000$ are in excellent agreement with Eq. (36) for $\left| {\overline{x}} \right| < 1$. Note that the coefficients of the quadratic term in Eq. (36) are very small. In particular, since $\left| {\overline{x}} \right| < 1$, the thickness of the liquid film is approximately constant inside the “contact” zone and is given by $c\left( \beta \right)$, the thickness where the pressure gradient is exactly zero.

Fig. 5

Comparison of the film thickness profile with Eq. (36) for two different $\beta$ values: a $\beta = 1000$ and b $\beta = 2000$

3 Numerical Method of Solving Full VEHL Problem

In this section, we highlight a numerical method to solve the VEHL lubrication problem which requires simultaneously solving the Reynolds equation and for the surface deformation. In the literature, the Reynolds equation for the sliding problem is usually solved using either relaxation [36, 37] or Newton–Raphson methods [43, 44]. In this work, we used a forward relaxation method [25] which is easier to implement and less memory-demanding compared with the Newton–Raphson method. The numerical method here differs from previous work [36] in two aspects: we consider viscoelasticity and using a normal force condition. Calculation of the deformation of the viscoelastic material requires extra computation time as the deformation depends not only the spatial distribution of the load but also the loading history. In the previous section, we have shown that this difficulty can be bypassed by integrating the temporal integrand analytically which results in an expression involving only the spatial integrand. This allows efficient evaluation of the viscoelastic deformation. As mentioned previously, the absolute surface deformation is not well-defined, which makes a displacement control loading scheme physically nonintuitive. Instead, we applied normal force control which requires us to find the relative position of the cylinder, $h_{0}$. This position is determined by the condition that the pressure satisfies Reynolds equation and normal force balance.

We use a central difference scheme to discretize the first and second derivatives in Eq. (10), i.e.,

$$ \left( {\frac{\partial f}{{\partial \overline{x}}}} \right)_{i} = \frac{{f_{i + 1} - f_{i - 1} }}{{2\Delta \overline{x}}};\quad \left( {\frac{{\partial^{2} f}}{{\partial \overline{x}^{2} }}} \right)_{i} = \frac{{f_{i + 1} - 2f_{i} + f_{i - 1} }}{{\left( {\Delta \overline{x}} \right)^{2} }}. $$

(37)

Using Eq. (37), the discretized form of Eq. (10) becomes:

$$ A_{i} \overline{p}_{i - 1} + B_{i} \overline{p}_{i} + C_{i} \overline{p}_{i + 1} = D_{i} , $$

(38)

where: $A_{i} = \left[ {\frac{{\left( {\bar{u}_{i} } \right)^{2} }}{{\left( {\Delta \bar{x}} \right)^{2} }}\left( {\frac{3}{4}\bar{u}_{{i - 1}} + \bar{u}_{i} - \frac{3}{4}\bar{u}_{{i + 1}} } \right)} \right];{\mkern 1mu} B_{i} = - 2\frac{{\left( {\bar{u}_{i} } \right)^{3} }}{{\left( {\Delta \bar{x}} \right)^{2} }};{\mkern 1mu} C_{i} = \left[ {\frac{{\left( {\bar{u}_{i} } \right)^{2} }}{{\left( {\Delta \bar{x}} \right)^{2} }}\left( { - \frac{3}{4}\bar{u}_{{i - 1}} + \bar{u}_{i} + \frac{3}{4}\bar{u}_{{i + 1}} } \right)} \right];{\mkern 1mu} D_{i} = - \frac{{\bar{u}_{{i + 1}} - \bar{u}_{{i - 1}} }}{{2\beta \Delta \bar{x}}} .$

The discretized form of film thickness is $\overline{u}_{i} = \overline{h}_{i} - \overline{w}_{i}$, where $\overline{h}_{i}$ and $\overline{w}_{i}$ are the position of the cylinder’s surface and the substrate surface’s deformation at $\overline{x}_{i}$. They are computed according to

$$ \overline{h}_{i} = \overline{h}_{0} + \frac{1}{2}\overline{x}_{i}^{2} , $$

(39)

$$ \overline{w}_{i} = \sum\limits_{k = 1}^{n} {\chi_{ik} \left( {\overline{x}_{i} ,\;\overline{x}_{k} } \right)\overline{p}_{k} } , $$

(40)

$$ \chi_{ik} = \left[ {\frac{1}{\pi }\ln \left| {\frac{{\overline{x}_{i} - \overline{x}_{k} }}{{\overline{r}_{0} - \overline{x}_{k} }}} \right| - \frac{f}{{\pi \left( {1 + f} \right)}}\rm{e}^{{\alpha \left( {\overline{x}_{i} - \overline{x}_{k} } \right)}} \rm{Ei}\left( { - \alpha \left( {\overline{x}_{i} - \overline{x}_{k} } \right)} \right)} \right] \cdot \Delta \overline{x}. $$

(41)

Note Eq. (40) is Eq. (17) in discretized form, where $n$ is the total number of grid points. The discretized form of the Reynolds Eq. (10) is solved using forward relaxation method where $\overline{p}_{i}^{{\rm{curt}}}$ in the current iteration is related to the previous iteration $\overline{p}_{i}^{{\rm{prev}}}$ by:

$$ \overline{p}_{i}^{{\rm{curt}}} = \overline{p}_{i}^{{\rm{prev}}} + \lambda_{p} \left( {D_{i} - A_{i} \overline{p}_{i - 1}^{{\rm{curt}}} - B_{i} \overline{p}_{i}^{{\rm{prev}}} - C_{i} \overline{p}_{i + 1}^{{\rm{prev}}} } \right)/B_{i} . $$

(42)

In Eq. (42), $\lambda_{p}$ is the relaxation factor which controls the convergence rate of the relaxation iteration. Large $\lambda_{p}$ usually results in faster convergence. However, it is also less stable and iteration is more prone to diverge. In our calculations, we found the values of $\lambda_{p}$ which optimize convergence rate and stability falls in a relatively large range, $\lambda_{p} = 0.01 - 0.8$. The relaxation factor also depends on the choice of parameters $\alpha$, $f$ and $\beta$. Usually, small $\alpha$ and large $f$, $\beta$ values require smaller $\lambda_{p}$ to ensure stable convergence.

Once the hydrodynamic pressure is found using the above scheme, we need to check if the normal force balance Eq. (12) is satisfied. The discretized form of Eq. (12) is:

$$ \sum\limits_{i = 1}^{n} {\overline{p}_{i} \Delta \overline{x}} = \frac{\pi }{2}. $$

(43)

If normal force balance is not satisfied, the film thickness is either too large or too small and the position of the cylinder, $\overline{h}_{0}$, should be adjusted. In our numerical scheme, $\overline{h}_{0}$ is updated every $n_{{\text{h}}}$ iterations using

$$ \overline{h}_{0}^{{\rm{curt}}} = \overline{h}_{0}^{{\rm{prev}}} + \lambda_{{\rm{h}1}} \left| {1 - \frac{2}{\pi }\sum\limits_{i = 1}^{n} {\overline{p}_{i}^{{\rm{curt}}} \Delta \overline{x}} } \right| + \lambda_{{\rm{h}2}} \frac{{\left\| {\overline{p}^{{\rm{curt}}} - \overline{p}^{{\rm{prev}}} } \right\|}}{{\left\| {\overline{p}^{{\rm{prev}}} } \right\|}}. $$

(44)

In Eq. (44), the adjustment of $\overline{h}_{0}$ includes two parts: the normalized normal force balance residual and the relative change of pressure in two iterations. Even though $\overline{h}_{0}$ is directly related to normal force balance, we found that including the contribution of the pressure change is very important for convergence when $\alpha < 0.1$. The parameters $\lambda_{{\rm{h}1}}$, $\lambda_{{\rm{h}2}}$ are relaxation factors associate with these two residuals. In our calculation, $\lambda_{{\rm{h}1}}$ is found to be in the range of $0.001 - 0.01$ and $\lambda_{{\rm{h}2}} = 10 - 20$ for $\alpha < < 1$ while $\lambda_{{\rm{h}2}} = 0$ works well for $\alpha \ge 1$. Note that smaller $n_{{\text{h}}}$ allows prompt adjustment of the cylinder position which potentially helps faster convergence. However, the iteration could become more unstable. We have found that an appropriate $n_{{\text{h}}}$ is in the range of $10 - 200$.

A flow chat of the numerical scheme is shown in Fig. 6. An initial guess of the pressure profile $\overline{p}^{{\rm{init}}}$ and $\overline{h}_{0}^{{\rm{init}}}$ has to be provided to start the iteration. $\overline{p}^{{\rm{init}}}$, $\overline{h}_{0}^{{\rm{init}}}$ are chosen to be the corresponding EHL solution with the target $\beta$ value. Note that a good initial guess is critical for the iteration to converge in a fast and stable pace.

Fig. 6

A flow chat summarizing the numerical scheme for solving Eqs. (10)–(12). For detailed description, see text above and Eqs. (37) to (44)

4 Numerical Results of the VEHL Problem

4.1 Hydrodynamic Pressure and Substrate Deformation

Figure 7a–c plot the normalized hydrodynamic pressure distribution $\overline{p}\left( {\overline{x}} \right)$ for different combinations of $\alpha ,\;\beta$ and $f$. The colored lines are the numerical results obtained by solving Eqs.(10–12). The black dashed lines are the dry sliding results from Eq. (24). Note $\alpha = 1$ in both Fig. 7a, b with f changing from 10 (Fig. 7a) to 100 (Fig. 7b). Recall that $f = E_{0} /E_{\infty } - 1$ so a larger $f$ indicates stronger viscoelasticity. Here we focus on highly viscoelastic solids such as rubber where $f \approx 100$ or higher. Figure 7a, b show that the hydrodynamic pressure peaks near the leading edge since the strain rate is highest here. Also, as $\beta$ increases, the hydrodynamic pressure approaches the dry sliding contact pressure. This is reasonable, since larger $\beta$ corresponds to higher normal loads or smaller sliding velocities; both conditions result in a thinner film. The main difference between the dry solution and the VEHL solution is near the leading edge, where the pressure of the dry solution drops abruptly to zero.

Fig. 7

Comparison of the hydrodynamic pressure profile with the dry sliding pressure Eq. (24). a $\alpha = 1$, $f = 10$, $\beta = 100 - 500$, b $\alpha = 1$, $f = 100$, $\beta = 100 - 500$, and c $\beta = 1000,f = 100$, $\alpha$ varies from $10^{ - 3}$ to $10^{3}$. In a–c, the dry sliding pressure cases are shown by the black broken lines

Figure 7c fixes $\beta$ and f while varying $\alpha$ by 6 orders of magnitude. Recall that $\alpha = a_{0} /V\tau$ is the ratio of time to slide the cylinder over half Hertzian contact width over the characteristic retardation time of the viscoelastic material. This figure shows that the hydrodynamic pressure is well approximated by the dry sliding pressure for all $\alpha$ values. The pressure is highly skewed for $\alpha = 0.1$ and $1$: pressure is concentrated at the leading edge. This means that if the time for the cylinder to slide over half the Hertzian contact width is comparable to the retardation time, the front half of the cylinder will experience much higher hydrodynamic pressure. For very large and small $\alpha$, the pressure is given by the elastic solution (Hertz pressure) corresponding to a relaxed or stiff substrate with modulus $E_{\infty }^{ * }$ and $E_{0}^{ * }$, respectively.

Figure 8a, b plot the position of the trailing edge $\overline{x}_{2}$ which is defined as the location where pressure first approaches zero. Here it is important to note that in our numerical calculation, the Reynolds condition [36] is applied to eliminate regions of negative pressure. In these figures, f = 100 and $\beta$ varies from 10 to 1000. The horizontal axis is $\alpha$ which varies from $10^{ - 3}$ to $10^{3}$. In the same figure, we also present the trailing edge of the dry sliding solution, $\overline{x}_{2}$ which is obtained from Eqs. (26), (29), and (30). Figure 8a shows that as $\beta$ increases, $\overline{x}_{2}$ approaches the dry sliding limit. It is interesting to note that $\overline{x}_{2} > 0$ for $\alpha \in \left( {0.1,\;1} \right)$. In this range of $\alpha$, the material is highly dissipative and hydrodynamic pressure is concentrated in the front part of the cylinder (see also Fig. 7b, c). This skew pressure distribution can cause significant stress concentration at the leading edge as we shall see in Fig. 9.

Fig. 8

Comparison of the trailing edge position $\overline{x}_{2}$ with the dry sliding prediction. a $\beta = 10,\;50,\;100,\;200$ and b $\beta = 10 - 1000$. Results show that for $\alpha = 0.1 - 1$, the rear position of the effective contact is larger than 0 which indicates that the hydrodynamic pressure concentrates in the region $\overline{x} > 0$

Fig. 9

The deformed viscoelastic substrate and the cylinder’s position for different $\alpha$ with constant $f$ and $\beta$,$f = 100,\;\beta = 1000$. Contour plots of $\overline{\sigma }_{yy}$ in the substrate are shown

Figure 9 shows contour plots of the normal stress component $\overline{\sigma }_{yy}$ near the leading edge. The calculation of $\overline{\sigma }_{yy}$ is given in SI. We focus on the range of $\alpha \in \left( {0.1,\;1} \right)$ where the pressure field is highly skewed. The result of the two limits where $\alpha \to 0$ and $\alpha \to \infty$ is given in the SI. In these two limits, the deformation of the substrate is almost symmetric and contour of $\overline{\sigma }_{yy}$ approaches to the Hertzian results with elastic moduli $E_{\infty }^{ * }$ and $E_{0}^{ * }$, respectively. For $\alpha = 0.1 - 1.0$, this asymmetric deformation is caused by the hydrodynamic pressure being concentrated more locally at a smaller region. With the skewed substrate deformation and concentrated pressure, one expects much higher counterreaction force acting on the rigid cylinder as shown schematically in Fig. 2. This is the friction force due to the viscoelastic deformation, $F_{\rm{v}}$.

4.2 Viscoelastic Dissipation: Loading and Unloading Cycles and the Viscoelastic Friction Force $F_{\rm{v}}$

The expression for the friction force $F_{v}$, Eq. (22) can be interpreted as the viscoelastic energy dissipated as a material point entering the leading edge and exiting the trailing edge. As this point enters the leading edge, it is actively loaded and it unloads to zero pressure as it exits the trailing edge. Figure 10 shows this loading and unloading cycle for a typical material point on the substrate surface for $f = 10,\;100$. The dry limit results calculated using Eqs. (24) and (17) (black dotted lines) are also plotted in the same figure for comparison. The area enclosed by the loading and unloading curves is the dissipated energy, $\overline{F}_{\rm{v}}$. In Fig. 10a, b, $\alpha = 1$, for which, we found numerically, the energy dissipation is approximately maximum. Results for a broad range of $\alpha$ are shown in Fig. 11.

Fig. 10

The loading and unloading cycles for a typical material point on the substrate’s surface. Dry sliding solution is plotted in comparison. a $f = 10$, and b $f = 100$. Different $\beta$ values are plotted to show the trend of approaching the dry limit solution

Fig. 11

Normalized friction force $\overline{F}_{\rm{v}}$ due to viscoelastic energy dissipation against $\alpha$ for different $\beta$. The dry sliding limit is the solid black line

Figure 11 plots the normalized friction force due to viscoelastic energy dissipation versus $\alpha$ for different values of β. The black solid line is the dry sliding friction force calculated using Eq. (31). Note that the dissipation or friction force $\overline{F}_{\rm{v}}$ reaches the maximum at roughly $\alpha = 1$ for different β. As expected, when $\overline{F}_{\rm{v}}$ approaches 0 when $\alpha \to 0$ or $\infty$. In these limits, the substrate is elastic. It is interesting to note that the dry sliding friction is an upper bound for $\overline{F}_{\rm{v}}$. This is because the liquid layer smooths out the skewed pressure distribution and hence reduces the friction force. The VEHL friction approaches the dry limit as β increases.

We summarize this section by emphasizing that the friction due to viscoelasticity of the substrate can be well approximated by the dry sliding solution and hence is effectively decoupled from the hydrodynamics for sufficiently large $\beta$. The situation is more complicated for the friction due to hydrodynamics since the gap size is expected to be sensitive to viscoelasticity. Nevertheless, the dry sliding solution can be exploited to determine this gap thickness, and this feature allows us to determine the hydrodynamic component of the friction force without solving the full lubrication problem, as we shall demonstrate below.

4.3 Liquid Film Thickness and Hydrodynamic Friction Force $F_{\rm{h}}$

Figure 12 plots the liquid film thickness profile for different $\alpha$ values while fixing $\beta ,\;f$. The liquid film thickness increases with $\alpha$ and varies by about an order of magnitude. This is not surprising since large $\alpha$ implies that the substrate underneath the cylinder is relaxed, with long-time modulus. Indeed, as $\alpha$ decreases, the substrate underneath the cylinder becomes effectively stiffer, and this decreases the size of the “effect contact zone”. To support the higher normal load, the liquid film thins to increase the hydrodynamic pressure.

Fig. 12

Film thickness profile for a large range of $\alpha$ values

To incorporate the effect of $\alpha$ and f into the hydrodynamic friction, we note that the scaling $c \approx O\left( {1/\sqrt \beta } \right)$ and $\overline{u} \approx O\left( {1/\sqrt \beta } \right)$ still holds for the VEHL case at large $\beta$ value except that $c$ and $\overline{u}$ now depends not only $\beta$, but also on $\alpha$ and $f$. Integrating of Eq. (6a) yields:

$$ \beta \overline{p},_{{\overline{x}}} \overline{u}^{3} = - \overline{u} + c\left( {\beta ,\;\alpha ,\;f} \right), $$

(45)

where c takes the form of:

$$ c = \frac{{\rho_{1} \left( {\alpha ,\;f} \right)}}{\sqrt \beta } + \frac{{\rho_{2} \left( {\alpha ,\;f} \right)}}{\beta }. $$

(46)

From our previous calculation of EHL in Sect. 2.2.2, we found:

$$ \rho_{1} \left( {\alpha \to \infty ,\;f} \right) = 0.197,\quad \rho_{2} \left( {\alpha \to \infty ,\;f} \right) = 0.951, $$

(47)

$$ \rho_{1} \left( {\alpha \to 0,\;f} \right) = \frac{0.197}{{\sqrt {1 + f} }},\quad \rho_{2} \left( {\alpha \to 0,\;f} \right) = \frac{0.951}{{1 + f}}. $$

(48)

We also have $\rho_{1} \left( {\alpha ,\;f = 0} \right) = 0.197$, $\rho_{2} \left( {\alpha ,\;f = 0} \right) = 0.951$ which are the elastic limits. A plot for $c$ versus $\beta$ for $f = 100$ for different $\alpha$ is shown in Fig. 13 where the symbols are the numerical $c$ values. The solid lines in Fig. 13 are calculated using the expression:

$$ c = \frac{0.197}{{\sqrt {\beta^{*} } }} + \frac{0.951}{{\beta^{*} }}\quad \rm{where}\;\beta^{*} \equiv \beta \left( {1 + f\rm{e}^{ - 1.41\alpha } } \right). $$

(49)

Fig. 13

Numerical result of $c$ versus $\beta$ for different $\alpha$ values (symbols). The solid black lines are calculated using by Eq. (24)

Figure 13 shows that Eq. (49) captures the numerical results well. This equation allows us to approximately determine the film thickness in the full viscoelastic sliding problem, as will be demonstrated below.

As shown in the previous section, for $\beta \ge 50$, the dry limit of $\overline{p}$ obtained from Eq. (24) is a good approximation for the hydrodynamic pressure. Using the dry limit of $\overline{p}$, we can solve the cubic Eq. (45) with c given by Eq. (49) for $\overline{u}$. This procedure allows us to determine the fluid film thickness in the “contact” zone for large $\beta$. The result of the asymptotic solution of $\overline{u}$ (for large $\beta$) is shown as symbols in Fig. 14a and the full solution of $\overline{u}$ is shown as solid lines for comparison.

Fig. 14

a Comparison of VEHL solution with asymptotic solution for the film thickness profile. The asymptotic solution is obtained by solving the cubic Eq. (45) with c given by Eq. (49) and P given by Eq. (24). b The normalized hydrodynamic friction force $\overline{F}_{\rm{h}}$ versus $\alpha$. Asymptotic solutions of $\overline{F}_{\rm{h}}$ calculated by using the dry limit of $\overline{p}$ and the asymptotic solution of $\overline{u}$ are shown in black solid lines

The above analysis demonstrates an important result: the hydrodynamic friction Eq. (18) can be determined using the dry sliding pressure and the gap thickness determined using the dry pressure and solving a cubic. The validity of this approximate solution is checked by comparing the solution of the full VEHL problem in Fig. 14b. In Fig. 14b we plot the normalized hydrodynamic friction force $\overline{F}_{\rm{h}}$ for a large range of $\alpha$. $\overline{F}_{\rm{h}}$ is calculated using Eq. (20). The black solid lines are the approximation solutions. For all practical purposes, the proposed approximation works. Both numerical and approximate solutions show that $\overline{F}_{\rm{h}}$ decreases with increasing $\beta$. For small $\alpha$, $\alpha < 0.1$ and large $\alpha$, $\alpha > 10$, $\overline{F}_{\rm{h}}$ plateaus indicating that $\overline{F}_{\rm{h}}$ is insensitive to $\alpha$ as the elastic limits are approached. As expected, $\overline{F}_{\rm{h}}$ peaks at $\alpha \approx 1$ for different $\beta$.

4.4 Total Friction in Viscoelastic Lubrication and Generalized Stribeck Surface

The total friction force $F_{{\rm{tot}}}$ is the sum of the viscoelastic friction $F_{\rm{v}}$ and the hydrodynamic friction $F_{\rm{h}}$. Using our approximation, $F_{{\rm{tot}}}$ and the corresponding friction coefficient $\mu_{{\rm{tot}}}$ are:

$$ F_{{\rm{tot}}} = F_{\rm{v}} + F_{\rm{h}} = \frac{{Na_{0} }}{R}\left[ {\left( {\overline{b} - \frac{1}{{\alpha \left( {1 + f} \right)}} - \overline{a}^{3} \overline{\Gamma }_{1} } \right) + \int_{ - \infty }^{\infty } {\left( {\frac{{\overline{p},_{{\overline{x}}} \overline{u}}}{\pi } + \frac{1}{{3\pi \beta \overline{u}}}} \right)\rm{d}\overline{x}} } \right] \equiv \frac{{Na_{0} }}{R}\overline{F}_{{\rm{tot}}} , $$

(50)

$$ \mu_{{\rm{tot}}} = \frac{{F_{{\rm{tot}}} }}{N} = \frac{{a_{0} }}{R}\left[ {\left( {\overline{b} - \frac{1}{{\alpha \left( {1 + f} \right)}} - \overline{a}^{3} \overline{\Gamma }_{1} } \right) + \int_{ - \infty }^{\infty } {\left( {\frac{{\overline{p},_{{\overline{x}}} \overline{u}}}{\pi } + \frac{1}{{3\pi \beta \overline{u}}}} \right)\rm{d}\overline{x}} } \right] = \mu_{\rm{v}} + \mu_{\rm{h}} , $$

(51)

where $\overline{a}$, $\overline{b}$, $\overline{\Gamma }_{1}$ are defined in Eqs. (26), (29), and (27), $\overline{p}$ is given by Eq. (24) and u is determined from the solution of the cubic Eq. (45).

Figure 15 plots the total friction force $\overline{F}_{{\rm{tot}}}$ (black line) against large range $\alpha$, $\alpha = 10^{ - 3} - 10^{3}$. Also plotted are the viscoelastic friction $\overline{F}_{v}$ and the hydrodynamic friction $\overline{F}_{\rm{h}}$. For very small $\alpha < 0.1$ and very large $\alpha > 10$ (i.e., very fast and very small loading rate), the total friction is mainly contributed by hydrodynamics as the substrate is elastic and no viscoelastic energy is dissipated. For moderate loading rates, $\alpha = 0.1 - 10$, the viscoelastic friction $\overline{F}_{\rm{v}}$ kicks in and contribute significantly to the total friction force. Comparing Fig. 15a, b shows that as $\beta$ increases viscoelastic dissipation is the dominant friction mechanism. In this regime, the calculation is much simpler since $\overline{F}_{\rm{v}}$ is completely determined by the dry friction solution.

Fig. 15

Total friction force $\overline{F}_{{\rm{tot}}}$ versus $\alpha$ for $f = 100$, a $\beta = 10$, and b $\beta = 500$. The components of $\overline{F}_{\rm{h}}$ and $\overline{F}_{\rm{v}}$ are also shown for comparison

In the EHL regime, it is common practice to use the Stribeck curve where the friction coefficient is plotted against the Hersey number. However, it must be noted that, even for an elastic substrate, the solution of the sliding problem cannot be expressed solely in terms of the Hersey number. Indeed, as shown above and by others [12, 34, 45], friction depends on the parameter $\beta$, which can be viewed as a generalized inverse Hersey number. Substrate viscoelasticity complicates the analysis as friction coefficient depends not only on $\beta$, but also on $\alpha$ and $f$. Thus, the generalization of the Stribeck curve is a Stribeck surface in the 4 dimensional space $\left( {\alpha ,\;\beta ,\;f,\;\mu_{{\rm{tot}}} } \right)$. Here, we present a slice of this 4 dimensional surface by fixing $f = 100$. In Fig. 16, we present 3D slices of the generalized Stribeck surfaces in $\left( {\alpha ,\beta ,\mu_{tot} } \right),\left( {\alpha ,\beta ,\mu_{{\text{v}}} } \right),\left( {\alpha ,\beta ,\mu_{h} } \right)$. Figure 16b shows that for large $\beta$, viscoelasticity controls the total friction force. The friction calculated using the dry sliding limit is shown in the same plot for comparison. However, for small $\alpha$, $\alpha < 0.01$ and large $\alpha$ regions, $\alpha > 100$, the hydrodynamic friction force contributes significantly to the total friction as shown in Fig. 16c. The elastic lubrication limit is shown in the same plot for comparison.

Fig. 16

Generalized Stribeck surfaces. a Total friction coefficient $\mu_{{\rm{tot}}}$ versus $\alpha ,\;\beta$. b and c Viscoelastic friction coefficient $\mu_{\rm{v}}$ and hydrodynamic friction coefficient $\mu_{\rm{h}}$ versus $\alpha ,\;\beta$

5 Discussion and Summary

In this work, we studied the lubricated sliding of a rigid cylinder on a viscoelastic substrate with an emphasis on how substrate viscoelasticity affects sliding friction. We developed a robust numerical algorithm and used it to solve the full viscoelastic lubrication problem. Our theoretical formulation shows that whereas EHL is governed solely by the generalized inverse Hersey number $\beta$, the full viscoelastic lubrication solution depends on two extra dimensionless parameters: $\alpha$ and $f$. The parameter $\alpha$ represents ratio of time taken to traverse the contact region to the characteristic viscoelastic relaxation time; $f$ is the ratio of short and long-time moduli (− 1) denoting the strength of viscoelasticity.

Our analysis suggests an approach that can further simplify the problem. We find that many results of the full viscoelastic lubrication problem can be obtained by the combination of two simper limiting cases. The first of these is the dry sliding limit in which the liquid layer is absent—the cylinder and viscoelastic substrate are in direct contact. The second one is the elastic lubrication limit in which the viscoelastic substrate is replaced by an elastic material. We have examined these two limits in detail. Our results show that the dry sliding contact pressure distribution is usually a good approximation of the hydrodynamic pressure in the lubricated case, especially in the large $\beta$ regime. The liquid film thickness can be calculated approximately using perturbation theory together with the dry contact pressure. The viscoelastic friction force due to viscoelastic energy dissipation dominates the total friction in this large $\beta$ regime. For small $\alpha$ regime, $\alpha < 0.01$, and large $\alpha$ regime, $\alpha > 100$, the hydrodynamic friction is the main source for the total friction. The dry limit solution summarized in this work, the scaling analysis for the elastic lubrication and the numerical scheme proposed for the full viscoelastic lubrication problem could be useful in other similar work. Also, the substrate is assumed to be standard viscoelastic solid in current work. One can linearly combine more characteristic retardation time into the model to fully approximate more realistic creep behavior of soft matter using similar methodology shown in this work.