Friction Force During Lubricated Steady Sliding of a Rigid Cylinder on a Viscoelastic Substrate

Abstract

We study the friction force during lubricated sliding of a rigid cylindrical indenter against a viscoelastic substrate in the iso-viscous visco-elasto-hydrodynamic lubrication (VEHL) regime. The substrate is represented by a foundation model. The solution is controlled by three dimensionless parameters. The first of these, λ, measures the time for the indenter to move one contact zone relative to the viscoelastic relaxation time; the second is the ratio of the long time to short time compliance of the substrate, $c_{\infty } /c_{0}$; the third parameter, β, is the ratio of average fluid flow rate to the sliding velocity. Although our solution works well for the full range of parameters, we focus on the “Hertz” regime (β >>1) where practically all the fluid in the contact region is squeezed out. This regime is quite common in soft contact lubrication problems and presents significant numerical difficulties. Our analysis gives insight into why these numerical difficulties arise. The friction force can be decomposed into two parts, one due to viscoelastic dissipation and the other from hydrodynamics. Although these two are generally coupled, in the Hertz limit, an important result is that the viscoelastic portion of the friction force can be well approximated by the solution of the corresponding “dry” sliding problem, in which there is no lubricating fluid layer. This provides a simple way to decouple the hydrodynamic portion of the friction force from the viscoelasticity of the substrate. We study how hydrodynamic pressure and film thickness vary with the controlling dimensionless parameters. Scaling laws for these relationships are given in closed form.

1 Introduction

Lubricated sliding, in which an intervening liquid layer separates two solid surfaces, is ubiquitous in nature and in technology. When the contacting solids are elastic and the liquid layer forms a continuous film in the contact region, we obtain an important subclass: Elasto-Hydrodynamic Lubrication (EHL) [1,2,3]. EHL theory has been extensively applied, traditionally with a heavy emphasis on stiff metal contacts such as in bearings [4, 5] and pistons [6, 7]. EHL theory is also relevant to contact between soft elastic materials and a hard surface, such as the sliding of rubbery tires or shoe soles on a lubricated hard surface. Many parts of our body rely on soft lubrication to function; examples are joints, eyelids and eyeballs with contact lenses. For more compliant materials the effect of deformation qualitatively alters the contact geometry and pressure profile, as well as hysteretic friction forces [8,9,10,11,12]. Material compliance and lubricant viscosity strongly affect friction behavior in the EHL regime. The Stribeck plot [13] shows that lubricated contact can be divided into three regimes. For high sliding or rolling velocities and small enough vertical loads, the liquid film is continuous and normal load is supported mainly by hydrodynamic pressure; friction is governed by fluid flow. As velocity decreases or normal load increases, the system enters the mixed lubrication regime, in which the liquid film starts to break apart, and the load is supported by both dry and lubricated contact. At very high loads or slow velocities, the system arrives in the boundary lubrication regime, where most of the liquid is squeezed out, and the solid surfaces come into intimate contact. Here adhesive forces form areas of “dry” contact and hysteretic forces from material deformation also begin to contribute to the friction response. In this regime sample roughness and inelasticity control the friction behavior.

EHL theory assumes that the contacting solids are elastic. However, many soft elastic solids such as rubber are viscoelastic. Viscoelasticity is a dissipative mechanism which can be used to significantly increase friction during sliding. However, as noted by Putignano [14], other than a handful of papers [15,16,17], the literature on how viscoelasticity affects lubricated contact mechanics is scant. The focus of this work is to study a special case of this class of problems in detail. Specifically, we report on a study of the lubricated sliding of a rigid cylinder on a soft, flat, and viscoelastic substrate. We focus on the regime where the liquid layer is continuous. We shall call this the VEHL (viscoelastic hydrodynamic lubrication) regime. Since the role of pressure-sensitive viscosity is negligible for typical soft solids [3], we assume that the liquid is Newtonian with a constant viscosity (iso-viscous). Our analysis is focused on the “Hertz” regime, in which the layer of liquid is thin and the elastic foundation deforms much as it would for dry frictionless indentation by the same indenter and load. The dominance of the Hertz regime is illustrated by our recent experiment [18, 19]. Briefly, we slid a spherical glass indenter on the lubricated surface of an elastic polydimethylsiloxane (PDMS) substrate. These tests were performed using different combinations of sliding velocity, normal load and sphere radius. Our results showed that, consistent with EHL theory, suitably normalized hydrodynamic friction plotted against the normalized sliding velocity collapses to a master curve, which means that elastohydrodynamic lubrication is controlled by a single dimensionless parameter $\beta$ (see below for definition), of which the inverse Hersey Number is an approximate version [13]. In our experiments, $\beta$ was found to be much larger than unity, which corresponds to the “Hertz” limit [18].

To put our work in context, many studies have examined lubricated sliding of elastic contact with a sphere-on-flat or cylinder-on-flat contact geometry to investigate the effects of properties such as material modulus, lubricant viscosity and surface roughness [13, 20,21,22,23,24,25,26,27,28,29]. Closely related to this work is a paper by Snoeijer et al. [30], who carefully studied lubricated sliding of a rigid cylinder on an elastic half space. Their focus is also on the “Hertz” regime. They showed that near the edge of the contact, the liquid film profile can be described by a similarity solution. More importantly, they showed that this 2D local solution can be applied to study the pressure and film thickness in 3D problems. Another closely related work is by Pandey et al. [16], who studied VEHL in a 2D geometry and presented asymptotic relations between the lift force and the sliding velocity.

The plan for the rest of this paper is as follows: Sect. 2 begins by summarizing the formulation of the VEHL problem. The main result in this section is to show that the viscoelastic lubrication problem can be broken down into two simpler problems: the first is the EHL problem in which the substrate has the short time modulus. The second is the “dry” viscoelastic problem, in which frictionless sliding takes place in the absence of a fluid layer. Full numerical solution is provided for the EHL problem. Highly accurate expressions which relate the liquid profile and the pressure distribution within the effective contact zone to $\beta$ are obtained. An exact closed-form solution is obtained for the second, dry, contact problem. We then use the solutions of these two problems to obtain approximate expressions for the film thickness, the pressure distribution and the friction force in the viscoelastic lubrication sliding problem. Section 3 uses the results in Sect. 2 to obtain a generalization of the Stribeck curve—a Stribeck surface. We conclude with summary and discussion in Sect. 4.

2 Theoretical Methods

2.1 Problem Statement and Formulation

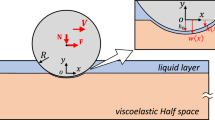
Figure 1 shows a schematic of the problem. An infinitely long rigid circular cylindrical indenter of radius R is sliding at a constant velocity V in the positive x direction on a viscoelastic substrate, which is modeled as a spring foundation. A coordinate system $\left( {x,y} \right)$ is attached to the moving cylinder. Here, y = 0 is the surface of the undeformed foundation and x = 0 is the horizontal coordinate of the center of the cylinder. The vertical displacement of the center of the cylinder is denoted by $h_{0}$ ($h_{0}$ < 0). The surface profile of the cylinder with respect to the moving coordinate system is $h\left( x \right)$. A layer of fluid lies between the cylinder and the foundation. The thickness of fluid layer is $d = h - w > 0$ where w is the displacement of the viscoelastic spring foundation. The compressive vertical line load required to maintain the indenter displacement $h_{0}$ is denoted by N. In this work compressive load and pressure are taken to be positive.

Fig. 1

A schematic of a steadily sliding rigid cylinder on a foundation of viscoelastic springs

We assume steady state sliding, and so field quantities are independent of time and depend only on x. The Reynolds’ equation for the fluid layer is then [31]

$$\left( {\frac{{p,_{x} \left( {h - w} \right)^{3} }}{12\eta }} \right),_{x} = - \left( \frac{V}{2} \right)\left( {h - w} \right),_{x} .$$

(1)

here, p is the fluid pressure field, $\eta$ is the fluid viscosity and a comma “,” denotes differentiation with respect to x. The thickness of the fluid layer is $d = h - w$. Using Hertz’s approximation for small contact [32], the surface of cylinder is approximated as a parabola, so

$$h = h_{0} + \frac{{x^{2} }}{2R}.$$

(2)

The springs in the foundation are assumed to be viscoelastic, that is, the displacement w is related to the pressure by a creep function $c\left( {t/t_{0} } \right)$[units $m^{3} /N$] where t denotes time and $t_{0}$ is a characteristic relaxation time in a creep test. Specifically, for a fixed material point $X_{m}$ on the surface of the foundation, we have

$$w\left( {X_{m} ,t} \right) = \int\limits_{ - \infty }^{t} {c\left( {\frac{{t - t^{\prime}}}{{t_{0} }}} \right)} \frac{{\partial p\left( {X_{m} ,t^{\prime}} \right)}}{{\partial t^{\prime}}}dt^{\prime}.$$

(3)

Steady state sliding implies that

$$\frac{{\partial p\left( {X_{m} ,t} \right)}}{\partial t} = - Vp,_{x} .$$

(4)

Equation (4) allows us to replace the time derivative by the spatial derivative in the moving coordinate system, so (3) can be rewritten as

$$w\left( x \right) = - \int\limits_{x}^{\infty } {c\left( {\frac{{x^{\prime} - x}}{{Vt_{0} }}} \right)} p,_{{x^{\prime}}} dx^{\prime}.$$

(5)

In the following, we shall assume that the foundation is a solid, so that $c\left( {t/t_{0} \to \infty } \right) = c_{\infty } > 0$, where $c_{\infty }$ is the long-time or relaxed compliance of the foundation. We will also denote the instantaneous compliance by $c\left( {t/t_{0} = 0} \right) = c_{0}$. Equations (1) and (5) are the governing equations for the lubricated sliding problem on a foundation of viscoelastic springs.

During sliding, as the material enters the leading edge of the (effective) contact region, it is compressed. Conversely, towards the rear (trailing edge) it relaxes. Thus, a typical material point experiences cyclic deformation, which results in hysteresis or viscoelastic dissipation. For a purely elastic solid there is no hysteresis and, in the Hertz limit, the pressure distribution and deformation are symmetrical about x = 0 and there is no net dissipation. This is not the case for viscoelastic foundations; the pressure distribution turns out to be asymmetrical.

2.1.1 Normalization

We normalize displacements, surface deformation w, and the cylinder profile h by $\left| {h_{0} } \right|$. The rest of the normalization is guided by the corresponding elastic “Hertz” contact problem in which the indenter is pushed vertically without sliding onto a spring foundation with instantaneous compliance $c_{0}$. For this case, the contact width is $2\sqrt {2R\left| {h_{0} } \right|}$ and the pressure distribution is [32]

$$p_{H} = \left\{ {\begin{array}{*{20}l} {\frac{{\left| {h_{0} } \right|}}{{c_{0} }}\left( {1 - \left( {x/\sqrt {2R\left| {h_{0} } \right|} } \right)^{2} } \right); \, \left| x \right| \le \sqrt {2R\left| {h_{0} } \right|} } \\ {0; \, \left| x \right| \ge \sqrt {2R\left| {h_{0} } \right|} } \\ \end{array} } \right..$$

(6)

Hence, we normalize all horizontal distances by $\sqrt {2R\left| {h_{0} } \right|}$ and pressure p by $c_{0} /\left| {h_{0} } \right|$. Then, the normalized form of Eq. (6) (Hertz pressure) is:

$$P_{H} = \left\{ {\begin{array}{*{20}l} {1 - X^{2}; \, \left| X \right| \le 1} \\ {0; \, \left| X \right| \ge 1} \\ \end{array} ,} \right.$$

(7)

and,

$$W = \frac{w}{{\left| {h_{0} } \right|}},\;\;H = \frac{h}{{\left| {h_{0} } \right|}} = - 1 + X^{2} ,\;\;X = \frac{x}{{\sqrt {2R\left| {h_{0} } \right|} }},D = \frac{d}{{\left| {h_{0} } \right|}} = H - W,\;\;P = \frac{{c_{0} }}{{\left| {h_{0} } \right|}}p.$$

(8)

The normalized governing Eqs. (1, 2, 5) are [after integrating Eq. (1) once]:

$$\begin{gathered} \beta P,_{X} D^{3} = - D + C, \, H = - 1 + X^{2} , \, W = - \int\limits_{X}^{\infty } {\phi \left( {\alpha \left( {X^{\prime} - X} \right)} \right)} \frac{\partial P}{{\partial X^{\prime}}}dX^{\prime} \hfill \\ \alpha = \frac{{\sqrt {2R\left| {h_{0} } \right|} }}{{Vt_{0} }}, \, \beta { = }\frac{{\left| {h_{0} } \right|^{3} }}{{6\eta Vc_{0} \sqrt {2R\left| {h_{0} } \right|} }}, \, \hfill \\ \end{gathered}$$

(9)

where $D = H - W$ is the normalized film thickness, $\, \phi \left( {t/t_{0} } \right) \equiv c\left( {t/t_{0} } \right)/c_{0}$ is the dimensionless creep function and C is a dimensionless integration constant. In the following we will use the standard viscoelastic solid model to illustrate ideas. In this case, the creep compliance function is given by

$$c\left( {t/t_{0} } \right) = c_{\infty } - \left( {c_{\infty } - c_{0} } \right)e^{{ - t/t_{0} }} .$$

(10)

where $t_{0}$ is the characteristic relaxation time in a creep test. With this model, the normalized solution depends on three dimensionless parameters (instead of one, $\beta$, for the corresponding elastic foundation hydrodynamic lubrication problem); these are $\alpha ,\beta$ and $c_{\infty } /c_{0}$. Note that the integration constant C depends on all three parameters.

2.1.2 Physical Meaning of Parameters

The parameter $c_{\infty } /c_{0}$ controls the amount of viscoelasticity; for a non-dissipative elastic solid, $c_{\infty } /c_{0} = 1$. It is typically much greater than 1 for highly dissipative solids. The parameter $\alpha$ represents the time to move the indenter by one contact zone length divided by the creep relaxation time. When it is very large/small compared to unity, the material behaves like a soft/stiff elastic solid. Dissipation is maximized when $\alpha$ takes intermediate values. The parameter β is the ratio of the pressure gradient due to elastic deformation, which scales as $\left( {\left| {h_{0} } \right|/c_{0} } \right)/\sqrt {2R\left| {h_{0} } \right|}$, to the hydrodynamic pressure gradient in the film which scales as $\left( {\eta V/\left| {h_{0} } \right|^{2} } \right)$. Alternatively, $1/\beta$ can be viewed as a normalized sliding velocity. It is the ratio of the sliding velocity and the average rate of fluid flow at a given indentation depth. To see this, we recall that in lubrication theory, the average flow rate in the film scales with the pressure gradient multiplied by the square of the fluid film thickness and divided by the viscosity. In our problem, the pressure gradient scales with $\left( {\left| {h_{0} } \right|/c_{0} } \right)/\sqrt {2R\left| {h_{0} } \right|}$ and the film thickness scales with $\left| {h_{0} } \right|$ [see Eq. (8)]. Hence the average flow rate scales with $\left| {h_{0} } \right|^{2} \left( {\left| {h_{0} } \right|/c_{0} } \right)/\eta \sqrt {2R\left| {h_{0} } \right|}$. It is interesting to note that $\beta$ carries little information about viscoelasticity whereas the parameters $\alpha$ and $c_{\infty } /c_{0}$ are independent of fluid flow.

2.2 Friction Force Due to Fluid Flow (Hydrodynamic Friction, $F_{f}$) and Friction Force Due to Viscoelastic Dissipation, $F_{vis}$

Two important quantities are the friction due to fluid flow ($F_{f}$) and that due to viscoelastic dissipation $F_{vis}$. The hydrodynamic friction $F_{f}$ (force per unit length) is computed by integrating the shear stress $\tau_{yx}$ acting on the indenter (see SI, Section 1).

$$F_{f} = \int_{ - \infty }^{\infty } {\left. {\tau_{yx} } \right|_{y = h} dx} = \frac{{\left| {h_{0} } \right|^{2} }}{{c_{0} }}\int_{ - \infty }^{\infty } {\left[ {\frac{{DP,_{X} }}{2} + \frac{1}{6\beta D}} \right]dX} \equiv \frac{{\left| {h_{0} } \right|^{2} }}{{c_{0} }}\overline{F}_{f} .$$

(11)

The viscoelastic friction force is the total dissipation (the area of the hysteresis loop) experienced by a material point as it moves from $\infty \to - \infty$ (see argument below)

$$F_{vis} = - \int_{ - \infty }^{\infty } {p\frac{dw}{{dx}}dx = } - \frac{{\left| {h_{0} } \right|^{2} }}{{c_{0} }}\int_{ - \infty }^{\infty } {P\frac{dW}{{dX}}dX \equiv \frac{{\left| {h_{0} } \right|^{2} }}{{c_{0} }}} \overline{F}_{vis} ,$$

(12)

here we emphasize that both these friction forces are normalized in the same way, that is, by $\left| {h_{0} } \right|^{2} /c_{0}$.

2.3 Two Special Problems

Important insights can be gained by examining two related, simpler, problems. The first is the special case of lubricated sliding on a purely elastic foundation. The second case is the non-lubricated (or ‘dry’, but still frictionless) limit where there is no fluid but the foundation is viscoelastic. As we shall see later, combination of the solutions to these simpler problems provides a useful approximation to the full viscoelastic lubrication problem.

2.3.1 Elastic Foundation

We identify foundation compliance with $c_{0}$ so Eq. (9) reduces to $W = - P$ and Eq. (9) becomes a first order nonlinear ordinary differential equation (ODE) in P:

$$\beta P,_{X} \left( {P - 1 + X^{2} } \right)^{3} = - \left( {P - 1 + X^{2} } \right) + C, \,$$

(13)

Equation (13) implies that the solution depends on a single parameter $\beta$. The integration constant associated with the solution of Eq. (9) and C are determined by the boundary conditions that the pressure vanishes at $X = \pm \infty$. There is little difficulty finding the solution numerically (see for example the closely related problem of two rotating cylinders [32].) However, these solutions by themselves do not provide enough insight, especially in the “Hertz” limit where $\beta > > 1$. For example, the corresponding problem in 3D, of a sphere undergoing lubricated sliding on an elastic foundation, is much harder to solve numerically as the ODE becomes a nonlinear partial differential equation (PDE) [19, 30, 33, 34]. In the literature, this PDE is usually solved by a relaxation method [19] which requires an initial guess for the pressure profile. However, the numerical solution is very sensitive to this initial guess when $\beta > > 1$. Intuitively, one may think that the Hertz pressure Eq. (7) would be a good initial guess. However, if one makes that choice, the numerical procedure diverges rapidly after a few iterations. Even with the “right” initial guess, it takes thousands of iterations for the numerical procedure to converge.

Here we highlight two ways to think about this limit. The first is geometrical and sheds light on the aforementioned numerical difficulty. Figure 2 plots the slope field of Eq. (13) in the (X, P) plane for $\beta = 10$. The normalized Hertz pressure (Eq. 7) (Hertz curve, $\gamma_{H}$) is indicated in Fig. 2 by a red solid line. We divide $\gamma_{H}$ into two parts: the first is $P_{H} = 1 - X^{2} ,$ where $X \in \left( { - 1,1} \right)$; the second is $P_{H} = 0,X \in \left( { - \infty , - 1} \right] \cup \left[ {1,\infty } \right)$. Note that the slope field on $\gamma_{H}$ is positive infinity as $P$ approaches $\gamma_{H}$ from the top side for any integration constant C > 0.¹ This means that the solution is always repelled from the Hertz curve for $X \in \left( { - 1,1} \right)$—this is the source of numerical instability. A scaling analysis (see SI, Section 2) shows that $C \simeq O\left( {1/\sqrt \beta } \right)$ for $\beta > > 1$. We solve Eq. (13) using an ODE solver and find that $C = 1/\sqrt {13\beta }$ for $\beta > 10$. The curve $\gamma_{0}$ where the slope field is exactly zero (nullcline) is readily determined using Eq. (13) and is

$$P = P_{H} + C = 1 - X^{2} + \frac{1}{{\sqrt {13\beta } }}.$$

(14)

Fig. 2

Slope field of Eq. (13) for C = 0.0877 ($\beta$ = 10). The red line ($\gamma_{H}$) is the Hertz pressure. For $X \in \left( { - 1,1} \right)$, the slope on $\gamma_{H}$ is positive infinity as P approaches $\gamma_{H}$ from above. The red arrows indicate infinite slope. Thus, solution is repelled from $\gamma_{H}$. The slope field on the blue curve indicates that the solution is trapped inside the “funnel”. The grey line shows the numerically computed solution (Color figure online)

For $\beta > > 1$, $\gamma_{0}$ is extremely close to $\gamma_{H}$; the gap between them is $\left( {13\beta } \right)^{ - 1/2}$. We also plot another curve $\gamma_{1}$ where the slope is -1. We plotted this curve to indicate that the exact solution is trapped between $\gamma_{H}$ where the slope is $+ \infty$ and the curve where the slope is negative such as $\gamma_{1}$.

Since the slope field for any curve above $\gamma_{0}$ is negative, the solution is attracted to $\gamma_{0}$. This means that the solution is slightly above $\gamma_{0}$ and $\gamma_{H}$ for $X \in \left( { - 1,1} \right)$- a very narrow region (see Fig. 2). In dynamical systems, such a region is called a funnel. The numerical solution is the grey line in Fig. 2.

A different approach is to treat the ODE Eq. (13) as a boundary layer problem, governed by the large parameter $\beta$. Figure 3b, c show the numerical pressure profile and the normalized fluid layer thickness $D \equiv H - W$ for $\beta = 100,500$. The normalized Hertz pressure, $P_{H} = 1 - X^{2}$ for $\left| X \right| \le 1$ is plotted in the same figure. Note that as $\beta$ increases, the pressure approaches the Hertz profile, consistent with slope field analysis.

Fig. 3

a Pressure profile for $\beta = 100$. Numerical result is given by the grey line, Hertz pressure by the red line, Eqs. (7), and the approximate solution (16) by the black line. b The gap between Hertz pressure and the numerical solution decreases with increasing $\beta$. c Normalized film thickness D versus position; the dotted line corresponds to Eq. (18) (Color figure online)

Note that D approaches zero and P approaches $P_{H}$ in $\Omega_{c} \subset \left( { - 1,1} \right)$ as $\beta$ increases. We will call $\Omega_{c}$ the contact zone even though there is no physical solid–solid contact due to the lubrication layer. Note that, since the pressure must be continuously differentiable everywhere, the convergence to the Hertz pressure cannot be uniform (the gradient of $P_{H}$ is discontinuous at $\left| X \right| = 1$). This means that there exist two internal boundary layers, one at the leading edge at X = 1, which we denote by $\Omega_{L}$, and the other $\Omega_{T}$, at the trailing edge at $X = - 1$ (see Figs. 3a or 2). Inside these boundary layers, the pressure gradient is continuous (see Fig. 3b). Outside these boundary layers and $\Omega_{c}$, i.e., $\left| X \right| \gg 1$, P goes to zero as (see derivation in SI, Section 3)

$$P \approx \frac{1}{{3\beta X^{3} }}.$$

(15)

Figure 3b shows that, for large $\beta$, the pressure profile inside the contact zone is well approximated by (see SI for a derivation, Section 3)

$$P = 1 - X^{2} + C\left( {1 + \frac{X}{5} + \frac{{3X^{2} }}{25} + ...} \right).$$

(16)

Equation (16) shows that the pressure inside the contact zone is always greater than the Hertz pressure for X > 0 and slightly above the nullcline [compare Eq. (16) with Eq. (14)], consistent with the slope field analysis. Figure 3a plots P versus X; the grey line is the numerical solution for $\beta = 100$, and the solid black line is (16). We also plot the Hertz pressure (red line) in Fig. 3a as a comparison. Clearly, the approximate solution, Eq. (16), is extremely accurate as long as X is inside the contact zone.

Note that the pressure distribution at the trailing edge is slightly negative. The maximum negative pressure, $P_{\min }$, occurs at $X_{\min } \simeq - 1 - \frac{0.397}{{\sqrt \beta }}$ and is well approximated by

$$P_{\min } = - \frac{B}{\sqrt \beta },$$

(17)

where $B = 0.611$ (see SI, Section 4). The existence of a region of negative pressure is frequent in lubrication problems [32]. For large negative pressure, the solution becomes unrealistic as the fluid often cavitates. However, cavitation is unlikely in our case since the maximum negative pressure goes to zero for large $\beta$ as indicated by Eq. (17).

The normalized film thickness $D$ inside the contact zone is given by Eq. (16) and $W = - P$, so

$$D \approx C\left( {1 + \frac{X}{5} + \frac{{3X^{2} }}{25} + ...} \right)\;\;\;C = \frac{1}{{\sqrt {13\beta } }},$$

(18)

in the contact zone and we assume that the minimum film thickness occurs at $X_{\min } = - 1$, so²

$$D_{\min } \approx \frac{1}{{\sqrt {13\beta } }}\left( {\frac{4}{5} + \frac{3}{25}} \right) \Rightarrow d_{\min } \approx \frac{{23\left| {h_{0} } \right|}}{{25\sqrt {13\beta } }}$$

(19)

Figure 3c shows that Eq. (18) is an excellent approximation for the film thickness inside the contact zone. The normalized friction force is calculated using Eqs. (11) and (18). In SI (Section 5), we show that it is very well approximated by:

$$\overline{F}_{f} = \frac{1.084}{{\sqrt \beta }} - \frac{0.3261}{\beta }\;\;\;\beta \ge 10.$$

(20)

Equations (19), (20) and (14) show that the maximum contact pressure, and friction force can be expressed in terms of minimum fluid layer thickness, the indentation depth and the compliance of the foundation; they are, for $\beta \ge 10$:

$$p_{\max } = \frac{{\left| {h_{0} } \right|}}{{c_{0} }}\left( {1 + \frac{25}{{23}}\frac{{d_{\min } }}{{\left| {h_{0} } \right|}}} \right),$$

(21)

$$F_{f} = \frac{{25\sqrt {13} d_{\min } }}{23}\frac{{\left| {h_{0} } \right|}}{{c_{0} }}\left[ {1.084 - 0.3261\left( {\frac{{25\sqrt {13} d_{\min } }}{{23\left| {h_{0} } \right|}}} \right)} \right] \approx \frac{{\left| {h_{0} } \right|^{2} }}{{c_{0} \sqrt \beta }} = \left( {2R\left| {h_{0} } \right|} \right)^{1/4} \sqrt {\frac{{6\eta V\left| {h_{0} } \right|}}{{c_{0} }}} .$$

(22)

Equation (22) shows that friction due to flow is directly proportional to fluid layer thickness and the indentation depth (which is independent of the radius of the cylinder). In addition, since the “effective” contact width is $a_{eff} \equiv \sqrt {2R \left| {h_{0} } \right|}$, the friction force is proportional to $a_{eff}^{3/2}$. Since the cylinder is infinite in the out-of-plane direction, $a_{eff}$ is also the effective area of contact per unit length of cylinder. In the SI Section 6, we give an expression for the thickness of the boundary layer near the exit. It turns out the friction force due to this boundary layer is small in comparison with the friction force given by (16), which ignores the effect of this layer.

Finally, the normal force N is related to $\left| {h_{0} } \right|$ by

$$\overline{N} \equiv \frac{{c_{0} N}}{{\left| {h_{0} } \right|\sqrt {2R\left| {h_{0} } \right|} }} = \frac{4}{3} + \frac{52}{{25\sqrt {13\beta } }}.$$

(23)

Combining Eqs. (22) and (23), we can express the friction as a function of the normal force,

$$F_{f} \approx \frac{3}{2}\sqrt {2\eta VN} .$$

(24)

Thus, in force control sliding where N is fixed, the friction force is independent of the radius of the indenter and the stiffness of the foundation. In contrast to Coulomb friction, the friction force is proportional to $\sqrt N$ and increases as the square root of the sliding velocity.

The average through thickness velocity $\overline{V}_{1}$ (relative to the moving frame) is obtained by integrating the velocity field

$$\overline{V}_{1} \equiv \frac{{v_{1} }}{V} = \left( {Y - H} \right)\left[ {6\beta P,_{X} \left( {Y - W} \right) + \frac{1}{D}} \right],$$

(25)

and dividing the result by D, i.e.,

$$\overline{V}_{1} \equiv \frac{{\overline{v}_{1} }}{V} \equiv \frac{1}{D}\int\limits_{W}^{H} {V_{1} } dY = - \beta P,_{X} D^{2} - 1/2$$

(26)

Using Eqs. (16) and (18), the leading order behavior of the average flow velocity inside the contact zone is

$$\overline{V}_{1} \left( {\left| X \right| < 1,\beta > > 1} \right) \approx \frac{2X}{{13}} - \frac{1}{2}.$$

(27)

The average flow (with respect to the cylinder) is approximately linear and is $- 9V/26$ at the leading edge $\left( {X = 1} \right)$ and $- 17V/26$ at the trailing edge $\left( {X = - 1} \right)$.

2.3.2 Dry Limit

Just as the Hertz limit provides an excellent approximation to the pressure distribution for the elastic foundation lubrication problem, the contact pressure of a rigid cylinder sliding on a non-lubricated and frictionless viscoelastic foundation turns out to be an excellent approximation to the viscoelastic contribution to friction. Note for this case $F_{f} = 0$ since the resistance to sliding is due entirely to viscoelastic dissipation. This is because we assume frictionless contact between the indenter and the surface of the viscoelastic foundation. For this case, the horizontal force resisting motion, denoted by $F_{vis}$, comes entirely from ploughing due to the asymmetry of the pressure distribution. This is illustrated schematically in Fig. 4. Thus, within the small contact approximation of Hertz

$$F_{vis} = - \int_{b}^{a} {p\frac{dw}{{dx}}dx} .$$

(28)

Fig. 4

Since the surface is frictionless, the traction acting on the indenter surface, $\sigma_{n}$ must be normal to the surface (red arrow). The horizontal component of this traction is $p\frac{dw}{{dx}}$ so $F_{vis}$ is given by Eq. (28) (Color figure online)

Note that Eq. (28) is identical to Eq. (12) except that the limits of integration are replaced by the position of the leading and trailing edges, which are denoted by a and b, respectively. These positions are well defined due to the absence of the fluid layer—the pressure field vanishes outside $\left[ {b,a} \right]$. At a and b, the pressure is exactly zero. The solution of the “dry” problem can be obtained in closed form. Details are given in the SI, Section 7. Here we summarize the key results, they are:

• 1. The solution depends only on two dimensionless parameters,$\alpha$ and $c_{\infty } /c_{0}$.

• 2. The normalized positions of the leading and trailing edges are, respectively

  $$\overline{a} = a/\sqrt {2R\left| {h_{0} } \right|} = 1,\;\;\;\frac{2}{{\lambda^{2} }}\frac{{\left( {\lambda \overline{b} + 1} \right) - e^{{ - \lambda \left( {1 - \overline{b}} \right)}} \left( {\lambda + 1} \right)}}{{\left( {1 - \overline{b}^{2} } \right)}} = - \frac{{c_{0} }}{{c_{\infty } }}\left( {1 - \frac{{c_{0} }}{{c_{\infty } }}} \right)^{ - 1} ,$$

  (29)
  $$\lambda \equiv \frac{{c_{\infty } \alpha }}{{c_{0} }} = \frac{{\sqrt {2R\left| {h_{0} } \right|} }}{{V\left[ {c_{0} t_{0} /c_{\infty } } \right]}}.$$

  (30)

  The position of the leading edge given by the first expression of Eq. (29) is exact and independent of velocity, while Eq. (29) is a transcendental equation for the normalized position of the trailing edge $\overline{b}$. In general, $- 1 < \overline{b} < 0.$ Note $\overline{b} \to - 1$ as $c_{0} /c_{\infty } \to 1$, recovering the Hertz solution for a spring foundation. The asymptotic solution of $\overline{b}$ for the cases of $\lambda > > 1$ and $0 < \lambda < < 1$ is given in the SI, Section 8.

• 3. The normalized pressure distribution inside the contact zone $\left[ {\overline{b},1} \right]$ is

  $$P\left( X \right) = \left[ {\left( {1 - \frac{{c_{0} }}{{c_{\infty } }}} \right)\frac{2}{{\lambda^{2} }}\left[ {\left( {\lambda X + 1} \right) - e^{ - \lambda } e^{\lambda X} \left( {\lambda + 1} \right)} \right] + \frac{{c_{0} }}{{c_{\infty } }}\left[ {1 - X^{2} } \right]} \right],\;\;\;\lambda \equiv \frac{{c_{\infty } \alpha }}{{c_{0} }}.$$

  (31)

  It is easy to verify that pressure profile given by Eq. (31) approaches the Hertz profile $P_{H}$ when $c_{0} /c_{\infty } \to 1$.

• 4. The normalized “ploughing” force is

  $$\overline{F}_{vis} = \left( {\frac{1}{2} - \overline{b}^{2} \left[ {1 - \frac{{\overline{b}^{2} }}{2}} \right]} \right)\frac{{c_{0} }}{{c_{\infty } }} + \frac{4}{{\lambda^{2} }}\left( {1 - \frac{{c_{0} }}{{c_{\infty } }}} \right)\left\{ {\frac{\lambda }{3}\left( {1 - \overline{b}^{3} } \right) + \frac{{\left( {1 - \overline{b}^{2} } \right)}}{2} - \frac{{\left( {\lambda + 1} \right)}}{{\lambda^{2} }}\left[ {\left( {\lambda - 1} \right) - \left( {\lambda \overline{b} - 1} \right)e^{{ - \lambda \left( {1 - \overline{b}} \right)}} } \right]} \right\}.$$

  (32)

  Equation (28) implies that $\overline{F}_{vis}$ is the area of the hysteresis loop experience by a material point after it enters the leading edge. In the next section, we will compare the “dry” solution with the full solution of the lubricated viscoelastic sliding problem.

• 5. The normal force acting on the cylinder,

  $$N = \left( {\left| {h_{0} } \right|\sqrt {2R\left| {h_{0} } \right|} /c_{0} } \right)\overline{N}\;{\text{where}}\;\;\overline{N} = \int\limits_{{\overline{b}}}^{1} {Pd\xi } ,$$

  (33)

  is the normalized normal force. Using Eq. (31), it is

  $$\overline{N} = \frac{2}{{\lambda^{2} }}\left( {1 - \frac{{c_{0} }}{{c_{\infty } }}} \right)\left[ {\left( {1 - \overline{b}} \right)\left( {1 + \frac{\lambda }{2} + \frac{\lambda }{2}\overline{b}} \right) - \frac{{\left( {1 + \lambda } \right)}}{\lambda }\left( {1 - e^{{ - \lambda + \lambda \overline{b}}} } \right)} \right] + \frac{{c_{0} }}{{c_{\infty } }}\left( {\frac{2}{3} - \overline{b} + \frac{1}{3}\overline{b}^{3} } \right).$$

  (34)

An important observation is that only λ (instead of α) appears in Eqs. (29–34). This suggests that the relevant time scale is $t_{R} \equiv c_{0} t_{0} /c_{\infty }$ [see Eq. (30)] which is the characteristic relaxation time in a relaxation tension test. Hence, the dimensionless parameter $\lambda = c_{\infty } \alpha /c_{0}$ is the time for the indenter to move one contact zone divided by $t_{R}$. For $\lambda \gg 1$, the foundation is fully relaxed with compliance $c_{\infty }$. For $\lambda \ll 1$, the foundation behaves as a stiff elastic foundation with compliance $c_{0}$. Since the transition from soft to stiff occurs at $\lambda \approx 1$, one expects maximum dissipation to occur at $\lambda \approx 1$ (see Fig. 5 below).

Fig. 5

Normalized pressure versus normalized displacement for a viscoelastic foundation with $c_{\infty } /c_{0} = 100$ and $\beta = 10$. $\overline{F}_{vis}$ is the area enclosed by each curve. Note for large and small $\lambda$ this area is zero as loading and unloading coincides

2.4 Numerical and Approximate Solution of the Viscoelastic Lubrication Problem

The integro-differential Eq. (9) are solved numerically for a foundation that obeys Eq. (10). Details of the numerical method are provided in the SI, Section 9. Figure 5 plots the hysteresis loop for a material point as it moves from $x = \infty$ to $x = - \infty$. The area of the hysteresis loop is $\overline{F}_{vis}$ defined by Eq. (12). In Fig. 5, we vary $\lambda$ while keeping $c_{\infty } /c_{0}$ and $\beta$ fixed at 100 and 10, respectively. As expected, the loading and unloading curves lie on top of each other for small and large $\lambda$ indicating that the foundation behaves like an elastic solid with compliances $c_{0}$ and $c_{\infty }$, respectively. Figure 5 also confirms our expectation that maximum energy dissipation occurs at $\lambda \approx 1$.

Figure 6 plots the pressure distribution for different values of $\beta$ and $\lambda$ with $c_{\infty } /c_{0} = 100$. The dry solution Eq. (31) (dotted line) is plotted in the same figure as a comparison. It is seen that for large $\beta$, there is very little difference between the dry and the lubricated solutions. Indeed, as long as $\beta > 20$, the agreement between the dry solution and the full lubrication solution is independent of $\lambda$ and $c_{\infty } /c_{0}$).

Fig. 6

Comparison of the normalized pressure of the viscoelastic lubrication problem with dry friction solution, $c_{\infty } /c_{0} = 100$, $\beta = 10 - 100$ are same for (a–c) while $\lambda$ is different. a $\lambda = 0.1$, b $\lambda = 1$, c $\lambda = 10$

Figure 7 compares $\overline{F}_{vis}$ obtained by solving the full lubrication problem with the “dry” analytical solution given by Eq. (32). Figure 7 shows that Eq. (32) is an excellent approximation for $\beta \gg 1$.

Fig. 7

Numerical solution of $\overline{F}_{vis}$ versus $\lambda$ for β = 10, 50 and 100. The dry analytical solution given by Eq. (32) is the solid black line

The asymmetry of the pressure distribution is reflected in $\overline{b}$, the position of the trailing edge. Numerical results of $\overline{b}$ versus $\lambda$ are presented in Fig. 8. The dry solution Eq. (29) corresponds to the limit where $\beta \to \infty$ (solid black line). As shown in Fig. 8, the dry solution provides a reasonable approximation to $\overline{b}$ for $\beta > 10$. The approximation is especially good where viscoelasticity is significant, that is, for $0.1 \le \lambda \le 10$. In this regime, $\beta \ge 10$ is sufficient to ensure excellent agreement between the full and dry solution.

Fig. 8

Numerical results for $\overline{b}$ versus $\lambda$ for $\beta = 10,50$ and 100 and $c_{\infty } /c_{0} = 100$ The dry solution is the solid black line, Eq. (29)

Next, we plot the normalized hydrodynamic friction $\overline{F}_{f}$ against $\lambda$ in Fig. 9. We also plot $\overline{F}_{vis}$ in the same plot as a comparison. Figure 9 shows that the maximum friction force due to both mechanisms are comparable for $c_{\infty } /c_{0} = 100$. The maximum friction due to viscoelastic dissipation occurs at $\lambda \approx 1$. Although the maximum of the hydrodynamic friction occurs at $\lambda = 0$, there is a wide range of $\lambda$ where $\overline{F}_{f}$ deviates little from its maximum.

Fig. 9

Comparison of hydrodynamic friction and friction due to viscoelastic dissipation for different values of $\beta$, with $c_{\infty } /c_{0} = 100$

2.4.1 Approximate Expressions for D and $\overline{F}_{f}$

In the section above, we have demonstrated that the dry solution provides an excellent approximation for $\overline{F}_{vis}$. Here we highlight an approximate method that combines the dry and the elastic lubrication solution to find the film thickness D and $\overline{F}_{f}$ for the full lubrication solution. The basic idea is that scaling analysis implies that for large $\beta$, C in Eq. (9) has the form:

$$C = \frac{{\rho \left( {\lambda ,c_{0} /c_{\infty } } \right)}}{\sqrt \beta }.$$

(35)

Recall that for an elastic substrate, $\rho$ is a numerical constant. Substituting Eq. (35) into Eq. (9) and making the transformation $D = C\hat{D}$, (9) becomes:

$$\rho^{2} P,_{X} = - \frac{1}{{\hat{D}^{2} }} + \frac{1}{{\hat{D}^{3} }}$$

(36)

Next, we note that, within the contact zone, $P,_{X}$ in Eq. (36) is well approximated by the dry solution and can be computed using Eq. (31). Since Eq. (36) is a cubic in $z \equiv 1/\hat{D}$, it can be solved in closed form. Since the algebra is quite messy, the solution is given in the SI. Once D is found, $\overline{F}_{f}$ can be evaluated using Eqs. (11) and (31). The only unknown in this procedure is $\rho$ which depends on $\lambda$ and $c_{0} /c_{\infty }$. Since small and large values of $\lambda$ correspond to an elastic foundation with compliance $c_{0}$ and $c_{\infty }$ , respectively,

$$\rho \left( {\lambda \to 0,\frac{{c_{0} }}{{c_{\infty } }}} \right) = \frac{1}{{\sqrt {13} }}, \, \rho \left( {\lambda \to \infty ,\frac{{c_{0} }}{{c_{\infty } }}} \right) = \frac{1}{{\sqrt {13} }}\sqrt {\frac{{c_{\infty } }}{{c_{0} }}} .$$

(37)

Also, $\rho \left( {\lambda ,c_{0} /c_{\infty } = 1} \right) = 1/\sqrt {13}$. A plot of C versus λ for $c_{\infty } /c_{0} = 100$ is shown in Fig. 10. The symbols are numerical results and the grey curves are obtained using the approximation:

$$C = \frac{1}{{\sqrt {13\beta^{*} } }} + \frac{0.03}{{\beta^{*} }}\;\;{\text{where}}\;\;\beta^{*} \equiv \beta c_{0} \left[ {\kappa k\left( {\omega_{1} \lambda } \right) + \left( {1 - \kappa } \right)k\left( {\omega_{2} \lambda } \right)} \right],$$

(38)

where $k\left( {t/t_{R} } \right) = \left( {1/c_{\infty } } \right) + \left[ {\left( {1/c_{0} } \right) - \left( {1/c_{\infty } } \right)} \right]e^{{ - t/t_{R} }}$ is the relaxation modulus, $\kappa = 0.15$; $\omega_{1} = 0.025$ and $\omega_{2} = 0.25$. Comparing Eqs. (38) with (35), we find

$$\rho = \left( {c_{0} \sqrt {13} } \right)^{ - 1} \left[ {\kappa k\left( {\omega_{1} \lambda } \right) + \left( {1 - \kappa } \right)k\left( {\omega_{2} \lambda } \right)} \right]^{ - 1} .$$

(39)

The approximation Eq. (38) is based on the simple idea that $\beta$ is proportional to the foundation stiffness $1/c_{0}$. In the viscoelastic problem the stiffness of the foundation is a function of position, hence we replace $1/c_{0}$ by the relaxation modulus $k\left( {t/t_{R} } \right)$ evaluated at $t/t_{R} = \omega \lambda$, where $\omega$ is a numerical factor of order one to account for the fact that a material point experiences different stiffness during sliding. Figure 11a plots the spatial distribution of normalized film thickness D for $\beta = 10,\;50,\;100$ and $c_{\infty } /c_{0} = 100$. The asymptotic solution obtained by solving the cubic Eq. (36) is plotted in the same figure as dashed lines. There is good agreement between the asymptotic and the numerical solution. Figure 11b plots the hydrodynamic friction $\overline{F}_{f}$ versus $\lambda$ for $\beta = 10,50,100$ and $c_{\infty } /c_{0} = 100$. The asymptotic solutions [by solving D from cubic and using Eq. (11)] are plotted as solid lines. Again, there is very good agreement between the asymptotic solution and the numerical result.

Fig. 10

Numerical results of C versus $\beta$ for different values of $\lambda$ (symbols). The grey lines are obtained using Eq. (39)

Fig. 11

a Comparison of the full lubrication solution and approximate expression for the film thickness [by solving Eq. (36)]. b Comparison of hydrodynamic friction obtained by numerical method and asymptotic solution. Results are for three normalized sliding velocities with $c_{\infty } /c_{0} = 100$

3 Friction Coefficient

Since friction is split into $F_{f}$ and $F_{vis}$, we define two friction coefficients:

$$\mu_{f} \equiv \frac{{F_{f} }}{N} = \sqrt {\frac{{\left| {h_{0} } \right|}}{2R}} \frac{{\overline{F}_{f} }}{{\overline{N}}},\;\;\mu_{vis} \equiv \frac{{F_{vis} }}{N} = \sqrt {\frac{{\left| {h_{0} } \right|}}{2R}} \frac{{\overline{F}_{vis} }}{N},$$

(40)

with

$$\mu_{\text{total}} = \mu_{f} + \mu_{vis} = \sqrt {\frac{{\left| {h_{0} } \right|}}{2R}} \frac{{\overline{F}_{f} + \overline{F}_{vis} }}{{\overline{N}}}.$$

(41)

The factor $\sqrt {\left| {h_{0} } \right|/2R}$ in Eqs. (40, 41) appears due to different normalization for the friction and normal forces [see Eqs. (11) and (33)]. The normal load $N$ in Eqs. (40, 41) is obtained by integrating the hydrodynamic pressure over the whole domain:

$$N = \frac{{\left| {h_{0} } \right|\sqrt {2R\left| {h_{0} } \right|} }}{{c_{0} }}\int_{ - \infty }^{\infty } {Pd\xi } \equiv \frac{{\left| {h_{0} } \right|\sqrt {2R\left| {h_{0} } \right|} }}{{c_{0} }}\overline{N}$$

(42)

The dry friction solution serves as a lower bound for the normal load as shown in Fig. 12. Similar to $\overline{b}$, the dry solution is very accurate where viscoelasticity is relevant, $0.1 \le \lambda \le 10$. Figure 13a–c plot the friction coefficients $\mu_{vis}$, $\mu_{f}$ and $\mu_{total}$ against $\lambda$ for different $\beta$. For convenience, the vertical axis is multiplied by $2R/\sqrt {\left| {h_{0} } \right|}$. Since the area of contact is proportional to $\sqrt {\left| {h_{0} } \right|}$ and both $\overline{F}_{vis} /\overline{N}$ and $\overline{F}_{f} /\overline{N}$ depend on $\sqrt {\left| {h_{0} } \right|}$ through the parameters $\lambda$ and $\beta$. These friction coefficients in general depend on the area of contact and hence friction does not obey the Coulomb model. Interestingly, the maximum friction coefficient for both mechanisms occurs at λ between 10 and 100. Note that, when $\lambda < 1$, the friction coefficient due to hydrodynamic flow $\left( {\mu_{f} } \right)$ increases linearly with area (recall $\lambda \propto \sqrt {\left| {h_{0} } \right|}$), which suggests that fatter tires have higher friction for the same normal force. Figure 13a shows that, for $1 < \lambda < 10^{2}$, $\mu_{f}$ increases faster than the area of contact since $\mu_{f}$ increases with $\lambda$ in this range. It is interesting to note that the maximum friction coefficient does not occur at $\lambda \approx 1$, instead, it occurs near $\lambda = \lambda_{peak} \approx 50$.

Fig. 12

$\overline{N}$ versus $\lambda$ for the dry case ($c_{\infty } /c_{0}$, $\beta = \infty$) and the viscoelastic hydrodynamic lubrication cases ($c_{\infty } /c_{0}$, $\beta = 10 - 100$)

Fig. 13

Friction coefficient components from: a the hydrodynamic part $\mu_{f}$; b the part of substrate viscoelasticity $\mu_{vis}$, c the total frictional coefficient $\mu_{total}$ versus different $\lambda$. $c_{\infty } /c_{0} = 100$ and $\beta = 10\sim 100$. The dry friction case corresponds to $c_{\infty } /c_{0} = 100$ and $\beta = \infty$

A convenient way of presenting results for an elastic substrate is to plot the Stribeck curve, that is, the friction coefficient against the Hersey number. Note, even for an elastic substrate, the solution of our problem cannot be expressed solely in terms of the Hersey number. Indeed, as shown above and by others [3, 30, 35], friction depends on the single parameter $\beta$, which one can view as a generalized Hersey number. For viscoelastic substrates, the friction coefficient depends on three dimensional parameters,$\beta ,\lambda ,c_{0} /c_{\infty }$. This means that the generalization of the Stribeck curve is a surface in four-dimensional space. Here we present a slice of this surface by fixing $c_{0} /c_{\infty }$ to be 100, and plot the friction coefficient $\mu_{total}$ against $\beta$ and $\lambda$. These results are shown in Fig. 14. In Fig. 14a, we plotted the special case where $c_{0} /c_{\infty } = 1$, which corresponds to an elastic substrate, as a reference. Clearly, in all cases viscoelasticity enhances friction. More interesting, the friction coefficient varies slowly for a fixed $\lambda$.

Fig. 14

The generalized Stribeck surface: a total friction coefficient $\mu_{total}$ as a function of $\beta$ and $\lambda$ with $c_{0} /c_{\infty } = 100$; b–c friction coefficient component $\mu_{f}$ and $\mu_{vis}$

4 Discussion and Summary

We have used a 1D model to study lubricated sliding on a viscoelastic substrate with focus on the large $\beta$ regime. Three dimensionless parameters are needed to determine the solution despite the simplicity of our model. Although the underlying physics are the same, 1D models are much easier to solve numerically. In 2D or 3D, numerical calculations are much more difficult even for elastic substrates. In addition to numerical difficulties, the large number of parameters requires many calculations and impedes understanding of the basic physics. Our analysis suggests an approach that can alleviate these difficulties. A key result is that many features of the full viscoelastic lubrication problem can be obtained by combining the solution of two simpler problems. The first is to replace the viscoelastic substrate by an elastic substrate; the second is the solution of dry (no lubricant) problem with a viscoelastic substrate. One simply solves the dry problem to find the pressure field and the friction force due to viscoelastic dissipation. In the large β regime, this “dry” pressure field and corresponding viscoelastic friction differ little from the pressure and friction of the full viscoelastic lubrication problem. The thickness of the lubrication layer can be obtained using perturbation theory using the dry pressure and this allows one to compute the hydrodynamic friction force without solving the full viscoelastic lubrication problem. We expect these insights are applicable to lubrication problems with more complex geometries such as such as sphere or ellipsoid.

In summary, we have accomplished the following:

• A detailed analysis of the elastic lubrication problem in the Hertz regime (large β). Accurate expressions for the hydrodynamic friction and film thickness are provided.

• A detailed analysis of the dry viscoelastic sliding contact problem. Accurate expressions for friction caused by viscoelastic dissipation are provided for a standard solid. Furthermore, the dry problem can be solved exactly (within quadrature) for any relaxation function.

• A detailed numerical study of the full viscoelastic lubrication problem in the large β regime. We demonstrated that many features of these numerical solutions can be obtained using the solutions of the first two problems.