Dynamics of a viscoelastic cylinder on a viscoelastic half-space

Abstract

The deceleration of a viscoelastic cylinder rolling with slipping on a viscoelastic half-space of the same material without driving forces and torques is studied. The interaction of the cylinder and the half-space is described from the solution of the 2D quasistatic contact problem of viscoelasticity (Goryacheva in J Appl Math Mech 37(5):877–885, 1973, Contact mechanics in tribology, Kluwer, Dordrecht, 1998). This solution states that the contact region consists of the slip and stick zones, and it is shifted forward in the direction of motion. Contact normal and shear stresses and, therefore, the resultant force and torque depend on the values of the linear velocity of the cylinder and creep ratio, as well as the mechanical properties of contacting bodies and sliding friction coefficient. The Cauchy problem for dynamical equations of the cylinder’s deceleration was solved numerically. The analysis of the deceleration process and changes in the contact normal and shear stress distributions in time for various initial conditions is presented.

1 Introduction

Accurate dynamical simulations of the systems with frictional contacts require adequate models of the forces and torques. Multibody dynamics involves the simulation of the systems consisting of rigid bodies connected by the joints and including constraints, and the accurate modeling of the contact interaction is of great importance [3]. The classical approach suggests a point-contact model for convex rigid bodies together with Coulomb’s law: It gives non-smooth systems [4,5,6,7]. For complex friction-induced dynamics (such as slip–stick oscillations), phenomenological models involving relative velocity are used [8, 9].

The Hertzian solution of the static problem on the contact interaction between two convex elastic bodies [10] gives rise to the Contensou-type dry friction models including a non-point-contact area [11,12,13,14,15]. These models exhibit the decrease in sliding friction force due to the relative spinning of the bodies that influences the dynamics of the systems [16, 17].

Phenomenological models of the deformable base as a 1D viscoelastic foundation started from [18] and developed in [19,20,21,22,23,24] were used to study the dynamics of a horizontal cylinder (or a sphere) that rolls and slides along a viscoelastic foundation. Similar models are used also for the analysis of multibody systems including cylinder–soil interaction [25]. The dynamics of the bodies was governed by ordinary differential equations, and the parametric analysis of the obtained solutions has been made. However, the use of the 1D models for the description of the foundation deformation is a strong simplification that causes qualitative distortion in the reaction force and torque in some areas of the phase space, especially for small creep ratios.

Coupling of the solutions of continuum mechanics contact problems with dynamics of the bodies is essential from a practical point of view and requires exhaustive numerical calculations [26, 27].

The attempts to use the exact solutions of the quasistatic contact problems for an elastic cylinder rolling with partial slip over an elastic half-space of the same material [28] and for a rigid cylinder sliding over the viscoelastic half-space [1, 2] in formulation and analysis of the dynamics of deceleration of the cylinder were made in [29, 30].

Here, we study the dynamics of a viscoelastic cylinder rolling with slipping on a viscoelastic half-space of the same material without driving forces and torques. The interaction of the cylinder and the supporting half-space is modeled by the solution of the 2D quasistatic problem of viscoelasticity, taking into account conditions of the partial slip within the contact region [1, 2]. The numerical solution of the Cauchy problem for dynamical equations taking into account the velocity-dependent stress distribution within the contact region describes the deceleration process and the contact characteristics evolution.

2 Problem formulation

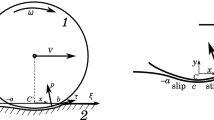
Consider a plane-parallel motion of a viscoelastic homogeneous cylinder 1 with mass m per unit length and radius R (Fig. 1) along a viscoelastic half-space 2 of the same material.

We introduce a fixed reference system $O\xi \eta \zeta$: The axis $O\xi$ belongs to the non-deformed boundary of the half-space, which is horizontal, $O\eta$ is directed vertically upwards, and $O\zeta$ is perpendicular to the plane of motion and is aligned with the axis of the cylinder. We denote the horizontal velocity of the cylinder’s center C by $\varvec{V} = V\varvec{e}_\xi$ and the angular velocity by $\varvec{\omega } = -\omega \varvec{e}_\zeta$. The positive value of $\omega$ corresponds to the clockwise rotation if viewed from the end of the $O\zeta$ axis (Fig.  1).

Fig. 1

Scheme of the contact

We assume that the velocity of the axis of the cylinder V and scaled angular velocity $\omega R$ are small compared to the wave propagation speeds in a viscoelastic body. In this assumption, according to the solution [31] of a similar problem about the dynamic frictional contact between an elastic foundation and a rigid sliding cylindrical punch, the full normal load and contact stresses are close to the equilibrium values. Therefore, for the modeling of the interaction between the cylinder and the half-space, we use the viscoelastic contact problem in a 2D quasistatic formulation [1, 2].

The relations between the strain and stress components in an isotropic viscoelastic body are taken in the following form (the case of plane strain):

$$\begin{aligned} \begin{aligned} \varepsilon _\xi + T_\varepsilon \dfrac{\partial \varepsilon _\xi }{\partial t}&= \frac{1-\nu ^2}{E}\left( \sigma _\xi + T_\sigma \dfrac{\partial \sigma _\xi }{\partial t}\right) - \frac{\nu (1+\nu )}{E}\left( \sigma _\eta + T_\sigma \dfrac{\partial \sigma _\eta }{\partial t}\right) , \\ \varepsilon _\eta + T_\varepsilon \dfrac{\partial \varepsilon _\eta }{\partial t}&= \frac{1-\nu ^2}{E}\left( \sigma _\eta + T_\sigma \dfrac{\partial \sigma _\eta }{\partial t}\right) -\frac{\nu (1+\nu )}{E}\left( \sigma _\xi + T_\sigma \dfrac{\partial \sigma _\xi }{\partial t}\right) , \\ \gamma _{\xi \eta } + T_\varepsilon \dfrac{\partial \gamma _{\xi \eta }}{\partial t}&= \frac{1+\nu }{E}\left( \tau _{\xi \eta } + T_\sigma \dfrac{\partial \tau _{\xi \eta }}{\partial t}\right) . \end{aligned} \end{aligned}$$

The values of $T_\varepsilon$ and $T_\sigma$ characterize the viscous properties of the body ($T_\varepsilon > T_\sigma$), E is Young’s modulus, and $\nu$ is Poisson’s ratio. The case of plane stress is considered similarly.

We introduce a moving Cartesian coordinate system $C'xyz$ with axes parallel to $O\xi \eta \zeta$ with the origin at the point $C'$ that is a projection of the cylinder’s axis onto the supporting plane (Fig. 1).

2.1 Contact conditions

Due to the assumption of small deformations, the non-deformed cylinder contour in the contact area is assumed to be parabolic: $y = f(x) = x^2/(2R)$. We assign the boundary conditions on the surface of the viscoelastic half-plane to the undeformed boundary ($y = 0$). The contact condition states that for all points of the contact area $x\in (-a,b)$ for displacements $u_y$ normal to the surface ($y=0$) the relation $u_y = f(x) + \mathrm {const}$ holds, so

$$\begin{aligned} \dfrac{\partial u_{y}}{\partial x} = \frac{x}{R},\quad y=0. \end{aligned}$$

The surfaces of the interacting bodies outside the contact area $(-a, b)$ are unloaded. We denote the contact pressure by

$$\begin{aligned} p(x) = -\sigma _y(x,0)>0. \end{aligned}$$

An equilibrium condition should be satisfied,

$$\begin{aligned} P = \iint \limits _{\varSigma } p(x)\,dx. \end{aligned}$$

Here, P is a full external vertical load that acts on the cylinder.

The contact region $x\in (-a,b)$ consists of stick and slip zones. For the same materials of the cylinder and the half-space, it was shown in [2] that there is one sticking $x\in (c,b)$ and one slipping $x\in (-a,c)$ area within the contact region, and the stick zone is located in the front side of the cylinder.

In the sticking area $x\in (c,b)$ the velocities of tangential displacement of contacting points of the cylinder and of the half-space are equal, so

$$\begin{aligned} V - \omega R + \dfrac{\partial u_{\xi 1}}{\partial t} = \dfrac{\partial u_{\xi 2}}{\partial t}. \end{aligned}$$

Shear and normal stresses relate as follows: $|\tau _{xy}| < \mu p(x)$. Here, $\mu$ is a friction coefficient.

In the slip zone $(-a, c)$, the normal and shear stresses satisfy the Amonton–Coulomb law:

$$\begin{aligned} \tau _{xy} = -\mu p(x) \mathrm {sgn} s_x. \end{aligned}$$

Here, $s_x$ is the difference between the velocities of tangential displacements of the points of the cylinder and the half-space on the boundary:

$$\begin{aligned} s_x = \dfrac{\partial u_{\xi _2}}{\partial t} - \dfrac{\partial u_{\xi _1}}{\partial t} - V + \omega R. \end{aligned}$$

The method of solving this contact problem is given in [2]. In Sect. 3, we give the necessary details of the solution.

2.2 Dynamical equations

The contact pressure p(x) and shear stresses $\tau _{xy}(x)$ act on each infinitesimal area element $\hbox {d}\varSigma$ of the contact area. So, the infinitesimal force on $\hbox {d}\varSigma$ is

$$\begin{aligned} \varvec{dF} = p(x)\, \hbox {d}\varSigma \,\varvec{n} + \tau _{xy}(x)\, \hbox {d}\varSigma \, \varvec{t} \end{aligned}$$

(1)

where $\varvec{n}$, $\varvec{t}$ are normal and tangent unit vectors to $\hbox {d}\varSigma$. The resultant force is

$$\begin{aligned} \varvec{F} = F_\xi \varvec{e}_\xi + F_\eta \varvec{e}_\eta \text { where } F_\xi = \iint \limits _{\varSigma } (\varvec{e}_\xi ,\,\varvec{dF}),\quad F_\eta = \iint \limits _{\varSigma } (\varvec{e}_\eta ,\,\varvec{dF}). \end{aligned}$$

The torque with respect to the cylinder’s axis is directed along $C\zeta$-axis. We denote its component by

$$\begin{aligned} M_\zeta = \iint \limits _{\varSigma } (\varvec{e}_\zeta ,[\varvec{r}\times \varvec{dF}]) \end{aligned}$$

where $\varvec{r}$ goes from C to $\hbox {d}\varSigma$. Besides, the gravity force $-mg\varvec{e}_\eta$ acts on the cylinder.

So the dynamical equations governing the motion of the cylinder are

$$\begin{aligned} ma_\eta&= F_\eta -mg, \end{aligned}$$

(2)

$$\begin{aligned} m{\dot{V}}&= F_\xi ,\quad J{\dot{\omega }} = -M_\zeta , \end{aligned}$$

(3)

where a dot denotes the derivative with respect to time.

Due to the viscoelastic properties of the materials, the height of the cylinder axis depends on its velocity: The lifting force decreases by deceleration, and the cylinder slowly sinks. However, in [31, Table 1] it is shown that for slow motions the normal load slightly differs from the equilibrium values: The relative deviation is within 10 % for the velocities V less than 20 % of the wave propagation speeds. Therefore, we will neglect this difference between static and dynamical load and assume that in Eq. (2) we have $a_\eta = 0$, and therefore, $F_\eta = mg$.

Friction force $F_\xi$ and the torque $M_\zeta$ in Eqs. (3) are functions of V and $\omega$ which are defined by the quasistatic solution of the contact problem. Thus, Eqs. (3) are closed with respect to the variables V, $\omega$. In this study, we analyze the Cauchy problem for Eqs. (3) with arbitrary initial conditions $V(0),\ \omega (0)$.

3 The contact problem analysis

3.1 The main dimensionless parameters and variables

It was shown [2] that the quasistatic viscoelastic contact problem is governed by two dimensionless parameters:

$$\begin{aligned} \alpha = \frac{T_\varepsilon }{T_\sigma }, \quad \kappa = \frac{R}{l_0} = \sqrt{\frac{E' R}{32 P}} \quad \left( E' = \frac{\pi E}{1-\nu ^2}\right) . \end{aligned}$$

Here, $\alpha \in [1,+\infty )$ is the ratio of the retardation to the relaxation times, and it is equal to unity for elastic materials; $\kappa$ is the ratio of the cylinder radius to the length $l_0= \sqrt{32 RP / E'}$ of the contact region at rest. Since the statement of the viscoelasticity problem assumes that the contact region is small compared to the cylinder radius [2], so $\kappa \gg 1$. Besides, the dynamical equations involve a third dimensionless parameter,

$$\begin{aligned} \gamma = \frac{PT_\varepsilon ^2}{mR}. \end{aligned}$$

(4)

It sets the ratio of the “dynamic” timescale, which is specified by the normal load and the cylinder radius, and the retardation time $T_\varepsilon$.

We introduce also the following dimensionless variables:

$$\begin{aligned} {\tilde{V}} = T_\varepsilon V/R,\quad {\tilde{\omega }} = T_\varepsilon \omega . \end{aligned}$$

Besides, we denote by

$$\begin{aligned} \delta = \frac{\omega R - V}{V} = \frac{{\tilde{\omega }}- {\tilde{V}}}{{\tilde{V}}} \end{aligned}$$

(5)

the creep ratio of the cylinder.

3.2 Equations determining the contact region and slip zone locations

The solution of the contact problem for a viscoelastic cylinder rolling over a viscoelastic half-space (stated in Sect. 2.1) is obtained in [2]. For $V>0$ and $\delta >0$, the dimensionless length of the contact area

$$\begin{aligned} \lambda = \frac{a+b}{l_0} = \kappa \frac{l}{R} \end{aligned}$$

is a (unique) solution of the equation

$$\begin{aligned} \begin{aligned}&\left[ 1-\lambda ^2\right] [I_0(\alpha \zeta ) K_1(\zeta ) + K_0(\zeta )I_1(\alpha \zeta )] + \frac{2}{\zeta }\left( \frac{1}{\alpha } - 1\right) \lambda ^2I_1(\alpha \zeta )K_1(\zeta ) = 0. \end{aligned} \end{aligned}$$

(6)

Here,

$$\begin{aligned} \zeta = \dfrac{a+b}{2 T_\varepsilon V} = \frac{\lambda }{2\kappa {\tilde{V}}} \end{aligned}$$

(7)

is the ratio of time per which each element travels a distance equal to the half width of the contact area to the retardation time $T_\varepsilon$; $I_0(x)$, $I_1(x)$, $K_0(x)$, and $K_1(x)$ are modified Bessel functions [32].

The dimensionless relative displacement of the contact area with respect to the axis $C'y$ is

$$\begin{aligned} \varepsilon = \frac{b-a}{b+a} = \frac{1}{2}\left( \lambda ^{-2}-1\right) \frac{K_0(\zeta )}{K_1(\zeta )}. \end{aligned}$$

(8)

The contact region consists of the slip zone $x\in (-a,c)$ and the stick zone $x\in (c,b)$. The parameter

$$\begin{aligned} \beta = \frac{b-c}{b+a} \end{aligned}$$

is a relative length of the stick zone.

If the following condition holds:

$$\begin{aligned} \delta <\delta _\alpha ^*({\tilde{V}}) = \frac{\mu \lambda (1+\varepsilon )}{2\kappa }, \end{aligned}$$

(9)

then there exists a (unique) solution $\beta$ of the equation:

$$\begin{aligned} \begin{aligned}&\left( 1+\varepsilon - \beta - \frac{2\delta \kappa }{\mu \lambda }\right) [I_0(\alpha \beta \zeta )K_1(\beta \zeta ) + I_1(\alpha \beta \zeta )K_0(\beta \zeta )] \\&\quad + \frac{1}{\zeta }\left( \frac{1}{\alpha }- 1\right) I_1(\alpha \beta \zeta )K_0(\beta \zeta ) = 0, \end{aligned} \end{aligned}$$

(10)

and, hence, the stick zone exists.

If Condition (9) is violated, then the cylinder moves along the half-space with full slip $c=b$. (The proof of this statement is given in the “Appendix.”) Figure 2 shows the dependence of the critical value $\delta _\alpha ^*$ on the dimensionless velocity ${\tilde{V}}$ for different values of $\alpha$: It decreases if ${\tilde{V}}$ or $\alpha$ grows. ($\delta ^*_\alpha$ is calculated for $\mu = 0.2$, $\kappa = 29.1$.)

Fig. 2

The dependence of $\delta _\alpha ^*({\tilde{V}})$ for $\alpha = 1;\,1.5;\,21.5;\,81.5$. Parameters $\mu = 0.2$, $\kappa = 29.1$

3.3 Pressure and shear stress distributions

The contact pressure inside the contact region is calculated from the following expression:

$$\begin{aligned} \frac{p({\tilde{x}})}{E'}= & {} -\frac{\alpha }{2\pi \kappa ^2{\tilde{V}}} \int \limits _{-{\tilde{a}}}^{{\tilde{x}}} \frac{\lambda ^2 + 4\left( x' - \kappa {\tilde{V}}\right) (\lambda \varepsilon - 2x') + 1}{16 \sqrt{ \left( x'+{\tilde{a}}\right) ({\tilde{b}} - x')}} \exp \left( \frac{\alpha }{\kappa {\tilde{V}}}({\tilde{x}}- x')\right) \,\hbox {d}x' \nonumber \\ {\tilde{x}}= & {} \frac{x}{l_0}\in [-{\tilde{a}},{\tilde{b}}],\quad {\tilde{a}} = \frac{\lambda (1-\varepsilon )}{2},\quad {\tilde{b}} = \frac{\lambda (1+\varepsilon )}{2}. \end{aligned}$$

(11)

The distribution of shear stresses is

• in the slip zone

  $$\begin{aligned} {\tau _{xy}({\tilde{x}})}/E' = \mu p({\tilde{x}})/E' \text { for } {\tilde{x}}\in (-{\tilde{a}},{\tilde{c}}), \quad \text {where } {\tilde{c}} = {\tilde{b}} - \lambda \beta , \end{aligned}$$

  (12)

• in the stick zone

  $$\begin{aligned} \frac{\tau _{xy}({\tilde{x}})}{E'}= & {} \mu \frac{p({\tilde{x}})}{E'}+\mu \frac{\alpha }{8\pi \kappa ^2{\tilde{V}}} \nonumber \\&\times \int \limits _{{\tilde{c}}}^{{\tilde{x}}} \left( 2\kappa {\tilde{V}}+ {\tilde{b}} - {\tilde{c}} - 2x' + 2 \kappa \frac{\delta }{\mu }\right) \sqrt{\frac{x'-{\tilde{c}}}{{\tilde{b}} - x'}} \exp \left( \frac{\alpha }{\kappa {\tilde{V}}}({\tilde{x}}- x')\right) \,\hbox {d}x' \nonumber \\&+\frac{\alpha {\tilde{C}}_2}{\pi \kappa {\tilde{V}}}\int \limits _{{\tilde{c}}}^{{\tilde{x}}} \frac{\exp \left( \frac{\alpha }{\kappa {\tilde{V}}}({\tilde{x}}- x')\right) }{\sqrt{(x'-{\tilde{c}})({\tilde{b}} - x')}}\,\hbox {d}x' \text { for } {\tilde{x}}\in ({\tilde{c}},{\tilde{b}}),\quad \text {where} \end{aligned}$$

  (13)
  $$\begin{aligned} {\tilde{C}}_2= & {} \frac{\mu \beta \lambda }{16\kappa }\left[ {\tilde{b}} + {\tilde{c}} - 2\kappa {\tilde{V}}- 2\kappa \frac{\delta }{\mu } + \left( {\tilde{b}} + {\tilde{c}} - 2\kappa \frac{\delta }{\mu }\right) \frac{K_1(\zeta \beta )}{K_0(\zeta \beta )}\right] . \end{aligned}$$

  (14)

  Integration of normal and shear stresses over the contact region gives the following expressions [2]:

  $$\begin{aligned} {Q}= & {} \int \limits _{-{\tilde{a}}}^{{\tilde{b}}} \tau _{xy}({\tilde{x}})\,l_0\,\hbox {d}{\tilde{x}}= {P}{\tilde{Q}},\nonumber \\ {\tilde{Q}}= & {} \left\{ \begin{array}{ll} \mu \left[ 1-\beta ^2\lambda ^2 - 2\beta \lambda ^2\left( 1+\varepsilon -\beta -\dfrac{2\delta \kappa }{\mu \lambda }\right) \dfrac{K_1(\beta \zeta )}{K_0(\beta \zeta )}\right] ,&{}\quad \text {if }\delta <\delta _\alpha ^*({\tilde{V}})\\ \mu , &{}\quad \text {if }\delta \ge \delta _\alpha ^*({\tilde{V}}) \end{array}\right. , \end{aligned}$$

  (15)
  $$\begin{aligned} M= & {} \int \limits _{-{\tilde{a}}}^{{\tilde{b}}} {\tilde{x}}\, p({\tilde{x}})\,l_0^2\,\hbox {d}{\tilde{x}}= PR{\tilde{M}},\nonumber \\ {\tilde{M}}= & {} \kappa ^{-1}\lambda \left[ \frac{\varepsilon }{2}\left( 1-\lambda ^2\right) + \frac{1}{2\zeta }\left( \lambda ^2-\frac{1}{\alpha }\right) \right] . \end{aligned}$$

  (16)

Fig. 3

a${\tilde{Q}}(\delta )$ for ${\tilde{V}}=0.1,\ 0.2,\ 0.4$, and $\alpha = 11$; b${\tilde{M}}({\tilde{V}})$ for $\alpha = 1.5,\ 21.5,\ 81.5$. Parameters $\mu = 0.2$, $\kappa = 29.1$

Figure 3 presents the graphs ${\tilde{Q}}(\delta )$ for ${\tilde{V}}=0.1,\ 0.2,\ 0.4$ and $\alpha = 11$ and ${\tilde{M}}({\tilde{V}})$ for $\alpha = 1.5,\ 21.5,\ 81.5$, respectively. For viscoelastic materials ($\alpha >1$), the function ${\tilde{Q}}$ depends on both ${\tilde{V}}$ and $\delta$, while ${\tilde{M}}$ does not depend on $\delta$. Besides, note that ${\tilde{M}}$ has the order of ${\mathcal {O}}(\kappa ^{-1})$.

For arbitrary (positive or negative) values of $\delta$ and ${\tilde{V}}$, Eqs. (15) and (16) are generalized in the following way¹:

$$\begin{aligned} {\tilde{Q}}= & {} \left\{ \begin{array}{ll} \mu \,\mathrm {sign}({\tilde{\omega }}- {\tilde{V}})\left[ 1-\beta ^2\lambda ^2 - 2\beta \lambda ^2\left( 1+\varepsilon -\beta -\dfrac{2|\delta | \kappa }{\mu \lambda }\right) \dfrac{K_1(\beta \zeta )}{K_0(\beta \zeta )}\right] , &{}\quad \text {if }\delta <\delta _\alpha ^*({\tilde{V}})\\ \mu \,\mathrm {sign}({\tilde{\omega }}- {\tilde{V}}), &{}\quad \text {if }\delta \ge \delta _\alpha ^*({\tilde{V}}) \end{array} \right. \end{aligned}$$

(17)

$$\begin{aligned} {\tilde{M}}= & {} \mathrm {sign}{\tilde{V}}\,\kappa ^{-1}\lambda \left[ \frac{\varepsilon }{2}\left( 1-\lambda ^2\right) + \frac{1}{2\zeta }\left( \lambda ^2-\frac{1}{\alpha }\right) \right] . \end{aligned}$$

(18)

Here, $\zeta$, $\varepsilon$, $\lambda$, and $\beta$ should be calculated from Eqs. (6) to (10) for the absolute value of ${\tilde{V}}$ and $\mu = \mu \,\mathrm {sign}\delta$.

3.4 Particular case of elastic materials $\alpha = 1$

For $\alpha = 1$, the algorithm gives Carter’s solution for the problem of the rolling with slipping of the elastic cylinder along the elastic half-space [28]. Since modified Bessel functions satisfy the equality

$$\begin{aligned} I_0(x)K_1(x) + I_1(x)K_0(x)\equiv \frac{1}{x}\quad \forall x>0, \end{aligned}$$

then Eq. (6) has a solution $\lambda \equiv 1$ for arbitrary values of ${\tilde{V}}$, and Eq. (8) gives $\varepsilon = 0$. Condition (9) of the partially sticking regime for $\alpha = 1$ gives

$$\begin{aligned} |\delta |<\delta _1^* = \frac{\mu }{2\kappa }, \end{aligned}$$

and from Eq. (10), we get $\beta = 1 - \frac{2|\delta |\kappa }{\mu }$. Equations (15, 16) give

$$\begin{aligned} {\tilde{Q}}= \left\{ \begin{array}{ll} 4\kappa \,\mathrm {sign}({\tilde{\omega }}- {\tilde{V}})\,|\delta |\left( 1-\dfrac{|\delta |\kappa }{\mu }\right) &{}\quad \text {if }|\delta |\le \delta _1^*,\\ \mu \,\mathrm {sign}({\tilde{\omega }}- {\tilde{V}}), &{}\quad \text {otherwise} \end{array}\right. \end{aligned}$$

and ${\tilde{M}}\equiv 0$.

Note that for the elastic case the function ${\tilde{Q}}$ depends only on $\delta$ and does not depend on ${\tilde{V}}$.

3.5 Friction force and moment

While interacting, both cylinder and plane deform. For the small deformations, the shape of the contact region can be described by the parabolic function

$$\begin{aligned} \varSigma = \left\{ y = k\frac{x^2}{2R}, \ x\in (-a,b)\right\} \end{aligned}$$

or in dimensionless variables

$$\begin{aligned} \varSigma = \left\{ {\tilde{y}} = \frac{y}{l_0} = \frac{k\,{\tilde{x}}^2}{2\kappa }, \ {\tilde{x}}\in (-{\tilde{a}},{\tilde{b}})\right\} . \end{aligned}$$

(19)

Since the cylinder and the half-space are of the same material, we assume that the displacements of the points at the vicinity of $C'$ are equal. It immediately gives $k=1/2$. Then, normal and tangent unit vectors to $\hbox {d}\varSigma$ and the length of $\hbox {d}\varSigma$ involved in Eq. (1) are:

$$\begin{aligned} \varvec{t} = \dfrac{2\kappa \varvec{e}_\xi + {\tilde{x}}\varvec{e}_\eta }{\sqrt{4\kappa ^2+{\tilde{x}}^2}} ,\quad \varvec{n} = \dfrac{-{\tilde{x}}\varvec{e}_\xi +2\kappa \varvec{e}_\eta }{\sqrt{4\kappa ^{2}+{\tilde{x}}^2}}, \quad \hbox {d}\varSigma = l_0\frac{\sqrt{4\kappa ^{2}+{\tilde{x}}^2}}{2\kappa }\,\hbox {d}{\tilde{x}}. \end{aligned}$$

Then, components $F_\xi$ and $F_\eta$ of the friction force $\varvec{F}$ are calculated by the following expressions:

$$\begin{aligned} F_\xi= & {} \iint \limits _{\varSigma } (\varvec{e}_\xi ,\,\varvec{dF}) = \int \limits _{-{\tilde{a}}}^{{\tilde{b}}} \left( -\frac{{\tilde{x}}}{2\kappa }p({\tilde{x}}) + \tau _{xy}({\tilde{x}})\right) \left( 1+{\mathcal {O}}(\kappa ^{-2})\right) \,l_0\hbox {d}{\tilde{x}},\\ F_\eta= & {} \iint \limits _{\varSigma } (\varvec{e}_\eta ,\,\varvec{dF}) = \int \limits _{-{\tilde{a}}}^{{\tilde{b}}} \left( p({\tilde{x}}) + \frac{{\tilde{x}}}{2\kappa }\tau _{xy}({\tilde{x}})\right) \left( 1+{\mathcal {O}}(\kappa ^{-2})\right) \,l_0\hbox {d}{\tilde{x}}. \end{aligned}$$

Neglecting here terms of order ${\mathcal {O}}(\kappa ^{-2})$, $O(\mu \kappa ^{-1})$, we obtain

$$\begin{aligned} F_\xi = Q - \frac{M}{2R} ,\quad F_\eta = P \end{aligned}$$

(20)

where Q and M are determined by Eqs. (15) and (16). Taking into account the assumption $F_\eta = mg$ (Sect. 2.2), we get that the vertical load P equals to the weight of the cylinder: $P = mg$.

To calculate the total moment with respect to the center of the cylinder $M_\zeta$, we recall the vector $\varvec{r}$ that goes from C to $\hbox {d}\varSigma$ and has components

$$\begin{aligned} \varvec{r} = l_0{\tilde{x}}\,\varvec{e}_x - R\left( 1 + {\mathcal {O}}(\kappa ^{-1})\right) \varvec{e}_y \end{aligned}$$

where the omitted term of order ${\mathcal {O}}(\kappa ^{-1})$ appears due to the deformation of the boundaries. Therefore, we get

$$\begin{aligned} M_\zeta = \iint \limits _{\varSigma } (\varvec{e}_\zeta ,\,[\varvec{r}\times \varvec{dF}]) = R\int \limits _{-{\tilde{a}}}^{{\tilde{b}}} \left( \tau _{xy}({\tilde{x}}) + \frac{{\tilde{x}}}{2\kappa } p({\tilde{x}})\right) \left( 1 + {\mathcal {O}}(\kappa ^{-2}) + {\mathcal {O}}(\mu \kappa ^{-1})\right) \,l_0\hbox {d}{\tilde{x}}. \end{aligned}$$

Neglecting here terms of order ${\mathcal {O}}(\kappa ^{-2})$, $O(\mu \kappa ^{-1})$, we obtain

$$\begin{aligned} M_\zeta = RQ + \frac{M}{2} \end{aligned}$$

(21)

for Q and M from Eqs. (15) and (16).

Fig. 4

Calculation scheme

4 Scheme of numerical integration

We study the Cauchy problem for Eqs. (3) numerically. Introducing dimensionless time, traction force, and torque,

$$\begin{aligned} {\tilde{t}} = t/T_\varepsilon ,\quad {\tilde{Q}} = Q/P,\quad {\tilde{M}} = M/(PR), \end{aligned}$$

we rewrite Eqs. (3) in dimensionless form,

$$\begin{aligned} \frac{\hbox {d}{\tilde{V}}}{\hbox {d}{\tilde{t}}} = \gamma \left( {\tilde{Q}}- \frac{{\tilde{M}}}{2}\right) ,\quad j\frac{\hbox {d} {\tilde{\omega }}}{\hbox {d}{\tilde{t}}} = -\gamma \left( {\tilde{Q}}+ \frac{{\tilde{M}}}{2}\right) , \end{aligned}$$

(22)

where $j=J/(mR^2)$ is a dimensionless moment of inertia that equals 1/2 for a homogeneous cylinder.

Initial data for the Cauchy problem are arbitrary values for ${\tilde{V}}(0)$ and ${\tilde{\omega }}(0)$; the scheme of numerical integration for Eqs. (22) is presented in Fig. 4.

For solving the nonlinear algebraic equations (6) and (10), we use the Brent–Dekker method for time-stepping—the variable-coefficient linear multistep Adams method in Nordsieck form; both algorithms are realized in GNU Scientific Library.²

The following dimension parameters were taken for the calculations:

$$\begin{aligned} \begin{aligned} R&\,{= }\,10 \text{ cm },\quad m = 35.5 \text{ kg/m },\quad \nu = 0.49,\quad E = 2.3\times 10^5 \text{ Pa } \\ T_\sigma&\, {=}\, {} 0.97 \text{ s },\quad T_\varepsilon = 10.7 \text{ s }.\ \end{aligned} \end{aligned}$$

Dimensionless parameters, hence, are

$$\begin{aligned} \begin{aligned} \alpha = 11,\quad \kappa = 2.91,\quad \gamma = 1.1\times 10^4. \end{aligned} \end{aligned}$$

5 Analysis of the numerical results

5.1 The deceleration process

Figure 5 illustrates the dependencies ${\tilde{V}}({\tilde{t}})$, ${\tilde{\omega }}({\tilde{t}})$ for three different initial conditions,

$$\begin{aligned} IC1:\ {\tilde{V}}(0)= & {} 1.5,\quad {\tilde{\omega }}(0) = 0.5,\\ IC2:\ {\tilde{V}}(0)= & {} -1.5,\quad {\tilde{\omega }}(0) = 0.5,\\ IC3:\ {\tilde{V}}(0)= & {} -1.5,\quad {\tilde{\omega }}(0) = -2. \end{aligned}$$

Condition (9) is violated initially ($\delta (0)>\delta _\alpha ^*$); material points of the cylinder and half-plane are slipping relative to each other.

Fig. 5

Dependence of ${\tilde{V}}({\tilde{t}})$ and ${\tilde{\omega }}({\tilde{t}})$ on time

On the full slipping regime, from Eq. (17) there follows ${\tilde{Q}}= \mu \mathrm {sign}({\tilde{\omega }}- {\tilde{V}})$, and since ${\tilde{M}}$ has the order ${\mathcal {O}}(\kappa ^{-1})$, the main term in the right-hand side of Eq. (22) is $\gamma {\tilde{Q}}$. It follows from Eq. (22) that

$$\begin{aligned} ({\tilde{\omega }}- {\tilde{V}})' = -\mu \gamma (1+j^{-1})\mathrm {sign}({\tilde{\omega }}-{\tilde{V}}) + {\mathcal {O}}(\kappa ^{-1}). \end{aligned}$$

The difference ${\tilde{\omega }}-V$ decreases almost linearly with time. Therefore, the graphs ${\tilde{V}}({\tilde{t}})$ and ${\tilde{\omega }}({\tilde{t}})$ approach each other.

After some finite time, the creep ratio $\delta (t)$ reaches the critical value $\delta _\alpha ^*$, so Condition (9) starts to be fulfilled and remains true further: The partial sticking regime of motion begins. Since then, the graphs ${\tilde{V}}({\tilde{t}})$ and ${\tilde{\omega }}({\tilde{t}})$ almost coincide. The absolute values of ${\tilde{V}}({\tilde{t}}), {\tilde{\omega }}({\tilde{t}})$ decrease till the full stop of the cylinder.

On full sliding and partial sticking regimes, the derivatives of plotted functions strongly differ; therefore on graphs, it looks like corners; however, scaling of the time-axis on the insert in Fig. 5 shows that the functions are smooth. Strictly speaking, the functions ${\tilde{V}}({\tilde{t}}),\ {\tilde{\omega }}({\tilde{t}})\in C ^2[0, +\infty )$ as ${\tilde{Q}}, {\tilde{M}}$ are continuously differentiable on their arguments.

Qualitatively, for all tested initial conditions, the process of deceleration is the following. If the absolute value of the creep ratio initially exceeds the critical value (i.e., $|\delta (0)|\ge \delta _\alpha ^*$), then the motion starts from the full slipping regime, and the functions ${\tilde{V}}({\tilde{t}})$ and ${\tilde{\omega }}({\tilde{t}})$ get closer; in finite time, the partial sticking regime starts ($|\delta (t^*)|<\delta _\alpha ^*$) and proceeds till the full stop of the cylinder; the absolute values of ${\tilde{V}}({\tilde{t}})$ and ${\tilde{\omega }}({\tilde{t}})$ decrease together. If the absolute value of the creep ratio initially is below the critical value, then we straightway get the second part of motion with the partial sticking regime. The details of the contact characteristics evolution for the motion with IC1 are described in the next paragraph.

5.2 The contact characteristics evolution during the deceleration

Figure 6 illustrates how the parameters $\lambda ,\ \varepsilon ,\ \beta$ depend on time for the motion with the initial conditions IC1. At each particular instant of time, these parameters depend on ${\tilde{V}}$ and $\delta$ as it follows from Fig. 4.

Fig. 6

The creep ratio $\delta$, the relative length of the contact area $\lambda$, the displacement of the contact zone $\varepsilon$, and the length of the sticking area $\beta$ as functions of time

For IC1, the creep ratio $\delta$ is negative at ${\tilde{t}}= 0$. Its absolute value grows till ${\tilde{t}}=1.5\times 10^{-4}$ when the sticking zone appears. At this time instant

$$\begin{aligned} \delta = -0.017,\quad \lambda = 0.311, \varepsilon = 0.7, \end{aligned}$$

so, Condition (9) is fulfilled. Since this instant, Eq. (10) has a solution for $\beta$. The function $\beta ({\tilde{t}})$ grows comparatively fast and achieves a value $\beta = 0.98$ at ${\tilde{t}}= 1.65\times 10^{-4}$ (see the blue dash-dot graph for $\beta ({\tilde{t}})$ in the insert).

The relative length of the contact zone $\lambda$ grows monotonously staying almost constant $\lambda \sim 0.3$ till ${\tilde{t}}= 2\times 10^{3}$. After that, it grows till $\lambda = 1$ that is its value at rest.

The displacement of the contact zone $\varepsilon$ grows monotonously till ${\tilde{t}}= 2\times 10^{3}$. Note that the inclination changes at ${\tilde{t}}=1.5\times 10^{-4}$ which is related to the change of the acceleration $\hbox {d}{\tilde{V}}/\hbox {d}{\tilde{t}}$ due to starting of the partially sticking regime of motion (Fig. 5). For ${\tilde{t}}> 2\times 10^{3}$, the function $\varepsilon ({\tilde{t}})$ decreases achieving the value $\varepsilon = 0$ at rest: It means that the pressure distribution becomes symmetric. Circles on the curves show the time instants for which the pressure and shear stress distributions are calculated in the next Section.

5.3 Evolution of the pressure and shear stress in the deceleration process

We take the motion with IC1 and plot the shear stresses distribution $\tau _{xy}({\tilde{x}})/E'$ calculated from Eq. (13). Besides, we added the graph $\mu p({\tilde{x}})/E'$ from Eq. (11) that is proportional to the pressure distribution. In the slipping subregion, the graphs coincide. The stresses are presented in Fig. 7 for the following instants of time (they are marked in Fig. 6 by empty black circles):

• 1. ${\tilde{t}}= 1.52\times 10^{-4}$: just after beginning of partially sticking regime (top left),

  $$\begin{aligned} \delta =-0.01,\quad \beta =0.45. \end{aligned}$$

• 2. ${\tilde{t}}= 4\times 10^{-4}$: the general case of partially sticking regime (top right),

  $$\begin{aligned} \delta = -0.0004,\quad \beta = 0.98. \end{aligned}$$

• 3. ${\tilde{t}}= 24\times 10^{-4}$: $\lambda$ grows, $\varepsilon$ decreases; hence, the pressure distribution becomes more symmetric (bottom left),

  $$\begin{aligned} \delta = -0.001,\quad \beta = 0.95. \end{aligned}$$

• 4. ${\tilde{t}}= 30\times 10^{-4}$: Contact stresses distribution almost at rest (bottom right),

  $$\begin{aligned} \delta = -6\times 10^{-5},\quad \beta = 0.998. \end{aligned}$$

Thus, in deceleration, the values of the shear stress are decreasing, and the contact region becomes symmetrical with respect to the axis $C'C$ (Fig. 1).

Fig. 7

Stress distribution at ${\tilde{t}}= 1.52\times 10^{-4}$ (top left), ${\tilde{t}}= 4\times 10^{-4}$ (top right), ${\tilde{t}}= 24\times 10^{-4}$ (bottom left), ${\tilde{t}}= 30\times 10^{-4}$ (bottom right). Shear stresses $\tau _{xy}(x)/E'$—solid lines, $\mu p(x)/E'$—dashed lines

6 Conclusions

The problem of the motion of a viscoelastic cylinder along a half-space of the same material is studied under the assumption that the boundary of the half-space is horizontal. The solution of the 2D quasistatic viscoelastic problem [2] gives the dependence of the pressure and shear stress distributions (and hence, the friction force and torque) on linear and angular velocities of the cylinder. Here the statement and the solution to this problem are recalled. The condition of the stick zone’s existence is explicitly formulated and proven; the resulting force and torque are calculated, taking into account the deformation of the boundary in the contact region. The Cauchy problem for dynamical equations that describe the motion is numerically solved under the assumption that only gravity acts (no driving force and torque). Initial values of the cylinder center’s linear and angular velocities give the initial creep ratio that defines the initial regime of motion.

It is concluded that if the absolute value of the creep ratio is above the critical value initially, the motion starts with full slipping between the cylinder and the half-space. Then, due to reaction force from the base, the creep ratio achieves the critical value in finite time, and the stick zone appears in the frontal part of the contact area. Further (or for corresponding initial conditions), the creep ratio stays below the critical value; the stick zone grows almost to the rear border of the contact area. Sticking of the materials decreases the shear stresses in the contact region, so the deceleration proceeds almost due to the non-symmetry of the contact pressure distribution. All contact characteristics (contact length and shift, normal and shear contact stress distribution) versus time during the deceleration process are calculated and analyzed.

The results can be used to control the free deceleration of deformable bodies from the same material by choosing the appropriate material properties, sliding friction coefficient, or initial velocities to start the process.

Appendix

Assertion. Equation (10) has a positive solution if and only if Condition (9) holds.

Proof

(Necessity). Since $\zeta >0$, $\alpha >1$, and the functions $I_{0,1}(z)$ and $K_{0,1}(z)$ are positive for real arguments, the second summand in Eq. (10) is always negative. So, if the equation has a positive solution, then

$$\begin{aligned} 1+\varepsilon - \beta - \dfrac{2\delta \kappa }{\mu \lambda }>0. \end{aligned}$$

It implies

$$\begin{aligned} \beta <1+\varepsilon - \dfrac{2\delta \kappa }{\mu \lambda }, \end{aligned}$$

and since we have a positive solution $\beta >0$, we get

$$\begin{aligned} \dfrac{2\delta \kappa }{\mu \lambda }<1+\varepsilon \end{aligned}$$

which is exactly Condition (9).

(Sufficiency). First, we rewrite Eq. (10) in the form:

$$\begin{aligned} \beta = 1+\varepsilon - \dfrac{2\delta \kappa }{\mu \lambda } + \dfrac{1-\alpha }{\alpha \zeta }\frac{I_1(\alpha \beta \zeta )K_0(\beta \zeta )}{I_0(\alpha \beta \zeta )K_1(\beta \zeta ) + I_1(\alpha \beta \zeta )K_0(\beta \zeta )}. \end{aligned}$$

Introducing a new variable $y=\alpha \beta \zeta$, we get an equation on y:

$$\begin{aligned} y= & {} \alpha \zeta \left( 1+\varepsilon - \dfrac{2\delta \kappa }{\mu \lambda }\right) + (1-\alpha )\varPhi (y)\nonumber \\&\text {where}\ \varPhi (y) = \frac{I_1(y)K_0(\alpha ^{-1}y)}{I_0(y)K_1(\alpha ^{-1}y) + I_1(y)K_0(\alpha ^{-1}y)}. \end{aligned}$$

(23)

Using the asymptotics for modified Bessel functions [32],

$$\begin{aligned} K_0(y)= & {} -\ln y (1+{o}(1)),\quad K_1(y) = \frac{1}{y}(1+{o}(1)),\\ I_0(y)= & {} 1+{o}(1),\quad I_1(y) = \frac{y}{2}(1+{o}(1)),\quad y\rightarrow 0, \end{aligned}$$

we get

$$\begin{aligned} \varPhi (y) = \dfrac{-y^2\ln (\alpha ^{-1}y)}{2\alpha -y^2\ln (\alpha ^{-1}y)} = 0 \text { while }y\rightarrow 0. \end{aligned}$$

Hence, due to Condition (9), the right-hand side of Eq. (23) is larger than its left-hand side at point $y = 0$. Further, for infinite values of y we have [32]

$$\begin{aligned} I_i(y)=\frac{e^{y}}{\sqrt{2\pi y}}(1+O(y^{-1})),\quad K_i(y)=\frac{\sqrt{\pi }e^{-y}}{\sqrt{2y}}(1+O(y^{-1})), \quad y\rightarrow \infty ,\quad i=1,2, \end{aligned}$$

and we get

$$\begin{aligned} I_i(y)K_j(\alpha ^{-1} y) = \frac{\exp \left( \left( 1-\frac{1}{\alpha }\right) y\right) }{2\sqrt{\alpha ^{-1}}y}\left( 1+O(y^{-1})\right) \Rightarrow \varPhi (y) \rightarrow \frac{1}{2} \text { while }y\rightarrow +\infty . \end{aligned}$$

Hence, the right-hand side of Eq. (23) tends to the finite value,

$$\begin{aligned} \alpha \zeta \left( 1+\varepsilon - \dfrac{2\delta \kappa }{\mu \lambda }\right) + \frac{1-\alpha }{2}. \end{aligned}$$

It means that for some finite value $y_*$ the right-hand side of Eq. (23) is smaller than its left-hand side.

As the functions in Eq. (23) are continuous, according to the Bolzano theorem, there exists a solution of Eq. (23).

Numerically, we get that the solution of this equation $0<\beta <1$ is unique when Condition (9) holds. $\square$