1 Introduction

The normal contact of linear, isotropic, homogeneous linear elastic bodies is a fundamental problem in contact mechanics. For this kind of problem, the solutions (e.g., the contact and interfacial shear stress) strongly rely on the types of boundary conditions at the interface which can be generally divided into two categories: normal and tangential ones. Consider a non-adhesive contact case. The normal boundary condition for the non-adhesive contact is characterized by the Kuhn–Tucker inequality [1]. Different cohesive models might be applied together with the Kuhn–Tucker inequality to the interface when adhesion is introduced. The three main commonly used tangential boundary conditions in the analytical and numerical models are:

  • Perfect Slip Condition

Interfacial shear stress is not considered, i.e., there is no friction existing between the two surfaces in contact.

  • Full Stick Condition

The interfacial shear stress is sufficient to prevent any slip between the contact interfaces of the elastic bodies.

  • Partial Slip Condition

The contact area is divided into two regions, the stick region and the slip region. In the stick region, the friction at the interface is sufficient to prevent any slip; in the slip region, the stress overcomes the friction and relative displacement can take place.

The current work considers the full stick case. When contact interfaces are under the full stick condition, the mating points from both interfaces have zero relative displacement along their tangent direction. This type of boundary condition occurs in many situations. Experimental results of a glass lens in torsional [2, 3] and sliding contact [4] confirmed the existence of the stick region before the onset of the global rotation and sliding. Recently, a delicate experiment done by Svetlizky and Fineberg [5] showed that the stick and slip regions in pre-sliding can be modeled as the propagation of the interfacial crack opening surfaces in full stick. This clearly indicates that the contact region is under the full stick condition right before being penetrated by the slip region. Due to the complex nature of the contact problem under the full stick condition, very little work was done on analytically solving the interfacial states for plane (2D) and spatial (3D) contact problems.

For the elastic contact under the plane stress/strain condition, several researchers have focused on the indenter with simple geometries and some of the results are summarized in Johnson’s classic book [6]. Johnson [6] gave the interfacial normal and shear stress between the rigid flat-end punch and an elastic half-space under the full stick condition. The solutions were solved based on the integral governing equation developed by Galin [7]. Since all the points on the flat end come into contact simultaneously, the punch results do not rely on the loading history. Johnson [6] also gave a solution for the sliding contact of the cylindrical punch under full stick assuming that the interaction between the interfacial normal and shear stresses is decoupled. Adhesive plane contact between a cylinder and a stretched flat of similar materials where the substrate was stretched was studied by Chen and Gao [8] and later they solved the similar contact problem between dissimilar materials [9]. A similar contact between a rigid cylinder and an elastic half-space was studied by Zhupanska [10]. In Zhupanska’s model, the half-space is not pre-stretched. Block and Keer [11] applied Galin’s formulation [7] for the non-periodic contact problem to the periodic contact problem based on the periodic Green’s function. The solution [11] to the rigid periodic flat-end punches in contact with an elastic half-space was given by analytically solving the coupled integral equations. Goodman’s approximation [12] was applied to the problem where the punch profile is periodically sinusoidal and closed-form solutions were obtained for the interfacial normal and shear stresses.

Most works on the analytical modeling of three-dimensional full stick contact belong to the axisymmetric case. Mossakovskii [13, 14] was the first to solve the axisymmetric normal contact problem under the full stick condition. Mossakovskii [14] presented the solutions for an elastic half-space in contact with a rigid indenter of different shapes: a flat-end cylinder, a parabolic shaped punch and a power law shaped punch. Because the interfacial normal and shear stresses are dependent on the loading history, Mossakovskii [13, 14] modeled the interfacial state of stresses incrementally. Goodman [12] gave an approximate solution of the Hertzian contact between dissimilar materials under the full stick condition. The interfacial normal stress is found by Hertzian contact based on Goodman’s approximation. Goodman [12] also used the incremental formulation to solve the interfacial shear stress. A more efficient analysis to the axisymmetric contact under the full stick condition was given by Spence [15]. He found a similar interfacial state of stresses is yielded at each step during the progressive loading, this behavior is usually referred to as self-similarity. He pointed out that the solution to the self-similar problem can be obtained directly without the application of the incremental technique. Solving the governing dual integral equations by the Wiener–Hopf technique [16] yields the interfacial normal and shear stresses. Based on the self-similarity technique, Borodich [17] solved the Hertzian contact between two nonlinear elastic anisotropic bodies under the full stick condition. Based on Mossakovskii’s analysis, Borodich and Keer [18] considered a contact between a rigid, axisymmetric punch and an isotropic elastic half-space under the adhesive (full stick) condition and found a relation between the contact stiffness, the contact area and the elastic modulus.

Numerical simulation is an effective approach for investigating the situation for both elastic and elastic–plastic contact. This method was used to find the stress distribution and displacement for elastic contact by Conway [19]. He considered that an elastic strip was compressed by a punch with the shapes of cylindrical and circular rollers in the full stick condition. Kosior et al. [20] used a numerical method to analyze the contact problem with friction between two elastic bodies. They used a domain decomposition method coupled with the boundary element method (BEM) to solve the contact problem of two elastic bodies. In an additional paper [21], they solved the same problem numerically by the finite element method (FEM) considering the contact between both a deformable spherical indenter and a deformable support. Brizmer et al. [22] used the FEM to investigate the effect of the contact condition (slip and full stick) and material properties on the termination of elasticity of the contact between an elastic plastic sphere and a rigid flat with the slip and full stick conditions.

All of the previous work assumed a spherical asperity geometry. The current work instead uses a sinusoidal or wavy geometry. The two-dimensional elastic sinusoidal contact was first solved by Westergaard [23]. Johnson, Greenwood and Higginson (JGH) [24] developed asymptotic solutions for the elastic contact of a three-dimensional sinusoidal profile. In their work, they provided a relationship between pressure and contact area for two limiting regimes: at the early stages of contact and near complete contact. Jackson and Streator [25] provided an empirical equation based on the experimental and numerical data, linking the two regimes. They investigated the analysis between rough surfaces that considered asperities using a sinusoidal geometry and proposed a non-statistical multi-scale model to predict the real contact area as a function of normal contact load. With the development of more multi-scale models between rough surfaces [26, 27], the contact problem of an elastic–plastic deformable sinusoidal surface and a rigid flat was investigated by several researchers for the perfect slip case [28,29,30]. Gao et al. [28] found a relationship between contact pressure, contact size, effective indentation depth and residual stress for the 2D elastic–plastic sinusoidal contact. Krithvasion and Jackson [29] provided an approximate solution for the elastic–plastic regimes and an empirical expression for predicting the contact area as a function of contact pressure. Jackson et al. [30] provided an analytical expression for the average pressure that causes complete contact.

As can be seen from the above literature review, most of the existing literature are about either spherical contact under the full stick condition or sinusoidal contact under the perfect slip condition. Very little work was done so far on the sinusoidal contact under the full stick condition, and an analytical solution for complete contact pressure is still missing for elastic contact under full stick condition, this case is very important for describing rough surface contact where there is a significant amount of friction. The main goal of this paper is to analyze the behavior of sinusoidal contact under the full stick condition. Therefore, the effects of contact conditions (perfect slip or full stick) are investigated in the present study for an elastic sinusoidal contact.

2 Methodology

2.1 Problem Statement

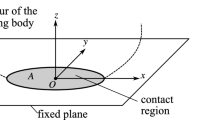
Consider a half-space with a bi-cosinusoidal waviness contour in purely normal contact with a rigid flat. The half-space is homogeneous, isotropic and linear elastic. The periodic bi-sinusoidal surface has the following expression:

$$h = \Delta \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(1)

where only one period is considered: \(\left\{ {\left( {x,y} \right)|x \epsilon \left[ {0,\lambda_{x} } \right),y \epsilon \left[ {0,\lambda_{y} } \right)} \right\}\) (Fig. 1). The wavelengths are \(\lambda_{x} = 2\pi /\alpha\) and \(\lambda_{y} = 2\pi /\beta\). The three-dimensional view and the contour of the surface are shown in Fig. 2 and Fig. 3, respectively. In order to compare the results with the equations in [24] and [30], in which the geometry are described as:

$$h = \Delta \left( {1 - \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)} \right)$$
(2)

a special case of \(\alpha = \beta\) will be considered in Sects. 2.4 and 2.5. The only difference of these two equations is a constant term, the amplitude, \(\Delta\). It should be much less than the wavelengths, i.e. \(\Delta \ll \lambda_{x} \left( {\lambda_{y} } \right)\), in order to exclude large deflections. Small ratio of amplitude to wavelength was also observed experimentally by Jackson [27] and Zhang and Jackson [31], so it is a reasonable assumption. The contacting interface is under the full stick condition. Since the interfacial normal and shear stresses depend on the loading stage [12, 14], generally, the contact problem should be formulated incrementally [12, 14]. In some special cases, (e.g., spherical contact), self-similarity can be used to simplify the formulation [16]. In order to avoid the complexity brought by the load-dependency, the contacting points are assumed to be achieved simultaneously, i.e., \(u_{x} \left( {x,y,0} \right) = u_{y} \left( {x,y,0} \right) = 0\).

Fig. 1
figure 1

Schematic representation of a half-space with bi-sinusoidal waviness in contact with a rigid flat surface. Only the xz cross section is shown

Full size image
Fig. 2
figure 2

Three-dimensional bi-sinusoidal wavy surface

Full size image
Fig. 3
figure 3

Schematic representation bi-sinusoidal waviness. Points A, B, C, D and E are the peaks. Points B’, C’, D’ and E’ are the valleys

Full size image

In order to simplify the contact problem, tangential loading and adhesion are not considered. Consider the special stage where the bi-sinusoidal waviness is initially in contact with the rigid flat everywhere. This stage is referred to as complete contact. At complete contact and under full stick, the contact problem belongs to the second type boundary value problem where the surface displacement components in [6] are prescribed by:

$$\begin{aligned} u_{x} \left( {x,y,0} \right) & = 0 \\ u_{y} \left( {x,y,0} \right) & = 0 \\ u_{z} \left( {x,y,0} \right) & = - h\left( {x,y} \right) \\ \end{aligned}$$
(3)

2.2 Interfacial State of Stress

Wavy or sinusoidal contact has been first studied by the work of Wastergaard [25]. In his work, a two-dimensional half-space contact under the perfect slip condition was analyzed. The cosinusoidal pressure distribution at the interface was given by:

$$\sigma_{z} \left( {x,0} \right) = p_{\text{slip}}^{*} \cos \left( {\alpha x + \beta y} \right)$$
(4)

and the normal elastic displacement due to the pressure in Eq. (4) was given by:

$$u_{z} = \left[ {2p_{\text{slip}}^{*} \left( {1 - \nu^{2} } \right)/E\zeta } \right]\cos \left( {\alpha x + \beta y} \right)$$
(5)

where \(\zeta = \sqrt {\alpha^{2} + \beta^{2} }\).

Johnson et al. [24] investigated the three-dimensional contact between an elastic half-space and a rigid flat, the bi-sinusoidal distribution of the surface pressure was given by:

$$\sigma_{z} \left( {x,y,0} \right) = p_{\text{slip}}^{*} {\text{cos}}\left( {\alpha x} \right){ \cos }\left( {\beta y} \right)$$
(6)

The elastic displacement due to this surface pressure is given by:

$$u_{z} = \left[ {2p_{\text{slip}}^{*} \left( {1 - \nu^{2} } \right)/E\left( {\alpha^{2} + \beta^{2} } \right)^{1/2} } \right]{ \cos }\left( {\alpha x} \right){ \cos }\left( {\beta y} \right)$$
(7)

Then, Tripp et al. [32] also investigated the three-dimensional half-space by using the potential method and considered the shear stress distribution:

$$\tau_{xz} \left( {x,y,0} \right) = q_{0} {\text{cos}}\left( {\alpha x} \right){ \cos }\left( {\beta y} \right)$$
(8)

and the elastic displacement components were given in terms of the potential function.

$$u_{x} = \left( {4\pi G} \right)^{ - 1} \left[ {2\phi_{zz} + 2\nu \phi_{xx} - z\phi_{xxz} } \right]$$
(9a)
$$u_{y} = \left( {4\pi G} \right)^{ - 1} \left[ {2\nu \phi_{xy} - z\phi_{xyz} } \right]$$
(9b)
$$u_{z} = \left( {4\pi G} \right)^{ - 1} \left[ {(1 - 2\nu )\phi_{xy} - z\phi_{xzz} } \right]$$
(9c)

where the Airy stress function for this case is given by:

$$\phi \left( {x,y,z} \right) = - \left( {2\pi q_{0} /\zeta^{3} } \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(10)

\(G\) is shear modulus, and given by \(G = E/\left( {2\left( {1 + \nu } \right)} \right)\) and \(q_{0}\) is the amplitude of shear stress.

Following Tripp et al.’s method, we assumed a bi-sinusoidal pressure distribution and shear stress distribution in both x and y directions. Generally, the unknown contact pressure, \(p\left( {x,y} \right)\), and the interfacial shear stresses, \(q_{x} \left( {x,y} \right)\), and \(q_{y} \left( {x,y} \right)\), can be expressed by the Fourier series with an infinite number of terms. Since the normal displacement, \(u_{z} \left( {x,y,0} \right)\), only contains a single sinusoidal term, a simplified form of the boundary stresses may be written as:

$$\begin{aligned} p\left( {x,y,0} \right) & = p_{11} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + p_{12} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right) \\ \quad + \, p_{21} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right) + p_{22} sin\left( {\alpha x} \right)\sin \left( {\beta y} \right) \\ \end{aligned}$$
(11a)
$$\begin{aligned} q_{x} \left( {{\text{x}},{\text{y}},0} \right) & = \tau_{x11} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + \tau_{x12} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right) \\ \quad + \, \tau_{x21} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right) + \tau_{x22} \sin \left( {\alpha x} \right)\sin \left( {\beta y} \right) \\ \end{aligned}$$
(11b)
$$\begin{aligned} q_{y} \left( {{\text{x}},{\text{y}},0} \right) & = \tau_{y11} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + \tau_{y12} \cos \left( {\alpha x} \right)sin\left( {\beta y} \right) \\ \quad + \, \tau_{y21} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right) + \tau_{y22} \sin \left( {\alpha x} \right)\sin \left( {\beta y} \right) \\ \end{aligned}$$
(11c)

where the normal stress constants \(p_{11}\), \(p_{12}\), \(p_{21}\), \(p_{22}\) and shear stress constants \(\tau_{x11}\), \(\tau_{x12}\), \(\tau_{x21}\), \(\tau_{x22}\), \(\tau_{y11}\), \(\tau_{y12}\), \(\tau_{y21}\), \(\tau_{y22}\), are initially unknown. Note that the mean value of \(q_{x } \left( {x,y} \right)\) and \(q_{y } \left( {x,y} \right)\) over each period are zero. The average value of \(p \left( {x,y} \right)\) is \(\bar{p}\) and is the minimum of the value which can exclude all the negative values in \(p \left( {x,y} \right)\). The addition of \(\bar{p}\) would be achieved by the application of a sufficient normal load.

Similarly to the calculation of displacement components on the sinusoidal surface of the plane contact in “Appendix 1”, the elementary solutions of the interfacial displacement components due to different bi-sinusoidal/cosinusoidal stress boundaries are listed in “Appendix 2”. The resultant interfacial displacement components, \(u_{x } \left( {x,y,0} \right)\), \(u_{y } \left( {x,y,0} \right)\), and \(u_{z } \left( {x,y,0} \right)\), due to the stress boundaries in Eq. (3) are the superposition of the corresponding elementary solutions. Substituting the interfacial displacement components into the boundary conditions for complete contact under full stick (see Eq. (3)) and combining the same bi-sinusoidal/cosinusoidal terms, then the above boundary conditions can be decomposed into 12 linear equations. After solving this linear system, only three out of the twelve unknowns are non-zeros:

$$p_{11} = p^{*} = \frac{{2\Delta E\zeta \left( {1 - \nu} \right)}}{{\left( {1 + \nu} \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}$$
(12a)
$$\tau_{x21} = q_{x}^{*} = \frac{{\Delta E\alpha \left( {1 - 2\nu} \right)}}{{\left( {1 + \nu} \right)\left( {8v^{2} - 12\nu + 5} \right)}}$$
(12b)
$$\tau_{y12} = q_{y}^{*} = \frac{{\Delta E\beta \left( {1 - 2\nu} \right)}}{{\left( {1 + \nu} \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}$$
(12c)

Note the complete contact pressure is reached when the average contact pressure is equal to \(p^{*}\) in the full stick condition. \(p^{*}\) now is denoted \(p_{\text{stick}}^{*}\), and Eq. (12a) becomes:

$$p_{\text{stick}}^{*} = \frac{{4\sqrt 2 \pi E\Delta f\left( {1 - \nu} \right)}}{{\left( {1 + \nu} \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}$$
(13)

In contrast, the complete contact pressure for the isotropic wave surfaces, \(\left( {\alpha = \beta = 2\pi /\lambda } \right)\), in the perfect slip condition is given by Johnson et al. [24]:

$$p_{\text{slip}}^{*} = \sqrt 2 \pi E^{\prime}\Delta f = \frac{\sqrt 2 \pi E\Delta f}{{1 - \nu^{2} }}$$
(14)

where \(E^{\prime}\) is the equivalent elastic modulus which is given by:

$$\frac{1}{E'} = \frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}$$
(15)

\(E_{1}\), \(v_{1}\) and \(E_{2}\), \(v_{2}\) are the elastic modulus and Poisson’s ratio of the contacting surfaces.

The elastic modulus of the rigid flat is considered to be \(\infty\), and Eq. (15) reduces to:

$$E' = \frac{{E_{1} }}{{1 - \nu_{1}^{2} }}$$
(16)

Since both Eqs. (13) and (14) have the \(E\Delta f\) term, the complete contact pressure in perfect slip condition,\(p_{\text{slip}}^{*}\), and in full stick condition, \(p_{\text{stick}}^{*}\) are normalized using \(E\Delta f\). Then the normalized complete contact pressure is plotted versus Poisson’s ratio (see Fig. 3). It can be seen from Fig. 3, as the Poisson’s ratio increases, the dimensionless complete contact pressure also increases in both stick and slip. The complete contact pressure is also much lower in stick than it is in slip. This is because the addition of traction in the stick case increases the overall stress in the contact and therefore lowers the pressure needed to cause strain to compress the surface. And the difference between the two curves decreases, they converge to the same value at \(\nu = 0.5\). This is because the influence of tangential traction on the normal pressure is small for high values of Poisson’s ratio, and the tangential stress under the full stick condition are low enough to make the complete contact pressure in stick and in slip similar. This observation was also found for the rigid flat punch indentation case as found in Johnson’s book [6]. For the compressible material (\(\nu < 0.5\)), the complete contact pressures in stick are lower than their corresponding value in slip; for the incompressible material (\(\nu = 0.5\)), the complete contact pressure in stick is exactly equal to the value in slip (Fig. 4).

Fig. 4
figure 4

Dimensionless complete contact pressure in full stick and prefect slip condition

Full size image

Dividing Eqs. (13) by (14), then the ratio between the stick and slip case is given by the following function of \(\nu\):

$$\frac{{p_{\text{stick}}^{*} }}{{p_{\text{slip}}^{*} }} = \frac{{4\left( {1 - \nu} \right)^{2} }}{{\left( {8\nu^{2} - 12\nu + 5} \right)}}$$
(17)

Figure 5 presents the ratio of the complete contact pressure in full stick over that in perfect slip. The ratio was found to be independent of the geometry and material properties, except for the Poisson’s ratio. The two limits are \(\frac{{p_{\text{stick}}^{*} }}{{p_{\text{slip}}^{*} }} = 0.8\) when \(\nu = 0\), and \(\frac{{p_{\text{stick}}^{*} }}{{p_{\text{slip}}^{*} }} = 1\) when \(\nu = 0.5\). The ratio increases as the Poisson’s ratio increases. That is because the tangential traction does not affect the ratio as much at the high values of Poisson’s ratio.

Fig. 5
figure 5

The ratio of complete contact pressure in full stick over perfect slip

Full size image

Consequently, the final forms of the contact pressure and the interfacial shear stresses under the full stick condition are:

$$p\left( {{\text{x}},{\text{y}}} \right) = p_{\text{stick}}^{*} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + \bar{p}$$
(18a)
$$q_{x} \left( {x,y} \right) = q_{x}^{*} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(18b)
$$q_{y} \left( {x,y} \right) = q_{y}^{*} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(18c)

Note that the complete contact is initially reached when \(\bar{p} = p_{\text{stick}}^{*}\).

2.3 General State of Stresses at Complete Contact

In order to determine the state of stresses of the half-space under the action of the boundary stresses, Eq. (13) can be decomposed into three sub-states for each surface traction \(p\left( {{\text{x}},{\text{y}}} \right)\), \(q_{x} \left( {{\text{x}},{\text{y}}} \right)\) and \(q_{y} \left( {{\text{x}},{\text{y}}} \right)\) individually. Then they can be superposed to find the complete solution. First we will neglect the final \(\bar{p}\) in Eq. (18a), Tripp et al. [32] provided the state of stresses of the half-space due to the application of a bi-cosinusoidal normal stress distribution, \(p\left( {x,y} \right) = p_{\text{stick}}^{*} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)\) on the boundary of a half-space:

$$\sigma_{x} = p_{\text{stick}}^{*} \left[ {\frac{{\alpha^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta } + 2\nu \left( {\beta /\zeta } \right)^{2} } \right]e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(19a)
$$\sigma_{y} = p_{\text{stick}}^{*} \left[ {\frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta } + 2\nu \left( {\alpha /\zeta } \right)^{2} } \right]e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(19b)
$$\sigma_{z} = p_{\text{stick}}^{*} \left( {1 + \zeta z} \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(19c)
$$\tau_{xy} = - p_{\text{stick}}^{*} \left( {\frac{\alpha \beta }{{\zeta^{2} }}} \right)\left( {1 - 2\nu - \zeta z} \right)e^{ - \zeta z} \sin \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(19d)
$$\tau_{yz} = p_{\text{stick}}^{*} \beta z e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(19e)
$$\tau_{xz} = p_{\text{stick}}^{*} \alpha z e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(19f)

In addition, Tripp et al. [32] also gave the closed-form solution of the state of stress of the half-space due to the action of a bi-cosinusoidal shear stress distribution, \(q_{x} \left( {x,y} \right) = q_{x}^{*} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)\), on the boundary. This boundary problem is solved by a known potential function. Following the same methodology, the state of stresses due to the boundary stress \(q_{x} \left( {x,y} \right) = q_{x}^{*} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)\) is

$$\sigma_{x} = - q_{x}^{*} \alpha /\zeta \left[ {2 + 2\nu \left( {\beta /\zeta } \right)^{2} - \left( {\alpha /\zeta } \right)\left( {\alpha z} \right)} \right]e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(20a)
$$\sigma_{y} = - q_{x}^{*} \alpha \left[ {\frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta } + 2\nu \left( {\alpha /\zeta } \right)^{2} } \right]e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(20b)
$$\sigma_{z} = - q_{x}^{*} \alpha ze^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(20c)
$$\tau_{xy} = q_{x}^{*} \beta /\zeta \left( {1 - \frac{{2\nu\alpha^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta }} \right)e^{ - \zeta z} sin\left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(20d)
$$\tau_{yz} = - q_{x}^{*} \frac{\alpha \beta }{\zeta }z e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(20e)
$$\tau_{xz} = q_{x}^{*} \left( {1 - \alpha^{2} z/\zeta } \right)e^{ - \zeta z} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(20f)

Similarly, a boundary stress distribution, \(q_{y} \left( {x,y} \right) = q_{y}^{*} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)\) will result in the following state of stress:

$$\sigma_{x} = - q_{y}^{*} \beta /\zeta \left( {2\nu \frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta }} \right) e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(21a)
$$\sigma_{y} = q_{y}^{*} \beta /\zeta \left[ {2 + 2\nu \left( {\alpha /\zeta } \right)^{2} - \left( {\beta /\zeta } \right)\left( {\beta z} \right)} \right]e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(21b)
$$\sigma_{z} = - q_{y}^{*} \beta ze^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(21c)
$$\tau_{xy} = q_{y}^{*} \alpha /\zeta \left( {1 - \frac{{2\nu\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta }} \right)e^{ - \zeta z} sin\left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(21d)
$$\tau_{yz} = q_{y}^{*} \left( {1 - \beta^{2} z/\zeta } \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(21e)
$$\tau_{xz} = - q_{y}^{*} \left( {\frac{\alpha \beta }{\zeta }} \right)z e^{ - \zeta z} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(21f)

Then, the state of stress due to the mutual action of the boundary tractions, \(p\left( {x,y} \right)\), \(q_{x} \left( {x,y} \right)\), and \(q_{y} \left( {x,y} \right)\) in Eq. (18), is the superposition of the contributions listed above:

$$\sigma_{x} = \left\{ {p_{\text{stick}}^{*} \left[ {\frac{{\alpha^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta } + 2\nu \left( {\beta /\zeta } \right)^{2} } \right] - q_{x}^{*} \alpha /\zeta \left[ {2 + 2\nu \left( {\frac{\beta }{\zeta }} \right)^{2} - \left( {\alpha /\zeta } \right)\left( {\alpha z} \right)} \right] - q_{y}^{*} \beta /\zeta \left( {2\nu \frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta }} \right)} \right\}e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(22a)
$$\sigma_{y} = \left\{ {p_{\text{stick}}^{*} \left[ {\frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta } + 2\nu \left( {\alpha /\zeta } \right)^{2} } \right] - q_{x}^{*} \alpha \left[ {\frac{{\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta } + 2\nu \left( {\frac{\alpha }{\zeta }} \right)^{2} } \right] + q_{y}^{*} \beta /\zeta \left[ {2 + 2\nu \left( {\alpha /\zeta } \right)^{2} - \left( {\beta /\zeta } \right)\left( {\beta z} \right)} \right]} \right\}e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(22b)
$$\sigma_{z} = \left\{ {p_{\text{stick}}^{*} \left( {1 + \zeta z} \right) - q_{x}^{*} \alpha z - q_{y}^{*} \beta z} \right\} e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(22c)
$$\tau_{xy} = \left[ { - p_{\text{stick}}^{*} \left( {\frac{\alpha \beta }{{\zeta^{2} }}} \right)\left( {1 - 2\nu - \zeta z} \right) + q_{x}^{*} \frac{\beta }{\zeta }\left( {1 - \frac{{2\nu \alpha^{2} }}{{\zeta^{2} }} - \frac{{\alpha^{2} z}}{\zeta }} \right) + q_{y}^{*} \frac{\alpha }{\zeta }\left( {1 - \frac{{2\nu\beta^{2} }}{{\zeta^{2} }} - \frac{{\beta^{2} z}}{\zeta }} \right)} \right]e^{ - \zeta z} \sin \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(22d)
$$\tau_{yz} = \left[ {p_{\text{stick}}^{*} \beta z - q_{x}^{*} \frac{\beta }{\zeta }\left( {\alpha z} \right) + q_{y}^{*} \left( {1 - \frac{{\beta^{2} z}}{\zeta }} \right)} \right] e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(22e)
$$\tau_{yz} = \left\{ {p_{\text{stick}}^{*} \alpha z + q_{x}^{*} \left( {1 - \alpha^{2} z/\zeta } \right) - q_{y}^{*} \left( {\frac{\alpha \beta }{\zeta }} \right)z } \right\}e^{ - \zeta z} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(22f)

After algebraic manipulation, it yields the following simplified forms of the state of stress:

$$\sigma_{x} = \frac{{\Delta E \left( { - \alpha^{2} + 2\nu \zeta } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(23a)
$$\sigma_{y} = \frac{{\Delta E \left( { - \beta^{2} + 2\nu \zeta } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(23b)
$$\sigma_{z} = \frac{{\Delta E \left( {\zeta^{2} z + 2z - 2\nu \zeta } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(23c)
$$\tau_{xy} = \frac{{\Delta E\alpha \beta z \left( {\zeta^{2} z + 2z - 2\nu \zeta } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z}\sin \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(23d)
$$\tau_{yz} = \frac{{\Delta E \beta \left( {\zeta z + 1 - 2\nu } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(23e)
$$\tau_{xz} = \frac{{\Delta E \beta \left( {\zeta z + 1 - 2\nu } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}} e^{ - \zeta z} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(23f)

In addition to the sinusoidal stresses, there is an average uniform pressure given in the last term of Eq. (18). Due to this uniform pressure, \(\bar{p} = p_{\text{stick}}^{*}\), and by employing Hooke’s law, the stress on the half-space is derived by:

$$\sigma_{x} = p_{\text{stick}}^{*} \left( {\frac{\nu }{1 - \nu }} \right)$$
(24a)
$$\sigma_{y} = p_{\text{stick}}^{*} \left( {\frac{\nu }{1 - \nu }} \right)$$
(24b)
$$\sigma_{z} = p_{\text{stick}}^{*}$$
(24c)

Note that the sign of the stresses in Eq. (15) follows the convention in contact mechanics, i.e., compressive stress is positive and tensile stress is negative. Carrying out the superposition, the stress field can be recombined from the Eqs. (14) and (15) with the following results:

$$\sigma_{x} = \frac{\Delta E }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}\left[ { \left( { - \alpha^{2} + 2\nu \zeta } \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + 2\nu } \right]$$
(25a)
$$\sigma_{y} = \frac{\Delta E }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}\left[ { \left( { - \beta^{2} + 2\nu \zeta } \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + 2\nu } \right]$$
(25b)
$$\sigma_{z} = \frac{\Delta E }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}\left[ { \left( {\zeta^{2} z + 2\zeta - 2\nu\zeta } \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\beta y} \right) + 2 - 2\nu } \right]$$
(25c)
$$\tau_{xy} = \frac{\Delta E\alpha \beta z }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z}\sin \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(25d)
$$\tau_{yz} = \frac{{\Delta E \beta \left( {\zeta z + 1 - 2\nu } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}e^{ - \zeta z} \cos \left( {\alpha x} \right)\sin \left( {\beta y} \right)$$
(25e)
$$\tau_{xz} = \frac{{\Delta E \alpha \left( {\zeta z + 1 - 2\nu } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}} e^{ - \zeta z} \sin \left( {\alpha x} \right)\cos \left( {\beta y} \right)$$
(25f)

2.4 The Maximum von Mises Stress

When considering the initiation of the plastic deformation, the von Mises (or distortion energy) criteria is considered to be a very effective method. It is given by:

$$\sigma_{\text{vm}} = \sqrt {\frac{1}{2}\left[ {\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {\sigma_{y} - \sigma_{z} } \right)^{2} + \left( {\sigma_{x} - \sigma_{z} } \right)^{2} + 6\left( {\tau_{xy}^{2} + \tau_{yz}^{2} + \tau_{xz}^{2} } \right)} \right]}$$
(26)

by substituting \(\sigma_{x}\), \(\sigma_{y}\), \(\sigma_{z}\), \(\tau_{xy}\), \(\tau_{yz}\), and \(\tau_{xz}\) from Eq. (25) into the Eq. (26), the von Mises stress is founded. Since for the current case, wavelengths in the x and y direction are equal (\(\alpha = \beta = 1/\lambda = f\)), the equation becomes:

$$\sigma_{\text{vm}} = \frac{\Delta E \zeta }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}\left\{ {\left[ {\left( {\frac{3}{2}\zeta z - 4\nu + 2} \right)e^{ - \zeta z} \cos \left( {\alpha x} \right)\cos \left( {\alpha y} \right) - 4\nu + 2} \right]^{2} + \frac{3}{4}\zeta^{2} z^{2} e^{ - 2\zeta z} \sin^{2} \left( {\alpha x} \right)\sin^{2} \left( {\alpha y} \right) + \frac{3}{2}\left( {\zeta z + 1 - 2\upsilon } \right)^{2} e^{ - 2\zeta z} \left[ {\cos^{2} \left( {\alpha x} \right)\sin^{2} \left( {\alpha y} \right) + \sin^{2} \left( {\alpha x} \right)\cos^{2} \left( {\alpha y} \right)} \right]} \right\}^{{\frac{1}{2}}}$$
(27)

In order to find the location of the maximum von Mises stress in the xy plane, the maximum of Eq. (27) will occur at the inflection point or where the gradient is nil. Therefore, carrying out the second-order derivation, and letting \(\frac{{\partial \sigma_{\text{vm}}^{2} }}{{\partial {\text{x}}\partial {\text{y}}}} = 0\), the location of the peak points, i.e. \(\left( {0,0} \right)\), \(\left( {0,\lambda } \right)\),\(\left( {\lambda ,0} \right)\),\(\left( {\lambda ,\lambda } \right)\), and (\(\lambda /2, \lambda /2\)). of \(\sigma_{\text{vm}}\) are determined. Substituting the 5 points into Eq. (27) results in the same equation for each case:

$$\sigma_{{{\text{vm}}0}} = \frac{\Delta E \zeta }{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}} \left| {\left[ {\left( {\frac{3}{2}\zeta z - 4\nu + 2} \right)e^{ - \zeta z} - 4\nu + 2} \right]} \right|$$
(28)

The differential of Eq. (28) is then becoming

$$\frac{{{\text{d}}\sigma_{{{\text{vm}}0}} }}{{{\text{d}}z}} = \frac{{\Delta E \zeta^{2} }}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}} \left| { - \frac{3}{2}\zeta z + 4\nu - \frac{1}{2}} \right|$$
(29)

The maximum von Mises stress is obtained by solving for the location z where\(d\sigma_{{{\text{vm}}0}} /dz = 0\). Hence, we can find the value of z where the von Mises reaches the maximum value. It is:

$$z_{0} = \frac{8\nu - 1}{3\zeta }$$
(30)

Since \(\zeta = \sqrt 2 \alpha = 2\sqrt 2 \pi /\lambda\), Eq. (30) yield to

$$z_{0} = \frac{8\nu - 1}{6\sqrt 2 \pi } \lambda$$
(31)

The location \(z_{0}\) is dependent only on the geometry parameter of wavelength, \(\lambda\), and the material parameter Poisson’s ratio, \(\nu\). Most of the Poisson’s ratios of typical engineering materials are in the range of \(0 \le \nu \le 0.5\). Considering this range, \(z_{0} < 0\), when \(0 \le \nu < \frac{1}{8}\) and \(z_{0} \ge 0\) when \(\frac{1}{8} \le \nu \le 0.5\). By definition, \(z_{0}\) should be always greater than or equal to zero, and therefore we need to discuss these two cases: When \(0 \le \nu \le \frac{1}{8}\), there is no solution for Eq. (29) in \(\left[ {0, \left. { + \infty } \right)} \right.\). Considering that Eq. (29) is a decreasing function, when \(z_{0} < 0\), it should be to be set to \(z_{0} = 0\). This physically means that the maximum stress is on the surface. When \(\frac{1}{8} \le \nu \le 0.5\), \(z_{0}\) is in \(\left[ {0, \left. { + \infty } \right)} \right.\) and then found to be: \(z_{0} = \frac{8\nu - 1}{6\sqrt 2 \pi } \lambda\). The values of \(z_{0} = \frac{8\nu - 1}{6\sqrt 2 \pi } \lambda\) and \(z_{0} = 0\) are then substituted back into Eq. (28) to find the maximum value of the von Mises stress for the full stick condition:

$$\begin{aligned} &{\text{For}}\;\nu < \frac{1}{8}, \left( {\sigma_{\text{vm}} } \right)_{ \hbox{max} } = \frac{{8\sqrt 2 \pi \left( {1 - 2\nu } \right)}}{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}\frac{\Delta }{\lambda } E \\ &{\text{For}}\;\nu \ge \frac{1}{8}, \left( {\sigma_{\text{vm}} } \right)_{ \hbox{max} } = \frac{{3\sqrt 2 \pi e^{{\left( {1 - 8\nu } \right)/3}} - 8\sqrt 2 \nu + 4\sqrt 2 }}{{\left( {1 + \nu } \right)\left( {8\nu ^{2} - 12\nu + 5} \right)}}\frac{\Delta }{\lambda } E \\ \end{aligned}$$
(32)

Based on the work in [30], the maximum von Mises stress expression is derived for perfect slip condition:

$$\left( {\sigma_{\text{vm}} } \right)_{ \hbox{max} } = \sqrt 2 \pi E^{\prime}\Delta f\left[ {\frac{3}{2}e^{{ - 2/3\left( {\nu + 1} \right)}} + \left( {\frac{1 - 2\nu}{1 - \nu}} \right)} \right]$$
(33)

The dimensionless maximum von Mises stress is plotted in Fig. 6. It is shown that the ratio will decrease as the Poisson’s ratio increases for both in stick and slip. The maximum von Mises stress under the full stick condition is lower than or equal to the corresponding value in slip. From the previous discussion, the maximum von Mises stress can occur either on the surface, \(z_{0}\) = 0, or somewhere under the surface,\(z_{0} = \frac{8\nu - 1}{6\sqrt 2 \pi } \lambda\), depending on the value of Poisson’s ratio. This is similar to that found in cylindrical contact by Green [33]. The transition is at \(\nu = \frac{1}{8}\), while the transition found in [33] was at \(\nu = 0.1938\), for the cylindrical contact.

Fig. 6
figure 6

Dimensionless maximum von Mises stress as a function of Poisson’s ratio

Full size image

2.5 Critical Value of Amplitude

The value of \(\sigma_{\text{vm}}\) is valid in the elastic deformation range and is used to calculate the critical amplitude during complete contact denoted \(\Delta_{\text{c}}\), provided by Jackson et al. [30]. The definition of the critical amplitude is: when \(\Delta \le \Delta_{\text{c}}\) the sinusoidal contact will deform purely elastically, for the entire range of loads, including when it has completely flattened out.

However, when \(\Delta > \Delta_{\text{c}}\), plastic deformation may occur before complete contact is reached. By setting the von Mises stress \(\sigma_{\text{vm}}\) equal to the yield strength, \(S_{\text{y}}\), and solving for \(\Delta\), the critical amplitude during complete contact \(\Delta_{\text{c}}\) is given as:

$$\begin{aligned} &{\text{For}}\;\nu < \frac{1}{8}, \Delta_{\text{c}} = \frac{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}{{8\sqrt 2 \pi \left( {1 - 2\nu } \right)}}\frac{Sy}{E} \lambda \\ &{\text{For}}\;\nu \ge \frac{1}{8}, \Delta_{\text{c}} = \frac{{\left( {1 + \nu } \right)\left( {8\nu^{2} - 12\nu + 5} \right)}}{{3\sqrt 2 \pi e^{{\left( {1 - 8\nu } \right)/3}} - 8\sqrt 2 \nu + 4\sqrt 2 }}\frac{Sy}{E} \lambda \\ \end{aligned}$$
(34)

The critical amplitude during complete contact for the perfect slip given in [30] is incorrect and the corrected equation is given in [34] as:

$$\Delta_{\text{c}} = \frac{{\sqrt 2 S_{y} \lambda }}{{\pi E^{\prime}\left[ {3 e^{{ - 2\left( {\nu + 1} \right)/3}} + 2\left( {\frac{1 - 2\nu }{1 - \nu }} \right)} \right]}}$$
(35)

The dimensionless critical values of amplitude for the perfect slip and full stick conditions are plotted in Fig. 7. It is noted that the value of the critical amplitude under the full stick is greater than the one in the perfect slip condition. This is because the tangential stresses in the contact interface under the full stick condition are nonexistent in the perfect slip condition. The additional tangential stress results in higher stresses in the material below a non-slip (i.e., full stick) surface compared to the slip case.

Fig. 7
figure 7

Dimensionless critical amplitude for prefect slip and full stick conditions

Full size image

3 Conclusions

An analytical, closed-form solution was provided to make predictions of the average pressure required to obtain complete contact between elastic wavy or sinusoidal surfaces in full stick. The value of the complete contact pressure in stick is lower than the value in slip. The ratio of the average complete contact pressure between perfect slip and full stick conditions are mostly affected by Poisson’s ratio.

This work also determines the location of the maximum von Mises stress in sinusoidal contact based upon the distortion energy theory as well. Similar to the cylindrical contact, the maximum von Mises stress occurs on the axis of symmetry, and it can occur either on the surface or under the surface, depending on Poisson’s ratio. For \(0 \le \nu < \frac{1}{8}\), the maximum von Mises stress occurs on the surface; for \(\frac{1}{8} \le \nu < 0.5\), the maximum von Mises stress occurs beneath the surface.

A critical amplitude of the sinusoidal surface is also derived. When the amplitude of the sinusoidal surface is less than the critical value, the deformation is always in the elastic range up to the initiation of complete contact; when the amplitude is greater than the critical value, the deformation will be able to enter the elastic–plastic range prior to complete contact. The critical value of amplitude is much higher in stick than in slip.

The limitations of the presented model need to also be mentioned. In practice, no such pure sinusoidal surface pattern may exist. However, due to the vibration of the tool, some machined surfaces show periodic patterns similar to the sinusoidal waviness [35]. There are also periodic biological and naturally occurring structures that may benefit from the model. In general, wavy geometries may also be effective at modeling the asperities and roughness of surfaces [25, 36]. In order to guarantee the assumption of small deformations (linear elasticity), the ratio of amplitude to wavelength is considered significant small (\(\Delta \ll \lambda\)) in the current work. Otherwise, deformation will distort the initial pattern of the sinusoidal surface. In practice, plasticity will of course occur in the complete contact case, especially for hard metallic materials [29, 30, 37,38,39]. For soft materials such as polymers and elastomers, this might not always occur. Regardless, plasticity is out of the scope of our current work.