1 Introduction

Analytical formulations of contact problems were established in books [1,2,3,4,5] and other researches. Recently, new analytical approaches have been developed but most of them were applied to single contact problems [6,7,8,9,10,11,12]. Jäger [13, 14] and Ciavarella [15, 16] proposed independently an approach for the solution of a quasi-static contact problem between two elastically similar half-planes under the constant normal and increasing tangential loading.

The analysis of a multiple contact problem is a generalization of a single contact problem but determining the extent of the contact and stick zones in multiple contacts is not a straightforward task. Hitherto, the most important analytical solutions of multiple contact problems were exhibited by Shtajerman [1], Muskhelishvili [2], Gladwell [3], Westergaard [17] and Barber [18,19,20]. But they did not present a general approach to determine the extent of the contact and stick zones. Manners [21] used Westergaard’s general approach to develop an analytical solution for multiple contacts between two rough, but nominally flat, surfaces where the initial gap function has a regular periodic form. He did not acquire the extent of the contact zones. Afterward, he presented a new numerical approach to calculate the extent of the contact zones in multiple contacts between two rough surfaces [22]. Sundaram and Farris [23] developed a semi-analytical approach to analyze quasi-static multiple contacts.

Ghanati and Adibnazari [24] derived the consistency condition in symmetric double contacts to determine the extent of the contact and stick zones in the symmetric indentation of a flat surface by an indenter with a concavity. They extended the analytical method based on the classical singular integral equations approach presented by Hills et al. [5] to analyze a generic quasi-static symmetric double contact problem between two elastically similar half-planes, under the constant normal and oscillatory tangential loading, by utilizing the Jäger–Ciavarella principle [13,14,15,16]. Following the previous work [24], in the present paper, we apply boundary conditions of nonsingular edges to determine the extent of the contact and stick zones in multiple contacts. It leads to the derivation of new side conditions that are named “the consistency conditions” for multiple contacts. These conditions appear when the number of nonsingular edges exceeds the number of discrete contact zones and are the most important contribution of this work. Finally, a generalized mathematical expression of the Jäger–Ciavarella principle is obtained that show all of the contact zones reach the full slip state simultaneously.

2 Problem definition and governing equations

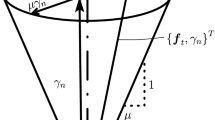
According to Fig. 1, in the first stage of loading, by applying the monotonically increasing normal force P and the planar moment M, the half-plane 1 with some concavities indents the flat half-plane 2 vertically. It results in multiple growing contact zones that may have singular edges or with just one inner singular point. In fact, during the first stage of loading, the value of the planar moment M that provides the vertical indentation of the lower half-plane (without rigid body rotation of the upper half-plane) is unknown. However, it is equal to the resultant moment of the contact pressure, which can be calculated at the end of the solution through the equilibrium equation of moments (see Table 1). It is obvious that for the symmetric indentation, the planar moment M will be zero. In the second and third stages of loading, the monotonically oscillating tangential force Q is applied in such a way that no rigid body motion is produced. In reality, these specified conditions and the basic theory associated with them are the same as in our previously published works [24,25,26] that are summarized in Table 1.

Fig. 1
figure 1

Schematic configuration of multiple contacts between two half-planes (1) and (2): a Initial contact points before loading, b Discrete contact zones after loading, assuming vertical indentation

Full size image
Table 1 A summary of problem specifications
Full size table

During the first stage of loading, the full stick state occurs in each contact zone. In the second stage of loading, slip initially occurs in the smooth edges or nonsingular edges. Subsequently, by increasing the tangential force, the stick zones shrink, and slip zones are created and grow inward of the contact zones. Therefore the number of the slip zones is the same as the number of the nonsingular edges. In the presence of the Coulomb friction with the constant coefficient \(\mu \), while \(Q<\mu P_0 \), the partial slip state occurs. However, for loading path defined in Table 1, slip does not occur in the sharp edges or singular edges unless \(Q=\mu P_0\) that is the full slip state and hence any singular edge of a contact zone is a singular edge of its stick zone as well. Consequently, in any complete contact zone, the full stick state occurs while \(Q<\mu P_0 \) [13, 15]. In other words, in any incomplete contact zone with two nonsingular edges, the partial slip state occurs with two slip zones and only one inner stick zone. In any incomplete contact zone with one nonsingular edge and one singular edge, the partial slip state occurs with one slip zone and one stick zone. In any complete contact zone with two singular edges, the partial slip state theoretically does not occur [13, 15]. Therefore, in the partial slip state or in the full stick state of multiple contacts, the number of the stick zones is the same as the number of the contact zones. Moreover, the number of the nonsingular edges of the stick zones is the same as the number of the nonsingular edges of the contact zones. According to the well-known Cattaneo problem [15], in the second stage of loading, the shear function q(x) in the stick area is considered as the aggregate of the slippery shear function \(-\mu p(x)\) and the corrective shear function \(q{*}(x)\) (see Table 1).

In the third stage of loading, initially the full stick state occurs in each contact zone. Subsequently, by further reduction in Q back-slip occurs and slip zones are created afresh whereas the sign of the slippery shear function in the slip zones changes. In this stage of loading, the shear function q(x) can be obtained by applying a superposition such a way that a reverse shear function with the slippery shear function \(2\mu p(x)\), and the corrective shear function \(-2q{*}(x)\) in the new stick area S, is superimposed on the shear function at the end of the second stage of loading with the slippery shear function \(-\mu p(x)\),and the corrective shear function \(q_0 {*}(x)\) in the stick area \(S_{0}\) [5] (see Table 1).

Fig. 2
figure 2

Multiple straight domains for the Plemelj and the Riemann–Hilbert problems

Full size image

3 Pressure and shear distribution functions

The general form of the inverse of a singular integral equation of the first kind in the straight domain L (see Fig. 2) is obtained by utilizing the known Plemelj formula and the general solution of the inhomogeneous Riemann–Hilbert problem [27] as follows:

$$\begin{aligned} \frac{1}{\pi }\int \limits _L {\frac{f(s)}{s-x}} \hbox {d}s=k(x), \Rightarrow f(x)=-\frac{X^{+}(x)}{\pi }\int \limits _L {\frac{k(s)}{X^{+}(s)(s-x)}} \hbox {d}s+F(x)X^{+}(x) , \quad \forall x\in L ; \end{aligned}$$
(1)

where f(x) and k(x) are complex functions of the real variable x and, F(x) is a polynomial with complex coefficients. \(X^{+}(x)\) denotes the limit of the function X(z) of the complex variable z (\(z=x+iy\hbox {; }i=\sqrt{-1})\) as \(z\mathop {\rightarrow }^{y>0}x\in L\), where X(z) is the general solution of the homogeneous Riemann–Hilbert problem as below:

$$\begin{aligned} X(z)=&\ \frac{E(z)}{\prod \limits _{j=1}^n {(z-a_j )^{\frac{1}{2}}(z-b_j)^{\frac{1}{2}}} } =\frac{E(z)}{\prod \limits _{j=1}^n {(r_j^a)^{\frac{1}{2}}\exp ({i\theta _j^a }/2) (r_j^b )^{\frac{1}{2}}\exp ({i\theta _j^b }/2)} } , \nonumber \\&\Rightarrow X^{+}(x) =\frac{-i\exp (-i(n-k)\pi )E(x)}{\sqrt{\left| {\prod \limits _{j=1}^n {(x-a_j )(x-b_j )} } \right| }} =\frac{-i(-1)^{n-k}E(x)}{\sqrt{\left| {\prod \limits _{j=1}^n {(x-a_j ) (x-b_j )} } \right| }};\nonumber \\&z\mathop {\longrightarrow }^{y>0}x\in \left[ {a_k ,b_k } \right] ; \quad k=1,2,\ldots ,n. ; \end{aligned}$$
(2)

and E(z) is a polynomial. Considering Eqs. (1) and (2), the real function p(x) in the \(k^{\mathrm{th}}\) contact zone and the real function \(q{*}(x)\) in the \(k^{\mathrm{th}}\) stick zone can be obtained by inverting the governing singular integral equations for the pressure and corrective shear distribution functions (see Table 1), as below:

$$\begin{aligned} p(x)= & {} \overline{X} _0 (x,a,b)\frac{\sum \limits _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _0 (s,a,b)(s-x)}\hbox {d}s+f_{n-1} (x)} } }{-(-1)^{n-k}\pi A} , \quad \forall x\in \left[ {a_k ,b_k } \right] , \quad k=1,2, \ldots ,n.; \end{aligned}$$
(3)
$$\begin{aligned} q{*}(x)= & {} \mu \overline{X} _0 (x,c,d)\frac{\sum \limits _{m=1}^n {\int _{ c_m}^{ d_m } {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _0 (s,c,d)(s-x)}\hbox {d}s+I_{n-1} (x)} } }{-\pi A(-1)^{n-k}}, \quad \forall x\in \left[ {c_k ,d_k } \right] ,\quad k=1,2, \ldots ,n.; \end{aligned}$$
(4)

where functions \(f_{n-1} (x)\) and \(I_{n-1}(x)\) are polynomials of order \(n-1\) with n arbitrary real constants, \(\frac{1}{\overline{X} _0 (x,a,b)}=\sqrt{| {\prod \limits _{j=1}^n {(x-a_j )(x-b_j )} } |}\) and \(\frac{1}{\overline{X} _0 (x,c,d)}=\sqrt{| {\prod \limits _{j=1}^n {(x-c_j )(x-d_j )} } |}\). Equation (3) is the same relation Shtajerman [1] acquired. Equations (3) and (4) are not the most general form of the inverse of the governing singular integral equations for the pressure and corrective shear distribution functions in Table 1, as Eq. (1) is. However, they are the general form of the traction distribution functions in uncoupled plane contact problems which satisfy boundary conditions in remote areas. According to Flamant’s solution the interior stress and displacement fields have to be zero in remote areas [5].

4 Side conditions

Assuming n is the number of the contact and stick zones, n unknown real constants exist in whichever of the functions \(f_{n-1}(x)\) (see Eq. (3)) and \(I_{n-1}(x)\) (see Eq. (4)). The positions of the singular edges are immobile during loading and the pressure and shear functions at them are theoretically infinite [15]. However, it is obvious that the positions of the nonsingular edges of the contact and stick zones are unknown. Therefore, assuming \(e\ ( 1 \le e\le 2n)\) is the number of the nonsingular edges of the contact and stick zones, \(n+e\) unknown parameters exist in whichever of p(x) and \(q{*}(x)\). These parameters can be obtained through the equilibrium equations of forces and side conditions. Side conditions are extracted by applying boundary conditions at edges. Initially, boundary conditions of the nonsingular edges have to be applied. These conditions for multiple contacts have not been applied as yet. In the next subsection, we apply these conditions and extract new side conditions and name them “the consistency conditions” for multiple contacts.

4.1 Consistency conditions

In any incomplete contact zone, |p(x)| decreases from the inside of the contact zone toward every nonsingular edge. Hence, for any nonsingular edge, one condition has to be applied which makes p(x) be zero at that edge [1]. Assuming \(a_{e1}\) (\(e 1=1,2,{\ldots },n\)) is the horizontal position of one of e nonsingular edges and \(p(a_{e1})=0\) is the first condition applied to p(x), by substituting \(\frac{x-a_{e1} }{(s-a_{e1})(s-x)} +\frac{1}{s-a_{e1}}\) for \(\frac{1}{s-x}\) in Eq. (3) and applying \(p(a_{e1})=0\), it can be deduced:

$$\begin{aligned} f_{n-1} (a_{e1} )=\sum \limits _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{-(-1)^{n-m}{h}'(s)}{\overline{X} _0 (s,a,b)(s-a_{e1} )}\hbox {d}s} } =E,\Rightarrow f_{n-1} (x)-E=(x-a_{e1} )f_{n-2} (x) ; \end{aligned}$$
(5)

therefore p(x) that satisfies \(p(a_{e1})=0\) is written as:

$$\begin{aligned} p(x)=\overline{X} _1 (x,a,b)\frac{\sum \limits _{m=1}^n {\hbox {sign}_a (m-e1) \int _{a_m }^{ b_m } {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _1 (s,a,b)(s-x)}\hbox {d}s+f_{n-2} (x)} } }{-\pi A(-1)^{n-k}\hbox {sign}_a (k-e1)}, \quad \forall x\in \left[ {a_k ,b_k } \right] , \quad k=1,2, \ldots ,n.;\nonumber \\ \end{aligned}$$
(6)

where function \(f_{n-2} (x)\) is a polynomial of order \(n-2\) with \(n-1\) arbitrary real constants and \(\overline{X} _1 (x,a,b)=| {x-a_{e1} } | \overline{X} _0 (x,a,b) \). sign\(_{a}(k-e\)1) represents the sign of (\(x-a_{e1}\)) for \(x\in [a_{k}, b_{k}]\). So for \(k=e1\), \(\hbox {sign}_{a}(0)\) is positive, because \(a_{e1}\) is the horizontal position of the left edge of the \(e1^{\mathrm{th}}\) contact zone. Similarly, for the second nonsingular edge with the horizontal position \(b_{e2} (e2=1 , 2, \ldots ,n )\), \(p(b_{e2})=0\) is applied to p(x) in Eq. (6) and the form of p(x) that satisfies \(p(a_{e1})=0\) and \(p(b_{e2})=0\) is obtained:

$$\begin{aligned} p(x)=\frac{\sum \limits _{m=1}^n {\hbox {sign}_a (m-e1)\hbox {sign}_b (m-e2)\int _{ a_m }^{ b_m } {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _2 (s,a,b)(s-x)}\hbox {d}s} } +f_{n-3} (x)}{\frac{-\pi A(-1)^{n-k}\hbox {sign}_a (k-e1)\hbox {sign}_b (k-e2)}{\overline{X} _2 (x,a,b)}}, \;\, \forall x\in \left[ {a_k ,b_k } \right] , \quad k=1,2, \ldots ,n.;\nonumber \\ \end{aligned}$$
(7)

where function \(f_{n-3} (x) \) is a polynomial of order \(n-3\) with \(n-2\) arbitrary real constants and \(\overline{X} _2 (x,a,b)=| {x-b_{e2} } | \overline{X} _1 (x,a,b)\). \(\hbox {sign}_{b}(k-e2)\) represents the sign of (\(x-b_{e2}\)) for \(x\in [a_{k},b_{k}]\). So for \(m=e2\), \(\hbox {sign}_{b}(0)\) is negative, because \(b_{e2}\) is the horizontal position of the right edge of the \(e2^{\mathrm{th}}\) contact zone. Analogously, for other nonsingular edges, this condition is applied to p(x) successively. If \(e\ge n\), by applying the \(n^{\mathrm{th}}\) condition, the polynomial disappears. For \(e>n\), it is assumed that \(\gamma _1 ,\gamma _2 , \ldots ,\gamma _{e-n} \) are the horizontal positions of the nonsingular edges that the condition \(p(x)=0\) at them has not been applied yet. Henceforth, by applying the condition \(p(x)=0\) at each \(\gamma _j \) (\(j=1,2,{\ldots },e-n\)), one side condition is obtained. Accordingly after applying the \((n+1)^{\mathrm{th}}\) to \((n+k_{0})^{\mathrm{th}}\) conditions to p(x) at \(\gamma _1 ,\gamma _2 , \ldots ,\gamma _{k_0 } \), \(k_{0}\) side conditions are achieved as below:

$$\begin{aligned} E^{k_0 }=\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{{h}'(s)\prod \limits _{j=1+k_0 }^{e-n} {(s-\gamma _j )} \prod \limits _{j=1}^{2n-e} {(s-\eta _j )} }{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}} } \hbox {d}s=0 ,\quad 1\le k_0<e-n ,\quad n<e<2n ; \end{aligned}$$
(8)

where \(\overline{X} _{2n} (x,a,b)=\sqrt{\left| {\prod \limits _{j=1}^n {(x-a_j )(x-b_j )} } \right| }\) and \(\eta _1 ,\eta _2 , \ldots ,\eta _{2n-e} \) are the specified horizontal positions of the singular edges that the condition \(p(x)=0\) at them cannot be applied. It is obvious that after applying the condition \(p(x)=0\) at all nonsingular edges, \(e-n\) side conditions are extracted. For \(k_{0}=e-n\), applying the \(e^{\mathrm{th}}\) condition to p(x) at \(\gamma _{e-n} \) gives the \((e-n)^{\mathrm{th}}\) side condition as below:

$$\begin{aligned} E^{e-n}=\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )}}{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s} } =0. \end{aligned}$$
(9)

These side conditions are independent but apparently their construction is dependent on the arrangement of applying the mentioned conditions to p(x). However, by performing a number of mathematical operations, a worthier form of these conditions can be deduced. Considering relation (8), it can be said that for \(k_{0}=e-n-1\), applying the \((e-1)^{\mathrm{th}}\) condition to p(x) at \(\gamma _{e-n-1} \) gives the \((e-n-1)^{\mathrm{th}}\) side condition as below:

$$\begin{aligned} E^{e-n-1}= & {} \sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{{h}'(s) (s-\gamma _{e-n} )\prod \limits _{j=1}^{2n-e} {(s-\eta _j )} }{(-1)^{n-m} \overline{X}_{2n} (s,a,b)}\hbox {d}s} } =\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{s{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )}}{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s-\gamma _{e-n} E^{e-n}} } =0, \nonumber \\&\Rightarrow E^{e-n-1}=\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{s{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )}}{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s} } =0; \end{aligned}$$
(10)

subsequently for \(k_{0}=e-n-2\), applying the \((e-2)^{\mathrm{th}}\) condition to p(x) at \(\gamma _{e-n-2} \) gives the \((e-n-2)^{\mathrm{th}}\) side condition as below:

$$\begin{aligned} E^{e-n-2}= & {} \sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{{h}'(s)(s-\gamma _{e-n} )(s-\gamma _{e-n-1}) \prod \limits _{j=1}^{2n-e} {(s-\eta _j )} }{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s} } \nonumber \\= & {} \sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{s^{2}{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )}}{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s-(\gamma _{e-n} +\gamma _{e-n-1} )E^{e-n-1}+\gamma _{e-n} \gamma _{e-n-1} E^{e-n}} } =0 ,\nonumber \\&\Rightarrow E^{e-n-2}=\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{s^{2}{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )}}{(-1)^{n-m}\overline{X} _{2n} (s,a,b)}\hbox {d}s} } =0; \end{aligned}$$
(11)

accordingly, \(e-n\) side conditions can be rewritten as:

$$\begin{aligned} E^{e-n-k_0 +1}=\sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{s^{k_0 -1}{h}'(s)\prod \limits _{j=1}^{2n-e} {(s-\eta _j )} }{(-1)^{n-m} \overline{X}_{2n} (s,a,b)}\hbox {d}s} } =0 ,\quad k_0 =1 , 2, \ldots ,e-n,\quad n<e<2n . \end{aligned}$$
(12)

Side conditions (12) are titled “the consistency conditions” and are independent of the arrangement of applying the mentioned conditions to p(x). Assuming \(e=2n\), the completely nonsingular form of p(x) is written as:

$$\begin{aligned} p(x)=\overline{X} _{2n} (x,a,b)\frac{\sum \limits _{m=1}^n {\int _{ a_m }^{ b_m} {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _{2n} (s,a,b)(s-x)}\hbox {d}s} }}{-\pi A(-1)^{n-k}}, \quad \forall x\in \left[ {a_k ,b_k } \right] , \quad k=1,2, \ldots ,n.; \end{aligned}$$
(13)

with n consistency conditions:

$$\begin{aligned} \sum _{m=1}^n {\int _{ a_m }^{ b_m } {\frac{(-1)^{n-m}s^{k_0 -1}{h}'(s)}{\overline{X} _{2n} (s,a,b)}\hbox {d}s} } =0 ,\quad k_0 =1 , 2, \ldots ,n. \end{aligned}$$
(14)

If \(n=1\), \(e=2\), \(a_{1}=a\) and \(b_{1}=b\), one consistency condition is extracted from relation (14) that is the same consistency condition previously acquired for an incomplete single contact [5]. Assuming \(n=2\), \(e=4\), \(-a_{1}=b_{2}=b\) and \(-b_{1}=a_{2}=a\), two consistency conditions are extracted from relation (14), but they are not independent and yield one consistency condition that is the same consistency condition acquired for incomplete symmetric double contacts in the previous work [24].

Due to the necessity of the continuity of the shear function q(x) in a contact zone, in any nonsingular edge of every stick zone \(q{*}(x)\) has to be zero. Therefore, for any nonsingular edge of the stick zones, one condition has to be applied which makes \(q{*}(x)\) be zero at that edge. These conditions can be applied to \(q{*}(x)\) at e nonsingular edges of the stick zones analogously to the aforementioned manner. If \(e=2n\), the completely nonsingular form of \(q{*}(x)\) is written as:

$$\begin{aligned} \frac{q{*}(x)}{\mu }=\overline{X} _{2n} (x,c,d)\frac{\sum \limits _{m=1}^n {\int _{ c_m }^{ d_m } {\frac{(-1)^{n-m}{h}'(s)}{\overline{X} _{2n} (s,c,d)(s-x)}\hbox {d}s} } }{-\pi A(-1)^{n-k}}, \quad \forall x\in \left[ {c_k ,d_k } \right] , \quad k=1,2, \ldots ,n.; \end{aligned}$$
(15)

with n consistency conditions:

$$\begin{aligned} \sum _{m=1}^n {\int _{ c_m }^{ d_m } {\frac{(-1)^{n-m}s^{k_0 -1}{h}'(s)}{\overline{X} _{2n} (s,c,d)}\hbox {d}s} } =0 ,\quad k_0 =1 , 2, \ldots ,n. ; \end{aligned}$$
(16)

where \(\overline{X} _{2n} (x,c,d)=\sqrt{| {\prod \limits _{j=1}^n {(x-c_j)(x-d_j )}}|}\). It is important to mention that Eqs. (13) and (15) are the inverse of the governing singular integral equations for the pressure and corrective shear distribution functions (see Table 1) even if consistency conditions (14) and (16) are not met. However applying the consistency conditions is essential in order to have access to the positions of the nonsingular edges such that the related boundary conditions at these edges and at infinity are simultaneously satisfied, when \(e > n\).

Henceforward, other boundary conditions and equilibrium of forces can be applied.

4.2 Conditions of rigid interconnections

In multiple contacts, in addition to the equilibrium equations and consistency conditions (for \(e > n)\), conditions of rigid interconnections are essential to determine the unknown parameters. The physical reasoning of these conditions is that multiple contacts occur between two solid bodies [1, 3]. There are \(n-1\) conditions of rigid interconnections to determine the unknown parameters in p(x). These conditions are obtained through integrating both sides of the governing singular integral equation for the pressure distribution function (see Table 1), over each noncontact zone between two successive contact zones. They can be written as follows:

$$\begin{aligned}&-\frac{A}{\pi }\int _{ b_m }^{ a_{m+1} } {\int \limits _L {\frac{p(s)}{x-s}} \hbox {d}s} \hbox {d}x=\int _{ b_m }^{ a_{m+1} } {{h}'(x)} \hbox {d}x=h(a_{m+1} )-h(b_m ) \nonumber \\&\quad \Rightarrow \frac{A}{\pi }\int _{ b_m }^{ a_{m+1}} {\int \limits _L {\frac{p(s)}{s-x}} \hbox {d}s} \hbox {d}x=h_0 (a_{m+1} ) -h_0 (b_m ),\quad m=1 , 2, \ldots ,n-1. \end{aligned}$$
(17)

Similarly, \(n-1\) conditions of rigid interconnections exist to determine the unknown parameters in \(q{*}(x)\) for the second and third stages of loading. These conditions are obtained through integrating both sides of the governing singular integral equation for the shear distribution function (see Table 1), over each nonstick zone between two successive stick zones. They can be written as below:

$$\begin{aligned} \frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _L {\frac{q(s)}{x-s}} \hbox {d}s} \hbox {d}x=\int _{ d_m }^{ c_{m+1} } {{g}'(x)} \hbox {d}x=g(c_{m+1} )-g(d_m ) , \quad m=1 , 2, \ldots ,n-1. \end{aligned}$$
(18)

Considering that the slip function g (x) in the stick zones is zero during the second stage of loading (see Table 1), Eq. (18) in the second stage of loading can be rewritten as below:

$$\begin{aligned}&\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{(x-s)}\hbox {d}s} } \hbox {d}x-\frac{A}{\pi }\mu \int _{ d_m }^{ c_{m+1} } {\int \limits _L {\frac{p(s)}{(x-s)}\hbox {d}s} } \hbox {d}x= 0 \nonumber \\&\quad \Rightarrow -\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{\mu (x-s)}\hbox {d}s} } \hbox {d}x=\int _{ d_m }^{ c_{m+1} } {{h}'(x)} \hbox {d}x=h(c_{m+1} )-h(d_m ) \nonumber \\&\quad \Rightarrow \frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{\mu (s-x)}\hbox {d}s} } \hbox {d}x=h_0 (c_{m+1} )-h_0 (d_m ) ,\quad m=1 , 2, \ldots ,n-1. \end{aligned}$$
(19)

Considering that the slip function g(x) in the stick zones during the third stage of loading is equal to the slip function at the end of the second stage of loading [15], Eq. (18) in the third stage of loading can be rewritten as below:

$$\begin{aligned}&-2\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{(x-s)}\hbox {d}s} } \hbox {d}x+\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _{S_0 } {\frac{q_0 {*}(s)}{(x-s)}\hbox {d}s} } \hbox {d}x+\frac{A}{\pi }\mu \int _{ d_m }^{ c_{m+1} } {\int \limits _L {\frac{p(s)}{(x-s)}\hbox {d}s} } \hbox {d}x \nonumber \\&\quad =\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _{S_0 } {\frac{q_0 {*}(s)}{(x-s)}\hbox {d}s} } \hbox {d}x-\frac{A}{\pi }\mu \int _{ d_m }^{ c_{m+1} } {\int \limits _L {\frac{p(s)}{(x-s)}\hbox {d}s} } \hbox {d}x \Rightarrow -\frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{\mu (x-s)}\hbox {d}s} } \hbox {d}x\nonumber \\&\quad =-\frac{A}{\pi }\mu \int _{ d_m }^{ c_{m+1} } {\int \limits _L {\frac{p(s)}{(x-s)}\hbox {d}s} } \hbox {d}x=\int _{ d_m }^{ c_{m+1} } {{h}'(x)} \hbox {d}x=h(c_{m+1} )-h(d_m ) \nonumber \\&\qquad \Rightarrow \frac{A}{\pi }\int _{ d_m }^{ c_{m+1} } {\int \limits _S {\frac{q{*}(s)}{\mu (s-x)}\hbox {d}s} } \hbox {d}x=h_0 (c_{m+1} )-h_0 (d_m ), \quad m=1 , 2, \ldots ,n-1. \end{aligned}$$
(20)

5 The mathematical expression of the principle of Jäger and Ciavarella

By considering the similarity between the mathematical processes of having access to p(x), \(q{*}(x)\) and their unknown parameters, it can be said that if p(x) in the contact area can be expressed as a function like \(T(x,\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P)\) during the first stage of loading (\(\lambda _1 ,\lambda _2 ,\ldots \) are geometric parameters), \(q{*}(x)\) in the stick area can be expressed as \(\mu T(x,\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P_0 -Q/\mu )\) during the second stage of loading and \(\mu T(x,\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P_0 -{(Q_0 -Q)}/{2\mu })\) during the third stage of loading . In reality, this can be the mathematical expression of the principle of Jäger and Ciavarella for quasi-static multiple contact problems between two elastically similar half-planes under the constant normal (including applied moments) and oscillatory tangential loading, when the number of the growing contact zones during the vertical indentation in the first stage of loading remains constant. Furthermore, it can be said that if the extent of the \(j^{\mathrm{th}}\) contact zone (\(b_j -a_j\)) can be expressed as a function like \(R_j (\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P)\) during the first stage of loading, the extent of its stick zone (\(d_j -c_j\)) can be expressed as \(R_j (\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P_0 -Q/\mu )\) during the second stage of loading and, \(R_j (\eta _1 ,\eta _2 ,\ldots ,\eta _{2n-e} ,\lambda _1 ,\lambda _2 ,\ldots ,A,P_0 -{(Q_0 -Q)}/{2\mu })\) during the third stage of loading . Therefore, it can be deduced conveniently that all of the contact zones reach the full slip state simultaneously.

6 Discussion

Generally, it would be mistaken to assume nonsingular edges of incomplete multiple contacts lie on a horizontal line that is parallel to the flat surface of the lower half-plane (before loading). Although within the contact zones h(x) can be equated with the indentation depth (\(\delta \)) minus the value of the overlap of two half-planes if they are allowed to interpenetrate each other freely, the actual extent of the contact zones during the normal loading is not the same as the overlapped extent in the free interpenetration figure [5] (see Fig. 3(a)). Making this mistaken assumption gives relations between roots of \(h_0 (x)-\delta \) that can be used to determine the positions of the nonsingular edges, regardless of the consistency conditions and the conditions of rigid interconnections. Westergaard [17] applied this assumption to indenter profiles that have the regular sinusoidal form. Hence the extent of the contact zones can be obtained only by the equilibrium equations, regardless of the consistency conditions and the conditions of rigid interconnections. This assumption may be in accordance with these side conditions in Westergaard’s problem as it occurs in every symmetric single contact problem (see Fig. 3(b)) and in the symmetric indentation of a flat surface by a bi-quadratic punch with the initial gap function \(h_0(x)={(x^{2}-\bar{{c}}^{2})^{2}}/{8R\bar{{c}}^{2}}\), where \(2\bar{{c}}\) is the horizontal distance between two initial contact points and R is the curvature radius of the indenter profile at two initial contact points. For this geometry, due to the symmetry (\(a_2 =-b_1 =a\) and \(b_2 =-a_1 =b\)), two consistency conditions extracted from relation (14) are not independent and yield one consistency condition as \(b^{2}+a^{2}=2\bar{{c}}^{2}\). Gladwell [3] solved this geometry by utilizing the Muskhelishvili potential function approach to obtain the pressure function and extracted this side condition by applying the boundary condition of remote areas to the Muskhelishvili potential function. This side condition is the relation between roots of \({(x^{2}-\bar{{c}}^{2})^{2}}/{8R\bar{{c}}^{2}}-\delta \) but as mentioned above, it cannot be applied to any indenter profile.

Fig. 3
figure 3

Comparison of the actual extent and the overlapped extent of the contact zone: a An asymmetric single contact. b A symmetric single contact

Full size image

In order to investigate the error that is caused by this assumption, it is applied to the symmetric indentation of a flat surface by two rigidly interconnected wedge-shaped punches with the small inner angles \(\phi _1\) and the small outer angles \(\phi _2\) and the horizontal distance \(2\bar{{c}}\) between two singular initial contact points (see Fig. 4). This geometry was solved in the previous study and the consistency condition was extracted as below [24]:

$$\begin{aligned} E(a,b)=\tan (\phi _1 )\int _{ a}^{ \bar{{c}}} {\frac{\hbox {d}x}{\sqrt{(x^{2}-a^{2})(b^{2}-x^{2})}}-\tan (\phi _2 ) \int _{\bar{{c}}}^{ b} {\frac{\mathrm{d}x}{\sqrt{(x^{2}-a^{2})(b^{2}-x^{2})}}} } =0; \end{aligned}$$
(21)

moreover, there is one condition of rigid interconnection that will be satisfied automatically due to the symmetry. Accordingly, the consistency Eq. (21) is utilized with the equilibrium equation of normal forces to determine the actual extent of the contact zones. These equations include elliptical integrals, hence the actual extent cannot be expressed in terms of an explicit function of the normal force P. However, a simple iterative algorithm, which was brought in the previous study [24], gives the consistent actual values of a and b that satisfy the consistency Eq. (21). Subsequently, the equilibrium equation of normal forces gives the values of P versus the corresponding values of the actual extent (\(b_{\mathrm{Actual}}-a_{\mathrm{Actual}}\)). Now the condition \(H_L (a,b)=\tan (\phi _2 )b+\tan (\phi _1 )a-(\tan (\phi _2 )+\tan (\phi _1 ))\bar{{c}}=0\) that makes the edges of the contact zones lie on a horizontal line, is considered instead of the consistency condition to calculate the overlapped extent of the contact zones during the normal loading. Initially, the overlapped values of a and b that satisfy this condition are calculated. Then, the equilibrium equation of normal forces is utilized to give the values of P versus the corresponding values of the overlapped extent (\(b_{\mathrm{Overlapped}}-a_{\mathrm{Overlapped}}\)).

Fig. 4
figure 4

Symmetric indentation of a flat surface by two rigidly interconnected wedge-shaped punches

Full size image

In Fig. 5, the overlapped extent is compared with the actual extent calculated through the consistency condition, for various geometric parameters. The percent error, which is expressed as \(Pe=\frac{\hbox {Actual extent}\,-\hbox {Overlapped extent}}{\hbox {Actual extent}}\times 100\), is calculated in various states and it is concluded that for given values of \(\phi _1\) and \(\phi _2\) the error depends on the dimensionless actual extent, which is expressed as \(\kappa =\frac{\hbox {Actual extent}}{\bar{{c}}}\), as indicated in Fig. 5d.

Fig. 5
figure 5

Comparison of the actual and overlapped extent of the contact zones in the symmetric indentation of a flat surface by two rigidly interconnected wedge-shaped punches: a\(\phi _1 = 0.11\ \hbox {rad}\), \(\phi _2 = 0.07\ \hbox {rad}\), b\(\phi _1 =\phi _2 = 0.18\ \hbox {rad}\), c\(\phi _1 = 0.07\ \hbox {rad}\), \(\phi _2 = 0.11\ \hbox {rad}\), d Percent error versus the dimensionless actual extent

Full size image

7 Conclusions

In the present study, the consistency conditions were derived through an analytical approach. These conditions accompanied with the conditions of rigid interconnections and the equilibrium equations form a system of equations that may be utilized to determine the extent of the contact and stick zones during the loading in a multiple contact problem with nonsingular edges when the number of them exceeds the number of discrete zones. If it is possible to find the uniquely correct solution of this system of equations, the positions of the nonsingular edges are calculated. Accordingly, the values of the pressure and shear functions in any nonsingular point of the contact and stick zones can be calculated by numerical computation of the integrals of the right-hand side of Eqs. (13) and (15), even if there is not a closed form solution for these integrals (as it is performed in the previous study [24]). Undoubtedly, having access to the solution of this system of equations in a more general problem is not a straightforward task. However, it is desired to improve numerical and semi-analytical solutions of quasi-static frictional multiple contacts by utilizing the consistency conditions and the mathematical expression of the principle of Jäger and Ciavarella in future researches.

Finally, the result of Sect. 6 shows that for the weak normal loading, the approximated extent of the contact zones in a multiple contact problem with nonsingular edges may be estimated conveniently by assuming that the extent of the contact zones is the same as the overlapped extent in the free interpenetration figure, regardless of the consistency conditions and the conditions of rigid interconnections. Obviously, the error caused by this assumption depends on geometric parameters. However, it can be said that for a given value of the normal force, this error increases remarkably with decreasing the distance between the contact zones.