Elastic–Plastic Sinusoidal Waviness Contact Under Combined Normal and Tangential Loading

Abstract

The behavior of an elastic plastic contact between a deformable three-dimensional sinusoidal asperity and a rigid flat under combined normal and tangential loading is investigated using the finite element method. The sliding inception is determined by the maximum shear stress criterion. The resulting junction growth and static friction coefficient are investigated. It is found that for a general case, at the low dimensionless contact pressures, the static friction coefficient decreases sharply with increasing contact pressure. However, at the medium contact pressures, the static friction coefficient nearly approaches a constant value (around 0.23). Nevertheless, as the contact pressure further increases, the static friction coefficient keeps on reducing at a linear rate. The effects of material properties, geometric properties and critical shear strength on the static friction coefficient are also studied. An empirical expression for the static friction coefficient is provided.

1 Introduction

The elastic–plastic contact of spheres under combined normal and tangential loading has been studied quite extensively, from the classical work of Mindlin [2] and Mindlin and Deresiewicz [3]. Mindlin used a predefined friction coefficient between two surfaces. He set an upper limit on the local shear stress, which is equal to the local normal pressure multiplied by the coefficient of friction. Whenever the computed shear stress exceeds the upper limit, local slip takes place. This is known as the local Coulomb friction law. The sliding of the entire surface occurs when the shear stresses over the entire contact area reach the upper limit, satisfying the Coulomb friction law. Mindlin also obtained the surface shear stress distribution in full stick and partial slip conditions. Keer et al. [4] followed Mindlin’s approach, finding the region for complete sliding of elastic bodies in contact. Hamilton [5] found the yield inception of spherical sliding contact by using Hertz contact pressure and the Mindlin shear stress distribution. Hills et al. [6] modified the stress distribution by considering the effect of the shear stress on surface displacements for two dissimilar elastic cylinders.

Bowden and Tabor [7] presented a different approach, which considered the start of surface slip in relation to the mechanical properties rather than a local friction law as in [2]. They used a failure mechanism related to the material properties to determine the sliding inception. They suggested that the tangential load at sliding inception was equal to the real contact area times the material shear strength. Courtney-Pratt and Eisner [8] measured the contact area of a metallic sphere pressed normally and segmentally again a smooth flat. They observed an increase in the contact area when the tangential load was increased. Tabor [9] defined this phenomenon as “junction growth,” explaining that a contact area that has already yielded plastically under a given preload must grow when it is subjected to an additional tangential loading, because the tangential loading can reduce its mean contact pressure in order to accommodate the additional shear stresses. Chang et al. [10] treats sliding inception as a failure mechanism based on that failure of small junctions between contact surfaces. They gave an explicit formula to calculate the maximum tangential loads that a single spherical asperity can support for a given preload against a rigid flat before sliding inception. Then, the total tangential load for the rough surface contact was obtained by using a statistical method. Kogut and Etsion [11] presented a semi-analytical approximate solution for the sliding inception for both elastic and plastic cases. They treated the sliding inception as a failure mechanism, and failure occurs either on the contact area or below it, depending on the status of normal loading.

Brizmer et al. [12] presented a new approach to determine the sliding inception for the full stick condition, which is known as the stiffness criterion. They considered that the sphere starts sliding when the instantaneous tangential stiffness is equal to a small predefined value. By using this criterion, Brizmer et al. [12] investigated several parameters such as junction stiffness, static friction force and static friction coefficient. The evolution of the contact area was also investigated in [13], and an empirical relation between the contact area and the normal preload was found by fitting the FEM results. The contact of a deformable sphere under combined normal and tangential loading by a rigid flat in the pre-sliding regime was also investigated by Zolotarevskiy et al. [14], and they developed a model for the evolution of static friction force and stiffness in the pre-sliding regime.

Some researchers also considered the partial slip condition, which means there is some local slip even though gross slip does not happen. Eriten et al. [15] developed a physics-based model. In their model, local Coulomb’s law was used to govern the interfacial strength. They set the product of the friction coefficient and normal stress to a critical friction shear stress. Following this approach, Patil and Eriten [16] showed that the static friction coefficient strongly depends on the interfacial strength, a material property. Mulvihill et al. [17] set the interfacial adhesional shear strength equal to a few different values related to the bulk yield strength. Based on the von Mises theory, Wu et al. [18] fixed the strength equal to a constant value and proposed a frictional model that transitioned from the KE model [11] to the BKE model [12] for the partial slip condition.

Several models that predict the static friction for elastic–plastic contact of rough surfaces under the full stick condition have been developed. These models incorporate the results of finite element analysis for different parameters, such as contact, adhesion and sliding inception of a single elastic–plastic spherical asperity in a statistical representation of surface roughness. Kogut et al. [19] developed a model that shows the strong effect of the external force and nominal contact area. They also found that the main dimensionless parameters affecting the static friction coefficient are plasticity index and the adhesion parameter. Cohen et al. [20] found the static friction is strongly affected by normal load, nominal contact area, mechanical properties, and surface roughness. Cohen et al. [21] investigated the effect of surface roughness on static friction and junction growth of an elastic–plastic spherical contact with a low plasticity index. Li et al. [22] extended the consideration of the plasticity index to a higher range. In these papers, junction growth was also investigated. In 2011, Ibrahim-Dickey et al. [23] also conducted static friction measurements of tin and used the Li et al. model [22] to compare to. It should be noted, however, that in all of these papers the asperities were modeled by spheres.

All of the previous works assumed a spherical asperity. However, real asperities on surfaces might not be shaped like spheres, especially at their base. At lower loads where the asperity base does not influence the result, the sphere works well. However, at higher loads, the effect of the complete asperity geometry and interaction with adjacent asperities becomes important. Even though statistical models use the assumption that only the peaks of the asperities are in contact, the asperities can still be heavily loaded and deformed (practically crushed in some cases). Recently, Greenwood [24] at the 2015 Leeds–Lyon Tribology Symposium suggested that more realistic asperity models like wavy surfaces should be considered. The current work uses a sinusoidal or wavy geometry. Sinusoidal contact has been studied since the works of Westergaard [25] and Johnson, Greenwood, Higginson (1985) [1]. Westergaard [25] first solved the two-dimensional elastic sinusoidal contact. Johnson, Greenwood, and Higginson (JGH) [1] developed asymptotic solutions for the elastic contact of a three-dimensional sinusoidal profile. In their work, they provided a relationship between pressure and contact area for two limiting regimes: at the early stages of contact and near complete contact. Jackson and Streator [26] provided an empirical equation based on the experimental and numerical data, linking the two regimes. They investigated the analysis between rough surfaces that considered asperities using a sinusoidal geometry and proposed a non-statistical multiscale model to predict the real contact area as a function of normal contact load.

In addition, for spectral-based and multiscale rough surface contact models, it is logical to use sinusoidal shapes for the asperities because the surface is often treated as a series of superposed harmonic waves (i.e., Fourier series or for fractals, the Mandelbrot function). For either statistical or multiscale models when the sinusoidal asperities are under heavy loads, they behave much differently than spheres due to the difference in geometry and also their periodic nature. The periodicity may also capture the effect of adjacent asperities better than spheres. With the development of more multiscale models between rough surfaces [27, 28], which could be applied to electrical [29] and thermal contact [30, 31], the contact problem of an elastic–plastic deformable sinusoidal surface and rigid flat was investigated by several researchers [32–35]. Gao et al. [32] found a relationship between contact pressure, contact size, effective indentation depth, and residual stress for the 2-D sinusoidal contact. Krithvasion and Jackson [33] provided an approximate solution for the elastic regimes and an empirical expression for predicting the contact area as a function of contact pressure. Jackson et al. [34] provided an analytical expression for the average pressure that causes complete contact. Rostami and Jackson [35] provided close-form equations that predict surface separation and stiffness for both elastic and elastic plastic cases.

As seen from the literature review above, most existing models considering the sinusoidal geometry are only under normal loading. Several researchers have investigated the case of deformable sinusoidal surface in contact with a flat. However, very little work was done on the sinusoidal contact under combined normal and tangential loading. The main goal of this paper is to use the FEM to investigate the contact performance parameters based on junction growth and the static friction coefficient for a deformable sinusoidal surface contacting a rigid flat. These relationships then might be used in spectral and fast Fourier transform (FFT)-based methods for modeling the contact and friction between rough surfaces.

2 Theoretical Model

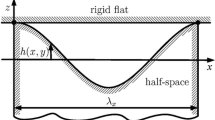
The current analysis use the same geometry used by Johnson et al. [1], Krithivasan and Jackson [33], and Jackson et al. [34], as shown in Fig. 1. The equation defining this sinusoidal surface is described by

$$h = \varDelta \left[ {1 - \cos \left( {\frac{2\pi x}{\lambda }} \right)\cos \left( {\frac{2\pi y}{\lambda }} \right)} \right]$$

(1)

where $h$ is the height of sinusoidal surface from its base, $\varDelta$ is the amplitude of the sinusoidal surface, and $\lambda$ is the wavelength of the sinusoidal surface.

Fig. 1

Topographical depiction of the three-dimensional sinusoidal surface geometry

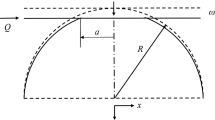
The cross section of a deformable sinusoidal asperity in contact with a rigid flat under combined normal and tangential loading is schematically shown in Fig. 2. The tangential load, $F_{\text{t}}$, is applied gradually, while the normal preload, $F_{\text{n}}$, remains constant. The thick and thin dashed lines show the contours of the sinusoidal asperity before and after applying normal preload, respectively, while the solid line shows the final contour of sinusoidal asperity after the application of the tangential load. The normal load produces an initial interference, $\omega_{0}$, while the additional tangential load combined with the normal preload produces the final interference, $\omega_{\text{s}}$.

Fig. 2

Contact of a deformable sinusoidal surface and a rigid flat under combined normal and tangential loading

2.1 Normal Loading

Complete contact is defined as when there are no gaps remaining between the two surfaces. The average contact pressure that causes complete contact for the elastic case is given by Johnson et al. [1]:

$$p^{*} = \sqrt 2 \pi E^{\prime}\Delta f$$

(2)

They provided two asymptotic solutions to the real contact area as well, which is given by:

when $\bar{p} \ll p^{*}$,

$$\left( {A_{\text{JGH}} } \right)_{1} = \frac{\pi }{{f^{2} }}\left[ {\frac{3}{8\pi }\frac{{\bar{p}}}{{p^{*} }}} \right]^{2/3}$$

(3)

when $\bar{p} \to p^{*}$,

$$\left( {A_{\text{JGH}} } \right)_{2} = \frac{1}{{f^{2} }}\left( {1 - \frac{3}{2\pi }\left[ {1 - \frac{{\bar{p}}}{{p^{*} }}} \right]} \right)$$

(4)

Jackson and Streator [26] provided an empirical fit based on the experimental and numerical data in

$${\text{For:}}\quad \frac{\bar{p}} {p^{*}} < 0.8: \quad A = (A_{\text{JGH}} )_{1} \left( 1 -\left\lceil \frac{\bar{p}} {p^{*}}^{1.51} \right\rceil \right) + ( A_{\text{JGH}} )_{2} \left(\frac{\bar{p}} {p^{*}} \right)^{1.04}$$

(5)

$${\text{For:}}\quad \frac{{\bar{p}}}{{p^{*} }}{ \ge }0.8:\quad A = \left( {A_{\text{JGH}} } \right)_{2}$$

(6)

For the elastic plastic case, Jackson et al. [34] defined a critical amplitude of a sinusoidal surface. When the amplitude is less than this value, the sinusoidal surface deforms elastically, when the amplitude is greater than this value, it deforms plastically. The critical amplitude given in [34] is incorrect, and the corrected equation is given as:

$$\varDelta_{\text{c}} = \frac{\sqrt 2 }{\pi }\frac{{S_{\text{y}} }}{{E^{\prime } }}\frac{1}{{f\left[ {3e^{{ - 2\left( {\upsilon + 1} \right)/3}} + 2\left( {\frac{1 - 2v}{1 - v}} \right)} \right]}}$$

(7)

And the resulting fit equation for contact pressure to cause complete contact is given by:

$$\frac{{p_{\text{ep}}^{*} }}{{p^{*} }} = \left[ {\frac{7.817}{{\left( {\varDelta /\varDelta_{\text{c}} } \right) + 6.817}}} \right]^{1.173} - C_{v} \left( {\frac{\varDelta }{{\varDelta_{\text{c}} }} - 1} \right)^{0.138}$$

(8)

where $C_{v}$ is a function of Poisson’s ratio; it is given in the form:

$$C_{v} = 0.0017\exp \left( {8.09\nu } \right) - 0.0567$$

(9)

Note that when $\varDelta = \varDelta_{c}$, $p_{\text{ep}}^{*} = p^{*}$. Equation (8) results in the same overall prediction as given in [34].

An empirical expression for contact area for elastic plastic sinusoidal contact is obtained by fitting the FEM results by Krithvason and Jackson [33],

$$A = A_{\text{ep}} \left( {1 - \left[ {\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}} \right]^{1.51} } \right) + \left( {A_{\text{JGH}} } \right)_{2} \left( {\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}} \right)^{1.04}$$

(10)

$$A_{\text{ep}} = 2\left( {\frac{{A_{c} }}{2}} \right)^{{\frac{1}{1 + d}}} \left( {\frac{{3\bar{p}}}{{4CS_{y} }}\lambda^{2} } \right)^{{\frac{d}{1 + d}}}$$

(11)

The expression for d is given by:

$$d = C_{1} \left( {\frac{{E^{\prime } }}{{S_{\text{y}} }}\frac{\varDelta }{\lambda }} \right)^{{C_{2} }}$$

(12)

where $C_{1} = 3.8$ and $C_{2} = 0.11$.

Three main contact conditions are generally considered: the perfect slip condition, the full stick condition, and the partial slip condition. The full stick condition implies that the contact points of the surface and the flat are prevented from further relative displacement once touching. While the perfect slip condition assumes no tangential stresses in the contact area. The Eqs. (2–11) are all for the perfect slip condition. The effect of contact conditions and material properties on the termination of elasticity in spherical contact was investigated by Brizmer et al. [36]. They found that the ratios of critical interference and load in the full stick condition over that in the perfect slip condition are independent of material properties except for the Poisson’s ratio. Eriten et al. [37] investigated the influence of friction on the onset of plastic yielding in these three contact conditions.

For the sinusoidal contact, we found that the ratio of complete contact pressure in full stick condition over that in perfect slip is independent of geometry and it is only slightly affected by the material properties, especially the Poisson’s ratio; the average difference is <4%. Hence, the contact pressure that causes complete contact can be considered to be equal to $p_{\text{ep}}^{*}$.

2.2 Combined Normal and Tangential Loading

The behavior of a contact between a deformable elastic plastic sphere and a rigid flat under normal and tangential loading was investigated by several researchers [11–14]. The sliding inception is treated as a failure mechanism based on plastic yield in [11], and sliding might actually initiate in the yielded material below the surface in some cases. The static friction coefficient equation found by fitting to FEM results in [11] is given as:

$$\mu_{\text{s}} = \left\{ {\begin{array}{ll} {0.516 \left( {\frac{{F_{\text{n}} }}{{F_{\text{c}} }}} \right)^{ - 0.345} ,} & {0 \le \frac{\omega }{{\omega_{\text{c}} }} \le 1} \hfill \\ { - 0.007 \left( {\frac{{F_{\text{n}} }}{{F_{\text{c}} }}} \right)^{2.104} + 0.083 \left( {\frac{{F_{\text{n}} }}{{F_{\text{c}} }}} \right)^{1.405} - 0.380 \left( {\frac{{F_{\text{n}} }}{{F_{\text{c}} }}} \right)^{0.701} + 0.822, } & {1 \le \frac{\omega }{{\omega_{\text{c}} }} \le 6.2} \hfill \\ \end{array} } \right.$$

(13)

Considering the full stick contact condition, the contact stiffness criterion was used to determine the sliding inception in [12–14] such that

$$\frac{{\left( {K_{\text{T}} } \right)_{i} }}{{\left( {K_{\text{T}} } \right)_{1} }} \le \alpha$$

(14)

where $\left( {K_{\text{T}} } \right)_{i}$ is the corresponding instantaneous tangential stiffness of the $i$th tangential loading step, and the $\left( {K_{\text{T}} } \right)_{1}$ is the initial tangential stiffness of the joint corresponding the first tangential loading step. And $\alpha$ is a predefined number that was chosen to determine the sliding inception by the criterion, i.e., the spherical asperity initiated sliding when the tangential stiffness drops by a factor $\alpha$. The corresponding tangential force at the moment of initial sliding is the maximum static friction force, $\left( {F_{\text{t}} } \right)_{ \hbox{max} }$.

From [12], the empirical equation of static friction coefficient is given as a function of $\frac{{F_{\text{n}} }}{{F_{\text{c}} }}$

$$\mu_{\text{s}} = 0.27\coth \left( {0.27\left( {\frac{{F_{\text{n}} }}{{F_{\text{c}} }}} \right)^{0.35} } \right)$$

(15)

And as a function of $\frac{\omega }{{\omega_{\text{c}} }}$

$$\mu_{\text{s}} = 0.26\coth \left( {0.27\left( {\frac{\omega }{{\omega_{\text{c}} }}} \right)^{0.46} } \right)$$

(16)

Another method for determining slip between surfaces is the maximum shear stress criterion. There is some local slip even though the gross slip does not happen (i.e., partial slip). A model was proposed by Wu et al. [18], in which the critical friction shear stress $\tau_{\text{c}}$ was set by the shear strength of the weaker material. i.e., once the frictional shear stress in the contact area reaches the shear strength, the local sliding occurs at this element. Once all the elements in the contact slide, the whole surface starts sliding. Considering the partial slip, the static friction coefficient is given by:

$$\mu_{\text{s}} = 0.3\coth \left( {0.57\left( {\frac{\omega }{{\omega_{\text{c}} }}} \right)^{0.41} } \right)$$

(17)

Note that Eqs. (13–17) are for spherical contact, but these equations can still be used for formulating empirical equations for the sinusoidal contact. Equations (13) and (15) are also used to compare with the results in the current work. Once the static friction coefficient is given, the maximum tangential load can be easily obtained by:

$$\left( {F_{\text{t}} } \right)_{\hbox{max} } = \mu_{\text{s}} F_{\text{n}}$$

(18)

3 The Finite Element Model

In the current work, a three-dimensional model was developed and the commercial FEM software ANSYS™ 17.0 was used to further analyze the combined normal and tangential loading of an elastic–plastic sinusoidal contact problem. The three-dimensional mesh consisted of more than 121,000 twenty-node brick elements (Solid 186). The sweep mesh option is selected. Conta 174 and Targe 170 elements formed the contact pair to model interaction between the surfaces. In order to make the simulation more efficient, the contacting surface of the rigid flat was modeled by a single element (Targe 170) with the size that can cover the largest contact area. The contact surface comprised of 174 elements arranged in a uniform mesh of 60 × 120 elements. The rigid target surface was associated with a “pilot node” which is an element with one node, whose motion governs the motion of the entire target surface. Forces and displacements for the entire target surface can be prescribed on just the pilot node. Due to the symmetry about the xz plane, it is sufficient to consider only one half of the sinusoidal volume (see Fig. 3).

Fig. 3

Finite elements model and boundary conditions

The uniform mesh of contact elements on the sinusoidal surface is used to predict the real contact area. By checking the contact status of each element during post-processing, the sticking contact area ratio is the sticking contact area normalized by apparent contact area, and it is given by the number of sticking elements over the total number of elements in contact. Similarly, the sliding contact area ratio is defined as well. The total contact area ratio is equal to the sum of the contact area ratios of sticking and sliding. In other words, the real contact area normalized by the apparent area of contact was given by the ratio of the number of elements in contact to the total number of elements over the surface.

In order to verify the accuracy of the three-dimensional FE model, for the normal loading step, the results in the first normal load for the elastic contact under a normal constant force were obtained and compared with the results in [1]. As shown in Fig. 4, the FEM data differ from the empirical equation slightly, but are in overall good agreement. The FEM results and the equations have the same trend. An average error of only 5% was found between the FEM data and the empirical Eqs. (5–6), but it appears that the FEM results are closer to the JGH data [1].

Fig. 4

Comparison of elastic model with JGH model

In order to verify the methodology of loading the surfaces, the complete contact case ($A_{r} = A_{n}$) was used. A critical interfacial shear strength, $\tau_{\text{c}}$, was defined as $\frac{{S_{\text{y}} }}{\sqrt 3 }$, and the static friction is calculated by: $\left( {F_{\text{t}} } \right)_{\hbox{max} } = \tau_{\text{c}} A_{0}$. As expected, the maximum tangential force extracted from the FEM results is exactly equal to the theoretical value.

A constant normal load, $F_{\text{n}}$, was applied as a single force at the pilot node, and then, a step-wide increase in the tangential displacement $U_{x}$ of the flat was added to simulate the gradually increasing tangential load. The instantaneous tangential force $F_{\text{t}}$ was obtained from the x component of the reaction at the pilot node. The sliding inception occurs when all the individual contact elements are sliding. When this occurs, the static friction coefficient is $\mu_{\text{s}} = \left( {F_{\text{t}} } \right)_{\hbox{max} } /F_{\text{n}}$.

For volume below the sinusoidal surface, the nodes on the bottom surface were constrained in all directions. All the nodes with the same y, z location on the yz plane were coupled to enforce periodicity, and the nodes on the xz plane were constrained to the zero displacement in the y direction to apply the symmetric boundary condition.

In this work, the material of the sinusoidal surface was assumed as elastic–plastic bilinear isotropic. However, the tangential modulus is sufficiently small so that the hardening is insignificant. During the first load step, the rigid flat is only displaced in the z direction, while the displacement in the x and y directions and the rotation about all of the axes are held to zero. Contact between the sinusoidal asperity and the rigid flat is accomplished by applying a constant preload $F_{\text{t}}$ in the z direction. This normal loading is followed by a displacement in the x direction applied on the rigid flat.

4 Results and Discussion

Before tangential loading, the sinusoidal surface and the rigid flat are assumed to be in the full stick condition. Once the tangential loading is applied, the maximum frictional shear stress criterion is used for governing the local sliding initiation. The local sliding occurs when the frictional stress at one element on the contact area reaches the critical interfacial shear strength value, $\tau_{\text{c}}$. The sliding of the asperity occurs when all the elements on the contact area slides. At that moment, the average shear stress over the real area of contact is equal to the critical shear strength, i.e., $\tau_{\text{ave}} = \tau_{\text{c}}$.

4.1 Effect of Pressure

The elastic plastic sinusoidal behavior was investigated over a wide range of material properties, geometry properties, dimensionless average contact pressures and dimensionless critical shear stresses. In order to formulate a fit for the FEM data, a benchmark case was set to analyze the problem between the deformable sinusoidal surface and a rigid flat. The material properties used for the benchmark case are: $E = 200\,{\text{GPa}}$, $S_{\text{y}} = 1\,{\text{GPa}}$, and $\nu = 0.3$. The dimensionless geometry ratio $\frac{\varDelta }{\lambda }$ was set to 0.02. The dimensionless average contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$ was set as 0.05. Based on the distortion energy (von Mises) theory, the critical shear strength, $\tau_{\text{c}}$, should satisfy the expression: $\tau_{\text{c}} \le \frac{1}{\sqrt 3 }S_{\text{y}} \approx 0.577S_{\text{y}}$. Therefore, the dimensionless critical shear strength $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$ was set as 0.577.

A range of $0.0001 \le \frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} \le 1$ were considered by the model while keeping all other properties the same as the benchmark case (see Fig. 5). This case covers the deformation range from elastic to deeply elastic–plastic. Therefore, only dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$ is varied parametrically. Figure 5 presents typical results for the instantaneous dimensionless tangential load as a function of normal dimensionless tangential displacement, as can be seen in Fig. 5, as the tangential loading progresses, the slopes of the curves decrease and gradually diminish. The tangential stiffness (the slope) decreases as the dimensionless tangential load increases. When the tangential load no longer increases and the stiffness becomes zero, slip occurs.

Fig. 5

Dimensionless tangential load $\frac{{F_{\text{t}} }}{{F_{\text{n}} }}$ versus the dimensionless tangential displacement $\frac{{U_{x} }}{{\omega_{0} }}$ for different dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$

An example of the typical growth of the contact area is presented in Fig. 6. Figure 6 presents the numerical results for the evolution of both the sticking and sliding states of the contact area. The lines with no mark are the contact area ratio of sticking contact area, while the lines with different marks are the contact area ratio of sliding contact area. When $\frac{{U_{x} }}{{\omega_{0} }} = 0$, the sticking contact area ratio is the sticking contact area before applying the tangential load. Then, the sliding contact area ratio is very low but not zero. For different average contact pressures, the dimensionless contact area ratio for sliding increases with increasing normal tangential displacement. As the dimensionless tangential displacement further increases, the sliding contact area ratio reaches a constant value. At that moment, all the elements are sliding. The dimensionless contact area for sticking shows a different decreasing trend. As the dimensionless tangential displacement increases, the sliding contact area ratio increases a little bit and then decreases until it reaches a constant value at last. The increase is caused by junction growth. As shown in Fig. 6, at the same dimensionless tangential displacement, both sticking and sliding contact area ratios of the higher contact pressures are higher than the contact area ratios at lower pressures. Another point that should be noted is that the total contact area ratio at the sliding inception is much higher than the one before applying tangential loading. For example, when the $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.7$, but the tangential loading is $\frac{{U_{x} }}{{\omega_{0} }} = 0$, the total contact area ratio is approximately 0.858 (obtained by adding both contacts area marked in Fig. 6, or 0.8553 + 0.002685), and the contact area ratio in the sliding inception $\left( {\frac{{U_{x} }}{{\omega_{0} }} = 0.44} \right)$ is approximately 0.9932 (almost complete contact). The increase is around 16%. This implies that an additional tangential load can cause the junction growth. That is probably because the formation of a junction by the normal contact pressure can support the additional loading.

Fig. 6

Portion of surface that is in slip or stick

Adding a tangential load to a given normal preload leads to an increase in the contact area, and as result, it can affect the coefficient of friction. The tangential load $\left( {F_{\text{t}} } \right)_{\hbox{max} }$ at the sliding inception is the static friction force for a single asperity. It is extracted from the finite element data for each case in Fig. 5. The static friction coefficient is obtained by $\frac{{\left( {F_{\text{t}} } \right)_{\hbox{max} } }}{{F_{\text{n}} }}$; however, note that this is only for a single asperity. To predict the friction coefficient for an actual rough surface contact, the asperity model needs to be included in a rough surface contact model. Figure 5 shows that the static friction coefficient is dependent on the average contact pressure. Hence, the static friction coefficient is plotted versus the dimensionless contact pressure.

As shown in Fig. 7, at the low dimensionless contact pressure $\left( {0.0001 \le \frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} \le 0.05} \right)$, the static friction coefficient decreases sharply with increasing contact pressure, and at the medium contact pressure $\left( {0.05 \le \frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} \le 0.3} \right)$, the static friction coefficient nearly approaches a constant value (around 0.23); as the contact pressure further increases, the static friction coefficient continues to reduce, and the relationship is nearly linear. One point to be noted is at the very low dimensionless contact pressure, such as $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.0001$ or $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.0002$, the coefficient is higher than one. This is because, the deformation is in the elastic range, and the surface can support more shear stress. An interesting finding observed in Fig. 7 is the static friction coefficient is still in nearly linear relationship even though the complete contact is reached.

Fig. 7

Static friction coefficient $\mu_{\text{s}}$ versus the dimensionless contact pressure

4.2 Effect of Material Properties

A parametric analysis of the material properties was considered. First, the elastic modulus, E, is now varied from 100 to 400 GPa, the Poisson’s ratio v = 0.3, yield strength $S_{\text{y}} = 1$ GPa, dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.05$, and the critical interfacial strength ratio $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }} = 0.577$. As shown in Fig. 8, as the elastic modulus increases, the curve decreases. At higher values of E, the curves seem to converge. The static friction is then plotted versus elastic modulus, as shown in Fig. 9. The static friction coefficient decreases with increasing elastic modulus. This is probably because as the elastic modulus decreases, the amount of deformation increases and the contact becomes smaller. Under the same contact pressure, the contact area with the larger elastic modulus has a smaller value, and therefore, the corresponding static friction coefficient is smaller.

Fig. 8

Dimensionless tangential load $F_{\text{t}} /F_{\text{n}}$ versus the dimensionless tangential displacement $U_{x} /\omega_{0}$ for different elastic modulus E

Fig. 9

Static friction coefficient versus elastic modulus

Next, the Poisson’s ratio $\nu$ is now varied from 0.1 to 0.49, the elastic modulus E = 200 GPa, yield strength $S_{\text{y}} = 1$ GPa, dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.05$, and the critical interfacial strength ratio $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }} = 0.577$. As shown in Fig. 10, as the Poisson’s ratio increases, the curve decreases. Figure 10 shows that at each loading step, the dimensionless tangential load with a higher Poisson’s ratio has a higher value. The static friction is then plotted versus Poisson’s ratio, and as can be seen in Fig. 11, the static friction coefficient decreases nearly linearly with increasing Poisson’s ratio. When $\nu$ is small, it has less expansion in the x and y directions, the surface separation is small, and the contact area becomes smaller. Thus, the static friction coefficient with higher values of $\nu$ is larger.

Fig. 10

Dimensionless tangential load $\frac{{F_{\text{t}} }}{{F_{\text{n}} }}$ versus the dimensionless tangential displacement $\frac{{U_{x} }}{{\omega_{0} }}$, for different Poisson’s ratio $\nu$

Fig. 11

Static friction coefficient versus Poisson’s ratio

Finally, the yield strength $S_{\text{y}}$ is now varied from 0.1 to 2.5 GPa, the elastic modulus E = 200 GPa, the Poisson’s ratio v = 0.3, yield strength $S_{\text{y}} = 1$ GPa, dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.05$, and the critical shear stress ratio $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }} = 0.577$; the results are shown in Fig. 12. As the yield strength increases, the magnitude of the curve also increases. This is because the increase in yield strength causes the asperity to resist more tangential load before slipping. The static friction is then plotted versus yield strength. Figure 13 shows that the static friction coefficient increases with increasing yield strength.

Fig. 12

Dimensionless tangential load $F_{\text{t}} /{\text{F}}_{\text{n}}$ versus the dimensionless tangential displacement $U_{x} /\omega_{0}$ for different yield strength $S_{\text{y}}$

Fig. 13

Static friction coefficient versus yield strength

4.3 Effect of $\frac{\varDelta }{\lambda }$

Next, a range of $\frac{\varDelta }{\lambda }$ were considered. The geometry property $\frac{\varDelta }{\lambda }$ is now varied from 0.001 to 0.05, as shown in Fig. 14. All other properties are held to the benchmark case value. As shown in Fig. 14, as $\frac{\varDelta }{\lambda }$ increases, the curve also decreases. This is because the contact area decreases by having a larger value of $\frac{\varDelta }{\lambda }$ (i.e., taller asperities).

Fig. 14

Dimensionless tangential load $\frac{{F_{\text{t}} }}{{F_{\text{n}} }}$ versus the dimensionless tangential displacement $\frac{{U_{x} }}{{\omega_{0} }}$ for different $\frac{\varDelta }{\lambda }$

The effect of $\frac{\varDelta }{\lambda }$ on the static friction coefficient is shown by the plot in Fig. 15. It can be seen that the static friction coefficient decreases when the $\varDelta /\lambda$ increases. Another point should be noted that the lower value of the ratio $\varDelta /\lambda$ can cause vary large static friction coefficient. For example, $\mu_{\text{s}} \approx 1.6$ when $\frac{\varDelta }{\lambda } = 0.001$; this is because the smooth surface results in a larger contact area and needs a large force to overcome the shear strength of the material. The shear stress plays an important role in the contact problems.

Fig. 15

Static friction coefficient versus geometry property

4.4 Effect of Interfacial Shear Strength

Last, a range of interfacial shear strength ratios were considered. The sliding is also governed by the critical interfacial shear strength $\tau_{\text{c}}$. When the shear stress exceeds the critical interfacial shear strength, local slipping occurs. In [18], the critical interfacial shear strength was set as $S_{\text{y}} /\sqrt 3$. However, the interfacial shear strength is not always equals to $S_{\text{y}} /\sqrt 3$, because of contaminants, lubrication and changes in temperature. Hence, a wide range of the critical shear stress ratios $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$ were considered in the model (see Fig. 16). The interfacial shear strength ratio $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$ was varied from 0.1 to 0.577. The elastic modulus E is 200 GPa, the Poisson’s ratio v = 0.3, yield strength $S_{\text{y}} = 1$ Gpa, geometry property $\frac{\varDelta }{\lambda }$ is set as 0.02, and dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.05$. As shown in Fig. 16, as the interfacial shear strength ratio increases, the curve levels off at a higher dimensionless tangential load. The initial stiffness increases with $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$ as well.

Fig. 16

Dimensionless tangential load $\frac{{F_{\text{t}} }}{{F_{\text{n}} }}$ versus the dimensionless tangential displacement $\frac{{U_{x} }}{{\omega_{0} }}$ for different $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$

Figure 17 presents the effect of critical interfacial shear strength on the static coefficient of friction. In this case, the dimensionless contact pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$ is chosen as 0.05. As shown in Fig. 17, the static friction coefficient increases with increasing dimensionless critical interfacial shear strength. This occurs because the asperity needs a larger force to overcome the local strength when the material has a large critical shear strength.

Fig. 17

Static friction coefficient versus interfacial shear strength ratio

Since the material properties, geometry properties, dimensionless contact pressure and dimensionless critical tangential stress are each varied independently from the benchmark case, an equation can be fit for each trend. It is very convenient to use an additional parameter $\psi$, which is proposed by Gao et al. [27]; it can be expressed in the form:

$$\psi = \frac{{E^{\prime } }}{{S_{\text{y}} }} \frac{\varDelta }{\lambda }$$

(19)

The static friction coefficient as a function of dependent parameter,$\psi$, dimensionless normal contact pressure, $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$, and the dimensionless critical shear strength, $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$, was fitted to all of the FEM data. And it is given by

$$\mu_{\text{s}} = \left[ {1.848\;\coth \left( {6.5 \psi^{2/3} \left( {\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}} \right)^{1/3} } \right) - 0.184 \psi^{{\frac{1}{4}}} \left( {\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}} \right)^{{\frac{1}{8}}} - 1.482} \right] \left[ {\left( {\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right)^{2} + 2\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right]$$

(20)

Again, note that Eq. (20) does not predict macroscale friction, but the local asperity friction is the case analyzed in this work.

A comparison between Eq. (20) and the FEM results of different case is shown in Figs. 18, 19 and 20. In Fig. 18, we can see that the model for static friction coefficient agrees fairly well with the FEM data based on the parameter $\psi$. The average error between the new model given by Eq. (20) and the FEM results when the $\psi$ is varied independently is <2%. Likewise, the plots in Figs. 19 and 20 show that the model also compares well for the cases where the dimensionless contact pressure, $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$, and the dimensionless critical shear strength, $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$, are varied (the errors in these cases are <4%).

Fig. 18

Comparison of the FEM results and the proposed model with different $\psi$

Fig. 19

Comparison of the FEM results and the proposed model with different $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$

Fig. 20

Comparison of the FEM results and the proposed model with different $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$

In order to compare the proposed model to the spherical contact models in [11, 12], it is necessary to present the expression of Eq. (20) in terms of $\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}$ instead of $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$. This could be done by manipulation that converts Eq. (20) to be a function of $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$, as shown in Appendix. The new equation is given by:

$$\mu_{\text{s}} = \left[ {1.848 \coth \left( {6.5 \varphi^{2/3} \left( {\left( {\frac{{F_{\text{c}} }}{{p_{\text{ep}}^{*} A_{n} }}} \right)\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}} \right)^{1/3} } \right) - 0.184 \varphi^{{\frac{1}{4}}} \left( {\left( {\frac{{F_{\text{c}} }}{{p_{\text{ep}}^{*} A_{n} }}} \right)\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}} \right)^{{\frac{1}{8}}} - 1.482} \right] \left[ {\left( {\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right)^{2} + 2\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right]$$

(21)

$p_{\text{ep}}^{*}$ can be calculated from Eq. (8).

Since the geometry and contact condition assumption of the proposed model are different from the sphere used in [11, 12], the same material properties in these papers are chosen. Ref. [12] by Brizmer et al. is now referred to as the BKE model, and Ref. [11] by Kogut and Etsion is referred to as the KE model. First, typical amplitudes-to-wavelength ratios ($\varDelta /\lambda$) are considered while keeping the critical shear stress ratio ($\tau_{\text{c}} /S_{\text{y}}$) constant (0.577). The effective static friction coefficient as a function of the dimensionless tangential load with different $\varDelta /\lambda$ is plotted in Fig. 21. As shown in Fig. 21, the proposed model has the same trend as the BKE model and the difference depends on the values of $\varDelta /\lambda$. Both the proposed model and the BKE model have higher values of the effective static friction coefficient than the KE model.

Fig. 21

Comparison of the KE and BKE model and the proposed model with different $\frac{\varDelta }{\lambda }$

Next, several interfacial shear strengths($\tau_{\text{c}} /S_{\text{y}}$) are considered, while keeping the amplitude-to-wavelength ratio($\varDelta /\lambda$) constant at a value of 0.02. The effective static friction coefficient is plotted as a function of the dimensionless tangential load with different $\tau_{\text{c}} /S_{\text{y}}$ in Fig. 22. As shown in Fig. 22, the proposed sinusoidal model again has the same trend as the BKE model. The sinusoidal model is always close or lower than the BKE model and differs quantitatively depending on the value of $\tau_{\text{c}} /S_{\text{y}}$. One observation is that when $\tau_{\text{c}} /S_{\text{y}} = 0.2$, the value of static friction coefficient is close to the value predicted by the KE model at low normal preloads.

Fig. 22

Comparison of the KE and BKE model and the proposed model with different $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}$

Since these previous works of Etsion’s group showed that plastically deforming material can effectively separate the contact surface from the bulk material below it, initial sliding is allowed to occur below the surface. The plastic deformation is related to the normal preload or interference [11, 12, 18] for spherical contact; the same situation is also found for this study. For the sinusoidal contact, it is also related to the wavelength ratio ($\varDelta /\lambda$). A typical metal is chosen with material properties $E = 200\,{\text{GPa}},\; \nu = 0.3,\; S_{\text{y}} = 1\,{\text{GPa}}$, and normalized pressure $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = 0.05$; critical interfacial shear strength ratio is chosen as $\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }} = 0.577$.

Figure 23 presents the equivalent plastic strain during tangential loading. As shown in Fig. 23a, the sinusoidal surface is only under the normal loading; there is no yield strain everywhere. The yield occurs on the surface and underneath of the surface on the annulus of the contact area, as shown in Fig. 23b. A further of tangential loading results in a larger yield area. The yield area extends from the annulus to the circle of the contact area. At the sliding inception, an elastic area exists in the middle of the contact area. As shown in Fig. 23c, for the case of $\varDelta /\lambda = 0.005$, the yield first occurs at the solid body below the surface. There is no yield on the surface; the plastic area on the surface becomes larger with the tangential load increases. At the sliding inception, the plastic area is extended to the whole contact area, and there is no elastic area in it, as shown in Fig. 24.

Fig. 23

Equivalent plastic strain during tangential loading ($\varDelta /\lambda = 0.001$). a Ft = 0, b Ft = 0.75 (Ft)_max, c Ft = (Ft)_max

Fig. 24

Equivalent plastic strain during tangential loading ($\varDelta /\lambda = 0.005$). a Ft = 0, b Ft = 0.625 (Ft)_max, c Ft = (Ft)_max

Considering the sliding inception as a failure mechanism, both FEM [11, 12] and experimental study [38] were carried out. They suggested that when the normal preload is less than the critical load, the failure occurs on the contact area. If the normal load exceeds the critical value, the failure occurs below the contact area. Etsion [39] revisited the Cattaneo–Mindlin concept of interfacial slip in tangentially loaded compliant bodies. He pointed out that sliding occurs under the surface for typical metallic materials, and interfacial slip can only occur in some special cases, such as when the interface is much weaker than any of the contacting bodies, or lubricated contact. Different from the full stick model, the sliding inception defined in the current work is when the gross relative displacement between the two surfaces in contact takes place. This may be different than the other definitions based on the plastic failure. However, the results show they have a reasonable agreement. For our cases, the slipping always occurs on the surface. At high pressures, an elastic island of hydrostatic stress can form, but it appears to be restrained by the surrounding material, and slip still occurs on the surface. It might be possible that slip can occur below the surface for higher amplitude-to-wavelength ratios ($\varDelta /\lambda$) not considered in this work. However, we choose a range that seems to be typical for rough surface asperities [29, 30, 40, 41].

5 Conclusion

Finite element simulations are carried out for a rigid flat on a deformable sinusoidal surface under combined normal and tangential loading at the asperity scale. This work used a finite element model to characterize the three-dimensional sinusoidal contact. A maximum shear stress criterion was used to determine the sliding inception. The phenomenon of growth of interference and contact area are described briefly. The static friction coefficient shows strong dependency on material properties, contact pressure and interfacial shear strength. An empirical expression of static friction coefficient was given considering these effects. This equation should be used in multiscale model to predict the static friction coefficient for the rough surface.

Appendix

The critical values for sinusoidal contact under normal load in the perfect slip condition are given in [33]:

$$\omega_{\text{cs}} = \left( {\frac{{\pi CS_{\text{y}} }}{2\pi f}} \right)^{2} \frac{1}{\varDelta }$$

(22)

$$F_{\text{cs}} = \frac{1}{6\pi }\left( {\frac{1}{{\varDelta f^{2} E^{\prime } }}} \right)^{2} \left( {\frac{C}{2}S_{\text{y}} } \right)^{3}$$

(23)

where $= 1.295 { \exp }\left( {0.736 \nu } \right)$, $\omega_{\text{cs}}$ is the critical interference under perfect slip condition and $F_{\text{cs}}$ is the critical force under the perfect slip condition.

The critical values for a sinusoidal surface in normal load under the full stick condition are given by [36] as

$$\omega_{\text{c}} = \omega_{\text{cs}} \left( {6.82\upsilon - 7.83\left( {\nu^{2} + 0.0586} \right)} \right)$$

(24)

$$F_{c} = F_{cs} \left( {8.88\upsilon - 10.13\left( {\nu^{2} + 0.089} \right)} \right)$$

(25)

where $\omega_{\text{c}}$ is the critical interference under full stick condition, and $F_{\text{c}}$ is the critical force under the full stick condition.

The term $\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }}$ in Eq. (20) can then be expressed as:

$$\frac{{\bar{p}}}{{p_{\text{ep}}^{*} }} = \frac{{\bar{p} A_{n} }}{{p_{\text{ep}}^{*} A_{n} }} = \frac{{F_{\text{n}} }}{{\left( {p_{\text{ep}}^{*} A_{n} /F_{\text{c}} } \right) F_{\text{c}} }} = \left( {\frac{{F_{\text{c}} }}{{p_{\text{ep}}^{*} A_{n} }}} \right)\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}$$

(26)

where $p_{\text{ep}}^{*}$ is the contact pressure to cause complete contact for elastic–plastic case.

By substituting Eq. (26) into Eq. (20), then Eq. (20) becomes:

$$\mu_{\text{s}} = \left[ {1.848 \coth \left( {6.5 \varphi^{2/3} \left( {\left( {\frac{{F_{\text{c}} }}{{p_{\text{ep}}^{*} A_{n} }}} \right)\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}} \right)^{1/3} } \right) - 0.184 \varphi^{{\frac{1}{4}}} \left( {\left( {\frac{{F_{\text{c}} }}{{p_{\text{ep}}^{*} A_{n} }}} \right)\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}} \right)^{{\frac{1}{8}}} - 1.482} \right] \left[ {\left( {\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right)^{2} + 2\frac{{\tau_{\text{c}} }}{{S_{\text{y}} }}} \right]$$

(27)

This equation is alternative version that is a function of $\frac{{F_{\text{n}} }}{{ F_{\text{c}} }}$.