1 Introduction

Porous medium systems consist of a connected solid phase and one or more fluids that fill the pore space. Boundaries between phases are interfaces, and the location where three phases intersect forms common curves. Such systems can be modeled from a macroscale perspective or a microscale perspective. Models formulated at the macroscale represent the state of the system in terms of quantities averaged over some region in space. Directly postulating macroscale models, although common, suffers from a lack of connection to the microscale physics. When the morphology and topology of the pore space is known, mechanistic models should be formulated at the microscale and solved (at least in some statistically representative sense) for each phase that is present. The importance of connecting microscale and macroscale models is becoming increasingly recognized, in part because of the rapid development of pore-scale experimental and modeling methods that provide a means to reveal fundamental aspects of microscale transport phenomena (Gray et al. 2015).

To bridge the physical behavior of systems at the microscale and at the macroscale, multiscale approaches have been developed. These approaches include the method of volume averaging (MVA) (Whitaker 1999), homogenization, hybrid mixture theory, and the thermodynamically constrained averaging theory (TCAT). TCAT methods have been the focus of substantial recent work, and a variety of model formulations have been developed. The TCAT approach was first introduced by Gray and Miller about a decade ago (Gray and Miller 2005; Miller and Gray 2005); however, elements of this theoretical approach were derived prior to the introduction of the formal TCAT structure (Gray 1999, 2000, 2002; Gray and Hassanizadeh 1989, 1998; Gray and Lee 1977; Gray et al. 1993, 2002). A recent book exhaustively details the general approach, the components of the method, and the derivation of three general classes of models (Gray and Miller 2014). Some of the important aspects of TCAT, not combined in alternative approaches, are as follows:

  1. 1.

    The inclusion of conservation and balance equations for phases, interfaces, common curves, and common points

  2. 2.

    The use of thermodynamic constraints that are upscaled from the microscale

  3. 3.

    The derivation and use of a set of macroscale equilibrium conditions

  4. 4.

    Formulation and use of the entropy production rate to constrain the form of closure relations

  5. 5.

    The development and use of kinematic equations based upon averaging theorems, which are separate from any conservation principle

Together, these components provide a means to derive models that are consistent across scales and naturally contain physics known to be important at the microscale in larger-scale models. The classes of models developed to date include: single-fluid-phase flow (Gray and Miller 2014), megascale models of single-fluid-phase flow (Gray and Miller 2009c), single-fluid-phase flow and species transport (Gray and Miller 2009b, 2014; Miller and Gray 2008), single-fluid-phase flow and heat transport (Gray and Miller 2009a), two-fluid-phase flow (Dye et al. 2015; Gray et al. 2015; Gray and Miller 2011, 2014; Jackson et al. 2009), two-fluid-phase flow and species transport (Rybak et al. 2015), and modeling of the transition between a two-fluid-phase porous medium system and a single-fluid-phase domain (Jackson et al. 2012).

TCAT model formulations have been developed to specify closure relations in either a general or specific functional form depending upon the application. For the specific closure relation forms, model parameters appear that depend upon the physical system being modeled. The evaluation, and prediction, of such parameters (e.g., macroscale transport parameters such as the effective diffusion tensor, thermal conductivity, resistance tensors) has received little attention to date for TCAT models. Typically, parameter estimation is carried out by solving an inverse problem based upon experimental observations, or direct numerical simulation of subscale systems. Since TCAT model formulations assure consistency across scales, microscale simulation can be used to determine macroscale parameters and validate the model forms derived.

In contrast to TCAT, the MVA is an upscaling approach that has been used to develop macroscale models and to provide a priori prediction of the derived macroscale closure parameters for certain microscale geometric and transport conditions. The existence of a representative elementary volume (REV) element is a requirement for this approach as well as the imposition of convenient scaling postulates (Wood 2009; Wood and Valdés-Parada 2013). Although macroscale property prediction is a powerful component of the theory, the MVA has been applied to develop models with phases alone, no thermodynamic constraints, and relatively simple physics compared to the TCAT formulations.

The overall goal of this work is to advance TCAT methods for modeling porous medium systems by incorporating means for parameter predictions. The specific objectives of this work are (1) to show how a general entropy inequality relation can be used to produce a particular closed model instance, (2) to introduce an approach for determining macroscale parameters for TCAT models based upon known microscale characteristics and modeling, (3) to evaluate macroscale parameters for a range of isotropic and anisotropic media using the new approach, and (4) to validate the parameter estimates using direct numerical simulation at the microscale.

Fig. 1
figure 1

Conceptual representation of the TCAT approach

Full size image

2 TCAT Framework

The components of the TCAT formulation approach are depicted in Fig. 1 and can be summarized as follows.

  1. 1.

    Primary restrictions are made, which specify the entities (phases, interfaces, common curves, and common points) and the phenomena (e.g., flow, species transport, heat transport) to be modeled, the thermodynamic theory to be relied upon at the microscale, and a requirement that the resulting macroscale model has a clear separation of length scales.

  2. 2.

    Based upon the primary restrictions, a set of macroscale equations is specified for the system corresponding to the entities and phenomena to be modeled. These macroscale equations include conservation equations for mass, momentum, and energy, a balance of entropy, thermodynamic equations, and macroscale conditions that must apply at equilibrium. As shown in Fig. 1, the macroscale equations are derived uniformly from the corresponding microscale equations by application of an averaging operator and simplified using a set of transport, divergence, and gradient theorems.

  3. 3.

    A macroscale entropy inequality (EI) is written by summing the entropy balance equations for all species and all entities and equating this summed equation to the rate of entropy production for the system, which must be greater than or equal to zero by the second law of thermodynamics.

  4. 4.

    The macroscale EI is augmented with a set of conservation and thermodynamic equations corresponding to the entities and processes being modeled. These equations are all arranged so that they are equal to zero; thus, adding the product of these equations with Lagrange multipliers for each equation to the EI does not change the inequality. The reason for augmenting the EI in this manner is to introduce the processes that result in entropy production into the EI. The Lagrange multipliers are thus free parameters that do not affect the inequality but will change the form of the resulting expression. The Lagrange multipliers are chosen such that a subset of the material derivatives vanish from the EI, which is desired so that the EI can be reduced to a flux-force form.

  5. 5.

    The augmented EI is arranged to yield a constrained EI (CEI). The CEI is an EI that is manipulated to produce an expression that is as close as possible to a flux-force form without introducing approximations. The CEI is an important intermediate formulation result because of its exact and general nature.

  6. 6.

    The simplified EI (SEI) is derived from the CEI by applying a set of approximations that allow for a strict flux-force form to be obtained. Additionally, secondary restrictions may be applied to simplify the SEI for a particular system of concern that may be simpler than the general model specified by the primary restrictions. For example, an isothermal system might be specified at this point.

  7. 7.

    The SEI, including potential secondary restrictions, is used to posit permissible forms of closure relations. The form of the SEI is a strict flux-force form comprised of expressions for the dissipative processes operative in the system. These processes can result in the production of entropy, so the inequality in the SEI provides a set of permissibility conditions on closure relations used to close a macroscale model. The closure relations are not unique, but they must meet permissibility constraints.

  8. 8.

    Evolution equations are specified using the averaging theorems and certain approximations to yield kinematic equations relating entity extents, such as volume fractions, specific interfacial areas, specific common curve lengths, and specific common point densities. These evolution equations are distinct from any conservation equation.

  9. 9.

    A macroscale model is formulated by combining the conservation equations, closure relations, and evolution equations. The closure relations may include state equations in a general functional form.

  10. 10.

    Computational or experimental means are used to produce specific, closed forms of a model complete with all needed model coefficients. Model evaluation, approximation evaluation, and validation can also be accomplished using microscale information.

The TCAT approach produces models that are consistent across scales, are thermodynamically consistent, and are of potentially higher fidelity than models that do not include interfaces and common curves. The execution of the steps summarized above results in a long, detailed calculation for each class of model considered. The starting point for specific model instance formulation and closure is the SEI. In the next section, we illustrate how an available SEI can be used to guide the closure of a specific model instance in a straightforward manner.

3 Model Formulation

We consider the case of diffusion of a single dilute, non-reactive species through a water-saturated isothermal porous medium system consisting of a macroscopically homogeneous, immobile, inert, non-deformable solid with a constant porosity. We further specify that mass and energy are not exchanged between entities. This system is specified to be a simple subset of an available model hierarchy that can be used to illustrate the general approach to model closure and to provide a formulation upon which an a priori closure scheme can be advanced.

The TCAT approach, as summarized in the previous section, involves formulating closed macroscale models that are consistent across scales with regard to thermodynamics and conservation principles and which are closed with relations that are provably consistent with the second law of thermodynamics. Miller et al. (2017) detailed the TCAT formulation of a macroscale model consistent with the system described in this work, which included all of the steps in the model-building approach. An alternative approach is to use available results to derive a model, thereby eliminating the majority of the work involved, while still producing a scale-consistent macroscale TCAT model. From the above description of the system to be modeled, it can be observed that the macroscale conservation equation that must be solved is given by

$$\begin{aligned} \frac{\partial {\left( {{\rho ^{w}}}{{\omega }^{{{i}\,}{\overline{w}}}} \right) }}{\partial {t}} +\nabla {{\varvec{\mathsf {\cdot }}}}\left( {{\rho ^{w}}}{{\omega }^{{{i}\,}{\overline{w}}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{{i}w}}}}} \right) =0 \end{aligned}$$
(1)

where \({{\rho ^{w}}}\) is the mass density of the water phase, \({{\omega }^{{{i}\,}{\overline{w}}}}\) is the mass fraction of species \({i}\) in the water phase, t is time, and \({{{\varvec{\mathrm u}}}^{{\overline{\overline{{i}w}}}}}\) is the deviation, or diffusion, velocity of the water phase. The superscripts denote macroscale quantities, and reactions and interphase mass exchange terms have been neglected. The closure problem for this system is the determination of an approximation for \({{{\varvec{\mathrm u}}}^{{\overline{\overline{{i}w}}}}}\). This can be deduced from an available SEI.

A general SEI for single-fluid-phase flow and species transport for the case of momentum transport of an entity, rather than for a species in an entity, is (Gray and Miller 2014)

(2)

where all terms are defined in the notation section.

The approach taken to derive this equation is consistent with the schematic illustration given by Fig. 1, and the details are provided by Gray and Miller (2014). We wish to simplify this SEI to the form needed to model species transport in the system previously detailed above. This study case is chosen for simplicity purposes, and the extensions to other more complicated applications is straightforward. This particular instance allows for reductions of the general SEI to a simpler form. To this end, we will refer to lines numbers in Eq. (2) and to the previously detailed model restrictions. The simplifications of this expression are summarized as follows.

  • The absence of mean advective transport allows for the elimination of Lines 1,2, and 17–26

  • The non-reactive species allows for the elimination of Lines 6 and 7

  • the lack of exchange of mass, momentum, and energy between entities allow for the elimination of Lines 8–11

  • The isothermal system restrictions allows for the elimination of Lines 3, and 12–17

  • The immobile, inert, incompressible solid phase allows for the elimination of Lines 27 and 28

With these simplifications, Eq. (2) reduces to

$$\begin{aligned}&-{{\sum \limits _{{{\alpha }} \in {{\mathscr {I}}}\ }\;}}{{\sum \limits _{{i} \in {{\mathscr {I}}_{s{}}}_{/N}\ }\;}}\dfrac{1}{{{{\theta }}^{{\overline{\overline{{{\alpha }}}}}}}} {{\epsilon }^{{\overline{\overline{{{\alpha }}}}}}}{\rho ^{{{\alpha }}}}{{\omega }^{{{i}\,}{\overline{{{\alpha }}}}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{{{i}{{\alpha }}}}}}}}{{\varvec{\mathsf {\cdot }}}}\nabla \left[ {{\mu }^{{\overline{{{i}{{\alpha }}}}}}_{}}+{{K}^{{\overline{\overline{{{i}{{\alpha }}}}}}}_E}+\dfrac{{{{\varvec{\mathrm u}}}^{{\overline{\overline{{{i}{{\alpha }}}}}}}}{{\varvec{\mathsf {\cdot }}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{{{i}{{\alpha }}}}}}}}}{2}+{{\psi }^{{\overline{{{i}{{\alpha }}}}}}_{}}\right. \nonumber \\&\left. \qquad -\left( {{\mu }^{{\overline{N{{\alpha }}}}}_{}}+{{K}^{{\overline{\overline{N{{\alpha }}}}}}_E}+\dfrac{{{{\varvec{\mathrm u}}}^{{\overline{\overline{N{{\alpha }}}}}}} {{\varvec{\mathsf {\cdot }}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{N{{\alpha }}}}}}}}{2}+{{\psi }^{{\overline{N{{\alpha }}}}}_{}} \right) \right] ={{\sum \limits _{{{\alpha }} \in {{\mathscr {I}}}\ }\;}}{{{{\Lambda }}^{{\overline{\overline{{{\alpha }}}}}}}}\ge 0. \end{aligned}$$
(3)

Because we are only concerned with binary species transport in the fluid phase, and kinetic energy terms are neglected, Eq. (3) can be written as

$$\begin{aligned} -\dfrac{1}{{\theta }} {{\epsilon }^{{\overline{\overline{w}}}}}{\rho ^{w}}{{\omega }^{{A\,}{\overline{w}}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{Aw}}}}}{{\varvec{\mathsf {\cdot }}}}\nabla \left( {{\mu }^{{\overline{Aw}}}_{}}+{{\psi }^{{\overline{Aw}}}_{}}-{{\mu }^{{\overline{Bw}}}_{}}-{{\psi }^{{\overline{Bw}}}_{}} \right) ={\Lambda }\ge 0\; \end{aligned}$$
(4)

or since the body force potential is only due to gravity, the porosity is constant, and the system is dilute, the difference in body force potentials is neglected, and the restricted SEI becomes

$$\begin{aligned} -\frac{1}{{\theta }}{{{\epsilon }^{{\overline{\overline{w}}}}}}{{\rho ^{w}}}{{\omega }^{{A\,}{\overline{w}}}}{{{\varvec{\mathrm u}}}^{{\overline{\overline{A w}}}}}{{\varvec{\mathsf {\cdot }}}}\nabla \left( {{\mu }^{{\overline{Aw}}}_{}}-{{\mu }^{{\overline{Bw}}}_{}} \right) ={{\Lambda }}\ge 0. \end{aligned}$$
(5)

This restricted SEI can be used to produce a closed model by deriving an approximation for \({{{\varvec{\mathrm u}}}^{{\overline{\overline{Aw}}}}}\), simplifying the resultant expression, and substituting into Eq. (1) as detailed in Miller et al. (2017). This closed macroscale model is

$$\begin{aligned} \frac{\partial {C^{Aw}}}{\partial {t}}=\nabla {{\varvec{\mathsf {\cdot }}}}\left[ {{\hat{\varvec{\mathsf {D}}}}}{{\varvec{\mathsf {\cdot }}}}\nabla C^{Aw} \right] \; \end{aligned}$$
(6)

where \(C^{Aw}={{\rho ^{w}}}{{\omega }^{{A\,}{\overline{w}}}}\) is the macroscopic fluid-phase concentration of the dilute species of interest, and \({{\hat{\varvec{\mathsf {D}}}}}\) is an effective diffusion tensor.

4 Parameter Evaluation

As mentioned in the introduction, an objective of this work is to derive an approach for evaluating and predicting closure relation parameter values for a macroscale TCAT model based upon microscale system characteristics. To meet this objective, elements used in the MVA (Whitaker 1999) will be used as inspiration to derive a similar parameter evaluation and estimation approach for TCAT models. The direct parameter evaluation method for TCAT differs from what has been done for the MVA, because deviations are non-local in the TCAT formulation and thus careful accounting for both a microscale and macroscale coordinate system are needed. The parameter evaluation approach detailed below will not always be a practical option; when systems become complex, the direct parameter estimation scheme can become intractable. For such problems, it may be best to approach parameter estimation in the conventional way by solving an inverse problem based upon a comparison of a macroscale TCAT model to experimental data, or microscale simulation results (Gray et al. 2015; Gray and Miller 2014).

In essence, the proposed approach develops parameter estimates from an equation for each dependent variable deviation from the macroscale average of the quantity. Once these deviation equations are known, equations defining the macroscale parameters in terms of microscale deviations can be computed, yielding a solution that provides an evaluation of these parameters. The steps involved in the procedure are detailed and then illustrated for the example case of diffusion in porous media using the previously derived TCAT model. The result is a model that combines the generality of TCAT with the ability for direct parameter evaluation present in the MVA.

4.1 Overview

Direct parameter evaluation can be accomplished, when possible, with the steps summarized as follows.

  1. 1.

    A closed microscale model is developed that corresponds to the macroscale model for which parameter estimates are sought.

  2. 2.

    The closed macroscale TCAT model is written in an equivalent unclosed form in terms of averages and deviations of the dependent variables.

  3. 3.

    A microscale deviation equation is formulated together with the corresponding boundary conditions in closed form and simplified.

  4. 4.

    The microscale deviation equation is solved over an REV, and the solution is used to provide a direct evaluation of the macroscale parameter.

4.2 Example Application

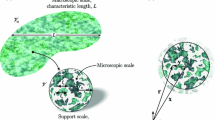
For the developments that follow, both microscale and macroscale coordinates will be used. We will use the coordinate decomposition \({{\varvec{\mathrm r}}} = {{\varvec{\mathrm x}}}+{\varvec{\mathrm \xi }}\) illustrated in Fig. 2. TCAT averages are computed about a domain \({\Omega }\) with point \({\varvec{\mathrm x}}\) located at the centroid of \({\Omega }\). Locations within \({\Omega }\) are defined relative to the centroid with the position vector \({\varvec{\mathrm \xi }}\). The position vector \({\varvec{\mathrm r}}\) is the vector sum of the macroscale position \({\varvec{\mathrm x}}\) and the microscale position relative to the centroid of \({\Omega }\), which is \({\varvec{\mathrm \xi }}\).

To illustrate the macroscale TCAT parameter evaluation approach summarized in Sect. 4.1, we consider parameter evaluation for the TCAT model developed in Sect. 3, detailing the steps involved in turn as follows.

Fig. 2
figure 2

An averaging domain, \(\Omega \), illustrating the relationship among \(\mathbf{x}\), \(\mathbf{r}\), and \({\varvec{\mathrm \xi }}\). For a particular averaging volume with the centroid fixed at \({\varvec{\mathrm x}}\), the variable \({\varvec{\mathrm r}}\) (or, equivalently, \({\varvec{\mathrm \xi }}\)) is the independent variable that locates points within the averaging domain. The variable \({\varvec{\mathrm x}}\) is fixed in this coordinate system

Full size image

Step 1 A closed microscale model is needed that corresponds to the closed macroscale model. Thus, the restrictions relied upon to develop the macroscale model should be consistent with the closed microscale model. In general, the TCAT approach does not require a closed microscale model, although it can be used to derive such a closed form (Gray and Miller 2014). The need for a closed microscale model is a result of the parameter estimation approach being considered.

The restrictions on the system considered were previously detailed in Sect. 3. For this case, an unclosed microscale model is given by

$$\begin{aligned} \frac{\partial {\left( {{\rho _{w}}}{{\omega }_{{{i}}{w}}}\right) }}{\partial {t}} +\nabla {{\varvec{\mathsf {\cdot }}}}\left( {{\rho _{w}}}{{\omega }_{{{i}}{w}}}{{{\varvec{\mathrm u}}}^{\,{}}_{{i}w}} \right) =0 \end{aligned}$$
(7)

where all other equations vanish from the final model formulation. A standard Fickian closure relation can be applied to Eq. (7) yielding a closed microscale model of the form

$$\begin{aligned} \frac{\partial {C_{Aw}({\varvec{\mathrm r}},t)}}{\partial {t}} - \nabla {{\varvec{\mathsf {\cdot }}}}\left( {{\hat{D}}}_{Aw}\nabla C_{Aw}({\varvec{\mathrm r}}, t) \right) =0\; \end{aligned}$$
(8)

subject to an appropriate set of auxiliary conditions needed to form a well-posed model.

It is useful to note the following relationships among derivatives (Gray et al. 1993). For any function \(f({{\varvec{\mathrm x}}}+{{\varvec{\mathrm \xi }}})\)

$$\begin{aligned} \nabla _{{\varvec{\mathrm r}}}f({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }})=\nabla _{{\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}}f({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}) =\nabla _{{\varvec{\mathrm x}}}f({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }})=\nabla _{{\varvec{\mathrm \xi }}}f({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}). \end{aligned}$$
(9)

Thus, Eq. (8) can be equivalently expressed by

$$\begin{aligned} \frac{\partial {C_{Aw}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }},t)}}{\partial {t}} - \nabla _{{\varvec{\mathrm x}}}\cdot \left[ {{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C_{Aw}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}, t) \right] =0\; \end{aligned}$$
(10)

Step 2 The unclosed macroscale model given by Eq. (1) can be written as

$$\begin{aligned} \frac{\partial {C^{Aw}(\mathbf{x},t)}}{\partial {t}}+\nabla _{{\varvec{\mathrm x}}}\cdot \left( C^{Aw}(\mathbf{x},t) {{{\varvec{\mathrm u}}}^{{\overline{\overline{Aw}}}}}({{\varvec{\mathrm x}}},t) \right) =0 \end{aligned}$$
(11)

We wish to express the second term in this equation as a function of averages of microscale quantities. To arrive at such an equation, we apply an averaging operator to Eq. (8) giving

$$\begin{aligned} {{{\left\langle \frac{\partial {C_{Aw}({\varvec{\mathrm r}},t)}}{\partial {t}} - \nabla _{{\varvec{\mathrm r}}}{{\varvec{\mathsf {\cdot }}}}\left( {{\hat{D}}}_{Aw}\nabla C_{Aw}({\varvec{\mathrm r}}, t) \right) \right\rangle _{{{\Omega }_{w}},{{\Omega }_{}}}}}} =0\; \end{aligned}$$
(12)

Equation (12) includes averages of differential operators, which we wish to eliminate. To do so, we can apply averaging theorems to the time derivative, T[3,(3,0),0]; the divergence, D[3,(3,0),0]; and the gradient, G[3,(3,0),0], where the theorem nomenclature refers to available averaging theorems (Gray et al. 1993; Gray and Miller 2013, 2014). Applying these theorems to Eq. (12) and simplifying for the case of an immobile and incompressible solid phase in the absence of interfacial mass transfer yields

$$\begin{aligned} \frac{\partial {\left( {{{\epsilon }^{{\overline{\overline{w}}}}}}C^{Aw}({\varvec{\mathrm x}},t)\right) }}{\partial {t}} - \nabla _{{\varvec{\mathrm x}}}{{\varvec{\mathsf {\cdot }}}}\Bigg [{{{\epsilon }^{{\overline{\overline{w}}}}}}{{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw} \left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}C_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{\Omega }}} \right| _{({\varvec{\mathrm x}},t)}\Bigg ] =0\; \end{aligned}$$
(13)

or, for the constant porosity case, as

$$\begin{aligned} \frac{\partial {C^{Aw}({\varvec{\mathrm x}},t)}}{\partial {t}} - \nabla _{{\varvec{\mathrm x}}}{{\varvec{\mathsf {\cdot }}}}\Bigg [{{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw}\left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}C_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}} \right| _{({\varvec{\mathrm x}},t)}\Bigg ] =0\; \end{aligned}$$
(14)

where \({{{\varvec{\mathrm n}}_{w}}}\) is the outward unit normal vector on the boundary of the water phase, the fluid domain \({{\Omega }_{w}}\) has boundary \({{\Gamma }_{w}}={{\Gamma }_{w \mathrm i}}\cup {{\Gamma }_{w \mathrm e}}\), \({{\Gamma }_{w \mathrm i}}\) is the internal boundary formed where the water phase intersects the solid phase, and \({{\Gamma }_{w \mathrm e}}\) is the external boundary where the water phase intersects the boundary \({{\Gamma }_{}}\) of the averaging region \({{\Omega }_{}}\). Note that the internal boundary term can be written explicitly by

$$\begin{aligned} \left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}C_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\right| _{({\varvec{\mathrm x}},t)}= \frac{1}{V_w} \int _{{\varvec{\mathrm \xi }}\in {{\Gamma }_{w \mathrm i}}({\varvec{\mathrm x}})} {{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }})C_{Aw}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }},t) \, \mathrm {d}A({\varvec{\mathrm \xi }})\; \end{aligned}$$
(15)

where \(V_w\) is the volume of the wetting phase in \({{\Omega }_{}}\).

It can be observed from Eqs. (11) and (14) that there is the following relationship between fluxes

$$\begin{aligned} C^{Aw}({\varvec{\mathrm x}},t) {{{\varvec{\mathrm u}}}^{{\overline{\overline{Aw}}}}}({{\varvec{\mathrm x}}},t)= -\left( {{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw}{\left\langle {{{\varvec{\mathrm n}}_{w}}}C_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}} \right) . \end{aligned}$$
(16)

As an alternative to the boundary term in Eq. (16), we can seek a form that depends upon a microscale deviation concentration instead of a microscale concentration. The microscale concentration can be expressed by the decomposition

$$\begin{aligned} C_{Aw}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }},t)= C^{Aw}({\varvec{\mathrm x}},t)+{\tilde{C}}_{Aw}({\varvec{\mathrm x}},{\varvec{\mathrm \xi }},t)\; \end{aligned}$$
(17)

where \({\tilde{C}}_{Aw}\) is a deviation concentration. The functional dependence of each variable is noted and is important. A microscale value depends upon the overall location \({\varvec{\mathrm r}}={\varvec{\mathrm x}} +{\varvec{\mathrm \xi }}\) and time; the macroscale concentration depends only upon the macroscale spatial coordinate \({\varvec{\mathrm x}}\) and time, and the deviation concentration depends upon \({\varvec{\mathrm x}}\), \({\varvec{\mathrm \xi }}\), and time, because the deviation is relative to a specific macroscale average, which is specified to be at the centroid location \({\varvec{\mathrm x}}\).

Spatial derivatives of the decomposed concentration can also be evaluated. The relationship given by Eq. (9) can be used along with Eq. (17) to deduce

$$\begin{aligned} \nabla _{{\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}} C_{Aw}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }},t)= \nabla _{{\varvec{\mathrm x}}} C_{Aw}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }},t)= \nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}},t) + \nabla _{{\varvec{\mathrm x}}}{\tilde{C}}_{Aw}({\varvec{\mathrm x}},{\varvec{\mathrm \xi }},t)\; \end{aligned}$$
(18)

and

$$\begin{aligned} \nabla _{{\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}} C_{Aw}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }},t)= \nabla _{{\varvec{\mathrm \xi }}} C_{Aw}({\varvec{\mathrm x}} +{\varvec{\mathrm \xi }},t)= \nabla _{{\varvec{\mathrm \xi }}}{\tilde{C}}_{Aw}({\varvec{\mathrm x}},{\varvec{\mathrm \xi }},t)\; \end{aligned}$$
(19)

Note that there is an important distinction to be pointed out between the deviations defined in the MVA and in TCAT. In the TCAT definitions, the value of the average within an averaging domain \(\Omega \) is always taken as the value at the centroid; deviations within the domain are computed relative to this single average value. Although this creates an inherently non-local definition for the deviations, it has the advantage that the average of the deviations is always identically zero. In the MVA, averages and deviations are defined locally pointwise. One can recover the MVA definitions for the deviations by setting \(\varvec{\xi }\) equal to zero in Eq. (17). Although this has the advantage of generating a local expression for the deviations, the average of the deviations in the MVA system is not necessarily zero.

Equations (14) and (17) can be combined to yield

$$\begin{aligned}&\frac{\partial {C^{Aw}({\varvec{\mathrm x}},t)}}{\partial {t}} - \nabla _{{\varvec{\mathrm x}}}\cdot \Big [{{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw}C^{Aw}({\varvec{\mathrm x}},t) \left. {\left\langle {{{\varvec{\mathrm n}}_{w}}} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\right| _{{\varvec{\mathrm x}}}\nonumber \\&\quad +\,{{\hat{D}}}_{Aw} \left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}} \right| _{({\varvec{\mathrm x}},t)}\Big ] =0\; \end{aligned}$$
(20)

where the \(C^{Aw}\) can be moved outside the averaging operator because it is a constant over the averaging domain. It can be shown that (Gray and Miller 2014; Whitaker 1999; Wood 2013)

$$\begin{aligned} \left. {\left\langle {{{\varvec{\mathrm n}}_{w}}} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\right| _{{\varvec{\mathrm x}}} = -\left( {{{\epsilon }^{{\overline{\overline{w}}}}}}\right) ^{-1} \nabla _{{\varvec{\mathrm x}}}{{{\epsilon }^{{\overline{\overline{w}}}}}}=0\; \end{aligned}$$
(21)

since the porosity is constant. Under these conditions, it follows that

$$\begin{aligned} \frac{\partial {C^{Aw}({\varvec{\mathrm x}},t)}}{\partial {t}} - \nabla _{{\varvec{\mathrm x}}}\cdot \Big [{{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw}\left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}} \right| _{({\varvec{\mathrm x}},t)}\Big ] =0\; \end{aligned}$$
(22)

and

$$\begin{aligned} C^{Aw}(\mathbf{x},t) {{{\varvec{\mathrm u}}}^{{\overline{\overline{Aw}}}}}({{\varvec{\mathrm x}}},t)= -\Bigg ({{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}({\varvec{\mathrm x}}, t) +{{\hat{D}}}_{Aw}\left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}} \right| _{({\varvec{\mathrm x}},t)}\Bigg )\; \end{aligned}$$
(23)

Note that, as we sought, Eq. (22) contains only averages and deviations of the dependent variable, \(C_{Aw}\). Also, by direct comparison with the closed macroscale mass balance given by Eq. (6), it follows that

$$\begin{aligned} {{\hat{\varvec{\mathsf {D}}}}}{{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm x}}} C^{Aw} = {{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} C^{Aw}+{{\hat{D}}}_{Aw}{\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\; \end{aligned}$$
(24)

Clearly, the term \({{\hat{D}}}_{Aw}{\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\) accounts for the influence of the morphology of the solid phase on the diffusion process. We will subsequently return to this expression to express the effective diffusion tensor \({{\hat{\varvec{\mathsf {D}}}}}\) in terms of microscale parameters. There are many options available for computing the averaging operator that appears in Eq. (24). For example, one may perform direct numerical simulations at the microscale or perform experiments to quantify this term for a given set of transport conditions. In the following, we show how to predict the values of this term by deriving and formally solving a problem for the concentration deviations. This approach is, at its core, simply a microscale simulation method. However, it is a specific microscale simulation method that is informed by the admissible solution forms for the deviation equations. Thus, the results provide efficient, and explicit, forms for the effective transport parameters (in this case, the diffusion tensor).

Step 3 A deviation equation is sought so that Eq. (24) can be solved, yielding an estimate of \({{\hat{\varvec{\mathsf {D}}}}}\). A deviation equation can be derived by subtracting the macroscale conservation of mass given by Eq. (22) from the microscale conservation of mass equation given by Eq. (10) and simplifying the resulting expression using the definitions given by Eqs. (17)–(19).

The boundary conditions that should be imposed on the external surfaces of the REV pose a particular problem; this has been discussed extensively by Wood and Valdés-Parada (2013). Conventionally, the approach has been to impose a weak condition on the boundaries, such as demanding that the external boundaries be periodic in \({\tilde{C}}_{Aw}\) and its normal derivative. Indeed, this weak condition is more a convenience than a necessity; however, comparison with experimental data in several studies (Whitaker 1999) suggests its pertinence.

Finally, at the internal boundaries, a no-flux condition is imposed. To develop a boundary condition for the deviations, we need to only use the decomposition defined by Eq. (18). Adopting each of these approximations, we find that a complete statement of the deviation equations is given by

$$\begin{aligned}&\frac{\partial {{\tilde{C}}_{Aw}({{\varvec{\mathrm x}}},{\varvec{\mathrm \xi }},t)}}{\partial {t}} = \nabla _{{\varvec{\mathrm x}}} {{\varvec{\mathsf {\cdot }}}}\Bigg ({{\hat{D}}}_{Aw}\nabla _{{\varvec{\mathrm x}}} {\tilde{C}}_{Aw}({{\varvec{\mathrm x}}},{\varvec{\mathrm \xi }},t) -\left. {{\hat{D}}}_{Aw}{\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\right| _{({{\varvec{\mathrm x}}},t)} \Bigg ), \end{aligned}$$
(25a)
$$\begin{aligned}&-{{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}) {{\varvec{\mathsf {\cdot }}}}{{\hat{D}}}_{Aw} \nabla _{{\varvec{\mathrm x}}} {\tilde{C}}_{Aw}({{\varvec{\mathrm x}}},{\varvec{\mathrm \xi }},t)= \underbrace{ {{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}){{\varvec{\mathsf {\cdot }}}}{{\hat{D}}}_{Aw} \nabla _{{\varvec{\mathrm x}}} {C}^{Aw}({\varvec{\mathrm x}},t)}_{\mathrm {source}} {\mathrm { on }}\ {{\Gamma }_{w \mathrm i}}({\varvec{\mathrm x}}), \end{aligned}$$
(25b)
$$\begin{aligned}&{\tilde{C}}_{Aw}({\varvec{\mathrm x}},\xi _i=0, t)={\tilde{C}}_{Aw}({\varvec{\mathrm x}},\xi _i=\xi _{il},t) \quad {\mathrm {for}}\quad i=1,\ldots ,n_d\ {\mathrm { on }}\ {{\Gamma }_{w \mathrm e}}({\varvec{\mathrm x}}), \end{aligned}$$
(25c)
$$\begin{aligned}&{{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}){{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm x}}} {\tilde{C}}_{Aw}({\varvec{\mathrm x}},\xi _i=0, t)= -{{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+\xi _{il}){{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm x}}} {\tilde{C}}_{Aw}({\varvec{\mathrm x}},\xi _i=\xi _{il}, t)\nonumber \\&\quad {\mathrm { for }}\quad i =1,\ldots ,n_d\ {\mathrm { on }}\ {{\Gamma }_{w \mathrm e}}({\varvec{\mathrm x}}),\quad {\mathrm {and}} \end{aligned}$$
(25d)
$$\begin{aligned}&{\tilde{C}}_{Aw}({\varvec{\mathrm x}},{\varvec{\mathrm \xi }},0)= \underbrace{ \mathscr {I}(\mathbf{x},\varvec{\xi })}_{\mathrm {source}}. \end{aligned}$$
(25e)

Note that here we have completed the system of equations by specifying an initial condition. In Eqs. (25c)–(25d), the spatial domain is indicated by \({{\Omega }_{}}=[0,\xi _{1l}]\times [0,\xi _{2l}]\times [0,\xi _{3l}]\), and \(n_d\) is the number of spatial dimensions. The vectors \(\xi _{il}\) are a set of lattice vectors used to define periodicity in the domain. Because of this periodicity, the boundary integral term in Eq. (25a) vanishes for the steady-state case, since the domain of integration is invariant with respect to location \({\varvec{\mathrm x}}\) within the periodic domain. The internal boundary condition is specified in terms of a constant macroscale gradient that applies everywhere in the domain, which could be used to write the right-hand side of Eq. (25a) in alternative forms under certain conditions.

Equation (25a) is an integro-differential equation that is non-local in space, which can be made local by specifying a fixed \({\varvec{\mathrm x}}\). One of the primary restrictions of the TCAT development for this problem is that an REV exists and that the characteristic size of the REV is substantially smaller than the characteristic size of \(\Omega ^0_w\) (\(\ell ^\mathrm{ma}\ll \ell ^\mathrm{me}\)). Thus, for the purposes of computing the spatial averaging operator \({{\hat{D}}}_{Aw}{\left\langle {{{\varvec{\mathrm n}}_{w}}}{\tilde{C}}_{Aw} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\), it suffices to solve Eqs. (25a)–(25e) over a single REV.

The problem for the concentrations deviations derived above contains two sources, namely the concentration gradient \(\nabla {C}^{Aw}(\mathbf{x},t)\) in the interfacial boundary condition and \(\mathscr {I}({\varvec{\mathrm x}},{\varvec{\mathrm \xi }})\) in the initial condition. As suggested by Wood and Valdés-Parada (2013), one may use integral equation formulations in terms of Green’s functions to solve this problem as

$$\begin{aligned} {\tilde{C}}_{Aw}({\varvec{\mathrm x}}, {\varvec{\mathrm \xi }},t)&= \int _{\mathbf{w}\in {{\Omega }_{w}}({{\varvec{\mathrm x}}}) } G({\varvec{\mathrm x}}, {\varvec{\mathrm \xi }},t; {\varvec{\mathrm w}},0) \mathscr {I}({\varvec{\mathrm w}},{{\varvec{\mathrm \xi }}})~\, \mathrm {d}V(\mathbf{w})\nonumber \\&\quad -\int _{\tau =0}^{\tau =t} \int _{\mathbf{w} \in {{\Gamma }_{w \mathrm i}}({\varvec{\mathrm x}})} G({\varvec{\mathrm x}}, {\varvec{\mathrm \xi }},t; {{\varvec{\mathrm w}}},\tau ) {{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm w}}+{\varvec{\mathrm \xi }}) {{\hat{D}}}_{Aw} \nonumber \\&\quad {{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm w}}} C^{Aw}({{\varvec{\mathrm w}}},t) \mathrm{d}A (\mathbf{w}) \, \mathrm {d}\tau \end{aligned}$$
(26)

with G being the Green’s function associated with the initial and boundary value problem of the concentration deviations. Note that \(\nabla C^{Aw}\) has been removed from the spatial integral but not from the temporal integral in the last term of the above equation. This implies that if this expression is substituted into Eq. (24), the effective diffusivity contains memory of the initial condition and the early stages of the transport process.

In many diffusive processes, the time for disturbances to relax at the microscale is much shorter than the time it takes them to relax at the macroscale. This motivates an additional point of simplification for the concentration deviations, which is supported by the separation of characteristic lengths already imposed, and explained previously in the literature (Whitaker 1999). On the basis of the order of magnitude estimates of the characteristic time scales at the microscale and the macroscale given by \(t_\mathrm{{mi}}^*= \mathcal {O}[(\ell _\mathrm{mi})^2/{{\hat{D}}}_{Aw}]\) and \(t_\mathrm{{ma}}^*= \mathcal {O}[(\ell ^\mathrm{ma})^2/{{\hat{D}}}_{Aw}]\); it follows that \(t_\mathrm{{mi}}^*\ll t_\mathrm{{ma}}^*\), since \(\ell _\mathrm{mi}\ll \ell ^\mathrm{ma}\). Under these conditions, the memory of the initial condition is lost, and the solution given by Eq. (26) can be reduced to

$$\begin{aligned} {\tilde{C}}_{Aw} ({{\varvec{\mathrm x}}, {\varvec{\mathrm \xi }}},t) = {{\varvec{\mathrm b}}}({{\varvec{\mathrm x}}, {\varvec{\mathrm \xi }}}) {{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm x}}} C^{Aw}(\mathbf{x},t). \end{aligned}$$
(27)

Here \({{\varvec{\mathrm b}}}({{\varvec{\mathrm x}}, {\varvec{\mathrm \xi }}})\) is a closure variable that is conveniently defined to represent the surface integral of the Green’s function. One can think of this variable as being the vector of deviation fields that would be generated by unit gradients of concentration in each of the three cardinal directions of the REV. Even without explicitly computing the Green’s function, this solution gives us the proper form for the localized microscale closure. Substitution of this result into Eq. (24) yields

$$\begin{aligned} {{\hat{\varvec{\mathsf {D}}}}}= {{\hat{D}}}_{Aw} {\varvec{\mathsf {I}}}+ {{\hat{D}}}_{Aw}\left\langle {{{\varvec{\mathrm n}}_{w}}}\otimes {{\varvec{\mathrm b}}} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}} \end{aligned}$$
(28)

where \(\otimes \) denotes the outer product. In contrast to Eq. (24), the above result does not require knowledge of the macroscopic concentration gradient, instead Eq. (28) provides the macroscale definition of the effective diffusion tensor, assuming that \({\varvec{\mathrm b}}\) is available. In order to derive the governing equations of \({\varvec{\mathrm b}}\), we substitute Eq. (27) into Eqs. (25a)–(25e), yielding (Whitaker 1999)

$$\begin{aligned}&\displaystyle \nabla _{{\varvec{\mathrm x}}}^2 {\varvec{\mathrm b}}({\varvec{\mathrm x}}, {\varvec{\mathrm \xi }}) = 0 {\text { in }}{{\Omega }_{w}}({\varvec{\mathrm x}}), \end{aligned}$$
(29a)
$$\begin{aligned}&\displaystyle -\,{{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}){{\varvec{\mathsf {\cdot }}}}\nabla _{{\varvec{\mathrm x}}} \otimes {\varvec{\mathrm b}}({\varvec{\mathrm x}}, {\varvec{\mathrm \xi }}) = {{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+{\varvec{\mathrm \xi }}) {\text { on }} {{\Gamma }_{w \mathrm i}}\; \end{aligned}$$
(29b)
$$\begin{aligned}&\displaystyle {\varvec{\mathrm b}}({\varvec{\mathrm x}},\xi _i=0)= \mathbf b ({\varvec{\mathrm x}},\xi _i=\xi _{il}), \quad {\text {for}}\quad i=1,\ldots ,n_d {\text { on }} {{\Gamma }_{w \mathrm e}}({\varvec{\mathrm x}}), \end{aligned}$$
(29c)
$$\begin{aligned}&\displaystyle {{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}})\cdot \nabla _{{\varvec{\mathrm x}}} \otimes {\varvec{\mathrm b}}({\varvec{\mathrm x}},\xi _i=0)= -\,{{{\varvec{\mathrm n}}_{w}}}({\varvec{\mathrm x}}+ \xi _{il})\cdot \nabla _{{\varvec{\mathrm x}}}\otimes \mathbf b ({\varvec{\mathrm x}},\xi _i=\xi _{il}), \nonumber \\&\displaystyle \quad {\text {for}}\quad i=1,\ldots ,n_d {\text { on }} {{\Gamma }_{w \mathrm e}}({\varvec{\mathrm x}})\; \end{aligned}$$
(29d)
$$\begin{aligned}&\displaystyle \left. {{{\left\langle {\varvec{\mathrm b}} \right\rangle _{{{\Omega }_{w}},{{\Omega }_{w}}}}}} \right| _{{\varvec{\mathrm x}}}={\varvec{\mathrm 0}}. \end{aligned}$$
(29e)

Note that, because this problem is treated as being steady in a periodic medium, the term \(\nabla _{{\varvec{\mathrm x}}} {{\varvec{\mathsf {\cdot }}}}\left. {\left\langle {{{\varvec{\mathrm n}}_{w}}}\otimes {\varvec{\mathrm b}} \right\rangle _{{{\Gamma }_{w \mathrm i}},{{\Omega }_{w}}}}\right| _{{\varvec{\mathrm x}}}\) is identically zero; thus, we have made this simplification on the right-hand side of Eq. (29a). Because the initial condition is not used, we have also added a constraint requiring the average of the deviations over the REV to be zero. Although this is identically true for averages in the TCAT formulation, we must explicitly impose this constraint in this set of equations in order to have a well-posed problem and thus to determine a unique solution.

One could also determine \({{\hat{\varvec{\mathsf {D}}}}}\) by solving the microscale balance for \(C_{Aw}\) directly (and then computing the deviations). However, this approach would require solutions for one linearly independent value of \(\nabla C^{Aw}\) per unknown tensor component (six solutions total for a three-dimensional system). In Eqs. (29a)–(29e), each component of the effective diffusion tensor is directly definable by a solution to the set of PDEs.

Step 4 The formulation specified above must be solved in a periodic unit cell that is representative of the porous medium morphology and topology. Here, the terminology “periodic unit cell” indicates an REV where all dependent variables are taken to be periodic at the boundaries. For particularly simple geometries, the fields of the vector \({\varvec{\mathrm b}}\) can be determined analytically (Chang 1983; Ochoa-Tapia et al. 1994). Generally, however, we would resort to numerical methods to compute the vector \({{\varvec{\mathrm b}}}\) in the REV (Ochoa-Tapia et al. 1994; Ryan et al. 1980). Examples of the computation of the effective diffusion tensor are described in the next section for a variety of periodic unit cells.

5 Computation of Macroscale Parameters

As mentioned above, the complexity of the porous medium topology must be included within the periodic unit cells for the determination of the \({\varvec{\mathrm b}}\) fields. An interesting question then arises about how much of the complexity is required to fully represent the processes of interest. Although there is no simple answer to this question, one can consider trying a sequence of unit cells of increasing complexity to answer this question, at least heuristically. In the following paragraphs we present predictions of the components of the diffusivity tensor in terms of isotropic and anisotropic periodic unit cells.

Fig. 3
figure 3

Examples of three-dimensional unit cells for the closure problem solution. The porosity values are 0.8 for unit cells (a) and (b); whereas for unit cells (c) and (d) porosity values are 0.56 and 0.84, respectively

Full size image

5.1 Isotropic Unit Cells

It is convenient to explore first the predictions resulting from using simple geometric representations of the solid phase in the unit cell. With this in mind, let us consider the periodic unit cells shown in Fig. 3 in which the solid phase is represented as a periodic array of in-line spheres and as random distributions of non-overlapping spheres. In addition, in this figure we included a non-periodic homothetic unit cell (Fig. 3b), which is known as Chang’s unit cell (Chang 1983). This type of unit cell represents an approximation of its periodic homothetic counterpart (i.e., Fig. 3a) and admits an analytic solution. In Chang’s unit cell, the periodic condition at the inlets and outlets of the unit cell is replaced by a homogeneous Dirichlet-type boundary condition. Interestingly, the solution of the closure problem in the unit cell depicted in Fig. 3b leads to the classic result from Maxwell (Maxwell 1881; Ochoa-Tapia et al. 1994) for dilute spheres in an infinite medium, and from Rayleigh (1892) as a first approximation to a periodic array of spheres

$$\begin{aligned} \frac{{{{\epsilon }^{{\overline{\overline{w}}}}}}{\hat{D}}}{{{\hat{D}}}_{Aw}} = \frac{2 {{{\epsilon }^{{\overline{\overline{w}}}}}}}{3-{{{\epsilon }^{{\overline{\overline{w}}}}}}}. \end{aligned}$$
(30)

Although analytical solutions are possible for simple geometries, they are generally not practical for complex ones. We solved the microscale problem given by Eqs. (29a)–(29e) numerically for the periodic unit cells shown in Fig. 3a, c and d using the finite element software COMSOL Multiphysics® 5.1. We performed standard convergence analyses for the spatial mesh in order to guarantee that the results were grid-independent. In all cases we noted that the off-diagonal components of the effective diffusivity tensor turned out to be negligible with respect to their diagonal counterparts. This means that, for the particular geometries considered in Fig. 3, we can approximate the diffusivity tensor as being isotropic, so that .

In Table 1, we compare the predictions of the diagonal components of the diffusivity tensor for the random distributions with those resulting from the closure problem solution for the simple unit cells in Fig. 3. We observe that the largest differences between the predictions of the effective diffusivity are found for the porosity value of 0.56, in particular those resulting from using Chang’s unit cell. Nevertheless, the relative error values are below 10%. Furthermore, when compared to the predictions resulting from representing the solid phase as a spherical obstacle with those from the random geometry, we observe that the relative errors are smaller than 5% in all cases considered here.

The above results show that, despite the simple nature of the unit cells in Fig. 3, they may be used to provide parameter estimates. The level of agreement between predictions made with simple unit cells and real porous media will depend upon the model. For example, more complicated situations such as highly convective mass transport, where the geometry is known to play a crucial role in the predictions of the dispersion tensor, would require more complex unit cells to provide reasonable estimates of model parameters. In any event, the unit cell concept allows the inclusion of actual three-dimensional porous medium images to evaluate model parameters, which illustrates how this direct evaluation approach could be applied for arbitrarily complex media.

Table 1 Predictions of the components of the effective diffusion tensor resulting from solving the closure problem in the three-dimensional unit cells depicted in Fig. 3
Full size table

5.2 Anisotropic Unit Cells

To compute the effective diffusion tensor for anisotropic structures, one follows essentially the same scheme as described in the previous section. For anisotropic systems, both the diagonal and off-diagonal components of the tensor have potentially non-negligible values. In Fig. 4, we provide an example REV geometry for two anisotropic systems. As for isotropic unit cells, these results were obtained using the finite element package COMSOL Multiphysics® 5.1. Standard grid refinement techniques were used to ensure convergence. Due to the orientation and shape of the obstacles considered in the unit cells depicted in Fig. 4, the diagonal components of the effective diffusivity tensor exhibit more differences between themselves compared to the predictions shown in Table 1. Furthermore, for the unit cell containing fiber-shaped obstacles, we observe that, as porosity decreases, the values of the off-diagonal components of the diffusivity tensor are comparable to their diagonal counterparts. Hence, the unit cells considered in Fig. 4 are anisotropic with respect to the diffusion process.

Fig. 4
figure 4

Computed components of the effective diffusion tensor for two anisotropic geometries. (Left) Ellipsoid with an aspect ratio of \(\sim 1.8\) tilted at \(45^{\circ }\). (Right) A bidisperse bundle of fibers titled at \(45^{\circ }\) with a diameter ratio of \(\sim 1.8\). Here, \({\hat{D}}_{ij}\) represents the ij- component of the effective diffusion tensor \({\hat{\mathbf{D}}}\), and \({\hat{D}}_{Aw}\) represents the molecular diffusion coefficient for species A

Full size image

5.3 Direct Numerical Simulation Validation

As a validation of the direct parameter evaluation method developed in this work, we compared the macroscopic flux computed using the computed value of the macroscale diffusivity tensor resulting from solving Eqs. (28) and (29), with the average of the microscale flux that was obtained by performing direct numerical simulation (DNS). The cases shown in Fig. 3a–c and Fig. 4 were all simulated in this manner. The results agreed in every case to 2–3 significant figures. The difference between the direct evaluation and the DNS decreased as the grid resolution of the numerical simulations increased. The close agreement in the results and pattern of decreasing errors with grid refinement for all cases was concluded to be a thorough validation of the method developed.

6 Discussion and Conclusions

In this work we have provided a means for a priori parameter estimation for macroscopic models developed using the TCAT approach. Since several entropy inequalities have been derived using the general TCAT approach, hierarchies of models can be derived for single and two-fluid-phase systems, fluid flow alone or fluid flow and species transport, energy transport, and the transition between a two-fluid porous medium system and single-fluid-phase domain. TCAT models can be derived relatively simply for a wide range of systems using available results to guide the formation of closure relations that can be combined with existing conservation equations to form complete closed models. To illustrate how these archival results can be used to accomplish such a model formulation, an available entropy inequality was used to formulate a closure relation and closed model for a case involving diffusion through a porous medium system. A similar approach could be used to formulate many other models.

TCAT models are typically formulated in a closed form that includes closure relation parameters. It is left that these parameters can be obtained for a given system by comparing experimental observations, or microscale simulations, with the TCAT macroscale model and solving an inverse problem. An attractive feature of the MVA is that it provides a priori estimates of parameter values for certain model systems. Borrowing from the general MVA approach, we developed a direct parameter evaluation approach for TCAT models. This approach was illustrated for the simple case of passive species diffusion in rigid and homogeneous porous media, and we derived an explicit expression for determining the effective diffusivity in terms of the concentration deviations. These deviations can be computed in a number of ways, such as from microscale simulations or experimental data. In this work, we derived, and formally solved, an initial and boundary value problem for the concentration deviations firstly under transient conditions and secondly under quasi-steady conditions.

The a priori parameter estimation approach was used to evaluate the macroscale diffusion tensor for several different types of porous media geometries. This advancement is not isolated to the case considered here, rather it can be applied more generally for a variety of cases, such as heat and or momentum transfer in porous media. The details of the derivation of this TCAT extension illustrates certain important differences between the MVA and TCAT approaches. One of these differences deals with way in which deviations are computed, which is central to the parameter evaluation approach. This difference for TCAT, where the mean of the deviations vanish over an REV, proves to be a useful attribute for parameter evaluation leading to exact results for certain identities arising in the formulation. The framework for parameter evaluation proposed here constitutes a convenient addition to the, already robust, TCAT modeling approach.