Upscaling Diffusion and Nonlinear Reactive Mass Transport in Homogeneous Porous Media

Abstract

In this work, we revisit the upscaling process of diffusive mass transfer of a solute undergoing a homogeneous reaction in porous media using the method of volume averaging. For linear reaction rate kinetics, the upscaled model exhibits a vis-à-vis correspondence with the mass transfer governing equation at the microscale. When nonlinear reactions are present, other methods must be adopted to upscale the nonlinear term. In this work, we explore a linearization approach for the purpose of solving the associated closure problem. For large rates of nonlinear reaction relative to diffusion, the effective diffusion tensor is shown to be a function of the reaction rate, and this dependence is illustrated by both numerical and analytical means. This approach leads to a macroscale model that also has a similar structure as the microscale counterpart. The necessary conditions for the vis-à-vis correspondence are clearly identified. The validation of the macroscale model is carried out by comparison with pore-scale simulations of the microscale transport process. The predictions of both concentration profiles and effectiveness factors were found to be in acceptable agreement. In an appendix, we also briefly discuss an integral formulation of the nonlinear problem that may be useful in developing more accurate results for the upscaled transport and reaction equations; this approach requires computing the Green function corresponding to the linear transport problem.

1 Introduction

Study of mass transport and reaction in multiscale systems is a relevant topic that involves applications ranging from transport in cellular media (Vafai 2010) to catalytic reactors (Froment et al. 2010). In media that are structured with a discrete hierarchy of scales, one often attempts to eliminate the redundant information associated with the microscale solution by developing effective medium equations that are applicable at the macroscale (cf., Cushman 2010; Pinder and Gray 2008). This process is generally referred as upscaling, and it can be carried out by a wide array of techniques including homogenization (Sanchez-Palencia 1970), thermodynamically constrained averaging theory (Gray and Miller 2014), volume averaging (Whitaker 1999), the generalized method of moments (Brenner 1980), mixture theory (Bowen 1967), and ensemble averaging (Saffman 1959). In these upscaling techniques, the information from the smaller scale is systematically filtered by identifying the corresponding time- and length-scale constraints and assumptions that allow reducing the number of degrees of freedom and to well bound the applicability of the upscaled model (Wood 2009; Wood and Valdés-Parada 2013). In this work, we derive an upscaled model for diffusive mass transport of a solute undergoing a chemical reaction with nonlinear kinetics in the fluid phase that saturates a homogeneous porous medium using the volume averaging method (Whitaker 1999).

Upscaling mass transport and reaction in porous media has been widely studied in the literature, and it remains a topic of wide interest (cf., Dadvar and Sahimi 2007; Ding et al. 2013; Edery et al. 2013; Habibi-Matin and Pop 2013; Hochstetler and Kitanidis 2013; Ko c̆ i et al. 2010; Pereira et al. 2014; Ratnakar et al. 2012). Due to recent increase in the computational capabilities, it is now feasible to carry out detailed pore-scale simulations of reactive transport in porous media using, for example, the lattice-Boltzmann method (Li et al. 2013; Machado 2012; Patel et al. 2014; Tian et al. 2014). Nevertheless, it is often desirable to develop upscaled theories of microscale processes to help reduce the number of degrees of freedom required to numerically simulate a problem and to eliminate redundant microscale information that is not, in itself, of primary interest. This motivates the derivation of rigorous upscaled models with a clear identification of their range of validity.

As mentioned above, most upscaled models are expressed in terms of effective medium coefficients that capture essential information from the microscale. For diffusive and reactive mass transfer in porous media, the main effective medium coefficients are the effective diffusivity and the effective reaction parameters [see, for example, Eqs. (1.4–68) in Whitaker 1999]. The issue of the dependence of the effective transport coefficients with the reaction rate has been extensively debated in the literature (cf., Park and Kim 1984; Sharratt and Mann 1987; Toei et al. 1973). In their study of substrate transport through grains coated by biofilms, Dykaar and Kitanidis (1996) showed the dependence of the effective medium coefficients with the Péclet and Damköhler numbers. Dadvar and Sahimi (2007) used pore network and continuum models and estimated the effective diffusivity under both reactive and nonreactive conditions, noticing significant differences between them. Recently, it has been shown (Valdés-Parada et al. 2011a; Valdés-Parada and Alvarez-Ramírez 2010), by means of the volume averaging method, that the effective transport coefficients involved in diffusion and dispersion in porous media depend, in general, on the nature and magnitude of the reaction rate. As mentioned above, the use of upscaled models is restricted to certain time and length-scale constraints and assumptions. For applications in which these constraints are not met, one may use nonlocal models as suggested by Wood and Valdés-Parada (2013).

The above works have been centered on reaction rates involving first-order kinetics. A study involving nonlinear kinetics (Michaelis–Menten type and second-order kinetics) using 3D pore network modeling was carried out by Dadvar and Sahimi (2007). These authors found that the effective diffusion coefficients under reactive and nonreactive conditions may differ considerably. Modeling nonlinear reactive transport in porous media has been carried out in the literature using both stochastic and deterministic approaches (cf., Giacobbo and Patelli 2007; Kang et al. 2010; Liu and Ewing 2005; Weerd et al. 1998; Wood et al. 2007; Wood and Whitaker 1998). In their study of reactive colloids in groundwater, Weerd et al. (1998) showed that nonlinear reactions lead to breakthrough curves that are steeper during contamination than in the linear case, which are in closer agreement with experimental data. Previous applications of the volume averaging method for studying mass transport with nonlinear reactions have been directed to the study of biofilms involving Michaelis–Menten kinetics (Wood and Whitaker 1998, 2000; Wood et al. 2002) under local mass equilibrium (Golfier et al. 2009) and nonequilibrium (Davit et al. 2010; Orgogozo et al. 2010) conditions. Moreover, the applications have not been restricted to diffusive transport but also to dispersion with heterogeneous nonlinear reactions as shown by Wood et al. (2007).

In the above-referenced works, the reaction term in the upscaled model, even when involving nonlinear kinetics, is of the same mathematical form as the reaction rate term in the pore-scale model. In other words, the structure of the macroscale model exhibits a vis-à-vis correspondence with its microscale counterpart. This often constitutes an approximation that needs to be validated in order to assure that the macroscopic models that are derived via upscaling are accurate. With this as a goal, in this work we study diffusive mass transfer of a solute undergoing a homogeneous reaction in homogeneous porous media. To derive the upscaled model, we employ the method of volume averaging involving a closure scheme to predict the corresponding effective medium coefficients. We first carry out our derivations assuming that the reaction rate is linear, and then, the analysis is extended to treat nonlinear reaction kinetics using a linearization approach. In both situations, the time- and length-scale constraints associated with the vis-à-vis approximation are clearly identified. In addition, we carry out a comparison with (direct) pore-scale simulations (PSS) to test the capabilities of the upscaled model. In addition, in the appendix, we outline an approach to generate implicit integral solutions of the closure problem; these solutions may be valuable when the conditions are such that the linearization of the reaction term is not accurate. To adopt this latter approach, the Green function for the linear part of the transport operator must be calculated.

2 Microscale Formulation

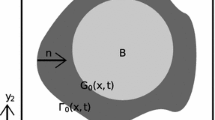
We begin by considering a rigid porous medium (Fig. 1) that is saturated by only one fluid phase (the $\gamma$-phase) that carries a solute (species $A$) forming a dilute solution. In this work, we consider only diffusive mass transport and a homogeneous reaction in the fluid phase. This means that the solid phase (the $\kappa$-phase) is assumed impermeable to mass transport. The governing initial and boundary-value problem for transport of species $A$ at the pore scale is given by

$$\begin{aligned} \frac{\partial c_{A\gamma }}{\partial t}&=\nabla \cdot \left( {\fancyscript{D}}_{A\gamma }\nabla c_{A\gamma }\right) -R(c_{A\gamma }),\quad \text {in }{\fancyscript{V}}_{\gamma , M}\end{aligned}$$

(1a)

$$\begin{aligned}&\quad -\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla c_{A\gamma }=0,\quad \text {at }{\fancyscript{A}}_{\gamma \kappa , M}\end{aligned}$$

(1b)

$$\begin{aligned} c_{A\gamma }&={\fancyscript{E}}\left( \mathbf{{x}},t\right) ,\quad \text {at }{\fancyscript{A}}_{\gamma \text {e}, M}\end{aligned}$$

(1c)

$$\begin{aligned} c_{A\gamma }&={\fancyscript{F}}\left( \mathbf {x}\right) ,\quad \text {when }t=0 \end{aligned}$$

(1d)

Here, $c_{A\gamma }$ is the molar concentration of species $A$ in the $\gamma$ phase, $R$ is the molar reaction rate owing to homogeneous chemical reaction, and ${\fancyscript{D}}_{A\gamma }$ is the mixture diffusion coefficient for species $A$ in the $\gamma$ phase. In this formulation, ${\fancyscript{A}}_{\gamma \kappa ,M}$ represents the surface of the $\gamma$–$\kappa$ interface contained within the macroscopic region shown in Fig. 1a, while ${\fancyscript{A}}_{\gamma \text {e},M}$ represents the entrances and exits of the $\gamma$ phase at the boundaries of the macroscopic region (see Fig. 2 in Wood and Valdés-Parada 2013); finally x is a position vector. Although in previous works a more relaxed notation has been used, we find it convenient to conserve the explicit relation between dependent and independent variables. Furthermore, unless explicitly indicated to be different from x, all spatial derivatives are taken with respect to x. In the following section, we will derive the macroscale model by volume averaging the pore-scale model and the benefits of using this notation will be clear. In each step of the averaging process, the corresponding length-scale constraints and assumptions are clearly identified.

Fig. 1

a Macroscopic region, averaging domain and characteristic lengths of the system. b Position vectors associated to the averaging domain

3 Spatial Smoothing for Linear Reactions

To begin the averaging process, we first associate each point in the macroscopic region ${\fancyscript{V}}_M$ with an averaging domain ${\fancyscript{V}}$ of characteristic size $r_0$ that contains portions of both the solid and fluid phases and an interface, i.e., ${\fancyscript{V}} ={\fancyscript{V}}_{\gamma }\cup {\fancyscript{A}}_{\gamma \kappa } \cup {\fancyscript{V}}_{\kappa }$. Here, ${\fancyscript{V}}_\gamma$ and ${\fancyscript{V}}_\kappa$ are the domains occupied by the $\gamma$-phase and $\kappa$-phase, respectively, within ${\fancyscript{V}}$, and ${\fancyscript{A}}_{\gamma \kappa }$ represents the interface between these two domains. For each $\mathbf{{x}}\in {\fancyscript{V}}_M$, we locate the centroid of an averaging volume, ${\fancyscript{V}}$, which is classically a compact uniform weighting function over a spherical volume with domain specified by

$$\begin{aligned} {\fancyscript{V}}\left( \mathbf{{x}}\right) =\{\mathbf{r}\in {\fancyscript{V}}_M:||\mathbf{y}||<r_0\} \end{aligned}$$

(2)

here $\mathbf{y}= \mathbf{r}-\mathbf{x}$ as illustrated in Fig. 1b. The magnitude of the averaging domain is given by $\left| {\fancyscript{V}} \right| = V$. The value of the weighting function, $m(\mathbf{x})$, is given by

$$\begin{aligned} m({\mathbf {r}}) = \left\{ {\begin{array}{ll} \tfrac{1}{V}&{}\quad \hbox {for } {\mathbf {r}}\in {\fancyscript{V}}(\mathbf{x}) \\ 0&{} \quad \hbox {otherwise} \end{array}} \right. \end{aligned}$$

(3)

Certainly, if $\mathbf{r} \in {\fancyscript{V}}_\gamma (\mathbf{x})$, we may define the weighting function as

$$\begin{aligned} m_\gamma (\mathbf{r})= \frac{1}{V_\gamma } \end{aligned}$$

(4)

For a piecewise smooth function defined everywhere, $\psi$, the intrinsic averaging operator over the averaging domain, is introduced as

$$\begin{aligned} \langle \psi \rangle ^\gamma |_\mathbf{x}= \int \limits _{\mathbf{r} \in {\fancyscript{V}}_\gamma \left( \mathbf{x}\right) } m_\gamma (\mathbf{r}) \left. \psi \right| _{\mathbf{r}} \, \mathrm{d}V\left( \mathbf{r}\right) =\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{V}}_\gamma \left( \mathbf{x}\right) } \left. \psi \right| _{\mathbf{r}} \, \mathrm{d}V\left( \mathbf{r}\right) \end{aligned}$$

(5)

Notice that the resulting average quantities are continuous, as they are defined for all $\mathbf{x}\in {\fancyscript{V}}_M$. Following Whitaker (1999), the next steps established in the method of volume averaging in order to upscale the microscale balance equations can be listed as

• 1. Application of the intrinsic averaging operator given by Eqs. (5) to Eq. (1a)

• 2. Interchange temporal differentiation and spatial integration using the general transport theorem and recall that the porous medium has been assumed to be rigid,

  $$\begin{aligned} \frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{V}}_\gamma \left( \mathbf{x}\right) }\left. \frac{\partial \psi }{\partial t}\right| _{\mathbf{r}}\mathrm{d}V\left( \mathbf{r}\right) = \frac{\partial \left. \langle \psi \rangle ^\gamma \right| _\mathbf{x}}{\partial t} \end{aligned}$$

  (6)

• 3. Interchange spatial differentiation and spatial integration using the spatial averaging theorem for intrinsic averages (Whitaker 1999),

  $$\begin{aligned} \langle \nabla \psi \rangle ^\gamma = \nabla \langle \psi \rangle ^\gamma +\langle \psi \rangle ^\gamma \varepsilon _\gamma ^{-1}\nabla \varepsilon _\gamma +\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }(\mathbf x)} \mathbf{n}_{\gamma \kappa }\psi ~ \mathrm{d}A(\mathbf{r}) \end{aligned}$$

  (7)

  here $\varepsilon _\gamma$ is the volume fraction of the $\gamma$-phase within the averaging domain, i.e., $\varepsilon _\gamma =V_\gamma /V$.

• 4. Use the interfacial boundary condition given by Eq. (1b) where applicable.

• 5. Decompose the point concentration, $c_{A\gamma }$, in terms of the averaged concentration, $\langle c_{A\gamma }\rangle ^\gamma$, and the concentration spatial deviation, ${\tilde{c}}_{A\gamma }$ (Gray 1975)

  $$\begin{aligned} \left. c_{A\gamma }\right| _{\mathbf{x}}=\left. \langle c_{A\gamma }\rangle ^\gamma \right| _{\mathbf{x}}+\left. {\tilde{c}}_{A\gamma }\right| _{\mathbf{x}} \end{aligned}$$

  (8)

  In the above expression, we only use averages that are computed when x is located in the fluid phase.

After conducting these steps, the unclosed average equation (valid everywhere in the domain of the porous medium ${\fancyscript{V}}_M$) can be written as (see Whitaker 1999, for details)

$$\begin{aligned} \frac{\partial \langle c_{A\gamma }\rangle ^\gamma }{\partial t}&= \nabla \cdot \left[ {\fancyscript{D}}_{A\gamma } \left( \nabla \langle c_{A\gamma }\rangle ^\gamma +\langle c_{A\gamma }\rangle ^\gamma \varepsilon _\gamma ^{-1} \nabla \varepsilon _\gamma +\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa } (\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }\langle c_{A\gamma }\rangle ^\gamma \mathrm{d}A(\mathbf{r})\right. \right. \nonumber \\&\left. \left. +\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }(\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }{\tilde{c}}_{A\gamma }\mathrm{d}A(\mathbf{r})\right) \right] -\big \langle R(c_{A\gamma })\big \rangle ^\gamma \end{aligned}$$

(9)

This equation is nonlocal since it involves a surface integral in which $\langle c_{A\gamma }\rangle ^\gamma$ is evaluated at points other than the averaging domain centroid, $\mathbf x$. In addition, notice that, up to this point, no expression has been provided for the reaction rate. In the following, we will treat it as a linear function and then extend the analysis to nonlinear expressions.

4 Closure: Linear Case

To complete the upscaling process, it is necessary to derive an expression for the concentration deviations in terms of $\langle c_{A\gamma }\rangle ^\gamma$ and, if necessary, of its derivatives. This is usually known as closure. To this end, it is necessary to derive and formally solve the initial and boundary-value problem for the concentration deviations. The governing differential equation for ${\tilde{c}}_{A\gamma }$ can be obtained by subtracting Eq. (9) from Eq. (1a), as suggested from Eq. (8). The result is expressed as follows

$$\begin{aligned} \frac{\partial {\tilde{c}}_{A\gamma }}{\partial t}&= \nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) -\nabla \cdot \left( \frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa } (\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }{\tilde{c}}_{A\gamma }\mathrm{d} A(\mathbf{r})\right) -\underbrace{{\fancyscript{D}}_{A\gamma }\nabla \cdot \left( \langle c_{A\gamma }\rangle ^\gamma \nabla \ln \varepsilon _\gamma \right) }_{\text {volume diffusive source}} \nonumber \\&-\,\underbrace{\nabla \cdot \left( \frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa } (\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }\langle c_{A\gamma }\rangle ^\gamma \mathrm{d} A(\mathbf{r}) \right) }_{\text {volume diffusive source}} -\underbrace{{\tilde{R}}\left( {\tilde{c}}_{A\gamma }+\langle c_{A\gamma }\rangle ^\gamma \right) }_{\text {volume reactive source}}, \quad \text {in } {\fancyscript{V}}_{\gamma ,M} \end{aligned}$$

(10a)

As a matter of consistency with Eq. (8), the reaction rate deviations are defined as

$$\begin{aligned} {\tilde{R}}(c_{A\gamma })= R(c_{A\gamma })-\big \langle R(c_{A\gamma })\big \rangle ^\gamma \end{aligned}$$

(10b)

Since $R$ is assumed to be a linear function, it follows that ${\tilde{R}}(c_{A\gamma })= R\left( {\tilde{c}}_{A\gamma }\right)$, thus becoming a homogeneous term in Eq. (10a).

From Eq. (1b) and the concentration decomposition given by Eq. (8), the interfacial boundary condition for ${\tilde{c}}_{A\gamma }$ can be expressed as

$$\begin{aligned} -\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla {\tilde{c}}_{A\gamma }= \underbrace{\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \langle c_{A\gamma }\rangle ^\gamma }_{\text {surface diffusive source}},\quad \text {at }{\fancyscript{A}}_{\gamma \kappa , M} \end{aligned}$$

(10c)

In a similar fashion, the second boundary condition and the initial condition are given by

$$\begin{aligned} {\tilde{c}}_{A\gamma }&= {\fancyscript{H}}\left( \mathbf{x},t\right) ,\quad \text {at }{\fancyscript{A}}_{\gamma \text {e},M} \end{aligned}$$

(10d)

$$\begin{aligned} {\tilde{c}}_{A\gamma }&= {\fancyscript{I}}_M\left( \mathbf{x}\right) , \quad \text { when }t=0 \end{aligned}$$

(10e)

here ${\fancyscript{H}}= {\fancyscript{E}}-\langle c_{A\gamma }\rangle ^\gamma$ and ${\fancyscript{I}}_M= {\fancyscript{F}}-\langle c_{A\gamma }\rangle ^\gamma$, respectively, are also sources of the initial and boundary-value problem for the concentration deviations, which is also nonlocal due to the second term on the right-hand side of Eq. (10a).

Using an integral equation formulation based on Green’s functions, as suggested by Wood and Valdés-Parada (2013), the formal solution for the concentration deviations can be expressed as

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)&=-\underbrace{\int \limits _{t_0=0}^{t_0=t}\int \limits _{\mathbf{r}\in {\fancyscript{V}}_{\gamma ,M}} G_M(\mathbf{x}, \mathbf{r}, t-t_0)\mathcal S_M(\mathbf{r}, t_0) \mathrm{d}V(\mathbf{r})\mathrm{d}t_0}_{\text {influence of the volume diffusive source}} \nonumber \\&\quad -\underbrace{\int \limits _{t_0=0}^{t_0=t}\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa ,M}} G_M(\mathbf{x}, \mathbf{r}, t-t_0) \mathbf{n}_{\gamma \kappa }(\mathbf{r})\cdot {\fancyscript{D}}_{A\gamma }\nabla _\mathbf{r} \langle c_{A\gamma }\rangle ^\gamma \left. \right| _{(\mathbf{r}, t_0)} \mathrm{d} A(\mathbf{r}) \mathrm{d}t_0}_{\text {influence of the surface diffusive source}}\nonumber \\&\quad +\underbrace{\int \limits _{t_0=0}^{t_0=t}\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \text {e},M}} G_M(\mathbf{x}, \mathbf{r}, t-t_0){\fancyscript{H}}(\mathbf{r}, t_0) \mathrm{d} A(\mathbf{r})\mathrm{d}t_0}_{\text {influence of the entrance and exit sources}}\nonumber \\&\quad +\underbrace{\int \limits _{\mathbf{r}\in {\fancyscript{V}}_{\gamma ,M}} G_M(\mathbf{x}, \mathbf{r}, t) {\fancyscript{I}}_M(\mathbf{r}) \mathrm{d}V(\mathbf{r})}_{\text {influence of the initial condition}} \end{aligned}$$

(11)

For the sake of brevity in presentation, we have introduced the notation

$$\begin{aligned} {\mathcal {S}}_M(\mathbf{r}, t_0)&= \nabla _\mathbf{r}\cdot \left( {\fancyscript{D}}_{A\gamma }\langle c_{A\gamma }\rangle ^\gamma \left. \right| _{(\mathbf{r}, t_0)} \nabla _\mathbf{r}\ln \varepsilon _\gamma (\mathbf{r})\right) \nonumber \\&+\nabla _\mathbf{r}\cdot \left( \frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma }\int \limits _{\mathbf{w}\in {\fancyscript{A}}_{\gamma \kappa } (\mathbf{r})}\mathbf{{n}}_{\gamma \kappa }\langle c_{A\gamma }\rangle ^\gamma \left. \right| _{(\mathbf{w}, t_0)} \mathrm{d} A(\mathbf{w}) \right) \end{aligned}$$

(12)

In Eq. (11), $G_M(\mathbf{x}, \mathbf{r}, t-t_0)$ denotes the associated Green’s function, which solves the following initial and boundary-value problem in the macroscopic domain

$$\begin{aligned}&\frac{\partial G_M(\mathbf{x},\mathbf{r}, t_0)}{\partial t}-\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla G_M(\mathbf{x},\mathbf{r}, t_0) \right) \nonumber \\&\quad +\nabla \cdot \left( \frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma }\int \limits _{\mathbf{w}\in {\fancyscript{A}}_{\gamma \kappa } (\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }(\mathbf{w}, t_0)G_M(\mathbf{w},\mathbf{r}, t_0) \mathrm{d} A(\mathbf{w})\right) \nonumber \\&\quad -R\left( G_M(\mathbf{x},\mathbf{r}, t_0) \right) = \delta (\mathbf{x}-\mathbf{r})\delta (t-t_0), \quad \text {in }{\fancyscript{V}}_{\gamma , M}\end{aligned}$$

(13a)

$$\begin{aligned}&\quad -\mathbf{n}_{\gamma \kappa }(\mathbf{x}, t_0)\cdot {\fancyscript{D}}_{A\gamma } \nabla G_M(\mathbf{x},\mathbf{r}, t_0) = 0, \quad \text {at }{\fancyscript{A}}_{\gamma \kappa ,M}\end{aligned}$$

(13b)

$$\begin{aligned}&G_M(\mathbf{x},\mathbf{r}, t_0)=0, ~\text {at }{\fancyscript{A}}_{\gamma \text {e},M}\end{aligned}$$

(13c)

$$\begin{aligned}&G_M(\mathbf{x},\mathbf{r}, t_0)=0, \text { when }t<t_0 \end{aligned}$$

(13d)

Certainly, the expression for the concentration deviations given in Eq. (11) may be substituted into Eq. (9) to close the averaged model. However, the resulting equation system would be nonlinear, nonlocal in both time and space, and strongly coupled to the microscale closure problem that needs to be solved in the whole macroscale domain. Under these conditions, it may be more feasible to solve the microscale equations (Eqs. 1) directly and then carry out the average (i.e., to perform pore-scale simulations). Unfortunately, this modeling choice would also require a complete knowledge of the microscopic geometry everywhere in the system, which is not always a tractable nor desirable line of work. For this reason, we will pursue an upscaling approach that requires imposing a set of length and timescale constraints and assumptions (see for instance Wood 2009; Wood and Valdés-Parada 2013) that allows reducing the number of degrees of freedom involved in the model. This approach is explained in detail in the following section.

5 Local Closure Problem

As a first simplification step, we seek for length-scale constraints that permit reducing the nonlocal transport equation given by Eq. (9), to a local transport equation. The development of these constraints is based on Taylor series expansions of $\langle c_{A\gamma }\rangle ^\gamma |_{\mathbf{r}}$ around the centroid of the averaging domain, x, and on the use of the geometrical theorems that allow evaluating volume integrals instead of surface integrals (see Section 2.1 in Quintard and Whitaker 1994).

Let $r_0$ be the characteristic length of the averaging domain, ${\fancyscript{V}}$ that satisfies the following length-scale constraints (Whitaker 1999)

• (i) $\ell _\gamma \ll r_0$

  This assumption implies that the characteristic length associated to the macroscopic scale is large compared to the characteristic length scale for the $\gamma$-phase. For a discussion about the meaning of characteristic lengths, see Section 3 in Wood and Valdés-Parada (2013).

• (ii) $r_0^2\ll L_{\varepsilon }L_{c_1}$

  where $L_{c_1}$ represents a characteristic length associated with the first derivative of $\langle c_{A\gamma }\rangle ^\gamma$, and $L_{\varepsilon }$ is the length scale associated to the porosity. If the porous medium is homogeneous (i.e., second-order spatially stationary in the sense of Wood 2013), the porosity is uniform and then $L_{\varepsilon }=\infty$, Consequently,

  $$\begin{aligned} \frac{1}{V_\gamma }\int \limits _{\mathbf{r} \in {\fancyscript{A}}_{\gamma \kappa }(\mathbf{x})}\mathbf{n}_{\gamma \kappa }\langle c_{A\gamma }\rangle ^\gamma |_{\mathbf{r}} \mathrm{d} A\left( \mathbf{r}\right)&\approx \frac{1}{V_\gamma }\int \limits _{\mathbf{r} \in {\fancyscript{A}}_{\gamma \kappa }(\mathbf{x})}\mathbf{n}_{\gamma \kappa }\mathrm{d} A\left( \mathbf{r}\right) \langle c_{A\gamma }\rangle ^\gamma |_{\mathbf{x}}\nonumber \\&=-\varepsilon _\gamma ^{-1}\nabla \varepsilon _\gamma \langle c_{A\gamma }\rangle ^\gamma \end{aligned}$$

  (14)

The length-scale constraints mentioned above are generally represented as $\ell _\gamma \ll r_0 \ll L$, where $L$ is conceived as the smallest large length scale associated with the problem under consideration. Under these conditions, the averaging domain can be regarded as a representative elementary volume (REV).

In item (ii) and in all this work, we use the term homogeneous in the same sense as Quintard and Whitaker (1987), i.e., A porous medium is homogeneous with respect to a given averaging volume and a given process when the effective transport coefficients in the volume-averaged transport equations are independent of position. A more formal statement of this concept is offered by Wood (2013), where the term homogeneous is interpreted to mean that the structure of the medium is second-order spatially stationary.

Imposing the length-scale constraint stated above transforms Eq. (9) into a local averaged equation valid in the bulk of the porous medium

$$\begin{aligned} \frac{\partial \langle c_{A\gamma }\rangle ^\gamma }{\partial t}= \nabla \cdot \left[ {\fancyscript{D}}_{A\gamma } \left( \nabla \langle c_{A\gamma }\rangle ^\gamma +\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }(\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }{\tilde{c}}_{A\gamma }\mathrm{d} A(\mathbf{r})\right) \right] -\big \langle R(c_{A\gamma })\big \rangle ^\gamma \end{aligned}$$

(15)

In addition, the term representing the volume diffusive source in the closure problem (see Eq. 12) becomes negligible with respect to the surface diffusive source. Furthermore, if $\ell _\gamma \ll L_{{\tilde{c}}}$, the nonlocal diffusion term can be discarded with respect to the local diffusion term in Eq. (10a), i.e.,

$$\begin{aligned} \nabla \cdot \left( \frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }(\mathbf{x})}\mathbf{{n}}_{\gamma \kappa }{\tilde{c}}_{A\gamma } \mathrm{d} A(\mathbf{r})\right) \ll \nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) \end{aligned}$$

In this way, we may write Eq. (10a) as follows

$$\begin{aligned} \frac{\partial {\tilde{c}}_{A\gamma }}{\partial t}=\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right)&- R\left( {\tilde{c}}_{A\gamma }\right) ,\quad \text {in }{\fancyscript{V}}_{\gamma , M} \end{aligned}$$

(16)

Despite these simplifications, the formal solution of the closure problem given by Eq. (11) still requires computing the associated Green’s functions in the entire macroscopic domain.

To simplify this solution, we will solve the closure problem in a more convenient domain that maintains the essential microscale information. Let ${\fancyscript{V}}$ be a representative region of the porous medium ${\fancyscript{V}}_M$, with characteristic length $r_0$. For the purpose of solving the closure problem, the representative region ${\fancyscript{V}}$ is modeled as a spatially periodic porous medium generated by three nonunique lattice vectors $\mathbf{l}_i$ ($i=1,2,3$) defining a representative unit cell $\varOmega$. The characteristic length, $\ell$, of the representative unit cell must be equal to or less than the characteristic length of the representative region, i.e., $\ell \le r_0$.

The use of spatially periodic models at the microscale is of primary importance in the method of volume averaging, and its main implications are provided below. As a matter of fact, other upscaling techniques share this modeling approach for the microscale geometry (see for instance, Bear and Cheng 2010; Sanchez-Palencia 1970). It is worth emphasizing that using a periodic domain for the closure problem solution is a convenient approximation but does not imply that the resulting macroscopic model would only be applicable to periodic geometries. The required length-scale constraint to treat the source terms of Eqs. (10a) and (10c) as constants in the unit cell is (Quintard and Whitaker 1994)

$$\begin{aligned} \ell \le r_0 \ll L_{c}, L_{c_1} \end{aligned}$$

(17)

thus, both $\langle c_{A\gamma }\rangle ^\gamma$ and $\nabla \langle c_{A\gamma }\rangle ^\gamma$ can be treated as position invariant within the representative unit cell $\varOmega$, and their values correspond to the cellular intrinsic average concentration and its gradient, respectively, evaluated at the centroid of the unit cell.

Furthermore, if $\ell \le r_0\ll \min {\left( L_c,L_{c_1}\right) }$, it is also concluded that

• (i) $\langle {\tilde{c}}_{A\gamma }\rangle ^\gamma |_\mathbf{x}=0$.

• (ii) The boundary condition at the entrances and exits of the macroscopic domain (i.e., Eq. 10d) is no longer necessary.

In this way, the initial and boundary-value problem defined in the porous medium ${\fancyscript{V}}_M$ and given by Eqs. (10a)–(10e) is simplified to a periodic and local closure problem defined in a unit cell $\varOmega$, which is bounded by the length-scale constraints established above, and it is given by

$$\begin{aligned}&\frac{\partial {\tilde{c}}_{A\gamma }}{\partial t}=\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) - R\left( {\tilde{c}}_{A\gamma }\right) ,\quad \text {in }\varOmega _\gamma \end{aligned}$$

(18a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla {\tilde{c}}_{A\gamma }= \underbrace{\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \langle c_{A\gamma }\rangle ^\gamma }_{\text {surface diffusive source}},\quad \text {at }{\partial \varOmega }_{\gamma \kappa } \end{aligned}$$

(18b)

$$\begin{aligned}&{\tilde{c}}_{A\gamma }\left( \mathbf{x}+\mathbf{l}_i\right) ={\tilde{c}}_{A\gamma }\left( \mathbf{x}\right) ,\quad i=1,2,3 \end{aligned}$$

(18c)

$$\begin{aligned}&{\tilde{c}}_{A\gamma }={\fancyscript{I}}\left( \mathbf{x}\right) ,\quad \text {when } t=0 \end{aligned}$$

(18d)

$$\begin{aligned}&\langle {\tilde{c}}_{A\gamma }\rangle ^\gamma =0 \end{aligned}$$

(18e)

In the above equations, $\varOmega _\gamma$ represents the domain occupied by the $\gamma$-phase within the unit cell, and $\varOmega$ and $\partial \varOmega _{\gamma \kappa }$ denote the solid–fluid interface in the unit cell. In addition, ${\fancyscript{I}}$ is the initial distribution of the concentration deviations in the unit cell.

At this point, it is convenient to re-formulate the formal solution of the closure problem in the unit cell. Once again, to achieve our goals we use integral equation formulations based on Green’s functions and express the solution as follows

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)&=-\underbrace{\int \limits _{t_0=0}^{t_0=t}\left( ~\int \limits _{\mathbf{r}\in \partial \varOmega _{\gamma \kappa }} {\fancyscript{G}}_\varOmega (\mathbf{x}, \mathbf{r}, t-t_0) \mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma } \mathrm{d} A(\mathbf{r})\right) \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma \mathrm{d}t_0}_{\text {influence of the surface diffusive source}}\nonumber \\&\quad +\underbrace{\int \limits _{\mathbf{r}\in \varOmega _{\gamma }} {\fancyscript{G}}_\varOmega (\mathbf{x}, \mathbf{r}, t) {\fancyscript{I}}(\mathbf{r}) \mathrm{d}V(\mathbf{r})}_{\text {influence of the initial condition}} \end{aligned}$$

(19)

In the above expression, ${\fancyscript{G}}_\varOmega (\mathbf{x}, \mathbf{r}, t-t_0)$ is the Green function that solves the following initial and boundary-value problem

$$\begin{aligned}&\frac{\partial {\fancyscript{G}}_\varOmega }{\partial t}-\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\fancyscript{G}}_\varOmega \right) -R({\fancyscript{G}}_\varOmega ) = \delta (\mathbf{x}-\mathbf{r})\delta (t-t_0), \quad \text {in }\varOmega _{\gamma }\end{aligned}$$

(20a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma } \nabla {\fancyscript{G}}_\varOmega = 0, \quad \text {at }\partial \varOmega _{\gamma \kappa }\end{aligned}$$

(20b)

$$\begin{aligned}&{\fancyscript{G}}_\varOmega \left( \mathbf{x}+\mathbf{l}_i\right) ={\fancyscript{G}}_\varOmega \left( \mathbf{x}\right) ,\quad i=1,2,3\end{aligned}$$

(20c)

$$\begin{aligned}&{\fancyscript{G}}_\varOmega =0,\quad \text { when }t<t_0\end{aligned}$$

(20d)

$$\begin{aligned}&\langle {\fancyscript{G}}_\varOmega \rangle ^\gamma =0 \end{aligned}$$

(20e)

Certainly, the closure problem solution in Eq. (19) is simpler than the one given in Eq. (11); however, it is pertinent to emphasize that, despite the simplification in the solution domain for the concentration deviations, the average concentration and its gradient are only constant in space but not in time. Consequently, if Eq. (19) is substituted into Eq. (15), the resulting expression would be nonlocal in time. For this reason, in the following paragraphs, we constrain the analysis to quasi-steady conditions. Before moving on, it is worth mentioning that the length-scale constraints imposed so far may be too severe in some applications. For example, if there are portions of the system exhibiting a linear average concentration profile, the concentration gradient would be constant, thus making it unnecessary to impose additional constraints.

6 Quasi-Steady Closure Problem

A common simplification in the method of volume averaging is to treat the closure problem as quasi-steady, even when the macroscopic reaction–diffusion process is unsteady. In order to derive the timescale constraint associated to the quasi-steady assumption of the closure problem, let us perform an order-of-magnitude analysis to Eq. (18a), the resulting estimates can be written as

$$\begin{aligned} \underbrace{\dfrac{\partial {\tilde{c}}_{A\gamma }}{\partial t}}_{\mathbf{O}\left( \frac{\Delta {\tilde{c}}_{A\gamma }}{t^*}\right) } =\underbrace{\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) }_{ \mathbf{O}\left( \frac{{\fancyscript{D}}_{\gamma }\Delta {\tilde{c}}_{A\gamma }}{\ell _\gamma ^2}\right) } - \underbrace{ R\left( {\tilde{c}}_{A\gamma }\right) }_{ \mathbf{O}\left( R\right) },\quad \text {in }\varOmega _\gamma \end{aligned}$$

(21)

From these estimates, the following constraint can be obtained,

$$\begin{aligned} \frac{1}{1+\frac{\ell _\gamma ^2 {\tilde{R}}}{{\fancyscript{D}}_{A\gamma } \Delta {\tilde{c}}_{A\gamma }}} \ll \frac{{\fancyscript{D}}_{A\gamma } t^*}{\ell _\gamma ^2} \end{aligned}$$

(22)

which, when satisfied, allows treating the closure problem as quasi-steady, and thus, Eq. (21) is simplified to

$$\begin{aligned} \nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) - R\left( {\tilde{c}}_{A\gamma }\right) =0,\quad \text {in }\varOmega _\gamma \end{aligned}$$

(23)

In the inequality (22), the term $\frac{\ell _\gamma ^2 {\tilde{R}}}{{\fancyscript{D}}_{A\gamma } \Delta {\tilde{c}}_{A\gamma }}$ can be regarded as a Thiele modulus for the closure problem, say $\phi _c^2$. It is convenient to introduce this dimensionless number since it relates the reaction rate to the diffusion rate. In this way, whenever $1\ll \phi _c^2$ the diffusive process is negligible with respect to the reactive transport, and for cases in which $\phi _c^2\ll 1$, the transport process is mainly diffusive. Therefore, if $1\ll \phi _c^2$, the timescale constraint reduces to $\Delta \tilde{c}_{A\gamma }/R\ll t^*$, and if $\phi _c^2\ll 1$, it results that $\ell _\gamma ^2/{\fancyscript{D}}_{A\gamma }\ll t^*$.

The following two corollaries arise from the quasi-steady assumption:

• 1. The influence of the initial condition over the ${\tilde{c}}_{A\gamma }$-fields becomes negligible.

• 2. The volume-averaged concentration and its derivatives can be assumed as constants in the timescale of ${\tilde{c}}_{A\gamma }$.

Therefore, the formal solution of the closure problem given by Eq. (19) simplifies to

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)=&\underbrace{\mathbf{b}(\mathbf{x}) \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma }_{\text {influence of the surface diffusive source}} \end{aligned}$$

(24)

As a matter of convenience, we defined the closure variable $\mathbf{b}$ as (Wood and Valdés-Parada 2013)

$$\begin{aligned} \mathbf{b}(\mathbf{x})= -\int \limits _{\mathbf{r}\in \partial \varOmega _{\gamma \kappa }} {\fancyscript{G}}_{rx}(\mathbf{x}, \mathbf{r}) \mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma } \mathrm{d} A(\mathbf{r}) \end{aligned}$$

(25)

In Eq. (24), ${\fancyscript{G}}_{rx}(\mathbf{x}, \mathbf{r})$ is the Green function associated to diffusion and reaction that solves the following boundary-value problem

$$\begin{aligned}&\nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\fancyscript{G}}_{rx}\right) - R({\fancyscript{G}}_{rx} ) = \delta (\mathbf{x}-\mathbf{r}), \quad \text {in }\varOmega _{\gamma }\end{aligned}$$

(26a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma } \nabla {\fancyscript{G}}_{rx} = 0, \quad \text {at }\partial \varOmega _{\gamma \kappa }\end{aligned}$$

(26b)

$$\begin{aligned}&{\fancyscript{G}}_{rx}\left( \mathbf{x}+\mathbf{l}_i\right) ={\fancyscript{G}}_{rx}\left( \mathbf{x}\right) ,\quad i=1,2,3\end{aligned}$$

(26c)

$$\begin{aligned}&\langle {\fancyscript{G}}_{rx}\rangle ^\gamma = 0 \end{aligned}$$

(26d)

In this way, the closure variable b solves the following boundary-value problem

$$\begin{aligned}&{\fancyscript{D}}_{A\gamma }\nabla ^2\mathbf{b} -R(\mathbf{b}) =0,\quad \text {in }\varOmega _\gamma \end{aligned}$$

(27a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \otimes \mathbf{b}=\mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma },\quad \text {at }\partial \varOmega _{\gamma \kappa }\end{aligned}$$

(27b)

$$\begin{aligned}&\mathbf{b}\left( \mathbf{x}+\mathbf{l}_i\right) =\mathbf{b}\left( \mathbf{x}\right) ,\quad i=1,2,3\end{aligned}$$

(27c)

$$\begin{aligned}&\langle \mathbf{b}\rangle ^\gamma =0 \end{aligned}$$

(27d)

At this point, let us assume that the reaction rate obeys a first-order kinetics, say $R(c_{A\gamma })= k c_{A\gamma }$. This allows, proposing the following decomposition

$$\begin{aligned} \mathbf{b}= k \mathbf{b}_{rx}+\mathbf{b}_\gamma \end{aligned}$$

(28)

here $\mathbf{b}_{rx}$ solves the following boundary-value problem

$$\begin{aligned}&{\fancyscript{D}}_{A\gamma }\nabla ^2\mathbf{b}_{rx} -k \mathbf{b}_{rx} =\mathbf{b}_\gamma ,\quad \text {in }\varOmega _\gamma \end{aligned}$$

(29a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \otimes \mathbf{b}_{rx}=0,\quad \text {at }\partial \varOmega _{\gamma \kappa }\end{aligned}$$

(29b)

$$\begin{aligned}&\mathbf{b}_{rx}\left( \mathbf{x}+\mathbf{l}_i\right) =\mathbf{b}_{rx}\left( \mathbf{x}\right) ,\quad i=1,2,3\end{aligned}$$

(29c)

$$\begin{aligned}&\langle \mathbf{b}_{rx}\rangle ^\gamma =0 \end{aligned}$$

(29d)

In Eq. (28), $\mathbf{b}_\gamma$ is defined in Eq. (65) and it solves the boundary-value problem given by Eqs. (1.4–58) in Whitaker (1999), which is independent of the reaction rate. At first sight, it is tempting to only solve the boundary-value problem given by Eqs. (27) and use Eq. (24) as the closure problem solution; however, this approach leads to a single effective diffusion-like coefficient that is dependent on the reaction rate (i.e., a diffusion–reaction coefficient, as shown by Valdés-Parada and Alvarez-Ramírez 2010). With the aim of making a distinction between an effective diffusivity (i.e., an effective medium coefficient that only depends of the porous medium structure) and a diffusion–reaction coefficient, we put forward the use of the decomposition given in Eq. (28). Nevertheless, it is worth stressing that solving the closure problem given by Eqs. (27) is simpler than solving the closure problem for $\mathbf{b}_{rx}$ (Eqs. 29) because the latter is coupled with the fields of $\mathbf{b}_\gamma$, given by Eq. (25). In summary, the closure problem solution strategy that we follow is to: (1) compute the fields of the closure variable $\mathbf{b}_\gamma$; (2) compute the fields of the closure variable $\mathbf{b}$; and (3) substitute these solutions into Eq. (28) to compute $\mathbf{b}_{rx}$. Notice that, for a given porosity, it is only necessary to recalculate steps (2) and (3) for different reaction rate coefficients. Finally, before proceeding with the derivation of the closed model, we discuss the case in which the reaction rate expression is nonlinear.

7 Linearization of the Closure Problem for Nonlinear Reactions

The developments provided so far have been restricted to situations involving a linear reaction rate; with the aim of extending the analysis to cases in which the reaction rate is nonlinear, we follow an approach similar to the one used by Whitaker (see Problem 1–11 in Whitaker 1999) in order to linearize the reaction rate term. This is accomplished by

• 1. Developing a Taylor series expansions of the reaction rate, $R$, around the average concentration, $\langle c_{A\gamma }\rangle ^\gamma$.

• 2. Neglecting nonlinear terms by performing an order-of-magnitude analysis based on the length-scale constraints established in the local theory presented in Sect. 5. This allows one to develop explicit constraints that indicate the range of validity of the linearized equation.

Note that in some instances, the range of validity of the constraints may prevent the linearized solution from being useful under a set of conditions for which one wants a solution. The idea of treating the nonlinear terms as source terms has a long history in the theory of nonlinear PDEs (cf., Flesch and Trullinger 1987; Stakgold and Holst 2011). The result is an implicit integral equation for the dependent variable, and iterative approaches must be used to determine the solution. Questions of existence and uniqueness of such solutions are often more difficult (or impossible) to prove, but when the solutions can be found, they may often be verified to be correct and physically relevant. We have detailed the nonlinear approach in the appendix; for the remainder of this section, we take the first critical step to the general nonlinear case by establishing the integral solution of the linear model.

The reaction rate of the species involved in the reaction–diffusion process is described by $R=R(c_{A\gamma })$, which can also be viewed as the composite function $R\circ c_{A\gamma }=R\left( c_{A\gamma }\left( \mathbf{r}\right) \right)$ defined in the $\gamma$-phase of the unit cell, i.e., for all $\mathbf{y}\in \varOmega _\gamma$. If $R\in C^\infty \left( \mathbb {R}^+\right)$, $R$ is an infinitely differentiable function in $\varOmega _\gamma$, and then, it can be locally defined by a convergent power series determined by its Taylor series. This means that, for every $c_{A\gamma }^*\in {\mathbb {R}}^+$, there exists some $r > 0$, known as the radius of convergence of the series, such that, for all $c_{A\gamma }\in (c_{A\gamma }^*-r, c_{A\gamma }^* + r) \subset {\mathbb {R}}^+$, the reaction rate function is given by (Arfken et al. 2013)

$$\begin{aligned} \left. R\right| _{c_{A\gamma }}&= \left. R\right| _{c_{A\gamma }^*} +\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{c_{A\gamma }^*}\left( c_{A\gamma }-c_{A\gamma }^*\right) +\frac{1}{2!}\left. \frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{ c_{A\gamma }^*}\left( c_{A\gamma }-c_{A\gamma }^*\right) ^2 +\cdots ,\nonumber \\&\quad |c_{A\gamma }-c_{A\gamma }^*|<r \end{aligned}$$

(30)

Since the local theory of the method of volume averaging is based on the local periodicity assumption, it follows that the concentration deviations are locally expressed in the unit cell $\varOmega \left( \mathbf{x}\right)$ as ${\tilde{c}}_{A\gamma }|_{\mathbf{r}}=c_{A\gamma }|_{\mathbf{r}}-\langle c_{A\gamma }\rangle ^\gamma |_{\mathbf{x}}$ for $\mathbf{x}\in \varOmega$ and $\mathbf{r}\in \varOmega _\gamma$. From the above discussion and taking $c_{A\gamma }^*=\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}$, there exists a range of positive values of $r$, such that, for all $c_{A\gamma }$ satisfying $\langle c_{A\gamma }\rangle ^\gamma -r<c_{A\gamma }<\langle c_{A\gamma }\rangle ^\gamma + r$, the reaction rate can be locally defined by its convergent Taylor series expansion about $\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}$ and can be expressed as

$$\begin{aligned} \left. R\right| _{c_{A\gamma }|_{\mathbf{r}}}&= \left. R\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} +\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} {\tilde{c}}_{A\gamma } |_{\mathbf{r}} +\left. \frac{1}{2!}\frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}{\tilde{c}}_{A\gamma }^2 |_{\mathbf{r}} +\cdots ,\nonumber \\&\quad |{\tilde{c}}_{A\gamma } |<r\left( \langle c_{A\gamma }\rangle ^\gamma \right) \end{aligned}$$

(31)

The intrinsic average of the reaction rate in the unit cell is

$$\begin{aligned} \langle \left. R\right| _{c_{A\gamma }}\rangle ^\gamma |_\mathbf{x}= \underbrace{\left. R\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} } _{\mathbf{O} \left( R (\langle c_{A\gamma }\rangle ^\gamma )\right) } +\underbrace{\left. \frac{1}{2!}\frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma |_\mathbf{x}} _{\mathbf{O} \left( \frac{ R \left( \langle c_{A\gamma }\rangle ^\gamma \right) }{\left( \langle c_{A\gamma }\rangle ^\gamma \right) ^2} \left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma \right) } +\cdots ,\quad |{\tilde{c}}_{A\gamma } |<r\left( \langle c_{A\gamma }\rangle ^\gamma \right) \end{aligned}$$

(32)

Subtracting Eq. (32) to Eq. (31), the spatial deviations of the reaction rate in the unit cell $\varOmega$ are given by

$$\begin{aligned} \left. {\tilde{R}}\right| _{c_{A\gamma }|_{\mathbf{r}}}&= \underbrace{\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} {\tilde{c}}_{A\gamma } |_{\mathbf{r}}} _{\mathbf{O} \left( \frac{ R \left( \langle c_{A\gamma }\rangle ^\gamma \right) }{ \langle c_{A\gamma }\rangle ^\gamma } {\tilde{c}}_{A\gamma } \right) } +\underbrace{\left. \frac{1}{2!}\frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\left( {\tilde{c}}_{A\gamma }^2 |_{\mathbf{r}} -\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma |_\mathbf{x}\right) } _{\mathbf{O} \left( \frac{ R \left( \langle c_{A\gamma }\rangle ^\gamma \right) }{ \left( \langle c_{A\gamma }\rangle ^\gamma \right) ^2} \left( {\tilde{c}}_{A\gamma }^2 -\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma \right) \right) } +\cdots ,\nonumber \\&|{\tilde{c}}_{A\gamma } |<r\left( \langle c_{A\gamma }\rangle ^\gamma \right) \end{aligned}$$

(33)

At this point, it is worth noting that no approximations have been made to the reaction rates, as long as the convergence of the series is guaranteed. In other words, if Eq. (33) is substituted into Eq. (24), the resulting expression would still be implicit and nonlinear. To attend this issue, the following inequality should be met

$$\begin{aligned} \left. \frac{1}{2!}\frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\left( {\tilde{c}}_{A\gamma }^2 |_{\mathbf{r}} -\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma |_\mathbf{x}\right) \ll \left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} {\tilde{c}}_{A\gamma } |_{\mathbf{r}} \end{aligned}$$

(34)

In order to derive the length-scale constraint that supports this assumption, we use the order-of-magnitude estimates provided in Eq. (33), and the result can be written as follows,

$$\begin{aligned} \frac{{\tilde{c}}_{A\gamma }^2 -\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma }{{\tilde{c}}_{A\gamma }} \ll \langle c_{A\gamma }\rangle ^\gamma \end{aligned}$$

(35)

To make further progress, we need to estimate the order of magnitude of the concentration deviations, for which we analyze Eq. (24) to arrive to

$$\begin{aligned} {\tilde{c}}_{A\gamma }= \mathbf{O}\left( \frac{\ell _\gamma \langle c_{A\gamma }\rangle ^\gamma }{L(1+\phi _c^2)}\right) \end{aligned}$$

(36)

Substituting this estimate into inequality (35) yields

$$\begin{aligned} \frac{\ell _\gamma }{L} \ll 1+\phi _c^2 \end{aligned}$$

(37)

This constraint not also supports the inequality given in (34), but also leads to the assumption that ${\tilde{c}}_{A\gamma }\ll \langle c_{A\gamma }\rangle ^\gamma$, which limits the range of application of the upscaled model. At this point, it is worth emphasizing that the results from order-of-magnitude estimates should be taken with caution, because the resulting constraints are usually more restrictive than needed. Certainly, a detailed analysis about the extents and limitations of the resulting upscaled model, as done by Battiato et al. (2009) and Battiato and Tartakovsky (2011) for reactions with linear kinetics, is desirable but lies beyond the scope of this work.

Under these conditions, we may simplify Eq. (33) to

$$\begin{aligned} \left. {\tilde{R}}\right| _{c_{A\gamma }|_{\mathbf{x+y_\gamma }}}= \left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} {\tilde{c}}_{A\gamma } |_{\mathbf{x+y}_\gamma } \end{aligned}$$

(38)

So that Eq. (23) can be written as

$$\begin{aligned} \nabla \cdot \left( {\fancyscript{D}}_{A\gamma } \nabla {\tilde{c}}_{A\gamma }\right) - \left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} {\tilde{c}}_{A\gamma } =0, \quad \text {in }\varOmega _\gamma \end{aligned}$$

(39)

This linearization scheme has been previously used to estimate effectiveness factors in catalytic systems (Valdés-Parada et al. 2006a), as well as in bioreactors (Valdés-Parada et al. 2005). Equation (39) is subject to the boundary conditions given by Eqs. (18b), (18c) and to the average constraint in Eq. (18e). Before moving on, it is convenient to summarize the scaling postulates involved in the closure problem in the following statement:

Let ${\fancyscript{V}}$ be a representative region of the porous medium ${\fancyscript{V}}_M$ of characteristic length $r_0$, and assumed to be a spatially periodic porous medium generated by the unit cell $\varOmega$ and with characteristic length $\ell \le r_{0}$, such that, $\ell \le r_0\ll \min {\left( L_c,L_{c1}\right) }$. If the length-scale associated with the pores $\ell _\gamma$ is constrained by $\ell _\gamma \ll \min \{L_{\tilde{c}}, L_c\} (1+\phi _c^2)$, implying that ${\tilde{c}}_{A\gamma }\ll \langle c_{A\gamma }\rangle ^\gamma$; and the characteristic time is large enough, so that $\frac{{\fancyscript{D}}_{A\gamma } t^{*}}{\ell _\gamma ^2}\gg (1+\phi _c^2)^{-1}$, then the closure problem can be treated as local, periodic, quasi-steady, and linear.

Under these conditions, the closure problem solution is given by Eq. (24), with b being

$$\begin{aligned} \mathbf{b}= \left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\mathbf{b}_{rx}+\mathbf{b}_\gamma \end{aligned}$$

(40)

and the problem for $\mathbf{b}_{rx}$, defined in Eqs. (29), is modified only in Eq. (29a) by substituting $k$ for $\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}$.

The derivations in this section show that, as long as the length-scale constraints and assumptions supporting the linearization scheme are met, one may handle the closure problem solution in the same manner as in the case in which $R$ is a linear function. As mentioned above, for cases where the problem is nonlinear, it may be possible to treat the nonlinear term as a source in the solution. This approach is explained in Appendix.

8 Closed Upscaled Model

In order to develop the closed form of the macroscopic reaction–diffusion equation in terms of effective transport coefficients, Eq. (24) is substituted into Eq. (15). The resulting equation can be written as

$$\begin{aligned} \frac{\partial \langle c_{A\gamma }\rangle ^\gamma }{\partial t}= \nabla \cdot \left( {{\mathbf {\mathsf{{D}}}}} _{\text {diff-rx}}\cdot \nabla \langle c_{A\gamma }\rangle ^\gamma \right) - \langle R( c_{A\gamma })\rangle ^\gamma \end{aligned}$$

(41)

where ${{\mathbf {\mathsf{{D}}}}}_{\text {diff-rx}}$ is the effective reaction–diffusion coefficient composed by the effective diffusivity tensor, ${{\mathbf {\mathsf{{D}}}}}_{\text {eff}}$, and a diffusion-like coefficient that is dependent on the reaction rate, ${{\mathbf {\mathsf{{D}}}}}_{\text {rx}}$,

$$\begin{aligned} {{\mathbf {\mathsf{{D}}}}}_{\text {diff-rx}}={{\mathbf {\mathsf{{D}}}}}_{\text {eff}}+{{\mathbf {\mathsf{{D}}}}}_{\text {rx}} \end{aligned}$$

(42)

These effective coefficients can be written in terms of the closure variables as follows,

$$\begin{aligned} {{\mathbf {\mathsf{{D}}}}}_{\text {diff-rx}}\left( \langle c_{A\gamma }\rangle ^\gamma \right) =&\underbrace{ {\fancyscript{D}}_{A\gamma }\left[ {{\mathbf {\mathsf{{I}}}}} +\frac{1}{V_\gamma }\int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }}\mathbf{{n}}_{\gamma \kappa }\left( \mathbf{r}\right) \mathbf{b}_{\gamma }\left( \mathbf{r }\right) \mathrm{d} A(\mathbf{r})\right] }_{{{\mathbf {\mathsf{{D}}}}}_{\text {eff}}} \nonumber \\&+\underbrace{\frac{{\fancyscript{D}}_{A\gamma }}{V_\gamma } \left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} \int \limits _{\mathbf{r}\in {\fancyscript{A}}_{\gamma \kappa }}\mathbf{{n}}_{\gamma \kappa }\left( \mathbf{r}\right) \mathbf{b}_{\text {rx}}\left( \mathbf{r},\langle c_{A\gamma }\rangle ^\gamma \right) \mathrm{d} A(\mathbf{r})}_{{{\mathbf {\mathsf{{D}}}}}_{\text {rx}}} \end{aligned}$$

(43)

Directing the attention to the reaction term in Eq. (41), we make use of the order-of-magnitude estimates provided in Eq. (32) and notice that

$$\begin{aligned} \left. \frac{1}{2!}\frac{\mathrm{d}^2R}{\mathrm{d} c_{A\gamma }^2}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\left\langle {\tilde{c}}_{A\gamma }^2 \right\rangle ^\gamma |_\mathbf{x} \ll \left. R\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} \end{aligned}$$

(44)

whenever the following constraint is met,

$$\begin{aligned} \sqrt{\langle {\tilde{c}}_{A\gamma }^2\rangle ^\gamma }\ll \langle c_{A\gamma }\rangle ^\gamma \end{aligned}$$

(45)

The length-scale constraint that supports this inequality has already been adopted in our derivations and it is given in (37). Under these circumstances, we have, from Eq. (32), the following approximation for the volume-averaged reaction rate

$$\begin{aligned} \langle \left. R\right| _{c_{A\gamma }}\rangle ^\gamma |_\mathbf{x}= \left. R\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} \end{aligned}$$

(46)

In this way, Eq. (41) takes its final form,

$$\begin{aligned} \frac{\partial \langle c_{A\gamma }\rangle ^\gamma }{\partial t}= \nabla \cdot \left( {{\mathbf {\mathsf{{D}}}}} _{\text {diff-rx}}\cdot \nabla \langle c_{A\gamma }\rangle ^\gamma \right) - R \left( \langle c_{A\gamma }\rangle ^\gamma \right) \end{aligned}$$

(47)

At this point, it is pertinent to provide the following comments regarding the upscaled model:

• Despite the familiar structure of Eq. (47), this is not a vis-à-vis model with respect to its microscale counterpart (Eq. 1a). The reason for this difference is due to the dependence of the coefficient ${{\mathbf {\mathsf{{D}}}}}_{\text {rx}}$ with $\langle c_{A\gamma }\rangle ^\gamma$. This is consistent with the previous study of diffusion and reaction in biofilms by Wood and Whitaker (1998) and, more recently, with studies of reactive transport in porous media with bimolecular reactions (Porta et al. 2012, 2013). Wood and Whitaker (1998) imposed an additional constraint for the reaction rate in their derivation of an upscaled model based on the local mass equilibrium assumption (see Eq. A.37 in Wood and Whitaker 1998),

  $$\begin{aligned} \frac{\ell _\gamma ^2}{{\fancyscript{D}}_{A\gamma }}\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma }\ll 1 \end{aligned}$$

  (48)

  This restriction allows neglecting ${{\mathbf {\mathsf{{D}}}}}_{\text {rx}}$ with respect to ${{\mathbf {\mathsf{{D}}}}}_{\text {eff}}$. This constraint is inherent in the derivation of local mass equilibrium models. As shown by Orgogozo et al. (2010), this constraint is not necessary in nonequilibrium models and will not be imposed in our work. Certainly, the functionality of the diffusion–reaction coefficient with the reaction rate will still be present even for linear reaction rate kinetics if no additional constraints are imposed (Valdés-Parada and Alvarez-Ramírez 2010).

• For nonlinear reaction rate kinetics, the price to be paid for maintaining the relationship between ${{\mathbf {\mathsf{{D}}}}}_{\text {rx}}$ and $\langle c_{A\gamma }\rangle ^\gamma$ is not only the nonlinearity of the upscaled model, but also the coupling with the closure problem. In other words, in order to compute the closure variable $\mathbf{b}_{rx}$, it is necessary to have the value of $\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma }$ as shown in Eq. (29a). This dependence of the closure problems with the macroscale concentration values has also been encountered in other problems, such as in transport of chemotactic bacteria in porous media (Valdés-Parada et al. 2009) or in the derivation of nonequilibrium models for mass transport and reaction in biofilm-coated porous media (Orgogozo et al. 2010).

• The closure problem and thus the upscaled model are restricted by the scaling postulates imposed so far. Briefly, the closure problem is local, periodic, linear, and quasi-steady. In future works, we will explore cases in which not all of these assumptions are met.

9 Computation of the Effective Diffusion Coefficient

The solution of the closure problems can be carried out by numerical or analytical means. In the first case, one can solve the boundary-value problems for $\mathbf{b}$ and $\mathbf{b}_\gamma$ using the commercial software Comsol Multiphysics$^{\textregistered }$ to perform the numerical solution. The strategy that we used is the following:

• 1. For a given porosity value, fix the closure Thiele modulus ($\varPhi ^2=R^\prime \left( \langle c_{A\gamma }\rangle ^\gamma /c_0\right) \ell ^2/{{\fancyscript{D}}_{A\gamma }}$).

• 2. Solve the closure problem for $\mathbf{b}_\gamma$ and $\mathbf{b}$ in a periodic unit cell as the one sketched in Fig. 2a.

• 3. Substitute the fields of the closure variables into Eq. (43) to compute the effective diffusivity.

Using this approach, we obtained the results shown in Fig. 3, for 2D and 3D unit cells for the $xx$-component of the effective diffusivity tensor. These results exhibit a sigmoidal-like shape and can be reproduced, for the range of values here studied, by means of the following expression

$$\begin{aligned} D_{\text {diff-rx}}^{xx}=D_\infty +\frac{D_{\text {eff}}-D_\infty }{1+\left( \frac{\varPhi ^2}{\varPhi _0^2}\right) ^n} \end{aligned}$$

(49)

where $D_{\text {eff}}$ is the $xx$-component of the effective diffusivity under nonreactive conditions (i.e., $\varPhi =0$), whereas $D_\infty$ is the value of $D_{\text {diff-rx}}^{xx}$ for $\varPhi \gg 1$. In addition, $\varPhi _0$ and $n$ are adjustable coefficients. In Table 1, we provide the values of all the coefficients involved in Eq. (49) for different porosity values using 2D and 3D periodic unit cells; in all cases, the correlation factor for the best-fit was equal to or larger than 0.999.

Fig. 2

Representative domains for the closure problem solution: a periodic unit cell, b Chang’s unit cell

Fig. 3

Effect of closure Thiele modulus, $\varPhi$, and porosity, $\varepsilon _\gamma$, on the effective reaction–diffusion coefficient predicted in 2D (left panel) and 3D (right panel) unit cells of a spatially periodic array of cylinders and spheres, and in cylindrical and spherical Chang’s unit cells. In the bottom plots, we provide the relative percent errors of the predictions from Chang’s unit cell with respect to those resulting from the spatially periodic unit cell in 2D and 3D

Table 1 Values of the coefficients involved in the best-fit expression for $D_{\text {diff-rx}}^{xx}$ using 2D and 3D periodic unit cells

A Chang unit cell (Chang 1982, 1983; Ochoa-Tapia et al. 1994), denoted as $\varGamma \subset {\mathbb {R}}^3$, is a nonperiodic domain conformed by two homothetic concentric regions $\varGamma _i\subset \varGamma _e$, in which $\varGamma _i$ is associated to the $\kappa$-phase, while the $\gamma$-phase is represented by the region comprised between the two concentric geometries, i.e., $\varGamma _\gamma =\varGamma _e-\varGamma _i$, and the $\gamma$–$\kappa$ interface coincides with the boundary of $\varGamma _i$, i.e., ${\fancyscript{A}}_{\gamma \kappa }=\partial \varGamma _i$. Since Chang’s unit cell is not periodic, homogeneous Dirichlet-type boundary conditions are enforced at $\partial \varGamma _e$, thus abandoning the periodic boundary conditions.

Although there are plenty homothetic geometries that may be considered, in this work we used cylindrical and spherical geometries as Chang’s unit cells for the sake of consistency with previous studies (Ochoa-Tapia et al. 1994). According to Fig. 2b, the $\gamma$-phase in a cylindrical Chang unit cell is described by $\varGamma _\gamma =\{(r,\theta ):r\in (a,\ell _\mathrm{ch}/2),\theta \in (0,2\pi )\}$, while for a spherical unit cell it is defined by $\varGamma _\gamma =\{(r,\theta ,\phi ):r\in (a,\ell _\mathrm{ch}/2),\theta \in (0,\pi ),\phi \in (0,2\pi )\}$. The characteristic length scale associated to these cells is $\ell =\ell _\mathrm{ch}$. Let $b_\gamma$ and $b$ be the scalar components of interest of the dimensionless closure variables $\mathbf{b}_{\gamma }/\ell$ and $\mathbf{b}/\ell$, respectively (i.e., $b_\gamma = \mathbf{b}_\gamma \cdot \mathbf{e}_x/\ell$ and $b = \mathbf{b}\cdot \mathbf{e}_x/\ell$). The closure problem in Chang’s unit cell is essentially the same one as in a periodic unit cell; the only difference is that the periodic boundary conditions at the entrances and exits are replaced by a homogeneous Dirichlet-type boundary condition. A discussion about the use of this boundary condition can be found in the work by Ochoa-Tapia et al. (1994). Due to the structure of the closure problem in Chang’s unit cell, it is not hard to realize that the structure of the solution is of the form,

$$\begin{aligned} \psi (r,\theta )&= \cos \theta ~v(r), \quad 2D\end{aligned}$$

(50a)

$$\begin{aligned} \psi (r,\theta ,\phi )&= \sin \theta \cos \phi ~v(r), \quad 3D \end{aligned}$$

(50b)

with $\psi$ representing either $b$ or $b_\gamma$. In the above expressions, $v(r)$ solves the following boundary-value problem

$$\begin{aligned}&\frac{1}{r^n}\frac{\mathrm{d}}{\mathrm{d}r}\left( r^n \frac{\mathrm{d} v}{\mathrm{d}r} \right) -\varPhi v =0, \quad \text { in } \varGamma _\gamma \end{aligned}$$

(51a)

$$\begin{aligned}&-\frac{\mathrm{d} v}{\mathrm{d}r} = \mathbf{e}_r\cdot \mathbf{e}_x, \quad \text { at } r=a\end{aligned}$$

(51b)

$$\begin{aligned}&v=0, \quad \text { at } r=\ell _\mathrm{ch}/2 \end{aligned}$$

(51c)

In Eq. (51a), $n=1,2$ corresponds to cylindrical and spherical coordinates, respectively. The closure problems for $b_\gamma$ and $b$ are recovered when $\varPhi =0$ and $\varPhi ^2=R^\prime \left( \langle c_{A\gamma }\rangle ^\gamma /c_0\right) \ell ^2/{{\fancyscript{D}}_{A\gamma }}$, respectively. The dimensionless number $\varPhi$ can be conceived as the Thiele modulus associated to the closure problem, in which $c_0$ is a characteristic concentration of species $A$ such that $c_{A\gamma }$ and, therefore, $\langle c_{A\gamma }\rangle ^\gamma$ are between 0 and 1. The resulting closure vectors derived from this approach are respectively substituted into Eq. (43), to obtain the analytical expressions for the effective transport coefficients (see for details, Ochoa-Tapia et al. 1991).

Cylindrical Chang’s Unit Cell

$$\begin{aligned}&\varepsilon _\gamma \frac{{D}_{\text {eff}}^{xx}}{{\fancyscript{D}}_{A\gamma }}= \frac{\varepsilon _\gamma }{2-\varepsilon _\gamma } \end{aligned}$$

(52a)

$$\begin{aligned}&\varepsilon _\gamma \frac{{ D}_{\text {diff-rx}}^{xx}}{{\fancyscript{D}}_{A\gamma }}= \varepsilon _\gamma +\frac{\varPhi ^{-2}\vartheta \left[ I_1\left( \varPhi \right) K_1\left( \vartheta \right) -I_1\left( \vartheta \right) K_1\left( \varPhi \right) \right] }{\left[ I_0\left( \vartheta \right) +I_2\left( \vartheta \right) \right] K_1\left( \varPhi \right) +\left[ K_0\left( \vartheta \right) +K_2\left( \vartheta \right) \right] I_1\left( \varPhi \right) } \end{aligned}$$

(52b)

where $\vartheta =\varepsilon _\kappa ^{\frac{1}{2}}\varPhi$, $\varepsilon _\kappa =4a^2/\ell _\mathrm{ch}^2$, $I_n$ and $K_n$ are the modified Bessel functions of order $n=0,1,2$.

Spherical Chang’s Unit Cell

$$\begin{aligned}&\varepsilon _\gamma \frac{{ D}_{\text {eff}}^{xx}}{{\fancyscript{D}}_{A\gamma }}= \frac{2\varepsilon _\gamma }{3-\varepsilon _\gamma } \end{aligned}$$

(53a)

$$\begin{aligned}&\varepsilon _\gamma \frac{{ D}_{\text {diff-rx}}^{xx}}{{\fancyscript{D}}_{A\gamma }}= \varepsilon _\gamma +\frac{\left( \varPhi \vartheta -1\right) \sinh \left( \varPhi -\vartheta \right) +\left( 1-\varepsilon _\gamma \right) \left( \varPhi -\vartheta \right) \cosh \left( \varPhi -\vartheta \right) }{\varepsilon _\gamma \left[ \vartheta \left( \vartheta -2\varPhi \right) +2\right] \sinh \left( \varPhi -\vartheta \right) -\left[ 2\left( \varPhi -\vartheta \right) +\varPhi \vartheta ^2\right] \cosh \left( \varPhi -\vartheta \right) } \end{aligned}$$

(53b)

where $\vartheta =\varepsilon _\kappa ^{\frac{1}{3}}\varPhi$, and $\varepsilon _\kappa =8a^3/\ell _\mathrm{ch}^3$. The comparison of these expressions with the numerical solutions in periodic unit cells is available in Fig. 3. From these results, it is clear that the analytical solutions from Chang’s unit cells qualitatively reproduce the dependence with the closure Thiele modulus and porosity. However, from a quantitative point of view (see Fig. 3c, d), the results from Chang’s unit cell overpredict those from the numerical solution in as much as 20 % for 2D geometries. As expected from previous studies (e.g., Ochoa-Tapia et al. 1991), the predictions from Chang’s unit cell are less accurate as the porosity increases and the differences with the numerical predictions in periodic unit cells are larger in 2D than in 3D geometries. These observations are also consistent with those found for first-order kinetics as shown in Fig. 5 of Valdés-Parada et al. (2011b).

At this point, it is opportune to ponder about the relevance of considering the functionality of the effective diffusion coefficient with the reaction rate. To this end, we computed the relative percent error of $D_{\text {eff}}$ (i.e., the passive diffusivity) with respect to $D^{xx}_{\text {diff-rx}}$ for the results provided in Fig. 3. We noticed that the percent error can go as high as 50 %, depending on the Thiele modulus value, which is quite considerable.

Finally, it is worth noting that, from the definition of the closure Thiele modulus, we can easily derive the dependence of the effective medium coefficient with $\langle c_{A\gamma }\rangle ^\gamma$, depending on the particular expression for the reaction rate. This fact will be further explored in the following section where we compare the predictions from the upscaled model with those resulting from performing PSS.

10 Comparison with Pore-Scale Simulations

Now that we have derived the closed macroscale model, we should ponder about its predictive capabilities. To this end, in this section we solve the upscaled and the microscale models and compare the average concentration profiles. For the purposes of this comparison exercise, we restrict the analysis to two dimensions and adopt a Michaelis–Menten expression for the reaction rate, i.e.,

$$\begin{aligned} R(c_{A\gamma })=\frac{k_1 c_{A\gamma }}{k_0+ c_{A\gamma }} \end{aligned}$$

(54)

The Michaelis–Menten expression is a nonlinear form of the reaction rate that is very typical in enzymatic reactions; its order ranges between 0 and 1 depending on the values of the coefficients $k_0$ and $k_1$ and it serves as a benchmark example to evaluate the model. We explored other nonlinear kinetic expressions (e.g., second-order, fractional-order kinetics) obtaining similar results. Thus, for the sake of brevity in presentation, we only report the results for the Michaelis–Menten kinetics.

In terms of the dimensionless variables,

$$\begin{aligned} X=\frac{x}{L};\quad Y=\frac{y}{L};\quad u=\frac{c_{A\gamma }}{c_\mathrm{in}},\quad \varPhi ^2_M=\frac{k_1 L^2}{{\fancyscript{D}}_{A\gamma }};\quad \gamma =\frac{k_0}{c_\mathrm{in}} \end{aligned}$$

(55)

the microscale equation to solve is

$$\begin{aligned} \frac{\partial ^2 u}{\partial X^2} +\frac{\partial ^2 u}{\partial Y^2} -\frac{\varPhi _M^2 u}{\gamma +u}=0 \end{aligned}$$

(56a)

This equation is subject to the following boundary conditions

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot \nabla u=0, \quad \text {at }{\fancyscript{A}}_{\gamma \kappa }\end{aligned}$$

(56b)

$$\begin{aligned}&X=0,1\quad u=1 \end{aligned}$$

(56c)

$$\begin{aligned}&Y=0,1\quad u=1 \end{aligned}$$

(56d)

In the above, $\varPhi _M$ can be regarded as a macroscale Thiele modulus, because it is expressed in terms of the macroscopic length $L$. In addition, as shown in Eqs. (56c) and (57), we imposed a constant concentration value at the extremes of the domain. We refer to the solution of the microscale equations as (direct) pore-scale simulations. In Fig, 4, we provide an example of the fields of $u$ taking $\varepsilon _\gamma =0.8$, $\varPhi _M=10$, $\gamma =1$ and $L=50\ell$. Due to the symmetry of the results, and with the aim of simplifying the computations, we reduce the solution domain to the stripe of in-line squares shown at the bottom of Fig. 4. Under these circumstances, we may introduce the change of variables $Y^*= Y/2-(1-2\ell /L)/4$ and replace the boundary conditions in Eq. (56d) to

$$\begin{aligned} Y^*=0,\frac{\ell }{L}\quad \frac{\partial u}{\partial Y^*}=0 \end{aligned}$$

(57)

In addition, the averaged model to be solved is given by the differential equation

$$\begin{aligned} D_{\text {diff-rx}}^{xx}\frac{\mathrm{d}^2 U }{d X^2}-\frac{\varPhi _M^2 U}{\gamma + U}=0 \end{aligned}$$

(58a)

which is subject to the boundary conditions,

$$\begin{aligned} X=0,1\quad U=1 \end{aligned}$$

(58b)

In the above expressions, $U= \langle c_{A\gamma }\rangle ^\gamma /c_\mathrm{in}$. We solved both microscale and macroscale models using Comsol Multiphysics. Standard tests of convergence and uniqueness were performed in order to guarantee the reliability of the numerical solutions. In Fig. 5, we provide two examples of the fields of $U$ resulting from solving Eqs. (58) and those arising from solving the microscale equations (Eqs. 56) and then taking the average (in an averaging domain corresponding to a single unit cell) of $u$. As can be observed, both models are in good agreement for all the conditions studied here. This is expected because the reaction is homogeneous, and thus, the volume fraction is more determinant than geometry in the average concentration predictions. However, for extremely large values of the macroscopic Thiele modulus (say, $\varPhi _M \gg 100$), the most important changes in concentration take place in a zone that is smaller than $\ell$. Under these circumstances, it is advisable to replace the boundary conditions given in Eq. (58b) by jump boundary conditions as suggested by Valdés-Parada et al. (2006b).

Fig. 4

Dimensionless concentration fields from pore-scale simulations using a Michaelis–Menten kinetics taking, $\varepsilon _\gamma =0.8$, $L=50\ell$, $\gamma =1$ and $\varPhi _M=10$. The plot provided at the bottom corresponds to a portion of the system that is far from the upper and lower boundaries influences

Fig. 5

Comparison of the concentration profiles obtained with the averaged model (black solid line) and using pore-scale simulations (red dashed line) for a Michaelis–Menten kinetics for different values of the macroscopic Thiele modulus taking a $\varepsilon _\gamma =0.4$ and b $\varepsilon _\gamma =0.8$; $\gamma =1$ and $L=100\ell$

To have a more quantitative insight about the comparison between the pore-scale simulations and the volume-averaged model, we compute the effectiveness factor for the system, $\eta$, defined as

$$\begin{aligned} \eta = \frac{\int _{X=0}^{X=1}\int _{Y^*=0}^{Y^*=\ell /L} R(U) \mathrm{d}Y^* \mathrm{d}X}{ \int _{X=0}^{X=1}\int _{Y^*=0}^{Y^*=\ell /L} \left. R(U)\right\| _{X=1} \mathrm{d}Y^* \mathrm{d}X} \end{aligned}$$

(59)

which is a parameter of interest in catalytic reactions. In Fig. 6, we present the predictions of the effectiveness factor using both pore-scale simulations and the averaged model as functions of $\varPhi _M$ for two porosity values. The relative percent error between both predictions is, in all cases, below 5 %, which is considered acceptable in many applications.

Fig. 6

Effectiveness factor predictions for two porosity values obtained with the averaged model (black solid line) and using pore-scale simulations (red dashed line) for a Michaelis–Menten kinetics for different values of the macroscopic Thiele modulus taking $\gamma =1$ and $L=100\ell$

Returning to the analytical and numerical predictions of the effective diffusivity, we used Chang’s unit cell expression for the effective diffusivity to compute $U$ and $\eta$. Interestingly, despite the clear differences between the analytical and numerical results shown in Fig. 3, we did not observe plausible differences between the pore-scale simulations and macroscale predictions of the effectiveness factor when using Chang’s unit cell. This is attributed to the fact that a macroscopic Thiele modulus value of 100 corresponds to a closure Thiele modulus value near 1, because $L=100\ell$. Under these circumstances, the differences between the analytical and numerical predictions of the effective diffusivity are not significant.

The computations performed so far have involved relatively simple geometries for both the unit cell and the solution domain in the pore-scale simulations. To overcome this issue, we built periodic unit cells consisting of random arrays of circles with a fixed size distribution. In Fig. 7, we show examples of the fields of the closure variables $b_x$ and $b_y$ taking $\varPhi _M=10$ for unit cells having fluid volume fractions of 0.4 (Fig. 7a, b) and 0.8 (Fig. 7c, d). In the unit cell with $\varepsilon _\gamma = 0.4$, there are 31 obstacles with radii ranging from $0.04\ell$ to $0.162\ell$, whereas in the unit cell corresponding to $\varepsilon _\gamma = 0.8$, there are 18 obstacles with radii ranging from $0.058\ell$ to $0.0836\ell$. With the closure variables fields, we computed the components of the effective diffusivity tensor and we noticed that the off-diagonal terms were negligible in comparison with the diagonal terms, which did not differ drastically between them. This implies that, even though the unit cell geometry is anisotropic, it can be concluded that the effective diffusivity is practically isotropic for the geometries treated in Fig. 7.

Fig. 7

Examples of the fields of the closure variables $b_x$ (a, c) and $b_y$ (b, d) in periodic unit cells involving a random distribution of solid obstacles with $\varepsilon _\gamma =0.4$ (a and b) and $\varepsilon _\gamma =0.8$ (c, d) for $\varPhi _M=10$

The unit cells shown in Fig. 7 were horizontally repeated 100 times in order to generate two new solution domains to carry out pore-scale simulations as shown in Fig. 8. As done before, we solved the dimensionless pore-scale equations to later compute the values of $\langle c_{A\gamma }\rangle ^\gamma /c_\mathrm{in}$ as a function of position for several values of $\varPhi _M$. Furthermore, taking into account the predictions of the effective diffusivity performed from the closure variable fields exemplified in Fig. 7, we solved the boundary-value problem given in Eqs. (58) to compute the predictions of the dimensionless volume-averaged concentration. This problem was also solved but using predictions of the effective diffusivity resulting from using arrays of squares in the unit cell for the same porosity and $\varPhi _M$ values used in Fig. 7. The resulting concentration profiles are shown in Fig. 9, and the maximum percent errors between the predictions from volume averaging and the pore-scale simulations are provided in Table 2; clearly, the largest deviations are exhibited in the system with a smaller volume fraction. As expected, the difference in the results increase with the reaction rate. We found that the maximum relative percent error could go as high as 400 % when using an array of squares in the unit cell, for $\varPhi _M=100$ and $\varepsilon _\gamma =0.4$, whereas if the unit cell with a random distribution of obstacles is considered, we obtained a difference that is always less than 7 % in all our computations. Certainly, this good agreement is also shared by the predictions obtained with the simple unit cell, but only for values of $\varPhi _M$ smaller than 10. Finally, it is worth mentioning that the averaging operator may be regarded as the response of an instrument probing intensive field variables (Baveye and Sposito 1984). Consequently, adopting a unit cell that closely resembles the actual geometry used in the pore-scale simulations yields better results than those produced by considering more idealized geometries.

Fig. 8

Examples of the dimensionless concentration fields from pore-scale simulations in domains built from horizontal repetitions of the unit cells in Fig. 7. In both examples, $L=100\ell$ and $\varPhi _M=10$

Fig. 9

Comparison of the concentration profiles obtained from pore-scale simulations (black solid line) with those resulting from the average model using arrays of squares (red dashed lined) and random distributions of obstacles (black dashed line) for the closure problem solution considering several values of the macroscopic Thiele modulus. a $\varepsilon _\gamma = 0.4$ and b $\varepsilon _\gamma = 0.8$

Table 2 Maximum percent errors in the concentration profiles predictions shown in Fig. 9 arising from the average model with respect to those from pore-scale simulations

11 Discussion and Conclusions

In this work, we revisited the upscaling process of the diffusive transport of a single chemical species undergoing a chemical reaction in the fluid phase that saturates a rigid and homogeneous porous medium. We used the method of volume averaging to derive the effective medium model (Eq. 47), and we identified the time- and length-scale constraints that lead to this particular structure of the model. These constraints are

$$\begin{aligned}&\ell _\gamma \ll r_0 \ll L\end{aligned}$$

(60a)

$$\begin{aligned}&\frac{\ell _\gamma }{L}\ll 1+\phi _c^2\end{aligned}$$

(60b)

$$\begin{aligned}&\frac{1}{1+\phi _c^2}\ll \frac{{\fancyscript{D}}_{A\gamma } t^*}{\ell _\gamma ^2} \end{aligned}$$

(60c)

It is important to recall that these constraints were derived from orders of magnitude estimates and may be over-restrictive. For instance, there may be situations in which fulfillment of these constraints translates in such a loss of information that hinders the predictive capabilities of the upscaled models.

In order to treat nonlinear reaction kinetics, we used a linearization scheme, based on Taylor series expansions, in order to derive a linear closure problem. As shown in Sect. 7, the length-scale constraint given in (60b) is essential for neglecting the nonlinear terms in the series expansion. At first sight, the macroscale model in Eq. (47) seems to exhibit a vis-à-vis resemblance with the governing equation at the microscale (Eq. 1a). Actually, this resemblance is only applicable to the reaction rate term, since the effective diffusivity turned out to be, in general, a nontrivial function of the reaction rate. This functionality was approximated by means of a logistic-type equation (49) that satisfactorily reproduces the numerical results. In addition, we solved the linear closure problem analytically using Chang’s unit cell and derived the expressions given in Eqs. (52) and (53) for 2D and 3D geometries, respectively. As shown in Fig. 3, the numerical and analytical predictions of the effective diffusivity as a function of the reaction rate are only in qualitative agreement.

With the aim of testing the predictive capabilities of the averaged model, we compared the concentration profiles and effectiveness factor predictions from the macroscale model with those resulting from performing pore-scale simulations in a 2D model of a porous medium consisting in a regular array of in-line squares and with random distributions of obstacles. As shown in the previous section, the agreement between both modeling approaches is quite acceptable. This is attributed to the homogeneity of the reaction rate in the system and to the fact that we built the solution domain for the pore-scale simulations from the same periodic unit cell used in the closure. As explained in the previous section, when comparing the concentration profiles corresponding to the largest Thiele modulus value for $\varepsilon _\gamma =0.4$, we noticed that the predictions resulting from using a simple unit cell (an array of squares) exhibit an error of 400 % relative to those from pore-scale simulations. Nevertheless, for smaller values, this difference may be as small as 5 %, thus showing the importance of the reaction rate and geometry over the predictions. Furthermore, if one would consider a system involving specific zones where considerably large reactions are taking place, one would require to use a hybrid modeling approach as suggested by Battiato et al. (2011).

Returning to the dependence of the effective diffusivity with the reaction rate, from the comparison with pore-scale simulations, we also noticed that, for the range of macroscopic Thiele modulus values here considered, it is acceptable to use either the logistic equation or the expressions arising from using Chang’s unit cell to predict the values of the effective diffusivity. This is attributed to the relatively small values of the closure Thiele modulus (about 1) that result even when taking values of the macroscopic Thiele modulus of 100. The cause of this disparity of values is the disparity of characteristic lengths between the microscale and the macroscale (for the system studied in Sect. 11, we took $L=100\ell$). The above suggests using the classical analytical expression for the effective diffusivity derived by Rayleigh (1892),

$$\begin{aligned} \frac{\varepsilon _\gamma D_{\text {eff}}^{xx} }{{\fancyscript{D}}_{A\gamma }}= \frac{\varepsilon _\gamma }{2-\varepsilon _\gamma } \end{aligned}$$

(61)

to predict the effectiveness factor dependence with the Thiele modulus for the conditions described in Fig. 6, and we found that the relative percent error with respect to pore-scale simulations was smaller than 10 % in all cases. Nevertheless, if one compares the predictions for the reactive diffusivity provided in Fig. 3 with those for passive diffusivity, the differences can go as high as 50 %. This leads us to conclude that, for systems satisfying the time- and length-scale constraints here identified, one may neglect the dependence of the diffusivity with the reaction rate for the purposes of predicting the effectiveness factor. Under these conditions, we may state that the averaged model has a vis-à-vis resemblance with the pore-scale model. Certainly, there are more complicated situations in which the agreement between the predictions from the upscaled model with pore-scale simulations are not as close as those shown here. Wood et al. (2007) studied the case of dispersive mass transport undergoing a heterogeneous reaction in a biofilm-coated porous medium. For a given representation of the porous medium geometry (see Fig. 5 in Wood et al. 2007), these authors concluded that the variance of the concentration field has a dramatic impact upon the shape of the effective reaction rate curve as determined by DNS. They attributed this behavior to the fact that order of operations of reaction and averaging cannot, in general, be freely interchanged.

It is worth mentioning that the vis-à-vis resemblance between the upscaled and microscale models applies for the structure of the model and not for the physical meaning of each term. In other words, the fact that both microscale and macroscale models include a diffusive term does not imply that the effective diffusivity is equal to the molecular diffusivity or that a volume-averaged concentration is equal to its microscale counterpart. Such equalities can only hold in systems in which the porous medium offers a negligible influence for transport, as, for instance, in systems with porosity values near the unity.

Finally, it is worth remarking that the linearization scheme used in this paper was a convenient tool to obtain a closed model that resembles its microscale counterpart, which appears to provide good agreement with pore-scale simulations. However, for situations in which this is not a reasonable approach, one may require the use of iterative schemes as explained in the appendix. In this case, the closure problem solution is implicit and the coupling between the closure problem and the upscaled model is more complicated than the one found for the linear problem. In addition, the computation of the related Green function will be an essential feature of the solution procedure. This alternative approach will be further explored in a future work.

Appendix

In this section, we describe an approach for solving closure problems in cases for which the linearization scheme described in Sect. 7 is not suitable. In this case, the closure problem is given by the following boundary-value problem:

$$\begin{aligned}&\nabla \cdot ({\fancyscript{D}}_{A\gamma }\nabla \tilde{c}_{A\gamma })-\tilde{R}(\tilde{c}_{A\gamma }+\langle c_{A\gamma }\rangle ^\gamma )=0, \quad \text {in }\varOmega _{\gamma }\end{aligned}$$

(62a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \tilde{c}_{A\gamma }= \mathbf{n}_{\gamma \kappa }\cdot {\fancyscript{D}}_{A\gamma }\nabla \langle c_{A\gamma }\rangle ^\gamma , \quad \text {at }\partial \varOmega _\gamma \end{aligned}$$

(62b)

$$\begin{aligned}&\tilde{c}_{A\gamma }(\mathbf{x}+\mathbf{l}_i)= \tilde{c}_{A\gamma }(\mathbf{x}), \quad i=1,2,3\end{aligned}$$

(62c)

$$\begin{aligned}&\langle \tilde{c}_{A\gamma }\rangle ^\gamma =0 \end{aligned}$$

(62d)

If we regard the reaction rate as a volumetric source term, the closure problem solution is given by

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)&=-\underbrace{\int \limits _{\mathbf{r}\in \varOmega _{\gamma }} {\fancyscript{G}}(\mathbf{x}, \mathbf{r}) {\tilde{R}}\left( {\tilde{c}}_{A\gamma }+\langle c_{A\gamma }\rangle ^\gamma \right) \mathrm{d}V(\mathbf{r})}_{\text {influence of the volumetric reactive source}}\nonumber \\&\quad \, -\underbrace{\int \limits _{\mathbf{r}\in \partial \varOmega _{\gamma \kappa }} {\fancyscript{G}}(\mathbf{x}, \mathbf{r}) \mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma } \mathrm{d} A(\mathbf{r}) \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma }_{\text {influence of the surface diffusive source}} \end{aligned}$$

(63)

where ${\fancyscript{G}}(\mathbf{x}, \mathbf{r})$ is the Green function associated to passive diffusive transport in the unit cell and it solves the following problem

$$\begin{aligned}&\nabla ^2 {\fancyscript{G}}=\delta (\mathbf{x}-\mathbf{r}), \quad \text {in } \varOmega _{\gamma }\end{aligned}$$

(64a)

$$\begin{aligned}&-\mathbf{n}_{\gamma \kappa }\cdot \nabla {\fancyscript{G}}= 0, \quad \text {at }\partial \varOmega _\gamma \end{aligned}$$

(64b)

$$\begin{aligned}&{\fancyscript{G}}(\mathbf{x}+\mathbf{l}_i)= {\fancyscript{G}} (\mathbf{x}), \quad i=1,2,3\end{aligned}$$

(64c)

$$\begin{aligned}&\langle {\fancyscript{G}}\rangle ^\gamma =0 \end{aligned}$$

(64d)

With the aim of simplifying Eq. (63), let us define

$$\begin{aligned} \mathbf{b}_\gamma (\mathbf{x}) = -\int \limits _{\mathbf{r}\in \partial \varOmega _{\gamma \kappa }} {\fancyscript{G}}(\mathbf{x}, \mathbf{r}) \mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma } \mathrm{d} A(\mathbf{r}) \end{aligned}$$

(65)

so that Eq. (63) takes the form

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)=&-\underbrace{\int \limits _{\mathbf{r}\in \varOmega _{\gamma }} {\fancyscript{G}}(\mathbf{x}, \mathbf{r}) {\tilde{R}}\left( {\tilde{c}}_{A\gamma }+\langle c_{A\gamma }\rangle ^\gamma \right) \mathrm{d}V(\mathbf{r})}_{\text {influence of the volumetric reactive source}} +\underbrace{\mathbf{b}_\gamma \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma }_{\text {influence of the surface diffusive source}} \end{aligned}$$

(66)

Certainly, Eq. (66) is an implicit solution as it requires knowledge of the concentration deviation fields in the first integral term. Under these conditions, the following iterative solution approach is advisable:

• 1. Compute the Green function for the linear portion of the operator for a given unit cell geometry. The nonlinear term is treated as a source term in this formulation. Note that the average concentration and its gradient are also source terms that parameterize the potential solution space. Thus, the general solution covering all possible conditions must be sought for all combinations of $\langle c_{A\gamma }\rangle ^\gamma$ and $\nabla \langle c_{A\gamma }\rangle ^\gamma$ as parameters.

• 2. For a particular set of values of $\langle c_{A\gamma }\rangle ^\gamma$ and $\nabla \langle c_{A\gamma }\rangle ^\gamma$, one must assume an initial value for the $\tilde{c}_{A\gamma }$ field.

• 3. Using the initial guess for $\tilde{c}_{A\gamma }$, compute ${\tilde{R}}({\tilde{c}}_{A\gamma }+\langle c_{A\gamma }\rangle ^\gamma )$.

• 4. Use Eq. (66) to compute the concentration deviations.

• 5. Verify whether the computed concentration deviation fields satisfy a convergence criterion. If the criterion is not met, correct the assumed fields and return to step 3.

• 6. Once a particular convergence criterion has been met, this process must be repeated for each combination of $\langle c_{A\gamma }\rangle ^\gamma$ and $\nabla \langle c_{A\gamma }\rangle ^\gamma$ required to adequately cover the solution domain of interest.

This scheme has been used in the past for studying diffusive and convective mass transport in a catalytic particle (Mandaliya et al. 2013; Valdés-Parada et al. 2008a, b) obtaining faster convergence rates than with traditional approaches. The idea of regarding the nonlinear term as a source in order to produce an implicit solution has been previously discussed at some length in the literature (Flesch and Trullinger 1987; Stakgold and Holst 2011). There are two potential disadvantages of this approach

• 1. The Green function for the linear component of the transport operator must be computed. It is possible to compute Green’s functions numerically, but the number of independent variables for these functions is essentially twice that of the underlying fields. This creates a significant computational burden.

• 2. Although the fields for $\tilde{c}_{A\gamma }$ can be, in principle, accurately computed for the nonlinear reaction, the resulting solution is not a simple one in terms of the average concentration and its gradients alone. However, higher-order approximation schemes can be developed from such solutions that involve only the average concentration and its (higer-order) gradients.

To conclude this section, it is illustrative to show that Eq. (66) leads to the same expression for the concentration deviations as given in Eq. (24) for the case in which the reaction rate can be linearized. In this case, Eq. (38) is applicable and Eq. (66) takes the form

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x}, t)=&-\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}} \int \limits _{\mathbf{r}\in \varOmega _{\gamma }} {\fancyscript{G}}(\mathbf{x}, \mathbf{r}) {\tilde{c}}_{A\gamma } |_{\mathbf{r}} \mathrm{d}V(\mathbf{r}) +\mathbf{b}_\gamma \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma \end{aligned}$$

(67)

Let us now substitute Eq. (66) into the integral term in the above expression to obtain

$$\begin{aligned} {\tilde{c}}_{A\gamma }(\mathbf{x})=&\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}\mathbf{b}_{rx} \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma +\mathbf{b}_\gamma \cdot \nabla \langle c_{A\gamma }\rangle ^\gamma \end{aligned}$$

(68)

where, on the basis of Eq. (25), the closure variable, $\mathbf{b}_{rx}$, is given by

$$\begin{aligned} \mathbf{b}_{rx}= \int \limits _{\mathbf{r}\in \varOmega _{\gamma }} \int \limits _{\mathbf{y_0}\in \partial \varOmega _{\gamma \kappa }} {\fancyscript{G}} (\mathbf{x}, \mathbf{r}) {\fancyscript{G}}_{rx}(\mathbf{r}, \mathbf{y}_0) \mathbf{n}_{\gamma \kappa }{\fancyscript{D}}_{A\gamma } \mathrm{d} A(\mathbf{y}_0) ~ \mathrm{d}V(\mathbf{r}) \end{aligned}$$

(69)

Equation (68) is equivalent to Eq. (24) thus concluding the demonstration. Certainly, in the case in which the reaction rate follows the first-order expression $R=kc_{A_\gamma }$, the above derivations are also applicable by simply replacing $\left. \frac{\mathrm{d}R}{\mathrm{d} c_{A\gamma }}\right| _{\langle c_{A\gamma }\rangle ^\gamma |_\mathbf{x}}= k$.