The joint aggregation of beliefs and degrees of belief

Abstract

The article proceeds upon the assumption that the beliefs and degrees of belief of rational agents satisfy a number of constraints, including: (1) consistency and deductive closure for belief sets, (2) conformity to the axioms of probability for degrees of belief, and (3) the Lockean Thesis concerning the relationship between belief and degree of belief. Assuming that the beliefs and degrees of belief of both individuals and collectives satisfy the preceding three constraints, I discuss what further constraints may be imposed on the aggregation of beliefs and degrees of belief. Some possibility and impossibility results are presented. The possibility results suggest that the three proposed rationality constraints are compatible with reasonable aggregation procedures for belief and degree of belief.

1 Introduction

There are two sorts of doxastic states that have received considerable attention from epistemologists. The first sort of doxastic state is belief. Belief is an all or nothing affair: For every proposition, φ, one either believes it or one does not. If one does not believe φ, one may either disbelieve φ (which is equivalent to believing not φ) or remain uncommitted (neither believing nor disbelieving). A second sort of doxastic state is degree of belief. The latter sort of state reflects the fact that beliefs may be held with varied degrees of conviction. Degrees of belief also correspond to personal (or subjective) probabilities, which are of considerable importance to decision theory. In order to cement the link between degree of belief and rational action, it is typically assumed that rational degrees of belief satisfy the axioms of probability.

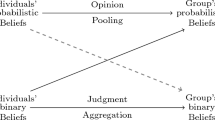
The two sorts of doxastic state give rise to two distinct aggregation problems. The first is the problem of aggregating beliefs: Given a group of agents, the problem is to pool individual beliefs regarding a domain of propositions, in order to form a collective belief set.¹ The second problem concerns the aggregation of degrees of belief: Given a group of agents, the problem is to pool their individual degrees of belief regarding a domain of propositions, in order to form collective degrees of belief.² The determination of what principles are appropriate in forming a collective doxastic state may vary by context, and depend on the relative importance of respecting procedural concerns (e.g., for the ‘fairness’ with which individual doxastic states have a bearing on the collective) versus veritistic concerns (e.g., for the tendency of the aggregation procedure to yield an accurate collective doxastic state). As a rough guide to forming intuitions about the relative importance of procedural and veritistic concerns, I will proceed upon the assumption that collective doxastic states will serve the purpose of guiding collective decision making (cf. Wagner 2010, p. 336).

Regardless of the importance one attaches to procedural and veritistic concerns, it is clear that both sorts of aggregation (i.e., of beliefs and of degrees of belief) have their place. In some cases, our goal is to form collective beliefs, on the basis of individual beliefs. Jury trials provide one sort of example. In more interesting cases, the members of a group need to aggregate their individual beliefs regarding a range of interrelated propositions. Such cases arise when a committee is charged with issuing yes/no verdicts regarding each element of a collection of related propositions. One example would be of a hiring committee that is charged with evaluating which qualifications a candidate meets (Pigozzi 2015). It is easy to imagine cases where it would be desirable for the members of a group to aggregate their degrees of belief. In fact, since degrees of belief are more fine-grained than beliefs (seeming to encode more information about an agent’s doxastic state), it might appear that it would always be preferable to aggregate degrees of belief, rather than beliefs. Nevertheless, it is clear that there are many circumstances where we want to form collective judgments, but we only have access to the beliefs of the members of a group, and not to their degrees of belief. In such cases, we will have to settle for aggregating beliefs.³

In addition to the problem of aggregating belief sets, and the problem of aggregating degrees of belief, there is the further problem of simultaneously aggregating beliefs and degrees of belief: Given a group of agents, the problem is to pool the individual belief sets in order to form a collective belief set, while at the same time pooling the individual degrees of belief in order to form collective degrees of belief.⁴Assuming we accede to some prior constraints on the manner in which rational beliefs and rational degrees of belief are related, the ‘joint problem’ of aggregating beliefs and degrees of belief is more than the sum of the two component problems. Assume, for example, that we endorse the rather modest constraint that it is only rational for an agent (or a collective) to believe a proposition, if the agent’s (or the collective’s) degree of belief for the proposition is greater than 0.5. If rational degree of belief constrains rational belief in this way, and we require that our aggregation procedures respect this constraint, then care must be taken in deciding how we aggregate beliefs and degrees of belief. If care is not taken, the result of aggregation may fail to satisfy the constraint.

One might dismiss the joint problem of aggregating beliefs and degrees of belief, appealing to the claim that degrees of belief are more fine-grained than beliefs. In particular, one might maintain that it is possible to provide necessary and sufficient conditions for rational belief specified wholly in terms of rational degree of belief. If belief were ‘reducible’ to degree of belief in the preceding sense, then one could dispense with (coarse-grained) belief, in favor of (fine-grained) degree of belief, in all cases where one had access to all of the facts about a relevant agent’s (or a relevant collective’s) degrees of belief. The suggestion is that, in the face of the joint problem of aggregating beliefs and degrees of belief, it would be sufficient to concern oneself with aggregating the relevant degrees of belief.

There are, of course, arguments against the claim that belief is reducible to degree of belief. One line of argument maintains that belief is sensitive to pragmatic and/or contextual considerations to which degree of belief is insensitive (Fantl and McGrath 2002; Hawthorne 2004; Weatherson 2005; Ganson 2008; Hawthorne 2009; Buchak 2014; Leitgeb 2014; Staffel 2016; Thorn 2017). Regardless of whether rational belief is reducible to rational degree of belief, it would be of value to know how to aggregate beliefs in a way that respects the relationship between rational belief and rational degree of belief. The value of such knowledge is analogous to the value of knowing the laws of chemistry even if those laws are reducible to the laws of fundamental physics. For example, knowledge of the laws of chemistry would be needed (up and above the laws of physics) in reasoning about a system for which we possess an adequate chemical description, but not a description in the language of fundamental physics. By analogy, knowledge of the appropriate principles of belief aggregation would be needed (up and above the appropriate principles for aggregating degrees of belief) in reasoning about the collective beliefs of a group, in cases where we do not have access to the degrees of belief of the members of the group.

The present article investigates the joint problem of aggregating beliefs and degrees of belief. My starting assumptions will consist of a number of rationality constraints on the inputs and outputs to the joint aggregation process. To begin with, I assume (1) that the belief sets that are the inputs and outputs to the aggregation process are consistent and closed under deductive consequences. I also assume (2) that the degrees of belief that are the inputs and outputs to the aggregation process satisfy the axioms of probability. Finally, I assume (3) that the inputs and outputs to the aggregation process satisfy a ‘context dependent’ version of the Lockean Thesis (Foley 1993, 2009; Leitgeb 2013, 2014):

The Lockean Thesis

For each individual/collective, there is some r (0.5 < r < 1) such that for the individual/collective, and each proposition, φ, it is rational for the individual/collective to believe φ if and only if the individual’s/collective’s rational degree of belief for φ is at least r.

The preceding version of the Lockean Thesis differs importantly from the ‘context independent’ version of the thesis, which requires some particular bound r that applies to every individual/collective. Indeed, as illustrated by the Lottery Paradox, the context independent version of the Lockean Thesis leads to inconsistency when combined with the claim that rational belief sets are consistent and closed under deductive consequences, and the claim that rational degrees of belief satisfy the axioms of probability (Kyburg 1961, p. 197). A key innovation of Leitgeb (2013, 2014) was to show how to consistently maintain the (context dependent) Lockean Thesis, while at the same time holding that rational belief sets are consistent and closed under deductive consequences, and that rational degrees of belief satisfy the axioms of probability.

The goal of the present article is to press forward with the insights of Leitgeb, and evaluate whether (1), (2), and (3) are compatible with reasonable constraints on the aggregation of beliefs and degrees of belief. The article will proceed as follows. Section 2 presents a formal framework for representing the aggregation of belief sets. Along with presenting a formal framework, I present three principles that any satisfactory belief aggregation procedure should satisfy. Section 3 parallels Sect. 2, and presents a framework for aggregating degrees of belief, along with three principles that any satisfactory procedure for aggregating degrees of belief should satisfy. In Sect. 4, it is shown that the core principles proposed in Sects. 2 and 3 are compatible with assumptions (1), (2), and (3). Further possibilities and impossibilities are also described. Section 5 summarizes the principal results of the paper.

Before proceeding, I should mention that several previous articles have observed various formal similarities between the problem of relating beliefs to degrees of belief and the problem of aggregating beliefs (Levi 2004; Douven and Romeijn 2007; Chandler 2013; Briggs et al. 2014; Cariani 2016; Dietrich and List 2018). Some papers have imported insights concerning the former problem in order to illuminate the latter problem (e.g., Douven and Romeijn 2007), while others have imported insights concerning the latter problem in order to illuminate the former problem (e.g., Dietrich and List 2018). Of particular interest, the paper of Dietrich and List (2018) introduced a means of ‘translating’ the problem of relating beliefs to degrees of belief into the problem of aggregating beliefs, which enables them to derive impossibility results for the former problem from impossibility results for the latter problem.

While the work presented here is obviously constrained by the impossibility results of Dietrich and List, those results will not feature explicitly in the discussion that follows. Indeed, given the three rationality assumptions that form the basis of my approach ((1), (2), and (3)), my options are very constrained regarding the relationship between rational belief and rational degree of belief, forcing me to reject a principle that Dietrich and List call “Propositionwise Independence”, which states that whether one believes a proposition should only depend upon one’s degree of belief in that proposition and not on one’s degree of belief in other propositions (Dietrich and List 2018, p. 228). In fact, a result of Leitgeb’s (2014), which is described in Sect. 4 (below), implies that the acceptance of (1), (2), and (3) comes at the cost of a strong form of context sensitivity for belief, such that whether it is rational for one to believe a proposition depends, not just upon one’s degree of belief in that proposition, but upon one’s degrees of belief in other propositions and upon the very possibilities that are individuated by one’s degree of belief function. As acknowledged by Leitgeb, the preceding form of context sensitivity is a significant cost (cf. Thorn 2017; Schurz 2017). In the present article, I assume that we have accepted this cost, and investigate what further costs (if any) are incurred as a result of accepting (1), (2), and (3).

2 Belief aggregation

I here consider the belief sets of agents whose belief contents are the elements of an algebra of propositions. Where W is the set of possible worlds, consider the algebra of propositions generated by a partition Π of W: Π = {w₁, …, w_k}. The finiteness of Π is taken as a simplifying assumption, with all results of the paper generalizing to the case where Π is infinite, except where noted. Any proposition, φ, expressible within Π, is identified with a subset S of Π, namely: φ = ∪S. Since our concern is exclusively with agents whose beliefs sets are closed under deductive consequences, the belief set of an agent may be identified with the strongest proposition believed by the agent. Formally, I characterize the belief set of an agent i using a k-tuple of 0 s and 1 s, namely:  b_i = 〈n_i1,…,n_ik〉. Within such tuples, 0 s are associated with propositions in Π that are disbelieved, and 1 s are associated with propositions in Π that are not disbelieved. Since the value “1” signifies non-disbelief, $n_{ij}$ = 1 does not imply that agent i believes w_j. Rather the strongest proposition believed by agent i is defined as φ_bi = ∪{w_j: $n_{ij}$ = 1}. This definition makes intuitive sense, for the following reasons: Whenever n_ij = 0, w_j is disbelieved by i, and its compliment, ¬w_j, is believed by i. Further, since the intersection of all ¬w_j such that n_ij = 0 is the strongest proposition believed by i, the compliment of the union of all w_j such that n_ij = 0 is the strongest proposition believed by i, and the latter set is the union of all w_j such that n_ij = 1.

In addition to being a tuple, b_i will serve as a belief function, defined as follows: b_i(φ) = 1 (agent i believes φ), if φ_bi ⊆ φ; and b_i(φ) = 0, otherwise. Note that if b_i(φ) = 0, then the agent i either disbelieves or suspends judgment regarding φ (with b_i(φ) = b_i(φ^c) = 0 implying suspension of judgment). Given the preceding, the belief set corresponding to a belief function b_i is simply {φ: b_i(φ) = 1}. Notice that belief sets, so defined, are closed under deductive consequences, relative to the algebra generated by Π. Next, notice that the belief set of an individual i is consistent if and only if ${\hbox{b}}_{i} =\langle n_{i1} , \ldots ,n_{ik} \rangle$ contains at least one “1”. For simplicity’s sake, I assume that our concern is only with consistent belief sets, thereby requiring that each tuple $n_{i1} , \ldots ,n_{ik}$ contains at least one “1”.

The problem with which we are faced is that of aggregating an ordered set, B, of n belief functions: B = 〈b₁, …, b_n〉 (where each b_i is defined over a k-sized partition of W). For the purpose of regimenting belief aggregation, it is convenient to regard the input to the aggregation process as an n by k matrix:

$$ \left[ {\begin{array}{*{20}c} {n_{11} } & \cdots & {n_{1k} } \\ \vdots & \ddots & \vdots \\ {n_{n1} } & \cdots & {n_{nk} } \\ \end{array} } \right] $$

Notice that the rows of the matrix are the elements of B (representing the belief sets of the individual agents), while the columns correspond to the elements of Π (the cells of the partition of W). The output of the aggregation process is the k-tuple b_B = 〈 n₁,…,n_k〉, which represents the strongest proposition believed by the collective. This (strongest believed) proposition is defined as φ_B = ∪{w_j: n_j = 1}. As with individuals, the fact that the collective believes a proposition φ is expressed as follows: b_B(φ) = 1, if φ_B ⊆ φ; and b_B(φ) = 0, otherwise. So, in addition to being a k-tuple, b_B is a belief function. The belief set of the collective is {φ : b_B(φ) = 1} (which is closed under deductive consequences). I also assume that b_B = $\langle n_{1} , \ldots ,n_{k} \rangle$ corresponds to a consistent belief set, and thus contains at least one “1”. In effect, the rational requirements of consistency and deductive closure are built into the present framework.

I assume that belief aggregation is determined by a function F_bel (i.e., F_bel(B) = b_B = $\langle n_{1} , \ldots ,n_{k} \rangle$), and espouse three highly plausible principles regarding F_bel. To begin with, I assume that the domain of F_bel is unrestricted:

Universality (U _b ):

All ordered sets of belief functions, B, are in the domain of F_bel.⁵

Next I assume that the order of the elements of B makes no difference to the output of F_bel:

Anonymity (A _b ):

For all B and g: if g: {1, …, n} → {1, …, n} is a permutation, and B′ = 〈b_g(1), …, b_g(n)〉, then b_B′ = b_B.

Similarly, I assume that the order of the elements of Π makes no difference to the output of F_bel:

Neutrality (N _b ):

For all B and f: if f : {1, …, k} → {1, …, k} is a permutation, B′ = 〈b′₁, …, b′_n〉, and for all i: b′_i = 〈$n_{if\left( 1 \right)}$, …, $n_{if\left( k \right)}$〉, then b_B′ = 〈$n_{f\left( 1 \right)}$, …, $n_{f\left( k \right)}$〉.

As an illustration of how N_b places constraints on F_bel, consider the following ordered set of belief functions:

In this case, N_b implies $n_{1}$ = $n_{3}$ (i.e., the collective attitude regarding w₁ and w₃ is identical). Indeed, where B′ is specified by f(1) = 3, f(2) = 2, and f(3) = 1, we have B′ = B, and thus b_B′ = 〈$n_{3}$, $n_{2}$, $n_{1}$〉 (given N_b), which implies that $n_{1}$ = $n_{3}$.

As an illustration of how N_b functions in conjunction with A_b, consider the following ordered set of belief functions:

In this case, the conjunction of A_b and N_b imply $n_{1}$ = $n_{3}$ (assuming U_b). To see why, consider the following ordered set of belief functions:

Since B′ results from switching the first and third rows of B, A_b tells us that F_bel(B′) = F_bel(B) = 〈$n_{1}$, $n_{2} , n_{3}$〉. Further, where B′′ is specified by f(1) = 3, f(2) = 2, and f(3) = 1, relative to B′, we have B′′ = B, and thus b_B′′ = 〈$n_{3}$, $n_{2}$, $n_{1}$〉 (given N_b), which implies that $n_{1}$ = $n_{3}$. By similar reasoning, it follows that $n_{1}$ = $n_{2}$, and so by the consistency requirement on b_B, we have b_B = 〈1, 1, 1〉.

Taken in conjunction, U_b, A_b, and N_b imply the negation of a condition that Douven and Romeijn (2007) call “Non-Unanimity at Disparity” (cf. Douven and Williamson 2006). Within the framework of this article, a ‘disparate’ set of belief functions, B, is one where |B| = |Π| (where |B| is the number of belief functions in B, and |Π| is the number of propositions in Π), and each element of B is a tuple $n_{i1} , \ldots ,n_{ik}$ that contains exactly one 0, and none of the tuples are identical. Non-Unanimity at Disparity demands that there be at least one disparate set of belief functions, B, and some proposition, φ, such that (i) b_B(φ) = 1, and (ii) there is some b_i ∈ B, such that b_i(φ) = 0. Douven and Romeijn assert that any aggregation procedure that does not satisfy Non-Unanimity at Disparity is “awkward”. Contrary to Douven and Romeijn, it is plausible to think (given the apparent plausibility of U_b, A_b, and N_b) that there is a class of possible sets of belief sets (i.e., disparate ones) where the individual belief sets pull in opposite directions with perfect symmetry, with the result that there is no non-arbitrary way of forming a collective belief set that includes any contingent claim.

It may now be observed that N_b is similar to a principle that was proposed by List and Pettit (2002), namely:

Systematicity (S):

There is a function, h, such that for all B and φ: b_B(φ) = h(b₁(φ),…, b_n(φ)).⁶

Notice that S is stronger than N_b, that is:

Fact 1.

S implies N_b, but N_b does not imply S.⁷

List and Pettit show that S conflicts with the conjunction of U_b and A_b, if one requires completeness among the outputs of aggregation, that is, if one requires that for all φ and B: b_B(φ) = 1 or b_B(φ^c) = 1. Completeness entails that all aggregate belief sets contain an element of the partition, Π, over which the aggregate belief set is defined. Given U_b, completeness applies in cases where Π is the finest partition of the space of possible worlds that our conceptual resources will admit, and demands collective belief in exactly one element of such ultra-fine partitions (irrespective of the beliefs of the individuals whose belief sets are the inputs to the aggregation process). Completeness is, thus, an extremely strong requirement, and it is apparent that correct norms of belief formation demand its rejection. I adhere to those demands and reject completeness. Since I do not require completeness, I could consistently accept S, along with the other principles that I favor. Nevertheless, there are further reasons for denying that S is a plausible constraint on belief aggregation. In particular, S in the presence of U_b and A_b implies a highly ‘incredulous’ belief aggregation function, as expressed by the following fact:

Fact 2.

If U_b, A_b, and S, then for all B, φ: b_B(φ) = 1 if and only if for all b_i in B: b_i(φ) = 1.⁸

Assuming U_b, A_b, and S, Fact 2 tells us that a collective will only believe a proposition if every member of the collective believes that proposition. Fact 2 shows that S induces a highly incredulous belief aggregation function (in the presence of U_b and A_b), and I believe that this counts as a decisive reason for rejecting S. Nevertheless, in what follows, I will remain neutral on the question of whether F_bel should satisfy S or merely N_b. As we shall see, it is possible to leave one’s options open in this respect, since the possibility results that are presented in Sect. 4 allow one to uphold S, if one desires. In fact, the possibility results presented in Sect. 4 show that the Lockean Thesis is compatible with an extremely broad range of belief aggregation functions, in the presence of reasonable constraints on degree of belief aggregation.

3 Degree of belief aggregation

Once again, where W is the set of possible worlds, I consider the algebra of propositions generated by a partition Π = {w₁, …, w_k} of W. As above, propositions are identified with subsets of Π, according to the condition: φ = ∪S, where S ⊆ Π. Formally, I identify the degree of belief function, p_i, of an agent i as a k-tuple of real numbers: $r_{i1} , \ldots ,r_{ik}$. I require that any such p_i be a probability function on Π, that is: $r_{ij}$ ∈ [0, 1] (for all i and j) and ∑_j $r_{ij}$ = 1 (for all i). More generally, i’s degrees of belief are specified by the schema: p_i(φ) = ∑_j $r_{ij}$, for j ∈ {j : w_j ⊆ φ}.

Similar to belief aggregation, the problem with which we are faced is that of aggregating an ordered set of n probability functions P = 〈p₁, …, p_n〉 (where each p_i is defined over a k-sized partition of W). The input to the aggregation process may be represented by an n by k matrix (where the rows of the matrix are the elements of P, and the columns correspond to the elements of Π):

$$ \left[ {\begin{array}{*{20}c} {r_{11} } & \cdots & {r_{1k} } \\ \vdots & \ddots & \vdots \\ {r_{n1} } & \cdots & {r_{nk} } \\ \end{array} } \right] $$

The output of the aggregation process is then a k-tuple p_P = 〈$r_{1} , \ldots ,r_{k}$〉. As with individual degrees of belief, it is assumed that p_P is a probability function, that is: $r_{j}$ ∈ [0, 1] (for all j), and ∑_j $r_{j}$ = 1. Similarly, p_P(φ) = ∑_j $r_{j}$, for j ∈ {j : w_j ⊆ φ}.

As usual, it is assumed that probability function aggregation is determined by a function F_prob (i.e., F_prob(P) = p_P = 〈$r_{1} , \ldots ,r_{k}$〉). I also endorse three standard principles regarding F_prob, which parallel the ones that I proposed for F_bel:

Universality (U _p ):

All ordered sets of probability functions, P, are in the domain of F_prob.⁹

Anonymity (A _p ):

For all P and g: if g: {1, …, n} → {1, …, n} is a permutation, and P′ = 〈p_g(1), …, p_g(n)〉, then p_P′ = p_P.

Neutrality (N _p ):

For all P and f: if f: {1, …, k} → {1, …, k} is a permutation, P′ = 〈p′₁, …, p′_n〉, and for all i: p′_i = 〈$r_{if\left( 1 \right)}$, …, $r_{if\left( k \right)}$〉, then p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉.

A principle stronger than N_p was introduced by Lehrer and Wagner (1981, 1983), and is similar to List and Pettit’s S:

Irrelevance of Alternatives (IA):

There is a function, h, such that for all P, w_i: p_P(w_i) = h(p₁(w_i),…, p_n(w_i)).

Although similar to S, IA does not lead to incredulity in the manner of S – recall Fact 2. Nevertheless, the problems that arise for S provide a reason for treating IA with caution. IA is also extremely restrictive, as illustrated by its interaction with the following highly plausible principle¹⁰:

Zero Unanimity (Z _p ):

For all P: if for all p_i in P: $r_{ij}$ = 0, then $r_{j}$ = 0.

Taken together, IA and Z are equivalent to linear weighting, in cases where |Π| > 2 (Lehrer and Wagner 1983):

Linear Weighting (LW):

There is a set of constants 〈c₁,…, c_n〉, such that (i) for all i: c_i ≥ 0, (ii) c₁ +… + c_n = 1, and (iii) for all P and j: p_P(w_j) = p₁(w_j)·c₁ +… + p_n(w_j)·c_n.

While LW appears to be reasonable, we will see below that the principle is incompatible with some plausible means of adhering to the Lockean Thesis. Assuming non-dictatorial weights (i.e., for all i: c_i ≠ 1), LW is also known to be incompatible with other widely endorsed principles, including:

Independence Preservation (IP):

For all P, φ, ψ: if for all p_i in P: p_i(φ∩ψ) = p_i(φ)p_i(ψ), then p_P(φ∩ψ) = p_P(φ)p_P(ψ).¹¹

Commutativity with Learning (CL):

For all P, φ, ψ: if for all p_i in P: p_i(φ) > 0, then p_P(ψ|φ) = p_P′(ψ), where P′ = 〈p₁(ψ|φ), …, p_n(ψ|φ)〉.¹²

Some have cited the incompatibility of LW and IP as grounds for rejecting LW (e.g., Laddaga 1977), and it is clear that there are some cases where we should require independence preservation, contrary to the prescriptions of LW (such as in the case described by Elkin and Wheeler 2018). Nevertheless, it is plausible to deny that IP holds generally, since the principle is implausible in the case where the probability functions to be aggregated mirror frequencies for disjoint and equinumerous samples (a case where LW is plausible). IP is also known to be highly restrictive, excluding many plausible aggregation functions (Genest and Wagner 1987).

CL tells us that we should reach the same collective degrees of belief, regardless of whether we (i) aggregate individual degrees of belief to form collective degrees of belief, and then update the collective degrees of belief by conditionalization upon given information φ, or (ii) update individual degrees of belief by conditionalization upon φ, and then aggregate individual degrees of belief to form collective degrees of belief. CL is an attractive principle, since it prohibits certain order effects that could make an aggregation process subject to manipulation according to when information is disclosed.¹³ While the principle is attractive, it is also highly restrictive, as observed by Genest (1984b), with further impossibility results concerning CL introduced by Russell, Hawthorne, and Buchak (2015). Because CL is so restrictive, the principle should probably be regarded as negotiable—nice to have but not a deal breaker if we have to give it up. Thus, we are left with several principles, including CL, IP, and LW, that are of interest, but should probably not be regarded as obligatory, due to their restrictiveness. Given the plausibility of Z, IA also seems overly restrictive, and should also be regarded as negotiable.

4 Belief and degree of belief aggregation together

I now consider some possibilities for the coordinated aggregation of beliefs and degrees of belief. My basic assumption is that rational beliefs and rational degrees of belief are related to each other according to the Lockean Thesis.¹⁴ In particular, I assume a context dependent version of the Lockean Thesis that says that for every individual/collective there is a bound r such that for each proposition, φ, it is rational for the individual/collective to believe φ if and only if the individual’s/collective’s rational degree of belief in φ is at least r. As shown by Leitgeb (2014), the satisfaction of the Lockean Thesis is closely related to the notion of p-stability:

Definition

A proposition φ is p-stable with respect to a probability function, p, if and only if for all S: if φ∩S ≠ ∅ and p(S) > 0, then p(φ|S) > 0.5.

Leitgeb (2014) has shown that if we embrace (1) consistency and deductive closure for belief sets, (2) probabilistic coherence for degrees of belief, and (3) the Lockean Thesis, then the strongest proposition believed by any given agent must be p-stable, where p is the degree of belief function for the respective agent. Furthermore, an agent will satisfy the Lockean Thesis with the bound r if and only if the strongest proposition, φ, believed by the agent is p-stable with probability at least r, and all other propositions that are p-stable are deductive consequences of φ, or have probability less than r. Given the preceding fact, I adopt the following criterion for the aptness of a belief function, b, for a probability function, p, relative to a bound r:

Definition

〈b, p〉 is Lockean at r if and only if (i) p(φ_b) ≥ r, (ii) φ_b is p-stable, and (iii) for all ψ: if ψ is p-stable, then φ_b ⊆ ψ or P(ψ) < r.

The goal of the present article is to canvass the possibility of instituting constraints on belief and degree of belief aggregation that are compatible with the Lockean Thesis. To simplify matters, I will limit my interest to pairs of aggregation functions that ensure the preservation of the satisfaction of the Lockean Thesis, under selected ‘appropriate conditions’, in the following sense: If the Lockean Thesis is satisfied by (the doxastic state of) each member of a group, and other appropriate conditions obtain, then the Lockean Thesis is satisfied by (the doxastic state of) the collective. A straightforward principle of the preceding sort omits any demand that appropriate conditions obtain, and simply demands that if the Lockean Thesis is satisfied by each member of a group, then the Lockean Thesis is satisfied by the collective. In other words:

Strict Preservation of the Locke an Thesis (SL)

For all B and P: if for all i: there exists an r: 〈b_i, p_i〉 is Lockean at r, then there exists an r: 〈b_B, p_P〉 is Lockean at r.

Notice that the antecedent of SL is very ‘flexible’ concerning which belief sets are compatible with which degrees of belief. Consider, for example, p = 〈0.993, 0.004, 0.002, 0.001〉, along with b₁ = 〈1, 0, 0, 0〉, b₂ = 〈1, 1, 0, 0〉, b₃ = 〈1, 1, 1, 0〉, and b₄ = 〈1, 1, 1, 1〉. Notice that 〈b₁, p〉 is Lockean at r = 0.993, 〈b₂, p〉 is Lockean at r = 0.997, 〈b₃, p〉 is Lockean at r = 0.999, and 〈b₄, p〉 is Lockean at r = 1. The flexibility of the relation between belief and degree of belief tolerated by SL allows agents with identical degrees of belief to adopt different beliefs and thereby exert differential impact on the beliefs of the collective. This is a good reason to canvas alternatives to SL. The flexibility of SL also yields the demand for a very incredulous belief set aggregation function, typically demanding that the collective suspend judgment regarding all contingent propositions.

An attractive alternative to SL is motivated by the idea that for every context, there is a single Lockean threshold, r, that applies to all individuals in that context. For any such context, it is plausible to demand that if each individual in the group satisfies the Lockean Thesis with the appropriate threshold r, then the collective should also satisfy the Lockean Thesis with the threshold r. We may express the present requirement more precisely, as a collection of aggregation principles for respective values of r:

Preservation of the Lockean Thesis at Level r (L _r )

For all B and P: if for all i: 〈b_i, p_i〉 is Lockean at r, then 〈b_B, p_P〉 is Lockean at r.

While the preceding constraints are appealing, they are incompatible with reasonable aggregation functions for belief and degree of belief, as illustrated by the following impossibility result:

Theorem 1

For all r: if 0.5 < r < 1, then {U_b, A_b, N_b, U_p, A_p, N_p, L_r} is inconsistent.

Theorem 1 shows that it would be too much to demand the satisfaction of instances of L_r. As an alternative, I will consider another principle that places different demands on when and how a collective should satisfy the Lockean Thesis. As a preliminary, I adopt a particular reductive thesis concerning the relationship between belief and degree of belief. According to this reductive thesis, an agent, i, counts as believing a proposition, φ, just in case φ is a logical consequence of the strongest proposition, φ_bi, that is p_i-stable, where p_i is i’s degree of belief function. Any agent who conforms to the present reductive thesis is credulous in the sense that she believes as many propositions as she can, while still adhering to the Lockean Thesis. The present conception of belief, which is endorsed by Arló-Costa and Pedersen (2012, p. 302), and entertained by Leitgeb (2013, pp. 1369–1370), is very attractive, assuming one wants to maintain the Lockean Thesis along with a reductive account of belief to degree of belief (cf. Cariani 2016, p. 402). This reductive thesis also provides us with the opportunity of combining the Lockean Thesis with reasonable principles of belief and degree of belief aggregation. In order to apply the reductive thesis, I introduce the following definition, which applies to a pair consisting of a belief function and a degree of belief function:

Definition

〈b, p〉 is credulous Lockean (abbreviated CL(b, p)) if and only if (1) φ_b is p-stable, and (2) for all S: if S is a subset of Π and ∪S is p-stable, then φ_b ⊆ ∪S.

Since there is a strongest p-stable proposition for each probability function p (Leitgeb 2014), it follows that for every p there is a unique belief function, b, such that 〈b, p〉 is credulous Lockean. Regarding the joint aggregation of beliefs and degrees of belief, I now propose the following principle:

Preservation of Lockean Credulity (PLC):

For all B, P: if for all i: CL(b_i, p_i), then CL(b_B, p_P).

It is demonstrable that PLC is consistent with the core principles of belief and degree of belief aggregation that were introduced in Sects. 2 and 3:

Theorem 2

{U_b, A_b, N_b, U_p, A_p, N_p, PLC} is consistent.

Theorem 2 follows directly from the following (far more general) result:

Theorem 3

For all F: if {F = F_bel, U_b, A_b, N_b} is consistent, then {F = F_bel, U_p, A_p, N_p, PLC} is consistent.¹⁵

In considering Theorem 3, note that a statement of the form “F = F_bel” expresses that the particular function F is the ‘correct’ belief aggregation function F_bel. So Theorem 3 tells us that the conjunction U_p, A_p, N_p, and PLC is compatible with any choice of belief aggregation function, so long as that function satisfies U_b, A_b, and N_b. In other words, Theorem 3 shows that our options are completely open regarding what further constraints we may adopt regarding F_bel, given our commitment to the conjunction U_p, A_p, N_p, and PLC. On the other hand, our options are far more constrained when it comes to F_prob. For example, PLC (in conjunction with other reasonable principles) is incompatible with linear weighting, LW, and Irrelevance of Alternatives, IA:

Theorem 4

{U_b, A_b, N_b, U_p, LW, PLC} is inconsistent.

Corollary

{U_b, A_b, N_b, U_p, IA, Z_p, PLC} is inconsistent.¹⁶

The failure of PLC to cohere with IA and LW is inconvenient, but tolerable to the degree that IA and LW are dubitable.¹⁷ Despite the failure of PLC to cohere with IA and LW, it is demonstrable that PLC does cohere with other, less dubitable, principles. In fact, if we wish to maintain the claim that PLC is compatible with reasonable aggregation functions, it is essential to go beyond Theorem 3, since the ‘substantive’ principles cited by Theorem 3, namely, A_b, N_b, A_p, and N_p, only require that acceptable aggregation functions be indifferent to the way that individuals and the elements of Π are ordered. Reasonable aggregation functions would also incorporate requirements to the effect that the ‘direction’ of the attitudes of the individuals in a collective exert the right sort of impact on the attitudes of the collective. The following four principles encapsulate some important ‘directionality’ requirements:

Unanimity (UN _b ):

For all B, j: if for all i: $n_{ij}$ = 0, then $n_{j}$ = 0, and if for all i: $n_{ij}$ = 1, then $n_{j}$ = 1.

Weak Dominance (WD _b ):

For all B, j, k: if for all i: $n_{ij}$ ≥ $n_{ik}$, then $n_{j}$ ≥ $n_{k}$.

Unanimity (UN _p ):

For all P, j: if for all i: $r_{ij}$ = 0, then $r_{j}$ = 0, and if for all i: $r_{ij}$ = 1, then $r_{j}$ = 1.¹⁸

Weak Dominance (WD _p ):

For all P, j, k: if for all i: $r_{ij}$ ≥ $r_{ik}$, then $r_{j}$ ≥ $r_{k}$.

The compatibility of PLC with the preceding principles is encapsulated by the following theorems:

Theorem 5

For all F: if {F = F_bel, U_b, A_b, N_b, UN_b} is consistent, then {F = F_bel, U_p, A_p, N_p, UN_p, PLC} is consistent.

Theorem 6

For all F: if {F = F_bel, U_b, A_b, N_b, WD_b} is consistent, then {F = F_bel, U_p, A_p, N_p, WD_p, PLC} is consistent.

Theorem 7

For all F: if {F = F_bel, U_b, A_b, N_b, UN_b, WD_b} is consistent, then {F = F_bel, U_p, A_p, N_p, UN_p, WD_p, PLC} is consistent.¹⁹

Although Theorems 5–7 are reassuring, it is demonstrable that both Independence Preservation (IP) and Commutativity with Learning (CL) are inconsistent with PLC, in the presence of other reasonable principles, as expressed by the following theorems (where Z_b consists of the first conjunct of UN_b):

Theorem 8

{U_b, A_b, N_b, Z_b, U_p, PLC, CL} is inconsistent.

Theorem 9

{U_b, A_b, N_b, Z_b, U_p, A_p, N_p, PLC, IP} is inconsistent.

If one doubts that Z_b is plausible, then one might dismiss the preceding theorems. Note, however, that maintaining either {U_b, A_b, N_b, U_p, PLC, CL} or {U_b, A_b, N_b, U_p, A_p, N_p, PLC, IP} (whose consistency is easily demonstrable²⁰) will require frequent violations of Z_b. Accepting such violations of Z_b, in the presence of A_b and N_b, will lead to a very incredulous belief set aggregation function (i.e., a belief set aggregation function that typically demands that the collective suspend judgment regarding all contingent propositions).

5 Conclusion

The present paper began by introducing the ‘joint problem’ of aggregating beliefs and degrees of belief. The joint problem is significant, because it is a potential source of constraints upon both belief aggregation and degree of belief aggregation. Indeed, if rational degree of belief and rational belief are subject to mutual constraints, then care must be taken in how we aggregate beliefs and degrees of belief, lest the result of joint aggregation be collective beliefs and degrees of belief that fail to satisfy the constraints.

In exploring the joint problem, the main goal of the paper was to investigate whether the Lockean Thesis is compatible with reasonable belief and degree of belief aggregation functions. While the Lockean Thesis is dubitable (see, e.g., Buchak 2014), it is typically regarded as highly attractive, because, among other reasons, it forbids cases where the rational degree of belief in one proposition, φ, is greater than the rational degree of belief in another proposition, ψ, and yet it is rational to believe ψ and it is not rational to believe φ. As shown by Leitgeb (2014), the Lockean Thesis is also very demanding: Assuming (1) consistency and deductive closure for belief sets, and (2) probabilistic coherence for degrees of belief, the Thesis implies that the determination of whether it is rational for an agent (or a collective) to believe a respective proposition is dependent, not just upon the agent’s degree of belief in the proposition, but also upon the agent’s degrees of belief in other propositions and upon the very possibilities that are individuated by the agent’s degree of belief function. Given the demandingness of the Lockean Thesis, it would have been reasonable to expect the Thesis to place significant constraints upon belief aggregation and/or degree of belief aggregation. The results of the preceding section bear out this expectation.

In evaluating the tenability of the Lockean Thesis in the context of the joint problem, I considered three ‘preservationist’ principles concerning when and how acceptable aggregation functions should yield collective beliefs and degrees of belief that satisfy the Lockean Thesis. Two of the principles proved to be unsatisfactory. One principle, SL, is unappealing, because it permits individuals within a group to have different beliefs, while having identical degree of belief functions. A second principle, L_r (for any setting of r in (0.5, 1)), is just too demanding, as it would require that we abandon at least one non-negotiable aggregation principle (as illustrated by Theorem 1). In the end, my investigation focused on a principle called Preservation of Lockean Credulity (PLC), though it is possible that I have overlooked other principles that warrant exploration.

As encapsulated by PLC, Theorem 7 shows that the Lockean Thesis is compatible with an ensemble of principles that may plausibly be regarded as specifying the non-negotiable core of belief and degree of belief aggregation, namely: universality of inputs (U_b and U_p), anonymity (A_b and A_p), neutrality (N_b and N_p), unanimity (UN_b and UN_p), and weak dominance (WD_b and WD_p). Theorem 7 also shows that our options are very open regarding the sort of belief aggregation function we may adopt, assuming a commitment to PLC. On the other hand, PLC closes off some other significant principles concerning degree of belief aggregation: Theorem 4 and its corollary show that Irrelevance of Alternatives (IA) and Linear Weighting (LW) are problematic, while Theorems 8 and 9 show that Independence Preservation (IP) and Commutativity with Learning (CL) are problematic. The impossibility results presented in Sect. 4 (i.e., Theorems 4, 8, and 9) bear out the claim that acceptance of the Lockean Thesis would place significant constraints on what degree of belief aggregation function one may adopt. On the other hand, the possibility results presented in Sect. 4 (i.e., Theorems 3, 5, 6, and 7) show that the cost of accepting the Lockean Thesis might well be tolerable.

Appendices

Appendix A: Lin and Kelly’s Symmetric Camera Shutter Rule

Motivated by the fact that there is no consistent context independent version of the Lockean Thesis with a threshold r < 1, Lin and Kelly (2012) proposed what they call the symmetric camera shutter rule. Like the Lockean Thesis the rule of Lin and Kelly includes a parameter r (0 < r < 1) that reflects an agent’s degree of credulity. Given a particular value r, the symmetric camera shutter rule demands the following relation between belief an degree of belief, where σ(w_i) = p(w_i)/max_j p(w_j):

$$ b\left( {w_{i} } \right) = 0\;if\;and\;only\;if\;\sigma\left( {w_{i} } \right) \le 1 - r. $$

In line with this condition, we can say that 〈b, p〉 is shutter fit at r (abbreviated SF_r(b, p)) just in case for all i: b(w_i) = 0 if and only if σ(w_i) ≤ 1  − r.

It is straightforward to define analogues of Lockean Credulity and PLC that apply to the symmetric camera shutter rule:

Definition

〈b, p〉 is credulous shutter fit (abbreviated CSF(b, p)) if and only if (1) there exists an r (0 < r < 1): 〈b, p〉 is shutter fit at r, and (2) for all b′: if φ_b′ ⊂ φ_b, then for all s (0 < s < 1): 〈b′, p〉 is not shutter fit at s.

Preservation of Shutter Fit Credulity (PSFC):

For all B, P: if for all i: CSF(b_i, p_i), then CSF(b_B, p_P).

It is, then, straightforward to demonstrate the analogue of Theorem 3 (and similarly for Theorems 5, 6, and 7):

Theorem 10

For all F: if {F = F_bel, U_b, A_b, N_b} is consistent, then {F = F_bel, U_p, A_p, N_p, PSFC} is consistent.²¹

Beyond the preceding, it turns out that the symmetric camera shutter rule is ‘more stable’ than the Lockean Thesis, as demonstrated by the behavior of the following analogues of the instances of L_r:

Preservation of Shutter Fit at Level r (SF_r):

For all B and P: if for all i: 〈b_i, p_i〉 is shutter fit at r, then 〈b_B, p_P〉 is shutter fit at r.

Unlike instances of L_r (for all r in (0.5, 1)), instances of SF_r are consistent with {U_b, A_b, N_b, U_p, A_p, N_p}, and more generally:

Theorem 11

For all F, r in (0, 1): if {F = F_bel, U_b, A_b, N_b} is consistent, then {F = F_bel, U_p, A_p, N_p, SF_r} is consistent.

However, both PSFC, along with all instances of SF_r, are still incompatible with LW (in the presence of other plausible principles):

Theorem 12

{U_b, A_b, N_b, U_p, A_b, N_b, LW, PSFC} is inconsistent.²²

Theorem 13

For all r in (0, 1): {U_b, A_b, N_b, U_p, LW, SF_r} is inconsistent.

Proof

For all r in (0, 1), we show that {U_b, A_b, N_b, U_p, LW, SF_r} is inconsistent. Consider an arbitrary r in (0, 1). Take the least n such that ((1 − (³√(n)/n))/(n − 1))/(³√(n)/n) ≤ 1 − r. Let |Π| = n. Let B = 〈b₁, …, b_n〉, where, for all i, b_i has the value 1 in the ith position, and the value 0 in all other positions. Let P = 〈p₁, …, p_n〉, where p₁ has the value v in the first position, and the value (1 − v)/(n − 1) in all other positions, where v = ³√(n)/n. For all i > 1: let p_i have the value 1 in the ith position and the value 0 in all other positions. Notice that A_b and N_b imply that b_B is a series of 1 s, and so b_B(w₁) = 1. Next notice that for all i: 〈b_i, p_i〉 is shutter-fit at r. (In particular, for all i > 1: σ_p1(w_i) = (1 − (³√(n)/n))/(n − 1))/(³√(n)/n) ≤ 1 − r.) So SF_r implies that 〈b_B, p_B〉 is shutter-fit at r. For reasons that follow, this implies that c₁ > 1/n. Assume c₁ ≤ 1/n, then p_P(w₁) ≤ (³√(n)/n)(1/n), and there exists an i such that p_P(w_i) ≥ (1 − (³√(n)/n))/(n − 1))(1/n) + 1/n, so that σ_P(w₁) ≤ (³√(n)/n)(1/n)/((1 − (³√(n)/n))/(n − 1))(1/n) + 1/n). But for all n > 1: (³√(n)/n)(1/n)/((1 − (³√(n)/n))/(n − 1))(1/n) + 1/n) ≤ ((1 − (³√(n)/n))/(n − 1))/(³√(n)/n). Assume not. Then for some n > 1: ³√(n²)((n −2)/n) + ³√(n)((n + 1)/n) − n > 0, which is absurd. So σ_P(w₁) ≤ 1 − r. The latter implies that b_B(w₁) = 0, which contradicts b_B(w₁) = 1. So c₁ > 1/n. By similar reasoning concerning permutations of B and P, it follows that for all i: c_i > 1/n, which contradicts LW.□

PSFC, along with all instances of SF_r, are also incompatible with CL and IP (in the presence of reasonable principles):

Theorem 14

{U_b, A_b, N_b, Z_b, U_p, PSFC, CL} is inconsistent.

Theorem 15

For all r in (0, 1): {U_b, A_b, N_b, Z_b, U_p, SF_r, CL} is inconsistent.

Theorem 16

{U_b, A_b, N_b, Z_b, U_p, A_p, N_p, PSFC, IP} is inconsistent.

Theorem 17

For all r in (0, 1): {U_b, A_b, N_b, Z_b, U_p, A_p, N_p, SF_r, IP} is inconsistent.

The proofs of Theorems 8 and 9 are annotated to indicate the modifications required to prove Theorems 14, 15, 16, and 17.

Appendix B: Proofs

Fact 2.

If U_b, A_b, and S, then for all B, φ: b_B(φ) = 1 if and only if for all b_i in B: b_i(φ) = 1.

Proof

The right to left direction of the consequent follows from the consistency requirement on b_B. To establish the left to right direction, it is sufficient to show that for all n, m: if 0 ≤ m < n, then there exists some sets of belief functions B, such that $n_{1j}$ + … + $n_{nj}$ = n − m, and $n_{j}$ = 1. If there are such sets of belief functions, then we have, for all m, such that 0 ≤ m < n, a proposition ¬w_j, that is believed by m of n agents, but not by the collective. It is straightforward to show that all of the needed B exist. By U_b, we have for all n and m, such that 0 ≤ m < n, some B such that the columns of B are the set of permutations of m 0 s and n − m 1 s. For each such B, $n_{i}$ = 1, for all $n_{i}$ in b_B, given A_b and N_b. The preceding holds, since, for each such B, each $n_{i}$ must take the same value, given A_b and N_b, which must be 1, by the consistency requirement on b_B.□

Theorem 1

For all r: if 0.5 < r < 1, then {U_b, A _b, N_b, U_p, A_p, N_p, L_r} is inconsistent.

Proof

Notice that for all r: if 0.5 < r < 1, then there exists n and ε: 0 < ε < 1/n and r = ((n − 1)/n) + ε. In light of the preceding, consider the instances of the following schema, for all n and ε: 0 < ε < 1/n. Let Π = {w₁, …, w_n}. Let B_n = 〈b₁, …, b_n〉, where b_i has the value 0 in the ith position, and the value 1 in all other positions. Let P_n = 〈p₁, …, p_n〉, where p_i has the value (1/n) − ε in the ith position, and the value (1/n) + (ε/(n − 1)) in all other positions. In this case, A_b and N_b imply that b_Bn has the value 1 in every position, and A_p and N_p imply p_Pn has the value 1/n in every position. Notice that for all i: 〈b_i, p_i〉 is Lockean at ((n − 1)/n) + ε, but 〈b_Bn, p_Pn〉 is not Lockean at ((n − 1)/n) + ε.□

Theorem 3

For all F: if {F = F_bel, U_b, A_b, N_b} is consistent, then {F = F_bel, U_p, A_p, N_p, PLC} is consistent.

Proof

To demonstrate the result, we show how to define a function F_prob that satisfies U_p, A_p, N_p, and PLC, given any aggregation function F_bel that satisfies A_b and N_b. Given any P, we define B* = 〈b*₁,…, b*_n〉 to be the (unique) set of belief functions, such that for all i: CL(b*_i, p_i) [or such that CSF(b*_i, p_i) or SF_r(b*_i, p_i) for the proofs of Theorems 12 and 13, respectively]. We then define F_prob by $r_{j}$ = 1/($n^{*}_{1}$ +···+ $n^{*}_{k}$), if $n^{*}_{j}$ = 1, and $r_{j}$ = 0, if $n^{*}_{j}$ = 0 (where $n^{*}_{1}$ through $n^{*}_{k}$ are determined via F_bel, given U_b). [Notice that, in the preceding step, we require that |{ $n^{*}_{j}$ | $n^{*}_{j}$ = 1}| is finite, which holds if Π is finite, but also assuming Z_b, since all p-stable sets are finite (Leitgeb 2013, p. 1366).] It follows immediately from the definition of F_prob that the combination of F_bel and F_prob satisfy PLC [or PSFC or SF_r, respectively]. The inputs to F_prob are not restricted; so U_p is also satisfied. A_p requires that for all P and g: if g: {1, …, n} → {1, …, n} is a permutation, and P′ = 〈p_g(1), …, p_g(n)〉, then p_P′ = p_P. We assume for arbitrary P and g, that g: {1, …, n} → {1, …, n} is a permutation, and P′ = 〈p_g(1), …, p_g(n)〉. We show that p_P′ = p_P. To begin with, notice that P determines B*, and P′ determines B′*, so that b′*_i = b*_g(i). But A_b, so B′* = B*, and thus p_P′ = p_P, given the definition of F_prob. So A_p is satisfied. N_p requires that for all P: if f: {1, …, k} → {1, …, k} is a permutation, P′ = 〈p′₁, …, p′_n〉, and for all i: p′_i = 〈$r_{if\left( 1 \right)}$, …, $r_{if\left( k \right)}$〉, then p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉. We assume for arbitrary P and f, that f: {1, …, k} → {1, …, k} is a permutation, P′ = 〈p′₁, …, p′_n〉, and for all i: p′_i = 〈$r_{if\left( 1 \right)}$, …, $r_{if\left( k \right)}$〉. We show that p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉. To begin with, notice that P determines B*, and P′ determines B′*, so that b′*_i = b*_g(i). But A_b, so B′* = B*, and thus p_P′ = p_P, given the definition of F_prob. So A_p is satisfied. N_p requires that for all P: if f: {1, …, k} → {1, …, k} is a permutation, P′ = 〈p′₁, …, p′_n〉, and for all i: p′_i = 〈$r_{if\left( 1 \right)}$, …, $r_{if\left( k \right)}$〉, then p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉. We assume for arbitrary P and f, that f: {1, …, k} → {1, …, k} is a permutation, P′ = 〈p′₁, …, p′_n〉, and for all i: p′_i = 〈$r_{if\left( 1 \right)}$, …, $r_{if\left( k \right)}$〉. We show that p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉. To begin with, notice that P determines B*, and P′ determines B′*, such that b*_i = 〈$n_{i1}$, …, $n_{ik}$〉 and b′*_i = 〈$n_{if\left( 1 \right)}$, …, $n_{if\left( k \right)}$〉. But N_b, so p_B′* = 〈$n_{f\left( 1 \right)}$, …, $n_{f\left( k \right)}$〉. So p_P′ = 〈$r_{f\left( 1 \right)}$, …, $r_{f\left( k \right)}$〉, given F_prob. So N_p is satisfied.□

Theorem 4

{U_b, A_b, N_b, U_p, LW, PLC} is inconsistent.

Proof

Let Π = {w₁, w₂}. Consider B₁ = 〈〈1, 0〉, 〈0, 1〉〉, and P₁ = 〈〈0.51, 0.49〉, 〈0.01, 0.99〉〉. Next consider B₂ = 〈〈1, 0〉, 〈0, 1〉〉, and P₂ = 〈〈0.99, 0.01〉, 〈0.49, 0.51〉〉. Notice that A_b and N_b imply that b_B1 = b_B2 = 〈1, 1〉. Notice that PLC (and similarly PSFC) imply that p_P1 = 〈0.5, 0.5〉, which, according LW, holds only if 0.51·c₁ + 0.01·c₂ = 0.5, and so where c₁ = 0.98 and c₂ = 0.02. But PLC (and similarly PSFC) also imply that p_P2 = 〈0.5, 0.5〉, which, according LW, holds only if 0.01·c₁ + 0.51·c₂ = 0.5, and so where c₁ = 0.02 and c₂ = 0.98, which is a contradiction.□

Theorem 5

For all F: if {F = F_bel, U_b, A_b, N_b, UN_b} is consistent, then {F = F_bel, U_p, A_p, N_p, UN_p, PLC} is consistent.

Proof

The proof proceeds as the proof of Theorem 5, save that we make the further assumption that UN_b, and show that F_prob satisfies UN_p. Assume not. Then there is a case where (i) $r_{j}$ ≠ 0 and for all i: $r_{ij}$ = 0, or a case where (ii) $r_{j}$ ≠ 1 and for all i: $r_{ij}$ = 1. In case (i), we have for all i: $n^{*}_{ij}$ = 0, given for all i: $r_{ij}$ = 0 (by the definition of B*). So $n^{*}_{j}$ = 0, given UN_b. And so $r_{j}$ = 0, by the definition of F_prob. In case (ii), we have for all i: $n^{*}_{ij}$ = 1 and for all i, k ≠ j: $n^{*}_{ik}$ = 0, given for all i: $r_{ij}$ = 1 (by the definition of B*). So $n^{*}_{j}$ = 1, and for all k ≠ j: $n^{*}_{k}$ = 0, given U_b and UN_b. So $r_{j}$ = 1, by the definition of F_prob.□

Theorem 6

For all F: if {F = F_bel, U_b, A_b, N_b, WD_b} is consistent, then {F = F_bel, U_p, A_p, N_p, WD_p, PLC} is consistent.

Proof

The proof proceeds as the proof of Theorem 5, save that we make the further assumption that WD_b, and show that F_prob satisfies WD_p. Let P, j, and k be arbitrary, with for all i: $r_{ij}$ ≥ $r_{ik}$. In that case, for all i: $n^{*}_{ij}$≥ $n^{*}_{ik}$, by the definition of F_prob. So $n^{*}_{j}$≥ $n^{*}_{k}$, given WD_b. So $r_{j}$ ≥ $r_{k}$, by the definition of F_prob.□

Theorem 8

{U_b, A_b, N_b, Z_b, U_p, PLC, CL} is inconsistent.

Proof

Let Π = {w₁, w₂, w₃}. Consider B = 〈〈1, 0, 0〉, 〈0, 0, 1〉〉, and P = 〈〈0.9, 0.09, 0.01〉, 〈0.01, 0.09, 0.9〉〉. Notice that A_b, N_b, and Z_b imply that b_B = 〈1, 0, 1〉. Without loss of generality, assume that p_p = 〈a, b, c〉. Then PLC implies that a > b, since CL(〈1, 0, 0〉, 〈0.9, 0.09, 0.01〉) and CL(〈0, 0, 1〉, 〈0.01, 0.09, 0.99〉) [and similarly CSF(〈1, 0, 0〉, 〈0.9, 0.09, 0.01〉) and CSF(〈0, 0, 1〉, 〈0.01, 0.09, 0.99〉)²³]. Now consider P′ = 〈〈90/99, 9/99, 0〉, 〈1/10, 9/10, 0〉〉, and B′ = 〈〈1, 0, 0〉, 〈0, 1, 0〉〉. Notice that A_b, N_b, and Z_b imply that b_B′ = 〈1, 1, 0〉. Now notice that CL implies that p_p′ = 〈a/(a + b), b/(a + b), 0〉. Finally, notice that CL(〈1, 0, 0〉, 〈90/99, 9/99, 0〉) and CL(〈0, 1, 0〉, 〈1/10, 9/10, 0〉) imply that CL(〈1, 1, 0〉, 〈a/(a + b), b/(a + b), 0〉), which is absurd, since CL(〈1, 0, 0〉, 〈a/(a + b), b/(a + b), 0〉), given a > b [and similarly with CSF in place of CL].□

Theorem 9

{U_b, A_b, N_b, Z_b, U_p, A_p, N_p, PLC, IP} is inconsistent.

Proof

Let Π = {w₁, w₂, w₃, w₄}. Consider B = 〈〈0, 0, 0, 1〉, 〈1, 0, 0, 0〉〉, and P = 〈〈0.01, 0.09, 0.09, 0.81〉, 〈0.81, 0.09, 0.09, 0.01〉〉.²⁴ Notice that A_b, N_b, and Z_b imply that b_B = 〈1, 0, 0, 1〉. Now notice that A_p and N_p imply that p_P(w₁) = p_P(w₄) and p_P(w₂) = p_P(w₃), and this implies that p_P(w₁∪w₂) = p_P(w₁∪w₃) = 1/2. Now notice that CL(〈0, 0, 0, 1〉, 〈0.01, 0.09, 0.09, 0.81〉) and CL(〈〈1, 0, 0, 0〉, 〈0.81, 0.09, 0.9, 01〉) [and similarly CSF(〈0, 0, 0, 1〉, 〈0.01, 0.09, 0.09, 0.81〉) and CSF(〈1, 0, 0, 0〉, 〈0.81, 0.09, 0.09, 0.01〉)]. So PLC implies that CL(〈1, 0, 0, 1〉, P_P) [and similarly CSF(〈1, 0, 0, 1〉, P_P)], which implies that p_P(w₁) > p_P(w₂), and thus p_P(w₁) > 1/4. Finally, notice that p₁((w₁∪w₂)∩(w₁∪w₃)) = p₁(w₁∪w₂)p₁(w₁∪w₃) and p₂((w₁∪w₂)∩(w₁∪w₃)) = p₂(w₁∪w₂)p₁(w₁∪w₃). So IP implies that p_P((w₁∪w₂)∩(w₁∪w₃)) = p_P(w₁∪w₂)p_P(w₁∪w₃). But p_P((w₁∪w₂)∩(w₁∪w₃)) = p_P(w₁), and, since p_P(w₁∪w₂) = p_P(w₁∪w₃), p_P(w₁) = 1/4, which is absurd.□