Introduction

Analytical chemistry, specifically electroanalytical chemistry, plays an important role in the fields of biochemistry, pharmaceuticals, chemistry, environment science and food production. In recent decades, biosensors have emerged from the laboratories into the everyday lives of many millions of people around the world. An electroanalytical biosensor based on the enzyme-catalysis is an analytical device that uses biological enzymes to detect the presence of chemical molecules.

In the biosensor field, electrochemical techniques, such as cyclic voltammetry (CV), and electrochemical impedance spectroscopy (EIS), have been proven to be advantageous for developing new methods for the determination of pharmaceutical [1, 2], environmental [3] and food [4] samples. Therefore, several researchers have pursued the investigation of the equivalent circuit model for the interface that consists of the electrode geometry and electrolyte parameter. Recently, an ultrasensitive enzyme biosensor was developed [5,6,7,8,9,10,11].

Preparing a novel ultrasensitive biosensor may be very expensive, as it may require many laboratory experiments. Therefore, it is wise to conduct computational experiments prior to physical experiments, which necessitates mathematical modeling and simulations of the biosensor. In chemical engineering, modeling and simulation are important tools for engineers and scientists to better understand the behavior of chemical processes [12,13,14,15,16,17]. Modeling methods are very useful for the design and optimization of chemical plants, for process control, and for training of operators and operational planning [18,19,20,21,22].

Mathematical models of enzyme biosensor responses can be created by solving partial differential equations (PDE) of the substrate diffusion and the biocatalytical conversion with the initial and the boundary conditions. Theoretical modeling of time dependent nonlinear differential equations for the electrochemical enzyme biosensors implies the use of a nonlinear term related to the Michaelis–Menten kinetic scheme, which can be solved analytically and numerically. For this purpose, this paper derives an analytical expression for the concentrations of the substrate and product for application in highly sensitive enzyme biosensors using the standard method of inverting a Laplace transform according to the Heaviside expansion theorem.

Kinetics and mathematical model

Kinetics model

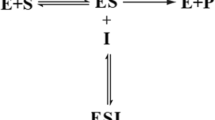
Electrochemical biosensors are constructed, for many cases, using a three-electrode system with a modified enzyme as the working electrode, Ag/AgCl as the reference electrode and platinum as the counter electrode. The use of electrochemical impedance spectroscopy (EIS) in this field may be applied to discriminate and quantify the different processes that determine a biosensor performance, such as the Ohmic resistance Rs, charge transfer resistance Rct, diffusion resistance Zw, and capacitance Cdl (Fig. 1). However, the kinetic model for an enzyme action, first elucidated by Michaelis and Menten (Eq. 1) suggests the binding of the free enzyme (E) to the reactant or substrate (S) forming an enzyme–substrate complex (ES). This complex undergoes a transformation, which releases the product (P) and enzyme (E) [23,24,25]. Note that substrate binding is reversible, but product release is not (Fig. 1).

$$E + S \begin{array}{*{20}c} {\mathop \to \limits^{k1} } \\ {\mathop \leftarrow \limits_{k2} } \\ \end{array} ES \mathop \to \limits^{k3} E + P$$
(1)

Here k1, k2 and k3 are the rate constants.

Fig. 1
figure 1

Kinetic reaction–diffusion in the biosensor process

Full size image

Mathematical model of highly sensitive biosensor

In biosensors, coupling of the substrate transport with the diffusion is described by Fick’s law with the enzyme-catalyzed reaction in the enzyme layer, which leads to the following equations:

$$\frac{{\partial c_{s} (x,t)}}{\partial t} = D_{s} \frac{{\partial^{2} c_{s} (x,t)}}{{\partial x^{2} }} - \frac{{ V_{m} c_{s} \left( {x,t} \right)}}{{k_{M} + c_{s} \left( {x,t} \right)}}$$
(2)
$$\frac{{\partial c_{p} (x,t)}}{\partial t} = D_{p} \frac{{\partial^{2} c_{p} (x,t)}}{{\partial x^{2} }} + \frac{{ V_{m} c_{s} (x,t)}}{{k_{M} + c_{s} \left( {x,t} \right)}}$$
(3)

Here x represents space between \(0\) and \(d\), with \(d\) is the thickness of the enzyme layer; \(c_{s} (x,t)\) and \(c_{p} (x,t)\) are the molar concentrations of the substrate \(S\) and the product \(P\) in the enzyme layer, respectively; \(V_{m}\) is the maximal enzymatic rate; \(k_{M}\) is the Michaelis constant; \(d\) is the thickness of the enzyme layer; and \(D_{s}\) and \(D_{p}\) are the diffusion coefficients.

For highly sensitive enzyme biosensors, the amount of substrate is small. Thus, the amount of the substrate \(c_{s}\) is negligible compared to the magnitude of The Michaelis constant, \(k_{M}\). Then, Eqs. 2 and 3 will be reduced to the following form:

$$\frac{{\partial c_{s} (x,t)}}{\partial t} = D_{s} \frac{{\partial^{2} c_{s} (x,t)}}{{\partial x^{2} }} - \frac{{ V_{m} }}{{k_{M} }}c_{s} \left( {x,t} \right)$$
(4)
$$\frac{{\partial c_{p} (x,t)}}{\partial t} = D_{p} \frac{{\partial^{2} c_{p} (x,t)}}{{\partial x^{2} }} + \frac{{ V_{m} }}{{k_{M} }}c_{s} \left( {x,t} \right)$$
(5)

With

$$\left\{ {\begin{array}{*{20}c} {c_{s} = 0, c_{p} = 0, t = 0; \quad 0 \le x \le d} \\ {\frac{{\partial c_{s} (x,t)}}{\partial x} = 0, c_{p} = 0, t > 0; \quad x = 0} \\ {c_{s} = c_{s}^{0} , c_{p} = 0, t > 0; \quad x = d} \\ \end{array} } \right.$$
(6)

Dimensionless form of the problem

The following parameters are used to convert the above Eqs. 4 and 5 into their normalized forms. We make the above nonlinear partial differential equations in a dimensionless form by defining the following parameters:

$$X = \frac{x}{d}, T = \frac{{D_{s} t}}{{d^{2} }}, C_{S} = \frac{{c_{s} }}{{c_{s}^{0} }}, C_{P} = \frac{{c_{p} }}{{c_{s}^{0} }}, D_{s} = D_{p} = D, a = \frac{{ V_{m} d^{2} }}{{D k_{M} }}$$

Then, Eqs. 4 and 5 reduce to the following dimensionless form:

$$\frac{{\partial C_{S} (X,T)}}{\partial T} = \frac{{\partial^{2} C_{S} (X,T)}}{{\partial X^{2} }} - a C_{S} \left( {X,T} \right)$$
(7)
$$\frac{{\partial C_{P} (X,T)}}{\partial T} = \frac{{\partial^{2} C_{P} (X,T)}}{{\partial X^{2} }} + a C_{S} \left( {X,T} \right)$$
(8)

The dimensionless initial and boundary conditions are:

$$\left\{ {\begin{array}{*{20}c} {\,C_{S} = 0,C_{P} = 0,T = 0;} & {0 \le X \le 1} \\ {\frac{{\partial C_{S} (X,T)}}{{\partial X}} = 0,C_{P} = 0,T > 0;} & {X = 0} \\ {C_{S} = 1,C_{P} = 0,T > 0;} & {X = 1} \\ \end{array} } \right.$$
(9)

Analytical solution of the reaction–diffusion problem for highly sensitive biosensor

By applying Laplace transformation to the partial differential Eqs. 7 and 8 and using the conditions Eq. 9, the following transformed differential equations are obtained. The expansion method and inversion of the Laplace transform are used to solve this system.

Analytical solution of kinetic of substrate concentration

The Laplace transform reduces the partial differential equation in Eq. 7 to the an ordinary differential equation (Eq. 10):

$$\frac{{\partial^{2} \overline{{C_{S} }} \left( {X,s} \right)}}{{\partial X^{2} }} - \left( {s + a} \right)\overline{{C_{S} }} \left( {X,s} \right) = 0$$
(10)

With boundary conditions:

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \overline{{C_{S} }} (X,s)}}{\partial X} = 0, } & {X = 0} \\ {\overline{{C_{S} }} = \frac{1}{s},} & {X = 1} \\ \end{array} } \right.$$
(11)

The general solution of this equation is:

$$\overline{{C_{S} }} \left( {X,s} \right) = A_{1} \left( s \right) e^{{\sqrt {s + a} X}} + A_{2} \left( s \right) e^{{ - \sqrt {s + a} X}}$$
(12)

With boundary conditions at \(X = 0\) and \(X = 1\), the solution becomes:

$$\overline{{C_{S} }} \left( {X,s} \right) = \left( {\frac{1}{ s} \frac{1}{{ e^{{\sqrt {s + a} }} + e^{{ - \sqrt {s + a} }} }}} \right)\left[ {e^{{\sqrt {s + a} X}} + e^{{ - \sqrt {s + a} X}} } \right]$$
(13)

We observe that the solution becomes a new function \(F\left( {X,s} \right)\):

$$F\left( {X,s} \right) = \overline{{C_{S} }} \left( {X,s} \right) = \frac{{e^{{\sqrt {s + a} X}} + e^{{ - \sqrt {s + a} X}} }}{{s (e^{{\sqrt {s + a} }} + e^{{ - \sqrt {s + a} }} )}}$$
(14)

The standard method of inverting a Laplace transform makes use of the residue theorem [26]. According the Heaviside expansion theorem [27], the inverse transform of F(s) are given by the residue theorem. That is, let:

$$F\left( {X,s} \right) = \frac{{P\left( {X,s} \right)}}{{Q\left( {X,s} \right)}}$$
(15)

Here, we have:

$$P\left( {X,s} \right) = e^{{\sqrt {s + a} X}} + e^{{ - \sqrt {s + a} X}}$$
(16)
$$Q\left( {X,s} \right) = s \left( {e^{{\sqrt {s + a} }} + e^{{ - \sqrt {s + a} }} } \right)$$
(17)

On the other hand, the solution of inverting a Laplace transform is:

$$f\left( t \right) = L^{ - 1} \left\{ {F\left( s \right)} \right\} = \mathop \sum \limits_{1}^{\infty } \rho_{n} (t)$$
(18)

If \(S_{n}\): is a simple pole of F(s), then \(\rho_{n} (t)\) is given by:

$$\rho_{n} \left( t \right) = \frac{{P\left( {S_{n} } \right)}}{{Q^{ '} \left( {S_{n} } \right)}} e^{{S_{n} t }}$$
(19)

Here \(Q^{'} \left( {s_{n} } \right)\), denoted \(\frac{dQ}{dt}\), is evaluated at the singular point of interest.

Recall that:

$$\frac{P\left( s \right)}{{Q^{ '} \left( {s_{n} } \right)}} = \mathop {\lim }\limits_{{s \to s_{n} }} \frac{P\left( s \right)}{{\left[ {\frac{{Q\left( s \right) - Q(s_{n} )}}{{s - s_{n} }}} \right]}} = \mathop {\lim }\limits_{{s \to s_{n} }} (s - s_{n} )\frac{P\left( s \right)}{Q\left( s \right)}$$
(20)

Therefore, the Q simple zero is located at:

  • The first simple pole when S = 0

$$\rho_{0} \left( t \right) = \mathop {\lim }\limits_{s \to 0} (s - 0)\frac{P\left( s \right)}{Q\left( s \right)} e^{st } = \frac{{e^{\sqrt a X} + e^{ - \sqrt a X} }}{{ (e^{\sqrt a } + e^{ - \sqrt a } )}}$$
(21)

  • The second pole: \(e^{{\sqrt {s + a} }} + e^{{ - \sqrt {s + a} }} = 0\)

When \(s_{n} = \frac{{ - \pi^{2} \left( {2n + 1} \right)^{2} - 4a}}{4}\)

Applying Eq. 19 gives:

$$\rho_{n} \left( T \right) = \frac{{\pi (2n + 1)\left( { - 1} \right)^{ - n} \left( {cos\frac{{\pi \left( {2n + 1} \right)}}{2}X} \right)}}{{ - (\pi^{2} \left( {2n + 1} \right)^{2} + 4a)/4}} e^{{\frac{{ - \pi^{2} \left( {2n + 1} \right)^{2} - 4a}}{4}T }}$$
(22)

We can use these results to invert a Laplace transform for the analytical solution of the substrate concentration. The analytical solution is given by:

$$C_{S} \left( {X,T} \right) = \frac{{e^{\sqrt a X} + e^{ - \sqrt a X} }}{{ \left( {e^{\sqrt a } + e^{ - \sqrt a } } \right)}} - 2 \mathop \sum \limits_{1}^{\infty } \left( { - 1} \right)^{ - n} \frac{{ \lambda_{n} e^{ - aT } }}{{\lambda_{n}^{2} + a}} cos(\lambda_{n} X) e^{{ - \lambda_{n}^{2} T }}$$
(23)

With: \(\lambda_{n} = \pi \left( {n + 1/2} \right)\)

Analytical solution of the kinetic product concentration

After adding Eqs. 7 and 8:

$$\frac{{\partial (C_{S} \left( {X,T} \right) + C_{P} \left( {X,T} \right))}}{\partial T} = \frac{{\partial^{2} (C_{S} \left( {X,T} \right) + C_{P} \left( {X,T} \right))}}{{\partial X^{2} }}$$
(24)

We need to introduce a new function \(C_{M} \left( {X,T} \right)\) as:

$$C_{M} \left( {X,T} \right) = C_{S} \left( {X,T} \right) + C_{P} \left( {X,T} \right)$$
(25)

We obtain a system of ordinary differential equations:

$$\frac{{\partial C_{M} (X,T)}}{\partial T} = \frac{{\partial^{2} C_{M} (X,T)}}{{\partial X^{2} }}$$
(26)

By applying the Laplace transformation in Eq. 26:

$$s \overline{{C_{M} }} \left( {X,s} \right) = \frac{{\partial^{2} \overline{{C_{M} }} \left( {X,s} \right)}}{{\partial X^{2} }}$$
(27)

With

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial \overline{{C_{M} }} \left( {X,s} \right)}}{\partial X} = 0,} & \quad ;\;{X = 0} \\ { \overline{{C_{M} }} = \frac{1}{s}, } & \quad \; {X = 1} \\ \end{array} } \right.$$
(28)

The analytical solution of Eq. 27 with the initial and boundary conditions of Eq. 28 in the form:

$$\overline{{C_{M} }} \left( {X,s} \right) = F\left( {X,s} \right) = \frac{{e^{\sqrt s X} + e^{ - \sqrt s X} }}{{s (e^{\sqrt s } + e^{ - \sqrt s } )}}$$
(29)

The analytical solution of Eq. 29 using the same method for solving Eq. 14 (case a = 0) is given by:

$$C_{M} \left( {X,T} \right) = 1 - 2 \mathop \sum \limits_{1}^{\infty } \frac{{\left( { - 1} \right)^{ - n} \left( {cos\lambda_{n} X} \right)}}{{\lambda_{n} }} e^{{ - \lambda_{n}^{2} T }}$$
(30)

Using Eqs. 23, 25 and 30, we have:

$$C_{P} \left( {X,T} \right) = \left[ {1 - \frac{{e^{\sqrt a X} + e^{ - \sqrt a X} }}{{ \left( {e^{\sqrt a } + e^{ - \sqrt a } } \right)}}} \right] - 2 \mathop \sum \limits_{1}^{\infty } \left( { - 1} \right)^{ - n} \frac{1 }{{\lambda_{n} }} cos(\lambda_{n} X) e^{{ - \lambda_{n}^{2} T }} + 2 \mathop \sum \limits_{1}^{\infty } \left( { - 1} \right)^{ - n} \frac{{ \lambda_{n} e^{ - aT } }}{{\lambda_{n}^{2} + a}} cos(\lambda_{n} X) e^{{ - \lambda_{n}^{2} T }}$$
(31)

After rearrangement, the solution of the dimensionless product concentration is given by:

$$C_{P} \left( {X,T} \right) = \left[ {1 - \frac{{e^{\sqrt a X} + e^{ - \sqrt a X} }}{{ \left( {e^{\sqrt a } + e^{ - \sqrt a } } \right)}}} \right] + 2\mathop \sum \limits_{1}^{\infty } \left( { - 1} \right)^{ - n} (\frac{{\lambda_{n}^{2} (e^{ - aT } - 1) - a}}{{\lambda_{n} (\lambda_{n}^{2} + a)}})cos(\lambda_{n} X) e^{{ - \lambda_{n}^{2} T }}$$
(32)

Results and discussion

Analytical solution validation

The analytical solutions are validated for a specific set of values. In this paper, the analytical data are validated through the numerical data obtained from the numerical modeling with the MATLAB program. The function pdex4 in MATLAB, which is a function of solving the initial boundary value problems for parabolic partial differential equations [28], is used to solve Eqs. 7 and 8 for the corresponding boundary conditions in Eq. 9.

Fig. 2 shows the response of the enzyme biosensor for various substrate and product concentrations, accepting two cases a = 0.1 and a = 1 with different times of t = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. In all the cases, the percentage of deviation for the analytical solution from the numerical result are calculated to be less than 1%. This conforms that the modeled data with analytical solution are very much similar to numerical data.

Fig. 2
figure 2

Mathematical modeling response of the enzyme biosensor with a dimensionless substrate, a with a = 1, b with a = 0.1 and a dimensionless product, c with a = 1, d with a = 0.1

Full size image

Reaction–diffusion effect

The mathematical model presented here in Eq. 23 for the substrate and Eq. 32 for the product utilizes well-developed enzyme-catalyzed reaction diffusion equations, which were applied to a highly sensitive enzyme biosensor. The mathematical solution results in Eqs. 23 and 32 indicate that the factor \(a = \frac{{ V_{m} d^{2} }}{{D k_{M} }}\) is the principal factor that controls the biosensor response.

In the case of biosensors, the diffusion modulus or Damkohler number (a) compares the rate of the enzyme reaction \((\frac{{ V_{m} }}{{ k_{M} }})\) with the diffusion \((\frac{ D }{{d^{2} }})\) through the enzyme layer [29].

Figs. 3 and 4 show the concentration profiles for different values of the Damkohler number. Small values of the Damkohler number indicate that the surface reaction dominates and that a significant amount of the reactant diffuses well into the membrane without reacting.

Fig. 3
figure 3

Mathematical modeling kinetics of the dimensionless substrate concentration in a highly sensitive enzyme biosensor

Full size image
Fig. 4
figure 4

Mathematical modeling kinetics of the dimensionless product concentration in a highly sensitive enzyme biosensor

Full size image

It can be seen from Fig. 3 that with the decrease in the Damkohler number, there is an increase in the dimensionless substrate concentration degradation.

As shown in Fig. 4, concentration of the product decreases when there is a decrease in the Damkohler number.

Conclusions

The mathematical model of a highly sensitive enzyme biosensor can be successfully used to investigate the response of biosensors when the enzyme reacts with its substrate to produce new product. An approximate analytical expression of substrate and final product has been derived using the standard method of inverting a Laplace transform according to the Heaviside expansion theorem to solve the coupled nonlinear time-dependent reaction–diffusion equations for the Michaelis–Menten expression that describes the concentrations of the substrate and the product within the enzymatic layer. Our results are compared with the numerical simulations in MATLAB, showing a good agreement is found between the two sets of results. The analytical method is an extremely simple approach and is promising to better understand the ultrabiosensor model.