Introduction

The energy derived from petroleum accounts for 41 % of total energy consumption [1], whereas the percentage used as fuel for transportation is of ca. 32.6 % [2]. In recent decades, heavy crude oil has been the subject of investigation to produce middle distillates that will contribute to satisfy the demand of fuels in several countries. For instance in Mexico, the availability of light crudes is decreasing while that of heavy oil is increasing due to its vast reserves. In fact, around 61 % of the total proved reserves is heavy, such percentages reach ca. 57 % for probable reserves and ~52 % for possible reserves [3].

Among all available processes for upgrading heavy petroleum, hydrocracking is a common route to produce commercial fuel fractions from heavy oil, because it allows for breaking heavy molecules into lighter ones in presence of selective catalysts and specific reaction conditions [4].

In order to investigate the effect of reaction conditions on the hydrocracking of heavy oil, kinetic models have been developed, from the simplest model that seems to be a discrete approach with few lumps to the most complete ones, using fundamental reaction mechanisms such as single event approach. As in many cases, the extreme models may not be convenient mainly by two reasons: (a) the enormous complexity of a petroleum feedstock undergoing hydrocracking, and (b) the unavailability of detailed experimental data for exhaustive models. In addition, the need of accounting for an efficient model to make predictions in line with gross experimental observations and in agreement with industrial operation commonly represents an issue, where only some data are available. In order to overcome these disadvantages, a milder approximation with robust modeling is frequently employed.

The main problem when dealing with hydrocracking of heavy oils is the huge amount of compounds undergoing different reactions. The use of discrete lumping is a well-known approach to deal with hydrocracking of heavy oils. A recent paper in the field [5] reports the use of seven lumps to represent the hydrotreatment of full-range middle distillate coal tar at different reaction conditions. The author claimed good agreement between experimental and model predictions. However, the need for describing as accurate as possible the boiling point distribution instead of a number of discrete lumps has given an impulse to the use of the continuous kinetic lumping model, which overcomes several disadvantages of discrete lumping including the number of model parameters to be estimated [6].

Very few reports in the literature take into account the transient behavior of hydrocracking reactors. Sildir et al. [7] have simulated the dynamic of nonisothermal performance of hydrocracking units but few details of feedstock, reactor behavior and model solution were given. Accounting for a dynamic reactor model to hydrocracking of heavy oil can be a useful computational tool because it allows for capturing additional phenomena apart from those obtained at steady-state condition [8].

In this sense, the development of a dynamic reactor model by using the continuous kinetic lumping approach is justifiable to allow for simulating the transient behavior aiming at studying in a deeper manner the hydrocracking of heavy oil in a bench scale unit.

The model

Continuous kinetic lumping model

The continuous kinetic lumping model was used with the following assumptions:

  • The kinetic regime prevails due to experiments were conducted isothermally with minimal inter and intra-gradients among phases.

  • First order dependence on hydrocarbon concentration is used due the hydrogen is in excess.

  • Axial and radial dispersion is negligible so that the reactor behaves as an ideal plug flow.

  • Steady-state operation was ensured and experimental information was obtained at that condition.

  • The higher the boiling point, the greater the value of rate constant.

  • The relationship between reactivity and boiling point is:

    $$\frac{k}{{k_{max} }} = \theta^{1/\alpha }$$
    (1)

    where

    $$\theta = \frac{TBP - TBP\left( l \right)}{TBP\left( h \right) - TBP\left( l \right)}$$
    (2)

Eq. 1 contains the following parameters: α is a model parameter and k max is the reactivity of the heaviest compound undergoing hydrocracking reaction.At steady-state, Laxminarasiham et al. [9] stated the continuous kinetic lumping model as:

$$0 = - v\frac{{dc\left( {k,\tau } \right)}}{dz} - kc\left( {k,z} \right) + \int_{k}^{{k_{max} }} p \left( {k,x} \right) \times x \times c\left( {k,z} \right) \times D\left( x \right) \times dx$$
(3)

Here:

$$p\left( {k,K} \right) = \frac{1}{{S_{0} \sqrt {2\pi } }}\left\{ {e^{{ - \left[ {\left\{ {\left( {k/K} \right)^{{a_{0} }} - 0.5} \right\}/a_{1} } \right]^{2} }} - e^{{ - \left( {0.5/a_{1} } \right)^{2} }} + \delta \left[ {1 - \left( {k/K} \right)} \right]} \right\}$$
(4)

z is a variable used to indicate the position within reactor of length L. Other symbols and variables are defined in nomenclature section.

Eq. 4 accounts for the yield distribution function having as model parameters: a 0, a 1 and \(\delta\). S 0 included in Eq. 4 is obtained from a mass balance criterion and from normalization conditions [10] as follows:

$$S_{0} = \int_{0}^{K} {\frac{1}{{\sqrt {2\pi } }}\left[ {e^{{ - \left[ {\left\{ {\left( {k/x} \right)^{{a_{0} }} - 0.5} \right\}/a_{1} } \right]^{2} }} - e^{{ - \left( {0.5/a_{1} } \right)^{2} }} + \delta \left[ {1 - \left( {k/x} \right)} \right]} \right]} \times D\left( x \right) \times dx$$
(5)

The species-type distribution function (D), which is necessary for proper coordinate transformation from discrete description to continuous approach, is given by:

$$D\left( k \right) = \frac{N\alpha }{{k_{\hbox{max} }^{\alpha } }}k^{\alpha - 1}$$
(6)

Here N is the total number of species in the mixture and k is the reactivity of any species.

It is assumed that reactivity of species varies directly with their boiling point, i.e. species with high boiling point hydrocrack faster than those of lower boiling point. From the work of McCoy et al. [10], the model that governs the binary fragmentation occurring in a plug-flow reactor at unsteady-state condition is properly written as:

$$\frac{\partial c}{\partial t} + v\frac{\partial c}{\partial z} = - kc + 2\int_{k}^{{k_{max} }} {k\left( {x'} \right) \times c\left( {t,x,x'} \right) \times \varOmega \left( {x,x'} \right) \times dx'}$$
(7)

Here k(x′) is the rate coefficient, Ω(x,x′) is the stoichiometric coefficient or kernel, x′ is any property of parent and x is the property of progeny.

Eq. 7 can be used for describing hydrocracking kinetics by replacing the distribution function and proper Jacobian to account for the transformation from discrete to continuous description [6]. Thus, the unsteady-state reactor model with continuous kinetic lumping approach can be written as:

$$\frac{{\partial c\left( {k,\tau ,t} \right)}}{\partial t} = - \frac{{\partial c\left( {k,\tau ,t} \right)}}{\partial \tau } - kc\left( {k,\tau ,t} \right) + \int_{k}^{{k_{max} }} p \left( {k,x} \right) \times x \times c\left( {k,\tau ,t} \right) \times D\left( x \right) \times dx$$
(8)

The conditions to solve Eq. 8 are:

$${\text{At}}\;t = 0\;z = 0,\;c = c_{0} \;z > 0,\;c = 0$$
$${\text{At}}\;z = L,\,\,\,t > 0\;\frac{\partial c}{\partial z} = 0$$

Here c 0 is the dimensionless concentration distribution function of feedstock.

Estimation of model parameters

Kinetic model parameters were determined from experimental information at steady-state and isothermal mode of operation at the three reaction temperatures. The series of steps to obtain these parameters can be found elsewhere [6]. Matlab software was used to solve Eq. 3 by minimizing the differences between experimental and calculated values to obtain the continuous kinetic lumping model parameters.

Simulation of unsteady-state hydrocracking reactor

Eq. 8 was used to simulate the dynamic behavior of hydrocracking reactor. It was discretized in z direction (τ) by using finite forward differences as follows:

$$\begin{aligned} \frac{{dc\left( {k_{i} ,\tau_{r} ,t} \right)}}{dt} & = - \frac{{c\left( {k_{i} ,\tau_{r} ,t} \right) - c\left( {k_{i} ,\tau_{r - 1} ,t} \right)}}{\Delta \tau } + c\left( {k_{i} ,\tau_{r} ,t} \right) \times \left[ { - k_{i} + I_{1i} } \right] \\ & \quad + \sum\limits_{j = i + 1}^{n + 1} {c\left( {k_{j} ,\tau_{r} ,t} \right) \times I_{2j} } + \sum\limits_{j = i + 1}^{n} {c\left( {k_{j} ,\tau_{r} ,t} \right) \times I_{3j} } \\ \end{aligned}$$
(9)

where

$$I_{1i} = \int_{{k_{i} }}^{{k_{i + 1} }} {p\left( {k_{i} ,x} \right) \times x \times \left( {\frac{{x - k_{i + 1} }}{{k_{i} - k_{i + 1} }}} \right) \times D\left( x \right)dx}$$
(10)
$$I_{2j} = \int_{{k_{j - 1} }}^{{k_{j} }} {p\left( {k_{i} ,x} \right) \times x \times \left( {\frac{{x - k_{j - 1} }}{{k_{j} - k_{j - 1} }}} \right) \times D\left( x \right)dx}$$
(11)
$$I_{3j} = \int_{{k_{j} }}^{{k_{j + 1} }} {p\left( {k_{i} ,x} \right) \times x \times \left( {\frac{{x - k_{j + 1} }}{{k_{j} - k_{j + 1} }}} \right) \times D\left( x \right) \times dx}$$
(12)

Details to arrive at Eqs. 10–12 are given in Elizalde and Ancheyta (2011) [6].

To calculate the weight fraction within the interval \(\theta_{j}\),\(\theta_{j + 1}\), that corresponds to dimensionless continuous concentration at any time and position within the reactor, the following equation is used:

$$\left. {wt(t,\tau ,\theta )} \right|_{j}^{j + 1} = \int_{{k_{j} }}^{{k_{j + 1} }} {c(t,\tau ,k)} \times D\left( k \right) \times dk$$
(13)

After that, the sum of those fractions is carried out as boiling point function to construct the cumulative weight function and verify the mass conservation:

$$\sum\limits_{j = 1}^{N} {wt_{j} } = 1$$
(14)

The kinetic model parameters together with Eq. 9 were used to simulate the dynamic behavior of hydrocracking reactor and profiles of concentration as function of reactor length and time were obtained. To solve Eq. 9, a similar strategy of that used in Elizalde and Ancheyta [6] was applied. First, integrals (I 1i , I 2j and I 3j ) were calculated; the concentration of component with the highest reactivity was determined for the first length segment followed by the concentration of components with lower reactivity. The procedure was repeated for each segment at the entire reactor length for the whole time of simulation.

Experimental

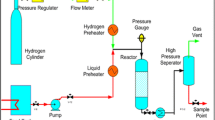
Experimental information was obtained at pressure of 9.8 MPa, temperature of 380–420 °C, 5000 standard cubic feet of hydrogen per barrel of oil and 1.0 h−1 of LHSV in an isothermal bench scale pilot reactor whose length is of 143 cm and internal diameter of 2.54 cm. Heavy crude oil was used as feedstock whose API is 21. Other relevant properties of the feed are: 3.51 wt% total sulfur, 3560 ppmw total nitrogen, 345.1 ppmw metals (Ni + V) and 39 wt% 538 °C + fraction. A NiMo/Al2O3 commercial catalyst was used and its main properties are: specific surface area of 175 m2/g, pore volume of 0.56 cm3/g, and average pore diameter of 127 Å. Prior to experimental runs, CS2 was used to activate the catalyst. ASTM D-5307 method was employed to characterize the feedstock and products regarding boiling point distributions.

Results and discussion

Steady-state reactor model

The model parameters of the continuous kinetic lumping approach were obtained by minimization of the sum of square differences between experimental and calculated concentrations of feedstock and products at each reaction condition. Fig. 1 shows the value of the model parameters as function of temperature. Similarly to other observations [10], an almost linear dependence of α, a 0 and δ with temperature was observed. It was also found that parameter a 1 does not change with temperature. Regarding the dependence of maximum reactivity (k max ) with temperature, an exponential relation was observed as previously reported [11].

Fig. 1
figure 1

Dependence of the continuous kinetic model parameters with temperature at 9.8 MPa. Predicted (lines) and experimental (symbols) data

Full size image

The optimal values of model parameters (Table 1) were used to simulate the experimental data at steady-state and the results are shown in Fig. 2. In general, excellent agreement between simulated and experimental information is observed. An increase of concentration of light and middle distillation fractions as reaction temperature increases is clearly seen.

Table 1 Parameters used in simulations
Full size table
Fig. 2
figure 2

Prediction of dimensionless distillation curves at 1.0 h−1 and 9.8 MPa. (open square) 420 °C, (open circle) 400 °C and (open triangle) 380 °C. Predicted (dotted lines) and experimental (symbols) data. (solid line) Feed

Full size image

Dynamic behavior of hydrocracking reactor

The values of parameters obtained at steady-state were used to simulate the dimensionless concentration evolution with time along the reactor length. As an example, Fig. 3 depicts the simulation of the dimensionless continuous concentration (c(t,τ,k)) at 380 °C, 9.8 MPa and LHSV of 1.0 h−1 for 0.5 h of run time. During simulation, the c(t,τ,k) of the compounds with the highest reactivity diminished whereas those compounds with milder reactivity (middle distillates) increased concentration. Evolution of c(t,τ,k) profiles were followed up until no noticeable changes on concentration at any point within reactor were detected.

Fig. 3
figure 3

Dynamic evolution of c curve as function of reactivity and reciprocal of LHSV at 380 °C and 9.8 MPa. Flash view at 0.5 h of time simulation

Full size image

By using data generated from continuous dimensionless concentration distribution and after proper transformation to cumulative weight by means of Eq. 14, by using similar procedure to that reported by Elizalde and Ancheyta [6], the profiles of cumulative weight fraction (wt) of hydrocracking products for each reaction temperature for the entire reactor length can be calculated. The information generated in Fig. 3 (380 °C, 9.8 MPa and LHSV of 1 h−1 and different times) was used to obtain the dynamic profiles of cumulative weight fraction and are plotted in Fig. 4a. From right to left, plane w − τ, the dynamic behavior of cumulative weight fraction is observed by means of surface representations. Each surface shown corresponds to a 6-min interval of simulation time. Clear evolution of the composition distribution as function of run time of simulation is shown, reaching the characteristic profile at the exit of reactor. A deep exploration of such a figure by means of rotation allows for observing that the main changes on concentration at the first instants are exhibited by those fractions having high reactivity (k → k max ) as shown in Fig. 4b. The fractions with lower boiling point (θ → 0) exhibit lower changes at short times due to their low content and reactivity, increasing their yields after times in which the most reactive fractions have attained the pseudo-steady state. All those behaviors contributed to the shape of the developed surfaces shown in Fig. 4a.

Fig. 4
figure 4

Profiles of cumulative weight fraction as function of dimensionless boiling point and reciprocal of LHSV. a Reaction conditions: 1.0 h−1 of LHSV, 380 °C and 9.8 MPa. From right to left in τ − c plane the effect of increasing time is shown. b View of rotation of a

Full size image

Fig. 5 plots of the evolution of oil factions with different reactivity against time of simulation. The operating conditions were 420 °C, 9.8 MPa and LHSV of 1.0 h−1. It is observed that all oil fractions appear at the same time, however its concentration at reactor exit changes with time because some of the low-reactivity pseudocomponents are hydrocracked/produced slower thus exhibiting small changes while those with the high reactivity are produced/hydrocracked faster as time-on-stream increases, so that their differences in concentration are also higher at longer times. It is observed that almost 1.5 h of operation was necessary to reach the pseudo-steady state. A zoom window was included in this plot to observe details of simulation at 0.5–0.8 h time range, that is, where the pseudo components start to be observable at exit reactor position. From the 0 to 0.5 h time range of simulation, neither products nor feedstock are detected at the exit of reactor due the flow rate condition that affects the molecules that have not still reached the exit reactor position. Dynamic profiles are in good agreement with literature reports [12]. It was found that the time to attain the pseudo-steady state at 380 and 400 °C (not shown) was also of ca. 1.5 h. This means that the dynamic behavior of the bench-scale reactor is not affected by the operating temperature. Based on these results, when recovering liquid product for further analysis, sampling has to be done after 1.5 h of time-on-stream.

Fig. 5
figure 5

Simulation of evolution profiles of pseudocomponents with different reactivity undergoing hydrocracking as function of time. Reaction conditions: 420 °C, 9.8 MPa and LHSV of 1.0 h−1. Profile of pseudocompounds with different reactivity (k) of: (dotted line) 1.14 h−1, (hyphen single mid dot hyphen) 1.66 h−1, (hyphen double mid dot hyphen) 1.98 h−1, (dashed line) 2.29 h, (solid line) 2.6 h−1

Full size image

The effect of LSHV on the dynamic profiles of pseudocomponents composition was investigated at 1.0 h−1 (base case), 0.5 and 2.0 h−1 keeping constant all the other operating parameters. It was assumed that the model parameters of the continuous kinetic approach do not vary with LHSV. Under LHSV = 0.5 h−1, the time to reach the pseudo-steady-state was about 3 h no matter the reaction temperature. As an example, the weight distribution function at the exit of reactor at reaction temperature of 400 °C is plotted in Fig. 6 for different time-on-stream. Only the fractions with boiling point within the interval of 0–600 °C were considered in this plot because they are the main products of industrial interest. In the interval of 1–2.8 h of TOS, the exit concentration changes drastically, approaching steady-state at 3.0 h of simulation. For light fractions whose boiling point was lower than 100 °C, small differences among profiles at different time-on-stream are observed. This behavior is because the operating conditions in this work are moderate and reaction severity is not such that hydrocracking of light fractions is carried out. For fractions with middle and high boiling point, the differences as time increases are higher due to these fractions are more reactive and thus they undergo more changes as extent of reaction increases before achieving pseudo-steady-state.

Fig. 6
figure 6

Simulation cumulative fraction at exit reactor at 400 °C, 9.8 MPa, LHSV of 2.0 h−1 and different times: (solid line) 1.2 h, (open square) 1.8 h, (filled circle) 2 h, (+++) 2.2 h, (–·–) 2.4 h, (dashed line) 2.6 h, (dotted line) 4 h

Full size image

The simulation conducted at 2.0 h−1 of LHSV (not shown) demonstrated that ca. 0.75 h are necessary to reach the pseudo-steady-state. Thus, an inverse variation between the time to reach the pseudo-steady-state and LHSV was observed. This effect can be attributed to the residence time of the reaction mixture within the reactor, that is, as the residence time increases, the time to attain the pseudo-steady-state is longer due to an increase of chemical reaction extent.

Based on all previous results, it can be stated that the present model can be useful to gain more insights about hydrocracking reactor operation either experimental or commercial. It can be further used to predict other important phenomena occurring during hydrocracking of heavy oil such as catalyst deactivation, reactor start-up, process control, among others. Also, extending the present model to other cases where some relevant phenomena are present such as deactivation by coke and non-isothermal reactor, will allow for identifying the need of modeling and experimental information for correct prediction of the behavior of those reactors.

Conclusions

The development of a dynamic reactor model for hydrocracking of heavy oil was carried out in this work. Some assumptions were necessary to test the validity of the proposed model and also reliable experimental information.

Since that kinetics of hydrocracking was described by the continuous lumping approach, and because that model contains tuning parameters, it was necessary to determine them from an isothermal bench scale hydrocracking reactor at steady-state condition.

The simulation of dynamic behavior of experimental reactor was carried out and the results allowed for establishing that under the assumptions and operating conditions of this work an inverse relationship between LHSV and the time to accomplish the pseudo-steady-state was found, that is, as contact time increases, so does the need of longer times for the stabilization of reactor regarding the product concentration due to complex reaction mechanisms.

It was also found that at the three tested reaction temperatures, the time to reach the pseudo-steady-state of reactor was almost equal, which was consequence of no variations on temperature as reaction proceeds.