1 Introduction

Quantum information theory has opened up the possibility of novel form of information processing tasks which are not possible in the region of classical information. Recently, one of remarkable approaches to quantum information processing has been remote state preparation (RSP), which is originally presented by several seminal perspectives [1–3]. RSP is dedicated to accomplishing an information-transmitted task that one sender transports a known quantum state to one receiver in distant location via local operations and classical communication (LOCC). Over the past decade, a large number of research groups focused on the topic about RSP, and reported enormous promising and feasible schemes both theoretically [4–16] and experimentally [17–22]. Very recently, another effective method of information-processing, so-called joint remote state preparation (JRSP), has been explored. In JRSP, the information of quantum state to be delivered is mathematically split into many pieces so as to guarantee the information security. Hence, the state cannot be restored by the receiver unless all the senders collaborate together. This is readily the main motivation for exploiting JRSP. To date, JRSP has received much attention, and a large number of proposals have been presented, e.g., JRSP of one-particle states [23–27], JRSP of two-particle states [26–34], JRSP of three-particle states [33–39], JRSP of four-particle states [40–43] and JRSP of multi-particle states [44–46] have been investigated.

It is well known that controlled information-processing is a hot topic in the field of quantum information communication. As a matter of fact, many authors have focused on it, and proposed many significant concepts, such as controlled teleportation [47, 48], controlled secure direct communication [49], controlled logic gates [50, 51], and so forth. In this paper, we will investigate another new approach, namely, multiparty-controlled joint remote state preparation (MCJRSP), which can be used for JRSP of arbitrary single- and two-particle states via the control of multi-agent. The receiver can get access to the desired state, as long as all the agents collaborate through LOCC. However, if one agent does not cooperate, the desired state cannot fully be recovered by the receiver, that is to say, the desired state is unable to be restored by anyone or several of the staff but the agents all collaborate. It deserves emphasizing that the state information is mathematically distributed to the senders rather than anyone of the agents. In this sense, the information delivery actually takes place between the senders and the receiver, while the agents are capable of supervising the whole preparation procedure including switching its occurrence. Thus, we claim that MCJRSP might be of importance to long-distance communication with multi-node in prospective quantum networks.

This paper is structured as follows. In the next section, our first MCJRSP scheme for an arbitrary single-particle state is expounded, which uses one multiple Greenberg–Horne–Zeilinger (GHZ) state as quantum channel. Additionally, success probability of the scheme (SPS) and classical information consumption (CIC) are calculated. And then we extend to generalize our second MCJRSP scheme for an arbitrary two-particle state in Sect. 3, which takes two GHZ-class states as quantum channels. SPS and CIC are figured out as well. In Sect. 4, some interesting points are discussed including the relations between the SPS and the employed entanglements, the generalization to the case of many-particle states and the feasibility of the proposed schemes. At last, we close the paper with a brief summary.

2 MCJRSP for an arbitrary single-particle state

In this scheme, there are (\(n+3\)) authorized participators, say, Alice, Bob, Dick, and \(n\) agents labeled by the sequence \(C_1,C_2,\ldots ,C_n\). Alice and Bob are the states’ senders while Dick as the receiver. Given both Alice and Bob are arranged to jointly prepare an arbitrary single-particle state within distant receiver’s site via the supervision of \(n\) agents, which can be written as

$$\begin{aligned} |\Phi \rangle =cos\theta |0\rangle +sin\theta {e^{i\varphi }}|1\rangle , \end{aligned}$$
(1)

where \(\theta \in [0,\pi /4]\) and \(\varphi \in [0,2\pi ]\). To begin with, the participants share one GHZ-class entangled state described as

$$\begin{aligned} |{\Psi }\rangle _{ABC_1\underbrace{{\cdots }}_{n-2}C_nD}=\sum _{i}^{0,1} \alpha _i|i\rangle ^{\bigotimes {n+3}} \end{aligned}$$
(2)

in advance, without loss of generality, we suppose that \(\alpha _0\) is real and the coefficients satisfy \(|\alpha _0|\le |\alpha _1|\). Particle \(A\) is hold by Alice, \(B\) by Bob, \(C_1\) by agent \(C_1, \ldots , D\) by \(\mathrm{Dick}\), respectively. To accomplish MCJRSP, Alice and Bob firstly make single-particle von Neumann measurements on particles \(A\) and \(B\) under a set of measuring basis \(\{|{\mathcal{M }}_i\rangle \}\) and \(\{|\mathcal{N }_j\rangle \}\), respectively. And \(\{|{\mathcal{M }}_i\rangle \}\) and \(\{|{\mathcal{N }}_j\rangle \}\) are given by

$$\begin{aligned} \left( \begin{array}{c} |{\mathcal{M }}_1\rangle \\ |{\mathcal{M }}_2\rangle \end{array}\right) =\left( \begin{array}{c@{\quad }c} cos\theta &{} sin\theta \\ sin\theta &{} -cos\theta \end{array} \right) \left( \begin{array}{c} |0\rangle \\ |1\rangle \end{array}\right) , \end{aligned}$$
(3)

and

$$\begin{aligned} \left( \begin{array}{c} |{\mathcal{N }}_1\rangle \\ |{\mathcal{N }}_2\rangle \end{array}\right) =\left( \begin{array}{c@{\quad }c} \frac{1}{\sqrt{2}} &{} \frac{1}{\sqrt{2}}e^{-i\varphi } \\ \frac{1}{\sqrt{2}} &{} -\frac{1}{\sqrt{2}}e^{-i\varphi } \end{array}\right) \left( \begin{array}{c} |0\rangle \\ |1\rangle \end{array}\right) , \end{aligned}$$
(4)

respectively. Thus, the whole system state can be redescribed as

$$\begin{aligned} |\Psi \rangle&= \sum _{i,j=1}^2|{\mathcal{M }}_i\rangle _{A} \otimes |{\mathcal{N }}_j\rangle _{B}\otimes |{\Omega }_{ij}\rangle _{C_1{\cdots }C_nD} \nonumber \\&= \frac{1}{\sqrt{2}}[|\mathcal{M }_1\rangle _{1}|\mathcal{N }_1\rangle _{2}({\alpha _0}{cos}\theta |0\rangle ^{\otimes {n+1}}+ {\alpha _1}{sin}{\theta }e^{i\varphi }|1\rangle ^{\otimes {n+1}})_{C_1{\cdots }C_nD}\nonumber \\&\quad +|\mathcal{M }_1\rangle _{1}|\mathcal{N }_2\rangle _{2}({\alpha _0}{cos}\theta |0\rangle ^{\otimes {n+1}}- {\alpha _1}{sin}{\theta }e^{i\varphi }|1\rangle ^{\otimes {n+1}})_{C_1{\cdots }C_nD}\nonumber \\&\quad +|\mathcal{M }_2\rangle _{1}|\mathcal{N }_1\rangle _{2}({\alpha _0}{sin}\theta |0\rangle ^{\otimes {n+1}}- {\alpha _1}{cos}{\theta }e^{i\varphi }|1\rangle ^{\otimes {n+1}})_{C_1{\cdots }C_nD}\nonumber \\&\quad +|\mathcal{M }_2\rangle _{1}|\mathcal{N }_2\rangle _{2}({\alpha _0}{sin}\theta |0\rangle ^{\otimes {n+1}}+ {\alpha _1}{cos}{\theta }e^{i\varphi }|1\rangle ^{\otimes {n+1}})_{C_1{\cdots }C_nD}], \end{aligned}$$
(5)

where \(|{\Omega }_{ij}\rangle _{C_1{\cdots }C_nD}\equiv {_{A} \langle {\mathcal{M }}_i|}{_{B}\langle {\mathcal{N }}_j}|\Psi \rangle _{ABC_1{\cdots }C_nD}\ (i,j=1,2)\). Subsequently, Alice and Bob inform Dick of their outcomes via classical channels (i.e., sending some classical bits). At the same time, the agents carry out the measurement on their own particles under the measuring basis \(\{|+\rangle ,|-\rangle \}\) respectively. By the way, \(\{|+\rangle ,|-\rangle \}\) is given by

$$\begin{aligned} |\pm \rangle =\frac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle ). \end{aligned}$$
(6)

Note that, both Alice (Bob) and Dick make an agreement in advance that bit ’0’ corresponds to the outcome \(|{\mathcal{M }}_1\rangle _{1}\,(|{\mathcal{N }}_1\rangle _{2})\), ’1’ to \(|{\mathcal{M }}_2\rangle _{1}\,(|{\mathcal{N }}_2\rangle _{2})\) hereafter. Besides, the agents and Dick make an agreement that the outcome \(|+\rangle \) corresponds to ’0’, while \(|-\rangle \) to ’1’. Thus, in terms of the received information bits, Dick exactly knows the collapse of his particle, and then can reconstruct the desired state after performing some appropriate unitary operations. Before illustrating it, it is declared that the outcomes \(|\mathcal{M }_i\rangle \) and \(|\mathcal{N }_j\rangle \) correspond to \((i,j)\) hereafter for short. Suppose that Alice’s and Bob’s measurement outcomes are (1,1). Then Alice sends bit ’0’ to Dick and Bob sends bit ’0’ through classical channels. Upon the classical messages, Dick readily realizes the remaining particles are in the state of

$$\begin{aligned} \frac{1}{N}({\alpha _0}{cos}\theta |0\rangle ^{\otimes {n+1}}+ {\alpha _1}{sin}{\theta }e^ {i\varphi }|1\rangle ^{\otimes {n+1}})_{C_1\cdots {C_n}D}, \end{aligned}$$
(7)

where \({N}={\sqrt{|{\alpha _0}{cos\theta }|^2+|{\alpha _1}{sin}\theta |^2}}\) is the normalized coefficient. Besides Dick will receive the all agent’s messages to inform their measuring outcome. Thus, extra \(n\) bits will be cost.

Given that Dick receives \(k\)’0’\(+(n-k)\)’1’(\(k\in \mathbb Z ^+\)) from the agents. Now we can classify them into two cases:

Case 1

\(k\) is even while \(n\) is odd, or \(n\) is even while \(k\) is odd.

In this case, based on the classical bits he realizes that his particle \(D\) is

$$\begin{aligned} \frac{1}{N}({\alpha _0}{cos}\theta |0\rangle - {\alpha _1}{sin}{\theta }e^{i\varphi }|1\rangle )_{D}. \end{aligned}$$
(8)

Next, he carries out an unitary transformation \(\sigma _z\) on his particle, where

$$\begin{aligned} \sigma _z=|0\rangle \langle 0|-|1\rangle \langle 1|. \end{aligned}$$
(9)

By doing this, the single-particle state will become

$$\begin{aligned} \frac{1}{N}({\alpha _0}{cos}\theta |0\rangle + {\alpha _1}{sin}{\theta }e^{i\varphi }|1\rangle )_{D}. \end{aligned}$$
(10)

Subsequently, he introduces an auxiliary particle \({A}^{\prime }\) with being in state of \(|0\rangle \), and then operates a bipartite unitary transformation \(U^1\), which is taken as

$$\begin{aligned} U^1=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{}0\\ 0 &{} \frac{{\alpha _0}}{{\alpha _1}} &{} 0 &{} \sqrt{1-\left( \frac{{\alpha _0}}{{\alpha _1}}\right) ^2}\\ 0&{} 0 &{} -1 &{}0\\ 0 &{} \sqrt{1-\left( \frac{{\alpha _0}}{{\alpha _1}}\right) ^2} &{} 0 &{} -\frac{{\alpha _0}}{{\alpha _1}} \end{array}\right) . \end{aligned}$$
(11)

Thus, the state of Dick’s particle will evolve as

$$\begin{aligned} \frac{1}{N}\left[ {\alpha _0}({cos}\theta |0\rangle + {sin}{\theta }e^{i\varphi }|1\rangle )_{D}|0\rangle _{{A}^{\prime }}+ {{\alpha _1}}\sqrt{1-\left( \frac{{\alpha _0}}{{\alpha _1}}\right) ^2}sin \theta {e}^{i\varphi }|1\rangle _{D}\otimes |1\rangle _{{A}^{\prime }}\right] .\nonumber \\ \end{aligned}$$
(12)

At last, he measures his auxiliary particle in the basis \(\{|0\rangle ,|1\rangle \}\). If \(|1\rangle _{{A}^{\prime }}\) is probed, his particle \(D\) will develop into a trivial state, that is MCJRSP fails in such situation; otherwise, \(|0\rangle _{{A}^{\prime }}\) is attained, he readily realizes the particle will be in \(({cos}\theta |0\rangle + {sin}{\theta }e^{i\varphi }|1\rangle )_{D}\equiv |\Phi \rangle _{D}\). In this sense, MCJRSP has been achieved in Dick’s site. At the same time, one can figure out the success probability

$$\begin{aligned} {P}=\left| \frac{{\mathcal{N }}}{\sqrt{2}}\right| ^2\times \left| \frac{{\alpha _0}}{\mathcal{N }}\right| ^2={|{\alpha _0}|^2}/{2}, \end{aligned}$$
(13)

and the CIC should be calculated as \(1+1+n=n+2\) bits in this case.

Case 2

Both \(k\) and \(n\) are even, or both \(k\) and \(n\) are odd.

After receiving the bits, he knows his particle is in the state of

$$\begin{aligned} \frac{1}{N}({\alpha _0}{cos}\theta |0\rangle + {\alpha _1}{sin}{\theta }e^{i\varphi }|1\rangle )_{D}, \end{aligned}$$
(14)

which is the same as Eq. (10). And applying the same analyzing methods as above, Dick can realize MCJRSP with the success probability of \({|{\alpha _0}|^2}/{2}\) and CIC of \(n+2\).

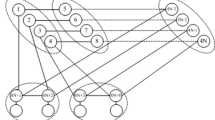
On the other hand, Alice’s and Bob’s outcome maybe (1, 2), if so, by the same analysis methods as the previous, it is found that one can accomplish MCJRSP for the arbitrary single-particle state with the same SPS and CIC as the above. However, if the outcome is one of the other two, i.e., (2, 1) or (2, 2), it is obvious that Dick can not convert his collapsed state into the desired state whatever the agents’ outcomes are. This displays MCJRSP fails in this case. Thus, the senders don’t send any messages to Dick so as to acquire economical classical resource consumption. Therefore, we can restart the preparation procedure to achieve MCJRSP. In all, our current scheme enables one to implement MCJRSP for an arbitrary single-particle state with SPS of \(2\times {P}=|{\alpha _0}|^2\) and CIC of \(n+2\) bits on average. For clarity, the quantum circuit has been shown in Fig. 1.

Fig. 1
figure 1

Quantum circuit diagram for MCJRSP of an arbitrary single-particle state. \({M_1}\) and \({M_2}\): two-particle projective measurement under the corresponding basis \(\{|{M_i}\rangle \}\) and \(\{|{N_j}\rangle \}\), respectively; The box with an index: a single-particle projective measurement under measuring basis \(\{|0\rangle ,|1\rangle \}\); DAUO: Dick’s approximate unitary operation on particle \(D\); \(U^1\): one local bipartite collective unitary transformation on Dick’s particles

Full size image

3 MCJRSP for an arbitrary two-particle state

Now let us extend the former scheme to a version for an arbitrary two-particle entangled state. Likewise, there are (\(n+3\)) legitimate participators, Alice, Bob, \({C}_1, {C}_2, \ldots , {C}_n\), and Dick. Alice and Bob are the states’ senders while Dick as the receiver. Given both Alice and Bob are designated to jointly prepare an arbitrary two-particle entangled state within distant receiver’s site under the control of the agents. In general, an arbitrary two-particle state reads as

$$\begin{aligned} |\widetilde{\Phi }\rangle =a|00\rangle +b{e^{i\xi _1}}|01\rangle +c{e^{i\xi _2}}|10\rangle +d{e^{i\xi _3}}|11\rangle , \end{aligned}$$
(15)

where \(a, b, c, d\) and \(\xi _i\) are real. At the start, the senders, the receiver and the agents share two GHZ-class entangled states

$$\begin{aligned}&|{\Psi }\rangle _{A_1B_1C_1\cdots {C_{n}}D_1}=\sum _{i}^{0,1} \beta _i|i\rangle ^{\bigotimes {n+3}}, \nonumber \\&|{\Psi }\rangle _{A_2B_2C_1^{\prime }\cdots {C_{n}^{\prime }}D_2}=\sum _{j}^{0,1} \gamma _j|j\rangle ^{\bigotimes {n+3}}, \end{aligned}$$
(16)

where, \(\beta _0\) and \(\gamma _0\) are real and the coefficients satisfy \(|\beta _0|\le |\beta _1|\) and \(|\gamma _0|\le |\gamma _1|\). Particles \(A_1\) and \(A_2\) are held by Alice, \(B_1\) and \(B_2\) by Bob, \(C_1\) and \(C_1^{\prime }\) by agent \({C}_1, \ldots , D_1\) and \(D_2\) by Dick. To realize MCJRSP, Alice and Bob operate two-particle projective measurements on the particle pairs \((A_1,A_2)\) and \((B_1,B_2)\) under a set of measuring basis \(\{|{{\widetilde{\mathcal{M }}}}_i\rangle \}\) and \(\{|{\widetilde{\mathcal{N }}}_j\rangle \}\), respectively. Here, \(\{|{\widetilde{\mathcal{M }}}_i\rangle \}\) and \(\{|{{\widetilde{\mathcal{N }}}}_j\rangle \}\) are given by

$$\begin{aligned} \left( \begin{array}{c} |{{\widetilde{\mathcal{M }}}}_1\rangle \\ |{{\widetilde{\mathcal{M }}}}_2\rangle \\ |{{\widetilde{\mathcal{M }}}}_3\rangle \\ |{{\widetilde{\mathcal{M }}}}_4\rangle \end{array}\right) =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a &{} b &{} c &{} d\\ b &{} -a &{} d &{} -c\\ c &{} -d &{} -a &{} b\\ d &{} c &{} -b &{} -a\end{array}\right) \left( \begin{array}{c} |00\rangle \\ |01\rangle \\ |10\rangle \\ |11\rangle \end{array}\right) , \end{aligned}$$
(17)

and

$$\begin{aligned} \left( \begin{array}{c} |{{\widetilde{\mathcal{N }}}}_1\rangle \\ |{{\widetilde{\mathcal{N }}}}_2\rangle \\ |{{\widetilde{\mathcal{N }}}}_3\rangle \\ |{{\widetilde{\mathcal{N }}}}_4\rangle \end{array}\right) =\frac{1}{2}\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 1 &{} e^{-i\xi _1} &{} e^{-i\xi _2} &{} e^{-i\xi _3}\\ 1 &{} -e^{-i\xi _1} &{} e^{-i\xi _2} &{} -e^{-i\xi _3}\\ 1 &{} -e^{-i\xi _1} &{} -e^{-i\xi _2} &{} e^{-i\xi _3}\\ 1 &{} e^{-i\xi _1} &{} -e^{-i\xi _2} &{} -e^{-i\xi _3} \end{array}\right) \left( \begin{array}{c} |00\rangle \\ |01\rangle \\ |10\rangle \\ |11\rangle \end{array}\right) , \end{aligned}$$
(18)

respectively. Since one can rewrite the total system state as

$$\begin{aligned} \sum _{i,j=1}^2&|{{{\widetilde{\mathcal{M }}}}}_i \rangle _{A_1A_2}\otimes |{{\widetilde{\mathcal{N }}}}_j\rangle _{B_1B_2} \otimes |{\widetilde{\Omega }}_{ij}\rangle _{C_1C_1^{\prime } \underbrace{\cdots }_{2n-2}{D_1D_2}}\nonumber \\ =&\frac{1}{2}[|{\widetilde{\mathcal{M }}}_1\rangle _{A_1A_2}| {\widetilde{\mathcal{N }}}_1\rangle _{B_1B_2}(a{\beta _0}{\gamma _0}| 00\rangle ^{\otimes {n+1}}+ b{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+c{\beta _1} {\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}} +d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_1\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_2 \rangle _{B_1B_2} (a{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}}-b{\beta _0}{\gamma _1} e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_1\rangle _{A_1A_2}|{\mathcal{{\widetilde{N}} }}_3 \rangle _{B_1B_2}(a{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}}- b{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|{\mathcal{\widetilde{M} }}_1\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_4\rangle _{B_1B_2} (a{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} +b{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle )_{C_1C_1^{\prime }\cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_2\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_1\rangle _{B_1B_2} (b{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} -a{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ d{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-c{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{{\widetilde{M}} }_2\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_2\rangle _{B_1B_2} (b{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} +a{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ d{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+c{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_2\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_3 \rangle _{B_1B_2}(b{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} +a{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- d{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-c{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_2\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_4 \rangle _{B_1B_2}(b{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} -a{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- d{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+c{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_3\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_1 \rangle _{B_1B_2}(c{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} -d{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- a{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+b{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_3\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_2 \rangle _{B_1B_2}(c{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} +d{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&- a{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-b{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_3\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_3 \rangle _{B_1B_2}(c{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} +d{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ a{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+b{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_3\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_4 \rangle _{B_1B_2}(c{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} -d{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ a{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-b{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_4\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_1 \rangle _{B_1B_2}(d{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} \!+\!c{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&-b{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-a{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_4\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_2 \rangle _{B_1B_2}(d{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} \!-\!c{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&-b{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+a{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_4\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_3 \rangle _{B_1B_2}(d{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} \!-\!c{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ b{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}-a{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}\nonumber \\&+|\mathcal{\widetilde{M} }_4\rangle _{A_1A_2}|\mathcal{\widetilde{N} }_4 \rangle _{B_1B_2}(d{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}} \!+\!c{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}\nonumber \\&+ b{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}+a{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}]. \end{aligned}$$
(19)

Subsequently, Alice and Bob inform Dick of their outcomes via classical channels, respectively. Specifically, both Alice (Bob) and Dick make an agreement in priori that bits ’00’ correspond to the outcome \(|{{\widetilde{\mathcal{M }}}}_{1}\rangle _{12}\) (\(|{{\widetilde{\mathcal{N }}}}_{1}\rangle _{34}\)), ’01’ to \(|{{\widetilde{\mathcal{M }}}}_{2}\rangle _{12}\) (\(|{{\widetilde{\mathcal{N }}}}_2\rangle _{34}\)), ’10’ to \(|{{\widetilde{\mathcal{M }}}}_{3}\rangle _{12}\) (\(|{{\widetilde{\mathcal{N }}}}_3\rangle _{34}\)), and ’11’ to \(|{{\widetilde{\mathcal{M }}}}_{4}\rangle _{12}\) (\(|{{\widetilde{\mathcal{N }}}}_4\rangle _{34}\)). Take an example, suppose that Alice’s and Bob’s measurement outcomes are (1,2). Then Alice sends bits ’00’ to Dick and Bob sends bits ’10’ through classical channels. Through the classical information, Dick readily obtains that the remaining particles have been in the state of

$$\begin{aligned}&\widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle ^{\otimes {n+1}}-b{\beta _0} {\gamma _1}e^{i\xi _1}|01\rangle ^{\otimes {n+1}}+ c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle ^{\otimes {n+1}}\nonumber \\&\quad -d{\beta _1} {\gamma _1}e^{i\xi _3}|11\rangle ^{\otimes {n+1}})_{C_1C_1^{\prime } \cdots {D_1D_2}}, \end{aligned}$$
(20)

where \({\widetilde{N}}=1/{\sqrt{|a{\beta _0}{\gamma _0}|^2+|b{\beta _0}{\gamma _1}|^2+ |c{\beta _1}{\gamma _0}|^2+|d{\beta _1}{\gamma _1}|^2}}\). And then the agents make single-particle projective measurements on their own particles under the basis \(\{|+\rangle ,|-\rangle \}\), and then \(C_l\) (\(l=1,\dots ,n\)) sends the measuring outcome of his particles \(C_l\) and \(C_l^{\prime }\) to Dick via bits ’\(\xi _l\zeta _l\)’(\(\xi _l,\zeta _l\in \{0,1\}\)). Besides, let \(p=\sum \nolimits _{l=1}^{n}{\xi _l}\), and \(q=\sum \nolimits _{l=1}^{n}{\zeta _l}\). According to the message, Dick can classify them into four types as follows:

  • (I) Both \(p\) and \(q\) are even.

In this case, Dick acquires that his particles are being in the state of

$$\begin{aligned} \widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle -b{\beta _0} {\gamma _1}e^{i\xi _1}|01\rangle +c{\beta _1}{\gamma _0} e^{i\xi _2}|10\rangle -d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle ) _{D_1D_2}, \end{aligned}$$
(21)

and then he carries out an unitary operation \(\sigma _z\) on his particle \(D_2\).

  • (II) Both \(p\) and \(q\) are odd.

In this case, the state of Dick’s particles is

$$\begin{aligned} \widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle +b{\beta _0}{\gamma _1} e^{i\xi _1}|01\rangle -c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle -d{\beta _1} {\gamma _1}e^{i\xi _3}|11\rangle )_{D_1D_2}. \end{aligned}$$
(22)

Accordingly, he performs an unitary operation \(\sigma _z\) on his particle \(D_1\).

  • (III) \(p\) is odd and \(q\) is even.

In this case, Dick’s particles have collapsed into

$$\begin{aligned} \widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle -b{\beta _0} {\gamma _1}e^{i\xi _1}|01\rangle -c{\beta _1}{\gamma _0} e^{i\xi _2}|10\rangle +d{\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle )_{D_1D_2}. \end{aligned}$$
(23)

Next, he makes an unitary operation \(\sigma _z\) on his particles \(D_1\) and \(D_2\), respectively.

  • (IV) \(p\) is even and \(q\) is odd.

In this case, Dick realizes that his particles’ state is

$$\begin{aligned} \widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle + b{\beta _0}{\gamma _1}e^{i\xi _1}|01\rangle + c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle +d{\beta _1} {\gamma _1}e^{i\xi _3}|11\rangle )_{D_1D_2}. \end{aligned}$$
(24)

Then, he executes an unitary operation \(I\) on his particles, respectively, where

$$\begin{aligned} I=|0\rangle \langle 0|+|1\rangle \langle 1|. \end{aligned}$$
(25)

Whatever the parity outcome is, the subsystem of Dick will collapse into

$$\begin{aligned} \widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle +b{\beta _0}{\gamma _1} e^{i\xi _1}|01\rangle +c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle +d {\beta _1}{\gamma _1}e^{i\xi _3}|11\rangle )_{D_1D_2}, \end{aligned}$$
(26)

after he makes the corresponding unitary operations mentioned before. Subsequently, in order to reconstruct the desired state, he introduces an auxiliary particle \(A^{\prime \prime }\) with being in \(|0\rangle \), and then makes a triplet unitary transformation \(U^{2}\), which is taken as a form of \(8\times 8\) matrix

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{}0 &{} 0 &{} 0 &{}0 &{} 0\\ 0 &{} \frac{\gamma _0}{\gamma _1} &{} 0 &{} 0 &{} 0 &{} \sqrt{1\!-\!\left( \frac{\gamma _0}{\gamma _1}\right) ^2}&{} 0 &{} 0\\ 0 &{} 0 &{} \frac{\beta _0}{\beta _1} &{}0 &{} 0 &{} 0 &{} \sqrt{1\!-\!\left( \frac{\beta _0}{\beta _1}\right) ^2} &{}0\\ 0&{} 0 &{} 0 &{}\frac{\beta _0\gamma _0}{\beta _1\gamma _1}&{}0&{} 0 &{} 0 &{} \sqrt{1\!-\!\left( \frac{\beta _0\gamma _0}{\beta _1\gamma _1}\right) ^2}\\ 0 &{} 0 &{}0 &{} 0&{} -1 &{} 0 &{} 0 &{}0\\ 0 &{} \sqrt{1\!-\!\left( \frac{\gamma _0}{\gamma _1}\right) ^2}&{} 0 &{} 0 &{} 0 &{} -\frac{\gamma _0}{\gamma _1} &{} 0 &{} 0\\ 0 &{} 0 &{} \sqrt{1\!-\!\left( \frac{\beta _0}{\beta _1}\right) ^2} &{}0 &{} 0 &{} 0 &{} -\frac{\beta _0}{\beta _1} &{}0\\ 0&{} 0 &{} 0 &{} \sqrt{1\!-\!\left( \frac{\beta _0\gamma _0}{\beta _1\gamma _1}\right) ^2}&{}0&{} 0 &{} 0 &{}-\frac{\beta _0\gamma _0}{\beta _1\gamma _1} \end{array}\right) .\nonumber \\ \end{aligned}$$
(27)

Thus, the state of Dick’s particle will develop into

$$\begin{aligned} \begin{aligned} {U}^{2}&\widetilde{N}(a{\beta _0}{\gamma _0}|00\rangle +b{\beta _0}{\gamma _1} e^{i\xi _1}|01\rangle + c{\beta _1}{\gamma _0}e^{i\xi _2}|10\rangle +d{\beta _1}{\gamma _1} e^{i\xi _3}|11\rangle )_{D_1D_2}\otimes |0\rangle _{A^{\prime \prime }}\\ =&\widetilde{N}\left[ {\beta _0}{\gamma _0}(a|00\rangle \!+\!be^{i\xi _1}|01\rangle \!+\! ce^{i\xi _2}|10\rangle \!+\!de^{i\xi _3}|11\rangle )_{D_1D_2}\otimes |0\rangle _{A^{\prime \prime }}\right. \\&\left. +\left( b{\beta _0}{\gamma _1}\sqrt{1\!-\!\left( \frac{\gamma _0}{\gamma _1}\right) ^2}e^{i\xi _1}|01\rangle + c{\beta _1}{\gamma _0}\sqrt{1-\left( \frac{\beta _0}{\beta _1}\right) ^2} e^{i\xi _2}|10\rangle \right. \right. \\&\left. \left. +d{\beta _1}{\gamma _1}\sqrt{1-\left( \frac{\beta _0\gamma _0}{\beta _1\gamma _1}\right) ^2} e^{i\xi _3}|11\rangle \right) _{D_1D_2}\otimes |1\rangle _{A^{\prime \prime }}\right] . \end{aligned} \end{aligned}$$
(28)

At last stage, he measures his auxiliary particle in the basis \(\{|0\rangle ,|1\rangle \}\). If \(|1\rangle _{A^{\prime \prime }}\) is probed, his particles \(D_1\) and \(D_2\) will collapse into a trivial state, that is our MCJRSP fails in this situation; otherwise, \(|0\rangle _{A^{\prime \prime }}\) is obtained, he realizes that the particles have readily been in \(|\widetilde{{\Phi }}\rangle \). That is to say, our MCJRSP succeeds in this case. At the same time, we can figure out the success probability should be

$$\begin{aligned} {P}^{\prime }={\frac{1}{4{|\mathcal{\widetilde{N} }}|^2}}\times | {\beta _0\gamma _0}{\mathcal{\widetilde{N} }}|^2=\frac{| \beta _0\gamma _0|^2}{4}. \end{aligned}$$
(29)

Of course, Alice’s and Bob’s outcome may be (1,1), (1,3), (1,4). If so, by the same analysis methods as the previous, it is found that Dick can achieve MCJRSP for the single-particle state with SPS of \({|\beta _0\gamma _0|^2}/{4}\) and CIC of \(4+2n\) bits. For simplicity, we don’t depict them one by one. As a summary, the senders’ measurement outcome \((i,j)\), the parity of \(p\) and \(q\), Dick’s appropriate unitary operations on his particles \(D_1\) and \(D_2\), and necessary triplet collective unitary transformation have been listed in Table 1, and for clearness the quantum circuit has been sketched in Fig. 2. However, if the outcome is one of other twelve outcomes, Alice confirms that Dick cannot convert his collapsed state into the desired state whatever the other agents’ outcomes are. This displays MCJRSP fails in these cases. Thus, Bob doesn’t send any messages to Dick any more. Therefore, we need to restart the preparation procedure.

Table 1 The senders’ measurement outcome \((i,j)\), the parity of \(p\) and \(q\) (\(p,q\)), Dick’s appropriate unitary operations on his particles \(D_1\) and \(D_2\) (DAUO), and triplet collective unitary transformation (\(U\))
Full size table
Fig. 2
figure 2

Quantum circuit diagram for MCJRSP of arbitrary two-particle states. \({\widetilde{M_1}}\) and \({\widetilde{M_2}}\): two-particle projective measurement under the corresponding basis \(\{|\widetilde{M_i}\rangle \}\) and \(\{|\widetilde{N_j}\rangle \}\), respectively; the box with an index: a single-particle projective measurement under measuring basis \(\{|0\rangle ,|1\rangle \}\), \(U^2\): one local triplet collective unitary transformation on Dick’s particles

Full size image

To sum up, we have proposed a MCJRSP scheme for an arbitrary two-particle state with SPS of \(4\times {\widetilde{P}}=|\beta _0\gamma _0|^2\), and the CIC equals to \(4+2n\) bits totally.

4 Discussions

Up to now, we have derived two MCJRSP schemes for arbitrary single- and two-particle states, which have, to our best knowledge, not been pointed out before. And the required quantum operations, classical information consumption and success probability are shown explicitly. Now we will have some interesting discussions on our schemes.

4.1 The relations between SPS and the employed quantum channels

In our first scheme, one GHZ-class entangled state is used as the quantum channels. The total SPS is \(|\alpha _0|^2\), which relates to the smaller coefficient of entanglement employed. As to the second scheme, the total SPS is \(|\beta _0\gamma _0|^2\), which relates to the smaller coefficients of entanglements employed as well. That indicates that the success probability is inherently determined by the shared entanglements set up in priori. For clarity, we have shown that relation charts between SPS and the employed channels in Fig. 3. From the figure, one can see that the SPS can be peaked, i.e., 50 and 25 %, respectively, when \(|\alpha _0|=|\beta _0|=|\gamma _0|=1/\sqrt{2}\) is hold. This indicates that maximally entangled states are taken as the quantum channels in this situation.

Fig. 3
figure 3

The diagram of relations between SPS and the employed channels. a Corresponds to the chart of the relation between SPS and the smaller coefficient of the employed channel in the first scheme, and b corresponds to the chart of that in the second scheme

Full size image

4.2 The generalization to the case of many-particle states

In previous sections, we firstly detail a MCJRSP scheme for an arbitrary single-particle state, and then extend to a two-particle version. Now, let us turn to briefly analyze both classical and quantum aspects of resource consumption with respect to MCJRSP for an arbitrary \(m\)-particle (\(m\ge 3\)) state.

  1. (1)

    Quantum resources: \(m\) \((n+3)\)-particle GHZ-class entangled states shared among two senders, one receiver and \(n\) agents, and an auxiliary particle;

  2. (2)

    Classical resources: \(m\times (n+2)\) classical bits to communicate among the participants, which is indispensable during the implementation.

In addition, the necessary quantum operations are embodied in the following:

  1. (a)

    Two \(m\)-particle projective measurements. Both of them are performed by two senders under the corresponding measuring basis, respectively.

  2. (b)

    \(m\) single-particle projective measurements performed by each agent under the basis \(\{|+\rangle ,|-\rangle \}\).

  3. (c)

    \(m\) appropriate single-particle unitary operations. The receiver needs to fulfill them perfectly after acquiring the state of his particles.

  4. (d)

    One \((m+1)\)-particle collective unitary operation and one single-particle projective measurement performed by the receiver.

4.3 The experimental feasibility

Now let us proceed to analyse the experimental feasibility of the schemes presented. In our MCJRSP proposals, one- and two-particle projective measurements and local two- and three-particle unitary transformations are considerably important during the preparations of the desired states. By far, projective measurement has received a great deal of attention [52–54]. Some researchers [52, 53] have conjectured that any projective measurement can be decomposed into a sequence of weak measurements, which cause only small changes to the state. Moreover, multi-particle projective measurement via linear optics, has been investigated by numerous spectacular works [55–58]. With regard to three-particle unitary transformations, it is well known that any many-particle unitary transformation can be decomposed into some single-particle rotation operations and a Controlled-Not gate transformation. In fact, single-particle rotating operations had been explored by various protocols [59, 60], and Controlled-Not gate had been successfully demonstrated via an all-optical system [61–63]. Thereby, our schemes, in principle, are feasible in the framework of linear optics, and further we expect that they could be demonstrated in prospective experiments.

5 Summary

To summarize, we have elaborated two efficient MCJRSP schemes for arbitrary single- and two-particle pure states with the control of multi-agent, respectively. With the assistance of GHZ-class entanglements and LOCC, our schemes can be realized with certain success probability in receiver’s location via the control of many agents. Importantly, our schemes can be easily extended to the case of many-particle states. Additionally, it has been revealed that SPS is only determined by the smaller coefficients of the employed channels. The experimental feasibility of the current schemes is analyzed as well, it is proved that our schemes are compatible with today’s technologies, and further we expect that they could be demonstrated in prospective experiments via all-optical systems. Remarkably, our work might be of importance to long-distance communication in prospective quantum networks.