1 Introduction

A principal goal of quantum information theory is to understand the resources necessary and sufficient for intact transmission of quantum states. One of the most remarkable schemes for the transmission of quantum state is the so-called quantum teleportation, brought out firstly by Bennett et al. [1], in which the transmission of an unknown qubit state can be achieved via an Einstein-Podolsky-Rosen (EPR) pair as the quantum channel with the help of two cbits classical communication. This approach has been developed quickly and made prominent progresses [2–5]. Subsequently, remote state preparation (RSP) has been brought forward gradually. It was investigated by Lo [6], Pati [7] and Bennett et al. [8] first. This so-called RSP can successfully propagate a pure known quantum state through employing a prior shared entanglement and some classical communication while the transmitted state are completely known by senders. The main difference between RSP and teleportation are in that, (1) in RSP Alice knows the state that she wants Bob to prepare, in particular, Alice need not own the state, but only know the information about the state, while in teleportation Alice must own the teleported state, but she need not know the state; (2) in RSP, the required resource can be traded off between classical communication cost and entanglement cost while in quantum teleportation, two bits of forward classical communication and one ebit of entanglement (an EPR pair) per teleported qubit are both necessary and sufficient, and neither resource can be traded off against the other [9]. So far a lot of RSP schemes [10–16] have been proposed.

Different from RSP, the schemes of joint remote state preparation (JRSP) [17–25] have also been suggested recently. That is a number of senders share the quantum state independently and they can jointly prepare the state for the remote receiver. When the state is characterized by a set of numbers {x,y,z,…} which can be split into subsets {x 1,y 1,z 1,…},{x 2,y 2,z 2,…},…,{x n ,y n ,z n ,…}, that are independently distributed to the n senders respectively. Apparently, neither a single sender nor most of the senders can prepare the state to the remote receiver. It is only when all the senders act cooperatively, the remote receiver can get the state he wants to prepare. In Refs. [17–25], they have chosen the Greenberger-Horne-Zeilinger (GHZ) states [26], W states [27] or EPR pairs [28] as the shared quantum channel to realize the JRSP. Most of them deal with JRSP of one- and two-qubit states. Recently, Luo et al. have proposed a scheme [29] to joint remotely prepare of an arbitrary three-qubit state using three maximally entangled GHZ states as quantum channel. We all know that an arbitrary three particle state is an important entangled state, it has important application in quantum information. Here we consider three non-maximally entangled GHZ states as quantum channel to joint remote the an arbitrary three particle state. Furthermore, we extended our method with the different information splitting which offers the better security environment.

Our paper is organized as follow: In Sect. 2 we propose a two-preparer JRSP scheme of a arbitray three qubits state via three non-maximally entangled GHZ states as the quantum channel. With the assistance of some special measurement bases, an arbitrary three qubit state can be jointly prepared by two senders. Using the three non-maximally entangled GHZ states as the quantum channel, we need introduce an auxiliary particle and make unitary transformation on particles. In Sect. 3 we extend the scheme in Sect. 2 to a different information splitting which not have to introduce an auxiliary particle. This method is more safety and economic. The conclusion is given in Sect. 4.

2 Joint Remote Preparation of a Three Qubit State Via GHZ States

The state we want to joint remotely prepare is as follow:

$$|\Phi\rangle=a|000\rangle+b|001\rangle+c|010\rangle+d|011\rangle+g|100\rangle+f|101\rangle +e|110\rangle+k|111\rangle. $$
(1)

Suppose that the boss Daisy has three non-maximally GHZ states

(2)
(3)

and

$$|\mathrm{GHZ}\rangle_3=(\gamma_1|000\rangle+\gamma_2|111\rangle)_{789},$$
(4)

with complex coefficients satisfying the normalization conditions \(\sum_{i=1}^{2}|\alpha _{i}|^{2}=\sum_{i=1}^{2}|\beta _{i}|^{2}=\sum_{i=1}^{2}|\gamma_{i}|^{2}=1\) and |α 1|>|α 2|, |β 1|>|β 2|, |γ 1|>|γ 2|. Suppose that Alice and Bob want to help Charlie joint remotely prepare the state in (1). Daisy knows the coefficients α i ,β,γ i and he can arrange Alice, Bob and Charlie to share the three non-maximally GHZ states as the quantum channel, that is, qubits 1,4,7 belong to Alice while qubits 2,5,8 and 3,6,9 belong to Bob and Charlie, respectively.

First, Alice and Bob each measures her/his qubits in an appropriate basis. Under the situation considered in this section Alice’s measurement basis {|φ i 〉147;i=1,2,3,4,5,6,7,8} is defined through the computational basis {|000〉,|001〉,|010〉,|011〉,|100〉,|101〉,|110〉,|111〉}147 as [29]

(5)

and Bob’s measurement basis {|ψ i 〉258; i=1,2,3,4,5,6,7,8} is

(6)

we define A n =|a n |2+|b n |2+|c n |2+|d n |2,B n =|f n |2+|e n |2+|g n |2+|k n |2. In (5)–(6), \(\mu _{n}=1/\sqrt{A_{n}+B_{n}},n=1, 2\). For n=1,2, the following equations are satisfied:

$$\left\{\begin{array}{l}A_n=B_n\\ [4pt]a_nb_n^*-a_n^*b_n-c_nd_n^*+c_n^*d_n=0 \\ [4pt]a_nc_n^*+a_n^*c_n+b_nd_n^*+b_n^*d_n=0\\ [4pt]a_nd_n^*+a_n^*d_n-b_nc_n^*-b_n^*c_n=0 \\ [4pt]g_nf_n^*-g_n^*f_n-e_nk_n^*+e_n^*k_n=0\\ [4pt]g_ne_n^*+g_n^*e_n+f_nk_n^*+f_n^*k_n=0 \\ [4pt]g_nk_n^*+g_n^*k_n-f_ne_n^*-f_n^*e_n=0.\end{array}\right.$$
(7)

With the bases |Ψ i 〉,i=1,…,8 defined in (5)–(6), the total state |Ψ〉= |GHZ〉123⊗|GHZ〉456⊗|GHZ〉789 can be rewritten as

$$|\Psi\rangle=\mu _{1}\mu _{2}\sum_{i,j=1}^{8}|\varphi _{i}\rangle _{147}|\varphi _{j}\rangle _{258}|\varphi _{ij}\rangle _{369},$$
(8)

where

(9)
(10)
(11)

From the boss Daisy, Alice knows the splitting coefficients a 1, b 1, c 1, d 1, e 1, f 1, g 1, k 1, and Bob knows a 2, b 2, c 2, d 2, e 2, f 2, g 2, k 2, but Charlie does not know a n , b n , c n , d n , e n , f n , g n , k n , a, b, c, d, e, f, g, k (n=1,2), where a 1 a 2=a, b 1 b 2=b, c 1 c 2=c, d 1 d 2=d, e 1 e 2=e, f 1 f 2=f, g 1 g 2=g, k 1 k 2=k. After Alice and Bob performing the projective measurement P 147, P 258 on qubits 1,4,7 and qubits 2,5,8 under the basis |φ〉147/258,i=1,…,8, respectively. Their measurement outcomes i, j are broadcast through classical communication. For i=j=1, the total state can be written as

(12)

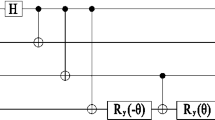
then, Charlie performs unitary transformation U 1=σ x on qubit 9. The unitary transformation U 1 will transform the state shown in (12) into

(13)

Next, Charlie introduces an auxiliary qubit M, see Ref. [30], which is prepared in state |0〉 M initially. The total state comes into

(14)

and Charlie makes another unitary transformation U 2 on particles 3, 6 and 9. When the original state is to be reincarnated the basis {|0000〉369M , |0010〉369M , |0100〉369M , |0110〉369M , |1000〉369M , |1010〉369M , |1100〉369M , |1110〉369M , |0001〉369M , |0011〉369M , |0101〉369M , |0111〉369M , |1001〉369M , |1011〉369M , |1101〉369M , |1111〉369M }, the unitary transformation U 2 can take the following form:

$$U_2=\left(\begin{array}{c@{\quad}c}M_1&M_2 \\[4pt]M_2& -M_1\end{array}\right),$$
(15)

where M i (i=1,2) is an 8×8 matrix and can be written as

(16)
(17)

where m i (i=1,2,3,4,5,6,7,8 and |m i |≤1) depend on the state of the particles 3, 6 and 9. Then we choose

(18)

The state in (19) will transform into the following state after the unitary transformation U 2:

(19)

Lastly, Charlie makes a measurement on the auxiliary qubit M. If the measurement is |0〉 M , they have successfully realized the JRSP with a probability of |α 2 β 2 γ 2|2. Otherwise, the JRSP has failed.

From (11), it seems we can’t get the state we wanted, for example i=1,j=3, even though we choose the different unitary matrix because the coefficient of each item can’t be known such as b 1 c 2≠b. Through calculating it is easy to find only when (i=j=1; i=1, j=2; i=2, j=1 and i=j=2) choosing the different unitary matrix we can get the state we want. So the total probability of successful is

(20)

Figure 1 displays the success probability P 1 as a function of real a 1 and e 1 for the possible collections of parameters.

Fig. 1
figure 1

The success probability P 1, (20), for JRSP of a general three-qubit state |Φ〉 via three non-maximally GHZ states |GHZ〉1, |GHZ〉2 and |GHZ〉3 as a function of a 1 and e 1 for \(a=b=c=d=e=f=k=g\allowbreak=1/\sqrt{8}\), \(\alpha_{1}=\beta_{1}=\gamma_{1}=\sqrt{2/3}\), \(\alpha_{2}=\beta_{2}=\gamma_{2}=\sqrt{1/3}\), |a 1|=|b 1|=|c 1|=|d 1|, |e 1|=|f 1|=|g 1|=|k 1|

Full size image

3 Joint Remote Preparation of a Three Qubit State Via GHZ States not Introducing an Auxiliary Particle

Now we extend our method to a different information splitting method in order not to introduce an auxiliary particle on the receiver’s side. In this case, follow the several same steps in the Sect. 2 till we get the form of the state as show in (9). Then we do the information splitting {a,b,c,d,e,f,g,k}→{{a 1,b 1,c 1,d 1,e 1,g 1,k 1},{a 2,b 2,c 2,d 2,e 2,f 2,g 2,k 2}}, Daisy first assigns each of a 1, b 1, c 1, d 1, e 1, f 1, g 1 and k 1 an arbitrary value. Then he determines a 2, b 2, c 2, d 2, e 2, f 2, g 2 and k 2 through the parameters involved as

(21)

Then substitute (21) into (9). It is transparent we get the state shown as follow:

(22)

The success probability is P 2:

$$P_2=(\mu _{1}\mu _{2})^{2}=\frac{1}{(A_1+B_1)(A_2+B_2)}, $$
(23)

which depends on the state to be prepared, the quantum channel used and the information splitting details. Compare with the former method, the biggest success probability is lower (P 2<P 1) while it’s easier to realize. Figure 2 displays the success probability P 2 as a function of real a 1 and e 1 for the possible collections of parameters.

Fig. 2
figure 2

The success probability P 2, (23), for JRSP of a general three-qubit state |Φ〉 via three non-maximally GHZ states |GHZ〉1, |GHZ〉2 and |GHZ〉3 not introducing an auxiliary particle as a function of a 1 and e 1 for \(a=b=c=d=e=f=k \allowbreak = g=1/\sqrt{8}\), \(\alpha_{1}=\beta_{1}=\gamma_{1}=\sqrt{2/3}\), \(\alpha_{2}=\beta_{2}=\gamma_{2}=\sqrt{1/3}\), |a 1|=|b 1|=|c 1|=|d 1|, |e 1|=|f 1|=|g 1|=|k 1|

Full size image

4 Conclusion

In conclusion, we have devised two new schemes for two parties to jointly prepare an arbitrary three particle state for a third remote party. Both schemes are probabilistic and use the three non-maximally entangled GHZ states as the quantum channel. The first scheme requires the receiver to possess an ancillary qubit while the second needn’t. It shows a judicious splitting of the information doesn’t prevent the receiver from doing any operation to obtain the target state. From the result we have gotten the second scheme has lower success probabilities but easier to complete. It’s proved that the second scheme is useful in particular circumstances when the receiver’s laboratory has limited resource/equipments. Compared our scheme with Luo’s [29] scheme, the present one has the following advantages. First, we used three non-maximally GHZ states as the shared quantum channel is the obvious advantage. Because the non-maximally entangled states are easier to be prepared than maximally entangled state in experiment and non-maximally entangled states have important application in quantum information. Second, we extend the method proposed in [29] to a different information splitting method in order not to introduce an auxiliary particle on the receiver’s side. Thus the second scheme of present paper proves to be useful in particular circumstances when the receiver’s laboratory has limited resource/equipments. We hope that with the existing technology it may be possible to easily implement the probabilistic JRSP scheme.