1 Introduction

Quantum entanglement is at the heart of quantum information theory. It combines three basic structural elements of quantum theory: superposition principle, quantum non-separability property, and exponential scaling of the state space with the number of partitions [1]. This unique resource, termed as particular non-classical correlations among separated quantum systems, can be used for efficiently achieving many tasks, including quantum secret sharing [2, 3], quantum dense coding [4], and quantum entanglement concentration [5–7], quantum computation [8–11], which are impossible in classical physics.

Quantum communication is concerned with the transmission, manipulation, and detection of quantum information, of which, quantum teleportation is used for transmitting an unknown quantum state from a sender (Alice) to a spatially separate receiver (Bob) with the aid of local operations and classical communication (LOCC). Notably, there also exists another situation that for an arbitrary target state, each sender knows partially of the classical information of the target state. In this case, it naturally arises an interesting question that whether it is possible to reconstruct the wanted state in a spatially separate site. Surprisingly, this can be achieved by the so-called remote state preparation (RSP) [12–14] and joint remote state preparation (JRSP).

The basic protocol of RSP involves two parties during the quantum communication process, say, Alice and Bob, which relies on correlations between two entangled qubits to similarly prepare Bob’s qubit in a particular state determined by Alice, conditioned on the result of a measurement on her qubit. This means RSP transmits a known state within LOCC, requiring that they succeed not exactly but only with high fidelity. However, unlike teleportation, RSP does not require the sender to perform full Bell-state analysis, which is currently experimental challenging for optical implementations. Meanwhile, it has been shown that classical communication cost for transmitting a known state via RSP is less than that of teleportation [14]. On the other hand, JRSP is designed for manipulation of quantum information in quantum communication, namely retrieval of the target state in a quantum networks between multi-sender and one receiver. In this case, the transmitted information is generally split into many subsets, and each sender owns one of the pieces. To recover the target state in receiver’s place, this protocol requires all senders to collaborate with each other. In this sense, the information security is essentially guaranteed to a large extent. Therefore, it is of practical significance to concentrate on RSP and JRSP on the demand for long-distance quantum communication and information processing.

Up to now, many theoretical investigations have been put forward for RSP [15–29] and JRSP [30–39]. For examples, optimal RSP [15], generalized RSP [16], faithful RSP [17], oblivious RSP [18, 19], RSP without oblivious conditions [20], and RSP for qubit states [21–29] have been explored. Remarkably, several RSP demonstrations have been reported by controlling over various degrees of the remotely prepared qubits [40–43]. To be explicit, Peng et al. investigated a RSP scheme by using NMR [40], Xiang et al. [41] and Peters et al. [42] proposed two RSP schemes with spontaneous parametric down-conversion. Julio et al. [43] reported the remote preparation of two-qubit hybrid entangled states, including a family of vector-polarization beams where single-photon states are encoded in the photon spin and orbital angular momentum, and then the desired state is reconstructed by means of spin-orbit state tomography and transverse polarization tomography. Recently, Liu et al. [44] demonstrated a novel implementation for arbitrary single-qubit states using Bell states as quantum resource with linear optical system. Nevertheless, after the transmission of entanglement through a practical channel with noise and storage into entangled systems, the employed Bell state, used as the entangled resource, will become a mixed entangled state or a partially entangled pure state. Furthermore, in comparison with the maximally entangled state, a partially entangled state is more general and relatively practical to be realized in the laboratory. Therefore, we explore single-photon-assistance RSP and JRSP protocols of an arbitrary single-photon state with partially entangled states as quantum channels. In particular, we also derive the success probability and classical communication cost (CCC) for the two communication protocols.

2 The RSP scheme

In this section, we will demonstrate how to remotely prepare an arbitrary single-photon pure state \(|P\rangle =\alpha |H\rangle +\beta \mathrm{e}^{i\theta }|V\rangle \) from a partially entangled biphotonic state with an ancillary single photon and linear optical elements, where H (V) denotes the horizontal (vertical) photon polarization, the real-valued \(\alpha \) and \(\beta \) satisfy the normalized condition, and \(\theta \in [0,2\pi )\). Assuming that the system of two photons A and B is in the following polarization entangled state

$$\begin{aligned} |\phi _{\text {in}}\rangle _{AB}=a|H_1\rangle _A |V_2\rangle _{B}+b|V_1\rangle _A |H_2\rangle _{B}, \end{aligned}$$
(1)

where a and b are complex numbers and satisfy the normalized condition \(|a|^2+|b|^2=1\), the subscripts 1 and 2 denote spatial modes of photon transmission, and A and B represent a pair of photons shared by two remote parties in quantum communication, say Alice and Bob. To be explicit, Alice is the sender of the desired state, and Bob is the receiver. Provided that photon A is at the Bob’s laboratory, while photon B at Alice’s location.

Fig. 1
figure 1

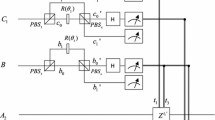
The setup for implementing RSP protocol of a single-photon state. PBS denotes polarizing beam splitter which transmits the horizontal component and reflect the vertical component, BS denotes beam splitter which is with the ratio of the transmission and reflection \(\alpha /\beta \), HWP denotes half-wave plate with included angle between its major axis and the horizontal direction \(\eta =22.5^\circ \), PM denotes phase modulator, and \(D_i\) denotes the i-th photon detector

Full size image

In order to remotely prepare each single-photon system in the desired state, Alice prepares a single photon C, the initial state of which is

$$\begin{aligned} |\phi \rangle _{C}=a|H_3\rangle _C+b|V_3\rangle _C. \end{aligned}$$
(2)

Thus, the state of the composite system ABC is expressed as

$$\begin{aligned} |\Phi \rangle _{ABC}= (a|H_1\rangle _A |V_2\rangle _{B}+b|V_1\rangle _A |H_2\rangle _{B}) \otimes (a|H_3\rangle _C+b|V_3\rangle _C). \end{aligned}$$
(3)

Alice can pick up the items with the same parameter ab with linear optical elements such as a polarizing beam splitter (PBS) and a post-selection. It is found that the a photon pair B and C have identical polarization states when the two items have the same parameter ab; otherwise, they are in two different polarization states. The experimental setup of generating entanglement for employing one pure partially entangled state as quantum channel is shown in Fig. 1. Alice lets his two photons B and C enter into PBS-1. When the two photons have the identical polarization states \(|H\rangle _B|H\rangle _C\) or \(|V\rangle _B|V\rangle _C\), they emit from the two outputs of the PBS. That is, each of the spatial modes of the PBS has one and only one photon in this time. Usually, one can call it as the two-mode instance. The polarization state \(|H\rangle _B|V\rangle _C\) will lead to the fact that the two photons emit from the same spatial mode, i.e., the upper mode, while the state \(|V\rangle _B|H\rangle _C\) will lead the two photons to emit from the down-spatial mode. That is, when the two photons emit from different spatial modes, Alice can pick up the state

$$\begin{aligned} |\phi ^1\rangle _{ABC}=ab(|H_1\rangle _A|V_4\rangle _{B}|V_5\rangle _{C}+|V_1\rangle _A |H_4\rangle _{B}|H_5\rangle _C) \end{aligned}$$
(4)

with occurrence probability of \(2|ab|^2\).

The element HWP in Fig. 1 represents a half-wave plate which operation is used to accomplish the transformation as follows

$$\begin{aligned}&|H\rangle \mapsto \frac{1}{\sqrt{2}}(|H\rangle +|V\rangle ),\nonumber \\&|V\rangle \mapsto \frac{1}{\sqrt{2}}(|H\rangle -|V\rangle ). \end{aligned}$$
(5)

After passing through the first HWP, the state of the composite system becomes

$$\begin{aligned} |\phi ^2\rangle _{ABC}&=\frac{1}{2}\left[ |H_1\rangle _A|V_4\rangle _{B}(|H_6\rangle _C-|V_6\rangle _{C})+|V_1\rangle _A |H_4\rangle _{B}(|H_6\rangle _C+|V_6\rangle _C)\right] \nonumber \\&=\frac{1}{{2}}\left[ |H_6\rangle _C(|H_1\rangle _{A}|V_4\rangle _B+|V_1\rangle _{A}|H_4\rangle _B)\right. \nonumber \\&\left. \quad +\,|V_6\rangle _C(|V_1\rangle _A|H_4\rangle _B-|H_1\rangle _A|V_4\rangle _B)\right] . \end{aligned}$$
(6)

If the photon detector \(D_1\) is triggered, that is, the state \(|H\rangle _C\) is probed by Alice, the subsystem AB will collapse into the standard Bell state \(|\phi ^+\rangle _{AB}=\frac{1}{\sqrt{2}}(|H_1\rangle _{A}|V_4\rangle _B+|V_1\rangle _{A}|H_4\rangle _B)\); Otherwise, the photon is detected in \(D_2\), this implies \(|V\rangle _C\) is attained, the remaining photons will collapse into the standard Bell state \(\frac{1}{\sqrt{2}}(|H_1\rangle _{A}|V_4\rangle _B-|V_1\rangle _{A}|H_4\rangle _B)\), which can be converted into \(|\phi ^+\rangle _{AB}\) by inserting a phase modulator PM-1 plate with transformations \(|H_4\rangle \rightarrow -|H_7\rangle \) and \(|V_4\rangle \rightarrow |V_7\rangle \).

To achieve the state with prescribed coefficients \(\alpha \) and \(\beta \), a polarization-independent beam splitter (BS-1) is used, the ratio of which transmission and reflection is equal to \(\alpha /\beta \). After passing the BS, the state of \(|\phi ^+\rangle _{AB}\) will evolve into

$$\begin{aligned} |\phi ^3\rangle _{AB}=\frac{1}{\sqrt{2}}\big [|H_1\rangle _A(\alpha |V_9\rangle _{B} +\beta |V_8\rangle _B)+|V_1\rangle _A(\alpha |H_9\rangle _{B}+\beta |H_8\rangle _B)\big ]. \end{aligned}$$
(7)

Incidentally, PM-2 is a phase modulator which is used to bring on a relative phase shift \(\mathrm{e}^{i\theta }\) to the state, namely the state of

$$\begin{aligned} |\phi ^4\rangle _{AB}=\frac{1}{\sqrt{2}}\left[ |H_1\rangle _A(\alpha |V_9\rangle _{B} +\beta {\mathrm{e}^{i\theta }}|V_8\rangle _B)+|V_1\rangle _A(\alpha |H_9\rangle _{B}+\beta {\mathrm{e}^{i\theta }}|H_8\rangle _B)\right] \end{aligned}$$
(8)

will be obtained as PM-2 is applied to the path 8.

Next, let the two photons pass the third PBS, and thus the systemic state is given by

$$\begin{aligned} |\phi ^5\rangle _{AB}=\frac{1}{\sqrt{2}}\left[ |H_1\rangle _A(\alpha |V_R\rangle _{B} +\beta {\mathrm{e}^{i\theta }}|V_L\rangle _B)+|V_1\rangle _A(\alpha |H_L\rangle _{B}+\beta {\mathrm{e}^{i\theta }}|H_R\rangle _B)\right] . \end{aligned}$$
(9)

Subsequently, photons A and B go through a HWP, respectively. This leads to the state of

$$\begin{aligned} |\phi ^6\rangle _{AB}&=\frac{1}{2}\left\{ |H_1\rangle _A\left[ \alpha (|H_{R_1}\rangle _B-|V_{R_1}\rangle _B)+\beta {\mathrm{e}^{i\theta }}(|H_{L_1}\rangle _B-|V_{L_1}\rangle _B)\right] \right. \nonumber \\&\left. \quad +\,|V_1\rangle _A\left[ \alpha (|H_{L_1}\rangle _B+|V_{L_1}\rangle _B)+\beta {\mathrm{e}^{i\theta }}(|H_{R_1}\rangle _B+|V_{R_1}\rangle _B)\right] \right\} \nonumber \\&=\frac{1}{2}\left[ |H_{R_1}\rangle _B(\alpha |H_1\rangle _A+\beta {\mathrm{e}^{i\theta }}|V_{1}\rangle _A)]+|V_{R_1}\rangle _B(-\alpha |H_1\rangle _A+\beta {\mathrm{e}^{i\theta }}|V_{1}\rangle _A)\right. \nonumber \\&\left. \quad +\,|H_{L_1}\rangle _B(\alpha |V_1\rangle _A+\beta {\mathrm{e}^{i\theta }}|H_{1}\rangle _A)+|V_{L_1}\rangle _B(\alpha |V_1\rangle _A-\beta {\mathrm{e}^{i\theta }}|H_{1}\rangle _A)\right] . \end{aligned}$$
(10)

From Eq. (10), one can see that if the detector \(D_3\) is triggered, Alice realizes his photon is the state of \(|H\rangle _B\) in the path \(R_1\), and then she informs Bob of this outcome via classical bits “00,” and Bob realizes that the output state \(|\phi _{\text {out}}\rangle \) of his photon has been the target state \(|P\rangle \). If any one of other detectors is triggered, Alice informs Bob of this outcome via classical channels, Bob realizes that his photon has been the target state as long as operating an appropriate unitary transformation U, which has been explicitly shown in Table 1. The total success probability (TSP) of the current scheme is \(2|ab|^2\) associated with the employed entanglement as shown in Fig. 2, and CCC is 2 cbits.

Table 1 OAD represents outcome of Alice detector, CCC represents classical communication cost, BCS represents Bob’s photon collapsed state and U represents appropriate unitary operations performed by Alice on her photon A
Full size table
Fig. 2
figure 2

The total success probability (TSP) is plotted as a function of the coefficient |a| from the employed channel

Full size image
Fig. 3
figure 3

The setup for implementing JRSP protocol of a single-photon polarization state. PBS denotes polarizing beam splitter which transmits the horizontal component and reflects the vertical component, BS-1 denotes a beam splitter which is with the ratio of the transmission and reflection \(\alpha _1/\beta _1\), BS-2 denotes a beam splitter which is with the ratio of the transmission and reflection \(\alpha _2/\beta _2\), HWP denotes half-wave plate with \(\eta =22.5^\circ \), PM denotes phase modulator, \(D_i\) denotes the i-th photon detector, and U denotes an unitary operation on Bob’s photon A

Full size image

3 The JRSP scheme

At this stage, we turn to present a feasible JRSP scheme for remotely preparing a single-photon pure state \(|{P}\rangle ={\alpha }|H\rangle +{\beta }\mathrm{e}^{i\theta }|V\rangle \) from a partially entangled GHZ state among multipartite agents. Assume that \({\alpha }=\alpha _1\cdot \alpha _2\), \({\beta }=\beta _1\cdot \beta _2\) and \({\theta }=\theta _1+\theta _2\), and Alice has knowledge of \(\alpha _1\), \(\beta _1\) and \(\theta _1\), while Bob knows the remaining information of the state. In this case, there is a system of three-photon ABC with a general polarization entangled state

$$\begin{aligned} |\varphi _\mathrm{{in}}\rangle _{ABC}=a|H_1\rangle _{A}|H_2\rangle _{B}|H_3\rangle _{C} +b|V_1\rangle _{A}|V_2\rangle _{B}|V_3\rangle _{C}, \end{aligned}$$
(11)

where the complex numbers a and b satisfy the normalized condition \(|a|^2+|b|^2=1\), and the subscripts 1, 2 and 3 represent spatial transmission modes of photons, and A, B and C represent the three photons shared by three remote parties in quantum communication, say Alice, Bob and Charlie. To be explicit, Alice and Bob are the senders of the wanted state, Charlie is the receiver, and photon A, B, and C belong to Charlie, Bob and Alice, respectively.

In order to remotely prepare each single-photon system in the desired state, Alice needs to prepare a single photon D in a state of

$$\begin{aligned} |\varphi \rangle _{D}=b|H_4\rangle _D+a|V_4\rangle _D. \end{aligned}$$
(12)

Thus, the state of the composite system of ABCD will be

$$\begin{aligned} |\Psi \rangle _{ABCD}=\big (a|H_1\rangle _{A}|H_2\rangle _{B}|H_3\rangle _{C}+b|V_1\rangle _{A}|V_2\rangle _{A} |V_3\rangle _{C}\big )\otimes \big (b|H_4\rangle _D+a|V_4\rangle _D\big ). \end{aligned}$$
(13)

Alice can pick up the items with the same parameter ab with linear optical elements, e.g., a polarization beam splitter (PBS) and a post-selection. It is not difficult to find that the two photons C and D have identical polarization states when the two items have the same parameter ab; otherwise, they are in two different polarization states. The experimental setup of jointly generating entanglement for arbitrary pure single-photon states is shown in Fig. 3. Alice lets his two photons C and D enter into PBS-1. Alice chooses the two outputs of the PBS via two-mode instance. That is, when C and D emit from different spatial modes, Alice can pick up

$$\begin{aligned} |{\varphi }^1\rangle _{ABCD}=ab\big (|H_1\rangle _A|H_2\rangle _{B}|H_6\rangle _{C}|H_5\rangle _{D}+|V_1\rangle _A |V_2\rangle _B|V_6\rangle _{C}|V_5\rangle _D\big ). \end{aligned}$$
(14)

with probability of \(2|ab|^2\).

Through a HWP, the state of the composite system evolves to

$$\begin{aligned} |{\varphi }^2\rangle _{ABCD}&=\frac{1}{\sqrt{2}}\left[ (|H_1\rangle _A|H_2\rangle _{B}|H_6\rangle _{C} (|H_5\rangle _D+|V_5\rangle _{D})\right. \nonumber \\&\left. \quad +|V_1\rangle _A |V_2\rangle _{B}|V_6\rangle _{C}(|H_5\rangle _D-|V_5\rangle _D)\right] \nonumber \\&=\frac{1}{\sqrt{2}}\left[ (|H_5\rangle _D(|H_1\rangle _{A}|H_2\rangle _B|H_6\rangle _C +|V_1\rangle _{A}|V_2\rangle _B|V_6\rangle _C)\right. \nonumber \\&\left. \quad +|V_5\rangle _D(|H_1\rangle _A|H_2\rangle _B|H_6\rangle _C-|V_1\rangle _A|V_2\rangle _B|V_6\rangle _C)\right] . \end{aligned}$$
(15)

When the photon detector \(D_1\) is triggered, i.e., Alice obtains the state \(|H\rangle _D\), the system ABC will collapse into a three-photon Greenberger–Horne–Zeilinger state \(|\varphi ^+\rangle _{ABC}=\frac{1}{\sqrt{2}}(|H_1\rangle _{A}|H_2\rangle _B|H_6\rangle _C +|V_1\rangle _{A}|V_2\rangle _B|V_6\rangle _C)\). Otherwise, the photon is detected in \(D_2\), this implies \(|V\rangle _D\) is attained, the subsystem ABC will collapse into the state \(\frac{1}{\sqrt{2}}(|H_1\rangle _{A}|H_2\rangle _B|H_6\rangle _C-|V_1\rangle _{A}|V_2\rangle _B|V_6\rangle _C)\), which can be converted into \(|\varphi ^+\rangle _{ABC}\) by inserting a phase modulator (PM-1) plate with transformations \(|H_6\rangle \rightarrow |H_7\rangle \) and \(|V_6\rangle \rightarrow -|V_7\rangle \).

To get \(\alpha _1\) and \(\beta _1\), Alice incorporates a polarization-independent beam splitter (BS-1) with the ratio of transmission and reflection coefficients equals to \(\alpha _1/\beta _1\). Meanwhile, PM-2 is added in path 9, which is a phase modulator with changing a relative phase \(\mathrm{e}^{i\theta _1}\) to the state. After going through the BS-1 and PM-2, the state of \(|\varphi ^+\rangle _{ABC}\) will evolve into

$$\begin{aligned} |\varphi ^3\rangle _{ABC}&=\frac{1}{\sqrt{2(\alpha _1^2+\beta _1^2)}}\Big [|H_1\rangle _A|H_2\rangle _B (\alpha _1|H_9\rangle _{C}\nonumber \\&\quad +\beta _1{\mathrm{e}^{i\theta _1}}|H_8\rangle _C)+ |V_1\rangle _A|V_2\rangle _B(\alpha _1|V_9\rangle _{C}+\beta _1{\mathrm{e}^{i\theta _1}}|V_8\rangle _C)\Big ]. \end{aligned}$$
(16)

To achieve JRSP, let the photon C pass PBS-3, the whole state is now reduced to

$$\begin{aligned} |\varphi ^4\rangle _{ABC}&=\frac{1}{\sqrt{2(\alpha _1^2+\beta _1^2)}}\Big [|H_1\rangle _A|H_2\rangle _B (\alpha _1|H_L\rangle _{C}\nonumber \\&\quad +\beta _1{\mathrm{e}^{i\theta _1}}|H_R\rangle _C)+ |V_1\rangle _A|V_2\rangle _B(\alpha _1|V_R\rangle _{C}+\beta _1{\mathrm{e}^{i\theta _1}}|V_L\rangle _C)\Big ]. \end{aligned}$$
(17)

Then, photons B and C will pass a HWP, which leads the above reduced state to

$$\begin{aligned} |\varphi ^5\rangle _{ABC}&=\frac{1}{2\sqrt{\alpha _1^2+\beta _1^2}}\Big \{|H_1\rangle _A|H_2\rangle _B \Big [\alpha _1(|H_{L_1}\rangle _C+|V_{L_1}\rangle _C)\nonumber \\&\quad +\beta _1{\mathrm{e}^{i\theta _1}} (|H_{R_1}\rangle _C+|V_{R_1}\rangle _C)\Big ]+|V_1\rangle _A|V_2\rangle _B \left[ \alpha _1(|H_{R_1}\rangle _C-|V_{R_1}\rangle _C)\right. \nonumber \\&\left. \quad +\beta _1{\mathrm{e}^{i\theta _1}} (|H_{L_1}\rangle _C-|V_{L_1}\rangle _C)\right] \Big \}\nonumber \\&=\frac{1}{2\sqrt{\alpha _1^2+\beta _1^2}}\Big [|H_{L_1}\rangle _C (\alpha _1|H_1\rangle _A|H_2\rangle _B\nonumber \\&\quad +\beta _1{\mathrm{e}^{i\theta _1}}|V_{1}\rangle _A|V_{2}\rangle _B) +|V_{L_1}\rangle _C(\alpha _1|H_1\rangle _A|H_2\rangle _B\nonumber \\&\quad -\beta _1{\mathrm{e}^{i\theta _1}}|V_{1}\rangle _A|V_{2}\rangle _B) +|H_{R_1}\rangle _C(\beta _1{\mathrm{e}^{i\theta _1}}|H_1\rangle _A|H_2\rangle _B\nonumber \\&\quad +\alpha _1|V_{1}\rangle _A|V_{2}\rangle _B)+|V_{R_1}\rangle _C(\beta _1{\mathrm{e}^{i\theta _1}} |H_1\rangle _A|H_2\rangle _B-\alpha _1|V_{1}\rangle _A|V_{2}\rangle _B)\Big ]. \end{aligned}$$
(18)

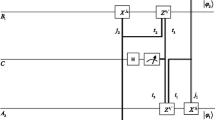
Without losing the generality, suppose that the detector \(D_3\) is triggered, Alice realizes his photon is the state of \(|H_{R_1}\rangle _C\), and then she informs Bob of this outcome via classical bits “10,” and Bob realizes that the output state of his photon has been the state of \(\frac{1}{\sqrt{\alpha _1^2+\beta _1^2}}(\alpha _1|V_1\rangle _A|V_2\rangle _B +\beta _1{\mathrm{e}^{i\theta _1}}|H_{1}\rangle _A|H_{2}\rangle _B)\). After that, Bob lets his photon pass a beam splitter (BS-2) with the ratio of transmission and reflection to be \(\alpha _2/\beta _2\) and a phase modulator (PM-4) with altering a phase of \(\theta _2\), the state of AB will become

$$\begin{aligned} |\varphi ^6\rangle _{AB}&=\frac{1}{\sqrt{(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}} \Big [\alpha _1|V_1\rangle _A(\alpha _2|V_{11}\rangle _B\nonumber \\&\quad +\,\beta _2{\mathrm{e}^{i\theta _2}}|V_{10}\rangle _B) +\beta _1\mathrm{e}^{i\theta _1}|H_{1} \rangle _A(\alpha _2|H_{11}\rangle _B+\beta _2{\mathrm{e}^{i\theta _2}}|H_{10}\rangle _B)\Big ]. \end{aligned}$$
(19)

Then, it will lead to

$$\begin{aligned} |\varphi ^7\rangle _{AB}&=\frac{1}{\sqrt{(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}} \Big [\alpha _1|V_1\rangle _A(\alpha _2|V_{12}\rangle _B\nonumber \\&\quad +\beta _2{\mathrm{e}^{i\theta _2}}|V_{14}\rangle _B)+\beta _1\mathrm{e}^{i\theta _1}|H_{1}\rangle _A (\alpha _2|H_{14}\rangle _B+\beta _2{\mathrm{e}^{i\theta _2}}|H_{12}\rangle _B)\Big ] \end{aligned}$$
(20)

on the basis of PBS-6. Subsequently, two HWPs in paths 12 and 14 will transfer \(|\varphi ^7\rangle _{AB}\) into

$$\begin{aligned}&\frac{1}{\sqrt{2(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}}\Big \{\Big [\alpha _1|V_1\rangle _A [\alpha _2(|H_{13}\rangle _B-|V_{13}\rangle _B)\nonumber \\&\quad +\beta _2{\mathrm{e}^{i\theta _2}}(|H_{15}\rangle _B-|V_{15}\rangle _B)] +\beta _1\mathrm{e}^{i\theta _1}|H_{1}\rangle _A[\alpha _2(|H_{15}\rangle _B\nonumber \\&\quad +|V_{15}\rangle _B)+\beta _2{\mathrm{e}^{i\theta _2}}(|H_{13}\rangle _B+|V_{13}\rangle _B)\Big ]\Big \}\nonumber \\&=\frac{1}{\sqrt{2(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}}\Big [|H_{13}\rangle _B (\alpha _1\alpha _2|V_1\rangle _A\nonumber \\&\quad +\beta _1\beta _2\mathrm{e}^{i(\theta _1+\theta _2)}|H_1\rangle _A)+|V_{13}\rangle _B (-\alpha _1\alpha _2|V_1\rangle _A\nonumber \\&\quad +\beta _1\beta _2\mathrm{e}^{i(\theta _1+\theta _2)}|H_1\rangle _A)+|H_{15}\rangle _B (\alpha _1\beta _2\mathrm{e}^{i\theta _2}|V_1\rangle _A\nonumber \\&\quad +\beta _1\alpha _2\mathrm{e}^{i\theta _1}|H_1\rangle _A)+|V_{15}\rangle _B (-\alpha _1\beta _2\mathrm{e}^{i\theta _2}|V_1\rangle _A+\beta _1\alpha _2\mathrm{e}^{i\theta _1}|H_1\rangle _A)\Big ]. \end{aligned}$$
(21)

According to Eq. (21), one can see that the target state has been recovered by Charlie with the operation of \(\sigma _x\) or \(\sigma _x\sigma _z\) on photon A, when Bob’s photon detector \(D_7\) or \(D_8\) is triggered. In this case, the success probability should be \(2|ab|^2\times \frac{1}{4}\times 2\times \left( \frac{1}{\sqrt{2(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}}\right) ^2 =\frac{|ab|^2}{2(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}\).

Table 2 The symbol “\(\surd \)” represents the triggered detector, the symbol “\(\times \)” represents the untriggered detector and U represents appropriate unitary recovering operations Charlie needs to make on his photon A
Full size table

In addition, Alice’s outcome may be one of other three outcomes \(|H_{L_1}\rangle _C\), \(|V_{L_1}\rangle _C\) and \(|V_{R_1}\rangle _C\). If so, the target state can be recovered in Charlie’s photon A by making the corresponding transformation on his photon. For clearness, possible positive outcomes of the senders’ detectors and Charlie’s required operations have been shown in Table 2, respectively. Therefore, the total success probability is \(\frac{2|ab|^2}{(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)}\) as shown in Figs. 4 and 5. From the figures, one can conclude that: (1) TSP increases with the increase of \(\alpha _1/\beta _1\) when \(\alpha =0\), i.e., the target state is reduced into \(|V\rangle \). (2) TSP will reach an extremum when \(\alpha _1/\beta _1=1\) and \(\alpha \ne 0\). (3) TSP is less than 0.5 all the time. (4) TSP is 25%, which is independent of the prepared state, if \(\alpha _1/\beta _1=1\) and \(|a|=1/\sqrt{2}\). Meanwhile, according to the required communication among Alice, Bob and Charlie, one can get that CCC is up to 4 cbits.

Fig. 4
figure 4

The TSP is plotted as a function of coefficient |a| with different ensembles of target states. Graph a: \(\alpha =0\) and Graph b: \(\alpha =1/\sqrt{2}\)

Full size image
Fig. 5
figure 5

The TSP is plotted as a function of coefficient \(\alpha \) with different values of \(\alpha _1/\beta _1\) when \(|a|=1/\sqrt{2}\)

Full size image

4 Extensions

4.1 RSP for a mixed state

In this subsection, we briefly derive RSP protocol for a mixed state with the current setup as displayed in Fig. 1. To prepare a mixed state, PBS-4, \(D_3\) and \(D_4\) are replaced by a polarization analyzer (called as PA-1) and PBS-5, \(D_5\) and \(D_6\) are replaced by another polarization analyzer (PA-2), and thus photon B is measured in a polarization-insensitive way. By this, one can prepare photon A in the mixed state. In terms of detection of photon B on path L or R, the mixed state is

$$\begin{aligned} \rho _A^L=\mathrm{Tr}_B\Big [(|H_L\rangle _B\langle H_L|+|V_L\rangle _B\langle V_L|)\rho _{AB}\Big ]=\alpha ^2|V_1\rangle _A\langle V_1|+\beta ^2|H_1\rangle _A\langle H_1| \end{aligned}$$
(22)

or

$$\begin{aligned} \rho _A^R=\mathrm{Tr}_B\Big [(|H_R\rangle _B\langle H_R|+|V_R\rangle _B\langle V_R|)\rho _{AB}\Big ]=\alpha ^2|H_1\rangle _A\langle H_1|+\beta ^2|V_1\rangle _A\langle V_1| \end{aligned}$$
(23)

where \(\rho _{AB}=|\phi ^5\rangle _{AB}\langle \phi ^5|\).

4.2 JRSP for a mixed state

For a mixed state, our JRSP setup shown as Fig. 2 is available as well. Here, we simply illustrate the JRSP protocol for a mixed state with the current setup. To prepare mixed states, PBS-7, \(D_7\) and \(D_8\) are replaced by a polarization analyzer and PBS-8, \(D_9\) and \(D_{10}\) are replaced by another polarization analyzer. In this way, photon B is measured in a polarization-insensitive way. Relying on such actions, one can prepare photon A in mixed states. According to detection of photon B on path 12 or 14, one can compute that the mixed state is given by

$$\begin{aligned} \rho _A^{12}=\mathrm{Tr}_B\left[ (|H_{12}\rangle _B\langle H_{12}|+|V_{12}\rangle _B\langle V_{12}|)\rho '_{AB}\right] =\alpha ^2|V_1\rangle _A\langle V_1|+\beta ^2|H_1\rangle _A\langle H_1| \end{aligned}$$
(24)

or

$$\begin{aligned} \rho _A^{14}=\mathrm{Tr}_B\left[ (|H_{14}\rangle _B\langle H_{14}|+|V_{14}\rangle _B\langle V_{14}|)\rho {'}_{AB}\right] =\alpha ^2|H_1\rangle _A\langle H_1|+\beta ^2|V_1\rangle _A\langle V_1| \end{aligned}$$
(25)

where \(\rho {'}_{AB}=|\varphi ^7\rangle _{AB}\langle \varphi ^7|\).

4.3 Single-photon-assisted JRSP with N-party

Note that our JRSP scheme can be extended to a N-sender (\(N>2\)) case. Suppose there are N sender, say, Alice\(_1\), Alice\(_2\), \(\ldots \), Alice\(_N\), who would like to recover a single-photon pure state \(|{P}\rangle ={\alpha }|H\rangle +{\beta }\mathrm{e}^{i\theta }|V\rangle \) in Bob’s site. Assume that \({\alpha }=\alpha _1\alpha _2\cdots \alpha _N\), \({\beta }=\beta _1\beta _2\cdots \beta _N\) and \({\theta }=\theta _1+\theta _2+\cdots +\theta _N\), and Alice\(_i\) has knowledge of \(\alpha _i\), \(\beta _i\) and \(\theta _i\). Now there is a system with a N-qubit GHZ-type state

$$\begin{aligned} |\psi _\mathrm{{in}}\rangle _{A_1A_2\cdots A_NB}=a|H_1\rangle _{A_1}\cdots |H_N\rangle _{A_N}|H_{N+1}\rangle _{B}+b|V_1\rangle _{A_1}\cdots |V_N\rangle _{A_N}|V_{N+1}\rangle _{B}, \end{aligned}$$
(26)

shared by multipartite participants. In Eq. (26), the complex numbers a and b satisfy the normalized condition, and the subscript \(i\ (i=1,2,\ldots ,N)\) represents spatial transmission modes of photons, and \(A_i\) labels the photons shared by those parties in quantum communication. To be explicit, photon \(A_i\) belongs to Alice\(_i\), and B to Bob. In order to remotely prepare each single-photon system in the desired state, Alice\(_1\) needs to prepare a single photon C with state of

$$\begin{aligned} |\varphi \rangle _{C}=b|H_{N+1}\rangle _C+a|V_{N+1}\rangle _C. \end{aligned}$$
(27)

By applying two-mode instances and the similar analysis methods as the case of two senders, Alice\(_i\ (i=3,4,\ldots ,N)\) can construct the same optical elements as those by Alice\(_2\), except that PM-\((i+2)\) added by Alice\(_i\) is with a relative phase \(\mathrm{e}^{\theta _i}\) in her path after the BS-i. For simplicity, we do not depict it any more. Upon classical communication for their measuring outcomes, Bob can realize which state his photon is. If his collapsed state can be converted into the desired state via appropriate unitary transformation, this shows that our JRSP can be successful; otherwise, Bob needs to restart the preparation procedure. Through some recursive calculations, one can obtain that TSP of the protocol is \(\frac{|ab|^2}{2^{(N-3)}(\alpha _1^2+\beta _1^2)(\alpha _2^2+\beta _2^2)\cdots (\alpha _N^2+\beta _N^2)}\) and CCC is up to \(2^N\) cbits.

5 Conclusion

To conclude, we have designed two optics-based implementations for RSP and JRSP of an arbitrary single-photon pure state by taking advantage of linear optics elements and partially entangled states as quantum resources, respectively. With the aid of suitable LOCC, our RSP protocol can be realized with certain success probability related to the employed entanglements, and the JRSP protocol can be achieved with a success probability characterized by the coefficients of both the employed entanglements and the ensembles of the target states, and we compute CCC for the two communication protocols as well, respectively. Interestingly, we have illustrated that the current proposals are available for implementing RSP and JRSP for a mixed state by means of the required replacement of photon detectors with polarization analyzers. In addition, the JRSP protocol can also be generalized to the case of N-sender with taking multi-photon partial entanglements as quantum channels. Furthermore, we believe that the present proposals might be importance of optics-based quantum communication in prospective multi-node quantum networks.