1 Introduction

Quantum correlations are an important resource theory and play a crucial role in several promising fields (Nielsen and Chuang 2010; Adesso et al. 2016). Quantifying these correlations in quantum systems is a significant challenge, and various measures have been proposed (Wootters 1998; Ollivier and Zurek 2001; Henderson and Vedral 2001; Paula et al. 2013a, b). Recently, local quantum uncertainty (LQU) has emerged as a discord-like correlation to assess quantum correlations in multipartite systems and possesses desirable traits required of a genuine NCC quantifier (Girolami et al. 2013; Wigner and Yanase 1963; Luo 2004). Additionally, LQU has a close relationship with quantum Fisher information (QFI), which makes it a common tool in quantum metrology (Giovannetti et al. 2011; Slaoui et al. 2019). QFI quantifies the precision with which a quantum state can estimate an unknown physical parameter. Experimental methods for extracting QFI from arbitrary quantum states are a major challenge and a subject of current interest (Yu et al. 2021; Beckey et al. 2022). More recently, local quantum Fisher information (LQFI) was demonstrated to be an effective means of quantifying NCC using QFI (Kim et al. 2018). This involves minimizing QFI with respect to a locally informative observable associated with a specific subsystem. Additionally, LQFI has the potential to serve as a valuable tool for elucidating the influence of quantum correlations and enhancing the precision and efficacy of quantum estimation protocols. LQU and LQFI have been studied in various specific two-qubit systems (Haseli 2020; Muthuganesan and Chandrasekar 2021; Mohamed and Eleuch 2022; Elghaayda et al. 2022; Benabdallah et al. 2022; Dahbi et al. 2023; Yurischev and Haddadi 2023; Dakir et al. 2023).

Quantum coherence (QC) is another essential concept in quantum physics that plays a critical role in numerous applications. As such, detecting and quantifying coherence is an essential task (Radhakrishnan et al. 2017). The difference between quantum and classical coherence has historically been revealed through phase space distributions and multi-point correlation functions (Glauber 1963; Sudarshan 1963; Scully et al. 1997). Recently, Baumgratz and co-workers developed a scheme for measuring coherence based on the framework of quantum information theory, which provides a more rigorous quantification of coherence (Baumgratz et al. 2014). Significant advancements in understanding the theory of QC have been completed, paving the way for better utilization as a resource in QIP (Yao et al. 2015; Hu et al. 2018).

One of the defining principles of quantum mechanics is the uncertainty relation, which limits the accuracy of joint measurements of incompatible observables. The most prominent uncertainty relation is expressed by (Kennard 1927; Robertson 1929):

$$\begin{aligned} \Delta \hat{\mathscr{Q}} \cdot \Delta \hat{\mathscr{R}} \ge \frac{1}{2}|\langle [\hat{\mathscr{Q}}, \hat{\mathscr{R}}]\rangle |, \end{aligned}$$
(1)

where \(\Delta \hat{\mathscr {Q}}=\sqrt{\left\langle \hat{\mathscr {Q}}^2\right\rangle -\langle \hat{\mathscr {Q}}\rangle ^2}, \Delta \hat{\mathscr {R}}=\sqrt{\left\langle \hat{\mathscr {R}}^2\right\rangle -\langle \hat{\mathscr {R}}\rangle ^2}\) denotes the mean quadratic deviations (i.e., the variances) of \(\hat{\mathscr {Q}}\) and \(\hat{\mathscr {R}}\), respectively, and \(|\langle [\hat{\mathscr {Q}}, \hat{\mathscr {R}}]\rangle |\) is the mean value of the commutator \([\hat{\mathscr {Q}}, \hat{\mathscr {R}}]=\hat{\mathscr {Q}} \hat{\mathscr {R}}-\hat{\mathscr {R}} \hat{\mathscr {Q}}\) in a quantum state \(|\psi \rangle\). However, the lower bound of inequality (1) is state-dependent, such that if the system is prepared in one of the eigenvectors of \(\hat{\mathscr {Q}}\) or \(\hat{\mathscr {R}}\), the inequality will be trivial, and \(|\langle [\hat{\mathscr {Q}}, \hat{\mathscr {R}}]\rangle |=0\). In this context, an innovative method for characterizing the uncertainty relation was proposed by Deutsch (Deutsch 1983) and subsequently elaborated on by Kraus (Kraus 1987). Eventually, Massen and Uffink reformulated an uncertainty relation utilizing Shannon entropy, expressed in the following form (Maassen and Uffink 1988):

$$\begin{aligned} H(\hat{\mathscr {Q}})+H(\hat{\mathscr {R}}) \ge \log _2 \frac{1}{c}, \end{aligned}$$
(2)

where \(H(\hat{\mathscr {X}})= -\sum _m p_m \log _2 p_m\) is the Shannon entropy of the observable \(\hat{\mathscr {X}} \equiv \lbrace \hat{\mathscr {Q}},\hat{\mathscr {R}} \rbrace\), \(p_m=\langle \phi ^{\hat{\mathscr {X}}}_m|{\hat{\rho }}|\phi ^{\hat{\mathscr {X}}}_m\rangle\) is the probability of obtaining the m-th outcome, \(|\phi ^{\hat{\mathscr {X}}}_m\rangle\) denotes the eigenvectors of the observables \(\hat{\mathscr {X}}\) (Rastegin 2016; Wang et al. 2017). The parameter \(c \equiv \max _{j,k}\lbrace |\langle \varphi ^{\hat{\mathscr {Q}}}_j |\Psi ^{\hat{\mathscr {R}}}_k\rangle |^2\rbrace\) is the maximal overlap of the observables \(\hat{\mathscr {Q}}\) and \(\hat{\mathscr {R}}\), where \(|\varphi ^{\hat{\mathscr {Q}}}_j\rangle\) and \(|\Psi ^{\hat{\mathscr {R}}}_k\rangle\) are the eigenvectors of \(\hat{\mathscr {Q}}\) and \(\hat{\mathscr {R}}\), respectively.

Recently, a novel uncertainty relation referred to as the entropic uncertainty relation (EUR) with quantum memory has been introduced. The relation employs a quantum particle, serves as a memory, and is more efficient than the previous inequality (2). Berta et al. proposed EUR and strictly proved the following inequality (Berta et al. 2010):

$$\begin{aligned} S(\hat{\mathscr {Q}}|B)+S(\hat{\mathscr {R}}|B)\ge S(A|B)-\log _2 c. \end{aligned}$$
(3)

The conditional von Neumann entropy, denoted by \(S(A|B)=S({\hat{\rho }}^{AB})-S({\hat{\rho }}^B)\), is a measure of the degree of entanglement between particle A and the quantum memory B. The left-hand side of inequality (3), \(S(\hat{\mathscr {X}}|B)=S({\hat{\rho }}^{\hat{\mathscr {X}},B})-S({\hat{\rho }}^B)\), represents the uncertainty in the measurement results of \(\hat{\mathscr {X}}\), conditioned on the underlying information reserved in the particle memory B. Furthermore, \(S({\hat{\rho }}^{\hat{\mathscr {X}},B})= \sum _i \nu _i \log _2 \nu _i\), where \({\hat{\rho }}^{\hat{\mathscr {X}},B}= \sum _i (\Pi _i^{\hat{\mathscr {X}}} \otimes {\hat{1\hspace{-4pt}1}}_B){\hat{\rho}}_{AB} (\Pi _i^{\hat{\mathscr {X}}} \otimes {\hat{1\hspace{-4pt}1}}_B)\) is the post-measurement state, \(\lbrace \nu _i \rbrace\) are the eigenvalues of \({\hat{\rho }}^{\hat{\mathscr {X}},B}\), and \(\Pi _i^{\hat{\mathscr {X}}}=|\phi _i^{\hat{\mathscr {X}}} \rangle \langle \phi _i^{\hat{\mathscr {X}}}|\) is the projector on the \(\hat{\mathscr {X}}\) eigenspace (Nielsen and Chuang 2010; Yang et al. 2019). Interestingly, the comparison between lower bounds reveals that the one of inequality (3) is tighter than (2) because particle A is entangled with the quantum memory B, and consequently, S(A|B) is negative. This leads to a reduction in the uncertainty of Bob’s prediction of Alice’s outcome. In particular, if the particles are maximally entangled, i.e., \(S(A|B) = -\log _2 d\) where d is the dimension of particle A (here, \(d=2\)), Bob can perfectly predict Alice’s measurement results. The EUR of inequality (3) has been successfully demonstrated in all-optical setups through various experiments (Prevedel et al. 2011; Li et al. 2011; Wang et al. 2019).

Quantum phase transitions (QPTs) remain a fundamental concept in the condensed matter field, and they occur by tuning external parameters (Sachdev 1999). Unlike thermal phase transitions, quantum fluctuations play a significant role at absolute zero temperature (Haravifard et al. 2015). To investigate these phenomena, quantum spin systems are commonly utilized, and NCCs measurements are crucial in detecting QPTs of interest (Hui et al. 2017). Spin models such as Ising, XY, and XXZ are frequently employed to study these systems (Huang 2014; Ait Chlih et al. 2022). Nonetheless, there exist practical exchange interactions in spin models that require consideration, particularly spin-orbit couplings (SOCs) in transition metal oxides. Recent advancements in materials synthesis and heterostructure design have significantly enhanced the development of new models for SOCs (Zvyagin 2020; Liu et al. 2021). It is crucial to consider the off-diagonal components when examining the properties of real magnetic materials. These off-diagonal exchange interactions are a unique form of SOCs that commonly emerge in materials with a spin liquid ground state (Zvyagin 2020). The Dzyaloshinskii-Moria (DM) coupling refers to the nonsymmetric under the exchange of spins off-diagonal components of the exchange interaction (Dzyaloshinsky 1958; Moriya 1960). The antisymmetric DM exchange interactions are fundamental to many magnetic phenomena, such as weak ferromagnetism, spin spirals, and skyrmion lattices (Kim et al. 2018; Mühlbauer et al. 2009). The symmetric off-diagonal components, also known as \(\Gamma\) couplings, are crucial in the interaction of orbitals in strongly correlated electron systems (Biskup et al. 2005; Oleś et al. 2006), particularly in the so-called compass models or in the so-called Kitaev materials, where their origin is related to pseudo-dipolar interactions (Rau et al. 2014; Nussinov and van den Brink 2015; Yadav et al. 2016). They are also crucial in Rydberg cold atoms with van der Waals interactions and optical lattices with trapped ultracold fermions (Yang et al. 2019; Simon et al. 2011).

In light of the above, the off-diagonal interactions offer promising features while probing critical phenomena related to QPTs at zero absolute temperature. From our perspective, we intend to study the impact of off-diagonal interactions on NCCs, QC, and EUR beyond zero temperature. Since near-zero temperature is a rather challenging task in most experimental setups, thermalization emerges as a viable alternative (Sun et al. 2021; Zhu et al. 2022). In the pursuit of inducing the thermal state of a quantum system within a heat bath, Jaynes proposed a justification for this observation based on the principle of maximum entropy (Jaynes 1957a, b). Among the distinct types of thermal states, Gibbs states emerge as the most relevant (Kliesch and Riera 2018). Endeavors to engineer Gibbs states present promising prospects for simulating the physical thermalization process in quantum computers (Poulin and Wocjan 2009; Rall et al. 2023; Rouzé et al. 2024).

In quantum information, temperature plays a destructive role in quantum systems, and several studies have reported the effects of temperature-induced decoherence on quantum features (Elghaayda et al. 2023; Ait Chlih et al. 2024a, b). To unveil the influence of off-diagonal interactions, the density matrix formalism and Gibbs state are utilized when considering a Heisenberg-type model, referred to as the \(XY-\Gamma\) spin chain (Zhao et al. 2022; Kheiri et al. 2024). A detailed discussion on the technical aspects of engineering the \(XY-\Gamma\) model using Atomic-Molecular-Optical (AMO) quantum simulation is presented (Zhao et al. 2022), which involves the use of coherent photon-mediated Raman transitions, enabling accurate and efficient simulation of the model. Therefore, this model is the subject of our in-depth examination at thermal equilibrium, and we examine its behavior and thermal state properties in detail. The paper unveils the impact of temperature on quantum resources and the significance of off-diagonal interaction in the \(XY-\Gamma\) spin chain model. It explores the behavior of EUR and mixedness in response to off-diagonal interaction at finite temperatures and the influence of the magnetic field. Furthermore, it reveals the potential for reducing measurement uncertainty and facilitating information transfer from qubit A to qubit B through a filtering operation.

The paper is structured as follows: Sec. 2 presents an exploration of the physical model’s solution, including an investigation of its thermal properties. Furthermore, Sec. 3 provides definitions and explicit formulas of quantum metrics, followed by a discussion of numerical results. Besides, the paper covers analytical expressions of EUR, its lower bound, and the mixedness in Sec. 4, followed by an analysis of its numerical results. In Sec. 5, we demonstrate a strategy that entails steering the measurement uncertainty by utilizing the filtering operation. Finally, Sec. 6 concludes the paper by summarizing the findings.

2 Physical model and thermal features

2.1 Solution of the effective spin Hamiltonian

The effective Hamiltonian, which comprises various types of couplings, such as XY, DM, and symmetric off-diagonal \(\Gamma\) interactions, is presented as Zhao et al. (2022):

$$\begin{aligned} \begin{aligned} \hat{\mathcal {H}}= \sum _{n=1}^N J\left( \frac{1+\delta }{2} {\hat{s}}_n^x \otimes {\hat{s}}_{n+1}^x+\frac{1-\delta }{2} {\hat{s}}_n^y \otimes {\hat{s}}_{n+1}^y\right) +\sum _{n=1}^N\left[ \Gamma \left( {\hat{s}}_n^x \otimes {\hat{s}}_{n+1}^y+\alpha {\hat{s}}_n^y \otimes {\hat{s}}_{n+1}^x\right) +h ({\hat{s}}_n^z \otimes {\hat{1\hspace{-4pt}1}} + {\hat{1\hspace{-4pt}1}} \otimes {\hat{s}}_{n+1}^z)\right] , \end{aligned}\end{aligned}$$
(4)

where \(J \equiv J_{n, n+1}^x+J_{n, n+1}^y\) denotes the coupling strength between the nearest-neighbor atoms; hereafter, we set \(J=1\) as the energy unit for simplicity; \(\delta \equiv \frac{J_{n, n+1}^x-J_{n, n+1}^y}{J}\) serves as the anisotropy parameter; \(\Gamma \equiv J_{n, n+1}^{\textrm{DM}}+J_{n, n+1}^{\textrm{SO}}\) characterizes the amplitude of off-diagonal exchange interactions, which reduces to the DM interaction for \(\alpha = -1\) and the symmetric off-diagonal exchange interaction for \(\alpha = 1\). The parameter \(\alpha \equiv \frac{J_{n, n+1}^{\textrm{SO}}-J_{n, n+1}^{\textrm{DM}}}{\Gamma }\) represents the relative coefficient of off-diagonal exchange couplings, and h denotes the strength of the transverse magnetic field (Zhao et al. 2022).

In this study, we assume the interaction of a bipartite (2 \(\times\) 2) system consisting of two spin-\(\frac{1}{2}\) qubits, say A and B. In this case, the above Hamiltonian is rewritten as follows:

$$\begin{aligned} \begin{aligned} \hat{\mathcal {H}}= \frac{1+\delta }{2} {\hat{s}}_A^x \otimes {\hat{s}}_{B}^x+\frac{1-\delta }{2} {\hat{s}}_A^y \otimes {\hat{s}}_{B}^y +\Gamma \left( {\hat{s}}_A^x \otimes {\hat{s}}_{B}^y+\alpha {\hat{s}}_A^y \otimes {\hat{s}}_{B}^x\right) +h ({\hat{s}}_A^z \otimes {\hat{1\hspace{-4pt}1}}_B + {\hat{1\hspace{-4pt}1}}_A\otimes {\hat{s}}_{B}^z). \end{aligned} \end{aligned}$$
(5)

In the standard computational basis \(\mathcal {B}=\{\vert {00} \rangle , \vert {01} \rangle , \vert {10} \rangle , \vert {11} \rangle \}\), the Hamiltonian (eq. (5)) takes the following X-shape:

$$\begin{aligned} \hat{\mathcal {H}}= \left( \begin{array}{cccc} 2h &{} 0 &{} 0 &{} \Theta ^* \\ 0 &{} 0 &{} \Upsilon &{} 0 \\ 0 &{} \Upsilon ^* &{} 0 &{} 0 \\ \Theta &{} 0 &{} 0 &{} -2h \end{array}\right) , \end{aligned}$$
(6)

with \(\Theta = \delta +i\Gamma (1+\alpha )\), and \(\Upsilon =1+i \Gamma (1-\alpha )\).

The Hamiltonian \(\hat{\mathcal {H}}\) satisfies the eigenvalues equations:

$$\begin{aligned} \hat{\mathcal {H}}\vert {\chi ^{ \pm }_1} \rangle = e^{\pm }_1 \vert {\chi ^{ \pm }_1} \rangle , \quad \text {and}\quad \hat{\mathcal {H}}\vert {\chi ^{ \pm }_2} \rangle = e^{\pm }_2\vert {\chi ^{ \pm }_2} \rangle , \end{aligned}$$
(7)

where

$$\begin{aligned} e^{\pm }_1=\pm \vert \Upsilon \vert \qquad \text {and} \qquad e^{\pm }_2= \pm \sqrt{4h^2 + \vert \Theta \vert ^2}, \end{aligned}$$
(8)

are the eigenvalues of the Hamiltonian \(\hat{\mathcal {H}}\), and its corresponding eigenstates are the following:

$$\begin{aligned} \vert {\chi ^{ \pm }_1} \rangle =\frac{1}{\sqrt{2}}\left[ \pm e^{i \varphi _1}\vert {01} \rangle +\vert {10} \rangle \right] \qquad \text {and} \qquad \vert {\chi ^{\pm }_2} \rangle =\sqrt{\frac{e^+_2 \pm 2h}{2e^+_2}}\left[ \pm e^{-i \varphi _2}\vert {00} \rangle + \frac{\vert \Theta \vert }{e^+_2 \pm 2h}\vert {11} \rangle \right] , \end{aligned}$$
(9)

with \(\varphi _1 = \arctan \left( \Gamma (1-\alpha )\right)\) and \(\varphi _2 = \arctan \left( \frac{\Gamma (1+\alpha )}{ \delta }\right)\). Also, in eq. (9) we noted \(|0\rangle =\left( \begin{array}{l}1 \\ 0\end{array}\right)\) and \(|1\rangle =\left( \begin{array}{l}0 \\ 1\end{array}\right)\), such that \(|u v\rangle\) denotes \(|u \otimes v\rangle\) (\(u,v=0,1\)).

In the current configuration, our focus lies on conveying the effect of the physical parameters of the system. As a result, we assume all parameters that influence the quantum characteristics of the system to be dimensionless (Mohr and Phillips Dec 2014).

To thoroughly investigate the impact of temperature, subjecting the \(XY-\Gamma\) spin chain system to a thermal bath is required. The following subsection delves into the concept of a thermal state, utilizing the Gibbs state formula. This will enable the production of a state that considers temperature and Hamiltonian parameters. Such an approach is crucial for understanding the interplay between temperature and the effective Hamiltonian parameters to explore the NCCs, QC, EUR, and mixedness within the \(XY-\Gamma\) spin chain model.

2.2 Thermal density matrix

Thermal equilibrium properties are obtained by fully characterizing the thermal state of the system (Greiner et al. 2012; Uffink 2006). The relevant manner of doing this is to use the Jaynes principle, which maximizes the von Neumann entropy (Jaynes 1957a). The result is the unique state that best represents the system at thermal equilibrium, known as the Gibbs ensemble (Jaynes 1957b). This process takes place in the presence of a heat bath at a specific temperature T (canonical ensemble), the thermal density operator of the system is described by the Gibbs operator as (Wehrl 1978):

$$\begin{aligned} \hat{\rho }(T)=\frac{1}{\mathcal {Z}}\exp \{-\beta \hat{\mathcal {H}}\}=\frac{1}{\mathcal {Z}}\sum _i \exp \{-\beta e^{\pm }_i\} \vert {\chi _i^{\pm }} \rangle \langle {\chi _i^{\pm }}\vert , \end{aligned}$$
(10)

where \(e_i^{\pm }\) and \(\vert {\chi _i^{\pm }} \rangle\) (\(i=1,2\)) denote the eigenvalues and the eigenstates of the Hamiltonian (eq. (5)) respectively. Here, \(\beta =\frac{1}{k_B T}\), where \(k_B\) represents Boltzmann’s constant (for the sake of simplicity, we assume \(k_B=1\)). The parameter T denotes the absolute temperature. Thus, \(\mathcal {Z}={\text {Tr}}\lbrace \exp \{-\hat{\mathcal {H}}/T\}\rbrace\) is the partition function of the system. In the standard computational basis \(\mathcal {B}=\lbrace \vert 00\rangle ,\vert 01\rangle ,\vert 10\rangle ,\vert 11\rangle \rbrace\), the density matrix \({\hat{\rho }}(T)\) is given by:

$$\begin{aligned} \hat{\rho }(T)=\left[ \begin{array}{llll} m^- &{} 0 &{} 0 &{} \kappa \\ 0 &{} n &{} o &{} 0 \\ 0 &{} o^* &{} n &{} 0 \\ \kappa ^* &{} 0 &{} 0 &{} m^+ \end{array}\right] , \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned}&m^{\pm }=\frac{1}{\mathcal {Z}}\left[ \cosh (e^+_2 T^{-1})\pm \frac{2h}{e^+_2}\sinh (e^+_2 T^{-1})\right] , \\&n=\frac{1}{\mathcal {Z}}\left[ \cosh (e^+_1 T^{-1})\right] , \\&o=\frac{1}{\mathcal {Z}}\left[ -e^{i \varphi _1}\sinh (e^+_1T^{-1})\right] , \\&\kappa =\frac{1}{\mathcal {Z}}\left[ -\frac{\vert \Theta \vert }{e^+_2}e^{-i \varphi _2}\sinh (e^+_2 T^{-1})\right] . \end{aligned} \end{aligned}$$

The system’s partition function can be expressed as \(\mathcal {Z}=2\left[ \cosh \left( e^+_1 T^{-1}\right) + \cosh \left( e^+_2 T^{-1}\right) \right]\). It is important to note that the thermal density operator \({\hat{\rho }}(T)\) must be Hermitian and satisfy certain constraints, such as \({\text {Tr}}\{{\hat{\rho }}\}=1\), \({\hat{\rho }}^2 \ne {\hat{\rho }}\), and \({\text {Tr}}\{{\hat{\rho }}^2\}\le 1\), since it represents a mixed density state.

3 NCCs and QC metrics

This section focuses on a comparative study of thermal features in the behavior of the NCCs, specifically LQU, LQFI, and QC via JSD, as well as revealing the influence of off-diagonal interactions and transverse magnetic field. To achieve this, we provide accurate definitions and mathematical formulas for the three trustworthy metrics. We then proceed to explore and analyze the numerical results.

3.1 NCCs via LQU

Quantifying the quantumness of a given system is a crucial area of research, and one such metric is the LQU (Girolami et al. 2013). LQU pertains to the minimum quantum uncertainty associated with a single measurement on one subsystem of a two-qubit system. To this end, the Wigner-Yanase skew information of a two-qubit system with \({\hat{\rho }}\) describing its state is used to compute LQU as (Girolami et al. 2013; Wigner and Yanase 1963):

$$\begin{aligned} {{\mathcal {L}}}\left( {{{\hat{\rho }}}} \right) = 1 - \max \left( {{l _{1}},{l_{2}},{l_{3}}} \right) , \end{aligned}$$
(12)

where \(l_{i=1,2,3}\) are the eigenvalues of the \(3\times 3\) symmetric matrix denoted by \({\mathbb {L}}\) whose entries are given by:

$$\begin{aligned} {\mathbb {L}}_{ij} \equiv \textrm{Tr} \left\{ \sqrt{{\hat{\rho }}} \left( {\hat{s}}_A^{i}\otimes \hat{1\hspace{-4pt}1}_B \right) \sqrt{{\hat{\rho }}} \left( {\hat{s}}_A^{j}\otimes \hat{1\hspace{-4pt}1}_B\right) \right\} , \end{aligned}$$
(13)

with \({\hat{s}}^{i,j} (i,j=x,y,z)\) denoting Pauli matrices. In our case, for the density matrix of eq. (11), the eigenvalues \(\{l_{i}\}\) are deduced from a straightforward calculation as follows:

$$\begin{aligned} l_{1}=-l_{2}=\frac{\left( \sqrt{N^-}+\sqrt{N^+}\right) \left( \sqrt{m^--M}+\sqrt{M+m^-}\right) }{\sqrt{2}}+\frac{\sqrt{2} \kappa \left( \sqrt{N^-}-\sqrt{N^+}\right) \left( \sqrt{m^--M}-\sqrt{M+m^-}\right) }{M-m^+}, \end{aligned}$$
(14)

and

$$\begin{aligned} l_{3}= \frac{4 \kappa ^2 \left( \sqrt{M+m^-} \sqrt{m^--M}+2 \sqrt{N^-} \sqrt{N^+}\right) +\left( m^--m^+\right) ^2 \left( m^-+m^++2 \sqrt{N^-} \sqrt{N^+}\right) }{4 \kappa ^2+\left( m^--m^+\right) ^2}, \end{aligned}$$
(15)

where \(M=m^++\sqrt{4 \kappa ^2+\left( m^--m^+\right) ^2}\) and \(N^{\pm }=n\pm o\).

3.2 NCCs via LQFI

As an alternative measure of discord-like correlation, we use the quantum Fisher information-based correlations quantifier (Elghaayda et al. 2022). The quantification of NCCs based on LQFI is defined as the minimum of QFI over all local Hamiltonians that act on a single part of a two-qubit system (Kim et al. 2018). For a given two-qubit state \({\hat{\rho }}=\sum _{i}\nu _i \left| \varphi _i\right\rangle \left\langle \varphi _i\right|\), where \(\nu _i \geqslant 0\) and \(\sum _{i}\nu _i=1\), the explicit closed formula of LQFI is given by:

$$\begin{aligned} \mathcal {F}({\hat{\rho }})=1-\max \{g_1,g_2,g_3 \}, \end{aligned}$$
(16)

where \(g_{i=1,2,3}\) are the eigenvalues of the matrix \({\mathcal {G}}\) and the elements of the symmetric \(3 \times 3\) matrix \({{\mathcal {G}}}\) are defined as follows:

$$\begin{aligned} {{{\mathcal {G}}}_{kl}} = \sum \limits _{i,j, \nu _i+\nu _j>0} {\frac{{2{\nu _i}{\nu _j}}}{{{\nu _i} + {\nu _j}}}\langle {\varphi _i}|{{\hat{s}}_k} \otimes \hat{1\hspace{-4pt}1}_B\left| {{\varphi _j}} \right\rangle \langle {\varphi _j}|{{\hat{s}}_l} \otimes \hat{1\hspace{-4pt}1}_B\left| {{\varphi _i}} \right\rangle }. \end{aligned}$$
(17)

We point out that the eigenvalues of the matrix \({\mathcal {G}}\) of the thermal state in eq. (11) are given by:

$$\begin{aligned}{} & {} \begin{array}{cc} \begin{aligned} g_1&{} =\frac{1}{\kappa ^2}\left( -\frac{N^+ \left( -m^--m^++M\right) \left( -2 \kappa +M-m^-\right) ^2}{m^-+m^++2 N^+-M}+\frac{N^+ \left( M+m^-\right) \left( 2 \kappa +m^--m^++M\right) ^2}{M+m^-+2 N^+}+\right. \\ &{}\left. \frac{N^- \left( M+m^-\right) \left( -2 \kappa +m^--m^++M\right) ^2}{M+m^-+2N^-}-\frac{N^- \left( -m^--m^++M\right) \left( 2 \kappa +M-m^-\right) ^2}{m^-+m^+-M+2N^-} \right) \end{aligned} \end{array}, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \quad \begin{array}{cc} \begin{aligned} g_2&{} =-\frac{N^- \left( -m^--m^++M\right) \left( -2 \kappa +M-m^-\right) ^2}{\kappa ^2 \left( m^-+m^++2 N^--M\right) }+\frac{N^- \left( M+m^-\right) \left( 2 \kappa +m^--m^++M\right) ^2}{\kappa ^2 \left( M+m^-+2 N^-\right) }\\ &{}+\frac{N^+ \left( M+m^-\right) \left( -2 \kappa +m^--m^++M\right) ^2}{\kappa ^2 \left( M+m^-+2 N^+\right) }+\frac{N^+ \left( m^-+m^+-M\right) \left( 2 \kappa +M-m^-\right) ^2}{\kappa ^2 \left( m^-+m^++2 N^+-M\right) } \end{aligned} \end{array}, \end{aligned}$$
(19)

and

$$\begin{aligned} g_3=\frac{m^- \left( m^--m^+\right) ^4}{\kappa ^4}+\frac{\left( 3 m^--m^+\right) \left( m^--m^+\right) ^2}{\kappa ^2}-\frac{16 \kappa ^2}{m^-+m^+}+\frac{16 m^- m^+}{m^-+m^+}-\frac{8 o^2}{n}+8 n. \end{aligned}$$
(20)

3.3 QC via JSD

To evaluate the QC, we choose a genuine metric based on the quantum version of the JSD (Radhakrishnan et al. 2016). Unlike relative entropy, which lacks the symmetry property of a distance measure, the JSD (Briët and Harremoës 2009; Radhakrishnan et al. 2016) uses entropy functions and adheres to the properties of distance. The JSD is defined as a distance measure between the state \({\hat{\rho }}\) and the closest incoherent state \({\hat{\rho }}_d\) and is given by:

$$\begin{aligned} \mathcal {J}({\hat{\rho }},{\hat{\rho }}_d)=S\left( \frac{{\hat{\rho }}+{\hat{\rho }}_d}{2} \right) -\frac{S({\hat{\rho }})}{2}-\frac{S({\hat{\rho }}_d)}{2}, \end{aligned}$$
(21)

where \({\hat{\rho }}_d\) is the diagonal part of the quantum state \({\hat{\rho }}\) in the computational basis and \(S={\text {Tr}}{\hat{\rho }}\log _2{\hat{\rho }}\) is the von Neumann entropy. By taking the square root of the JSD, the resulting measure satisfies both the distance axioms and the triangle inequality, thus offering metric advantages and all known criteria for a QC quantifier (Radhakrishnan et al. 2016). The coherence based on JSD, denoted as \(\mathcal {C}_{JS}\), is formally defined as the square root of JSD as Radhakrishnan et al. (2016):

$$\begin{aligned} \mathcal {C}_{JS}({\hat{\rho }}) \equiv \sqrt{\mathcal {J}({\hat{\rho }},{\hat{\rho }}_d)}. \end{aligned}$$
(22)

In our case, for the density matrix of eq. (11), the analytical expression of JSD takes the form:

$$\begin{aligned} \mathcal {J}\left( {\hat{\rho }}, {\hat{\rho }}_d\right) = \frac{1}{2 \log (2)}\left[ \sum _{i=1}^4 \mu _i \log \mu _i+ 2n \log n + m^- \log m^- + m^+ \log m^+ -2 \sum _{j=1}^4 \tau _j \log \tau _j\right] , \end{aligned}$$
(23)

where \(\mu _i\) are eigenvalues of the density matrix of eq. (11), and \(\tau _j\) are eigenvalues of the matrix \(\frac{{\hat{\rho }}+{\hat{\rho }}_d}{2}\).

3.4 Numerical results and discussion

To accurately assess the extent of NCCs and QC regarding specific physical parameters such as temperature, anisotropy, off-diagonal exchange interactions, and the uniform transverse magnetic field in our proposed model, we aim to visualize the variations of \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\). While our formalism applies to a general case, for the sake of simplicity, we constrain our discussion to the case where \(\delta =0.3\) for all numerical plots in this work.

Fig. 1
figure 1

\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of T with \(\Gamma =3.0\), \(h=0.7\) for \(\alpha =0.5\) in (a), and \(\alpha = -0.5\) in (b)

Full size image

In Fig. 1, we have plotted the variations of \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\) with respect to temperature T. Obviously, all quantities decrease as the temperature increases until they reach their minimum value for a higher temperature regime. We can observe that both \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) exhibit a similar pattern: they exponentially decay as T increases, and they vanish at specific high temperatures. Through this analysis, one verifies an important property of LQU with LQFI, which is: \(\mathcal {F}({\hat{\rho }}) \ge \mathcal {L}({\hat{\rho }})\) (Luo 2004).

At lower temperatures, the amount of NCCs is maximum, that is, \(\mathcal {F}({\hat{\rho }}) = \mathcal {L}({\hat{\rho }}) \approx 0.95\) when \(\alpha = 0.5\) (Fig. 1a). However, when \(\alpha =-0.5\) the amount of NCCs is enhanced and the system becomes maximally correlated, \(\mathcal {F}({\hat{\rho }}) = \mathcal {L}({\hat{\rho }})=1.0\) (Fig. 1b). So the negative values of \(\alpha\) promote the NCCs in the system. Furthermore, focusing on the QC quantified by \(\mathcal {C}_{JS}\) one can see that its maximum amount for both plots is presented when T is lower, such that \(\mathcal {C}_{JS}\approx 0.54\) in Fig. 1a and \(\mathcal {C}_{JS}\approx 0.56\) in Fig. 1b and decreases when increasing T. This reveals the impact of the relative coefficient of off-diagonal interaction \(\alpha\) on the level of NCCs and QC presented in the current system. Remarkably, \(\mathcal {C}_{JS}\) is less sensitive to temperature compared to \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {L}({\hat{\rho }})\); this is observed for high-temperature regimes, which demonstrate its resilience against temperature-induced decoherence. From the above analysis, one draws the following statement: increasing temperature reduces the quantum resources in the system. Interestingly, these quantum resources are more pronounced when considering the relative coefficient \(\alpha\) in the region \(\alpha < 0\).

Fig. 2
figure 2

\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\alpha\) with \(\delta =0.3\), \(h=0.7\), \(T=0.3\) for various values of \(\Gamma\)

Full size image

Figure 2 illustrates the behaviors of \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\) as functions of the relative coefficient \(\alpha\) while varying the intensity of the magnetic field h. The remaining parameters are fixed at \(\Gamma =1.5\) and \(T=0.3\). It is worth noting that Fig. 2a and b show similar pattern. It is observed that the minimum values of NCCs are strictly dependent on the selected values of h. For instance, when \(h=0.1\), the minimum values of NCCs are located at \(\alpha =0.1\). On the other hand, when \(h=0.5\), the minimum values of NCCs are located at \(\alpha \approx 0\). As the magnetic field h increases, the minimum values of NCCs are spotted in the negative region of the off-diagonal interaction \(\alpha\). It can be inferred that an increase in the value of h decays \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) in the two regions of the \(\alpha\). It is important to note that large magnetic field strengths, such as \(h=1.0\) and 1.5, significantly impact NCCs. When \(\alpha > 0\), \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) increase almost linearly until \(\alpha =1\). However, when \(\alpha < 0\), \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) initially decrease and then rise until \(\alpha =-1\). On the other hand, \(\mathcal {C}_{JS}({\hat{\rho }})\) undergoes a moderate change when the magnetic h field is varied. Lower values of h have less influence on \(\mathcal {C}_{JS}({\hat{\rho }})\). Note that the minimum value of \(\mathcal {C}_{JS}({\hat{\rho }})\) also depends on the intensity of the magnetic field. Higher values of h show minimum values of \(\mathcal {C}_{JS}({\hat{\rho }})\) in the region of \(\alpha < 0\). However, the enhancement of \(\vert \alpha \vert\) always promotes the generation of \(\mathcal {C}_{JS}({\hat{\rho }})\) in the system.

Based on this analysis, we can observe that unlike the NCCs present in the system, the QC quantified by \(\mathcal {C}_{JS}({\hat{\rho }})\) exhibits permanent resistance to the increase in the magnetic field h. However, despite the differences between NCCs and QC, we have demonstrated that incorporating the off-diagonal interaction into the XY spin chain can effectively modulate and enhance the level of NCCs and QC in the system. Moreover, it can mitigate the adverse impact of the transverse magnetic field h.

Fig. 3
figure 3

\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\alpha\) with \(\delta =0.3\), \(\Gamma =1.5\), \(T=0.3\) for various values of h

Full size image

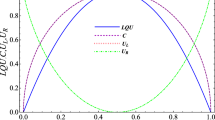
Figure 3 illustrates the impact of the amplitude of off-diagonal interaction \(\Gamma\), on \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\). The remaining parameters are held constant at \(h=0.7\) and \(T=0.3\). The primary objective of this analysis is to demonstrate that controlling \(\Gamma\) results in the improvement of NCCs and QC in the system. This is evident when comparing the curves of \(\Gamma =0.5\) to \(\Gamma =3.0\). Although minimal NCCs are observed for weak values of \(\alpha\), \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) are enhanced with increasing \(\vert \alpha \vert\) values up to \(\pm 1\). A similar trend is exhibited for QC, such that the increase in \(\Gamma\) enhances the value of \(\mathcal {C}_{JS}({\hat{\rho }})\), and the system displays more QC. Furthermore, upon comparing the range of \(\alpha < 0\) and \(\alpha > 0\) of the off-diagonal interaction, it is observed that the quantum resources saturate at their maximum values (\(\mathcal {L}({\hat{\rho }})=\mathcal {F}({\hat{\rho }})=1\), and \(\mathcal {C}_{JS}({\hat{\rho }}) \approx 0.56\)) promptly in the region where \(\alpha < 0\) as the amplitude \(\Gamma\) increases. Hence, the system is more resourceful in the \(\alpha < 0\) region.

Fig. 4
figure 4

\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\Gamma\) with \(\delta =0.3\), \(\alpha =0.5\), \(T=0.3\) for various values of h

Full size image

The graph depicted in Fig. 4 showcases the variations of \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\Gamma\) while varying the magnetic field h in the case of \(\alpha =0.5\). The symmetrical evolution of the three metrics with respect to \(\Gamma =0\) is demonstrated in all plots of Fig. 4, indicating that the highest amount of quantum resources is presented in weak values of h in the absence of off-diagonal interaction (\(\Gamma =0\)). Upon analyzing the curves of \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) corresponding to \(h=0.1\), we can observe that increasing the parameter \(\Gamma\) tends initially to drop these NCCs, then followed by a gradual increase for high values of \(\Gamma\). This characteristic concerns only \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) and not \(\mathcal {C}_{JS}({\hat{\rho }})\).

Fig. 5
figure 5

\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\) and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\Gamma\) with \(\delta =0.3\), \(\alpha =-0.5\), \(T=0.3\) for various values of h

Full size image

The graph presented in Fig. 5 illustrates the variations of \(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\), and \(\mathcal {C}_{JS}({\hat{\rho }})\) as a function of \(\Gamma\), while varying the magnetic field h for \(\alpha =-0.5\). As compared to Fig. 4, unlike the characteristic of the weak magnetic field h, the plots indicate that the drop of NCCs is not presented with increasing \(\vert \Gamma \vert\). However, for relatively high values of h (e.g., 1.0 and 1.5), \(\mathcal {L}({\hat{\rho }})\) and \(\mathcal {F}({\hat{\rho }})\) show a sudden drop, followed by a rise for high values of \(\vert \Gamma \vert\). This unique characteristic is specific to NCCs and is not presented in QC.

Both analyses of Figs. 4 and 5 lead to the following primary statement: the increase of h tends to decay the amount of NCCs and QC in the system. However, this decay is counteracted when incorporating the off-diagonal interaction \(\alpha\) and increasing its amplitude \(\Gamma\).

4 EUR and mixedness for XY-\(\Gamma\) spin chain

4.1 EUR

Fig. 6
figure 6

A sketch of the uncertainty game: (1) Bob sends particle A to Alice via a quantum channel, (2) Alice measures particle A using either \(\hat{\mathscr {Q}}\) or \(\hat{\mathscr {R}}\) and (3) sends the measure choice to Bob via a classic message

Full size image

To evaluate the dynamic features of the EUR in the two-qubit \(XY-\Gamma\) spin chain thermal state ( eq. (11)), we assume \(\hat{\mathscr {Q}} \equiv {\hat{s}}^x\) and \(\hat{\mathscr {R}} \equiv {\hat{s}}^z\) as the two incompatible observables. Accordingly, the two post-measurement states \({\hat{\rho }}^{{\hat{s}}^x, B}\) and \({\hat{\rho }}^{{\hat{s}}^z B}\) of inequality (3) are, respectively, given as follows:

$$\begin{aligned} {\hat{\rho }}^{{\hat{s}}^x, B}=\frac{1}{2}\left( \begin{array}{cccc} m^- +n &{} 0 &{} 0 &{} o^* + \kappa \\ 0 &{} m^+ +n &{} o + \kappa ^* &{} 0 \\ 0 &{} o^* + \kappa &{} m^- +n &{} 0 \\ o + \kappa ^* &{} 0 &{} 0 &{} m^+ +n \end{array}\right) , \end{aligned}$$
(24)

and

$$\begin{aligned} {\hat{\rho }}^{{\hat{s}}^z, B}=\left( \begin{array}{cccc} m^- &{} 0 &{} 0 &{} 0 \\ 0 &{} n &{} 0 &{} 0 \\ 0 &{} 0 &{} n &{} 0 \\ 0 &{} 0 &{} 0 &{} m^+ \end{array}\right) . \end{aligned}$$
(25)

After obtaining the post-measurement states, the corresponding von Neumann entropies are given by:

$$\begin{aligned} S\left( {\hat{\rho }}^{{\hat{s}}^x, B}\right) =S_{\text{ bin } }\left( \frac{1-\sqrt{1-4 \varpi }}{2}\right) +1, \end{aligned}$$
(26)

and

$$\begin{aligned} S\left( {\hat{\rho }}^{{\hat{s}}^z, B}\right) =-m^- \log _2 m^- - m^+ \log _2 m^+ -2n \log _2 n, \end{aligned}$$
(27)

where the binary entropy denotes \(S_{\text{ bin } }(\Xi )=-\Xi \log _2 \Xi -(1-\Xi ) \log _2(1-\Xi )\) and \(\varpi = m^- n+n^2 +n m^+ + m^+ m^- -\vert \kappa \vert ^2 -\vert o \vert ^2 - o^* \kappa ^* - o \kappa\).

On account of \({\hat{\rho }}^B={\text {Tr}}_A({\hat{\rho }}(T))\), the eigenvalues of \(B^{\prime }\) s reduced density matrix are \(m^- + n\) and \(m^+ + n\), the left-hand side (LHS) of inequality (3) is:

$$\begin{aligned} \mathcal {U}_\mathcal {L}=S\left( {\hat{\rho }}^{{\hat{s}}^x, B}\right) +S\left( {\hat{\rho }}^{{\hat{s}}^z, B}\right) -2 S_{\text {bin}}\left( m^-+n \right) . \end{aligned}$$
(28)

Furthermore, the eigenvalues of \({\hat{\rho }}(T)\) obtained in eq. (11) are given by \(\nu _{1,2}=\frac{1}{2}\left( \tau \pm \sqrt{\tau ^2-4\,m^- m^+ +4 \vert \kappa \vert ^2}\right)\) and \(\nu _{3,4}=\frac{1}{2}\left( \zeta \pm \sqrt{\zeta ^2-4 n^2 +4 \vert o \vert ^2}\right)\), where \(\tau =\) \(m^- + m^+\) and \(\zeta = 2n\). The overlap, denoted by c (inequality (3), between two Pauli observables is a constant value of \(\frac{1}{2}\). Consequently, the lower bound of the right-hand side (RHS) of inequality (3) is explicitly given as:

$$\begin{aligned} \mathcal {U}_\mathcal {R}=1-S_{\text {bin}}\left( m^-+n \right) -\sum _i \nu _i \log _2 \nu _i. \end{aligned}$$
(29)

Finally, we hold the exact expressions of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {U}_\mathcal {R}\) by inserting the matrix elements (eq. (11)) into the equations for the left-hand side (LHS) and the RHS, as in eq. (28) and eq. (29), respectively (Fig. 6).

4.2 Mixedness

Many studies have attempted to understand the dynamic behaviors of EUR. They suggest that the degree of EUR is closely related to the mixedness \(\mathcal {M}\) of the systematic state. To determine the mixedness of an arbitrary state \({\hat{\rho }}\), we use the following expression:

$$\begin{aligned} \mathcal {M}=\frac{d}{d-1} \left( 1-{\text {Tr}}\{{\hat{\rho }}^2\} \right) , \end{aligned}$$
(30)

where d denotes the dimension of the system state \({\hat{\rho }}\), and \(0 \le \mathcal {M} \le 1\). The state \({\hat{\rho }}\) is pure when \({\text {Tr}}\{{\hat{\rho }}^2\}=1\) (i.e., \(\mathcal {M}=0\)). Otherwise, it is mixed whenever \({\text {Tr}}\{{\hat{\rho }}^2\} < 1\) (i.e., \(\mathcal {M} \le 1\)). In the case of the thermal state \({\hat{\rho }}(T)\) (Eq. (11)) the mixedness is explicitly given as:

$$\begin{aligned} \mathcal {M}=\frac{4}{3}\left( 1-(m^-)^{2}-2\vert \kappa \vert ^2 -2n^2 - 2\vert o\vert ^2 - (m^+)^{2} \right) . \end{aligned}$$
(31)

4.3 Numerical results and discussion

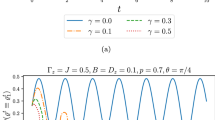
In what follows, we analyze the EUR \(\mathcal {U}_\mathcal {L}\), its lower bound \(\mathcal {U}_\mathcal {R}\), and the mixedness \(\mathcal {M}\) of the two-qubit \(XY-\Gamma\) spin chain model. We examine how these quantities behave regarding the system’s parameters and temperature T. Figure 7a portrays the behavior of \(\mathcal {U}_\mathcal {L}\), \(\mathcal {U}_\mathcal {R}\), and \(\mathcal {M}\) as the temperature T changes while keeping all other parameters constant. When \(T=0\), \(\mathcal {U}_\mathcal {L}=\mathcal {U}_\mathcal {R}=0\). The higher temperature leads to an expansion of measurement uncertainty and mixedness. Upon analysis, it becomes apparent that the variation trend of the measurement uncertainty and mixedness is considerably contrasting to that of NCCs (\(\mathcal {L}({\hat{\rho }})\), \(\mathcal {F}({\hat{\rho }})\)) and QC (\(\mathcal {C}_{JS}({\hat{\rho }})\)) as the temperature increases Fig. 1a. Besides, the expansion of EUR arises from thermal fluctuations that occur as the temperature rises. This can be evaluated by the mixedness \(\mathcal {M}\) of the state \({\hat{\rho }}(T)\) (eq. (11)), which indicates the same trend as \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {U}_\mathcal {R}\). Based on this, a strong correlation between the uncertainty measure and the level of mixedness is revealed. In other words, the EUR reaches its highest value when the mixedness of the state is at its highest, and vice versa.

We turn to Fig. 7b in which we explore the behavior of the same quantities of interest as a function of the parameter \(\Gamma\) at finite temperature. The plots of Fig. 7b show the monotonic decrease of \(\mathcal {U}_\mathcal {L}\), \(\mathcal {U}_\mathcal {R}\), and \(\mathcal {M}\). This reduction highlights the significant role played by the off-diagonal interaction in decreasing the EUR, which in turn leads to the reduction of the quantum state mixedness. Reducing EUR is crucial to accurately predict the measurement result by the owner of the particle serving as memory. In this scenario, we have shown how the destructive effect of temperature T is counteracted by increasing the amplitude \(\Gamma\) of the off-diagonal coupling.

Fig. 7
figure 7

EUR with its lower bound and mixedness: \(\mathcal {U}_\mathcal {L}\), \(\mathcal {U}_\mathcal {R}\) and \(\mathcal {M}\) versus temperature T in (a), and versus \(\Gamma\) in (b)

Full size image

The following Fig. 8 examines the behaviors of the EUR \(\mathcal {U}_\mathcal {L}\) and its relationship with the mixedness \(\mathcal {M}\) as a function of the relative coefficient of the exchange interaction \(\alpha\) and the transverse magnetic field h at a finite temperature. Both functions reach their maximum values in the region where \(\alpha\) and h are null. The role of the magnetic field is dependent on the range of the coefficient \(\alpha\) considered. In Fig. 8a, when \(\alpha \le 0\), the EUR decreases as h increases. However, for values of \(\alpha\) approaching -1 and low magnetic field intensities, the EUR is minimal and improves as \(\vert h \vert\) increases up to a maximum, then decreases again for high h intensities. For the range of \(\alpha > 0\), the area where \(\mathcal {U}_\mathcal {L}\) is influential is decreased, and values of \(\alpha\) approaching 1 exhibit lower uncertainties. It is important to note that the increase in the intensity of \(\vert h \vert\) has a minor influence on the increase in the EUR \(\mathcal {U}_\mathcal {L}\). The mixedness \(\mathcal {M}\) depicted in Fig. 8b can be analyzed similarly. The results show that when \(\alpha \le 0\), the magnetic field h enhances the mixedness \(\mathcal {M}\) during its evolution. However, this behavior is the opposite for higher intensity of \(\vert h \vert\). On the other hand, when \(\alpha > 0\), the increase in magnetic field leads to a decrease in the mixedness \(\mathcal {M}\) until it eventually disappears.

Fig. 8
figure 8

Contour plots of (a) \(\mathcal {U}_\mathcal {L}\) and (b) \(\mathcal {M}\) versus the parameters \(\alpha\) and h

Full size image

In Fig. 9, the contour plots are presented to compare the effect of the parameters \(\Gamma\) and h in two distinct regions of the relative coefficient \(\alpha\), i.e., \(\alpha =-0.5\) (Fig. 9a) and \(\alpha =0.5\) (Fig. 9b). An analysis of Fig. 9a and b shows that the weak intensities of h and low values of \(\Gamma\) result in large amounts of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\). The amounts of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) decrease considerably for large values of the \(\Gamma\) parameter. This trend is slightly different when the two qubits are initially subjected to a certain magnetic field intensity, e.g., \(\vert h \vert = 2\). The parameter \(\Gamma\) can play the opposite role, increasing the EUR and the mixedness. For large values of \(\Gamma\), \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) present their minimums until they vanish. Consequently, the impact of the magnetic field h influences the impact of \(\Gamma\), and explicitly, the larger \(\vert h \vert\) is, the stronger the increase in the amplitude \(\Gamma\) of the off-diagonal interaction is required to reduce the level of mixedness and mitigate the measurement uncertainty.

Figure 9c and d highlight the contour plots of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) where \(\alpha = 0.5\). In this scenario, the EUR and the mixedness are high at low values of \(\vert h \vert\) and \(\Gamma\). However, as the amplitude \(\Gamma\) increases, \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) decrease significantly. The magnetic field h also contributes to the collapsing of these two quantities. Unlike the case where \(\alpha = -0.5\), the intensity of the magnetic field, \(\vert h \vert\), does not affect the parameter \(\Gamma\). Hence, for any value of h, the decrease of mixedness and uncertainty is mainly governed by the enhancement of the amplitude \(\Gamma\) of the off-diagonal exchange coupling.

Fig. 9
figure 9

Contour plots of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) as functions of parameters \(\Gamma\) and h. We set \(\alpha =-0.5\) in (a), (b) and \(\alpha =0.5\) in (c), (d)

Full size image

5 Steering measurement uncertainty with filtering operation

Quantum systems are known to be vulnerable to decoherence effects that ultimately lead to their ephemeral nature. To tackle this issue, several researchers have been working on developing different methods to mitigate decoherence, with a particular emphasis on local operations such as quantum weak measurement, reversal measurement, non-Hermitian operation, and filtering operation (Kim et al. 2012; Wang et al. 2014, 2019). The present study aims to investigate a variant of local filtering operation, which is typically classified as a type of weak measurement with null result (Siomau and Kamli 2012; Karmakar et al. 2015). Our purpose is to determine whether the effectiveness of this operation has any adverse impact on reducing measurement uncertainty. In the following, we will delve into the operational aspects of how this approach affects our concern. To commence, let us briefly recapitulate the concept of filtering operation (FO). Generally, it is commonly represented by the following operator (Karmakar et al. 2015):

$$\begin{aligned} \hat{\mathcal {S}}_i=\left( \begin{array}{cc} \sqrt{1-q_{i}} &{} 0 \\ 0 &{} \sqrt{q_i} \end{array}\right) . \end{aligned}$$
(32)

This operator refers to the non-trace-preserving map, where \(\hat{\mathcal {S}}_i\) represents the operator acting on particle \(i(i \in \{A, B\})\) and the FO strength is controlled by the parameter \(0< q_i < 1\). Herein, we assume that such operation is performed solely on particle A, while B is free from any operations, that is, \(\hat{\mathcal {S}}_B= {\hat{1\hspace{-2.5pt}\text {l}}}_B\) and \(q_A \equiv q\). Then, the post-operation state \({\hat{\varrho }}(T)\) of the system is given by:

$$\begin{aligned} {\hat{\varrho }}(T)=\frac{\left( \hat{\mathcal {S}}_A \otimes \hat{1\hspace{-4pt}1}_B\right) {\hat{\rho }}(T)\left( \hat{\mathcal {S}}_A \otimes \hat{1\hspace{-4pt}1}_B\right) ^{\dagger }}{{\text {Tr}}\left[ \left( \hat{\mathcal {S}}_A \otimes \hat{1\hspace{-4pt}1}_B\right) {\hat{\rho }}(T) \left( \hat{\mathcal {S}}_A \otimes \hat{1\hspace{-4pt}1}_B\right) ^{\dagger }\right] }. \end{aligned}$$
(33)

So, the measurement uncertainty \(\mathcal {U}_\mathcal {L}\) and the mixedness \(\mathcal {M}\) for the state \({\hat{\varrho }}(T)\) can be obtained analytically by linking eqs. (28) with eq. (33) and linking eq. (31) with eq. (33). By performing FO on qubit A, one can probe the relationship between the strength of the FO, denoted by "q", the measurement uncertainty, and the mixedness of interest. The following numerical results provide information on this matter.

Fig. 10
figure 10

Steered EUR \(\mathcal {U}_\mathcal {L}\) and mixedness \(\mathcal {M}\) versus temperature T in (a, b) and versus \(\Gamma\) in (c, d)

Full size image

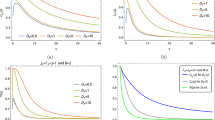
To demonstrate how the FO affects the dynamic evolution of measurement uncertainty \(\mathcal {U}_\mathcal {L}\) and mixedness \(\mathcal {M}\), we have plotted in Fig (10) their evolution as a function of temperature T and amplitude \(\Gamma\) for various FO strengths q, while setting the remaining system parameters. By examining the figure, it becomes evident that by adjusting the values of q, the FO can effectively reduce the measurement uncertainty during incompatible measurements. Indeed, it is observed that during the FO experienced by the qubit A, the operation is controlled by the parameter q in such a way that the reduction is more effective when the value of q is closer to 0 or 1. The operation is symmetric with respect to \(q=0.5\) (see also, eq. (32)), which is equivalent to the case of no operation.

Upon analyzing Fig. 10a, it is noted that the measurement uncertainty exhibits an increasing trend with a rise in FO strength q for low-temperature values. However, the situation is thoroughly different for high-temperature cases, as an increase in FO strength q results in a considerable decrease in measurement uncertainty. Based on this analysis, it can be concluded that FO can significantly decrease the measurement uncertainty in most cases, except for low-temperature scenarios. However, achieving a zero-temperature condition can be challenging in most experiments. In addition, the dependence of mixedness \(\mathcal {M}\) on the filtering parameter q is similar to that of measurement uncertainty, as illustrated in Fig. 10b. However, it remains unaffected by q at low-temperature values, which sets it apart from the case of \(\mathcal {U}_\mathcal {L}\). This intriguing observation suggests that mixedness cannot be viewed as the sole source of the dynamic evolution of EUR \(\mathcal {U}_\mathcal {L}\).

Furthermore, the variations of \(\mathcal {U}_\mathcal {L}\) and \(\mathcal {M}\) as a function of the parameter \(\Gamma\), while varying the parameter q is depicted in Fig. 10c and d. The findings reveal that the impact of FO on \(\mathcal {U}_\mathcal {L}\) is more pronounced for smaller values of \(\Gamma\), whereas the opposite holds for larger values. Similarly, the mixedness \(\mathcal {M}\) exhibits a comparable pattern, while the strength of q has no bearing on \(\mathcal {M}\) for larger values of \(\Gamma\). Nevertheless, the FO scheme proves to be an effective tool for mitigating decoherence and steering both EUR and mixedness to a significant extent. This feature is highly desirable for enhancing the efficiency of quantum protocols, particularly quantum key distribution.

Fig. 11
figure 11

Contour plots of steered EUR as a function of parameters \(\alpha\) and h for different values of FO parameter q: (a) \(q=0.6\), (b) \(q=0.7\), (c) \(q=0.8\), (d) \(q=0.9\)

Full size image

The ensuing analysis explores the influence of the magnetic field h on the measurement uncertainty \(\mathcal {U}_\mathcal {L}\) in the range of the relative coefficient of the off-diagonal interaction (\(-1 \le \alpha \le 1\)) while controlling the FO parameter q. As depicted in the contour plots of Fig. 11, we observe that the sign of h affects \(\mathcal {U}_\mathcal {L}\) differently, thereby breaking the symmetry demonstrated in Fig. 8 due to the local operation on the qubit A. Additionally, the evolution of \(\mathcal {U}_\mathcal {L}\) is significantly influenced by the parameter \(\alpha\). Specifically, we note that the EUR is higher when \(\alpha \le 0\) and \(h \le 0\), and the area of higher \(\mathcal {U}_\mathcal {L}\) spreads further as the parameter q approaches 1 (as evidenced by Fig. 11a to d). Conversely, we can attain the minimum of EUR when \(\alpha > 0\) and \(h \le 0\), and controlling the parameter q (e.g., \(q=0.8\) in Fig. 11c and \(q=0.9\) in Fig. 11d), we can minimize this uncertainty further for values below 0.25. This outcome is not evident in Fig. 8.

Overall, the filtering operation demonstrates its efficacy in mitigating the detrimental impact of temperature-induced decoherence. Notably, even when this local non-unitary operation is exclusively implemented on qubit A, the memory qubit B immediately experiences the effects. This is due to the entanglement between the two particles, as indicated by the conditional entropy \(S(A/B)=-\log _2 d <0\) of inequality (3), which enables the exchange of information between the qubits. Consequently, the filtering operation can minimize measurement uncertainty and facilitate the transfer of information from qubit A to qubit B, ultimately improving the accuracy of guessing Alice’s measurement result.

6 Conclusion

To sum up, we have investigated the dynamics of NCCs, QC, EUR, and mixedness of a two-qubit \(XY-\Gamma\) spin chain system at thermal equilibrium using the Gibbs state. We analyzed the impact of temperature (T), relative coefficient of off-diagonal exchange coupling (\(\alpha\)), its amplitude (\(\Gamma\)), and transverse magnetic field (h) on the LQU, LQFI, and QC based on JSD. We have found that increasing the temperature adversely affects the quantum resources in the system. However, incorporating off-diagonal interaction and increasing its amplitude \(\Gamma\) within the \(XY-\Gamma\) spin chain effectively regulates and enhances the levels of NCCs and QC in the system. Similarly, strengthening the relative coefficient \(\alpha\) of off-diagonal interaction compensates for the adverse effects of the transverse magnetic field. Furthermore, the system exhibits higher resourcefulness when the relative coefficient of off-diagonal interaction is in the region \(\alpha < 0\).

The second part of the investigation focuses on the EUR, its lower bound, and the mixedness of the system. The results show that increasing the temperature T expands these quantities, which is opposite to the behavior observed in NCCs and QC. It is demonstrated that the EUR reaches its highest value when the mixedness of the state is at its highest, and vice versa. The findings also highlight the significant role played by the off-diagonal interaction in decreasing EUR and mixedness. Thus, the study demonstrates how the destructive effect of temperature T can be counteracted by increasing the amplitude \(\Gamma\) of the off-diagonal coupling. Additionally, the study emphasizes the influence of the magnetic field on EUR and mixedness, revealing that the impact of the magnetic field depends on the range of the coefficient \(\alpha\) considered. Moreover, the study reveals that the magnetic field’s influence on EUR is closely tied to the role of the amplitude \(\Gamma\) of the off-diagonal interaction.

We successfully demonstrate the effectiveness of the filtering operation (FO) strategy in minimizing measurement uncertainty. The findings show that this strategy effectively mitigates the negative effects of temperature-induced decoherence and the increased measurement uncertainty caused by the magnetic field h. It is important to note that even when this local non-unitary operation is applied selectively to qubit A, it immediately affects the memory qubit B, thus limiting the transfer of information from qubit A to qubit B in quantum communication protocols. However, by precisely controlling the \(XY-\Gamma\) system parameters and fine-tuning the strength of the FO parameter, we can significantly reduce measurement uncertainty, enabling the transfer of information from qubit A to qubit B. These findings contribute significantly to improving the accuracy of NCCs and QC, thereby reducing measurement uncertainty in the two-qubit \(XY-\Gamma\) system that employs the off-diagonal parameter as the main interaction in the current system under a transverse magnetic field within a thermal bath.

In quantum systems, understanding and utilizing \(\Gamma\) interactions can lead to the design of more realistic models with enhanced coherence properties. This is critical for quantum information processing, where the preservation of quantum coherence over extended periods remains paramount for efficient computation and error correction. The symmetric off-diagonal interaction \(\Gamma\) plays a crucial role in stabilizing the spin liquid phase, which is fundamental for maintaining coherence in quantum systems. Moreover, further research suggests that \(\Gamma\) interactions need to be considered to explain the potential observed in experiments for quantum spin liquids (Luo et al. 2021a, b; Yang et al. 2020). The symmetric off-diagonal interaction \(\Gamma\) also finds application in the engineering of Mott insulators (Arakawa and Yonemitsu 2021).

Although this paper presents a promising avenue for considering the symmetric off-diagonal \(\Gamma\) interactions in spin chain systems for quantum information applications, ongoing research to fully unlock the potential of \(\Gamma\) interactions in quantum information applications is required. In this direction, we advocate for further exploration of the potential of the two-qubit \(XY-\Gamma\) spin chain as a quantum channel for quantum teleportation and dense coding protocols.