1 Introduction

Nonlinear evolution equations (NLEEs) have a number of significant applications in various fields of science, namely, solid-state physics, quantum mechanics, optical fibers and many others (Eslami and Rezazadeh 2016; Rezazadeh 2018; Akinyemi et al. 2022; Abbagari et al. 2022; Ahmad et al. 2021, 2022; Akram et al. 2023, 2022; Asjad et al. 2023; Majid et al. 2023. The solutions of nonlinear evolution equations in mathematical physics and other branches of science are a major interest of research. The exact traveling wave solutions of nonlinear evolution equations provide a deeper insight into the dynamical framework of the governing models (Arshed et al. 2021; Raza et al. 2021; Rizvi et al. 2023a, b). Owing to the importance of traveling wave solutions, particularly solitons and solitary wave solutions, many researchers have proposed useful numerical and analytical methods to determine traveling wave solutions (Nasreen et al. 2023; Seadawy et al. 2020; Kumar et al. 2023). Various mathematical techniques have been established successfully such as, sine-Gordon equation expansion (Yamgoué et al. 2019), enhanced \((\frac{G'}{G})\) expansion (Islam 2015), modified simple equation (Biswas et al. 2018), extended Kudryashov (Hassan et al. 2014), exp-function (Hafez et al. 2015), new extended \((\frac{G'}{G})\) expansion (Hoque and Akbar 2014), Frobenius integrable decomposition (Ma et al. 2007), trial solution (Biswas et al. 2016), simple equation (Roshid and Bashar 2019), extended and modified rational expansion method (Seadawy et al. 2023), new extended direct algebraic method (Nasreen et al. 2023) and Darboux transformation (Feng and Zhang 2018; Xu and He 2012) methods. Analytical solutions of many NLEEs represent solitons, breathers and lump solutions (Feng et al. 2020; Sulaiman et al. 2020; Shen et al. 2021; Manukure et al. 2018; Ding et al. 2019; Ismael et al. 2023). During propagation, a soliton preserves its shape while interacting with other waves and has constant velocity (Kedziora et al. 2014; Nasreen et al. 2023).

A generalized \((2+1)\)-dimensional NLEE (Tahami and Najafi 2017) can be considered, as

$$\begin{aligned} r_{xt} + r_xr_{xy} + pr_{xx}r_y + qr_{xxxy} = 0, \end{aligned}$$
(1.1)

where p, q are arbitrary constants.

Equation (1.1) becomes \((2+1)\)-dimensional Calogero–Bogoyavlenskii–Schiff (CBS) equation for \(p = \frac{1}{2}\), \(q = \frac{1}{4}\), as

$$\begin{aligned} r_{xt} + r_xr_{xy} + \frac{1}{2}r_{xx}r_y + \frac{1}{4}r_{xxxy} = 0, \end{aligned}$$
(1.2)

where the terms \(r_x r_{xy}\) and \(r_{xx}r_y\) indicate the nonlinearity of the wave. The derivation of the CBS equation is attributed to Bogoyavlenskii and Schiff who used different approaches to retrieve the afore-mentioned equation. Schiff utilized the self-dual Yang–Mills equation to present the CBS equation, whereas Bogoyavlenskii derived the CBS equation using the modified Lax-formalism (Peng 2006; Toda et al. 1999; Schiff 1992). In recent years, many scholars paid much attention to the \((2+1)\)-dimensional CBS equation. Yu et al. (1998) proposed a new \((2+1)\)-dimensional CBS equation by adding \(\frac{1}{4}\partial ^{-1}_x r_{yyy}\) in Eq. (1.2), which can be written, as

$$\begin{aligned} r_{xt} + r_xr_{xy} + \frac{1}{2}r_{xx}r_y + \frac{1}{4}r_{xxxy} + \frac{1}{4}\partial ^{-1}_xr_{yyy} = 0, \end{aligned}$$
(1.3)

where \(\partial ^{-1}_x\,f = \int \,f\,dx\).

In the framework of \((2+1)\)-dimensional equations, several integrable models have been recently constructed. These integrable systems have various applications in nonlinear optics, hydrodynamics, plasma and field theories (Wazwaz 2017; Kumar et al. 2022). The CBS equation clarifies the interaction between long propagating and Riemann waves (Kumar et al. 2023).

An extended \((2+1)\)-dimensional CBS equation is attained by adding the flux term \(\omega\) \(r_{xy}\) in Eq. (1.3) (Wazwaz 2012; Mabrouk and Rashed 2019), as

$$\begin{aligned} r_{xt} + r_xr_{xy} + \frac{1}{2}r_{xx}r_y + \frac{1}{4}r_{xxxy} + \frac{1}{4}\partial ^{-1}_xr_{yyy} + \omega r_{xy} = 0, \end{aligned}$$
(1.4)

where \(\omega\) is an arbitrary constant. This extended CBS equation retains the integrability after the addition of the flux term. The proposed mathematical model has applications in a wide range of theoretical physics problems and scientific domains. Many experts have focused their attention on understanding the extended CBS model in recent years. Several approaches have been used to get accurate solutions for the extended CBS equation, which includes several complicated functions and, as a result, shows a multitude of unique behaviors. These closed-form solutions are achieved in the form of solitons and other solitary waves which play crucial roles in the field of plasma physics, fluid dynamics and nonlinear optics. The presence of solitary wave solutions is important in the nonlinear wave phenomena and propagation of waves (Nasreen et al. 2023; Kumar et al. 2022).

The main objective of this manuscript is the theoretical investigation of the dynamical behavior of Eq. (1.4) by finding the exact closed-form solitons and other traveling wave solutions. The traveling wave transformation is applied along with the extended trial equation method (ETEM) and modified auxiliary equation method (MAEM) to extract many accurate analytical solutions of the considered model. The graphical depiction of obtained solutions using these methods is used to analyze the physical interpretation of the governing equation. The ETEM is an extension of the trial method that was proposed to solve some time fractional differential equations, including the generalized third-order fractional KdV equation (Pandir et al. 2013). The MAEM was developed to find the solitary wave solutions of various NLEEs utilizing an auxiliary equation (Khater et al. 2019). These schemes are proficient and valuable to investigate the considered model.

The remaining paper is organized in the following way: Sect. 2 presents the conversion of Eq. (1.4) into an ordinary differential equation (ODE). Section 3 presents the mathematical analysis and application of the extended trial equation method on the considered model. Section 4 presents the mathematical analysis and application of the modified auxiliary equation method. The graphical simulations of the obtained solutions are presented in Sect. 5. The presented work is concluded in Sect. 6.

2 Conversion of extended CBS equation into an ODE

Differentiating Eq. (1.4) with respect to x leads to the \((2+1)\)-dimensional extended CBS equation in the following form.

$$\begin{aligned} 4r_{xtx} + 4r_{x}r_{xxy} + 6r_{xx}r_{xy} + 2r_{xxx}r_{y} + r_{xxxxy} + r_{yyy} + 4\omega r_{xxy} = 0. \end{aligned}$$
(2.1)

The traveling wave transformation can be considered, as

$$\begin{aligned} r(x, y, t)=\Phi (\theta ),\quad \theta = ax + by - ct, \end{aligned}$$
(2.2)

where a, b and c are any constants. Substituting Eq. (2.2) into Eq. (2.1), it reduces to

$$\begin{aligned} a^4b\Phi '''''(\theta ) + 6a^3b\Phi '(\theta )\Phi '''(\theta ) + (4\omega a^2b - 4a^2c + b^3)\Phi {'''}(\theta ) + 6a^3b(\Phi ''(\theta ))^2 = 0, \end{aligned}$$
(2.3)

which implies that

$$\begin{aligned} a^4b\Phi '''''(\theta ) + 6a^3b\Phi '(\theta )\Phi {'''}(\theta ) + \eta \Phi {'''}(\theta ) + 6a^3b(\Phi ''(\theta ))^2 = 0, \end{aligned}$$
(2.4)

where \(\eta = 4\omega a^2b - 4a^2c + b^3\). Integrating Eq. (2.4) twice, yields the relation

$$\begin{aligned} a^4b\Phi '''(\theta ) + \eta \Phi '(\theta ) + 3a^3b(\Phi '(\theta ))^2 = 0. \end{aligned}$$
(2.5)

Using the substitution

$$\begin{aligned} \Phi '(\theta ) = \nu (\theta ), \end{aligned}$$
(2.6)

leads to

$$\begin{aligned} a^4b\nu ''(\theta ) + 3a^3b \nu ^2(\theta ) + \eta \nu (\theta ) = 0. \end{aligned}$$
(2.7)

3 Mathematical analysis using ETEM

The brief description of the extended trial equation method is given as follows:

The nonlinear partial differential equation is considered, as

$$\begin{aligned} P(r, r_{x}, r_{y}, r_{t}, r_{xx}, r_{xy}, r_{xt},r_{yy},\ldots )=0, \end{aligned}$$
(3.1)

where P is a polynomial.

According to the traveling wave hypothesis, Eq. (3.1) is reduced to an ODE of the form

$$\begin{aligned} Q(\Phi , \Phi ', \Phi '', \Phi ''',\ldots )=0, \end{aligned}$$
(3.2)

where \((')= \frac{d}{d\theta }\). The solution of Eq. (3.2) is assumed, as

$$\begin{aligned} \Phi = \sum _{j=0} ^{\vartheta }\gamma _{j} \Omega ^j, \end{aligned}$$
(3.3)

where

$$\begin{aligned} (\Omega ^{'})^2 = \Lambda (\Omega ) = \frac{\Gamma (\Omega )}{\Psi (\Omega )}=\frac{\tau _{\rho }\Omega ^\rho +\cdots +\tau _{1}\Omega +\tau _{0}}{\chi _{\varsigma } \Omega ^\varsigma +\cdots +\chi _{1} \Omega +\chi _{0}}. \end{aligned}$$
(3.4)

Using the Eqs. (3.3)–(3.4), the following expressions for \((\Phi ^{'})^2\) and \(\Phi ''\) are obtained.

$$\begin{aligned} (\Phi ')^2 =\frac{\Gamma (\Omega )}{\Psi (\Omega )}\left( \sum _{j=0} ^{\vartheta }j\gamma _j\Omega ^{j-1}\right) ^2, \end{aligned}$$
(3.5)

and

$$\begin{aligned} \Phi '' = \frac{\Gamma '(\Omega )\Psi (\Omega )-\Gamma (\Omega )\Psi '(\Omega )}{2\Psi ^2(\Omega )}\left( \sum _{j=0} ^{\vartheta }j\gamma _j\Omega ^{j-1}\right) +\frac{\Gamma (\Omega )}{\Psi (\Omega )}\left( \sum _{j=0} ^{\vartheta }j(j-1)\gamma _j\Omega ^{j-2}\right) , \end{aligned}$$
(3.6)

where \(\Gamma (\Omega )\) and \(\Psi (\Omega )\) are polynomials in \(\Omega\). Putting Eqs. (3.5)–(3.6) into Eq. (3.2), a relation of the following form is obtained.

$$\begin{aligned} \Theta (\Omega ) = \varrho _\epsilon \Omega ^\epsilon +\cdots +\varrho _1\Omega + \varrho _0 = 0. \end{aligned}$$
(3.7)

Balancing the highest power nonlinear term and the term with the highest order derivative yields a relation in \(\vartheta\), \(\rho\) and \(\varsigma\), which is used to select suitable values of \(\vartheta\), \(\rho\) and \(\varsigma\). Equating all coefficients of \(\Theta (\Omega )\) equals to zero yields a set of algebraic equations containing free parameters, as

$$\begin{aligned} \varrho _i = 0, \quad i = 0,1,\ldots ,s. \end{aligned}$$
(3.8)

Solving the system (3.8), the values of \(\tau _0,\ldots ,\tau _\rho\), \(\chi _0,\ldots ,\chi _\varsigma\) and \(\gamma _0,\ldots ,\gamma _\vartheta\) are determined. Equation (3.4) can be expressed in integral form, as

$$\begin{aligned} \pm (\theta -\theta _0) = \int \frac{d\Omega }{\sqrt{\Lambda (\Omega )}} = \int \sqrt{\frac{\Gamma (\Omega )}{\Psi (\Omega )}}\,d\Omega . \end{aligned}$$
(3.9)

Equation (3.9) is solved using a complete discrimination system for polynomials to classify the roots of \(\Psi (\Omega )\) and obtain the exact solutions of Eq. (3.2). The solutions of Eq. (3.2) provide the exact traveling wave solutions of Eq. (3.1) after some simplification.

3.1 Application of ETEM

According to balancing principle, the highest order derivative term \(\nu ''\) is equated with the nonlinear term \(\nu ^2\), as

$$\begin{aligned} \rho = \vartheta + \varsigma + 2. \end{aligned}$$
(3.10)

For \(\vartheta = 1\) and \(\varsigma = 0\), \(\rho = 3\) is obtained. Hence, Eqs. (3.3) and (3.6) yield the following relations for the solution of Eq. (2.7).

$$\begin{aligned} \nu = \gamma _0 + \gamma _1\Omega , \end{aligned}$$
(3.11)
$$\begin{aligned} \nu '' = \frac{\gamma _1(3\tau _3\Omega ^2 + 2\tau _2\Omega + \tau _1)}{2\chi _0}. \end{aligned}$$
(3.12)

Putting Eqs. (3.11)–(3.12) into Eq. (2.7), then solving the algebraic system determined by collecting the coefficients of \(\Omega\) with the help of Mathematica, the following values are retrieved.

$$\begin{aligned} \tau _1= & {} \frac{-2\gamma _0(\eta + 3a^3b\gamma _0)\chi _0}{a^4b\gamma _1},\quad \tau _2 = \frac{(-\eta - 6a^3b\gamma _0 )\chi _0}{a^4b}, \\ \nonumber \quad \tau _3= & {} \frac{-2\gamma _1\chi _0}{a},\quad \tau _0 = \tau _0, \quad \gamma _0 = \gamma _0, \quad \gamma _1 = \gamma _1, \quad \chi _0 = \chi _0. \end{aligned}$$

Putting these results into Eqs. (3.4) and (3.9), the following relation is obtained.

$$\begin{aligned} \pm (\theta - \theta _0) = K \int \frac{d\Omega }{\sqrt{\Delta (\Omega )}}, \end{aligned}$$
(3.13)

where

$$\begin{aligned} \Delta (\Omega ) = \Omega ^3 + \frac{\tau _2}{\tau _3}\Omega ^2 + \frac{\tau _1}{\tau _3}\Omega + \frac{\tau _0}{\tau _3}, \quad K = \sqrt{\frac{\chi _0}{\tau _3}}. \end{aligned}$$
(3.14)

Integrating Eq. (3.13), substituting the result in Eq. (3.11) and using the transformation Eqs. (2.2) and (2.6), the solutions are obtained as follows:

For \(\Delta (\Omega ) = (\Omega - \lambda _1)^3\)

$$\begin{aligned} r(x,y,t)= & {} (\gamma _0 + \lambda _1\gamma _1)\left( ax + by - \frac{t(b^3 - \eta + 4a^2b \omega )}{4a^2}\right) \nonumber \\{} & {} -\frac{4 K^2\gamma _1}{\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) - \theta _0}+E_1, \end{aligned}$$
(3.15)

where \(E_1\) is the integration constant.

For \(\Delta (\Omega ) = (\Omega - \lambda _1)^2(\Omega - \lambda _2)\) and \(\lambda _2 > \lambda _1\)

$$\begin{aligned} r(x,y,t)= & {} (\gamma _0 + \lambda _1\gamma _1)\left( ax + by - \frac{t(b^3 - \eta + 4a^2b \omega )}{4a^2}\right) -2K\gamma _1\sqrt{\lambda _1 - \lambda _2} \nonumber \\{} & {} \times \tanh \left( \frac{\sqrt{\lambda _1 - \lambda _2}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2} - \theta _0\right) }{2K}\right) + E_2, \end{aligned}$$
(3.16)

where \(E_2\) is the integration constant.

For \(\Delta (\Omega ) = (\Omega - \lambda _1)(\Omega - \lambda _2)^2\) and \(\lambda _1 > \lambda _2\)

$$\begin{aligned} r(x,y,t)= & {} (\gamma _0 + \gamma _1\lambda _1)\left( ax + by - \frac{t(b^3 - \eta + 4a^2b \omega )}{4a^2}\right) -2K\gamma _1\sqrt{\lambda _1 - \lambda _2} \nonumber \\{} & {} \times \coth \left( \frac{\sqrt{\lambda _1 - \lambda _2}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2} - \theta _0\right) }{2K}\right) + E_3, \end{aligned}$$
(3.17)

where \(E_3\) is the integration constant.

For \(\Delta (\Omega ) = (\Omega - \lambda _1)(\Omega - \lambda _2)(\Omega - \lambda _3)\) and \(\lambda _1> \lambda _2 > \lambda _3\)

$$\begin{aligned} r(x,y,t)= & {} (\gamma _0 + \gamma _1\lambda _3) \left( ax + by - \frac{t(b^3 - \eta + 4a^2b \omega )}{4a^2} \right) \nonumber \\{} & {} +2\gamma _1K\sqrt{\lambda _1-\lambda _3} \left[ \frac{\sqrt{\lambda _1 - \lambda _3}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2} - \theta _0\right) }{2K}\right. \nonumber \\{} & {} -EllipticE\left. \left( sn\left( \frac{\sqrt{\lambda _1 - \lambda _3}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2} - \theta _0\right) }{2K}, \ell \right) , \ell \right) \right] +E_4,\nonumber \\ \end{aligned}$$
(3.18)

where

$$\begin{aligned} \ell ^2 = \frac{\lambda _2-\lambda _3}{\lambda _1-\lambda _3}, \quad EllipticE[r,z] = \int _{0}^{r}\left( \sqrt{\frac{1-z^2m^2}{1-m^2}}\right) \,dm \end{aligned}$$

and \(E_4\) is the integration constant.

Here \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\) are the zeros of polynomial equation

$$\begin{aligned} \Delta (\Omega ) = 0. \end{aligned}$$
(3.19)

Taking \(\gamma _0 = -\gamma _1\lambda _1\) and \(\theta _0 = 0\), the solutions Eqs. (3.15)–(3.17) can be simplified, as rational function solution

$$\begin{aligned} r(x,y,t) = -\frac{4 K^2\gamma _1}{ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}} + E_1, \end{aligned}$$
(3.20)

traveling wave solution

$$\begin{aligned} r(x,y,t) = -2K \gamma _1\sqrt{\lambda _1-\lambda _2}\tanh \left( \frac{\sqrt{\lambda _1-\lambda _2}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}\right) + E_2, \end{aligned}$$
(3.21)

singular soliton solution

$$\begin{aligned} r(x,y,t) = -2K \gamma _1\sqrt{\lambda _1-\lambda _2}\coth \left( \frac{\sqrt{\lambda _1-\lambda _2}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}\right) + E_3, \end{aligned}$$
(3.22)

respectively.

Furthermore, for \(\gamma _0 = -\gamma _1\lambda _3\) and \(\theta _0 = 0\), Eq. (3.18) can be simplified, as traveling wave solution

$$\begin{aligned} r(x,y,t)= & {} 2\gamma _1K\sqrt{\lambda _1-\lambda _3}\left[ \frac{\sqrt{\lambda _1 - \lambda _3}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}\right. \nonumber \\{} & {} \left. -EllipticE\left( sn\left( \frac{\sqrt{\lambda _1 - \lambda _3}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}, \ell \right) , \ell \right) \right] + E_4. \nonumber \\ \end{aligned}$$
(3.23)

Remark When the modulus term \(\ell \rightarrow\)1, then the solution Eq. (3.22), becomes

$$\begin{aligned} r(x,y,t)= & {} 2\gamma _1K\sqrt{\lambda _3-\lambda _1}\left[ \frac{\sqrt{\lambda _3 - \lambda _1}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}\right. \nonumber \\{} & {} \left. -EllipticE\left( \tanh \left( \frac{\sqrt{\lambda _3 - \lambda _1}\left( ax + by - \frac{t(b^3 -\eta + 4 a^2b \omega )}{4a^2}\right) }{2K}\right) , l\right) \right] + E_4, \nonumber \\ \end{aligned}$$
(3.24)

where \(\lambda _1 = \lambda _2\).

4 Mathematical analysis using MAEM

According to the modified auxiliary equation method, the nonlinear partial differential equation is taken, as

$$\begin{aligned} P(r, r_{x}, r_{y}, r_{t}, r_{xx}, r_{xy}, r_{xt},r_{yy},\ldots )=0, \end{aligned}$$
(4.1)

where P is a polynomial. Using the traveling wave transformation Eq. (4.1) is converted to an ODE of the form

$$\begin{aligned} Q(\Phi , \Phi ', \Phi '', \Phi ''',\ldots )=0, \end{aligned}$$
(4.2)

where \((')= \frac{d}{d\theta }\). The solution of Eq. (4.2) is expressed, as

$$\begin{aligned} \Phi (\theta )= p_0 + \sum _{i=1}^{M}p_iY^{ig(\theta )} + \sum _{i=1}^{M}q_iY^{-ig(\theta )}, \end{aligned}$$
(4.3)

where \(p_0\), \(p_i\), Y and \(q_i\) are constants to be determined. The unknown constants \(p_i\)’s, \(q_i\)’s cannot be zero simultaneously and the function \(g(\theta )\) satisfies the auxiliary equation

$$\begin{aligned} g'(\theta ) = \frac{\beta + \alpha Y^{-g(\theta )} + \delta Y^{g(\theta )}}{\ln (Y)}, \end{aligned}$$
(4.4)

where \(\beta\), \(\alpha\) and \(\delta\) are parameters to be calculated and \(Y>0\), \(Y\ne 0\). Using the homogenous balancing principle, the value of M can be induced, but in some cases, M is not retrieved as a positive integer. A positive integer value of M is determined by the following suitable transformation in these cases.

Case 1 When \(M=\frac{m}{n}\), where m and n are co-prime, the following transformation is utilized.

$$\begin{aligned} \Phi (\theta ) = (U(\theta ))^\frac{m}{n}. \end{aligned}$$
(4.5)

Case 2 When \(M=-p\) is a negative integer, the following transformation is utilized.

$$\begin{aligned} \Phi (\theta ) = (U(\theta ))^{-p}. \end{aligned}$$
(4.6)

Putting either Eqs. (4.5) and (4.6) into Eq. (4.2), the integer value of M can be obtained by homogenous balancing principle. Inserting Eq. (4.3) along with Eq. (4.4) into Eq. (4.2), collecting all the coefficients of \(Y^{ig(\theta )}\), where \((i= 0,\pm 1,\pm 2,\ldots ,\pm M)\), and equating them to zero, a system of equations can be deduced by using software like Mathematica, Maple to retrieve the values of unknowns \(p_0, p_i, q_i\), \(\beta\), \(\alpha\), \(\delta\), a, b, c where \((i = 1,2,\ldots ,M)\).

The function \(Y^{g(\theta )}\) assumes the following values.

If \(\beta ^2 - 4\alpha \delta < 0\) and \(\delta \ne 0\) then

$$\begin{aligned} Y^{g(\theta )} = \frac{-\beta +\sqrt{-\beta ^2 + 4\alpha \delta }\tan \left( \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right) }{2\delta }, \end{aligned}$$
(4.7)

or

$$\begin{aligned} Y^{g(\theta )} = -\frac{\beta +\sqrt{-\beta ^2 + 4\alpha \delta }\cot \left( \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right) }{2\delta }. \end{aligned}$$
(4.8)

If \(\beta ^2 - 4\alpha \delta > 0\) and \(\delta \ne 0\) then

$$\begin{aligned} Y^{g(\theta )} = -\frac{\beta +\sqrt{\beta ^2 - 4\alpha \delta }\tanh \left( \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right) }{2\delta }, \end{aligned}$$
(4.9)

or

$$\begin{aligned} Y^{g(\theta )} = -\frac{\beta +\sqrt{\beta ^2 - 4\alpha \delta }\coth \left( \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right) }{2\delta }. \end{aligned}$$
(4.10)

If \(\beta ^2 - 4\alpha \delta = 0\) and \(\delta \ne 0\) then

$$\begin{aligned} Y^{g(\theta )} = -\frac{2+\beta \theta }{2\delta \theta }. \end{aligned}$$
(4.11)

The exact solution of Eq. (4.1) can be attained by putting the values of \(p_0\), \(p_i\), \(q_i\), \(\alpha\), \(\beta\), \(\delta\) and substituting the corresponding values of \(Y^{g(\theta )}\) from Eqs. (4.7–4.11) into Eq. (4.3) with transformation Eq. (2.2).

4.1 Application of MAEM

According to the homogenous balancing principle, the highest order derivative term \(\nu ''\) and nonlinear term \(\nu ^2\) are balanced for \(M = 2\), Eq. (4.3) takes the form for solution of Eq. (2.7).

$$\begin{aligned} \nu (\theta ) = p_0 + p_1Y^{g(\theta )} + p_2Y^{2g(\theta )} + q_1Y^{-g(\theta )} + q_2Y^{-2g(\theta )}, \end{aligned}$$
(4.12)

where \(p_0\), \(p_1\), \(p_2\), \(q_1\) and \(q_2\) are arbitrary constants to be evaluated. Putting Eq. (4.12) with auxiliary equation Eq. (4.4) into Eq. (2.7) and equating all the coefficients of \(Y^{ig(\theta )}\) to zero, where \((i = 0, \pm 1,\pm 2,\pm 3,\pm 4)\), an algebraic set of equations is determined. The following solution sets are determined for the unknown constants.

Set 1: \(p_0 = -\frac{1}{3}a(\beta ^2 + 2\alpha \delta )\), \(p_1 = -2a\beta \delta\), \(p_2 = -2a\delta ^2\), \(q_1=0\), \(q_2=0\), \(b = \frac{\eta }{a^4(\beta ^2-4\alpha \delta )}\). Set 2: \(p_0 = -\frac{1}{3}a(\beta ^2 + 2\alpha \delta )\), \(p_1 = 0\), \(p_2 = 0\), \(q_1 = -2a\alpha \beta\), \(q_2 = -2a\alpha ^2\), \(b = \frac{\eta }{a^4(\beta ^2-4\alpha \delta )}\).

Set 3: \(p_0 = -2a\alpha \delta\), \(p_1 = -2a\beta \delta\), \(p_2 = -2a\delta ^2\), \(q_1 = 0\), \(q_2 = 0\), \(b = -\frac{\eta }{a^4(\beta ^2-4\alpha \delta )}\). Set 4: \(p_0 = -2a\alpha \delta\), \(p_1 = 0\), \(p_2 = 0\), \(q_1 = -2a\alpha \beta\), \(q_2 = -2a\alpha ^2\), \(b = -\frac{\eta }{a^4(\beta ^2-4\alpha \delta )}\).

Family 1 The following solutions are determined using Set 1. For \(\beta ^2 - 4\alpha \delta < 0\) and \(\delta \ne 0\),

$$\begin{aligned} r(x,y,t) = -\frac{1}{3}\,a(\beta ^2 - 4\alpha \delta )\theta - a\sqrt{-\beta ^2 + 4\alpha \delta }\tan \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] + k_{11}, \end{aligned}$$
(4.13)

or

$$\begin{aligned} r(x,y,t) = -\frac{1}{3}\,a(\beta ^2 - 4\alpha \delta )\theta + a\sqrt{-\beta ^2 + 4\alpha \delta }\cot \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] + k_{12}. \end{aligned}$$
(4.14)

For \(\beta ^2 - 4\alpha \delta > 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t) = -\frac{1}{3}\,a(\beta ^2 - 4\alpha \delta )\theta + a\sqrt{\beta ^2 - 4\alpha \delta }\tanh \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] + k_{13}, \end{aligned}$$
(4.15)

or

$$\begin{aligned} r(x,y,t) = -\frac{1}{3}\,a(\beta ^2 - 4\alpha \delta )\theta + a\sqrt{\beta ^2 - 4\alpha \delta }\coth \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] + k_{14}, \end{aligned}$$
(4.16)

where \(\theta = ax + by -ct\), \(c = \frac{b^3-\eta +4a^2b\omega }{4a^2}\) and \(k_{1j}\) \((j = 1,2,3,4)\) are integration constants.

Family 2 The following solutions are determined using Set 2.

For \(\beta ^2 - 4\alpha \delta < 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t)= & {} \frac{ \left( a({\beta }^2 - 4 {\alpha } {\delta })^\frac{7}{2} \,\text {sec}^2 \left[ \frac{1}{2}\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}{\theta }\right] \right) }{\left( 3(-({\beta }^2 - 4 {\alpha } {\delta })^2)^\frac{3}{2} \left( {\beta }- \sqrt{{-\beta }^2 +4 {\alpha } {\delta }} \tan \left[ \frac{1}{2}\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }} {\theta } \right] \right) ^2\right) } \nonumber \\{} & {} \times \left[ 2 {\alpha }{\delta }\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}{\theta } + \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }} \right. \nonumber \\{} & {} \times \left. \left( -3 {\beta } + {\beta }^2 {\theta } - 2 {\alpha }{\delta }{\theta }\right) \cosh \left( \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}\theta \right) \right. \nonumber \\{} & {} \left. + \left( -3\beta ^2+\beta ^3\theta +6\alpha \delta - 4\alpha \beta \delta \theta \right) \sinh \left( \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}\theta \right) \right] + k_{21}, \end{aligned}$$
(4.17)

or

$$\begin{aligned} r(x,y,t)= & {} \frac{ \left( a({\beta }^2 - 4 {\alpha } {\delta })^\frac{3}{2} \,\csc ^2 \left[ \frac{1}{2}\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}{\theta }\right] \right) }{\left( 3(-({\beta }^2 - 4 {\alpha } {\delta })^2)^\frac{1}{2} \left( {\beta }+ \sqrt{{-\beta }^2 +4 {\alpha } {\delta }} \cot \left[ \frac{1}{2}\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}{\theta } \right] \right) ^2\right) } \nonumber \\{} & {} \times \left[ -2 {\alpha } {\delta }\sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}{\theta } + \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }} \right. \nonumber \\{} & {} \times \left. \left( -3 {\beta } + {\beta }^2 {\theta } - 2 {\alpha }{\delta }{\theta }\right) \cosh \left( \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}\theta \right) \right. \nonumber \\{} & {} \left. + \left( -3\beta ^2+\beta ^3\theta +6\alpha \delta - 4\alpha \beta \delta \theta \right) \sinh \left( \sqrt{{-\beta }^2 + 4 {\alpha } {\delta }}\theta \right) \right] + k_{22}. \end{aligned}$$
(4.18)

For \(\beta ^2 - 4\alpha \delta > 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t)= & {} \frac{- \left( a \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \,\text {sech}^2 \left[ \frac{1}{2}\sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta }\right] \right) }{3 \left( {\beta }+ \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \tanh \left[ \frac{1}{2}\sqrt{{\beta }^2 -4 {\alpha } {\delta }} {\theta }\right] \right) ^2} \nonumber \\{} & {} \times \left[ 2 {\alpha }{\delta }\sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta } + \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \right. \nonumber \\{} & {} \times \left. \left( -3 {\beta } + {\beta }^2 {\theta } - 2 {\alpha }{\theta } {\delta }\right) \cosh \left( \sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta }\right) \right. \nonumber \\{} & {} \left. +\left( -3\beta ^2+\beta ^3\theta +6\alpha \delta -4\alpha \beta \delta {\theta }\right) \sinh \left( \sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta }\right) \right] + k_{23}, \end{aligned}$$
(4.19)

or

$$\begin{aligned} r(x,y,t)= & {} \frac{- \left( a \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \,\text {csch}^2 \left[ \frac{1}{2}\sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta }\right] \right) }{3 \left( {\beta }+ \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \coth \left[ \frac{1}{2} \sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta } \right] \right) ^2} \nonumber \\{} & {} \times \left[ - 2 {\alpha }{\delta }\sqrt{{\beta }^2 -4 {\alpha } {\delta }}{\theta } + \sqrt{{\beta }^2 -4 {\alpha } {\delta }} \right. \nonumber \\{} & {} \times \left. \left( -3 {\beta } + {\beta }^2 {\theta } - 2 {\alpha } {\delta }\theta \right) \cosh \left( \sqrt{{\beta }^2 -4 {\alpha } {\delta }}\theta \right) \right. \nonumber \\{} & {} \left. +\left( -3\beta ^2+\beta ^3\theta +6\alpha \delta -4\alpha \beta \delta \theta \right) \sinh \left( \sqrt{{\beta }^2 -4 {\alpha } {\delta }}\theta \right) \right] + k_{24}, \end{aligned}$$
(4.20)

where \(\theta = ax + by -ct\), \(c = \frac{b^3-\eta +4a^2b\omega }{4a^2}\) and \(k_{2j}\) \((j = 1,2,3,4)\) are integration constants.

Family 3 The following solutions are determined using Set 3.

For \(\beta ^2 - 4\alpha \delta < 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t) = -a\sqrt{-\beta ^2 + 4\alpha \delta }\tan \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] + k_{31}, \end{aligned}$$
(4.21)

or

$$\begin{aligned} r(x,y,t) = a\sqrt{-\beta ^2 + 4\alpha \delta }\cot \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] + k_{32}. \end{aligned}$$
(4.22)

For \(\beta ^2 - 4\alpha \delta > 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t) = a\sqrt{\beta ^2 - 4\alpha \delta }\tanh \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] + k_{33}, \end{aligned}$$
(4.23)

or

$$\begin{aligned} r(x,y,t) = a\sqrt{\beta ^2 - 4\alpha \delta }\coth \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] + k_{34}, \end{aligned}$$
(4.24)

where \(\theta = ax + by -ct\), \(c = \frac{b^3-\eta +4a^2b\omega }{4a^2}\) and \(k_{3j}\) \((j = 1,2,3,4)\) are integration constants.

Family 4 The following solutions are determined using Set 4.

For \(\beta ^2 - 4\alpha \delta < 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t) = -\frac{4a\alpha \delta }{\beta -\sqrt{-\beta ^2 + 4\alpha \delta }\tan \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] }+ k_{41}, \end{aligned}$$
(4.25)

or

$$\begin{aligned} r(x,y,t) = -\frac{4a\alpha \delta }{\beta +\sqrt{-\beta ^2 + 4\alpha \delta }\cot \left[ \frac{1}{2}\sqrt{-\beta ^2 + 4\alpha \delta }\theta \right] }+k_{42}. \end{aligned}$$
(4.26)

For \(\beta ^2 - 4\alpha \delta > 0\) and \(\delta \ne 0\)

$$\begin{aligned} r(x,y,t) = -\frac{4a\alpha \delta }{\beta +\sqrt{\beta ^2 - 4\alpha \delta }\tanh \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] }+ k_{43}, \end{aligned}$$
(4.27)

or

$$\begin{aligned} r(x,y,t) = -\frac{4a\alpha \delta }{\beta +\sqrt{\beta ^2 - 4\alpha \delta }\coth \left[ \frac{1}{2}\sqrt{\beta ^2 - 4\alpha \delta }\theta \right] } + k_{44}, \end{aligned}$$
(4.28)

where \(\theta = ax + by -ct\), \(c = \frac{b^3-\eta +4a^2b\omega }{4a^2}\) and \(k_{4j}\) \((j = 1,2,3,4)\) are integration constants.

5 Graphical simulations and comparison of results

Some of the retrieved solutions are demonstrated through graphical simulations to observe the wave behavior of the \((2+1)\)-dimensional extended CBS equation. The graphs are plotted for suitably assigned parametric values. A variety of dynamical structures are observed corresponding to various obtained solutions including kink soliton, dark-bright singular soliton and periodic wave solutions.

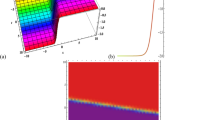
Figure 1 shows the graphs of solution (3.20) for \(K = \eta =a=y = 1\), \(\gamma _1=\omega = 2\), \(b = -1\), \(E_1 = 0\). The graphical illustration represents a dark-bright singular soliton solution.

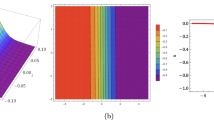
Figure 2 shows the graphs of solution (3.21) for \(K=\eta = a=y = 1\), \(\gamma _1=\omega = 2\), \(b = -1\), \(E_2 = 0\), \(\lambda _1 = 2\), \(\lambda _2 = 4\). The graphical illustration represents a singular periodic wave solution.

Figure 3 shows the graphs of solution (3.22) for \(K=\eta =a=y = 1\), \(\gamma _1 = \omega = 2\), \(b = -1\), \(E_3 = 0, \lambda _1 = 4, \lambda _2 = 2\). The graphical illustration represents a dark-bright singular soliton solution.

Figure 4 shows the graph of solution (4.13) for \(\beta = \eta =a=y=\omega = 1\), \(\alpha =\delta = 2\), \(k_{11} = 0\). The graphical illustration represents a singular periodic wave solution.

Figure 5 shows the graph of solution (4.15) for \(\alpha =\eta =a=y = 1\) , \(\beta = 4\), \(\delta = 2\), \(\omega = -1, k_{13} = 0\). The graphical illustration represents a traveling wave solution.

Figure 6 shows the graph of solution (4.25) for \(\alpha =\omega = 2\), \(\beta =\delta =a=y = 1\), \(\eta = -1, k_{41} = 0\). The graphical illustration represents a periodic wave solution.

Figure 7 shows the graph of solution (4.27) for \(\alpha =\omega = 2\), \(\beta = 4\), \(\delta =a=y =1\), \(\eta = -1\), \(k_{43} = 0\). The graphical illustration represents the kink soliton solution.

Fig. 1
figure 1

Graph of dark–bright singular soliton solution (3.20) in (a) for \(K = \eta = a = y = 1, \gamma _1 = \omega = 2\), \(b = -1, E_1 = 0\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 2
figure 2

Graph of singular periodic wave solution (3.21) in (a) for \(K = \eta = a = y = 1, \gamma _1 = \omega = 2, b = -1, E_2 = 0, \lambda _1 = 2, \lambda _2 = 4\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 3
figure 3

Graph of dark–bright singular soliton solution (3.22) in (a) for \(K=\eta =a=y = 1\), \(\gamma _1 = \omega = 2\), \(b = -1, E_3 = 0\), \(\lambda _1 = 4, \lambda _2 = 2\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 4
figure 4

Graph of singular periodic wave solution (4.13) in (a) for \(\beta = \eta =a=y=\omega = 1\), \(\alpha =\delta = 2\), \(k_{11} = 0\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 5
figure 5

Graph of traveling wave solution (4.15) in (a) for \(\alpha = \eta =a=y = 1\) , \(\beta = 4\), \(\delta = 2\), \(\omega = -1\), \(k_{13} = 0\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 6
figure 6

Graph of periodic wave solution (4.25) in (a) for \(\alpha =\omega = 2\), \(\beta =\delta =a=y = 1\), \(\eta = -1\), \(k_{41} = 0\) with its 2D graph in (b) and density plot in (c)

Full size image
Fig. 7
figure 7

Graph of kink type soliton solution (4.27) in (a) for \(\alpha =\omega = 2\), \(\beta = 4\), \(\delta =a=y = 1\), \(\eta = -1, k_{43} = 0\) with its 2D graph in (b) and density plot in (c)

Full size image

The proposed extended trial equation method and modified auxiliary equation method are applied for the first time in this work to explore the considered CBS model. The proposed techniques have produced a diverse range of exact traveling wave solutions to the (2+1)-dimensional extended CBS model. The comparison of the proposed study with the existing literature reveal that the obtained results confirm some of the previously obtained wave behavior and also include some novel results (Tripathy and Sahoo 2021; Shen et al. 2021; Khalique and Maefo 2021; Ali et al. 2021; Chen et al. 2020). Hence, the achieved solutions demonstrate the effectiveness of the recommended approaches.

6 Conclusion

The \((2+1)\)-dimensional extended CBS equation is theoretically investigated to construct the exact traveling wave solutions including solitons. The extended trial equation method and modified auxiliary equation method are applied to retrieve the explicit accurate closed-form solution expressions. The traveling wave solutions in terms of hyperbolic, trigonometric and rational functions are obtained. The behavior of the retrieved exact solutions is demonstrated by surface plots, line plots and density plots choosing suitable values of parameters. Kink soliton, dark-bright singular soliton and periodic wave solutions are exhibited by the graphical simulations. These results gives us different forms of solitary waves which help to understand the real-world problems. The kink soliton is characterized by the sudden change in wave form from one asymptotic state to another. The bright-dark singular soliton has a localized increase in the wave amplitude followed by a localized decrease in the wave amplitude. The periodic waves are characterized by the repetitive wave form after certain intervals of time. Periodic wave solutions can be used in plasma physics and nonlinear optics to describe the propagation of periodic traveling waves. Kink solitons in nonlinear fibers can cause self-steepness or nonlinear effects, influencing the high-intensity short-pulse characteristics. Kink solitons can be applied between two optical logic units or domains as polarization switches. Owing to the cross-polarization of light fields in birefringent, dark-bright solitons can be produced. They are widely used in telecommunication and ultrafast optics. The visual depiction shows that the modified auxiliary equation approach has more accurate and valuable results for the proposed model than the extended trial equation method. All soliton types are not provided by the single scheme so to enhance the capability of the considered model these methods have been described. The obtained results exhibit that the presented methods are effective and useful for determining the solutions of \((2+1)\)-dimensional extended CBS equation. The obtained results will be helpful in understanding the relevant physical system in plasma physics, optics and fluid dynamics.