1 Introduction

Water waves have been thought to be one of the most common phenomena in nature, the study of which helps in designing the related industries [1,2,3,4,5,6,7]. The Kadomtsev–Petviashvili (KP)-type equations have been seen in fluid mechanics, nonlinear optics and plasma physics [8,9,10,11,12,13,14,15]. People have also obtained the B-type KP hierarchy by imposing an extra condition between the Lax operator and its adjoint of the KP hierarchy [16,17,18,19,20]. To study the B-type KP hierarchy, researchers have presented a generalized (\(3+1\))-dimensional B-type KP equation for the water waves [21,22,23],

$$\begin{aligned} \begin{aligned} u_{ty}-u_{xxxy}-3(u_xu_y)_x+3u_{xz}=0, \end{aligned} \end{aligned}$$
(1)

where \(u=u(x,y,z,t)\) is a real function of the scaled spatial coordinates x, y, z and temporal coordinate t, the subscripts denote the partial derivatives. The higher-order, multiple rogue waves and lumps for Eq. (1) have been obtained based on the solutions in terms of the Gramian [21]. Multiple wave solutions for Eq. (1) have been constructed by means of the multiple exp-function algorithm [22]. N-soliton solutions formed by the linear combinations of the exponential traveling waves have been constructed [23].

Breathers, lumps and rogue waves have attracted researchers’ attention because of their applications in fluid mechanics, nonlinear optics, plasma physics and other fields [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. It has been considered that there are three types of the breathers, namely the Akhmediev breathers, Kuznetsov–Ma breathers and Peregrine solitons [36, 41,42,43,44,45,46]. As a kind of the rational solutions, lumps have been considered as the waves localized in all directions in the space [33,34,35]. Rogue waves have been seen as the large-amplitude waves unexpectedly appearing in the oceans [36,37,38, 47, 48]. A potential mechanism for the formation of the rogue waves has been associated with the modulation instability [45, 49,50,51,52]. Peregrine solitons have been considered as the prototype of the rogue waves in the oceans [36]. It has been reported that three types of the breathers are mutually related, especially the Peregrine solitons have been considered as the limiting form of the Akhmediev or Kuznetsov–Ma breathers [53, 54].

To our knowledge, the breather solutions and hybrid solutions which are composed of the breathers, lumps, line rogue waves and kink solitons for Eq. (1) have not been studied via the KP hierarchy reduction. In Sect. 2, we will construct the solutions in terms of the Gramian which are different from those in Ref. [21] for Eq. (1). In Sect. 3, we will derive one kind of the breather solutions for Eq. (1), which can be reduced to the homoclinic orbits under certain conditions. According to the long-wave limit method [33, 55], we will also construct the rational solutions including the lumps and line rogue waves for Eq. (1). In Sect. 4, one kind of the hybrid solutions composed of the breathers, lumps and line rogue waves for Eq. (1) will be obtained. In Sect. 5, another kind of the breather solutions and hybrid solutions which are composed of the breathers, lumps and kink solitons for Eq. (1) will be constructed. In Sect. 6, we will give our conclusions.

2 Gramian solutions for Eq. (1)

By virtue of the dependent variable transformation [21]

$$\begin{aligned} u=2(\ln f)_x, \end{aligned}$$
(2)

where \(f=f(x,y,z,t)\) is a real function, Eq. (1) can be converted into the following bilinear form [14]:

$$\begin{aligned} (D_yD_t-D_x^3D_y+3D_xD_z)f\cdot f=0, \end{aligned}$$
(3)

where D is the Hirota’s bilinear differential operator defined as [56]

$$\begin{aligned}&D_x^{l_1}D_y^{l_2}D_z^{l_3}D_t^{l_4}f\cdot g =\Big (\frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\Big )^{l_1}\Big (\frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\Big )^{l_2}\\&\qquad \Big (\frac{\partial }{\partial z}-\frac{\partial }{\partial z'}\Big )^{l_3}\Big (\frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\Big )^{l_4}\quad f(x,y,z,t)\\&\qquad g(x',y',z',t')|_{x=x',y=y',z=z',t=t'}, \end{aligned}$$

with g as a function of the formal variables \(x',y',z'\) and \(t'\), \(l_1,l_2,l_3\) and \(l_4\) being the non-negative integers.

Referring to Refs. [57,58,59,60], the bilinear equation in the KP hierarchy,

$$\begin{aligned} \begin{aligned} (D_{x_1}^3D_{x_2}+2D_{x_3}D_{x_2}-3D_{x_1}D_{x_4})\tau _n\cdot \tau _n=0, \end{aligned} \end{aligned}$$
(4)

admits the Gramian solutions,

$$\begin{aligned} \begin{aligned} \tau _n=|m_{ij}^{(n)}|_{1\le i,j\le N}, \end{aligned} \end{aligned}$$
(5)

where the matrix element \(m_{ij}^{(n)}\) satisfies the following differential and difference relations:

$$\begin{aligned} \begin{aligned}&\partial _{x_1} m_{ij}^{(n)}=\varphi _i^{(n)}\psi _j^{(n)},\\&\partial _{x_2} m_{ij}^{(n)}=(\partial _{x_1}\varphi _i^{(n)})\psi _j^{(n)}-\varphi _i^{(n)}(\partial _{x_1}\psi _j^{(n)}),\\&\partial _{x_3} m_{ij}^{(n)}=(\partial ^2_{x_1}\varphi _i^{(n)})\psi _j^{(n)}+\varphi _i^{(n)}(\partial ^2_{x_1}\psi _j^{(n)})\\&\qquad \qquad -\,(\partial _{x_1}\varphi _i^{(n)})(\partial _{x_1}\psi _j^{(n)}),\\&\partial _{x_4} m_{ij}^{(n)}=(\partial ^3_{x_1}\varphi _i^{(n)})\psi _j^{(n)}-(\partial ^2_{x_1}\varphi _i^{(n)})(\partial _{x_1}\psi _j^{(n)})\\&\qquad \qquad +\,(\partial _{x_1}\varphi _i^{(n)})(\partial ^2_{x_1}\psi _j^{(n)})-\varphi _i^{(n)}(\partial ^3_{x_1}\psi _j^{(n)}),\\&m_{ij}^{(n+1)}=m_{ij}^{(n)}+\varphi _i^{(n)}\psi _j^{(n+1)},~~\partial _{x_k}\varphi _i^{(n)}=\varphi _i^{(n+k)},\\&\partial _{x_k}\psi _j^{(n)}=-\,\psi _j^{(n-k)},~~(k=1,2,3,4). \end{aligned} \end{aligned}$$
(6)

\(m_{ij}^{(n)}\), \(\varphi _i^{(n)}\) and \(\psi _j^{(n)}\) are the functions of the variables \(x_1,x_2,x_3\) and \(x_4\), “\(\partial \)” means the partial derivative, n is an integer and N is a positive integer. Proof process about \(\tau _n\) being the solutions of Bilinear Form (4) can be found in Ref. [21].

In order to construct the breather solutions for Eq. (1), satisfying (6), we choose

$$\begin{aligned} \begin{aligned}&m_{ij}^{(n)}=\delta _{ij}+\frac{1}{p_i+q_j}\varphi _i^{(n)}\psi _j^{(n)},\\&\varphi _i^{(n)}=p_i^n(p_i+q_i)e^{r_i},\\&\psi _j^{(n)}=(-\,q_j)^{-n}e^{s_j}, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&r_i=p_ix_1+p_i^2x_2+p_i^3x_3+p_i^4x_4+r_i^0,\\&s_j=q_jx_1-q_j^2x_2+q_j^3x_3-q_j^4x_4+s_j^0, \end{aligned} \end{aligned}$$

where \(p_i\), \(q_j\), \(r_i^0\) and \(s_j^0\) are the complex constants, \(\delta _{ij}=1~(i=j)\) and \(\delta _{ij}=0~(i\ne j)\).

We set \(f=\tau _0\) and take the independent variable transformations:

$$\begin{aligned} \begin{aligned} x_1=-\,x,~x_2=Iy,~x_3=2t,~x_4=Iz, \end{aligned} \end{aligned}$$

where \(I=\sqrt{-\,1}\), and then Bilinear Form (4) can be reduced to Bilinear Form (3). With certain parameters \(p_i\) and \(q_j\) given in [61], we can prove that \(f=\tau _0\) is a real function. Therefore, Gramian solutions for Bilinear Form (3) can be written as

$$\begin{aligned} \begin{aligned} f=\Big |\delta _{ij}+\frac{p_i+q_i}{p_i+q_j}e^{r_i+s_j}\Big |_{N\times N}, \end{aligned} \end{aligned}$$
(7)

where

$$\begin{aligned} \begin{aligned}&r_i=-\,p_ix+Ip_i^2y+2p_i^3t+Ip_i^4z+r_i^0,\\&s_j=-\,q_jx-Iq_j^2y+2q_j^3t-Iq_j^4z+s_j^0, \end{aligned} \end{aligned}$$

and then, by virtue of the transformation \(u=2(\ln f)_x\), we can obtain the Gramian solutions which are different from those in [21] for Eq. (1).

3 The first kind of the breather and rational solutions for Eq. (1)

3.1 The first kind of the breather solutions for Eq. (1)

In Appendix A, we construct the first kind of the breather solutions for Eq. (1). Setting \(M=1\) in Eq. (24), we can obtain the first-order breather solutions for Eq. (1) as

$$\begin{aligned}&u=2(\ln f)_x,\end{aligned}$$
(8a)
$$\begin{aligned}&f=1+e^{\zeta _1}+e^{\zeta ^*_1}+A_{12}e^{\zeta _1+\zeta ^*_1}, \end{aligned}$$
(8b)

where

$$\begin{aligned} \begin{aligned}&\zeta _1=-\,I\lambda _1x+2I\varLambda _1\lambda _1y-I\lambda _1(\varLambda _1\lambda _1^2+4\varLambda _1^3)z\\&\quad \qquad -\,\frac{I\lambda _1}{2}(\lambda _1^2+12\varLambda _1^2)t+\zeta _1^0,\\&A_{12}=1-\frac{\lambda _1^2}{(\varLambda _1-\varLambda _1^*)^2}. \end{aligned} \end{aligned}$$

Take \(\varLambda _1=\varLambda _{1R}+I\varLambda _{1I}\) with \(I=\sqrt{-1}\), \(\varLambda _{1R}\) and \(\varLambda _{1I}\) as the real constants, and we rewrite \(\zeta _1=\zeta _{1R}+I\zeta _{1I}\), where

$$\begin{aligned} \begin{aligned}&\zeta _{1R}=-\,2\lambda _1\varLambda _{1I}y+\lambda _1\varLambda _{1I}(\lambda _1^2-4\varLambda _{1I}^2\\&\quad \qquad +\,12\varLambda _{1R}^2)z+12\lambda _1\varLambda _{1R}\varLambda _{1I}t+\zeta _1^0,\\&\zeta _{1I}=-\,\lambda _1x+2\lambda _1\varLambda _{1R}y\\&\quad \qquad -\,\lambda _1\varLambda _{1R}(\lambda _1^2-12\varLambda _{1I}^2+4\varLambda _{1R}^2)z\\&\quad \qquad -\,\frac{\lambda _1}{2}(\lambda _1^2-12\varLambda _{1I}^2+12\varLambda _{1R}^2)t. \end{aligned} \end{aligned}$$
(9)

It can be found that the behavior of the first-order breather is affected by \(\varLambda _{1R},~\varLambda _{1I}\) and \(\lambda _1\), and the asymptotic behavior of the first-order breather is \(u\rightarrow 0\) as \(\zeta _{1R}\rightarrow \pm \,\infty \). Moreover, the first-order breather is localized along the direction of the line \(\zeta _{1R}=0\) and periodic along the direction of the line \(\zeta _{1I}=0\). Calculation shows that \(\varLambda _{1I}\) and \(\lambda _1\) cannot be zero; otherwise, the first-order breather solutions will be equal to zero. Because \(\zeta _{1R}\) only contains the expressions of y and t but not the expression of x, the first-order breather is parallel to the x axis on the (x, y) and (x, z) planes. However, on the (y, z) plane, the first-order breather has an angle with the y and z axis. Particularly, when the coefficient of z in \(\zeta _{1R}\) is equal to zero, i.e., \(\lambda _1^2-4\varLambda _{1I}^2+12\varLambda _{1R}^2=0\), the first-order breather will be parallel to the z axis on the (y, z) plane.

We note that when \(\frac{\partial \zeta _{1R}}{\partial z}=0\) or \(\frac{\partial \zeta _{1R}}{\partial t}=0\), which means that the coefficient of z or t in \(\zeta _{1R}\) is equal to zero, and the localized behavior of the breather only appears in the t axis. Those breathers will be reduced to the periodic line waves on the (x, z) or (x, t) plane, where the periodic line waves begin from the constant plane, then form the periodic waves, and finally return to the plane. That kind of the solution is also called the homoclinic orbit [62, 63]. Because \(\varLambda _{1I}\) and \(\lambda _1\) cannot be zero, there is no such solution on the (x, y) plane.

The higher-order breather solutions for Eq. (1) can be obtained similarly. For instance, when \(M=2\), the second-order breather solutions for Eq. (1) are

$$\begin{aligned} u&=2(\ln f)_x,\end{aligned}$$
(10)
$$\begin{aligned} f&=\varDelta _2\left| \begin{array}{cc} \frac{1}{I\lambda _1e^{\zeta _1}}+\frac{1}{I\lambda _1} &{} \frac{-\,1}{I\left( \varLambda _1-\varLambda _1^*\right) }\\ \frac{1}{I\left( \varLambda _1-\varLambda _1^*\right) } &{} \frac{-\,1}{I\lambda _1e^{\zeta _1^*}}+\frac{-\,1}{I\lambda _1}\\ \frac{1}{I\left( \varLambda _1-\varLambda _2+\frac{\lambda _1+\lambda _2}{2}\right) } &{} \frac{-\,1}{I\left( \varLambda _2-\varLambda _1^*+\frac{\lambda _1-\lambda _2}{2}\right) }\\ \frac{1}{I\left( \varLambda _1-\varLambda _2^*+\frac{\lambda _1-\lambda _2}{2}\right) } &{} \frac{-\,1}{I\left( \varLambda _2^*-\varLambda _1^*+\frac{\lambda _1+\lambda _2}{2}\right) }\\ \end{array}\right. \nonumber \\&\qquad \left. \begin{array}{cc} \frac{1}{I\left( \varLambda _2-\varLambda _1+\frac{\lambda _1+\lambda _2}{2}\right) } &{} \frac{1}{I\left( \varLambda _2^*-\varLambda _1+\frac{\lambda _1-\lambda _2}{2}\right) }\\ \frac{-\,1}{I\left( \varLambda _1^*-\varLambda _2+\frac{\lambda _1-\lambda _2}{2}\right) } &{} \frac{-\,1}{I\left( \varLambda _1^*-\varLambda _2^*+\frac{\lambda _1+\lambda _2}{2}\right) }\\ \frac{1}{I\lambda _2e^{\zeta _2}}+\frac{1}{I\lambda _2} &{} \frac{-\,1}{I\left( \varLambda _2-\varLambda _2^*\right) }\\ \frac{1}{I\left( \varLambda _2-\varLambda _2^*\right) } &{} \frac{-\,1}{I\lambda _2e^{\zeta _2^*}}+\frac{-\,1}{I\lambda _2} \end{array}\right| , \end{aligned}$$
(11)

where

$$\begin{aligned}&\zeta _k=-\,I\lambda _kx+2I\varLambda _k\lambda _ky-I\lambda _k(\varLambda _k\lambda _k^2+4\varLambda _k^3)z\end{aligned}$$
(12a)
$$\begin{aligned}&\quad \qquad -\,\frac{I\lambda _k}{2}(\lambda _k^2+12\varLambda _k^2)t+\zeta _k^0,~~(k=1,2) \nonumber \\&\varDelta _2=\lambda _1^2\lambda _2^2e^{\zeta _1+\zeta _1^*+\zeta _2+\zeta _2^*}. \end{aligned}$$
(12b)
Fig. 1
figure 1

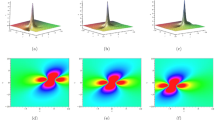
The second-order breathers via Solutions (10) with \(\varLambda _1=0.4+I,~\lambda _1=2,~\varLambda _2=-\,\frac{1}{3}+\frac{2}{3}I,~ \lambda _2=\frac{2}{3}\) and \(\zeta _1^0=\zeta _2^0=0\). a\(z=0\); b\(x=0\); c\(y=0\)

Full size image

From the above analysis on the first-order breather solutions, we know that there are three forms of the second-order breathers, which contain two first-order breathers, two homoclinic orbits and the mixed form consisting of one first-order breather and one homoclinic orbit, as shown in Fig. 1. Since \(\zeta _{1R}\) in Eqs. (12) only contains the expressions of y and t but not the expression of x, which means that the x direction shows only the periodicity, so that the second-order breathers are still parallel to the x axis on the (x, y) and (x, z) planes. However, on the (y, z) plane, we can construct the breathers which are parallel to the z axis or have an angle to the y and z axes. Because \(\text {Im}(\varLambda _1)\) (where \(\hbox {Im}(\bullet )\) is the imaginary part of \(\bullet \)) and \(\lambda _1\) in Solutions (10) cannot be zero, the second-order breathers on the (y, z) plane can be parallel to the z axis but not to the y axis. We find two interaction forms of the second-order breathers. The two first-order breathers propagate along the same direction and undergo an overtaking interaction when \(\text {Re}(\varLambda _1)\cdot \text {Re}(\varLambda _2)>0\) (where \(\hbox {Re}(\bullet )\) is the real part of \(\bullet \)) in Solutions (10). However, when \(\text {Re}(\varLambda _1)\cdot \text {Re}(\varLambda _2)<0\) in Solutions (10), the two first-order breathers propagate in the opposite direction and undergo a head-on interaction.

If we take \(\frac{\partial \text {Re}(\zeta _1)}{\partial z}=0\) or \(\frac{\partial \text {Re}(\zeta _2)}{\partial z}=0\) in Solutions (10), we can obtain the mixed form of the second-order breather solutions consisting of one first-order breather and one homoclinic orbit, as shown in Fig. 1. It can be seen that the mixed solutions only contain one first-order breather when \(|t|\ge 0\), and the first-order breather is parallel to the x axis. When \(|t|\rightarrow 0\), periodic line waves arise from the constant background and interact with the first-order breather. Moreover, let both \(\frac{\partial \text {Re}(\zeta _1)}{\partial z}=0\) and \(\frac{\partial \text {Re}(\zeta _2)}{\partial z}=0\) in Solutions (10), and we can obtain the second-order breather solutions consisting of two homoclinic orbits.

3.2 Rational solutions for Eq. (1)

According to the long-wave limit method [23, 39], we construct the rational solutions for Eq. (1) in Appendix B. We note that the rational solutions have also been obtained via another method in [21]. When \(M=1\), the rational solutions for Eq. (1) can be written as

$$\begin{aligned}&u=2(\ln f)_x,\nonumber \\&f=|\theta _1|^2-\frac{1}{(\varLambda _1-\varLambda _1^*)^2}, \end{aligned}$$
(13)

with

$$\begin{aligned} \begin{aligned} \theta _1=I(x-2\varLambda _1y+4\varLambda _1^3z+6\varLambda _1^2t). \end{aligned} \end{aligned}$$

Let \(\varLambda _1=a+Ib\) with a and b as the real constants, and the rational solutions can be rewritten as

$$\begin{aligned} \begin{aligned} u=\frac{16b^2(x+hy+mz+nt)}{1+4b^2[(x+hy+mz+nt)^2+(ry+pz+qt)^2]}, \end{aligned} \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned}&m=4a(a^2-3b^2),~n=6(a^2-b^2),~p=4b(b^2-3a^2),\\&q=-\,12ab,~h=-\,2a,~r=2b. \end{aligned} \end{aligned}$$

Next, we give two types of the rational solutions:

  1. 1.

    Lumps. We take the (x, z) plane as an example. From Eq. (14), when \(y=0\), at any fixed t, when (x, z) goes to the infinity, \(u\rightarrow 0\). Hence that solution indicates a lump moving on a constant background, and that lump has two extreme points at \((\frac{1}{2b},0)\) and \((-\,\frac{1}{2b},0)\) with the maximum and minimum being 4b and \(-\,4b\), respectively.

  2. 2.

    Line rogue waves. When \(p=0\) in Solutions (14), i.e., \(4b(b^2-3a^2)=0\), the lumps will be reduced to the line rogue waves on the (x, z) plane. Different from that of the soliton, the amplitude of the line rogue wave varies with t, and the maximum and minimum amplitudes of the line rogue waves are 4b and \(-\,4b\), respectively. We note that because b cannot be zero (otherwise u is equal to zero), there is no such line rogue waves on the (x, y) plane.

Fig. 2
figure 2

The second-order rational solutions via Solutions (15) with \(\varLambda _1=\frac{1}{2}+\frac{\sqrt{3}}{2}\) and \(\varLambda _2=-\,\frac{1}{2}+\frac{\sqrt{3}}{2}\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image

When \(M=2\), the second-order rational solutions are

$$\begin{aligned} \begin{aligned}&u=2(\ln f)_x,\\&f=\begin{vmatrix} \theta _1&\frac{1}{\varLambda _1-\varLambda _1^*}&\frac{1}{\varLambda _1-\varLambda _2}&\frac{1}{\varLambda _1-\varLambda _2^*}\\ \frac{1}{\varLambda _1-\varLambda _1^*}&\theta _1^*&\frac{-\,1}{\varLambda _1^*-\varLambda _2}&\frac{-\,1}{\varLambda _1^*-\varLambda _2^*}\\ \frac{1}{\varLambda _2-\varLambda _1}&\frac{1}{\varLambda _2-\varLambda _1^*}&\theta _2&\frac{1}{\varLambda _2-\varLambda _2^*}\\ \frac{-\,1}{\varLambda _2^*-\varLambda _1}&\frac{-\,1}{\varLambda _2^*-\varLambda _1^*}&\frac{1}{\varLambda _2-\varLambda _2^*}&\theta _2^* \end{vmatrix}, \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{aligned} \theta _k=I(x-2\varLambda _ky+4\varLambda _k^3z+6\varLambda _k^2t).~(k=1,2). \end{aligned} \end{aligned}$$
Fig. 3
figure 3

The second-order rational solutions via Solutions (15) with \(\varLambda _1=0.2+0.6I\) and \(\varLambda _2=-\,\frac{1}{3}+\frac{\sqrt{3}}{3}\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image

The second-order rational solutions contain the two lumps, two line rogue waves and the mixed form consisting of one lump and one line rogue wave, as shown in Fig. 2. Similar to the second-order breathers, there are also two kinds of the interaction forms from the two lumps, as shown in Fig. 2. We show the evolution of the two line rogue waves in Fig. 2c. It can be seen that the two line rogue waves arise from a constant background, then reach their maximum amplitudes at \(t=0\) and finally disappear into the background again. We also find that the amplitude at the location of the interaction between the two line rogue waves is zero and the wave pattern forms two curvy wavefronts which are separated, as seen in Fig. 3c. We illustrate the mixed solution consisting of one lump and one line rogue wave in Fig. 3, from which we find that the lump exists all the time and moves on the constant background but the line rogue wave exists only for a period of t. When the amplitude of the line rogue wave reaches the maximum value, the line rogue wave crosses over the lump and the lump is divided into two parts.

4 Hybrid solutions for Eq. (1)

We give the hybrid solutions for Eq. (1) in Appendix C. When \({\widetilde{N}}={\widehat{N}}=1\) in Eq. (26), rational- and exponent-type solutions can be written as

$$\begin{aligned} \begin{aligned}&u=2(\ln \varDelta _0F)_x,\\&F=\\&\begin{vmatrix} \theta _1&\frac{1}{\varLambda _1-\varLambda _1^*}&\frac{2}{2(\varLambda _1-\varLambda _2)-\lambda _2}&\frac{2}{2(\varLambda _1-\varLambda _2^*)+\lambda _2} \\ \frac{1}{\varLambda _1-\varLambda _1^*}&\theta _1^*&\frac{-\,2}{2(\varLambda _1^*-\varLambda _2)-\lambda _2}&\frac{-\,2}{2(\varLambda _1^*-\varLambda _2^*)+\lambda _2} \\ \frac{-\,2I}{2(\varLambda _1-\varLambda _2)+\lambda _2}&\frac{2I}{-\,2(\varLambda _1^*-\varLambda _2)-\lambda _2}&\frac{-I}{\lambda _2e^{\zeta _2}}+\frac{-I}{\lambda _2}&\frac{I}{\varLambda _2-\varLambda _2^*} \\ \frac{-\,2I}{2(\varLambda _1-\varLambda _2^*)-\lambda _2}&\frac{2I}{-\,2(\varLambda _1^*-\varLambda _2^*)+\lambda _2}&\ \frac{-I}{\varLambda _2-\varLambda _2^*}&\frac{I}{\lambda _2e^{\zeta _2^*}}+\frac{I}{\lambda _2} \end{vmatrix}, \end{aligned} \end{aligned}$$
(16)

where \(\varDelta _0=\lambda _2^2e^{\zeta _2+\zeta _2^*}\) and

$$\begin{aligned} \begin{aligned}&\theta _1=I(x-2\varLambda _1y+4\varLambda _1^3z+6\varLambda _1^2t),\\&\zeta _2=-\,I\lambda _2x+2I\varLambda _2\lambda _2y-I\lambda _2(\varLambda _2\lambda _2^2+4\varLambda _2^3)z\\&\quad \qquad -\,\frac{I\lambda _2}{2}(\lambda _2^2+12\varLambda _2^2)t+\zeta _2^0. \end{aligned} \end{aligned}$$

Based on the above analysis on the breather and rational solutions, we know that the hybrid solutions are composed of the lumps, breathers, line rogue waves and homoclinic orbits. We show the rational and exponent solutions in Fig. 4. It can be seen that the breather is parallel to the x axis on the (x, y) plane but has an angle with the y and z axes on the (y, z) plane.

Fig. 4
figure 4

Hybrid solutions via Solutions (16) with \(\varLambda _1=-\,\frac{2}{5}+\frac{2\sqrt{3}}{5}I,~\varLambda _2=0.3+I\) and \(\lambda _2=1\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image

We find that the breather and lump move in the opposite directions and form the head-on interaction when \(\text {Re}(\varLambda _1)\cdot \text {Re}(\varLambda _2)<0\) in Eq. (16). However, when \(\text {Re}(\varLambda _1)\cdot \text {Re}(\varLambda _2)>0\) in Eq. (16), the breather and lump move in the same direction and form the overtaking interaction. If we set \([\text {Im}(\varLambda _1)]^2=3[\text {Re}(\varLambda _1)]^2\) in Eq. (16), we can obtain the hybrid solutions consisting of one breather and one line rogue wave, as shown in Fig. 4c. It can be seen that the breather moves on the (x, z) plane and the line rogue wave only exists for a limited period of t in Fig. 4c. If we set \(\lambda _2^2-4[\text {Im}(\varLambda _2)]^2+12[\text {Re}(\varLambda _2)]^2=0\) in Eq. (16), we can obtain the hybrid solutions consisting of one homoclinic orbit and one line rogue wave.

5 The second kind of the breather and hybrid solutions for Eq. (1)

5.1 The second kind of the breather solutions for Eq. (1)

In Appendix D, we construct the second kind of the breather solutions for Eq. (1). Different from the first kind of the breather solutions for Eq. (1), the second kind of the breather solutions emerges from some different characteristics. For example, when \(M=1\) in Eq. (29), the first-order breather solutions for Eq. (1) can be written as

$$\begin{aligned}&u=2(\ln f)_x,\end{aligned}$$
(17a)
$$\begin{aligned}&f=1+e^{\zeta _1}+e^{\zeta ^*_1}+A_{12}e^{\zeta _1+\zeta ^*_1}, \end{aligned}$$
(17b)

where

$$\begin{aligned} \begin{aligned}&\zeta _1=\lambda _1x-2I\varLambda _1\lambda _1y-I\varLambda _1\lambda _1(\lambda _1^2+4\varLambda _1^2)z\\&\quad \qquad -\,\frac{\lambda _1}{2}(\lambda _1^2+12\varLambda _1^2)t+\zeta _1^0,\\&A_{12}=\frac{(\varLambda _1+\varLambda _1^*)^2}{(\varLambda _1+\varLambda _1^*)^2-\lambda _1^2}. \end{aligned} \end{aligned}$$

Take \(\varLambda _1=\varLambda _{1R}+I\varLambda _{1I}\), and we rewrite \(\zeta _1=\zeta _{1R}+I\zeta _{1I}\), where

$$\begin{aligned}&\zeta _{1R}=\lambda _1x+2\lambda _1\varLambda _{1I}y\nonumber \\&\quad \qquad \lambda _1\varLambda _{1I}(\lambda _1^2-4\varLambda _{1I}^2+12\varLambda _{1R}^2)z\nonumber \\&\quad \qquad -\,\frac{\lambda _1}{2}(\lambda _1^2-12\varLambda _{1I}^2+12\varLambda _{1R}^2)t+\zeta _1^0,\nonumber \\&\zeta _{1I}=-\,2\lambda _1\varLambda _{1R}y-\lambda _1\varLambda _{1R}(\lambda _1^2-12\varLambda _{1I}^2+4\varLambda _{1R}^2)z\nonumber \\&\quad \qquad -\,12\lambda _1\varLambda _{1I}\varLambda _{1R}t. \end{aligned}$$
(18)

The first-order kinky breather in Fig. 5 shows both the features of the breather and kink. Kinky breather is also localized along the direction of the line \(\zeta _{1R}=0\) and periodic along the direction of the line \(\zeta _{1I}=0\). We find that the kinky breather in Fig. 5 does not need to be parallel to the x axis on the (x, y) and (x, z) planes because \(\zeta _{1R}\) in Eq. (18) contains four variables x,  y,  z and t. Moreover, the imaginary part in Eq. (17b) will disappear when \(\zeta _{1I}=0\), and then the kinky breather will be reduced to the kink soliton.

Fig. 5
figure 5

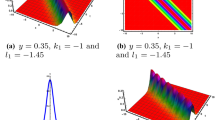
The first-order kinky breather via Solutions (17) with \(\varLambda _1=0.6-\frac{2}{3}I\) and \(\lambda _1=\frac{1}{2}\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image
Fig. 6
figure 6

The second-order kinky breathers via Solutions (19) with \(\varLambda _1=\frac{3}{4}I,~\lambda _1=1,~\varLambda _2=\frac{3}{5}-\frac{2}{3}I\) and \(\lambda _2=\frac{1}{2}\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image

When \(M=2\) in Eq. (29), the second-order kinky breather solutions for Eq. (1) can be written as

$$\begin{aligned}&u=2(\ln f)_x\end{aligned}$$
(19)
$$\begin{aligned}&f=\varDelta _2\left| \begin{array}{cc} \frac{-\,1}{\lambda _1e^{\zeta _1}}+\frac{-\,1}{\lambda _1} &{} \frac{1}{\varLambda _1+\varLambda _1^*-\lambda _1}\\ \frac{-\,1}{\varLambda _1+\varLambda _1^*+\lambda _1} &{} \frac{-\,1}{\lambda _1e^{\zeta _1^*}}+\frac{-\,1}{\lambda _1}\\ \frac{1}{\varLambda _2-\varLambda _1-\frac{\lambda _1+\lambda _2}{2}} &{} \frac{1}{\varLambda _2+\varLambda _1^*-\frac{\lambda _1+\lambda _2}{2}}\\ \frac{-\,1}{\varLambda _1+\varLambda _2^*+\frac{\lambda _1+\lambda _2}{2}} &{} \frac{-\,1}{\varLambda _2^*-\varLambda _1^*+\frac{\lambda _1+\lambda _2}{2}} \end{array}\right. \nonumber \\&\quad \left. \begin{array}{cc} \frac{1}{\varLambda _1-\varLambda _2-\frac{\lambda _1+\lambda _2}{2}} &{} \frac{1}{\varLambda _2^*+\varLambda _1-\frac{\lambda _1+\lambda _2}{2}}\\ \frac{-\,1}{\varLambda _1^*+\varLambda _2+\frac{\lambda _1+\lambda _2}{2}} &{} \frac{-\,1}{\varLambda _1^*-\varLambda _2^*+\frac{\lambda _1+\lambda _2}{2}}\\ \frac{-\,1}{\lambda _2e^{\zeta _2}}+\frac{-\,1}{\lambda _2} &{} \frac{1}{\varLambda _2+\varLambda _2^*-\lambda _2}\\ \frac{-\,1}{\varLambda _2+\varLambda _2^*+\lambda _2} &{} \frac{-\,1}{\lambda _2e^{\zeta _2^*}}+\frac{-\,1}{\lambda _2} \end{array}\right| , \end{aligned}$$
(20)

where

$$\begin{aligned}&\zeta _k=\lambda _kx-2I\varLambda _k\lambda _ky-I\varLambda _k\lambda _k(\lambda _k^2+4\varLambda _k^2)z\\&\quad -\,\frac{\lambda _k}{2}(\lambda _k^2+12\varLambda _k^2)t+\zeta _k^0,~~(k=1,2)\\&\varDelta _2=\lambda _1^2\lambda _2^2e^{\zeta _1+\zeta _1^*+\zeta _2+\zeta _2^*}. \end{aligned}$$

We find that the second-order kinky breather solutions contain two first-order kinky breathers, two kink solitons and the mixed solutions consisting of one first-order kinky breather and one kink soliton. If we set \(\text {Re}(\varLambda _k)=0\) in Eq. (19), the kinky breather will be reduced to the kink soliton. We can construct the mixed solutions consisting of one kinky breather and one kink soliton when \(\hbox {Re}(\varLambda _1)=0\) and of two kink solitons when \(\hbox {Re}(\varLambda _1)=\hbox {Re}(\varLambda _2)=0\) in Eq. (19). We find that the kinky breather and kink soliton move in the opposite directions when \(\text {Im}(\varLambda _1)\cdot \text {Im}(\varLambda _2)<0\) or move in the same direction when \(\text {Im}(\varLambda _1)\cdot \text {Im}(\varLambda _2)>0\) in Eq. (19).

Fig. 7
figure 7

Hybrid solutions via Solutions (21) with \(\varLambda _1=\frac{\sqrt{3}}{3}-\frac{1}{3}I,~\varLambda _2=\frac{2}{3}+I,~\lambda _2=\frac{1}{2}\) and \(y=0\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image
Fig. 8
figure 8

Hybrid solutions via Solutions (21) with \(\varLambda _1=\frac{\sqrt{3}}{4}-\frac{1}{4}I,~\varLambda _2=\frac{3}{2}I,~\lambda _2=\frac{3}{2}\) and \(y=0\). a \(z=0\); b \(x=0\); c \(y=0\)

Full size image

5.2 Hybrid solutions for Eq. (1)

Based on the second kind of the breather solutions, we construct the hybrid solutions for Eq. (1) in Appendix E. According to Eq. (26), when \({\widetilde{N}}={\widehat{N}}=1\), the hybrid solutions can be written as

$$\begin{aligned} \begin{aligned}&u=2(\ln \varDelta _0F)_x,\\&F=\\&\begin{vmatrix} \theta _1&\frac{1}{\varLambda _1+\varLambda _1^*}&\frac{2}{2(\varLambda _1-\varLambda _2)-\lambda _2}&\frac{2}{2(\varLambda _1+\varLambda _2^*)-\lambda _2} \\ \frac{-\,1}{\varLambda _1+\varLambda _1^*}&\theta _1^*&\frac{-\,2}{2(\varLambda _1^*+\varLambda _2)+\lambda _2}&\frac{-\,2}{2(\varLambda _1^*-\varLambda _2^*)+\lambda _2} \\ \frac{-\,2}{2(\varLambda _1-\varLambda _2)+\lambda _2}&\frac{-\,2}{-\,2(\varLambda _1^*+\varLambda _2)+\lambda _2}&\frac{-\,1}{\lambda _2e^{\zeta _2}}+\frac{-\,1}{\lambda _2}&\frac{1}{\varLambda _2+\varLambda _2^*-\lambda _2} \\ \frac{-\,2}{2(\varLambda _1+\varLambda _2^*)+\lambda _2}&\frac{-\,2}{-\,2(\varLambda _1^*-\varLambda _2^*)+\lambda _2}&\ \frac{-\,1}{\varLambda _2+\varLambda _2^*+\lambda -2}&\frac{-\,1}{\lambda _2e^{\zeta _2^*}}+\frac{-\,1}{\lambda _2} \end{vmatrix}, \end{aligned} \end{aligned}$$
(21)

where \(\varDelta _0=\lambda _2^2e^{\zeta _2+\zeta _2^*}\) and

$$\begin{aligned} \begin{aligned}&\theta _1=-\,x+2I\varLambda _1y+4I\varLambda _1^3z+6\varLambda _1^2t,\\&\zeta _2=\lambda _2x-2I\varLambda _2\lambda _2y-I\varLambda _2\lambda _2(\lambda _2^2+4\varLambda _2^2)z\\&\quad \qquad -\,\frac{\lambda _2}{2}(\lambda _2^2+12\varLambda _2^2)t+\zeta _2^0. \end{aligned} \end{aligned}$$
(22)

That kind of the hybrid solutions, composed of the kinky breathers, lumps and kink solitons, is shown in Figs. 7 and 8. Hybrid solutions composed of one kinky breather and one lump is shown in Fig. 7. Similarly to that in Fig. 6, if we set \(\text {Im}(\zeta _2)=0\) in Eq. (22), the kinky breather will be reduced to the kink soliton and we can obtain the hybrid solutions composed of one kink soliton and one lump. When we set \([\text {Re}(\varLambda _1)]^2=3[\text {Im}(\varLambda _1)]^2\) in Eq. (22), we can derive the hybrid solutions composed of one kinky breather and one line rogue wave, as shown in Fig. 7. Moreover, if we set \([\text {Re}(\varLambda _1)]^2=3[\text {Im}(\varLambda _1)]^2\) and \(\text {Im}(\zeta _2)=0\) in Eq. (22), which means that the kinky breather is reduced to the kink soliton and the lump is reduced to the line rogue wave, we can obtain the hybrid solutions composed of one kink soliton and one line rogue wave, as shown in Fig. 8.

6 Conclusions

Water waves have been thought to be one of the most common phenomena in nature, the study of which helps in designing the related industries. In this paper, a generalized (\(3+1\))-dimensional B-type KP equation for the water waves, i.e., Eq. (1), has been studied. Different from those in Ref. [21], Gramian Solutions (7) for Eq. (1) have been constructed via the KP hierarchy reduction. Based on Solutions (7), we have derived the first- and second-order breather solutions, i.e., Solutions (8) and Solutions (10). We have found that the first-order breather is parallel to the x axis on the (x, y) and (x, z) planes and can be reduced to the homoclinic orbits. For the higher-order breather solutions, we have constructed the mixed solutions consisting of the breathers and homoclinic orbits, as shown in Fig. 1. According to the long-wave limit method, rational Solutions (25) for Eq. (1) have been derived. Two types of the rational solutions, i.e., lump and line rogue wave solutions, have been analyzed, as shown in Figs. 2 and 3 . We have found that the lumps can be reduced to the line rogue waves. We have also constructed the hybrid solutions composed of the breathers, lumps and line rogue waves, i.e., Solutions (26), for Eq. (1). Characteristics of those hybrid solutions have been graphically analyzed, as shown in Fig. 4.

Taking the parameters given in Eq. (28) for Gramian Solutions (7), we have also derived the kinky breather solutions for Eq. (1), i.e., Solutions (29). The first- and second-order kinky breathers are shown in Figs. 5 and 6 . We have found that it is not necessary for the kinky breathers to be parallel to the x axis, i.e., the kinky breathers can have an angle to the x axis, and the kinky breathers can be reduced to the kink solitons. For the higher-order kinky breather solutions, we have constructed the mixed solutions consisting of the kinky breathers and kink solitons. Meanwhile, we have derived another kind of the hybrid solutions, i.e., Solutions (30), for Eq. (1), which are composed of the breathers, lumps, line rogue waves and kink solitons. Characteristics of those hybrid solutions have also been graphically analyzed, as shown in Figs. 7 and 8.