Introduction

Nonlinear evolution equations are widely used as models describing many important dynamical systems in various fields of science, particularly in fluid mechanics, solid-state physics, plasma physics, and nonlinear optics. In the study of nonlinear physical events, the exploration of soliton wave solutions that possesses nonlinear partial differential equations (NPDEs) is crucial. In the last several decades, this field has been researched. Various intriguing computational strategies are used to integrate a variety of this field. In order to understand better the nonlinear phenomena as well as further applications in practical life, it is important to seek their more exact traveling wave solutions [1]. Based on developments in computing tools, investigations of the precise solutions of these equations are currently rather spectacular. The Jacobi elliptic function expansion method [2], the Exp-function method [3], the F-expansion method [4], the sub-ODE method [5], the parameter-expansion method [6], the inverse scattering method [7], the variational iteration method [8], the tanh-method [9], the extended tanh-method [10], the homogeneous balance method [11], the homotopy perturbation method [12], the sine-Gordon method [13], the generalized Riccati equation mapping method [14], the improved Sardar sub-equation method [15], the Kudryashov method [16], modified Hirota method [17] are a few methods for computing exact solutions of NPDEs in literature.

The Schamel–KdV is considered in this study as follows [18]:

$$\begin{aligned} u_t+u_x\left( \alpha \sqrt{u}+\beta \,u\right) +\delta \,u_{xxx}=0,\,\,\,\beta \delta \ne {0}, \end{aligned}$$
(1)

where \(\alpha ,\,\beta ,\) and \(\delta \) are the activation trapping, convection, and dispersion coefficients, respectively. This equation reduces to the following:

  • The Schamel equation when \(\beta =0,\) give as

    $$\begin{aligned} u_t+\alpha \,u_x\sqrt{u}+\delta \,u_{xxx}=0. \end{aligned}$$
    (2)

  • The well-known KdV equation when \(\alpha =0,\) given as

    $$\begin{aligned} u_t+\beta \,uu_x+\delta \,u_{xxx}=0. \end{aligned}$$
    (3)

The Schamel equation governs the propagation of ion-acoustic waves in a cold-ion plasma where certain electrons do not behave isothermally throughout the wave’s passage but are trapped. The Korteweg–De Vries (KdV) equation, on the other hand, is a mathematical model of waves on shallow water surfaces. In the presence of solitary waves, the Schamel–Korteweg–de Vries (S–KdV) model is utilized to simulate the effect of surface for deep water. This model, which incorporates leading order nonlinearity and dispersion, is a general model of weakly nonlinear long waves. Exact solutions of this equation play a vital role in the study of NPDEs occurring in several fields to comprehend the physical shape provided by nonlinear models. Electromagnetic theory, physical chemistry, geophysics, fluid motion, elastic medium, nuclear physics, optic fibers, energy physics, gravity, statistical, condensed material physics, biostatistics, natural physics, chemical mechanics, compound physics, electrochemistry, fluid mechanics, audial, cosmology, ionized physics, and other fields are examples. To compute the solutions of this equation, the modified Kudrayshov technique [19,20,21] will be used. Kudrayshov’s technique is shown to be a powerful mathematical technique for investigating nonlinear evolution issues. For instance, Hosseini [22], Mayeli [23] and Ansari [24] works on the uses of Kudryashov’s approach. Ahmet Bekir [25] work on the application of the modified Kudryashov approach in [26]. The implementation of the modified Kudryashov technique in this study highlights our main goal and demonstrates its capacity to handle nonlinear equations, allowing it to be utilized to solve many types of nonlinearity models.

As follows, we organized the layout of the rest of our work: In Sect. 2, we present the methodology of the modified Kudryashov method. The mathematical analysis is presented in Sect. 3. In Sect. 4, we provided the discussion and results. Finally, the conclusion of our work is given in Sect. 5.

Methodology of the Modified Kudryashov Method

First, we consider the NLPDE of the form:

$$\begin{aligned} G\left( u,u_x,u_t,u_{\text {xx}},u_{\text {xt}},u_{\text {tt}},\text {...}\right) =0, \end{aligned}$$
(4)

where \(u=u(x,t)\) is the unknown function and G is a polynomial. Using the transformation \(u(x,t)=U(\xi ),\,\,\xi =\kappa {x}+\omega {t}\) varies according to given equation, this will carries the Eq. (4)) to the nonlinear ODE of the form

$$\begin{aligned} H(U,\,U^{\prime },\,U^{\prime \prime },\,\cdots )=0, \end{aligned}$$
(5)

H is the polynomial in U and the derivatives are ordinary with respect to \(\xi .\) Suppose the solution of Eq. (5) is of the form

$$\begin{aligned} U(\xi )=a_0+\sum _{j=1}^N a_j Q^j(\xi ),\,\,\,a_N\ne {0}, \end{aligned}$$
(6)

where the constants \(a_j\) \((j=0,1,\ldots ,N)\) will be determine and positive integer N is calculated by balancing principle. The function \(Q(\xi )\) satisfies the ODE

$$\begin{aligned} Q^{\prime }(\xi )=(Q^2(\xi )-Q(\xi ))\ln (A), \end{aligned}$$
(7)

where \(Q(\xi )=\frac{1}{\text {dA}^{\xi }+1}\) and \(A\ne {0,\,1}.\) Susbtituting Eqs. (7) and (6) into Eq. (5) and using mathematical teachnique we obtained a set of algebraic equations in parameters \(a_j,\, (j=0,1,\ldots ,N),\,k,\) and \(\omega .\) Finally obtained new exact solutions for the Eq. (4) by arranging the extracted values in Eq. (6).

Mathematical Analysis

Consider the wave transformation

$$\begin{aligned} u(x,t)=v(x,t)^2,\,\,\,v(x,t)=V(\eta ),\,\,\,\eta =k x-\omega {t}, \end{aligned}$$
(8)

then, Eq. (1) reduces to nonlinear odes of form:

$$\begin{aligned} \delta \,k^3(VV^3+3V^{\prime }V^{\prime \prime })+kV^{\prime }(\alpha \,V^2+\beta \,V^3)-\omega {VV^{\prime }}=0. \end{aligned}$$
(9)

By balancing principle we obtained \(N=1.\) The solutions for Eq. (9) can be consider as:

$$\begin{aligned} u(\xi )=a_0+a_1Q(\xi ), \end{aligned}$$
(10)

satisfies the above equation

$$\begin{aligned} Q^{\prime }(\xi )= & {} \ln (a)(Q(\xi )^2-Q(\xi )),\\ Q(\xi )= & {} \frac{1}{d\,a^{\xi }+1}. \end{aligned}$$

Putting Eq. (10) along with its first two derivatives and collecting the coefficients of \(Q^i,\) we obtained the following system:

$$\begin{aligned} \begin{aligned}&-a_0a_1\delta \,k^3\ln ^3(a)-\alpha \,a_0^2a_1k\ln (a)-a_0^3a_1\beta \,k\ln (a)+a_0a_1\omega \ln (a)=0,\\ \quad&-4a_1^2\delta \,k^3\ln ^3(a)+7a_0a_1\delta \,k^3\ln ^3(a)-2\alpha \,a_0a_1^2k\ln (a)+\alpha \,a_0^2a_1k\ln (a)\\&\quad -3a_0^2a_1^2\beta \,k\ln (a)+a_0^3a_1\beta \,k\ln (a)+a_1^2\omega \ln (a)-a_0a_1\omega \ln (a)=0,\\&\quad 19a_1^2\delta \,k^3\ln ^3(a)-12a_0a_1\delta \,k^3\ln ^3(a)-\alpha \,a_1^3k\ln (a)\\&\quad \qquad +2\alpha \,a_0a_1^2k\ln (a)-3a_0a_1^3\beta \,k\ln (a)+3a_0^2a_1^2\beta \,k\ln (a)-a_1^2\omega \ln (a)=0,\\&\quad -27a_1^2\delta \,k^3\ln ^3(a)+6a_0a_1\delta \,k^3\ln ^3(a)\\&\quad +\alpha \,a_1^3k\ln (a)-a_1^4\beta \,k\ln (a)+3a_0a_1^3\beta \,k\ln (a)=0,\\&\quad 12a_1^2\delta \,k^3\ln ^3(a)+a_1^4\beta \,k\ln (a)=0. \end{aligned} \end{aligned}$$
(11)

Family I The following cases arise

Case I

$$\begin{aligned} a_0=-\frac{4\alpha }{5\beta },\,\,\,a_1=\frac{4\alpha }{5\beta },\,\,\,k=-\frac{75\beta \omega }{16\alpha ^2},\,\,\,\delta =-\frac{1024\alpha ^6}{421875\beta ^3\omega ^2\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_1(x,t)=-\frac{4\alpha \,d\,a^x}{5\beta \,a^{\omega {t}}+5\beta \,d\,a^x}. \end{aligned}$$
(12)

Case II

$$\begin{aligned} a_0=0,\,\,\,a_1=-\frac{4\alpha }{5 \beta },\,\,\,k=-\frac{75\beta \omega }{16\alpha ^2},\,\,\,\delta =-\frac{1024\alpha ^6}{421875\beta ^3\omega ^2\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_2(x,t)=-\frac{4\alpha }{5\beta (d\,a^{x-\omega {t}}+1)}. \end{aligned}$$
(13)

Family II The following cases arise

Case I

$$\begin{aligned} a_0=\frac{15\omega }{4\alpha {k}},\,\,\,a_1=-\frac{15\omega }{4\alpha \,k}\,\,\,\beta =-\frac{16\alpha ^2 k}{75\omega },\,\,\,\delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_3(x,t)=\frac{15d\omega \,a^x}{4\alpha \,k\,a^{\omega {t}}+4\alpha \,d\,k\,a^x}. \end{aligned}$$
(14)

Case II

$$\begin{aligned} a_0=0,\,\,\,a_1=\frac{15 \omega }{4 \alpha \,k},\,\,\,\beta =-\frac{16\alpha ^2k}{75\omega },\,\,\,\delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_4(x,t)=\frac{15\omega }{4\alpha \,k(d\,a^{x-\omega {t}}+1)}. \end{aligned}$$
(15)

Family III The following cases arise

Case I

$$\begin{aligned} a_0=-\frac{4\alpha }{5\beta },\,\,\,a_1=\frac{4\alpha }{5\beta },\,\,\,\omega =-\frac{16\alpha ^2k}{75\beta },\,\,\, \delta =-\frac{4\alpha ^2}{75\beta \,k^2\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_5(x,t)=\frac{4\alpha }{5\beta }\left( \frac{1}{d\,a^{x+\frac{16\alpha ^2kt}{75\beta }}+1}-1\right) . \end{aligned}$$
(16)

Case II

$$\begin{aligned} a_0=0,\,\,\,a_1=-\frac{4\alpha }{5\beta },\,\,\,\omega =-\frac{16\alpha ^2k}{75\beta },\,\,\, \delta =-\frac{4\alpha ^2}{75\beta \,k^2\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_6(x,t)=-\frac{4\alpha }{5\beta \left( d\,a^{x+\frac{16\alpha ^2kt}{75\beta }}+1\right) }. \end{aligned}$$
(17)

Family IV The following cases arise

Case I

$$\begin{aligned} a_0=-\sqrt{\frac{3\omega }{2\beta \,k}},\,\,\,a_1=\sqrt{\frac{6\omega }{\beta \,k}},\,\,\,\delta =-\frac{\omega }{2k^3\ln ^2(a)},\,\,\,\alpha =0. \end{aligned}$$

Then,

$$\begin{aligned} u_7(x,t)=\sqrt{\frac{3\omega }{2\beta \,k}}\left( \frac{-d\,a^x+a^{\omega {t}}}{d\,a^x+a^{\omega {t}}}\right) . \end{aligned}$$
(18)

Case II

$$\begin{aligned} a_0=\sqrt{\frac{3\omega }{2\beta \,k}},\,\,\,a_1=-\sqrt{\frac{6\omega }{\beta \,k}},\,\,\,\delta =-\frac{\omega }{2k^3\ln ^2(a)},\,\,\,\alpha =0. \end{aligned}$$

Then,

$$\begin{aligned} u_8(x,t)=\sqrt{\frac{3\omega }{2\beta \,k}}\left( \frac{d\,a^x-a^{\omega {t}}}{d\,a^x+a^{\omega {t}}}\right) . \end{aligned}$$
(19)

Case III

$$\begin{aligned} a_0=-i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\,a_1=i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\, \alpha =\frac{5i}{4}\sqrt{\frac{3\beta \omega }{k}},\,\,\,\delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_9(x,t)=-\frac{id\sqrt{3\omega }\,a^x}{\sqrt{\beta \,k}(a^{\omega {t}}+d\,a^x)}. \end{aligned}$$
(20)

Case IV

$$\begin{aligned} a_0=i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\,a_1=-i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\, \alpha =-\frac{5i}{4}\sqrt{\frac{3\beta \omega }{k}},\,\,\,\delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{10}(x,t)=\frac{id\sqrt{3\omega }\,a^x}{\sqrt{\beta \,k}(a^{\omega {t}}+d\,a^x)}. \end{aligned}$$

Case V

$$\begin{aligned}&a_0=0,\,\,\,a_1=-i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\,\alpha \\&\qquad =\frac{5i}{4}\sqrt{\frac{3\beta \omega }{k}},\,\,\, \delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{11}(x,t)=-\frac{i\sqrt{3\omega }}{\sqrt{\beta \,k}(d\,a^{x-\omega {t}}+1)}. \end{aligned}$$
(21)

Case VI

$$\begin{aligned} a_0=0,\,\,\,a_1=i\sqrt{\frac{3\omega }{\beta \,k}},\,\,\,\alpha =-\frac{5i}{4}\sqrt{\frac{3\beta \omega }{k}},\,\,\, \delta =\frac{\omega }{4k^3\ln ^2(a)}. \end{aligned}$$
$$\begin{aligned} u_{12}(x,t)=\frac{i\sqrt{3\omega }}{\sqrt{\beta \,k}(d\,a^{x-\omega {t}}+1)}. \end{aligned}$$

Family V The following cases arise

Case I

$$\begin{aligned} a_0=a_1=-\frac{15\omega ^{\frac{2}{3}}\root 3 \of {-\frac{\delta }{2}}\ln ^{\frac{2}{3}}(a)}{2\alpha },\,\,\, k=\frac{\left( -\frac{1}{2}\right) ^{\frac{2}{3}}\root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\, \beta =-\frac{8(-1)^{\frac{2}{3}}\root 3 \of {2}\,\alpha ^2}{75\root 3 \of {\delta }\,\omega ^{\frac{2}{3}}\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{13}(x,t)=-\frac{15d\,\omega ^{\frac{2}{3}}\root 3 \of {-\frac{\delta }{2}}\, a^x\ln ^{\frac{2}{3}}(a)}{2\alpha \,a^{2\alpha \,d\,a^x+\omega {t}}}. \end{aligned}$$
(22)

Case II

$$\begin{aligned} a_0=0,\,\,\,a_1=-\frac{15\root 3 \of {-\frac{\delta }{2}}\omega ^{\frac{2}{3}}\ln ^{\frac{2}{3}}(a)}{2 \alpha },\,\,\,k=\frac{\left( -\frac{1}{2}\right) ^{\frac{2}{3}}\root 3 \of {\omega }}{\root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\,\,\,\beta =-\frac{8(-1)^{\frac{2}{3}}\root 3 \of {2}\alpha ^2}{75\root 3 \of {\delta }\omega ^{\frac{2}{3}} \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{14}(x,t)=-\frac{15\root 3 \of {-\frac{\delta }{2}}\,\omega ^{\frac{2}{3}} \ln ^{\frac{2}{3}}(a)}{2\alpha \left( d\,a^{x-\omega {t}}+1\right) }. \end{aligned}$$
(23)

Case III

$$\begin{aligned} a_0=\frac{15\root 3 \of {\delta }\omega ^{\frac{2}{3}}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha },\,\,\, a_1=-\frac{15\root 3 \of {\delta }\omega ^{\frac{2}{3}}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha },\,\,\, k=\frac{\root 3 \of {\omega }}{2^{\frac{2}{3}}\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\, \beta =-\frac{8\root 3 \of {2}\alpha ^2}{75\root 3 \of {\delta }\omega ^{\frac{2}{3}}\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{15}(x,t)=\frac{15d\root 3 \of {\delta }\omega ^{\frac{2}{3}}a^x\ln ^{\frac{2}{3}}(a)}{\root 3 \of {2}(2\alpha \,a^{\omega {t}}+2\alpha \,d\,a^x)}. \end{aligned}$$
(24)

Case IV

$$\begin{aligned} a_0=0,\,\,\,a_1=\frac{15\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}}\alpha ,\,\,\,k=\frac{\root 3 \of {\omega }}{2^{2/3}\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\, \beta =-\frac{8\root 3 \of {2}\alpha ^2}{75\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{16}(x,t)=\frac{15\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha (d\,a^{x-\omega {t}}+1)}. \end{aligned}$$
(25)

Case V

$$\begin{aligned}&a_0=\frac{15(-1)^{2/3}\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha },\,\,\, \beta =\frac{8\root 3 \of {-2}\alpha ^2}{75\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)},\,\,\, a_1=-\frac{15(-1)^{2/3}\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha },\,\,\,\\&\qquad k=-\frac{\root 3 \of {-1}\root 3 \of {\omega }}{2^{2/3}\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{17}(x,t)=\frac{15(-1)^{2/3}d\root 3 \of {\delta }\omega ^{2/3}a^x \ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}(\alpha \,a^{\omega {t}}+\alpha \,d\,a^x)}. \end{aligned}$$
(26)

Case VI

$$\begin{aligned} a_0=0,\,\,\,a_1=\frac{15(-1)^{2/3} \root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}\alpha },\,\,\,k=-\frac{\root 3 \of {-1} \root 3 \of {\omega }}{2^{2/3}\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\, \beta =\frac{8\root 3 \of {-2}\alpha ^2}{75\root 3 \of {\delta }\omega ^{2/3}\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{18}(x,t)=\frac{15(-1)^{2/3}\root 3 \of {\delta }\omega ^{2/3} \ln ^{\frac{2}{3}}(a)}{2\root 3 \of {2}(\alpha \,d\,a^{x-\omega {t}}+\alpha )}. \end{aligned}$$
(27)

Family VI The following cases arise

Case I

$$\begin{aligned} a_0=-\frac{4\alpha }{5\beta },\,\,\,\omega =\frac{32i\alpha ^3}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }\ln (a)},\,\,\, a_1=\frac{4\alpha }{5\beta },\,\,\,k=-\frac{2i\alpha }{5\sqrt{3}\sqrt{\beta }\sqrt{\delta }\ln (a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{19}(x,t)=-\frac{4\alpha \,d\,a^x}{5\beta \,d\,a^x+5\beta \,e^{\frac{32i\alpha ^3t}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }}}}. \end{aligned}$$
(28)

Case II

$$\begin{aligned} a_0=0,\,\,\,\omega =\frac{32i\alpha ^3}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }\ln (a)},\,\,\, a_1=-\frac{4\alpha }{5\beta },\,\,\,k=-\frac{2 i\alpha }{5\sqrt{3}\sqrt{\beta }\sqrt{\delta }\ln (a)}. \end{aligned}$$

Then

$$\begin{aligned} u_{20}(x,t)=-\frac{4\alpha }{5\left( \beta +\beta \,d\,a^x\,e^{-\frac{32i\alpha ^3t}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }}}\right) }. \end{aligned}$$
(29)

Case III

$$\begin{aligned} a_0=-\frac{4\alpha }{5\beta },\,\,\,\omega =-\frac{32i\alpha ^3}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta } \ln (a)},\,\,\,a_1=\frac{4\alpha }{5\beta },\,\,\,k=\frac{2i\alpha }{5\sqrt{3}\sqrt{\beta }\sqrt{\delta }\ln (a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{21}(x,t)=\frac{4\alpha \left( -1+\frac{1}{1+d\,a^x\,e^{\frac{32i\alpha ^3t}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }}}}\right) }{5\beta }. \end{aligned}$$
(30)

Case IV

$$\begin{aligned} a_0=0,\,\,\,\omega =-\frac{32i\alpha ^3}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }\ln (a)},\,\,\, a_1=-\frac{4\alpha }{5\beta },\,\,\,k=\frac{2 i\alpha }{5\sqrt{3}\sqrt{\beta }\sqrt{\delta }\ln (a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{22}(x,t)=-\frac{4\alpha }{5\left( \beta +\beta \,d\,a^x\,e^{\frac{32i\alpha ^3t}{375\sqrt{3}\beta ^{3/2}\sqrt{\delta }}}\right) }. \end{aligned}$$
(31)

Family VII The following cases arise

Case I

$$\begin{aligned} a_0=-\frac{(-1)^{5/6}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\root 3 \of {2}\sqrt{\beta }},\,\,\, \alpha =0,\,\,\,a_1=\frac{(-1)^{5/6}2^{2/3}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\, k=\frac{\root 3 \of {-\frac{1}{2}}\root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{23}(x,t)=\frac{(-1)^{5/6}2^{2/3}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }\left( d\,a^{x-\omega {t}}+1\right) }-\frac{(-1)^{5/6}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\root 3 \of {2}\sqrt{\beta }}. \end{aligned}$$
(32)

Case II

$$\begin{aligned} a_0=\frac{(-1)^{5/6}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\root 3 \of {2}\sqrt{\beta }},\,\,\, \alpha =0,\,\,\,a_1=-\frac{(-1)^{5/6}2^{2/3}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\, k=\frac{\root 3 \of {-\frac{1}{2}}\root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{24}(x,t)=\frac{(-1)^{5/6}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\root 3 \of {2}\sqrt{\beta }}- \frac{(-1)^{5/6}2^{2/3}\sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }(d\,a^{x-\omega {t}}+1)}. \end{aligned}$$
(33)

Case III

$$\begin{aligned} \begin{aligned} a_0&=-\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\, k=\frac{\left( -\frac{1}{2}\right) ^{2/3}\root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\\ a_1&=\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\, \alpha =\frac{5\root 6 \of {-1}\sqrt{3}\sqrt{\beta }\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{25}(x,t)=\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }\left( d\,a^{x-\omega {t}}+1\right) }-\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }}. \end{aligned}$$
(34)

Case IV

$$\begin{aligned} \begin{aligned} a_0&=\frac{\root 6 \of {-1}\root 3 \of {2} \sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,a_1=-\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\\ k&=\frac{\left( -\frac{1}{2}\right) ^{2/3} \root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\, \alpha =-\frac{5\root 6 \of {-1}\sqrt{3}\sqrt{\beta }\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{26}(x,t)=\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }}-\frac{\root 6 \of {-1} \root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }\left( d\,a^{x-\omega {t}}+1\right) }. \end{aligned}$$
(35)

Case V

$$\begin{aligned} a_0=0,\,\,\,a_1= & {} -\frac{\root 6 \of {-1} \root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=\frac{\left( -\frac{1}{2}\right) ^{2/3} \root 3 \of {\omega }}{\root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\nonumber \\&\alpha =\frac{5 \root 6 \of {-1} \sqrt{3} \sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2\ 2^{2/3}}, \end{aligned}$$
$$\begin{aligned} u_{27}(x,t)=-\frac{\root 6 \of {-1} \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(36)

Case VI

$$\begin{aligned} a_0=0,~a_1= & {} \frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=\frac{\left( -\frac{1}{2}\right) ^{2/3}\root 3 \of {\omega }}{\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\,\nonumber \\&\alpha =-\frac{5\root 6 \of {-1}\sqrt{3}\sqrt{\beta }\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{2^{5/3}}, \end{aligned}$$

Then,

$$\begin{aligned} u_{28}(x,t)=\frac{\root 6 \of {-1}\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }\left( d\,a^{x-\omega {t}}+1\right) }. \end{aligned}$$
(37)

Case VII

$$\begin{aligned} \begin{aligned} a_0&=-\frac{i\root 3 \of {2}\sqrt{3} \root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,a_1=\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\\ k=&\frac{\root 3 \of {\omega }}{2^{2/3}\root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\,\alpha =\frac{5i\sqrt{3}\sqrt{\beta }\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{2\ 2^{2/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{29}(x,t)=\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }\left( d\,a^{x-\omega {t}}+1\right) }-\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }}. \end{aligned}$$

Case VIII

$$\begin{aligned} \begin{aligned} a_0&=\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,a_1=-\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\\ k&=\frac{\root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\,\,\,\alpha =-\frac{5 i \sqrt{3}\sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{30}(x,t)=\frac{i\root 3 \of {2}\sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }}-\frac{i \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-\omega {t}}+1\right) }. \end{aligned}$$

Case IX

$$\begin{aligned} a_0=0,\,\,\,a_1= & {} -\frac{i \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=\frac{\root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\,\,\,\nonumber \\&\alpha =\frac{5 i \sqrt{3} \sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2^{5/3}}, \end{aligned}$$

Then,

$$\begin{aligned} u_{31}(x,t)=-\frac{i \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(38)

Case X

$$\begin{aligned} a_0=0,\,\,\,a_1= & {} \frac{i \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=\frac{\root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\,\,\,\nonumber \\&\alpha =-\frac{5 i \sqrt{3} \sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned}$$

Then,

$$\begin{aligned} u_{32}(x,t)=\frac{i \root 3 \of {2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(39)

Case XI

$$\begin{aligned} \begin{aligned} a_0&=-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,a_1=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\\ k&=-\frac{\root 3 \of {-1} \root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)},\,\,\,\alpha =\frac{5 (-1)^{5/6} \sqrt{3} \sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{33}(x,t)=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }}. \end{aligned}$$
(40)

Case XII

$$\begin{aligned} \begin{aligned} a_0&=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,a_1=-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\\ k&=-\frac{\root 3 \of {-1} \root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\,\alpha =-\frac{5(-1)^{5/6} \sqrt{3} \sqrt{\beta }\root 6 \of {\delta }\root 3 \of {\omega }\root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} u_{34}(x,t)=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }}-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(41)

Case XIII

$$\begin{aligned}&a_0=0,\,\,\,\alpha =\frac{5 (-1)^{5/6} \sqrt{3} \sqrt{\beta } \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2\ 2^{2/3}},\,\,\,a_1=-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,\\&\qquad k=-\frac{\root 3 \of {-1} \root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{35}(x,t)=-\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(42)

Case XIV

$$\begin{aligned}&a_0=0,\,\,\,a_1=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=-\frac{\root 3 \of {-1} \root 3 \of {\omega }}{2^{2/3} \root 3 \of {\delta }\ln ^{\frac{2}{3}}(a)},\,\,\,\\&\qquad \alpha =-\frac{5(-1)^{5/6} \sqrt{3} \sqrt{\beta }\root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{2^{5/3}}. \end{aligned}$$

Then,

$$\begin{aligned} u_{36}(x,t)=\frac{i \root 3 \of {-2} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(43)

Case XV

$$\begin{aligned} a_0=-\frac{i \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }},~\alpha =0,\,\,\,a_1=\frac{i 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }} ,\,\,\,k=-\frac{\root 3 \of {\omega }}{\root 3 \of {2} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{37}(x,t)=\frac{i 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }-\frac{i \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }}. \end{aligned}$$
(44)

Case XVI

$$\begin{aligned} a_0=\frac{i \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }},\,\,\,\alpha =0,\,\,\,a_1=-\frac{i 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,k=-\frac{\root 3 \of {\omega }}{\root 3 \of {2} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{38}(x,t)=\frac{i \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }}-\frac{i 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(45)

Case XVII

$$\begin{aligned} a_0= & {} -\frac{\root 6 \of {-1} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }},\,\,\,\alpha =0,\,\,\,a_1=\frac{\root 6 \of {-1} 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,\nonumber \\&k=-\frac{(-1)^{2/3} \root 3 \of {\omega }}{\root 3 \of {2} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{39}(x,t)=\frac{\root 6 \of {-1} 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }-\frac{\root 6 \of {-1} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }}. \end{aligned}$$
(46)

Case XVIII

$$\begin{aligned} a_0= & {} \frac{\root 6 \of {-1} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }},\,\,\,\alpha =0,\,\,\,a_1=-\frac{\root 6 \of {-1} 2^{2/3} \sqrt{3}\root 6 \of {\delta } \root 3 \of {\omega }\root 3 \of {\ln (a)}}{\sqrt{\beta }},\,\,\,\nonumber \\&k=-\frac{(-1)^{2/3} \root 3 \of {\omega }}{\root 3 \of {2} \root 3 \of {\delta } \ln ^{\frac{2}{3}}(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{40}(x,t)=\frac{\root 6 \of {-1} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\root 3 \of {2} \sqrt{\beta }}-\frac{\root 6 \of {-1} 2^{2/3} \sqrt{3} \root 6 \of {\delta } \root 3 \of {\omega } \root 3 \of {\ln (a)}}{\sqrt{\beta } \left( d a^{x-t \omega }+1\right) }. \end{aligned}$$
(47)

Family VIII The following cases arise

Case I

$$\begin{aligned} a_0=\frac{15 \delta k^2 \ln ^2(a)}{\alpha },\,\,\,a_1=-\frac{15 \delta k^2 \ln ^2(a)}{\alpha },\,\,\, \omega =4 \delta k^3 \ln ^2(a),\,\,\,\beta =-\frac{4 \alpha ^2}{75 \delta k^2 \ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{41}(x,t)=\frac{15 d \delta k^2 a^x \ln ^2(a)}{\alpha d a^x+\alpha e^{4 \delta k^3 t \ln ^3(a)}}. \end{aligned}$$
(48)

Case II

$$\begin{aligned} a_0=0,\,\,\,a_1=\frac{15 \delta k^2 \ln ^2(a)}{\alpha },\,\,\,\omega =4 \delta k^3 \ln ^2(a),\,\,\,\beta =-\frac{4 \alpha ^2}{75 \delta \,k^2\ln ^2(a)}. \end{aligned}$$

Then,

$$\begin{aligned} u_{42}(x,t)=\frac{15 \delta k^2 \ln ^2(a)}{\alpha d a^{x-4 \delta k^3 t\ln ^2(a)}+\alpha }. \end{aligned}$$
(49)

Family IX. The following cases arise

Case I

$$\begin{aligned} a_0=-\frac{i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\alpha =0,\,\,\,a_1=\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\omega =-2 \delta k^3 \ln ^2(a). \end{aligned}$$

Then,

$$\begin{aligned} u_{43}(x,t)=-\frac{i \sqrt{3} \sqrt{\delta } k \ln (a) \left( d a^{2 \delta k^3 t \ln ^2(a)+x}-1\right) }{\sqrt{\beta } \left( d a^{2 \delta k^3 t \ln ^2(a)+x}+1\right) }. \end{aligned}$$
(50)

Case II

$$\begin{aligned}&a_0=\frac{i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\alpha =0 ,\\&\qquad a_1=-\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\, \omega =-2 \delta k^3 \ln ^2(a), \end{aligned}$$

Then,

$$\begin{aligned} u_{44}(x,t)=\frac{i \sqrt{3} \sqrt{\delta } k \ln (a) \left( d a^{2 \delta k^3 t \ln ^2(a)+x}-1\right) }{\sqrt{\beta } \left( d a^{2 \delta k^3 t \ln ^2(a)+x}+1\right) }. \end{aligned}$$
(51)

Case III

$$\begin{aligned} a_0= & {} -\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,a_1=\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\omega =4 \delta k^3 \ln ^2(a),\,\,\,\nonumber \\&\alpha =\frac{5}{2} i \sqrt{3} \sqrt{\beta } \sqrt{\delta } k \ln (a), \end{aligned}$$

Then,

$$\begin{aligned} u_{45}(x,t)=-\frac{2 i \sqrt{3} d \sqrt{\delta } k a^x \ln (a)}{\sqrt{\beta } \left( d a^x+e^{4 \delta k^3 t \ln ^3(a)}\right) }. \end{aligned}$$
(52)

Case IV

$$\begin{aligned} a_0= & {} \frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,a_1=-\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\omega =4 \delta k^3 \ln ^2(a),\,\,\,\nonumber \\&\alpha =\frac{1}{2} (-5) i \sqrt{3} \sqrt{\beta } \sqrt{\delta } k \ln (a). \end{aligned}$$

Then,

$$\begin{aligned} u_{46}(x,t)=\frac{2 i \sqrt{3} d \sqrt{\delta } k a^x \ln (a)}{\sqrt{\beta } \left( d a^x+e^{4 \delta k^3 t \ln ^3(a)}\right) }. \end{aligned}$$
(53)

Case V

$$\begin{aligned} a_0=0,\,\,\,a_1=-\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }},\,\,\,\omega =4 \delta k^3 \ln ^2(a),\,\,\,\alpha =\frac{5}{2} i \sqrt{3} \sqrt{\beta } \sqrt{\delta } k \ln (a), \end{aligned}$$

Then,

$$\begin{aligned} u_{47}(x,t)=-\frac{2 i \sqrt{3} \sqrt{\delta } k\ln (a)}{\sqrt{\beta }\left( d\,a^{x-4 \delta k^3 t \ln ^2(a)}+1\right) }. \end{aligned}$$
(54)

Case VI

$$\begin{aligned} a_0=0,\,\,\,\alpha =\frac{1}{2} (-5) i \sqrt{3} \sqrt{\beta } \sqrt{\delta } k\ln (a),\,\,\,\omega =4 \delta k^3 \ln ^2(a),\,\,\,a_1=\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta }}. \end{aligned}$$

Then,

$$\begin{aligned} u_{48}(x,t)=\frac{2 i \sqrt{3} \sqrt{\delta } k \ln (a)}{\sqrt{\beta } \left( d a^{x-4 \delta k^3 t \ln ^2(a)}+1\right) }. \end{aligned}$$
(55)

Discussion and Results

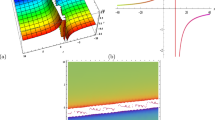
The graphical representations of some solitons (in particular; the dark and singular solitons), and breather structures have been shown in this section. Solitons are solitary waves that keep their shape and speed while moving at a steady speed. They are common in nature and have several applications in nonlinear dynamics [27,28,29,30,31,32,33,34]. Breathers, on the other hand, have important applications in a variety of physical domains, including hydrodynamics, quantized superfluid, optics, and many others [35, 36]. For a given parameter values, a family of dark, singular solitons, as well as breather solutions, is illustrated. The nature of nonlinear waves is seen in 3D, 2D, and contour plots created using Eq. (4) (Figs. 1, 2, 3, 4, and 5).

Fig. 1
figure 1

The wave simulations of Eq. (16) solution with \(a=5,\,\alpha =0.5,\,\beta =0.4,\,d=0.8,\) and \(k=0.1\)

Full size image
Fig. 2
figure 2

The wave simulations of Eq. (17) solution with \(a=5,\,\alpha =0.5,\,\beta =0.4,\,d=0.8,\) and \(k=0.1\)

Full size image
Fig. 3
figure 3

The wave simulations of Eq. (28) solution with \(a=5,\,\alpha =5,\,\beta =0.4,\,d=0.8,\) and \(\delta =0.1\)

Full size image
Fig. 4
figure 4

The wave simulations of Eq. (32) solution with \(a=5,\,\beta =0.4,\,d=0.8,\,\delta =0.1,\) and \(\omega =7\)

Full size image
Fig. 5
figure 5

The wave simulations of Eq. (33) solution with \(a=2,\,\beta =0.4,\,d=0.8,\,\delta =0.1,\) and \(\omega =7\)

Full size image

Conclusion

In this study, we describe a modified kudrayshov approach for generating a large number of innovative S-KdV equation traveling wave solutions. The exact solutions provided here may be beneficial in the theoretical and numerical investigations of the considered equation since they may explain a variety of novel wave characteristics. Traveling wave solutions with some free parameters can be found using the modified kudrayshov method. The results show that the proposed technique is a promising tool since it can provide a wide range of novel traveling wave solutions for various physical nonlinear models.