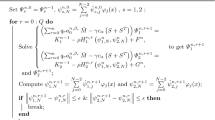Novel numerical methods based on graded, adaptive and uniform meshes for a time-fractional advection-diffusion equation subjected to weakly singular solution

Abstract

This paper presents adaptive, graded and uniform mesh schemes to approximate the solution of a fractional order advection-diffusion model, which generally shows a weak singularity at the initial time level. The temporal fractional derivative in the underlying problem is described in a Caputo form and is discretized by means of L1 scheme on a nonuniform mesh. The space derivative is discretized on a uniform mesh employing a fourth-order compact finite difference scheme. The adaptive grid is generated via equidistribution of a positive monitor function. Stability and convergence results for the proposed method on graded mesh are established. Numerical examples are provided to study the accuracy and efficiency of the proposed techniques and to support the theoretical results. A discussion about the advantages of the graded and adaptive meshes over the uniform one is also presented. The CPU times for the proposed numerical schemes are provided.

1 Introduction

Fractional differential equation has emerged as strong tools in the study of various physical and biological phenomena and modelling of material system and financial processes, for example, see [1,2,3,4,5,6,7,8]. Such equations can be used to simulate practical phenomena more accurately then integer order one [32]. The advection-diffusion (AD) equation is employed in groundwater hydrology research to model the transport of passive tracers carried by fluid flow in porous medium [9] and in neurology [10]. It is also used to describe the transport dynamics in complex systems. In this study, we consider the following time-fractional advection-diffusion (TFAD) equation:

$$\begin{aligned} D^{\alpha }_t\chi (x,t)-a\frac{\partial ^2 \chi (x,t)}{\partial x^2}+b\frac{\partial \chi (x,t)}{\partial x}=f(x,t),\;\; \alpha \in (0,1), \; (x,t)\in (0,1)\times (0,T], \end{aligned}$$

(1)

subject to the IC (initial condition)

$$\begin{aligned} \chi (x,0)={g}(x) \end{aligned}$$

(2)

and BCs (boundary conditions)

$$\begin{aligned} \chi (0,t)=0,\;\chi (1,t)=0. \end{aligned}$$

(3)

Here, a and b are real positive constants, $f(x,t) \in C([0,1]\times [0,T])$ and ${g}(x) \in C[0,1].$ Further, $D^{\alpha }_t\chi (x,t)$ denotes the Caputo derivative of order $\alpha ,$ which is defined as [11]:

$$\begin{aligned} D^{\alpha }_t\chi (x,t)= \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-s)^{-\alpha }\frac{\partial \chi (x,s)}{\partial s}ds, \ \alpha \in (0,1). \end{aligned}$$

(4)

Equation (1) describes how the field variable $\chi (x,t)$ in a medium varies under the influence of advection and diffusion processes. The solution of the problem considered has a weak singularity at $t=0$. The regularities of the solution satisfy

$$\begin{aligned} \left| \frac{\partial \chi (x,t)}{\partial t} \right| \le \hat{C}_1 (1+t^{\alpha -1 }),\ \forall \ t \in (0,T], \end{aligned}$$

(5)

$$\begin{aligned} \left| \frac{\partial ^k \chi (x,t)}{\partial x^k} \right| \le \hat{C}_2 \quad \text{ for } \ k=0,1,2,3,4,5,6, \end{aligned}$$

(6)

where $\hat{C}_1$ and $\hat{C}_2$ are constants independent of t and x. In [50], the existence and uniqueness of the solution to the Caputo time-fractional diffusion equation with Dirichlet boundary condition have been investigated. The maximum principle was applied for proving the uniqueness result. Li and Wang [51] prove existence and uniqueness of the solution to the Caputo time-fractional convection diffusion reaction equation. Further, the reader can refer to [43, 52]. Due to the weak singularity and nonlocality character of the time-fractional operator, it is very difficult in obtaining the exact solution of time-fractional model problems. Many powerful computational techniques have been used in recent years by researchers to approximate the solutions of several time-fractional problems, for instance, see [33,34,35,36,37,38, 40, 41]. On the other hand, various numerical schemes were used for solving the TFAD equations. Zhuang et al. [13] designed an implicit meshless scheme for solving the time-dependent fractional AD equation with the Caputo time derivative. In this method, the L1 method is employed for approximation of Caputo temporal fractional derivative on uniform mesh, while an implicit meshless approach based on the moving least squares technique is employed for discretization of space derivative. Azin et al. [14] developed a hybrid numerical scheme based on Chebyshev cardinal functions and the modified Legendre functions to approximate the solution of (1) over a bounded time domain and an unbounded space domain. Li et al. [15] proposed a series of high-order numerical schemes on uniform mesh to solve Caputo-type advection-diffusion equation. The authors first constructed a series of high-order numerical algorithms to approximate the Caputo derivative and then derived a high-order finite difference scheme for solving Caputo-type advection-diffusion equation. In [16], Cao et al. presented a new high-order difference scheme on uniform mesh to solve Caputo-type AD equation. Mardani [17] proposed a meshless method, which is based on the moving least square (MLS) approximation, for solving a time-fractional advection-diffusion model with variable coefficients. In this approach, the time-fractional derivative (TFD) is approximated by a finite difference scheme on uniform mesh. It is important to point out that in [13,14,15,16,17], numerical schemes based on uniform mesh (simpler mesh) are designed to approximate the time-fractional derivative. Further, the weak singularity was not considered in these papers. The optimal rate of convergence in time direction was obtained by considering the exact solution which is smooth enough. Moreover, various numerical techniques were proposed for solving the time-fractional diffusion and reaction-diffusion problems, see [21,22,23,24,25,26,27,28,29,30,31] and their references. The authors of these papers ignored weak singularity at $t=0$ and considered numerical examples with smooth analytical solutions to show that their methods have the optimal order convergence in the time direction. Furthermore, most of the above-stated methods are of lower orders of convergence in space direction.

In the current work, we aim to develop robust numerical techniques for solving (1)–(3) subjected to both smooth and nonsmooth analytical solutions. We derive graded and adaptive mesh numerical schemes for (1)–(3). In these methods, the Caputo time-fractional derivative is approximated by means of L1 scheme on nonuniform grids and the space derivatives are approximated by using a compact finite difference (CFD) scheme on uniform mesh. The graded and adaptive meshes on the time domain are constructed to overcome the weak singularity at $t=0$, which produce a fine mesh near $t=0$. The adaptive mesh is generated via equidistribution of a monitor function [18,19,20]. The theoretical results on the stability and convergence for the graded mesh technique are introduced. We consider three test problems to demonstrate the efficiency and accuracy of the suggested method and to support the theoretical results. The comparison between the results obtained with graded and adaptive meshes and those obtained with the uniform mesh is presented. The CPU times for the proposed techniques are provided. Numerical methods based on graded mesh or adaptive mesh were proposed in [42,43,44,45,46,47,48,49] to solve various kinds of boundary value problems for ordinary differential equation or partial differential equations.

The outline of this paper is as follows: Section 2 contains the description of the discretization scheme on the graded mesh. The adaptive mesh generation algorithm is described in Section 3. The proposed method on graded mesh is analyzed rigorously for the stability and convergence in Section 4. In Section 5, three test problems are solved and the numerical results are presented to show the robustness of proposed numerical algorithms. Finally, the conclusions are discussed in Section 6.

2 Derivation of a graded mesh numerical scheme

In this section, a graded mesh technique is derived for solving the TFAD model (1)–(3).

2.1 Time discretization

We discretize (1)–(3) over the domain [0, T], where $T>0.$ Let $t_m=T(m/\mathcal {N})^r,$$m=0,1,..., \mathcal {N}$ be the temporal grid points, where $\mathcal {N}$ be a positive integer and r is the grading parameter. Let the temporal mesh size be $\uptau _m=t_{m}-t_{m-1},$ $m=1,2,..., \mathcal {N}$. If $r=1,$ then the mesh is uniform. We approximate the Caputo TFD by employing the L1 scheme on the nonuniform mesh as follows

$$\begin{aligned} D_t^{\alpha } \chi (x,t_m)= & {} \frac{1}{\Gamma (1-\alpha )}\sum _{k=1}^{m}\int _{t_{k-1}}^{t_{k}}(t_m-s)^{-\alpha }\frac{\partial \chi (x,s)}{\partial s}ds \nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\sum _{k=1}^{m}\left[ (t_m-t_{k-1})^{1-\alpha }-(t_m-t_{k})^{1-\alpha }\right] \delta _t^-\chi (x,t_k)+\hat{\mathcal {R}}^m, \end{aligned}$$

(7)

where $\delta _t^-\chi (x,t_k)=\frac{\chi (x,t_k)-\chi (x,t_{k-1})}{\uptau _k}$ with $\uptau _k=t_{k}-t_{k-1},$ $\forall$ $1\le k\le \mathcal {N}$ and $\hat{\mathcal {R}}^m$ is the truncation error.

Lemma 1

([12]) Assume that the solution of TFAD problem satisfies (5). Then, we have the following bound for each $(x,t_m) \in \left( 0,1\right) \times \left( 0,T\right)$:

$$\begin{aligned} |\hat{\mathcal {R}}^m| \le m^{-min\{2-\alpha , r\alpha \}}, \quad m=1,2,...,\mathcal {N}. \end{aligned}$$

(8)

Considering (1) at $t=t_{m}$ yields

$$\begin{aligned} D^{\alpha }_t\chi (x,t_m)= a\frac{\partial ^2 \chi (x,t_m)}{\partial x^2}-b\frac{\partial \chi (x,t_m)}{\partial x}+f(x,t_m),\;\; 1\le m \le \mathcal {N}. \end{aligned}$$

(9)

Equations (2) and (3) can be expressed as follows

$$\begin{aligned} \chi (x,t_0)={g}(x), \end{aligned}$$

(10)

$$\begin{aligned} \chi (0,t_m)=0,\;\chi (1,t_m)=0, 1\le m \le \mathcal {N} . \end{aligned}$$

(11)

2.2 Spatial discretization

Here, we discretize (9)–(11) in space direction by means of a fourth-order CFD technique. We introduce uniform spatial grids with spatial step $\triangle x$ on the interval [0, 1] such that $\{0=x_{0}<x_{1}<..<x_n<.....<x_{\mathcal {M}}=1\}$, where $x_n=n\triangle x,$ $n=0,1,...,\mathcal {M}$ and $\mathcal {M}$ is the number of mesh elements.

The second-order central finite difference approximation ${\delta }^2_{x}v(x_{n})$ for $v''(x_{n})$ is defined by

$$\begin{aligned} {\delta }^2_{x}v(x_{n})=\frac{v(x_{n-1})-2v(x_{n})+v(x_{n+1})}{\triangle x^2},\hspace{0.1cm}n=1,2,...,\mathcal {M}-1. \end{aligned}$$

(12)

The second-order central difference approximation ${\delta }_{x}v(x_{n})$ for $v'(x_{n})$ is defined by

$$\begin{aligned} {\delta }_{x}v(x_{n})=\frac{v(x_{n+1})-v(x_{n-1})}{2\triangle x},\hspace{0.1cm}n=1,2,...,\mathcal {M}-1. \end{aligned}$$

(13)

Denote $F(x_n)=F_n,$ $F'(x_n)=F'_n,$ $v(x_{n})=v_{n},$ $v'(x_{n})=v'_{n}$ and $v''(x_{n})=v''_{n}.$

Theorem 1

Suppose the solution v(x) belongs to the function space $C^6[0,1].$ The fourth-order compact difference scheme for the problem

$$\begin{aligned} -a\frac{\partial ^2 v(x)}{\partial x^2}+b\frac{\partial v(x)}{\partial x}=F(x),\hspace{0.1cm}0<x<1, \end{aligned}$$

(14)

is given by

$$\begin{aligned} (-a+p \triangle x^2) {\delta }^2_{x} v_{n}+b \delta _{x}v_{n}=\frac{\triangle x^2}{12}{\delta }^2_{x} F_{n}+q{\triangle x^2}{\delta }_{x} F_{n}+F_{n}+O(\triangle x^4), \end{aligned}$$

(15)

where $p=-\frac{b^2}{12a}$ and $q=-\frac{b}{12a}.$

Proof

Inserting the Taylor’s series expansions for $v_{n+1}$ and $v_{n-1}$ into (12) and (13) yields

$$\begin{aligned} v''_{n}={\delta }^2_{x}v_{n}-\hat{T}_{1}, \end{aligned}$$

(16)

where

$$\begin{aligned} \hat{T}_{1}=\frac{\triangle x^2}{12}v_{n}^{(4)}+\frac{\triangle x^4}{360}v_{n}^{(6)}+O(\triangle x^6) \end{aligned}$$

and

$$\begin{aligned} v'_{n}={\delta }_{x}v_{n}-\hat{T}_{2}, \end{aligned}$$

(17)

where

$$\begin{aligned} \hat{T}_{2}=\frac{\triangle x^2}{6}v_{n}^{(3)}+\frac{\triangle x^4}{120}v_{n}^{(5)}+O(\triangle x^6). \end{aligned}$$

Using (16) and (17), we obtain the following difference approximation for (14) at $x=x_{n}:$

$$\begin{aligned} -a{\delta }^2_{x}v_{n}+b{\delta }_{x}v_{n}+{\hat{T}}_{3}=F_{n}, \end{aligned}$$

(18)

where

$$\begin{aligned} {\hat{T}}_{3}=a\hat{T}_{1}-b\hat{T}_{2}. \end{aligned}$$

(19)

To obtain a fourth-order scheme, one needs to approximate $v_{n}^{(3)}$ and $v_{n}^{(4)}$ in (19). For this purpose, we differentiate (14) w.r.t. x and then set $x=x_n$ to get

$$\begin{aligned} -a v^{(3)}_{n}+bv''_{n}=F'_n. \end{aligned}$$

(20)

Further, differentiating twice (14) w.r.t. x and then setting $x=x_n$ produces

$$\begin{aligned} -a v^{(4)}_{n}+bv^{(3)}_{n}=F''_n. \end{aligned}$$

(21)

Using (20) in (21), we obtain

$$\begin{aligned} v^{(4)}_n=\frac{b^2}{a^2}v''_{n}-\frac{b}{a^2}F'_{n}-\frac{F''_{n}}{a}. \end{aligned}$$

(22)

By (22) and (20), it follows from (19) that

$$\begin{aligned} {\hat{T}}_{3}=-\frac{b^2}{12a}{\Delta x}^2 v''_n -\frac{{\Delta x}^2}{12} F''_n -\frac{b{\Delta x}^2}{12a} F'_n+O(\triangle x^4). \end{aligned}$$

(23)

Using (16) and (17) in (23) gives

$$\begin{aligned} {\hat{T}}_{3}=-\frac{b^2{\Delta x}^2}{12a}{\delta }^2_x v_n -\frac{{\Delta x}^2}{12} {\delta }^2_x F_n -\frac{b{\Delta x}^2}{12a} {\delta _x}F_n+O(\triangle x^4). \end{aligned}$$

(24)

Inserting (24) into (18) produces the following fourth-order CFD approximation for the problem (14):

$$\begin{aligned} (-a+p \triangle x^2) {\delta }^2_{x} v_{n}+b \delta _{x}v_{n}=\frac{\triangle x^2}{12}{\delta }^2_{x} F_{n}+q{\triangle x^2}{\delta }_{x} F_{n}+F_{n}+O(\triangle x^4), \end{aligned}$$

(25)

which completes the proof. $\square$

Now, let

$$\begin{aligned} \hat{G}(x,t)=D_t^{\alpha }\chi (x,t). \end{aligned}$$

(26)

At the point $(x_{n},t_{m})$, (26) leads to

$$\begin{aligned} \hat{G}(x_{n},t_{m})= D_t^{\alpha } \chi (x_{n},t_{m}) . \end{aligned}$$

(27)

Using (7) in (27), we get

$$\begin{aligned} \nonumber \hat{G}(x_{n},t_{m})= & {} \frac{1}{\Gamma (2-\alpha )}\sum _{k=1}^{m}\left[ (t_m-t_{k-1})^{1-\alpha }-(t_m-t_{k})^{1-\alpha }\right] \delta _t^-\chi (x_n,t_k)\\= & {} \mathcal {B} \bigg [\beta _{m,1}\chi (x_n,t_m)+\sum _{k=1}^{m-1}\left[ \beta _{m,k+1}-\beta _{m,k}\right] \chi (x_n,t_{m-k})-\beta _{m,m}\chi (x_n,t_0)\bigg ], \end{aligned}$$

(28)

where

$$\begin{aligned} \mathcal {B}=\frac{1}{\Gamma (2-\alpha )}, \beta _{m,k}=\frac{(t_m-t_{m-k})^{1-\alpha }-(t_m-t_{m-k+1})^{1-\alpha }}{{\uptau }_{m-k+1}}\,. \end{aligned}$$

(29)

When $l=1,$ we obtain $\beta _{m,1}={\uptau }_{m}^{-\alpha }.$ By (27), it follows from (9) that

$$\begin{aligned} -a\frac{\partial ^2 \chi (x_n,t_m)}{\partial x^2}+b \frac{\partial \chi (x_n,t_m)}{\partial x}=f(x_n,t_m)-\hat{G}(x_n,t_m). \end{aligned}$$

(30)

By means of Theorem 1, equation (30) at the point $(x_{n},t_{m})$ can be written as

$$\begin{aligned} {\begin{matrix} &{}(-a+p \triangle x^2) {\delta }^2_{x} \chi (x_n,t_m)+b \delta _{x}\chi (x_n,t_m)=\frac{\triangle x^2}{12}{\delta }^2_{x} (f(x_{n},t_{m})-\hat{G}(x_{n},t_{m}))\\ &{}+q{\triangle x^2}{\delta }_{x} (f(x_{n},t_{m})-\hat{G}(x_{n},t_{m}))\\ &{}+f(x_{n},t_{m})-\hat{G}(x_{n},t_{m})+O(\triangle x^4). \end{matrix}} \end{aligned}$$

(31)

We denote $\chi ^{m}_{n}=\chi (x_{n},t_{m})$ and $f^{m}_{n}=f(x_{n},t_{m}),\ 0 \le m \le \mathcal {N}; 0 \le n \le \mathcal {M}$. Thus, by (28) and (31), one has

$$\begin{aligned} {\begin{matrix} &{}\left( \frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\mathcal {B}\beta _{m,1}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\right) \chi ^{m}_{n-1}+\left( \frac{2a}{\triangle x^2}-2p+\frac{5 \beta _{m,1} \mathcal {B} }{6} \right) \chi ^{m}_{n}\\ {} &{} +\left( \frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}q \mathcal {B} \triangle x }{2}\right) \chi ^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{} \chi ^{m-k}_{n-1}+\frac{5}{6}\chi ^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )\chi ^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\chi ^{0}_{n-1}+\frac{5}{6}\chi ^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\chi ^{0}_{n+1}\bigg ]\\ {} &{} +\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )f^{m}_{n-1}+\frac{5}{6}f^{m}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x }{2}\bigg )f^{m}_{n+1}+ \hat{\mathcal {R}}^m_n, \hspace{0.1cm} n=1,2,...,\mathcal {M}-1,\hspace{0.1cm}m\ge 1, \end{matrix}} \end{aligned}$$

(32)

where $\hat{\mathcal {R}}^m_n$ represents the truncation error at $(x_n,t_m),$ which is defined by

$$\begin{aligned} |\hat{\mathcal {R}}^m_n| \le \hat{C} (m^{-min\{2-\alpha ,r\alpha \}}+ \triangle x^4), \end{aligned}$$

(33)

where $\hat{C}$ is a positive constant. Equation (11) is discretized as

$$\begin{aligned} \chi ^{m}_{0}=0,\hspace{0.1cm} \chi ^{m}_{\mathcal {M}}=0,\hspace{0.1cm}m\ge 1. \end{aligned}$$

(34)

The IC (10) is discretized as

$$\begin{aligned} \chi ^{0}_{n}=g_(x_{n})=g_{n},\hspace{0.1cm}n=0,1,2,...,\mathcal {M}. \end{aligned}$$

(35)

Denoting $\hat{\chi }^{m}_{n}$ as an approximation of $\chi ^{m}_{n}$ and neglecting $\hat{\mathcal {R}}^{m}_{n}$ in (32) yields the following finite difference discretization for (1)-(3):

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\hat{\chi }^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5\beta _{m,1}\mathcal {B}}{6} \bigg ) \hat{\chi }^{m}_{n}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p+\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\hat{\chi }^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{}\hat{\chi }^{m-k}_{n-1}+\frac{5}{6}\hat{\chi }^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )\hat{\chi }^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\hat{\chi }^{0}_{n-1}+\frac{5}{6}\hat{\chi }^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\hat{\chi }^{0}_{n+1}\bigg ]\\ {} &{} +\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )f^{m}_{n-1}+\frac{5}{6}f^{m}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x }{2}\bigg )f^{m}_{n+1}, \hspace{0.1cm} n=1,2,...,\mathcal {M}-1,\hspace{0.1cm}m\ge 1, \end{matrix}} \end{aligned}$$

(36)

with

$$\begin{aligned} \hat{\chi }^{m}_{0}=0,\hspace{0.1cm}m\ge 1, \end{aligned}$$

(37)

$$\begin{aligned} \hat{\chi }^{m}_{\mathcal {M}}=0,\hspace{0.1cm}m\ge 1, \end{aligned}$$

(38)

$$\begin{aligned} \hat{\chi }^{0}_{n}=g_{n},\hspace{0.1cm}n=0,1,2,...,\mathcal {M}. \end{aligned}$$

(39)

3 An adaptive numerical method

An adaptive mesh technique for solving the TFAD model (1)–(3) is presented in this section. We note that the graded mesh technique for solving the problem considered is defined by (32) and the complete discrete method based on adaptive grid can be obtained by altering the truncation error term in (32) with the truncation error term given in (42). The truncation error $\bar{\mathcal {R}}^m$ for TFD in (7) relative to the adaptive mesh is defined by

$$\begin{aligned} |\bar{\mathcal {R}}^m| \le C \max _{1\le k\le m}(\uptau _{k})^{1-\alpha }\int _{t_{k-1}}^{t_{k}}\left| \frac{\partial ^2\chi (x,s)}{\partial t^2}\right| ds\,. \end{aligned}$$

(40)

Taking into account (40) and (31), we obtain

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\mathcal {B}\beta _{m,1}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\chi ^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5 \beta _{m,1} \mathcal {B} }{6} \bigg ) \chi ^{m}_{n}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}q \mathcal {B} \triangle x }{2}\bigg )\chi ^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{} \chi ^{m-k}_{n-1}+\frac{5}{6}\chi ^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )\chi ^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\chi ^{0}_{n-1}+\frac{5}{6}\chi ^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\chi ^{0}_{n+1}\bigg ]\\ {} &{} +\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )f^{m}_{n-1}+\frac{5}{6}f^{m}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x }{2}\bigg )f^{m}_{n+1}+ \bar{\mathcal {R}}^m_n, \hspace{0.1cm} n=1,2,...,\mathcal {M}-1,\hspace{0.1cm}m\ge 1. \end{matrix}} \end{aligned}$$

(41)

The truncation error $\bar{\mathcal {R}}^m_n$ in (41) is defined by

$$\begin{aligned} |\bar{\mathcal {R}}^m_n| \le \mathcal {C}\left( \max _{1\le m\le \mathcal {N},1\le n\le \mathcal {M}}\uptau _{m}^{1-\alpha }\int _{t_{m-1}}^{t_{m}}\left| \frac{\partial ^{2}\chi (x_{n},s)}{\partial t^{2}}\right| ds+\triangle x^4\right) \,. \end{aligned}$$

(42)

where C denotes a positive constant. Denoting $\bar{\chi }^{m}_{n}$ as an approximation of $\chi ^{m}_{n}$ and neglecting $\bar{\mathcal {R}}^{m}_{n}$ in (41) yields the following numerical scheme for (1)–(3):

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\bar{\chi }^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5\beta _{m,1}\mathcal {B}}{6} \bigg ) \bar{\chi }^{m}_{n}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p+\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\bar{\chi }^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{}\bar{\chi }^{m-k}_{n-1}+\frac{5}{6}\bar{\chi }^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )\bar{\chi }^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\bar{\chi }^{0}_{n-1}+\frac{5}{6}\bar{\chi }^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\bar{\chi }^{0}_{n+1}\bigg ]\\ {} &{} +\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )f^{m}_{n-1}+\frac{5}{6}f^{m}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x }{2}\bigg )f^{m}_{n+1}, \hspace{0.1cm} n=1,2,...,\mathcal {M}-1,\hspace{0.1cm}m\ge 1. \end{matrix}} \end{aligned}$$

(43)

with

$$\begin{aligned} \bar{\chi }^{m}_{0}=0,\hspace{0.1cm}m\ge 1, \end{aligned}$$

(44)

$$\begin{aligned} \bar{\chi }^{m}_{\mathcal {M}}=0,\hspace{0.1cm}m\ge 1, \end{aligned}$$

(45)

$$\begin{aligned} \bar{\chi }^{0}_{n}=g_{n},\hspace{0.1cm}n=0,1,2,...,\mathcal {M}. \end{aligned}$$

(46)

3.1 Algorithm for adaptive mesh generation

Here we present an algorithm for generating the adaptive grid and for approximating the solution of (1)–(3) on the adaptive grid by employing (43)–(46).

Since the solution $\chi (x,t)$ of the problem (1) shows a weak singularity at $t=0$, a nonuniform adaptive time grid is generated by means of equidistribution of a positive monitor function, which is defined by (48). This kind of monitor function (48) has been employed in [18,19,20, 39]. Let $\Theta ^{\mathcal {N}}=\{ 0=t_{0}<t_{1}<...<t_{m}<...<t_{\mathcal {N}}= T\}$ be the time mesh. The time mesh $\Theta ^{\mathcal {N}}$ is called equidistributed if

$$\begin{aligned} \int _{t_{m-1}}^{t_m} \hat{M}(\mu ) d\mu =\frac{1}{\mathcal {N}} \int _{0}^{T} \hat{M}(\mu ) d\mu ,\ m= 1,2,....\mathcal {N}. \end{aligned}$$

(47)

The monitor function $\hat{M}(\mu )$ in (47) is approximated by

$$\begin{aligned} \hat{M}_{n}^{m}=\hat{M}(x_{n},t_m)=1+ \sqrt{ \bigl \vert \delta _{t}^{2}\hat{\chi }_{n}^{m} \bigr \vert },\quad t\in (t_{m-1},t_{m} ). \end{aligned}$$

(48)

In above equation, $\delta _{t}^{2}\hat{\chi }_{n}^{m}$ denotes the central difference approximation of $\hat{\chi }(x_n,t)$ on nonuniform temporal mesh. The following algorithm is proposed to solve (47):

Step I

Consider $\hat{\jmath } =0,$ where $\hat{\jmath }$ represents the iteration number. Take the uniform temporal mesh $\Theta ^{\mathcal {M},\mathcal {N},(0)}= \{(x_{n},t_{m}^{(0)} ) \vert \ 0\le \ n\le \mathcal {M}, 0\le m\le \mathcal {N} \}$ as the initial value for the iteration. Go to the step II with $\hat{\jmath } =0.$

Step II

Solve (43)–(46) for $\{ \bar{\chi }_{n}^{m,(\hat{\jmath } )} \}$ on $\Theta ^{\mathcal {M},\mathcal {N},(\hat{\jmath } )}= \{ (x_{n},t_{m}^{(\hat{\jmath } )} ) \vert 0\le n\le \mathcal {M}, 0\le m\le \mathcal {N} \}$. Set $\uptau _{m}^{(\hat{\jmath } )}=t_{m}^{(\hat{\jmath } )}-t_{m-1}^{(\hat{\jmath } )}$ for each m. Compute

$$\begin{aligned} \xi _{n}^{m,(\hat{\jmath } )}=\sum _{k=1}^{m} \uptau _{k}^{(\hat{\jmath })}\hat{M}_{n}^{k,(\hat{\jmath } )} \end{aligned}$$

(49)

and pick out $\jmath$ such that

$$\begin{aligned} \xi _{\jmath }^{\mathcal {N},(\hat{\jmath } )}=\max _{1\le n< \mathcal {M}} \bigl \{ \xi _{n}^{\mathcal {N},(\hat{\jmath } )} \bigr \}. \end{aligned}$$

(50)

The monitor function $\hat{M}_{n}^{k,(\hat{\jmath } )}$ in (49) was evaluated at the k-th grid point of the current grids. We set $\hat{M}_{n}^{0,(\hat{\jmath } )}=\hat{M} _{n}^{1,(\hat{\jmath } )}$ and $\hat{M}_{n}^{\mathcal {N},(\hat{\jmath } )}=\hat{M}_{n}^{\mathcal {N}-1,(\hat{\jmath } )}.$

Step III

Choose a constant $\hat{\psi }> 1$. If

$$\begin{aligned} \frac{ {\max _{1\le m\le \mathcal {N}}\uptau _{m}^{(\hat{\jmath } )}\hat{M}_{\jmath }^{m,(\hat{\jmath } )}}}{\xi _{\jmath }^{\mathcal {N},(\hat{\jmath } )}}\le \frac{ \hat{\psi }}{\mathcal {N}}, \end{aligned}$$

(51)

then go to step V, else continue step IV.

Step IV

Set $I_{m}^{(\hat{\jmath } )}=m\xi _{\jmath }^{\mathcal {N},(\hat{\jmath } )}/\mathcal {N}, \ m=0,1,..., \mathcal {N}.$ Interpolate $(I_{m}^{(\hat{\jmath } )},t_{m}^{(\hat{\jmath } +1)} )$ to $(\xi _{\jmath } ^{m,(\hat{\jmath } )},t_{m}^{(\hat{\jmath } )} )$. Generate a new mesh

$$\begin{aligned} \Theta ^{\mathcal {M},\mathcal {N},(\hat{\jmath } +1)}=\left\{ \bigl (x_{n},t_{m}^{(\hat{\jmath } +1)} \bigr )|0 \le n\le \mathcal {M}, 0\le m\le \mathcal {N}\right. \bigr \} . \end{aligned}$$

(52)

Step V

Set $\Theta ^{\mathcal {M},\mathcal {N},*}=\Theta ^{\mathcal {M},\mathcal {N},(\hat{\jmath } )}$ and $\{ \bar{\chi }_{n}^{m,*} \} = \{ \bar{\chi }_{n}^{m,(\hat{\jmath } )} \},$ then stop.

Remark 1

It is observed that the coefficient matrix of (36)–(39) or (43)–(46) is strictly diagonally dominant with nonpositive off-diagonal elements and positive diagonal elements. Hence, the systems defined by (36)–(39) and (43)–(46) are solvable.

4 Stability and convergence

In this section, we study the stability and convergence for the numerical scheme (36)–(39).

4.1 Stability

Here, we present the stability bound of the present numerical scheme (36) for the considered time-fractional problem. We introduce $L^{\infty }$-norm for any mesh function $U^m_n$, as follows

$$\begin{aligned} ||U^m|| _\infty =\displaystyle \max _{0\le n\le \mathcal {M}}|U^m_n| \quad \text{ and } \quad ||U|| _\infty = \displaystyle \max _{0\le m\le \mathcal {N}}\displaystyle \max _{0\le n\le \mathcal {M}}|U^m_n|. \end{aligned}$$

(53)

Lemma 2

The solution of (36) satisfies

$$\begin{aligned} ||\chi ^m||_\infty \le \frac{1}{\beta _{m,1}} \bigg [ \frac{1}{\mathcal {B}}||f^m||_\infty +\beta _{m,m} ||\hat{\chi }^0||_\infty +\sum _{k=1}^{m-1} (\beta _{m,k}-\beta _{m,k+1}) ||\hat{\chi }^{m-k}||_\infty \bigg ], \end{aligned}$$

(54)

for $m=1,2,\dots ,\mathcal {N}$.

Proof

Fix $m\in \{{1,2,...,\mathcal {N}}\}$. Choose $n_0$ such that $| \hat{\chi }^m_{i_{0}}|=\displaystyle \max _{0\le n\le \mathcal {M}}|\hat{\chi }^m_n|=||\hat{\chi }^m||_\infty$. Then, (36) at the mesh point $(x_{i_{0}},t_m)$ is

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\hat{\chi }^{m}_{i_{0}-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5\beta _{m,1}\mathcal {B}}{6} \bigg ) \hat{\chi }^{m}_{i_{0}}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\hat{\chi }^{m}_{i_{0}+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{}\hat{\chi }^{m-k}_{i_{0}-1}+\frac{5}{6}\hat{\chi }^{m-k}_{i_{0}}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )\hat{\chi }^{m-k}_{i_{0}+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\hat{\chi }^{0}_{i_{0}-1}+\frac{5}{6}\hat{\chi }^{0}_{i_{0}}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\hat{\chi }^{0}_{i_{0}+1}\bigg ]\\ {} &{} +\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )f^{m}_{i_{0}-1}+\frac{5}{6}f^{m}_{i_{0}}+\bigg (\frac{1}{12}+\frac{q \triangle x }{2}\bigg )f^{m}_{i_{0}+1}. \end{matrix}} \end{aligned}$$

(55)

By taking $L^{\infty }$-norm in (55) one has

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5 \beta _{m,1}\mathcal {B}}{6} \bigg ) ||\hat{\chi }^m||_\infty \le \bigg (\frac{2a}{\triangle x^2}-2p-\frac{\beta _{m,1}\mathcal {B}}{6} \bigg ) ||\hat{\chi }^m||_\infty \\ {} &{}+ ||f^m||_\infty +\beta _{m,m}\mathcal {B} ||\hat{\chi }^0||_\infty +\mathcal {B}\sum _{k=1}^{m-1}( \beta _{m,k}-\beta _{m,k+1}) ||\hat{\chi }^{m-k}||_\infty . \end{matrix}} \end{aligned}$$

(56)

Equation (56) simplifies to

$$\begin{aligned} ||\chi ^m||_\infty \le \frac{1}{\beta _{m,1}} \bigg [ \frac{1}{\mathcal {B}}||f^m||_\infty +\beta _{m,m} ||\hat{\chi }^0||_\infty +\sum _{k=1}^{m-1} (\beta _{m,k}-\beta _{m,k+1}) ||\hat{\chi }^{m-k}||_\infty \bigg ]. \end{aligned}$$

Thus, we get the desired result.$\square$

Lemma 3

The following properties hold for the coefficients $\beta _{m,k}$ defined in (29):

$$\begin{aligned} {\begin{matrix} &{}(i)\quad \beta _{m,k+1}\le \beta _{m,k}\, \\ {} &{}(ii) \quad \frac{(t_m-t_{m-k})^{-\alpha }}{\Gamma (1-\alpha )}\le \beta _{m,k} \le \frac{(t_m - t_{m-k+1})^{-\alpha }}{\Gamma (1-\alpha )}. \end{matrix}} \end{aligned}$$

Proof

Using the mean value theorem one can prove (i). Then, using (i) one can obtain (ii).

Let us define real numbers $D_{m,i}$, for $m=1,2,...,\mathcal {N}$ and $i=1,2,...,m-1$ such that

$$\begin{aligned} D_{m,m} = 1, \quad D_{m,i}=\sum _{k=1}^{m-i} {\uptau _{m-k}^{\alpha }} (\beta _{m,k}-\beta _{m,k+1})D_{m-k,i}. \end{aligned}$$

(57)

In view of Lemma 3, it can be seen that $D_{m,i}>0$ for all m and i.$\square$

Lemma 4

The solution of (36) satisfies

$$\begin{aligned} ||\hat{\chi }^m||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \frac{1}{\beta _{m,1} \mathcal {B} } \sum _{i=1}^{m} D_{m,i} ||f^i||_{\infty }, \end{aligned}$$

(58)

for $m=1,2,\dots ,\mathcal {N}$.

Proof

We use mathematical induction on m to prove the lemma. For $m=1,$ (54) reduces to

$$\begin{aligned} ||\chi ^1||_{\infty } \le \frac{1}{\beta _{1,1}} \bigg [ \beta _{1,1}||\chi ^0||_{\infty } +\frac{1}{\mathcal {B}}||f^1||_{\infty }\bigg ] = ||\chi ^0||_{\infty } + \frac{D_{1,1}}{\mathcal {B}\beta _{1,1}} ||f^1||_{\infty }. \end{aligned}$$

Thus, (58) is valid for $m=1.$ Next, we assume that (58) holds true for all $1\le m \le j-1,$ that is,

$$\begin{aligned} ||\hat{\chi }^m||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \frac{1}{\beta _{m,1}\mathcal {B}} \sum _{i=1}^{m} D_{m,i} ||f^i||_{\infty },\ \text{ for } \ 1\le m \le j-1. \end{aligned}$$

(59)

Now, we prove that the assertion (58) is valid for $m=j.$ Considering (54) at $m=j$, yields

$$\begin{aligned} ||\hat{\chi }^j||_\infty \le \frac{1}{\beta _{j,1}} \bigg [ \frac{1}{\mathcal {B}}||f^j||_\infty +\beta _{j,j} ||\hat{\chi }^0||_\infty +\sum _{k=1}^{j-1} (\beta _{j,k}-\beta _{j,k+1}) ||\hat{\chi }^{j-k}||_\infty \bigg ]. \end{aligned}$$

(60)

Taking into account (59), it follows from (60) that

$$\begin{aligned} ||\hat{\chi }^j||_\infty \le \frac{1}{\beta _{j,1}} \bigg [ \frac{1}{\mathcal {B}}||f^j||_\infty +\beta _{j,j} || \hat{\chi }^0||_\infty +\sum _{k=1}^{j-1} (\beta _{j,k}-\beta _{j,k+1}) \bigg (||\hat{\chi }^0||_{\infty } + \frac{1}{\mathcal {B}\beta _{j-k,1}} \sum _{i=1}^{j-k} D_{j-k,i} ||f^i||_{\infty }\bigg ) \bigg ]. \end{aligned}$$

The above equation simplifies to

$$\begin{aligned} ||\hat{\chi }^j||_\infty \le \frac{1}{\beta _{j,1}} \bigg [ \frac{1}{\mathcal {B}}||f^j||_\infty +\beta _{j,1} ||\hat{\chi }^0||_\infty +\frac{1}{\mathcal {B}}\sum _{k=1}^{j-1} \frac{1}{\beta _{j-k,1}}(\beta _{j,k}-\beta _{j,k+1}) \sum _{i=1}^{j-k} D_{j-k,i} ||f^i||_{\infty } \bigg ]. \end{aligned}$$

Now arranging the terms we get

$$\begin{aligned} {\begin{matrix} &{}||\hat{\chi }^j||_\infty \le \frac{1}{ {\mathcal {B}}\beta _{j,1}} ||f^j||_\infty + ||\hat{\chi }^0||_\infty +\frac{1}{\mathcal {B}\beta _{j,1}}\sum _{i=1}^{j-1} ||f^i||_{\infty }\sum _{k=1}^{j-i} \frac{1}{\beta _{j-k,1}}(\beta _{j,k}-\beta _{j,k+1}) D_{j-k,i} \\ {} &{}= \frac{1}{ {\mathcal {B}}\beta _{j,1}} ||f^j||_\infty + ||\hat{\chi }^0||_\infty +\frac{1}{\mathcal {B}\beta _{j,1}}\sum _{i=1}^{j-1} ||f^i||_{\infty }\sum _{k=1}^{j-i} {\uptau _{j-k}^{\alpha }} (\beta _{j,k}-\beta _{j,k+1})D_{j-k,i}. \end{matrix}} \end{aligned}$$

(61)

Using (57) in (61), one has

$$\begin{aligned} ||\hat{\chi }^j||_\infty \le \frac{1}{\mathcal {B} \beta _{j,1}} ||f^j||_\infty + ||\hat{\chi }^0||_\infty +\frac{1}{\mathcal {B}\beta _{j,1}}\sum _{i=1}^{j-1} ||f^i||_{\infty } D_{j,i}. \end{aligned}$$

In view of (57), the above equation can be written as

$$\begin{aligned} ||\hat{\chi }^j||_\infty \le \frac{D_{i,i}}{\mathcal {B}\beta _{j,1}} ||f^j||_\infty + ||\hat{\chi }^0||_\infty +\frac{1}{\mathcal {B}\beta _{j,1}}\sum _{i=1}^{j-1} ||f^i||_{\infty } D_{j,i}. \end{aligned}$$

(62)

Equation (62) simplifies to

$$\begin{aligned} ||\hat{\chi }^j||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \frac{1}{\mathcal {B}\beta _{j,1}} \sum _{i=1}^{j} D_{j,i} ||f^i||_{\infty }. \end{aligned}$$

Thus, (58) is valid for $m=j.$ Therefore, the assertion (58) is valid for all value of m. $\square$

Lemma 5

Let the parameter $\lambda$ satisfy $\lambda \le r\alpha$ and the real number $D_{m,i}$ be defined by (57). Then, for $1\le m\le \mathcal {N}$, we have

$$\begin{aligned} \uptau _m^\alpha \sum _{i=1}^{m} i^{-\lambda }D_{m,i} \le \frac{T^\alpha \mathcal {N}^{-\lambda }}{1-\alpha }. \end{aligned}$$

(63)

Proof

One can prove the lemma following the arguments used in Lemma 4.3 of [12].$\square$

Theorem 2

The solution of (36) satisfies

$$\begin{aligned} ||\hat{\chi }^m||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \Gamma (1-\alpha ) T^{\alpha } ||f||_{\infty }. \end{aligned}$$

Proof

From lemma 4, we have

$$\begin{aligned} {\begin{matrix} ||\hat{\chi }^m||_{\infty } &{} \le ||\hat{\chi }^0||_{\infty } + \frac{1}{\mathcal {B} \beta _{m,1}} \sum _{i=1}^{m} D_{m,i} ||f^i||_{\infty } = ||\hat{\chi }^0||_{\infty } + \frac{1}{\mathcal {B} \beta _{m,1}} \sum _{i=1}^{m} D_{m,i} \displaystyle \max _{0\le n\le \mathcal {M}}|f^{i}_{n}| \\ {} &{} \le \displaystyle \max _{0\le i\le \mathcal {N}} \bigg [\displaystyle \max _{0\le n\le \mathcal {M}} |f^i_n|\bigg ] \frac{1}{\mathcal {B} \beta _{m,1}}\sum _{i=1}^{m} D_{m,i}. \end{matrix}} \end{aligned}$$

(64)

Setting $\lambda =0$ in (63), one has

$$\begin{aligned} \uptau _m^\alpha \sum _{i=1}^{m} D_{m,i} \le \frac{T^\alpha }{1-\alpha }. \end{aligned}$$

(65)

Using (65) in (64) yields

$$\begin{aligned} ||\hat{\chi }^m||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \Gamma (2-\alpha ) \frac{T^\alpha }{1-\alpha } ||f||_{\infty }. \end{aligned}$$

The above equation implies that

$$\begin{aligned} ||\hat{\chi }^m||_{\infty } \le ||\hat{\chi }^0||_{\infty } + \Gamma (1-\alpha ) T^{\alpha } ||f||_{\infty }. \end{aligned}$$

(66)

We now state and prove the main stability theorem. $\square$

Theorem 3

The numerical scheme defined by (36) is unconditionally stable.

Proof

Let $\tilde{\chi }_n^m$ be the approximate solution of (36). The error $\bar{e}_n^m=\tilde{\chi }_n^m-\hat{\chi }_n^m,$ $n=0,1,..,\mathcal {M};\hspace{0.1cm}m=0,1,..,\mathcal {N}$ satisfies

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\bar{e}^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5\beta _{m,1}\mathcal {B}}{6} \bigg ) \bar{e}^{m}_{n}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )\bar{e}^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\bar{e}^{m-k}_{n-1}\\ {} &{}+\frac{5}{6}\bar{e}^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg ) \bar{e}^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )\bar{e}^{0}_{n-1}+\frac{5}{6}\bar{e}^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )\bar{e}^{0}_{n+1}\bigg ],\\ {} &{} \hspace{6.5cm} n=1,2,..,\mathcal {M}-1,\hspace{0.1cm}m=1,2,..,\mathcal {N}-1. \end{matrix}} \end{aligned}$$

(67)

Taking into account Lemma 2 and Theorem 2, one has

$$\begin{aligned} ||\bar{e}^m||_{\infty } \le ||\bar{e}^0||_{\infty }, \ 1\le m\le \mathcal {N}, \end{aligned}$$

(68)

where $||\bar{e}^m||_{\infty }=\displaystyle \max _{1\le n\le \mathcal {M}-1} |\bar{e}^{m}_{n}|.$ This demonstrates that the proposed numerical scheme (36) is unconditionally stable.$\square$

5 Convergence analysis

In this section, we study the convergence analysis of the numerical scheme based on graded mesh described by (36). Let $e_n^m = \chi _n^m - \hat{\chi }_n^m$ for $0 \le n \le \mathcal {M}$ and $0 \le m \le \mathcal {N}$. Then, subtracting (36) from (33), one obtain the following error equation

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )e^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5\beta _{m,1}\mathcal {B}}{6} \bigg ) e^{m}_{n}\\ {} &{} +\bigg (\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )e^{m}_{n+1} =\mathcal {B}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )e^{m-k}_{n-1}\\ &{}+\frac{5}{6}e^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )e^{m-k}_{n+1}\bigg ] +\mathcal {B}\beta _{m,m}\bigg [\bigg (\frac{1}{12}-\frac{q \triangle x }{2}\bigg )e^{0}_{n-1}+\frac{5}{6}e^{0}_{n}+\bigg (\frac{1}{12}+\frac{q \triangle x}{2}\bigg )e^{0}_{n+1}\bigg ] +\hat{R}_{n}^{m},\\ {} &{} \hspace{7cm} n=1,2,..,\mathcal {M}-1,\hspace{0.1cm}m=1,2,..,\mathcal {N}-1, \end{matrix}} \end{aligned}$$

(69)

where $\hat{\mathcal {R}}^m_n$ is defined by (33). As the error terms at initial time level are zero, it follows from (69) that

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{-a}{\triangle x^2}-\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}-\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )e^{m}_{n-1}+\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5 \beta _{m,1}\mathcal {B}}{6} \bigg ) e^{m}_{n}\\ {} &{} +\bigg (\bigg [\frac{-a}{\triangle x^2}+\frac{ b}{2\triangle x} +p +\frac{\beta _{m,1}\mathcal {B}}{12}+\frac{\beta _{m,1}\mathcal {B}q\triangle x }{2}\bigg )e^{m}_{n+1} = {\mathcal {B}}\sum _{k=1}^{m-1}\left[ \beta _{m,k}-\beta _{m,k+1}\right] \bigg [\bigg (\frac{1}{12}-\frac{q\triangle x }{2}\bigg )\\ {} &{}e^{m-k}_{n-1}+\frac{5}{6}e^{m-k}_{n}+\bigg (\frac{1}{12}+\frac{q\triangle x }{2}\bigg )e^{m-k}_{n+1}\bigg ] +\hat{R}_{n}^{m}, \hspace{0.1cm} n=1,2,...,\mathcal {M}-1,\hspace{0.1cm}m\ge 1. \end{matrix}} \end{aligned}$$

(70)

Considering similar arguments as used in Lemma 2, we can obtain the following result

$$\begin{aligned} {\begin{matrix} &{}\bigg (\frac{2a}{\triangle x^2}-2p+\frac{5 \beta _{m,1} \mathcal {B}}{6} \bigg ) ||e^m||_\infty \le \bigg (\frac{2a}{\triangle x^2}-2p-\frac{\beta _{m,1}\mathcal {B}}{6} \bigg ) ||e^m||_\infty \\ {} &{}+ \mathcal {B} \bigg [\sum _{k=1}^{m-1}( \beta _{m,k}-\beta _{m,k+1}) ||e^{m-k}||_\infty \bigg ]+||\hat{R}^m||_\infty , \end{matrix}} \end{aligned}$$

(71)

which is equivalent to

$$\begin{aligned} ||e^m||_\infty \le \frac{1}{\beta _{m,1}\mathcal {B}} ||\hat{R}^m||_\infty + \frac{1}{\beta _{m,1}} \sum _{k=1}^{m-1} (\beta _{m,k}-\beta _{m,k+1}) ||e^{m-k}||_\infty . \end{aligned}$$

(72)

Lemma 6

The solution of (70) satisfies

$$\begin{aligned} ||e^m||_{\infty } \le \frac{1}{\mathcal {B}\beta _{m,1}} \sum _{i=1}^{m} D_{m,i} ||\hat{R}^i||_{\infty }. \end{aligned}$$

(73)

Proof

We use induction on m to prove the result. When $m=1,$ (72) reduces to

$$\begin{aligned} ||e^1||_{\infty } \le \frac{1}{\mathcal {B}\beta _{1,1}} ||\hat{R}^1||_{\infty }, \end{aligned}$$

which suggests that (73) holds true for $m=1$. Let’s assume that (73) holds true for $1\le m \le j-1,$ that is

$$\begin{aligned} ||e^m||_\infty \le \frac{1}{\mathcal {B}\beta _{m,1}} \sum _{i=1}^{m} D_{m,i} ||\hat{R}^i||_{\infty }, \ \text {for} \ 1\le m \le j-1. \end{aligned}$$

(74)

Now, we prove that (73) holds true for $m=j.$ Considering (72) at $m=j$ yields

$$\begin{aligned} ||e^j||_\infty \le \frac{1}{\beta _{j,1}\mathcal {B}} ||\hat{R}^j||_\infty + \frac{1}{\beta _{j,1}} \sum _{k=1}^{j-1} (\beta _{j,k}-\beta _{j,k+1}) ||e^{j-k}||_\infty . \end{aligned}$$

(75)

Taking into account (74), it follows from (75) that

$$\begin{aligned} {\begin{matrix} ||e^j||_{\infty } &{}\le \frac{1}{\mathcal {B}\beta _{j,1}} \bigg [ ||\hat{R}^j||_\infty +\sum _{k=1}^{j-1} (\beta _{j,k}-\beta _{j,k+1})\frac{1}{\beta _{j-k,1}} \sum _{i=1}^{j-k} D_{j-k,i} ||\hat{R}^i||_{\infty } \bigg ] \\ {} &{}\le \frac{1}{\mathcal {B}\beta _{j,1}} \bigg [\sum _{k=1}^{j-1}\sum _{i=1}^{j-k} \frac{1}{\beta _{j-k,1}} (\beta _{j,k}-\beta _{j,k+1}) D_{j-k,i}||\hat{R}^i||_{\infty } + ||\hat{R}^j||_{\infty } \bigg ]\\ {} &{}\le \sum _{i=1}^{j-1}\frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^i||_{\infty }\sum _{k=1}^{j-i} \frac{1}{\beta _{j-k,1}} (\beta _{j,k}-\beta _{j,k+1}) D_{j-k,i}+ \frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^j||_{\infty }. \end{matrix}} \end{aligned}$$

The last inequality is equivalent to

$$\begin{aligned} {\begin{matrix} ||e^j||_{\infty } \le \sum _{i=1}^{j-1}\frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^i||_{\infty }\sum _{k=1}^{j-i} {\uptau _{j-k}^{\alpha }} (\beta _{j,k}-\beta _{j,k+1}) D_{j-k,i}+ \frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^j||_{\infty }. \end{matrix}} \end{aligned}$$

(76)

Using (57) in (76), one has

$$\begin{aligned} {\begin{matrix} ||e^j||_{\infty } \le \sum _{i=1}^{j-1}\frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^i||_{\infty } D_{j,i}+ \frac{1}{\mathcal {B}\beta _{j,1}}||\hat{R}^j||_{\infty }. \end{matrix}} \end{aligned}$$

The above equation simplifies to

$$\begin{aligned} ||e^j||_{\infty } \le \frac{1}{\mathcal {B}\beta _{j,1}}\sum _{i=1}^{j} D_{j,i} ||\hat{R}^i||_{\infty }. \end{aligned}$$

Thus, (73) is valid for $m=j.$ Therefore, the conclusion of Lemma 6 is proved. We now state and prove the main convergence theorem.$\square$

Fig. 1

The generation of temporal mesh points for different $\alpha$: Top: Graded mesh, Bottom: Adapted mesh (at last time level)

Fig. 2

The generation of adapted moving meshes for $\alpha = 0.1$

Fig. 3

The generation of adapted moving meshes for $\alpha = 0.4$

Fig. 4

The generation of adapted moving meshes for $\alpha = 0.6$

Theorem 4

Let $\chi (x,t)$ be the exact solution of (1)–(3) and $\hat{\chi }_{m}^n$ be the discrete solution of (36)–(39). Then, there exist a constant $C^{*}$ independent of $\Delta x$ and $\beta _{m,1}$ such that

$$\begin{aligned} ||e^m||_{\infty } \le {C^*}\left( \mathcal {N}^{-\min \{2-\alpha ,\, \, r\alpha \}}+\Delta x^4\right) . \end{aligned}$$

Proof

From lemma 6, we have

$$\begin{aligned} ||e^m||_{\infty } \le \frac{1}{\mathcal {B}\beta _{m,1}}\sum _{i=1}^{m} D_{m,i} ||\hat{R}^i||_{\infty }. \end{aligned}$$

(77)

In view of (33), (77) yields

$$\begin{aligned} ||e^m||_{\infty } \le \frac{1}{\mathcal {B}\beta _{m,1}} \sum _{i=1}^{m} D_{m,i} \hat{C}\bigg (\Delta x^4+i^{-\min \{2-\alpha ,r\alpha \}}\bigg ). \end{aligned}$$

(78)

Taking into account (63), it follows from (78) that

$$\begin{aligned} {\begin{matrix} ||e^m||_{\infty } &{} \le \Gamma (2-\alpha ) \hat{C} \bigg [\frac{\Delta x^4T^{\alpha }}{1-\alpha }+ \frac{\mathcal {N}^{-\min \{2-\alpha ,r\alpha \}}T^{\alpha }}{1-\alpha }\bigg ] \\ &{} \le \Gamma (1-\alpha ) T^{\alpha } \hat{C} \bigg (\Delta x^4+\mathcal {N}^{-\min \{2-\alpha ,r\alpha \}}\bigg ) \\ &{}= C^{*} \bigg (\mathcal {N}^{-\min \{2-\alpha ,r\alpha \}} + \Delta x^4\bigg ). \end{matrix}} \end{aligned}$$

Hence, Theorem 4 is proved. $\square$

Fig. 5

3D plots of numerical solutions on adapted, graded and uniform meshes for Example 1 when $\alpha = 0.1$

Fig. 6

3D plots of numerical solutions on graded, adapted and uniform meshes for Example 1 when $\alpha = 0.8$

Table 1 The ROC in time for adapted mesh, graded mesh with $r=2(2-\alpha )/\alpha$ and uniform mesh for example 1, when $\mathcal {M=N}$

Table 2 The ROC in time for graded mesh with $r=(2-\alpha )/\alpha$ for example 1

Table 3 The ROC in time for graded mesh with $r=(2-\alpha )/(2\alpha )$ for example 1

Table 4 The ROC in space for graded mesh with $r=(2-\alpha )/\alpha$, when $\alpha =0.8$ and $\mathcal {N}=12000$ for example 1

Table 5 The ROC in space for adaptive mesh, when $\alpha =0.8$ and $\mathcal {N}=12000$ for example 1

6 Numerical results

Here, three numerical examples of the form (1)–(3) are presented to illustrate the efficiency and robustness of proposed methods. It is worth mentioning that the exact solution to the first test problem has a weak singularity at the initial time $t=0,$ while the solution of second one is smooth and the exact solution to the third problem is not known. We calculate the $L_{\infty }$ norm error and the maximum $L_{2}$ norm error in the computed solution corresponding to the graded mesh using the following formulae

$$\begin{aligned} L_{\infty }^{\mathcal {N},\mathcal {M}}=\max _{\begin{array}{c} 0\le m\le \mathcal {N}, 0\le n\le \mathcal {M} \end{array}}|\hat{\chi }^{m}_{n}-{\chi }(x_{n}, t_{m})| \end{aligned}$$

(79)

and

$$\begin{aligned} L_{2}^{\mathcal {N},\mathcal {M}}=\max _{\begin{array}{c} 0\le m\le \mathcal {N} \end{array}} \bigg (\Delta x {\sum _{n=1}^{\mathcal {M}-1}(\hat{\chi }^{m}_{n}-{\chi }(x_{n}, t_{m}))^2}\bigg )^{\frac{1}{2}}, \end{aligned}$$

(80)

where ${\hat{\chi }}_n^m$ and $\chi (x_n,t_m)$ respectively denotes the computed solution and exact solution. We compare the numerical results obtained with the graded and adaptive meshes with the results obtained with the uniform mesh.

Example 1

Let us consider (1)–(3) with $a=b=1,$ ${g}(x)=4x^2(1-x)^2$ and $T=1$. The analytical solution is given by

$$\begin{aligned} \chi (x,t)=(2 x (1-x))^2 (t^{\alpha }+\sin (x)). \end{aligned}$$

(81)

The solution of above problem exhibits a weak singularity at $t=0$. The right-hand side source function f(x, t) can be obtained by inserting (81) into left-hand side of (1).

The presented schemes are employed to approximate the solution of this problem for various values of $\alpha ,$ $\mathcal {N}$ and $\mathcal {M}$. Figure 1 shows the formation of mesh points at final time level corresponding to the adaptive mesh technique and graded mesh technique for $\alpha = 0.1, \,\, 0.4,$ and 0.6,  when $\mathcal {N}=\mathcal {M}=64.$ As it can be seen in Fig. 1 that the concentration of mesh points near $t=0$ for $\alpha =0.1$ is higher than that for $\alpha =0.6.$ Figs. 2, 3 and 4 show the time evolution of mesh geometry on the adaptive mesh technique for $\alpha = 0.1,$ $\alpha = 0.4$ and $\alpha =0.6,$ respectively. It can be noted from the figures that the number of iterations (NOI) increases as $\alpha$ decreases. In particular, the NOI (within given tolerance) for $\alpha =0.1,$ $\alpha =0.4$ and $\alpha =0.6$ are 24,  7 and 4 respectively. The 3D plots of the numerical results on graded, adapted and uniform grids for $\alpha =0.1$ and 0.8 are depicted in Figs. 5 and 6, respectively. One can observe from the Figures that there is an initial layer in the solution profile which is consistent with (5). Further, one can observe from Figs. 5 and 6 that as $\alpha$ decreases the layer at $t=0$ becomes sharper.

Fig. 7

Maximum absolute errors on adapted, graded and uniform meshes for $\alpha = 0.4$

Fig. 8

Maximum absolute errors on adapted, graded and uniform meshes for $\alpha = 0.6$

Fig. 9

Maximum absolute errors on adapted, graded and uniform meshes for $\alpha = 0.8$

Fig. 10

3D plots of absolute errors on adapted, graded and uniform meshes for $\alpha = 0.8$

Next, we calculate the $L_{\infty }$ norm errors of presented schemes in time direction for different values of $\alpha .$ Table 1 lists the $L_{\infty }$ norm errors, the rate of convergence (ROC) and CPU time corresponding to the graded mesh with $r=2(2-\alpha )/\alpha ,$ adaptive mesh and uniform mesh for $\alpha =0.4,\,\, 0.6$ and 0.8. It can be noted from the tables that the scheme based on graded mesh yields much better accuracy (in temporal direction) as compared to the methods on adapted and uniform grids. Further, the method with adaptive mesh produces an approximation to the solution of the TFAD equation using more computational resources, both in terms of storage and CPU time. Moreover, we have calculated the errors on the graded mesh with $r=(2-\alpha )/\alpha$ and $r=(2-\alpha )/(2\alpha ),$ as listed in Tables 2 and 3, respectively for different values of $\alpha$. One can observe from Tables 1, 2, and 3 that in the case of grading parameter $r=(2-\alpha )/(2\alpha ),$ the rate of convergence is $(2-\alpha )/2,$ while for $r=2(2-\alpha )/\alpha$ and $r=(2-\alpha )/\alpha ,$ the optimal rate $(2-\alpha )$ is obtained. Further, the method on graded mesh with $r=2(2-\alpha )/\alpha$ produces more accurate solution than the method with $r=(2-\alpha )/\alpha .$ Furthermore, the uniform mesh method fails to provide an optimal $(2-\alpha )-$th order of convergence in time.

Table 6 The ROC in time for uniform mesh for example 2

Table 7 The ROC in time for adapted mesh, graded mesh with $r=(2-\alpha )/\alpha$ and uniform mesh for example 3

Next, we calculate the convergence rates of proposed schemes in space with respect to $L_{\infty }$ and $L_2$ norm errors. To do so, we calculate the errors for various values of $\mathcal {M}$ by fixing $\mathcal {N}$ (viz. $\mathcal {N}=12000$). Table 4 lists the $L_2$ norm and $L_{\infty }$ norm errors and the rates of convergence obtained by the method on graded mesh with $r=(2-\alpha )/\alpha$ for $\alpha =0.8$. Table 5 lists the $L_2$ norm and $L_{\infty }$ norm errors and the rates of convergence obtained by the method on adapted mesh for $\alpha =0.8.$ The tables indicate that the computed solution converges to the exact solution with fourth-order accuracy and confirm that the numerical results are in agreement with the theoretical results in Theorem 4. The $L_{\infty }$ norm errors obtained on graded mesh with $r=(2-\alpha )/\alpha ,$ adapted grid and uniform grid for $\alpha =0.4,\,\, 0.6$ and 0.8,  are depicted in Figs. 7, 8 and 9, respectively. From the figures, one can observe that the error decreases with the increase in $\mathcal {M},\mathcal {N}$ and the scheme based on graded mesh yields much better accuracy as compared to the methods on adapted and uniform grids. The 3D plots of the absolute errors (in time) obtained by the methods on graded, adapted and uniform grids for $\alpha =0.8$ are shown in Fig. 10 when $\mathcal {M}=\mathcal {N}=64.$ It can be observed from the Figures that the error increases towards $t=0$ and the present method with graded grid gives far better results as compared to the method with adapted grid or uniform grid.

Table 8 The ROC in space for adapted mesh, graded mesh with $r=(2-\alpha )/\alpha$ and uniform mesh, when $\mathcal {N}=12000$ for example 3

Fig. 11

3D plots of numerical solutions on adapted, graded and uniform meshes for Example 3 when $\alpha = 0.1$

Example 2

Consider (1)–(3) with $a=b=1,$ ${g}(x)=4x^2(1-x)^2,$ and $T=1$. The exact solution of this problem is $\chi (x,t)=(2 x (1-x))^2 (t^{3+\alpha }+\sin (x)).$ This example has a smooth solution at $t=0$.

The proposed scheme based on uniform mesh is employed to approximate the solution of this problem for several values of $\alpha ,$ $\mathcal {M}$ and $\mathcal {N}$. The $L_{\infty }$ errors for $\alpha =0.4, 0.6$ and 0.8 are reported in Table 6. One can conclude from the table that the uniform mesh method has an optimal rate convergence (i.e., $(2-\alpha )$) in time direction in the case when the exact solution to the TFAD problem is smooth.

Example 3

Consider (1)–(3) with $a=b=1,$ ${g}(x)=\sin x,$ $T=1$ and $f(x,t)=(1+t^4)(x^2-\pi x)+t^2.$ The exact solution of this problem is not known.

The proposed schemes on graded mesh with $r=(2-\alpha )/\alpha ,$ adapted mesh and uniform mesh are employed to approximate the solution of this problem for several values of $\alpha ,$ $\mathcal {M}$ and $\mathcal {N}$. The $L_{\infty }$ errors for $\alpha =0.4, 0.6$ and 0.8 are reported in Table 7. One can observe from the table that the graded and adaptive mesh methods yield the optimal rate of convergence O($\mathcal {N}^{-(2-\alpha )}$) in time, while the uniform mesh yields the suboptimal order convergence, that is, the order is close to $\alpha$. Table 8 presents the $L_{\infty }$ norm errors and the corresponding rates of convergence in space obtained by the methods on adapted mesh, graded mesh with $r=(2-\alpha )/\alpha$ and uniform mesh for $\alpha =0.8.$ The table indicates that the computed solution converges to the exact solution with fourth-order accuracy. The 3D plots of the numerical solutions on graded, adapted and uniform grids for $\alpha =0.1$ are depicted in Fig. 11. One can observe from the Figure that there is an initial layer in the solution profile.

7 Conclusions

In this article, efficient and robust numerical schemes based on graded and adaptive meshes have been developed for solving the TFAD model with weakly singular solution. The temporal derivative is described in the sense of Caputo. We have constructed adaptive moving mesh algorithm and graded mesh technique to deal with the weak singularity at the initial time. The space derivative is discretized by a high-order difference scheme. It has been shown that the graded mesh method is unconditionally stable. Convergence result of the method based on graded mesh has been established. Three numerical examples were solved to demonstrate the applicability and efficiency of proposed methods. The computed results suggest that the method based on graded or adapted mesh well approximate the solution of a given TFAD problem and yields the optimal $(2-\alpha )-$th order of convergence in time. The results obtained with the graded or adaptive mesh are better as compared to those obtained with the uniform mesh in terms of numerical accuracy. The uniform mesh method has the $\alpha -$th order of convergence in time in the case when the solution is nonsmooth. The method with adaptive grid produces an approximation to the solution of the TFAD problem using more computational resources. In the subsequent paper, we will design and analyze robust numerical scheme based on adaptive and graded meshes for the efficient numerical solution of a TFAD model with variable coefficients.