An $H^1$-Galerkin mixed finite element method for time fractional reaction–diffusion equation

Abstract

In this article, an $H^1$-Galerkin mixed finite element (MFE) method for solving time fractional reaction–diffusion equation is presented. The optimal time convergence order $O(\varDelta t^{2-\alpha })$ and the optimal spatial rate of convergence in $H^1$ and $L^2$-norms for variable $u$ and its gradient $\sigma$ are derived. Moreover, some numerical results are shown to support our theoretical analysis.

1 Introduction

In this article, we consider the time fractional reaction–diffusion equation

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}-\frac{\partial ^2 u(x,t)}{\partial x^2}+pu(x,t)=f(x,t),(x,t)\in \varOmega \times J,\\&u(x_L,t)=u(x_R,t)=0, t\in \bar{J},\\&u(x,0)=u_0(x), x\in \varOmega . \end{aligned}\right. \end{aligned}$$

(1)

In Eq. (1), $\varOmega =[x_L,x_R], J=(0,T]$ is the time interval with $0<T<\infty$. $u_0(x)$ and $f(x,t)$ are given functions, $p$ is a non-negative constant and $\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}$ is Caputo fractional-order derivative operator defined by

$$\begin{aligned} \frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}=\frac{1}{\varGamma (1-\alpha )}\int \limits _0^t\frac{\partial u(x,\tau )}{\partial \tau }\frac{d\tau }{(t-\tau )^{\alpha }}, \end{aligned}$$

(2)

where $0<\alpha <1$.

Generally, the fractional partial differential equations (PDEs) can be grouped into three categories: time fractional PDEs [1–3], space fractional PDEs [4–6] and space–time fractional PDEs [7]. Recently, more and more efficient numerical methods, such as finite difference methods [4, 8–21], finite element methods [1–3, 22, 23], spectral methods [24] and LDG methods [25, 26], have been found and studied for fractional PDEs. From the current literatures, we can find that a lot of numerical methods have been studied and developed for fractional PDEs. However mixed finite element methods for solving fractional PDEs have not been reported.

Over the past few decades, more and more mathematical scholars have studied some mixed finite element methods for partial differential equations. Pani (in 1998) [27] proposed an $H^1$-Galerkin MFE method for solving the linear parabolic equations. Compared to classical mixed methods, this method has several distinct characteristics: First, it is free of the LBB consistency condition; Second, the polynomial degrees of the finite element spaces $V_h$ and $W_h$ may be different; Third, the optimal $H^1$-error estimates for both the scalar unknown $u$ and its gradient $\sigma$ are obtained. In view of the method’s attractive features, the one has been used to seek the numerical solutions of some integer order partial differential equations [28–39]. However the numerical analysis of $H^1$-Galerkin MFE method of fractional PDEs has not been studied and discussed.

In this article, our aim is to propose the $H^1$-Galerkin MFE method for time fractional reaction–diffusion equation. We discretize the time fractional derivative by a high order difference method and approximate the spatial direction by the $H^1$-Galerkin MFE method. We derive some optimal a priori error estimates for the scalar unknown $u$ and the gradient term $\sigma$ in the $L^2$ and $H^1$-norms. We provided a numerical example to illustrate the effectiveness of the studied method.

The layout of the paper is as follows. In Sect. 2, we formulate an $H^1$-Galerkin mixed scheme for time fractional reaction diffusion equation (1) and give two important lemmas for a priori error analysis. In Sect. 3, we introduce a high order difference method for time fractional order derivative. In Sect. 4, we derive the detailed proof of the a priori error estimates for fully discrete scheme. In Sect. 5, we obtain some numerical results to confirm our theoretical analysis. In Sect. 6, we give some remarks and extensions about the $H^1$-Galerkin MFE method for fractional PDEs.

Throughout this paper, the notations and definitions of Sobolev spaces as in Ref. [40] are used.

2 An $H^1$-Galerkin MFE formulation

In order to get the $H^1$-Galerkin mixed formulation, we first split Eq. (1) into the following lower-order system of two equations by introducing an auxiliary variable $\sigma =\frac{\partial u(x,t)}{\partial x}$

$$\begin{aligned} \left\{ \begin{aligned} (a)&~\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}-\frac{\partial \sigma (x,t)}{\partial x}+pu(x,t)=f(x,t),\\ (b)&~\sigma -\frac{\partial u(x,t)}{\partial x}=0. \end{aligned}\right. \end{aligned}$$

(3)

Now we multiply the first equation in (3) by $-\frac{\partial w}{\partial x},w\in H^1$ and integrate with respect to space from $x_L$ to $x_R$ to arrive at

$$\begin{aligned} -\Big (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }},\frac{\partial w}{\partial x}\Big )+\Big (\frac{\partial \sigma }{\partial x},\frac{\partial w}{\partial x}\Big )-p\Big (u,\frac{\partial w}{\partial x}\Big )=-\Big (f,\frac{\partial w}{\partial x}\Big ), \end{aligned}$$

(4)

where $(q,z)\doteq \int _{x_{L}}^{x_R}q(x)\cdot z(x)dx$.

By the application of integration by parts with $\frac{\partial u(x_L,\tau )}{\partial \tau }=\frac{\partial u(x_R,\tau )}{\partial \tau }=0,$ we can obtain

$$\begin{aligned}&-\Big (\frac{\partial ^{\alpha }u}{\partial t^{\alpha }},\frac{\partial w}{\partial x}\Big )-p\Big (u,\frac{\partial w}{\partial x}\Big )\nonumber \\&\quad =-\Big (\frac{1}{\varGamma (1-\alpha )}\int \limits _0^t\frac{\partial u(x,\tau )}{\partial \tau }\frac{d\tau }{(t-\tau )^{\alpha }},\frac{\partial w}{\partial x}\Big )-p\Big (u,\frac{\partial w}{\partial x}\Big )\nonumber \\&\quad =\Big (\frac{1}{\varGamma (1-\alpha )}\int \limits _0^t\frac{\partial ^2 u(x,\tau )}{\partial \tau \partial x}\frac{d\tau }{(t-\tau )^{\alpha }},w\Big )+p\Big (\frac{\partial u}{\partial x},w\Big )\nonumber \\&\quad +\frac{1}{\varGamma (1-\alpha )}\int \limits _0^t\frac{\partial u(x,\tau )}{\partial \tau }\cdot w(x,t)\Big |_{x_L}^{x_R}\frac{d\tau }{(t-\tau )^{\alpha }}+ pu(x,t)\cdot w(x,t)\Big |_{x_L}^{x_R}\nonumber \\&\quad =\Big (\frac{1}{\varGamma (1-\alpha )}\int \limits _0^t\frac{\partial \sigma (x,\tau )}{\partial \tau }\frac{d\tau }{(t-\tau )^{\alpha }},w\Big )+p(\sigma ,w)\nonumber \\&\quad =\Big (\frac{\partial ^{\alpha }\sigma (x,t)}{\partial t^{\alpha }}+p\sigma ,w\Big ). \end{aligned}$$

(5)

Substitute (5) into (4) to get

$$\begin{aligned} \Big (\frac{\partial ^{\alpha }\sigma }{\partial t^{\alpha }},w\Big )+\Big (\frac{\partial \sigma }{\partial x},\frac{\partial w}{\partial x}\Big )+p(\sigma ,w)=-\Big (f,\frac{\partial w}{\partial x}\Big ). \end{aligned}$$

(6)

Multiply the second equation in (3) by $\frac{\partial v}{\partial x},v\in H_0^1$ and integrate with respect to space from $x_L$ to $x_R$ to obtain

$$\begin{aligned} \Big (\frac{\partial u}{\partial x},\frac{\partial v}{\partial x}\Big )=\Big (\sigma ,\frac{\partial v}{\partial x}\Big ),\forall v\in H_0^1. \end{aligned}$$

(7)

Combining (6) with (7), the mixed weak formulation can be described as

$$\begin{aligned} \left\{ \begin{aligned} (a)&~\Big (\frac{\partial u}{\partial x},\frac{\partial v}{\partial x}\Big )=\Big (\sigma ,\frac{\partial v}{\partial x}\Big ),\forall v\in H_0^1,\\ (b)&~\Big (\frac{\partial ^{\alpha }\sigma }{\partial t^{\alpha }},w\Big )+\Big (\frac{\partial \sigma }{\partial x},\frac{\partial w}{\partial x}\Big )+p(\sigma ,w)=-\Big (f,\frac{\partial w}{\partial x}\Big ),\forall w\in H^1. \end{aligned}\right. \end{aligned}$$

(8)

Choosing the finite dimensional subspaces $V_h$ and $W_h$ of $H_0^1$ and $H^1$, respectively, with the following approximation properties: for $1\le p\le \infty$ and $k,~r$ positive integers [27]

$$\begin{aligned}&\displaystyle \inf _{v_h\in V_h}\{\Vert v-v_h\Vert _{L^p}+h\Vert v-v_h\Vert _{W^{1,p}}\}\le Ch^{k+1}\Vert v\Vert _{W^{k+1,p}},v\in ~H_{0}^{1}\cap W^{k+1,p},&\\&\displaystyle \inf _{w_h\in W_h}\{\Vert w-w_h\Vert _{L^p}+h\Vert w-w_h\Vert _{W^{1,p}}\}\le Ch^{r+1}\Vert w\Vert _{W^{r+1,p}},w\in ~W^{r+1,p}.&\end{aligned}$$

Then the semidiscrete $H^1$-Galerkin mixed finite element scheme is described by

$$\begin{aligned} \left\{ \begin{aligned} (a)&~\Big (\frac{\partial u_h}{\partial x},\frac{\partial v_h}{\partial x}\Big )=\Big (\sigma _h,\frac{\partial v_h}{\partial x}\Big ),\forall v_h\in V_h,\\ (b)&~\Big (\frac{\partial ^{\alpha }\sigma _h}{\partial t^{\alpha }},w_h\Big )+\Big (\frac{\partial \sigma _h}{\partial x},\frac{\partial w_h}{\partial x}\Big )+p(\sigma _h,w_h)=-\Big (f,\frac{\partial w_h}{\partial x}\Big ),\forall w_h\in W_h. \end{aligned}\right. \end{aligned}$$

(9)

For a priori error estimates for fully discrete scheme, we introduce two projection operators [27, 41] in Lemma 1 and Lemma 2.

Lemma 1

We define an elliptic projection $P_hu\in V_h$ for the variable $u$ by

$$\begin{aligned} (u_x-P_{h}u_x,v_{hx})=0,v_h~\in V_h . \end{aligned}$$

(10)

Then the following estimates hold, for $j = 0,1$

$$\begin{aligned} \Vert u-P_hu\Vert _j\le C_{\star }h^{k+1-j}\Vert u\Vert _{k+1}. \end{aligned}$$

(11)

Lemma 2

Further, we also define an elliptic projection $R_h\sigma \in W_h$ of $\sigma$ as the solution of

$$\begin{aligned} \mathfrak {B}(\sigma -R_h{\sigma },w_{h}) =0,w_h~\in W_h, \end{aligned}$$

(12)

where $\mathfrak {B}(\sigma ,w)=(\sigma _x,w_x)+(\lambda +p)(\sigma ,w)$. Here $\lambda >0$ is chosen to satisfy

$$\begin{aligned} \mathfrak {B}(w,w)\ge \mu _0\Vert w\Vert _{1}^{2},w~\in H^1,\mu _0>0. \end{aligned}$$

Then the following estimates are found: for $j = 0,1$

$$\begin{aligned} \Vert \sigma -R_h\sigma \Vert _j\le C_*h^{r+1-j}\Vert \sigma \Vert _{r+1},~\Vert \sigma _t-R_h\sigma _t\Vert _j\le C_*h^{r+1-j}\Vert \sigma _t\Vert _{r+1}. \end{aligned}$$

(13)

Remark 1

When the reaction term coefficient $p>0$, we can also choose the parameter $\lambda =0$ and ensure that the $\mathfrak {B}(w,w)$ is $H^1$-coercive.

3 Discretization of time-fractional derivative

For the discretization of time-fractional derivative, let $0=t_0<t_1<t_2<\cdots <t_M=T$ be a given partition of the time interval $[0,T]$ with step length $\varDelta t=T/M$ and nodes $t_n=n\varDelta t$ ($n=0,1,\cdots ,M$), for some positive integer $M$. For a smooth function $\phi$ on $[0,T]$, define $\phi ^n=\phi (t_n)$.

Lemma 1

, [23] The time fractional order derivative $\frac{\partial ^{\alpha }\sigma (x,t)}{\partial t^{\alpha }}$ at $t=t_{n}$ is discretized by, for $0<\alpha <1$

$$\begin{aligned} \frac{\partial ^{\alpha }\sigma (x,t_{n})}{\partial t^{\alpha }} = \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n} \Big [(n-k+1)^{1-\alpha }-(n-k)^{1-\alpha }\Big ] \frac{\sigma ^k-\sigma ^{k-1}}{\varDelta t} +E_0^{n},\nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} E_0^{n}&= \frac{1}{\varGamma (1-\alpha )}\sum _{k=1}^{n} \int \limits _{t_{k-1}}^{t_{k}}\Big [\Big (\tau -\frac{t_k+t_{k-1}}{2}\Big )\frac{\partial ^2 \sigma (x,t_{k-\frac{1}{2}})}{\partial t^2}+O((\tau -t_{k-\frac{1}{2}})^2)\nonumber \\&+O(\varDelta t^2)\Big ]\frac{d\tau }{(t_{n}-\tau )^{\alpha }}. \end{aligned}$$

(15)

Proof

Using Taylor expansion at time $t=t_{k-\frac{1}{2}}$, we can arrive at

$$\begin{aligned} \frac{\partial \sigma (x,t_{k-\frac{1}{2}})}{\partial t} =\frac{\sigma ^k-\sigma ^{k-1}}{\varDelta t}+O(\varDelta t^2). \end{aligned}$$

(16)

By (16), Taylor expansion and some simple calculations of definite integral, we have

$$\begin{aligned}&\frac{\partial ^{\alpha }\sigma (x,t_{n})}{\partial t^{\alpha }}\nonumber \\&\quad =\frac{1}{\varGamma (1-\alpha )} \sum _{k=1}^{n}\int \limits _{t_{k-1}}^{t_{k}}\frac{\partial \sigma (x,\tau )}{\partial \tau }\frac{d\tau }{(t_{n}-\tau )^{\alpha }}\nonumber \\&\quad =\frac{1}{\varGamma (1-\alpha )}\sum _{k=1}^{n} \int \limits _{t_{k-1}}^{t_{k}}\Big [\frac{\sigma ^k-\sigma ^{k-1}}{\varDelta t} +\frac{\partial \sigma (x,\tau )}{\partial \tau }-\frac{\partial \sigma (x,t_{k-\frac{1}{2}})}{\partial t}+O(\varDelta t^2)\Big ]\frac{d\tau }{(t_{n}-\tau )^{\alpha }}\nonumber \\&\quad =\frac{1}{\varGamma (1-\alpha )}\sum _{k=1}^{n} \frac{\sigma ^{k}-\sigma ^{k-1}}{\varDelta t}\int \limits _{t_{k-1}}^{t_{k}}\frac{d\tau }{(t_{n}-\tau )^{\alpha }}\nonumber \\&\quad +\frac{1}{\varGamma (1-\alpha )}\sum _{k=1}^{n} \int \limits _{t_{k-1}}^{t_{k}}\Big [\Big (\tau -\frac{t_k+t_{k-1}}{2}\Big )\frac{\partial ^2 \sigma (x,t_{k-\frac{1}{2}})}{\partial t^2}+O((\tau -t_{k-\frac{1}{2}})^2)+O(\varDelta t^2)\Big ]\frac{d\tau }{(t_{n}-\tau )^{\alpha }}\nonumber \\&\quad = \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n} \Big [(n-k+1)^{1-\alpha }-(n-k)^{1-\alpha }\Big ] \frac{\sigma ^k-\sigma ^{k-1}}{\varDelta t} +E_0^{n}. \end{aligned}$$

(17)

$\square$

So, the conclusion of Lemma 1 can be obtained by the above calculations.

Lemma 2

[23, 24] The truncation error $E_0^{n}$ is bounded by

$$\begin{aligned} |E_0^{n}|\le C_0\varDelta t^{2-\alpha }. \end{aligned}$$

(18)

4 Error estimates for fully discrete scheme

In the following analysis, for deriving the convenience of theoretical process, we now denote

$$\begin{aligned} B^{\alpha }_{n-k}=(n-k+1)^{1-\alpha }-(n-k)^{1-\alpha }~ \text {and}~ D_t\sigma ^{k}=\frac{\sigma ^{k}-\sigma ^{k-1}}{\varDelta t}. \end{aligned}$$

Based on the discrete formula (14) of time-fractional derivative, we obtain the time semi-discrete scheme of (8)

$$\begin{aligned} \left\{ \begin{aligned} (a)&~~\Big (\frac{\partial u^{n}}{\partial x},\frac{\partial v}{\partial x}\Big )=\Big (\sigma ^{n},\frac{\partial v}{\partial x}\Big ),\forall v\in H_0^1,\\ (b)&~~\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }(D_t \sigma ^{k},w)+\Big (\frac{\partial \sigma ^{n}}{\partial x},\frac{\partial w}{\partial x}\Big )+p(\sigma ^n,w)\\&=-\Big (f^{n},\frac{\partial w}{\partial x}\Big )+(E_0^{n},w),\forall w\in H^1. \end{aligned}\right. \end{aligned}$$

(19)

Now, we look for the solution $(u^{n}_h,\sigma ^{n}_h)\in V_{h}\times W_{h},(n=0,1,\cdots ,M-1)$ by the fully discrete procedure

$$\begin{aligned} \left\{ \begin{aligned} (a)&~~\Big (\frac{\partial u^{n}_h}{\partial x},\frac{\partial v_h}{\partial x}\Big )=\Big (\sigma _h^{n},\frac{\partial v_h}{\partial x}\Big ),\forall v_h\in V_h,\\ (b)&~~\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }(D_t \sigma _h^{k},w_h)+\Big (\frac{\partial \sigma _h^{n}}{\partial x},\frac{\partial w_h}{\partial x}\Big )+p(\sigma ^n_h,w_h)\\&=-\Big (f^{n},\frac{\partial w_h}{\partial x}\Big ),\forall w_h\in W_h. \end{aligned} \right. \end{aligned}$$

(20)

For the convenience of the analysis, we now decompose the errors as

$$\begin{aligned} u(t_n)-u^n_h&= (u(t_n)-P_h{u}^n)+(P_h{u}^n-u^n_h)=\phi ^n+\vartheta ^n;\\ \sigma (t_n)-\sigma ^n_h&= (\sigma (t_n)-R_h{\sigma }^n) +(R_h{\sigma }^n-\sigma ^n_h)=\varrho ^n+\delta ^n. \end{aligned}$$

Subtracting (20) from (19) and using two projections (10) and (12), we get the error equations

$$\begin{aligned} \left\{ \begin{aligned} (a)&~~\Big (\frac{\partial \vartheta ^{n}}{\partial x},\frac{\partial v_h}{\partial x}\Big )=\Big (\delta ^{n},\frac{\partial v_h}{\partial x}\Big )+ \Big (\varrho ^{n},\frac{\partial v_h}{\partial x}\Big ),\forall v_h\in V_h,\\ (b)&~~\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }(D_t \delta ^{k},w_h)+\mathfrak {B}(\delta ^n,w_h)\\&=-\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }(D_t \varrho ^{k},w_h)+\lambda (\varrho ^n,w_h)+(E_0^{n},w_h),\forall w_h\in W_h. \end{aligned}\right. \end{aligned}$$

(21)

In the following discussion, we will derive the proof for the fully discrete a priori error estimates.

Theorem 1

Supposing that $u_h^0=P_h{u}(0)$ and $\sigma _h^0=R_h{\sigma }(0)$, then there exists a positive constant $C_0$ free of space–time mesh $h$ and $\varDelta t$ such that

$$\begin{aligned} \begin{aligned} \Vert \sigma ^n-\sigma ^{n}_h\Vert&\le C_0(\sigma ,T,\alpha )(\varDelta t^{2-\alpha }+(\lambda +1+\varDelta t^{-\alpha })h^{r+1}),\\ \Vert u^n-u^{n}_h\Vert _j&\le C_0(u,\sigma ,T,\alpha )(\varDelta t^{2-\alpha }+(\lambda +1+\varDelta t^{-\alpha })h^{r+1}+h^{k+1-j}),j=0,1. \end{aligned} \end{aligned}$$

(22)

Proof

Noting that $\sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \delta ^{k}=\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}$, then Eq (21b) may be rewritten as

$$\begin{aligned}&\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }(D_t \delta ^{n-k},w_h)+\mathfrak {B}(\delta ^n,w_h)\nonumber \\&\quad =-\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }(D_t \varrho ^{k},w_h)+\lambda (\varrho ^n,w_h)+(E_0^{n},w_h). \end{aligned}$$

(23)

$\square$

We take $w_h=\delta ^{n}$ in (23) and multiply by $\varGamma (2-\alpha )\varDelta t^{\alpha }$ to arrive at

$$\begin{aligned}&\sum _{k=0}^{n-1}B_k^{\alpha }(\delta ^{n-k}-\delta ^{n-k-1}, \delta ^{n})+\varGamma (2-\alpha )\varDelta t^{\alpha }\mathfrak {B}(\delta ^n,\delta ^n)\nonumber \\&\quad =-\sum _{k=0}^{n-1}B_{k}^{\alpha }( \varrho ^{n-k}-\varrho ^{n-k-1},\delta ^n)\nonumber \\&\quad +\lambda \varGamma (2-\alpha )\varDelta t^{\alpha }(\varrho ^n,w_h)+\varGamma (2-\alpha )\varDelta t^{\alpha }(E_0^{n},\delta ^n). \end{aligned}$$

(24)

By the simple calculation, we get the following equalities

$$\begin{aligned}&\sum _{k=0}^{n-1}B_k^{\alpha }(\delta ^{n-k}-\delta ^{n-k-1},\delta ^{n})\nonumber \\&\quad = \left( \sum _{k=0}^{n-1}B_{k}^{\alpha }\delta ^{n-k}- \sum _{k=1}^{n}B_{k-1}^{\alpha }\delta ^{n-k},\delta ^{n}\right) \nonumber \\&\quad =\Vert \delta ^{n}\Vert ^2+ \left( \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha }) \delta ^{n-k},\delta ^{n}\right) +B_{n-1}^{\alpha }\left( \delta ^{0},\delta ^{n}\right) , \end{aligned}$$

(25)

and

$$\begin{aligned}&\sum _{k=0}^{n-1}B_k^{\alpha }(\varrho ^{n-k}-\varrho ^{n-k-1},\delta ^{n})\nonumber \\&\quad =(\varrho ^n,\delta ^{n})+ \left( \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha })\varrho ^{n-k}, \delta ^{n}\right) +B_{n-1}^{\alpha }(\varrho ^{0},\delta ^{n}). \end{aligned}$$

(26)

Substitute (25) and (26) into (24) to arrive at

$$\begin{aligned}&\Vert \delta ^{n}\Vert ^2+\varGamma (2-\alpha )\varDelta t^{\alpha }\mathfrak {B}(\delta ^n,\delta ^n)\nonumber \\&\quad =-(\varrho ^n,\delta ^{n})- \left( \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha })\varrho ^{n-k},\delta ^{n}\right) - \left( \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha })\delta ^{n-k},\delta ^{n}\right) \nonumber \\&\quad -B_{n-1}^{\alpha }(\varrho ^0+\delta ^{0},\delta ^{n})+\lambda \varGamma (2-\alpha )\varDelta t^{\alpha }(\varrho ^n,\delta ^n)+\varGamma (2-\alpha )\varDelta t^{\alpha }(E_0^{n},\delta ^n). \end{aligned}$$

(27)

For (27), we take advantage of Cauchy–Schwarz inequality to have

$$\begin{aligned}&\Vert \delta ^{n}\Vert ^2+\varGamma (2-\alpha )\varDelta t^{\alpha }\mathfrak {B}(\delta ^n,\delta ^n)\nonumber \\&\quad \le \Big ( \Vert \varrho ^n\Vert +\sum _{k=1}^{n-1} \Big |B_{k}^{\alpha }-B_{k-1}^{\alpha } \Big |\Vert \varrho ^{n-k}\Vert +\sum _{k=1}^{n-1}\Big |B_{k}^{\alpha }-B_{k-1}^{\alpha }\Big |\Vert \delta ^{n-k}\Vert \nonumber \\&\quad +B_{n-1}^{\alpha }(\Vert \varrho ^{0}\Vert +\Vert \delta ^{0}\Vert )+\lambda \varGamma (2-\alpha )\varDelta t^{\alpha }\Vert \varrho ^n\Vert +\varGamma (2-\alpha )\varDelta t^{\alpha }\Vert E^n_{0}\Vert \Big )\Vert \delta ^n\Vert .\qquad \end{aligned}$$

(28)

Noting that $0<B_{k}^{\alpha }<B_{k-1}^{\alpha }<1$ and $\Vert \varrho ^{n-k}\Vert \le \Vert \varrho \Vert _{L^{\infty }(L^2)}$ in (28), we get

$$\begin{aligned}&\Vert \delta ^{n}\Vert ^2+\varGamma (2-\alpha )\varDelta t^{\alpha }\mathfrak {B}(\delta ^n,\delta ^n)\nonumber \\&\quad \le \Big ( \sum _{k=1}^{n-1}\Big [B_{k-1}^{\alpha }-B_{k}^{\alpha }\Big ]\Vert \delta ^{n-k}\Vert +(2+\lambda \varGamma (2-\alpha )\varDelta t^{\alpha }-B_{n-1}^{\alpha })\Vert \varrho \Vert _{L^{\infty }(L^2)}\nonumber \\&\quad +B_{n-1}^{\alpha }(\Vert \varrho ^{0}\Vert +\Vert \delta ^{0}\Vert )+\varGamma (2-\alpha )\varDelta t^{\alpha }\Vert E^n_{0}\Vert \Big )\Vert \delta ^n\Vert . \end{aligned}$$

(29)

Noting that $\delta ^0=0$ in (29) and $\varGamma (2-\alpha )\varDelta t^{\alpha }\mathfrak {B}(\delta ^n,\delta ^n)\ge \varGamma (2-\alpha )\varDelta t^{\alpha }\mu _0\Vert \delta ^n\Vert _0^2>0$, we have

$$\begin{aligned}&\Vert \delta ^{n}\Vert \le \Big ( \sum _{k=1}^{n-1}\Big [B_{k-1}^{\alpha }-B_{k}^{\alpha }\Big ]\Vert \delta ^{n-k}\Vert +(2+\lambda \varGamma (2-\alpha )\varDelta t^{\alpha }-B_{n-1}^{\alpha })\Vert \varrho \Vert _{L^{\infty }(L^2)}\nonumber \\&\quad +B_{n-1}^{\alpha }\Vert \varrho ^{0}\Vert +\varGamma (2-\alpha )\varDelta t^{\alpha }\Vert E^n_{0}\Vert \Big ). \end{aligned}$$

(30)

Using the Lemma in [24], we have

$$\begin{aligned} \Vert \delta ^{n}\Vert&\le \frac{2}{B_{n-1}^{\alpha }}\Vert \varrho \Vert _{L^{\infty }(L^2)}+\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{B_{n-1}^{\alpha }}\Vert E^n_{0}\Vert \nonumber \\&\le (n\varDelta t)^{\alpha }\varDelta t^{-\alpha }\frac{(2+\lambda \varGamma (2-\alpha )\varDelta t^{\alpha })n^{-\alpha }}{B_{n-1}^{\alpha }}\Vert \varrho \Vert _{L^{\infty }(L^2)}\nonumber \\&+\frac{\varGamma (2-\alpha )n^{-\alpha }(n\varDelta t)^{\alpha }}{B_{n-1}^{\alpha }}\Vert E^n_{0}\Vert . \end{aligned}$$

(31)

Noting that $(n\varDelta t)^{\alpha }\le T^{\alpha }$ and $\frac{n^{-\alpha }}{B_{n-1}^{\alpha }}\rightarrow \frac{1}{1-\alpha }$, we have

$$\begin{aligned} \Vert \delta ^{n}\Vert \le (2\varDelta t^{-\alpha }+\lambda \varGamma (2-\alpha )) \frac{T^{\alpha }}{1-\alpha }\Vert \varrho \Vert _{L^{\infty }(L^2)}+ \frac{\varGamma (2-\alpha )T^{\alpha }}{1-\alpha }\Vert E^n_{0}\Vert . \end{aligned}$$

(32)

By (13) and Lemma 1, we have

$$\begin{aligned} \Vert \delta ^{n}\Vert \le C_*(2\varDelta t^{-\alpha }+\lambda \varGamma (2-\alpha ))\frac{T^{\alpha }}{1-\alpha }h^{r+1}\Vert \sigma \Vert _{r+1}+\frac{C_0\varGamma (2-\alpha ) T^{\alpha }}{1-\alpha }\varDelta t^{2-\alpha }.\qquad \end{aligned}$$

(33)

Taking $v_h=\vartheta ^n$ in (21) and using Cauchy–Schwarz inequality, Poincare inequality, (33) and (13), we get

$$\begin{aligned} \Vert \vartheta ^n\Vert&\le C_1 \Big \Vert \frac{\partial \vartheta ^{n}}{\partial x}\Big \Vert \le C_1(\Vert \delta ^{n}\Vert + \Vert \varrho ^{n}\Vert )\nonumber \\&\le C_1C_*(2\varDelta t^{-\alpha }+\lambda \varGamma (2-\alpha ))\frac{T^{\alpha }}{1-\alpha }h^{r+1}\Vert \sigma \Vert _{r+1}\nonumber \\&+\frac{C_1C_0\varGamma (2-\alpha )T^{\alpha }}{1-\alpha }\varDelta t^{2-\alpha }+C_*h^{r+1}\Vert \sigma \Vert _{r+1}. \end{aligned}$$

(34)

Combining (11), (13), (33) and (34) with triangle inequality, we have the estimates for $\Vert \sigma ^n-\sigma _h^n\Vert , \Vert u^n-u_h^n\Vert$ and $\Vert u^n-u_h^n\Vert _1$.

Remark 2

(i) It is not hard to see from the proof of Theorem 1 that if we choose the reaction term coefficient $p=0$, the conclusions will have not any change based on the projection (12) with the chosen parameter $\lambda >0$.

(ii) When the reaction term coefficient $p>0$, we can also get the results of Theorem 1 with the vanished parameter $\lambda$.

Theorem 2

With the same condition to Theorem 1, one have the following a priori error estimate for $0<C_2,C(\lambda )\in R$ free of space-time mesh $h$ and $\varDelta t$

$$\begin{aligned} \Vert \sigma ^n-\sigma ^{n}_h\Vert _1\le C_2(u,\sigma ,T,\alpha )(\varDelta t^{2-\frac{3\alpha }{2}}+\varDelta t^{-\frac{3\alpha }{2}}h^{r+1}+h^{r})+C(\lambda )\varDelta t^{-\alpha }h^{r+1}.\qquad \end{aligned}$$

(35)

Proof

Take $w_h=\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}$ in (23) to arrive at

$$\begin{aligned}&\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}\Big \Vert ^2+\mathfrak {B}\Big (\delta ^n,\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}\Big )\nonumber \\&\quad =-\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }\left( D_t \varrho ^{k},\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}\right) \nonumber \\&\quad +\left( \lambda \varrho ^n+E_0^{n},\frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}\right) \nonumber \\&\quad \le \frac{1}{2}\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \varrho ^{k}\Big \Vert ^2+\frac{1}{4}\Vert E_0^{n}\Vert ^2+C(\lambda )\Vert \varrho ^n\Vert ^2\nonumber \\&\quad +\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}B_{k}^{\alpha }D_t \delta ^{n-k}\Big \Vert ^2. \end{aligned}$$

(36)

$\square$

Multiply by $\varGamma (2-\alpha )\varDelta t^{\alpha }$ and use the similar calculation to (25) to get

$$\begin{aligned}&\mathfrak {B}(\delta ^{n},\delta ^n)\nonumber \\&\quad \le - \Big (\sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha })\frac{\partial \delta ^{n-k}}{\partial x},\frac{\partial \delta ^{n}}{\partial x}\Big )-B_{n-1}^{\alpha }\Big (\frac{\partial \delta ^{0}}{\partial x},\frac{\partial \delta ^{n}}{\partial x}\Big )\nonumber \\&\quad -(\lambda +p)\left( \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha }) \delta ^{n-k},\delta ^{n}\right) -(\lambda +p)B_{n-1}^{\alpha }(\delta ^{0}, \delta ^{n})+C(\lambda )\Vert \varrho ^n\Vert ^2\nonumber \\&\quad +\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{4}\Vert E_0^{n}\Vert ^2+\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{2}\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \varrho ^{k}\Big \Vert ^2\nonumber \\&\quad \le \frac{1}{2}\mathfrak {B}(\delta ^{n},\delta ^n)+\frac{1}{2} \sum _{k=1}^{n-1}\Big |B_{k}^{\alpha }-B_{k-1}^{\alpha }\Big |^2\Big [\Big \Vert \frac{\partial \delta ^{n-k}}{\partial x}\Big \Vert ^2+\Vert \delta ^{n-k}\Vert ^2\Big ]+\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{4}\Vert E_0^{n}\Vert ^2\nonumber \\&\quad +\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{2}\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \varrho ^{k}\Big \Vert ^2+C(\lambda )\Vert \varrho ^n\Vert ^2. \end{aligned}$$

(37)

Now, we estimate the last term on the right hand side of (37). Using the similar result to (26), we have

$$\begin{aligned}&\frac{\varGamma (2-\alpha )\varDelta t^{\alpha }}{2}\Big \Vert \frac{\varDelta t^{1-\alpha }}{\varGamma (2-\alpha )}\sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \varrho ^{k}\Big \Vert ^2\nonumber \\&\quad =\frac{\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}\Big \Vert \varDelta t \sum _{k=1}^{n}B_{n-k}^{\alpha }D_t \varrho ^{k}\Big \Vert ^2\nonumber \\&\quad =\frac{\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}\Big \Vert \varrho ^n+ \sum _{k=1}^{n-1}(B_{k}^{\alpha }-B_{k-1}^{\alpha }) \varrho ^{n-k}+B_{n-1}^{\alpha }\varrho ^{0}\Big \Vert ^2\nonumber \\&\quad \le \frac{3\varDelta t^{-\alpha }}{4\varGamma (2-\alpha )}\left( \Vert \varrho ^n\Vert ^2+ \sum _{k=1}^{n-1}|B_{k}^{\alpha }-B_{k-1}^{\alpha }|^2 \Vert \varrho ^{n-k}\Vert ^2+(B_{n-1}^{\alpha })^2\Vert \varrho ^{0}\Vert ^2\right) .\qquad \end{aligned}$$

(38)

Substitute (38) into (37) to get

$$\begin{aligned}&\mathfrak {B}(\delta ^{n},\delta ^n)\nonumber \\&\quad \le \sum _{k=1}^{n-1}\Big |B_{k}^{\alpha }-B_{k-1}^{\alpha } \Big |^2\Big [\Big \Vert \frac{\partial \delta ^{n-k}}{\partial x}\Big \Vert ^2+\Vert \delta ^{n-k}\Vert ^2\Big ]\nonumber \\&\quad +\frac{1}{2}\varGamma (2-\alpha )\varDelta t^{\alpha }\Vert E_0^{n}\Vert ^2+C(\lambda )\Vert \varrho ^n\Vert ^2\nonumber \\&\quad +\frac{3\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}\left( \Vert \varrho ^n\Vert ^2+ \sum _{k=1}^{n-1}|B_{k}^{\alpha }-B_{k-1}^{\alpha }|^2\Vert \varrho ^{n-k}\Vert ^2+(B_{n-1}^{\alpha })^2\Vert \varrho ^{0}\Vert ^2\right) .\quad \quad \quad \end{aligned}$$

(39)

Noting that $B_{k}^{\alpha }/B_{k-1}^{\alpha }<1$ and $2a_1a_2+2a_1a_3+\cdots +2a_{n-1}a_n+\sum _{i=1}^{n}a_i^2\le n\sum _{i=1}^{n}a_i^2\le n(a_1+a_2+\cdots +a_n)^2,\forall a_i\in R^+$, we easily get

$$\begin{aligned}&\Big \Vert \frac{\partial \delta ^{n}}{\partial x}\Big \Vert + \Vert \delta ^{n}\Vert \nonumber \\&\quad \le C_2\left[ \sum _{k=1}^{n-1}\Big (B_{k-1}^{\alpha }-B_{k}^{\alpha }\Big )\Big [\Big \Vert \frac{\partial \delta ^{n-k}}{\partial x}\Big \Vert +\Vert \delta ^{n-k}\Vert \Big ]\right. \nonumber \\&\quad +\frac{1}{2}\sqrt{\varGamma (2-\alpha )\varDelta t^{\alpha }}\Vert E_0^{n}\Vert +\sqrt{C(\lambda )}\Vert \varrho ^n\Vert \nonumber \\&\quad \left. +\sqrt{\frac{3\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}}\left( \Vert \varrho ^n\Vert + \sum _{k=1}^{n-1}\Big (B_{k-1}^{\alpha }-B_{k}^{\alpha }\Big )\Vert \varrho \Vert _{L^{\infty }(L^2)}+B_{n-1}^{\alpha }\Vert \varrho ^{0}\Vert \right) \right] \!.\quad \quad \quad \end{aligned}$$

(40)

Using mathematical induction, we have

$$\begin{aligned}&\Big \Vert \frac{\partial \delta ^{n}}{\partial x}\Big \Vert + \Vert \delta ^{n}\Vert \le \frac{C_2(n\varDelta t)^{\alpha }\varDelta t^{-\alpha }n^{-\alpha }}{B^{\alpha }_{n-1}}\left[ \sqrt{\varGamma (2-\alpha )\varDelta t^{\alpha }}\Vert E_0^{n}\Vert \right. \nonumber \\&\quad \left. +\left( \sqrt{C(\lambda )}+\sqrt{\frac{3\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}}\right) \Vert \varrho \Vert _{L^{\infty }(L^2)}\right] . \end{aligned}$$

(41)

Noting that $(n\varDelta t)^{\alpha }\le T^{\alpha }$ and $\frac{n^{-\alpha }}{B_{n-1}^{\alpha }}\rightarrow \frac{1}{1-\alpha }$ again, we get

$$\begin{aligned}&\Big \Vert \frac{\partial \delta ^{n}}{\partial x}\Big \Vert + \Vert \delta ^{n}\Vert \le \frac{C_2T^{\alpha }\varDelta t^{-\alpha }}{1-\alpha }\Big [\sqrt{\varGamma (2-\alpha )\varDelta t^{\alpha }}\Vert E_0^{n}\Vert \nonumber \\&\quad +\left( \sqrt{C(\lambda )}+\sqrt{\frac{3\varDelta t^{-\alpha }}{2\varGamma (2-\alpha )}}\right) \Vert \varrho \Vert _{L^{\infty }(L^2)}\Big ]\nonumber \\&\quad \le \frac{C_2T^{\alpha }}{1-\alpha }\Big (\sqrt{C(\lambda )}\varDelta t^{-\alpha }+\sqrt{\frac{3}{2\varGamma (2-\alpha )}}\varDelta t^{-\frac{3\alpha }{2}}\Big )h^{r+1}\Vert \sigma \Vert _{r+1}\nonumber \\&\quad +\frac{C_2T^{\alpha }}{1-\alpha }\sqrt{\varGamma (2-\alpha )}\varDelta t^{2-\frac{3\alpha }{2}}. \end{aligned}$$

(42)

Combining (13), (42) with triangle inequality, we get the conclusion of theorem.

5 Some numerical results

Now we consider a numerical example [24] to test our theoretical analysis of a priori error estimates. In (1), we take space-time interval $[0,1]\times [0,1]$, the source term $f(x,t)=\frac{2}{\varGamma (3-\alpha )}t^{2-\alpha }\sin (2\pi x)+4\pi ^2t^2\sin (2\pi x)$, the coefficient $p=0$ of the convection term and the initial value $u(x,0)=0$. We easily find that the exact solution is $t^2\sin (2\pi x)$.

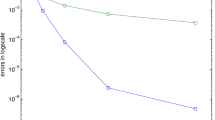
In Tables 1 and 2, for a fixed spatial step $h=1/800$ and some different time meshes $\varDelta t_1=1/25, \varDelta t_2=1/50, \varDelta t_3=1/100$, we can see that the orders of convergence for $u$ and $\sigma$ are close to $1.5, 1.3$ and $1.1$ with different $\alpha =0.5,0.7,0.9$, respectively. The convergence results are consistent with the results $O(\varDelta t^{2-\alpha })$ of the theoretical analysis.

In Tables 3 and 4, we obtain the optimal second-order convergence rate for $u$ and $\sigma$ in $L^2$-norm and the optimal first-order $H^1$-norm error results for the changed spatial meshes $h_1=1/25, h_2=1/50, h_3=1/100$ and the fixed time step $\varDelta t=1/800$. These numerical results of optimal a priori error estimates confirm the conclusions for the $H^1$-Galerkin MFE method.

Table 1 The convergence results of time for $u$ with fixed $h=1/800$ and different $\alpha$

Table 2 The convergence results of time for $\sigma$ with fixed $h=1/800$ and different $\alpha$

Table 3 Spatial convergence results for $u$ with fixed $\varDelta t=1/800$ and different $\alpha$

Table 4 Spatial convergence results for $\sigma$ with fixed $\varDelta t=1/800$ and different $\alpha$

6 Some concluding remarks and extensions

As far as we know, MFE methods for solving fractional PDEs have not been seen in the current literatures. In this article, our aim is to study an $H^1$-Galerkin MFE method for solving time fractional order reaction diffusion equation. We obtain some optimal a priori error estimates for the scalar unknown $u$ and its gradient $\sigma$ in $L^2$ and $H^1$-norms. For verifying the effectiveness of our method, we provide some numerical results by using Matlab procedure.

In the near future, we will study the $H^1$-Galerkin MFE method to solve the fractional telegraph equation [7], the variable-order fractional advection diffusion equation [10] and so on. At the same time, we are trying to find some new discrete methods for approximating fractional derivatives and study some other MFE procedures [37, 42] based on moving finite element method [1] for solving the fractional PDEs.