1 Introduction

In the last decades, fractional differential equations have been extensively studied because of their powerful potential to depict many processes in science and engineering. Compared with the integer-order differential equations, the fractional differential equations can provide a much more accurate and adequate description of the physical processes involving memory and hereditary properties. Though some fractional differential equations with special form, e.g., linear equations, can be solved by analytical methods, e.g., the Laplace transform method, the Mellin transform method or the Fourier transform method, the analytical solutions of many generalized fractional differential equations (e.g., nonlinear fractional differential equations and multi-term fractional differential equations) are rather difficult to obtain. Hence, developing numerical methods is of great importance in practical applications. The specific nature of the fractional operators involves computational challenges which, if not properly addressed, may lead to unreliable or even wrong results. The numerical methods for solving fractional differential equations can be broadly divided into two classes.

  1. (a)

    Fractional differential equations with smooth solutions Unfortunately, The majority of numerical methods developed in the literature are just methods that were devised originally for standard integer-order operators then applied in a naive way to their fractional-order counterparts without a proper knowledge of the features of fractional-order problems leading unexpected results. There have been various numerical methods to solve fractional differential equations, such as finite element methods [17], finite difference methods [7, 25], and spectral methods [3, 11].

  2. (b)

    Fractional differential equations with nonsmooth solutions Solutions of fractional differential equations typically exhibit weak singularities [8]. This topic is discussed in more detail in the survey chapter [35]. This singularity is a consequence of the weakly singular behavior of the kernels of fractional integral and derivatives. From a physical perspective, its importance is related to the natural emergence of completely monotone relaxation functions in models whose dynamics is governed by these operators. It is shown in [34] that imposing excessive smoothness requirements on the solutions to a partial differential equation (e.g., for the sake of simplifying the error analysis or for obtaining a higher convergence order) has drastic implications regarding the class of admissible problems. Up to now, a few numerical methods have been proposed for fractional differential equations with non-smooth solutions, such as the use of nonuniform grids (see, e.g. [15, 44]), the nonpolynomial/singular basis (see, e.g. [2, 41]), nonsmooth transformations [43], and Lubich’s correction method (see, e.g. [45, 48]). Lubich’s method consists of adding suitable correction terms to the corresponding numerical approximation, which makes the new approximation exact for low regularity terms of the solutions while still maintaining high accuracy for high regularity terms.

Multi-term time fractional differential equations are motivated by their flexibility to describe complex multirate physical processes, see, e.g. [6, 26, 36]. They are proposed to improve the modeling accuracy in depicting the anomalous diffusion process, successfully capturing power-law frequency dependence [18], adequately modeling various types of viscoelastic damping [4], properly simulating the unsteady flow of a fractional Maxwell fluid [37] and Oldroyd-B fluid [12]. Coupled systems of fractional-order differential equations equipped with received considerable attention in anomalous diffusion [33]. To gain insights into the behavior of the solution of such models, there has been substantial interest in deriving a closed form solution. Daftardar-Gejji et al. [5] obtained the linear and non-linear diffusion-wave equations of fractional order by Adomian decomposition method. Existence, uniqueness and a priori estimates for a class of these equations were obtained by Luchko [27] based on an appropriate maximum principle and the Fourier method. Ding et al. [9] presented the analytical solutions for the multi-term time-space fractional advection–diffusion equations with mixed boundary conditions. Ming et al. [28] proposed Analytical solutions of multi-term time fractional differential equations and application to unsteady flows of generalized viscoelastic fluid. Li et al. [22] investigated the well-posedness and the long-time asymptotic behaviour for initial-boundary value problems of multi-term time-fractional diffusion equations. Using Luchko’s Theorem and the equivalent relationship between the Laplacian operator and the Riesz fractional derivative, Jiang et al. [16] proposed some new analytic techniques to solve three types of multi-term time-space Caputo–Riesz fractional advection diffusion equations with nonhomogeneous Dirichlet boundary conditions.

The analytical solutions obtained in these studies are for the linear case and involve special functions and infinite series, and thus are inconvenient for numerical evaluation. Hence, efficient and accurate numerical approaches are demanded to deal with this model, especially the nonlinear case. Dehghan et al. [7] developed high-order finite difference method and Galerkin spectral method for the numerical solution of multi-term time-fractional differential equations. Alikhanov [1] investigated the finite difference methods for the Dirichlet and Robin boundary value problems of a multi-term variable-distributed order diffusion equation. Wang and Wen [39] proposed high-order compact exponential finite difference method for the multi-term time-fractional diffusion equation, based on the L1 formula on a general nonuniform time mesh. Wei [40] proposed and analyzed a fully discrete local discontinuous Galerkin method for a class of multi-term time fractional diffusion equations. Wang et al. [38] proposed an efficient spectral Galerkin method using the \(L2-1_{\sigma }\) formula for time discretization and the Legendre–Galerkin spectral method for space discretization to solve the three-dimensional multi-term time-space fractional diffusion equation. Zaky [42] developed a Legendre spectral tau method to handle the multi-term time-fractional diffusion equations. Fu et al. [13] presented a semi-analytical boundary-only collocation technique for solving multi-term time-fractional diffusion-wave equations. Shi et al. [32] studied nonconforming quasi-Wilson finite element fully-discrete approximation for two dimensional multi-term time fractional diffusion-wave equation on regular and anisotropic meshes. Hendy [14] constructed a fully implicit difference scheme for the numerical solution of the multi-term time-space fractional advection–diffusion model.

The L1-type schemes have a wide range of applicability in solving fractional differential equations in time [29]. Most reports on L1-type methods refer to the efficiency analysis of numerical schemes for linear fractional differential equations [24], whereas only few works have discussed the stability and the convergence of L1-type schemes for nonlinear time-fractional differential equations [14, 20, 21]. These results are for the single-order fractional problems. It is observed that a direct application of the discrete fractional Grönwall inequality proposed in [24] for the analysis of nonlinear multi-term time fractional diffusion equations discretization on nonuniform graded mesh cannot be achieved, motivating us to consider this case of study.

Our aim in this paper is twofold. First, we provide a novel discrete fractional Grönwall inequality for the numerical analysis of nonlinear multi-term time fractional differential equations equations using L1-type schemes on a nonuniform graded mesh. Second, we continue our work [15, 44] and propose and analyze an efficient numerical method for the following coupled system of nonlinear multi-term time-space fractional diffusion equations:

$$\begin{aligned}&\sum _{r=1}^m q_r\frac{\partial ^{\beta _{r}}\psi _1}{\partial t^{\beta _{r}}} -\gamma \,\frac{\partial ^\alpha \psi _1}{\partial |x|^\alpha }\nonumber \\&\quad =\rho F_1(\psi _1,\psi _2)+f_1(x,t),\quad x \in \Omega ,\ t \in I, \end{aligned}$$
(1.1)
$$\begin{aligned}&\sum _{r=1}^m q_r\frac{\partial ^{\beta _{r}}\psi _2}{\partial t^{\beta _{r}}} -\gamma \,\frac{\partial ^\alpha \psi _2}{\partial |x|^\alpha }\nonumber \\&\quad =\rho F_2(\psi _1,\psi _2)+f_2(x,t),\quad x \in \Omega ,\ t \in I, \end{aligned}$$
(1.2)
$$\begin{aligned}&\psi _\mathrm {i}(x , 0) = \phi _\mathrm {i}(x), \qquad x \in \Omega , \quad \mathrm {i} \in \{1,2\}, \end{aligned}$$
(1.3)
$$\begin{aligned}&\psi _\mathrm {i} (x , t) =0, \qquad x\in \partial \Omega ,\ t \in I, \end{aligned}$$
(1.4)

where \(F_1\) and \(F_2\) are nonlinear functions, and \(\Omega =(a , b) \subset {\mathbb {R}}\) and \(I=(0,T] \subset {\mathbb {R}}\) are the space and time domains, respectively. The parameters \(\gamma ,\,\rho\) are positive constants. the parameter \(q_m\) is strictly positive. The boundary of \(\Omega\) is denoted by \(\partial \Omega\), \(\phi _{\mathrm {i}}(x)\) is a known sufficiently smooth function, and \(\frac{\partial ^{\beta _r} \psi }{\partial t ^{\beta _r}}\ (1>\beta _m>\cdots>\beta _{2}>\beta _1>0)\) represents the Caputo fractional derivative. The Caputo fractional derivative \(\frac{\partial ^{\beta _r} \psi }{\partial t ^{\beta _r}}\) is defined as [29, 30]

$$\begin{aligned} \frac{{\partial ^{\beta _r}}}{{\partial t^{\beta _r}}}f(x,t) =\frac{1}{{\Gamma \left( {1 - {\beta _r}}\right) }}\int _0^t {(t - s)^{-{\beta _r}}} \frac{{\partial f(x,s)}}{{\partial s}}\mathrm{d}s, \end{aligned}$$
(1.5)

where \(\Gamma (\cdot )\) denotes the Gamma function. The Riesz space fractional derivative of order \(\alpha\) with respect to \(x \in \Omega\), namely \(\frac{\partial ^{\alpha }}{\partial |x|^{\alpha }}\), is defined as [29, 30]

$$\begin{aligned} \frac{\partial ^{\alpha }f(x)}{\partial |x|^{\alpha }} :=c_{\alpha }\left( {}_{a}{D}_{x}^{\alpha }f(x) + {}_{x}{D}_{b}^{\alpha } f(x)\right) , \end{aligned}$$
(1.6)

\(c_{\alpha }=\frac{-1}{2\cos {\frac{\pi \alpha }{2}}}\), \({}_{a}D_{x}^{\alpha }\psi\) and \({}_{x}D_\mathrm{b}^{\alpha }\psi\) are the left- and right-Riemann–Liouville derivatives of order \(\alpha\), defined as [29, 30]

$$\begin{aligned} {}_{a}{D}_{x}^{\alpha }f(x)&= \frac{1}{\Gamma (2-\alpha )} \frac{\partial ^{2}}{\partial x^{2}}{\int _{a}^{x}}\frac{f(\xi ) \mathrm {d}\xi }{(x-\xi )^{\alpha -1}}, \end{aligned}$$
(1.7)
$$\begin{aligned} {}_{x}{D}_\mathrm{b}^{\alpha }f(x)&= \frac{1}{\Gamma (2-\alpha )} \frac{\partial ^{2}}{\partial x^{2}}\int _{x}^\mathrm{b}\frac{f(\xi ) \mathrm {d}\xi }{(\xi -x)^{\alpha -1}}. \end{aligned}$$
(1.8)

The paper is organized as follows. In Sect. 2, some definitions and lemmas on the spaces of fractional derivatives are introduced. In Sect. 3, we develop the L1 spectral Galerkin scheme for a coupled system of nonlinear multi-term time-space fractional diffusion equations. The convergence is rigorously proved in Sect. 4 by providing a generalized discrete form for the fractional Grönwall inequality which enables us to overcome the difficulties caused by the sum of Caputo time-fractional derivatives and the positivity of the reaction term over the nonuniform time mesh. In Sect. 5, the numerical experiments are shown to confirm the theoretical analysis, and the conclusions follow in Sect. 6.

2 Preliminaries

In this section, based on Ervin and Roop [10], we present some definitions and lemmas on the spaces of fractional derivatives, which are useful for the rigorous analysis of convergence.

We write \((\cdot ,\cdot )\) for the inner product on the space \(L^2(\Omega )\) with the \(L^2\)norm \(\Vert \cdot \Vert _{L^{2}({\Omega } )}\). For convenience, we denote \(\Vert \cdot \Vert _{L^{2}({\Omega } )}\) as \(\Vert \cdot \Vert\).

Definition 1

(Left fractional derivative space) For \(\eta >0\), we define the semi-norm

$$\begin{aligned} |\psi |_{J_{L}^{\eta }(\Omega )}=\left\Vert {_a D_{x}^{\eta }\psi }\right\Vert , \end{aligned}$$
(2.1)

and the norm

$$\begin{aligned} \left\Vert {\psi }\right\Vert _{J_{L}^{\eta }(\Omega )}=\left( |\psi |^{2}_{J_{L}^{\eta } (\Omega )}+\left\Vert {\psi }\right\Vert ^{2}\right) ^{1/2}, \end{aligned}$$
(2.2)

and denote \(J_{L}^{\eta }({\Omega })\) and \(J_{L,0}^{\eta }({\Omega })\) as the closure of \(C^{\infty }(\Omega )\) and \(C_0^{\infty }(\Omega )\) with respect to \(\left\Vert {\cdot }\right\Vert _{J_{L}^{\eta }(\Omega )}\), respectively.

Definition 2

(Right fractional space) For \(\eta >0\), we define the semi-norm

$$\begin{aligned} |\psi |_{J_{R}^{\eta }(\Omega )}=\left\Vert {_x D_{b}^{\eta }\psi }\right\Vert , \end{aligned}$$
(2.3)

and the norm

$$\begin{aligned} \left\Vert {\psi }\right\Vert _{J_{R}^{\eta }(\Omega )}=\left( |\psi |^{2}_{J_{R}^{\eta } (\Omega )}+\left\Vert {\psi }\right\Vert ^{2}\right) ^{1/2}, \end{aligned}$$
(2.4)

and denote \(J_{R}^{\eta }\) and \(J_{R,0}^{\eta }\) as the closure of \(C^{\infty }(\Omega )\) and \(C_0^{\infty }(\Omega )\) with respect to \(\left\Vert {\cdot }\right\Vert _{J_{R}^{\eta }(\Omega )}\), respectively.

Definition 3

(Symmetric fractional derivative space) Let \(\eta >0\) and \(\eta \ne n-\frac{1}{2},\ n\in {\mathbb {N}}\), we define the semi-norm

$$\begin{aligned} |\psi |_{J_S^{\eta }({\Omega })}= |({}_{a} {{\mathcal {D}}}_{x}^{\eta }\psi , {}_{x}{{\mathcal {D}}}_{b}^{\eta }\psi )|) |^{1/2}, \end{aligned}$$
(2.5)

and the norm

$$\begin{aligned} \Vert \psi \Vert _{J_S^{\eta }({\Omega })}=\left( \Vert \psi \Vert ^2 +|\psi |_{J_S^{\eta }({\Omega })}^2\right) ^{1/2}, \end{aligned}$$
(2.6)

and denote \(J_{S}^{\eta }({\Omega })\) and \(J_{S,0}^{\eta }({\Omega })\) as the closure of \(C^{\infty }({\Omega })\) and \(C_{0}^{\infty }({\Omega })\) with respect to \(\Vert \cdot \Vert _{J_{S}^{\eta }({\Omega })}\), respectively.

Definition 4

(Fractional Sobolev space) For \(\eta >0\), we define the semi-norm

$$\begin{aligned} |\psi |_{H^{\eta }({\Omega })} =\Vert |\xi |^{\eta }{\mathcal {F}}(\hat{\psi })(\xi ) \Vert _{L^2({\mathbb {R}})}, \end{aligned}$$
(2.7)

and the norm

$$\begin{aligned} \Vert \psi \Vert _{H^{\eta }({\Omega })} =\left( \Vert \psi \Vert ^2 +|\psi |_{H^{\eta }({\Omega })}^2\right) ^{\frac{1}{2}}, \end{aligned}$$
(2.8)

and denote \(H^\eta (\Omega )\) and \(H_0^\eta (\Omega )\) as the closure of \(C^{\infty }({\Omega })\) and \(C_{0}^{\infty }({\Omega })\) with respect to \(\Vert \cdot \Vert _{H^{\eta }({\Omega })}\), respectively. Here, \({\mathcal {F}}(\hat{\psi })(\xi )\) is the Fourier transformation of the function \(\hat{\psi }\), and \(\hat{\psi }\) is the zero extension of \(\psi\) outside \(\Omega\).

Lemma 1

( [10]) The spaces \(J_{L}^{\eta },\ J_{R}^{\eta },\ J_{s}^{\eta }\) and \(H^{\eta }\) are equivalent with equivalent semi-norms and norms if \(\eta \ne n-\frac{1}{2},\ n\in {\mathbb {N}}\).

Lemma 2

(Adjoint property) Let \(1<\eta <2,\) then for any \(\psi \in H_{0}^{\eta }(\Omega )\) and \(\nu \in H_{0}^{\eta /2}(\Omega )\), we get

$$\begin{aligned} \left( {}_{a}D_{x}^{\eta }\psi ,\nu \right)&=\left( {}_{a} D_{x}^{\eta /2} \psi ,{}_{x} D_{b}^{\eta /2}\nu \right) , \quad \left( {}_{x}D_{b}^{\eta } \psi ,\nu \right) \nonumber \\&=\left( {}_{x} D_{b}^{\eta /2}\psi ,{}_{a} D_{x}^{\eta /2}\nu \right) . \end{aligned}$$
(2.9)

The following lemma and remark summarize the properties of the interpolation operator \(I _N\).

Lemma 3

(see [31]) Let \(s \ge 1\). If \(\psi _j \in H ^s (\Omega )\) then there exists a constant \(C > 0\) independent of N, such that \(\left\Vert {\psi _j - I _N \psi _j}\right\Vert _l \le C N ^{l - s} \left\Vert {\psi _j}\right\Vert _s\), for any \(0 \le l \le 1\).

Remark 1

A smooth solution of a fractional differential equation does not mean a smooth source term and vice versa. Therefore, the regularity order s of the solution \(\psi _i\) is not the same as the regularity order r of the source term \(f_j\), i.e \(\left\Vert {I _N f_j - f_j}\right\Vert \le C N^{-r}\left\Vert {\psi _j}\right\Vert _{r}, \forall f_j \in H ^r (\Omega ).\)

Lemma 4

(see [10]) Let \(\eta >0\) and \(u \in J _{L , 0} ^\eta (\Omega ) \cap J _{R , 0} ^\eta (\Omega )\). Then

$$\begin{aligned} \left( {} _a D _x ^\eta u , {} _x D _b ^\eta u \right)&= \cos (\pi \eta ) \left\Vert {{} _{- \infty } D _x ^\eta \hat{u}}\right\Vert ^2 _{L ^2 ({\mathbb {R}})} \nonumber \\&= \cos (\pi \eta ) \left\Vert {{} _x D _\infty ^\eta \hat{u}}\right\Vert ^2 _{L ^2 ({\mathbb {R}})}. \end{aligned}$$
(2.10)

Let \(P_n^{(\alpha ,\beta )}(x)\) be the Jacobi polynomial of degree n with \(\alpha ,\beta >-1\) defined on \(\Lambda =(-1,1)\). The Jacobi polynomials are defined by the three-term recurrence (cf. [31]):

$$\begin{aligned}&P_{n+1}^{(\alpha ,\beta )}(x)=\left( a_{n}^{(\alpha ,\beta )}x -b_{n}^{(\alpha ,\beta )} \right) P_{n}^{(\alpha ,\beta )}(x) -c_{n}^{(\alpha ,\beta )}P_{n-1}^{(\alpha ,\beta )}(x),\;\; n\ge 1,\nonumber \\&P_0^{(\alpha ,\beta )}(x)=1,\;\;\; P_1^{(\alpha ,\beta )}(x)=\frac{1}{2} (\alpha +\beta +2)x+\frac{1}{2}(\alpha -\beta ), \end{aligned}$$
(2.11)

where

$$\begin{aligned} a_{n}^{(\alpha ,\beta )}&=\frac{(2n+\alpha +\beta +1)(2n+\alpha +\beta +2)}{2(n+1)(n+\alpha +\beta +1)}, \end{aligned}$$
(2.12)
$$\begin{aligned} b_{n}^{(\alpha ,\beta )}&=\frac{(\beta ^2-\alpha ^2)(2n+\alpha +\beta +1)}{2(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )}, \end{aligned}$$
(2.13)
$$\begin{aligned} c_{n}^{(\alpha ,\beta )}&=\frac{(n+\alpha )(n+\beta )(2n+\alpha +\beta +2)}{(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )}. \end{aligned}$$
(2.14)

We have

$$\begin{aligned} P_{n}^{(\alpha ,\beta )}(-1)=(-1)^nP_{n}^{(\beta ,\alpha )}(1), \,P_{n}^{(\alpha ,\beta )} (1)=\frac{\Gamma (n+\alpha +1)}{n!\Gamma (\alpha +1)}. \end{aligned}$$
(2.15)

For \(\alpha ,\beta >-1\), the Jacobi polynomials are orthogonal with respect to the Jacobi weight function: \(\omega ^{(\alpha ,\beta )}(x) = (1-x)^{\alpha }(1+x)^{\beta }\), namely,

$$\begin{aligned} \int _{-1}^1 {P}_n^{(\alpha ,\beta )}(x) {P}_{m}^{(\alpha ,\beta )} (x) \omega ^{(\alpha ,\beta )}(x) \, {\text {d}}x =\gamma _n^{(\alpha ,\beta )}\delta _{mn}, \end{aligned}$$
(2.16)

where \(\delta _{mn}\) is the Kronecker symbol, and

$$\begin{aligned} \gamma _n^{(\alpha ,\beta )} =\frac{2^{\alpha +\beta +1} \Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{(2n+\alpha +\beta +1) n!\,\Gamma (n+\alpha +\beta +1)}. \end{aligned}$$
(2.17)

In particular, the Legendre polynomial is defined as \(L _i (x) = J ^{0 , 0} _i (x)\). Let us denote by \(I_N\) the Legendre–Gauss–Lobatto interpolation operator \(I_N :C(\bar{\Omega }) \rightarrow {\mathcal {W}} _N\) as \(\psi (x_k ) = I_N \psi (x_k ) \in {\mathcal {P}} _N,\quad k=0,1,\ldots ,N\).

In what follows, we shall use the Legendre–Gauss–Lobatto interpolation and quadrature. Let \(\{x_j\}_{j=0}^N\) be the zeros of \((1-x^2)L'_i (x)\), and let \(\{\omega _j\}_{j=0}^N\) be the corresponding weights (cf. [31]). Then, the Legendre–Gauss–Lobatto quadrature has the exactness

$$\begin{aligned} \int ^1_{-1}f(x ) {\text {d}}x = \sum _{j=0}^Nf(x _j) {\omega }_j, \quad \forall f \in {{\mathcal {P}}}_{2N-1}, \end{aligned}$$
(2.18)

where \({{\mathcal {P}}}_N\) denotes the set of all polynomials of degree less than or equal to N.

3 The numerical algorithm

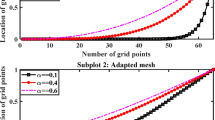
In this section, we shall develop a robust scheme for the problem (1.1)–(1.4) with a nonsmooth solution in time direction. The scheme employs the Legendre–Galerkin spectral method in space and an L1-type approximation with graded mesh for the time-fractional derivative. In spite of the assumption that the initial conditions and source terms are smooth, the solutions of the fractional differential equation can be nonsmooth and even have a strong singularity at \(t = 0\). Hence, the rate of convergence may be deteriorate significantly. To make up for the lost of accuracy near \(t = 0\), we refer to the nonuniform L1 approach in   [23].

Definition 5

For a positive integer M, let \(\left\{ {t_{i}=T(i/M)^{\gamma }} \right\} _{i=0}^M\) be the graded mesh with a grading parameter \(\gamma > 1\) and \(\tau _i:=t_i-t_{i-1}\) for \(i=1,\ldots , M\). Let \(\{ {\psi ^n } \} _{n = 0} ^M\) be a sequence of real functions defined on \(\Omega\). The nonuniform discrete time-fractional difference Caputo operator \(\Delta _M^\beta\) is given by

$$\begin{aligned}&\Delta _M ^\beta \psi _{j}^n = \sum _{i = 1} ^n a_{n - i}^{n,\beta } \delta _t \psi _{j}^i = \sum _{i = 0} ^n {b _{n - i}^{n,\beta } \psi _{j}^i} , \nonumber \\&\qquad \forall n = 1 , \ldots , M, \end{aligned}$$
(3.1)

where \(a_{n - i}^{n,\beta }=\frac{\omega _{2-\beta }(t_n-t_{i-1}) -\omega _{2-\beta }(t_n-t_i)}{\tau _{i}},\ 1\le i\le n\), \(\omega _{\beta }(t)=\frac{t^{\beta -1}}{\Gamma (\beta )},\,t>0\), \(b_{0}^{n,\beta }= a_0^{n,\beta }\), \(b_n ^{n,\beta }= - a_{n - 1}^{n,\beta }\), \(b_{n - i} ^{n,\beta }= a_{n - i}^{n,\beta } - a_{n - i - 1}^{n,\beta }\), \(\forall i = 1 , \ldots , n - 1\) and \(\delta _t \psi _j ^i = \psi _j ^i - \psi _j ^{i - 1}.\)

The integral mean-value theorem says that the nonuniform L1 coefficient (3.1) satisfies

$$\begin{aligned} a_{n - i+1}^{n,\beta }<\omega _{1-\beta }(t_n-t_{i-1}) < a_{n - i}^{n,\beta },\quad 1\le i\le n. \end{aligned}$$
(3.2)

Let \(\psi _j^n\) be the discrete approximation of solution \(\psi _{j}(x,t_n) \, \forall j \in \{1,2\},\) for \(x\in \Omega\). At each time level n, the fractional temporal component of (1.1)–eqrefusl2v can be approximated using (3.1), i.e.,

$$\begin{aligned}&\sum _{r=0}^m q_{r}\Delta _M ^{\beta _r} \psi _{1}^n - \gamma \,\frac{\partial ^\alpha \psi _{1}^n}{\partial |x|^\alpha } =\rho \,F_1(\psi _{1}^n,\psi _{2}^n)+f_{1}^n,\nonumber \\&\sum _{r=0}^m q_{r}\Delta _M ^{\beta _r} \psi _{2}^n - \gamma \,\frac{\partial ^\alpha \psi _{2}^n}{\partial |x|^\alpha } =\rho \,F_2(\psi _{1}^n,\psi _{2}^n)+f_{2}^n. \end{aligned}$$
(3.3)

The approximation space \({\mathcal {W}}_N\) is defined as

$$\begin{aligned} {\mathcal {W}}_N = {\mathcal {P}} _N (\Omega ) \cap H_0^{1} (\Omega ). \end{aligned}$$

Then the L1/spectral Galerkin scheme of (1.1)–(1.4) can be expressed as follows: for \(n = 1,\, 2,\ldots ,M\), \(j=1,2,\) find \(\psi _{j,N}^n \in {\mathcal {W}}_N\) such that

$$\begin{aligned}&\sum _{r=0}^m q_{r}a_{0}^{n,\beta _r} \left( {\psi _{1,N}^n ,v_N} \right) -\gamma \left( {\frac{{\partial ^\alpha \psi _{1,N}^n }}{{\partial \left| x \right| ^\alpha }} ,v_N} \right) \nonumber \\&\quad =\sum _{r=0}^m q_{r}a_{n-1}^{n,\beta _r} \left( {\psi _{1,N}^0 ,v_N} \right) \nonumber \\&\qquad -\sum _{r=0}^m q_{r}\sum _{i=1}^{n-1}b_{n-i}^{n,\beta _r} \left( {\psi _{1,N}^i ,v_N} \right) \nonumber \\&\qquad +\rho \left( I_N(F_{1}(\psi _{1,N}^n, \psi _{2,N}^n)),v_N \right) +(I_Nf_{1}^n,v_N),\nonumber \\&\sum _{r=0}^m q_{r}a_{0}^{n,\beta _r} \left( {\psi _{2,N}^n ,v_N} \right) -\gamma \left( {\frac{{\partial ^\alpha \psi _{2,N}^n }}{{\partial \left| x \right| ^\alpha }} ,v_N} \right) \nonumber \\&\quad =\sum _{r=0}^m q_{r}a_{n-1}^{n,\beta _r} \left( {\psi _{2,N}^0 ,v_N} \right) \nonumber \\&\qquad -\sum _{r=0}^m q_{r}\sum _{i=1}^{n-1}b_{n-i}^{n,\beta _r} \left( {\psi _{2,N}^i ,v_N} \right) \nonumber \\&\qquad +\rho \left( I_N(F_{2}\left( \psi _{1,N}^n, \psi _{2,N}^n)\right) ,v_N \right) +\left( I_Nf_{2}^n,v_N\right) ,\nonumber \\&\psi _{1,N}^0 = P_N\phi _1,\ \psi _{2,N}^0 = P_N\phi _2, \nonumber \\&n=1,\dots ,M,\ \quad v_N \in {\mathcal {W}}^0 _N, \end{aligned}$$
(3.4)

where \(P_N\) is an appropriate projection operator, its related properties are given in the following theorem.

Lemma 5

(see [47]) Let \(\epsilon\) and s be real numbers satisfying \(s > \frac{\alpha }{2}\). For any function \(\psi _j \in H _0 ^{\frac{\alpha }{2}} (\Omega ) \cap H ^s (\Omega )\), there exists a projector operator \(P _N\) such that the following error estimates hold:

$$\begin{aligned} \left\Vert {\psi _j - P _N \psi _j}\right\Vert \le C N ^{- s} \left\Vert {\psi _j}\right\Vert _s , \quad \text {if } \alpha \ne \tfrac{3}{2}, \end{aligned}$$
(3.5)

and

$$\begin{aligned} \left\Vert {\psi _j - P _N \psi _j}\right\Vert \le C N ^{\epsilon - s} \left\Vert {\psi _j}\right\Vert _s, \quad \text {if } \alpha = \tfrac{3}{2} \, \& \, 0< \epsilon < \tfrac{1}{2}. \end{aligned}$$
(3.6)

The function space \({\mathcal {W}}_N\) can be expressed as

$$\begin{aligned} {\mathcal {W}}_N =\text {span} \left\{ {\varphi _n (x), n = 0,1,\ldots ,N - 2} \right\} , \end{aligned}$$
(3.7)

in which \(\varphi _n (x)\) is defined as follows:

$$\begin{aligned} \varphi _n (x)= & {} L_n (\hat{x}) - L_{n + 2} (\hat{x}), \ \hat{x} \in [ - 1,1], x \nonumber \\= & {} \frac{{(b - a)\hat{x} + a + b}}{2} \in [a,b], \end{aligned}$$
(3.8)

where \(L_n (\hat{x})\) is the Legendre polynomial of order n. We expand the approximate solution as

$$\begin{aligned} \psi _{j,N}^n = \sum \limits _{i = 0}^{N - 2} {\hat{\psi }_{j,i}^n \varphi _i (x)},\ j \in \{1,2\}, \end{aligned}$$
(3.9)

where \(\hat{\psi }_{j,i}^n\) are unknown coefficients. Plugging the above expression into (3.4) and taking \(v_N = \varphi _k ,\ 0 \le k \le N - 2\), we obtain the following matrix form representation using Lemma 2:

$$\begin{aligned}&\left( \sum _{r=0}^m q_{r} a_0^{n,\beta _r} \bar{M} - \gamma c_\alpha \left( {S + S^\mathrm{T} } \right) \right) \Psi _j^n \nonumber \\&\quad =K_j^{n - 1} +\rho H_j^n+F_j^n, \quad j \in \{1,2\}, \end{aligned}$$
(3.10)

where

$$\begin{aligned} K_j ^{n - 1}&= - \sum _{r=0}^m q_{r}\sum _{q = 0} ^{n - 1} {b^{n,\beta _r} _{n - q}\bar{M} \Psi _j^q}\nonumber \\ h_{j,i}^n&= \int _\Omega {\varphi _i (x)I_NF_j\left( \psi _{1,N}^n,\psi _{2,N}^n\right) \mathrm{d}x},\nonumber \\ s_{ij}&= \int _\Omega {{}_aD_x^{\frac{\alpha }{2}} \varphi _i (x){}_xD_b^{\frac{\alpha }{2}} \varphi _j (x)\mathrm{d}x},\nonumber \\ S&= \left( {s_{ij} } \right) _{i,j = 0}^{N - 2} ,\nonumber \\ m_{ij}&= \int _\Omega {\varphi _i (x)\varphi _j (x)\mathrm{d}x} ,\nonumber \\ \bar{M}&= \left( {m_{ij} } \right) _{i,j = 0}^{N - 2} ,\nonumber \\ H_j^n&= \left( {h_{j,0}^n ,h_{j,1}^n , \ldots ,h_{j,N - 2}^n } \right) , \nonumber \\ \Psi _j^n&= \left( {\hat{\psi } _{j,0}^n ,\hat{\psi } _{j,1}^n , \ldots ,\hat{\psi } _{j,N - 2}^n } \right) ^\mathrm{T},\nonumber \\ f_{i,j}^n&=\int _{\Omega }\varphi _i (x)I_Nf_j^n\mathrm{d}x,\nonumber \\ F_j^n&=\left( f_{0,j}^n,f_{1,j}^n,\ldots ,f_{{N-2},j}^n \right) ^\mathrm{T}. \end{aligned}$$
(3.11)

Lemma 6

( [31, 46]) The elements of the stiffness matrix S are given as

$$\begin{aligned} s_{ij} = a_i^j - a_i^{j + 2} - a_{i + 2}^j + a_{i + 2}^{j + 2}, \quad \forall i,j=0,1,\dots ,N-2, \end{aligned}$$
(3.12)

where

$$\begin{aligned} a_i^j&= \int _\Lambda {{}_aD_x^{\frac{\alpha }{2}} L_i (\hat{x}){}_xD_b^{\frac{\alpha }{2}} L_j (\hat{x})\mathrm{d}x}\nonumber \\&=\left( {\frac{{b - a}}{2}} \right) ^{1 - \alpha } \frac{{\Gamma (i + 1)\Gamma (j + 1)}}{{\Gamma \left( i-\frac{\alpha }{2} + 1\right) \Gamma \left( j - \frac{\alpha }{2} + 1\right) }}\nonumber \\&\quad \times \sum \limits _{r = 0}^N \varpi _r^{ - \frac{\alpha }{2}, -\frac{\alpha }{2}} P_i^{\left( \frac{\alpha }{2}, - \frac{\alpha }{2}\right) }\nonumber \\&\quad \left( x_r^{ - \frac{\alpha }{2}, - \frac{\alpha }{2}} \right) P_j^{\left( - \frac{\alpha }{2},\frac{\alpha }{2}\right) } \left( x_r^{ - \frac{\alpha }{2}, - \frac{\alpha }{2}} \right) , \end{aligned}$$
(3.13)

and \(\left\{ {\varpi _r^{ - \frac{\alpha }{2}, - \frac{\alpha }{2}}, x _r^{ - \frac{\alpha }{2}, - \frac{\alpha }{2}} } \right\} _{i =0}^N\) are the set of Jacobi–Gauss weights and nodes corresponding to the Jacobi parameters \(-\frac{\alpha }{2}, - \frac{\alpha }{2}\). The mass matrix \(\bar{M}\) is symmetric whose nonzero elements are

$$\begin{aligned} m_{ij} = m_{ji} = \left\{ \begin{array}{l} \frac{b-a}{{2j + 1}} + \frac{b-a}{{2j + 5}},\quad i = j, \\ - \frac{b-a}{{2j + 5}},\quad \quad i = j + 2. \\ \end{array} \right. \end{aligned}$$
(3.14)

Noticing that \(H_r^n = H_r^{n } (\psi _{1,N}^n,\psi _{2,N}^n )\), we can solve the nonlinear system (3.10) by the following iteration algorithm:

figure a

4 Theoretical analysis

The present section is devoted to present sharp error estimates in the following theorem for the nonuniform L1-Galerkin spectral scheme (3.4). In the sequel, C and \(C_{\psi }\) will denote generic positive constants independent of M, N and n, and may be different under different circumstances. We define the following space of functions:

$$\begin{aligned}&C^{\beta }\left( [0,T];X\right) \\&\quad :=\left\{ f \in C^{\beta }\left( [0,T];X\right) : \underset{0<\tau <T}{\sup }\right. \\&\qquad \quad \left. \frac{\left\Vert {u(\cdot ,t+\tau ) -u(\cdot ,t)}\right\Vert _{C\left( [0,T-\tau ];X\right) }}{\tau ^{\beta }}\le \infty \right\} , \end{aligned}$$

and fix the following notation

$$\begin{aligned}&A(\psi _j,w)\nonumber \\&\quad =-\gamma c_{\alpha }\left [ \left( {}_{a}D_{x}^{\alpha /2} \psi _j,{}_{x}D_{b}^{\alpha /2}w\right) +\left( {}_{x}D_{b}^{\alpha /2} \psi _j,{}_{a}D_{x}^{\alpha /2}w\right) \right] . \end{aligned}$$
(4.1)

Define the orthogonal projection operator \(P_N:H_{0}^{\frac{\alpha }{2}}(\Omega )\rightarrow {{\mathcal {W}}_N}\) such that

$$\begin{aligned} A(\psi _j-P_{N}\psi _j,w)=0,\ \forall w \in {\mathcal {W}}_N. \end{aligned}$$
(4.2)

For convenience of theoretical analysis, we give the following semi-norm and norm, respectively,

$$\begin{aligned}&|\psi _j|_{\alpha /2}:=A(\psi _j,\psi _j)^{1/2},\nonumber \\&\left\Vert {\psi _j}\right\Vert _{\alpha /2}:=\left( \left\Vert {\psi _j}\right\Vert ^2+|\psi _j|_{\alpha /2}^2\right) ^{1/2}. \end{aligned}$$
(4.3)

The following two lemmas is deduced from [19] and used to obtain the truncation error for the multi-term fractional operator approximation

Lemma 7

Let \(\left\{ {t_{n}=T(n/M)^{\gamma }} \right\} _{n=0}^M\) be the graded mesh with a grading parameter \(\gamma \ge 1\). Then for \(\psi _j^n,\quad j \in \{1,2\},\) satisfies (1.1)–(1.4), the the truncating error in time can be represented by

$$\begin{aligned} \left| R_{t}^{n,\beta _{r}}\right|&=\left| \frac{\partial ^{\beta _{r}}}{\partial t ^{\beta _{r}}}\psi _j(t_{n})-\Delta _{M}^{\beta _r}\psi (t_{n})\right| \nonumber \\&\le t_{n}^{-\beta _{r}}\left( (\tau _1/t_n)f^{1,\beta _r} +\underset{p=2,\ldots ,n}{\max } f^{p,\beta _r}\right) ,\nonumber \\&\qquad \qquad \forall n=1,\dots ,M,\quad r=1,\ldots ,m, \end{aligned}$$
(4.4)

where

$$\begin{aligned} f^{1,\beta _r}&:=\tau _1^{\beta _r}\underset{s\in (0,t_1)}{\sup }\nonumber \\&\quad \left( s^{1-\beta _r}\left| \delta _t(\psi _j(t_1))-\partial _{s}\psi _j(s)\right| \right) ,\nonumber \\ f^{p,\beta _r}&:=\tau _j^{2-\beta _r}t_{p}^{\beta _r} \underset{s\in (t_{p-1},t_p)}{\sup }\nonumber \\&\quad \left( s^{1-\beta _r}\left| \partial ^{2}_{s}\psi _j(s)\right| \right) ,\quad \forall p\ge 2. \end{aligned}$$
(4.5)

Lemma 8

( [19]) Suppose that \(|\partial _{t}^l\psi _j(t)| \le 1+t^{\beta _{m}-l},\) for \(l=1,2\) and \(t \in (0,T],\) then

$$\begin{aligned} \left| R_{t}^{n,\beta _r}\right|&\le t_{n}^{-\beta _{m}}\left( (\tau _1/t_n) f^{1,\beta _m} +\underset{p=2,\ldots ,n}{\max }f^{p,\beta _1}\right) \nonumber \\&\le t_n^{-\beta _m}M^{-\min \{\gamma \beta _{m},2-\beta _m\}},\nonumber \\&\qquad \forall n=1,\dots ,M, \end{aligned}$$
(4.6)

and the consistency error for the multi term fractional derivative in time given as

$$\begin{aligned}&\left| R_{t}^n\right| =\sum _{r=1}^m q_r \left| R_{t}^{n,\beta _r}\right| \le \mathbf {c}t_n^{-\beta _m}M^{-\min \{\gamma \beta _{m},2-\beta _m\}},\nonumber \\&\mathbf {c}=\sum _{r=1}^m q_r,\quad \forall n=1,\ldots ,M. \end{aligned}$$
(4.7)

Now, the following lemma is devoted to introduce a proper discrete fractional Grönwall inequality.

Lemma 9

(Nonuniform discrete fractional Grönwall inequality [23, 24]) For any finite time \(t_{M}=T>0,\) and a given nonnegative sequence \((\lambda _{l})_{l=0}^{M-1}\), assume that there exists a constant \(\lambda ,\) independent of time steps, such that \(\lambda \ge \sum _{l=0}^{M-1}\lambda _{l}\) and let \(\{ \nu ^n \} _{n = 1} ^M\) and \(\{\zeta ^n, g^n \} _{n = 1} ^M\) be sequences of non-negative numbers satisfying

$$\begin{aligned}&\Delta _M^\beta (\nu ^n)^2 \le \sum _{l=1}^n\lambda _{n-l} (\nu ^l)^2 + \nu ^n (\zeta ^n+ g^n), \nonumber \\&\qquad \forall \,n = 1 , \ldots , M. \end{aligned}$$
(4.8)

If the time grids satisfy

$$\begin{aligned} \tau _{i-1}\le \tau _{i},\quad 2\le i \le M, \end{aligned}$$
(4.9)

then with the maximum time step

$$\begin{aligned} \tau _{M} \le \root \beta \of {\frac{1}{2\Gamma (2-\beta )\lambda }}, \end{aligned}$$

the following inequality holds:

$$\begin{aligned} \nu ^n&\le 2 \left( \nu ^0 +\max _{1 \le j \le n} \sum _{l=1}^j P_{j-l}^{(j)} \zeta ^l\right. \nonumber \\&\quad \left. +\nu _{1+\beta }(t_n)\max _{1 \le j \le n}g^j\right) E _\beta (2 \lambda t _n ^\beta ),\nonumber \\&\qquad \forall 1 \le n \le M, \end{aligned}$$
(4.10)

where \(P_{n-j}^{(n)}\) is the discrete convolution kernel defined in [23] and \(E _\beta (t)\) is the Mittag-Leffler function. Moreover, the convolution summation \(\sum _{l=1}^j P_{j-l}^{(j)}\zeta ^l\) in (4.10) is meaningful since it can be bounded by \(\omega _{1+\beta }(t_j)\max _{1 \le l \le j}\zeta ^l\).

Remark 2

The boundedness estimate (4.10) is also valid if the condition (4.8) is replaced by

$$\begin{aligned} \Delta _M^\beta \nu ^n \le \sum _{l=1}^n\lambda _{n-l}\nu ^l +\zeta ^n+ g^n, \qquad \forall \,n = 1 , \ldots , M. \end{aligned}$$

In the following lemma, we clarify how to extend the Grönwall Lemma 9 for the multi-term fractional operators.

Theorem 1

For any time \(\{t_{M}=T>0\},\) and a given non-negative constant \(\lambda\). Suppose that the grid function \(\{\nu ^n|n\ge 0\},\) such that \(\nu ^0\ge 0,\) satisfies

$$\begin{aligned} \sum _{r=1}^m q_r \Delta _{M}^{\beta _{r}}\nu ^{k}\le \lambda \nu ^{k} +(\zeta ^k+\eta ^k),\quad k\ge 1, \end{aligned}$$
(4.11)

where \(\Delta _{M}^{\beta _{r}}\) is the fractional difference operator defined in (3.1), \(q_r>0,\) and \(\{\zeta ^k,\eta ^k,\, 1\le k\le M\},\) are non-negative sequences. If the time grid fulfills \(\tau _{k-1}\le \tau _k,\, 2\le k \le M,\) with the maximum time-step restriction

$$\begin{aligned} \tau _{M} \le \root \beta _m \of {\frac{q_m}{2\Gamma (2-\beta _m)\lambda }}, \end{aligned}$$

it holds that

$$\begin{aligned} \nu ^k \le \frac{2}{q_m}\omega _{1+\beta _{m}}(t_k) \left( \sum _{l=1}^k(\zeta ^l+\eta ^l)+\nu ^0 W\right) E _{\beta _{m}} \left( 2 \frac{\lambda }{q_m} t _k ^{\beta _m}\right) , \, \forall 1 \le k \le M. \end{aligned}$$
(4.12)

Proof

Multiply both sides of (4.11) by \(\tau _M\) and summing over k from \(1 \rightarrow j\) for both sides of (4.11), we conclude

$$\begin{aligned}&\tau _M \sum _{r=1}^m q_r \sum _{k=1}^{j}\sum _{s = 1}^k a_{k - s}^{k,\beta _{r}} \left( \nu ^s-\nu ^{s-1}\right) \nonumber \\&\quad \le \lambda \tau _M \sum _{k=1}^{j}\nu ^{k}+\tau _M \sum _{k=1}^{j}(\zeta ^k+\eta ^k),\quad k\ge 1. \end{aligned}$$
(4.13)

Since

$$\begin{aligned}&\tau _M \sum _{k=1}^{j}\sum _{s = 1} ^k a_{k - s}^{k,\beta _r} \left( \nu ^s-\nu ^{s-1}\right) \nonumber \\&\quad = \tau _M\sum _{s=1}^{j}\left( \nu ^s-\nu ^{s-1}\right) \sum _{k=s}^{j}a_{k - s}^{k,\beta _r} \nonumber \\&\quad =\tau _M\sum _{s=1}^{j}\nu ^s\sum _{k=s}^{j}a_{k - s}^{k,\beta _r} -\tau _M\sum _{s=1}^{j}\nu ^{s-1}\sum _{k=s}^{j}a_{k - s}^{k,\beta _r} \nonumber \\&\quad =\tau _M\sum _{s=2}^{j+1}\nu ^{s-1}\sum _{k=s-1}^{j}a_{k-s+1}^{k,\beta _r}\nonumber \\&\qquad -\tau _M\sum _{s=2}^{j}\nu ^{s-1}\sum _{k=s}^{j}a_{k - s}^{k,\beta _r}-\tau _M\nu ^0 \sum _{k=1}^{j}a_{k - 1}^{k,\beta _r}\nonumber \\&\quad =\tau _M\nu ^j a_{0}^{j,\beta _r}-\tau _M\nu ^0 \sum _{k=1}^{j}a_{k - 1}^{k,\beta _r}\nonumber \\&\qquad +\tau _M\sum _{s=2}^{j}\nu ^{s-1}\left [ \sum _{k=s-1}^{j}a_{k-s+1}^{k,\beta _r} -\sum _{k=s}^{j}a_{k-s+1}^{k,\beta _r} \right] \nonumber \\&\quad =\tau _M\sum _{s=1}^j a_{j-s}^{j,\beta _r}\,\nu ^s -\tau _M\nu ^0\sum _{k=1}^{j}a_{k-1}^{k,\beta _r}, \end{aligned}$$
(4.14)

then

$$\begin{aligned}&\tau _M\sum _{r=1}^m q_r \sum _{k=1}^{j} \sum _{s = 1} ^k a_{k - s}^{k,\beta _{r}} \left( \nu ^s-\nu ^{s-1}\right) \nonumber \\&\quad =\tau _M\sum _{r=1}^m q_r\sum _{s=1}^j a_{j-s}^{j,\beta _r}\,\nu ^s\nonumber \\&\qquad -\tau _M\nu ^0\sum _{r=1}^m q_r\sum _{k=1}^{j}a_{k-1}^{k,\beta _r}. \end{aligned}$$
(4.15)

Denote

$$\begin{aligned} \sum _{r=1}^m q_r\sum _{k=1}^{j}a_{k-1}^{k,\beta _r}:=W>0, \end{aligned}$$

then according to (4.13) and (4.15), we deduce

$$\begin{aligned}&\tau _M\sum _{r=1}^m q_r\sum _{s=1}^j a_{j-s}^{j,\beta _r}\,\nu ^s\nonumber \\&\quad \le \lambda \tau _M \sum _{k=1}^{j}\nu ^{k}\nonumber \\&\qquad +\tau _M\sum _{k=1}^{j}(\zeta ^k+\eta ^k)+\tau _M\nu _0 W,\quad k\ge 1. \end{aligned}$$
(4.16)

Assume that

$$\begin{aligned} \tau _M\sum _{k=1}^j\nu ^k=y^j,\quad y^0=0 \end{aligned}$$

then

$$\begin{aligned} \frac{y^k-y^{k-1}}{\tau _M}=\nu ^k\ge 0,\quad k\ge 1. \end{aligned}$$

According to that, (4.16) can have the following form:

$$\begin{aligned}&\sum _{r=1}^m q_r\sum _{s=1}^j a_{j-s}^{j,\beta _r}\,\left( y^s-y^{s-1}\right) \nonumber \\&\quad =\sum _{r=1}^m q_r\Delta _{M}^{\beta _{r}}y^j\le \lambda y^{j}\nonumber \\&\qquad +\tau _M\sum _{k=1}^j(\zeta ^k+\eta ^k)+\tau _M\nu _0 W. \end{aligned}$$
(4.17)

Now, as

$$\begin{aligned} (y^s-y^{s-1})\ge 0, \end{aligned}$$

after using the assumption of the positivity of \(q_m\), we get

$$\begin{aligned}&\Delta _{M}^{\beta _{m}}y^j\nonumber \\&\quad \le \frac{1}{q_m}\left [ \lambda y^{j}+\tau _M\sum _{k=1}^j (\zeta ^k+\eta ^k)+\tau _M\nu _0 W\right] ,\nonumber \\&\qquad \quad 1\le j \le M. \end{aligned}$$
(4.18)

Now, applying Lemma 9, we get

$$\begin{aligned} y^j&=\tau _M\sum _{k=1}^j\nu ^k\nonumber \\&\le \frac{2\tau _M}{q_m}\omega _{1+\beta _{m}}(t_j)\nonumber \\&\quad \left( \sum _{k=1}^j(\zeta ^k+\eta ^k)+\nu _0 W\right) E _{\beta _{m}} \left( 2 \frac{\lambda }{q_m} t _j ^{\beta _m}\right) , \end{aligned}$$
(4.19)

then the proof is fulfilled. \(\square\)

The following theorem is devoted to study the convergence analysis.

Theorem 2

Let \(\{\psi _1,\psi _2\}\) and \(\{\psi _{1,N}^n,\psi _{2,N}^n\}\) be solutions of (1.1)–(1.4) and (3.4), and \(\psi _i \in C^{\beta }\left( [0,T];L^2(\Omega )\right) \cap C( [0,T;H _0 ^{\frac{\alpha }{2}} (\Omega ) \cap H ^s (\Omega ))\), and suppose that \(\{\psi _1,\psi _2\}\) is sufficiently regular in spatial directions and has a regularity hypothesis on temporal derivatives of \(\{\psi _1,\psi _2\}\) reads \(\left\Vert {\frac{\partial ^{2}\psi _j}{\partial t^{2}}}\right\Vert _{L^{\infty }(I)}\le C(1+t^{\beta _{m}-2})\). Assume also that \(\frac{\partial ^{\beta }\psi _j}{\partial t^{\beta }}\in C( [0,T;H _0 ^{\frac{\alpha }{2}} (\Omega ) \cap H ^s (\Omega ))\). Also, the functions \(F_j\) in (1.1)-(1.4) are Lipschitz, \(f_j \in C(0,T;H ^r (\Omega ))\) and \(\phi _i \in H _0 ^{\frac{\alpha }{2}} (\Omega ) \cap H ^s (\Omega )\), then, if \(\tau _M\le \root \beta _m \of {\frac{q_m}{2\Gamma (2-\beta _m)\lambda }}\) holds, the Galerkin spectral scheme (3.4) admits a unique solution \(\{\psi _{1,N}^n,\psi _{2,N}^n\}\) under smoothly graded meshes \(t_n=T(n/M)^{\gamma }\) satisfying

$$\begin{aligned}&\left\Vert {\psi _{1,N} ^n - \psi _1 (x , t _n)}\right\Vert +\left\Vert {\psi _{2,N} ^n - \psi _2 (x , t _n)}\right\Vert \nonumber \\&\quad \le \mathbf {C} \left( M ^{-\min \{\gamma \beta _m,2-\beta _m\}} + N ^{- s}+ N ^{- r} \right) ,\nonumber \\&\quad \qquad \text {if } \alpha \ne \tfrac{3}{2}, \end{aligned}$$
(4.20)
$$\begin{aligned}&\left\Vert {\psi _{1,N} ^n - \psi _1 (x , t _n)}\right\Vert +\left\Vert {\psi _{2,N} ^n - \psi _2 (x , t _n)}\right\Vert \nonumber \\&\quad \le \mathbf {C} \left( M ^{-\min \{\gamma \beta _m,2-\beta _m\}} + N ^{\epsilon - s}+ N ^{\epsilon - r}\right) , \nonumber \\&\quad \qquad \text {if } \alpha = \tfrac{3}{2}\, \mathrm{and }\, 0< \epsilon < \frac{1}{2}, \end{aligned}$$
(4.21)

such that \(\mathbf {C}\) is a positive constant independent of \(N,\,M\) and n. Particularly, the numerical solution \(\{\psi _{1,N}^n,\psi _{2,N}^n\}\) achieves an optimal time convergence order \(O(M^{\beta _m-2})\) for the optimal grid parameter \(\gamma _{opt}=(2-\beta _m)/\beta _m\).

Proof

The following variational form can be given thanks to (7), (3.3) at \(i=1\) and using the notation (4.1),

$$\begin{aligned}&\left( \sum _{r=1}^m q_{r}\Delta _M ^{\beta _r} \psi _{1}^n,\nu _1\right) +A(\psi _1^n,\nu _1) \nonumber \\&\quad -\rho \, \left( F_1(\psi _{1}^n,\psi _{2}^n),\nu _1\right) -\left( f_{1}^n,\nu _1\right) +\left( R_t^n,\nu _1\right) =0. \end{aligned}$$
(4.22)

Let \(e_1=\psi _1-\psi _{1,N},\quad \zeta _1=\psi _1-P_{N}\psi _1\) and \(\eta _1=P_{N}\psi _1-\psi _{1,N},\) we get \(e_1^{n}=\zeta _1^{n}+\eta _1^{n}.\) Using Lemma 5, we have the following estimate in the case of \(\alpha \ne \frac{3}{2},\)

$$\begin{aligned} \left\Vert {e^{n}_1}\right\Vert \le \left\Vert {\zeta ^{n}_1}\right\Vert +\left\Vert {\eta ^{n}_1}\right\Vert \le CN^{-s}\left\Vert {\psi _1}\right\Vert _{s}+\left\Vert {\eta _1^{n}}\right\Vert . \end{aligned}$$
(4.23)

The full discretization of the first equation in (3.4) can be rewritten generally as

$$\begin{aligned}&\left( \sum _{r=1}^m q_{r}\Delta _M ^{\beta _r}\psi _{1,N}^{n},\nu _1\right) \nonumber \\&\quad +A(\psi _{1,N}^n,\nu _1)-\rho \left( I_N\left( F_1 (\psi _{1,N}^n,\psi _{2,N}^n)\right) ,v_1 \right) \nonumber \\&\quad -(I_Nf_{1}^n,v_1)+\left( R_t^n,\nu _1\right) =0. \end{aligned}$$
(4.24)

Then the error weak form is achieved by taking \(\nu _1=\eta _1^{n}\),

$$\begin{aligned}&\left( \sum _{r=1}^m q_{r}\Delta _M ^{\beta _r}e_{1}^{n},\eta _1^n\right) +A(e_{1,N}^n,\eta _1^n)\nonumber \\&\quad -\rho \left( I_N(F_1\left( \psi _{1,N}^n,\psi _{2,N}^n)\right) -F_1(\psi _{1}^n,\psi _{2}^n),\eta _1^n \right) \nonumber \\&\quad -(I_Nf_{1}^n-f_{1}^n,\eta _1^n)+\left( R_t^n,\eta _1^n\right) =0. \end{aligned}$$
(4.25)

Starting from the first term in the left-hand side of (4.25) and according to [24],

$$\begin{aligned} \left( \Delta _{M}^{\beta _r}e_{1}^{n},\eta _1^{n}\right)&=\left( \Delta _{M}^{\beta _r}\eta _1^{n},\eta _{1}^{n}\right) +\left( \Delta _{M}^{\beta }\zeta _1^{n},\eta _1^{n}\right) \nonumber \\&\ge \frac{1}{2}\Delta _{M}^{\beta _r}\left\Vert {\eta _1^n}\right\Vert ^{2} +\left( \Delta _{M}^{\beta _r}\zeta _1^{n},\eta _1^{n}\right) . \end{aligned}$$
(4.26)

For the second term in the left-hand side of (4.25) and by considering (4.1) and (4.3), we get

$$\begin{aligned} A (e_1^n,\eta _1^n)=A (\zeta _1^n,\eta _1^n)+A (\eta _1^n,\eta _1^n) =|\eta _1^n|_{\alpha /2}^{2}. \end{aligned}$$
(4.27)

Substituting those results into (4.25), we deduce

$$\begin{aligned}&\sum _{r=1}^m q_{r}\Delta _M ^{\beta _r} \left\Vert {\eta _1^n}\right\Vert ^{2}+ 2|\eta ^n_1|_{\alpha /2}^{2}\nonumber \\&\quad \le 2\sum _{r=1}^m q_{r}\left( \Delta _M ^{\beta _r} \zeta ^n , \eta _1^n \right) \nonumber \\&\qquad +2\rho \, \left( I_N\left( F_1(\psi _{1,N}^n,\psi _{2,N}^n)\right) -F_1(\psi _{1}^n,\psi _{2}^n),\eta _1^n \right) \nonumber \\&\qquad +2\left( I_{N}f_{1}^n-f_{1}^{n},\eta _1^{n}\right) +2\left( R_t^n,\eta _1^{n}\right) . \end{aligned}$$
(4.28)

Neglecting the second positive term in the left-hand side of (4.28) and using Lemma 5 to bound the first term in the right-hand side of (4.28) at \(\alpha \ne \frac{3}{2}\), we obtain

$$\begin{aligned}&\sum _{r=1}^m q_{r}\Delta _M ^{\beta _r}\left\Vert {\eta _1^n}\right\Vert ^{2}\nonumber \\&\quad \le 2 C N^{-s}\sum _{r=1}^m q_{r}\left\Vert {\Delta _M ^{\beta _r} \psi _{1}^n}\right\Vert _{s}\left\Vert {\eta _1^n}\right\Vert \nonumber \\&\qquad +2\rho \, \left( I_N\left( F_{1}(\psi _{1,N}^n,\psi _{2,N}^n)\right) -F_{1}(\psi _{1}^n,\psi _{2}^n),\eta _1^n \right) \nonumber \\&\qquad +2\left( I_{N}f_{1}^n-f_{1}^{n},\eta _1^{n}\right) +2\left( R_t^n,\eta _1^{n}\right) . \end{aligned}$$
(4.29)

On the other hand, we use (4.23), Lemma 3 and the Lipschitz condition on F to reach

$$\begin{aligned}&\left\Vert {I _N F_1 (\psi _{1,N}^n,\psi _{2,N}^n)-F_1(\psi _{1}^n,\psi _{2}^n)}\right\Vert \nonumber \\&\quad \le \left\Vert {I _N \left( F_1 (\psi _{1,N}^n,\psi _{2,N}^n) -F_1 (\psi _{1}^n,\psi _{2}^n)\right) }\right\Vert \nonumber \\&\qquad + \left\Vert {I _N F_1 (\psi _{1}^n,\psi _{2}^n) - F_1 (\psi _{1}^n,\psi _{2}^n)}\right\Vert \nonumber \\&\quad \le \mathrm {C} \left( \left\Vert {F_1 (\psi _{1,N}^n, \psi _{2,N}^n) - F_1 (\psi _{1}^n,\psi _{2}^n)}\right\Vert \right) \nonumber \\&\qquad + \mathrm {C} N ^{- s} \left( \left\Vert {\psi _{1,N}^n}\right\Vert _s +\left\Vert {\psi _{2,N}^n}\right\Vert _s\right) \nonumber \\&\quad \le \mathrm {C} N ^{- s} \left( \left\Vert {\psi _{1,N}^n}\right\Vert _s +\left\Vert {\psi _{2,N}^n}\right\Vert _s\right) \nonumber \\&\qquad + \mathrm {C}\left( \left\Vert {\eta _1^n}\right\Vert +\left\Vert {\eta _2^n}\right\Vert \right) . \end{aligned}$$
(4.30)

In the following, rearrange terms conveniently, take the absolute value and use the triangle inequality. Next, use Young’s inequality and Lemma 3 side by side to (4.29) to obtain

$$\begin{aligned}&\sum _{r=1}^m q_{r}\Delta _M ^{\beta _r}\left\Vert {\eta _1^n}\right\Vert ^{2} \nonumber \\&\quad \le 2 C N^{-s}\sum _{r=1}^m q_{r}\left\Vert {\Delta _M ^{\beta _r} \psi _{1}^n}\right\Vert _{s}\left\Vert {\eta _1^n}\right\Vert \nonumber \\&\qquad +2 \rho \left\Vert {I_N(F_1(\psi _{1,N}^n,\psi _{2,N}^n)) -F_1(\psi _{1}^n,\psi _{2}^n)}\right\Vert \left\Vert {\eta _1^n}\right\Vert \nonumber \\&\qquad + 2 \left\Vert {I _N f_{1}^n - f_{1}^n}\right\Vert \left\Vert {\eta _1^n}\right\Vert +\left( R_t^n,\eta _1^{n}\right) \nonumber \\&\quad \le \tilde{C} \left( \left( N ^{- s}+N ^{- r}\right) ^2 + \left\Vert {\eta _1^n}\right\Vert ^2+\left\Vert {\eta _1^n}\right\Vert \left\Vert {\eta _2^n}\right\Vert +(R_t^{n})^2 \right) , \end{aligned}$$
(4.31)

such that \(\tilde{C}=6\times \max \{2 C\sum _{r=1}^m q_{r} \left\Vert {\Delta _M ^{\beta _r}\psi _{1,N}^n}\right\Vert _{s},2C \left\Vert {\psi _{1,N}^n}\right\Vert _s, 2C\left\Vert {\psi _{1,N}^n}\right\Vert _r\), \(2\rho C \left( \left\Vert {\psi _{1,N}^n}\right\Vert _s +\left\Vert {\psi _{2,N}^n}\right\Vert _s \right) , 2\rho C,4\}\).

Similarly, by following the same steps for (1.1) at \(i=2\) and its numerical form in (3.4), we conclude

$$\begin{aligned}&\sum _{r=1}^m q_{r}\Delta _M ^{\beta _r}\left\Vert {\eta _2^n}\right\Vert ^{2} \nonumber \\&\quad \le \bar{C} \left( \left( N ^{- s}+N ^{- r}\right) ^2 +\left\Vert {\eta _2^n}\right\Vert ^2+\left\Vert {\eta _1^n}\right\Vert \left\Vert {\eta _2^n}\right\Vert +(R_t^{n})^2 \right) , \end{aligned}$$
(4.32)

such that \(\bar{C}=6\times \max \{2 C\sum _{r=1}^m q_{r} \left\Vert {\Delta _M^{\beta _r} \psi _{2,N}^n}\right\Vert _{s},2C\left\Vert {\psi _{2,N}^n}\right\Vert _s ,2C\left\Vert {\psi _{2,N}^n}\right\Vert _r\), \(2\rho C\left( \left\Vert {\psi _{2,N}^n}\right\Vert _s +\left\Vert {\psi _{1,N}^n}\right\Vert _s \right) ,2\rho C,4\}\). Adding (4.31) and (4.32) together, we obtain

$$\begin{aligned}&\sum _{r=1}^m q_{r}\Delta _M ^{\beta _r} \left( \left\Vert {\eta _1^n}\right\Vert ^{2}+\left\Vert {\eta _2^n}\right\Vert ^{2}\right) \nonumber \\&\quad \le 4\hat{C} \left( \left\Vert {\eta _1^n}\right\Vert ^2+\left\Vert {\eta _2^n}\right\Vert ^2 +(R_t^{n})^2+\left( N ^{- s}+N ^{- r}\right) ^2\right) , \end{aligned}$$
(4.33)

where \(\hat{C}=\max \{\bar{C},\tilde{C}\}.\) A direct application of Theorem 1 and Lemma 8 yields the result. Then the proof is fulfilled when \(\alpha \ne \frac{3}{2}\) and the desired result is obtained. The proof when \(\alpha = \frac{3}{2}\) and \(0< \epsilon < \frac{1}{2}\) can be derived similarly. \(\square\)

5 Numerical results

Consider the following coupled system of ten-term fractional diffusion equations:

$$\begin{aligned}&\sum _{r=1}^{10} \frac{\partial ^{\beta _{r}}\psi _1}{\partial t^{\beta _{r}}} -\frac{\partial ^\alpha \psi _1}{\partial |x|^\alpha }\nonumber \\&\quad =\sin \left( {\psi _1 } \right) + \psi _2^2+f_1(x,t), \quad x \in (0,1),\ t \in (0,1], \end{aligned}$$
(5.1)
$$\begin{aligned}&\sum _{r=1}^{10} \frac{\partial ^{\beta _{r}}\psi _2}{\partial t^{\beta _{r}}} -\frac{\partial ^\alpha \psi _2}{\partial |x|^\alpha }\nonumber \\&\quad =\sin \left( {\psi _2 } \right) + \psi _1^2+f_2(x,t), x \in (0,1),\ t \in (0,1]. \end{aligned}$$
(5.2)

We choose the fractional orders \(\beta _r= \frac{{1 + 2m -r}}{{4m}}\) and \(\alpha =1.5\). The nonsmooth solutions \(\psi _1 (x,t) =t^{\beta _m} x(1 - x)^2 sin\left( {\pi x} \right)\) and \(\psi _2 (x,t) =(t^{\beta _m} + t)x^2 (1 - x)^2 \mathrm{cos}\left( {\pi x} \right)\) are used to generate the source functions \(f_1\) and \(f_2\) and the initial-boundary conditions. Tables 1 and 2 show the convergence rates of the approximate solutions of \(\psi _1\) and \(\psi _2\) in temporal and spatial directions, respectively.

Table 1 Numerical temporal accuracy of \(\psi _1\) and \(\psi _2\) with \(N=100\)
Full size table
Table 2 Numerical spatial accuracy of \(\psi _1\) and \(\psi _2\) with \(\gamma =3\) and \(M=1600\)
Full size table

6 Conclusion

Due to the lack of a discrete fractional Grönwall-type inequality, the techniques of analyzing the L1 difference schemes can not be applied directly to multi-term fractional diffusion equations that contains positive reaction term on a nonuniform time mesh, especially when the maximum order of the fractional derivatives is not an integer. This limitation was overcome in Theorem 1 by exploiting a novel discrete fractional Grönwall inequality for the L1 scheme over a nonuniform time mesh. This inequality was a main result. Then we proposed a finite difference/spectral method to solve coupled systems of nonlinear multi-term time-space fractional diffusion equations with non-smooth solutions in the time direction. The proposed method combined the strength of the L1 scheme with temporal nonuniform mesh and the Galerkin–Legendre method. Finally, we illustrated the use of Theorem 1 by outlining some convergence estimates of the scheme. The numerical results accompanying our analysis supported our theoretical contributions. The proposed approach extended our earlier work [44] that uses the L1 approximation to the single-order fractional derivatives.