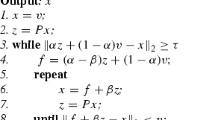An adaptively preconditioned multi-step matrix splitting iteration for computing PageRank

Abstract

The multi-step matrix splitting iteration (MPIO) for computing PageRank is an efficient iterative method by combining the multi-step power method with the inner-outer iterative method. In this paper, with the aim of accelerating the computation of PageRank problems, a new method is proposed by preconditioning the MPIO method with an adaptive generalized Arnoldi (GArnoldi) method. The new method is called as an adaptive GArnoldi-MPIO method, whose construction and convergence analysis are discussed in detail. Numerical experiments on several PageRank problems are reported to illustrate the effectiveness of our proposed method.

1 Introduction

In our world, web search engines have become one of the most commonly used tools for information retrieval. When we use a web search engine to search something, we not only hope to obtain the search results as soon as possible, but also hope to get the most relevant web pages. Hence, it is necessary to measure the importance of web pages and order them. Based on the hyperlink structure of web pages, Google’s PageRank is regarded as an efficient method to determine the importance of web pages [1]. From the view of numerical solutions, it requires to solve the following linear system

$$ Ax = x, \quad A = \alpha P + (1-\alpha)ve^{\mathrm{T}}, $$

(1)

where $A\in \mathbb {R}^{n\times n}$ is called a Google matrix, $x\in \mathbb {R}^{n}$ is a PageRank vector, α ∈ (0,1) is a damping factor, $P\in \mathbb {R}^{n\times n}$ is a column-stochastic matrix, $e=[1,1,\cdots ,1]^{\mathrm {T}} \in \mathbb {R}^{n}$ and v = e/n.

It is well-known that the power method is a classical method for computing PageRank. When the damping factor is small such as α = 0.85, the power method has a fast convergence. On the contrary, if the damping factor is large such as α ≥ 0.99, then the power method suffers from slow convergence. In fact, the closer the damping factor α is to 1, the closer the Google matrix A is to the original web link graph. In other words, the PageRank vector derived from large α perhaps gives a “truer” PageRanking than small α [2,3,4]. Hence, it is meaningful to improve the power method for large values of α. Gu et al. [5] proposed a two-step matrix splitting iterative method (denoted as “PIO”) for computing PageRank, where the power method is combined with the inner-outer iteration [6]. With this idea in mind, Wen et al. [7] presented a multi-step matrix splitting iterative method (called as “MPIO”) by applying multi-step power method to combine with the inner-outer iteration. In addition, many strategies based on Arnoldi process are considered to speed up the power method. For instance, Wu and Wei [4] developed a Power-Arnoldi algorithm by periodically combining the power method with the thick restarted Arnoldi algorithm [8]. Hu et al. [9] proposed a variant of the Power-Arnoldi algorithm by using the power method with the extrapolation process based on trace (PET) [10]. Gu et al. [11] presented a GMRES-Power algorithm based on a periodic combination of the power method with the GMRES method [12, 13]. More numerical methods based on the Arnoldi process or the power method, please refer to [14,15,16,17,18,19,20,21,22,23,24].

Considering a weighted inner product into the Arnoldi process, Yin et al. [25] proposed an adaptive generalized Arnoldi (GArnoldi) method for computing PageRank. And then Wen et al. [26] developed an adaptive Power-GArnoldi algorithm by treating the adaptive GArnoldi method as an accelerated technique for the power method. Motivated by these works, we try to construct a new method by preconditioning the MPIO method with the adaptive GArnoldi method in this paper. One reason is that the MPIO method usually converges faster than the power method for computing PageRank [7]. Another reason is that the adaptive GArnoldi method with a weighted inner product can improve the robustness of the standard Arnoldi method with the Euclidean norm [25]. The new method is called as an adaptive GArnoldi-MPIO method, whose implementation and convergence would be analyzed in detail. It is worth noting that our new method is different from the Arnoldi-MSPI method in [19], since the latter used the thick restarted Arnoldi algorithm [8] to preprocess the multi-step splitting iteration.

The remainder of this paper is organized as follows. In Section 2, we briefly review the MPIO method and the adaptive GArnoldi method for computing PageRank. In Section 3, we give the construction of the adaptive GArnoldi-MPIO method and discuss its convergence. In Section 4, numerical experiments are used to illustrate the effectiveness of our proposed method. Finally, conclusions are presented in Section 5.

2 The MPIO iteration and the adaptive GArnoldi method for computing PageRank

In this section, we briefly review the MPIO iteration [7] and the adaptive GArnoldi method [25] for computing PageRank.

2.1 The MPIO iteration

According to the idea of the PIO iteration [5], Wen et al. [7] proposed a MPIO iteration by combining the multi-step power method with the inner-outer iteration. The MPIO iteration can be depicted as follows.

The MPIO iteration. Given an initial guess x⁽⁰⁾. For k = 0,1,⋯, compute

$$ \left\{ \begin{array}{l} x^{\left( k+\frac{1}{m_{1}+1}\right)} = \alpha Px^{\left( k\right)} + (1-\alpha)v, \\ x^{\left( k+\frac{2}{m_{1}+1}\right)} = \alpha Px^{\left( k+\frac{1}{m_{1}+1}\right)} + (1-\alpha)v, \\ {\cdots} \\ x^{\left( k+\frac{m_{1}}{m_{1}+1}\right)} = \alpha Px^{\left( k+\frac{m_{1}-1}{m_{1}+1}\right)} + (1-\alpha)v, \\ (I - \beta P)x^{(k+1)} = (\alpha-\beta)Px^{\left( k+\frac{m_{1}}{m_{1}+1}\right)} + (1-\alpha)v, \end{array} \right. $$

(2)

until the sequence $\{x^{(k)}\}_{k=0}^{\infty }$ converges, where α ∈ (0,1), β ∈ (0,α) and m₁ (m₁ ≥ 2) is a multiple iteration parameter. Note that, if m₁ = 1, then the MPIO iteration is reduced to the PIO iteration [5].

From the construction of the MPIO iteration, we can see that the first m₁ steps of (2) are easy to implement since only matrix-vector products are used, while for the last step of (2), there is a computational problem when solving the linear system with I − βP. In order to overcome this problem, Gleich et al. [6] employed an inner Richardson iteration by setting

$$ f = (\alpha - \beta)Px^{\left( k+\frac{m_{1}}{m_{1}+1}\right)} + (1-\alpha)v, $$

(3)

such that the inner linear system is defined as (I − βP)y = f. Then x^(k+ 1) can be computed by the inner iteration

$$ y^{(j+1)} = \beta P y^{(j)} + f, \quad j = 0,1,2, {\cdots} ,l-1, $$

(4)

where $y^{(0)} = x^{\left (k+\frac {m_{1}}{m_{1}+1}\right )}$ and y^(l) = x^(k+ 1).

For the whole iterations, the stopping criteria of the outer iteration (the last step of (2)) and the inner iteration (4) are set as

$$ \|(1-\alpha)v - (I-\alpha P)x^{(k+1)}\|_{2} < tol, $$

(5)

and

$$ \|f - (I-\beta P)y^{(j+1)}\|_{2} <\eta, $$

(6)

respectively, where tol and η are the prescribed tolerances. The corresponding algorithm of the MPIO iteration for computing PageRank is presented as follows [7, 19].

Note that, in Algorithm 1, we use the 2-norm of the residual as the stopping criterion for being consistent with the choices of the following methods.

2.2 The adaptive GArnoldi method

The Arnoldi process with weighted inner products, instead of the Euclidean norm, can be viewed as a generalization of the standard Arnoldi process. By changing the weights with the current residual vector corresponding to the approximate PageRank vector, Yin et al. [25] proposed an adaptive GArnoldi method for computing PageRank, which can be described as follows.

Some remarks about Algorithm 2 are given as follows.

• In the first line, the input parameter A is the Google matrix as shown in (1), v = e/n is used as an initial vector, m is the steps of the GArnoldi process and tol is a prescribed tolerance.

• In the step 3, there is a GArnoldi process, in which the matrix $G\in \mathbb {R}^{n\times n}$ is a symmetric positive define (SPD) matrix. In the line 3.5, there is a G-inner product defined as $(x,y)_{G} = x^{\mathrm {T}}Gy, \forall x\in \mathbb {R}^{n}, y\in \mathbb {R}^{n}$. Correspondingly, in the line 3.1 and 3.7, there is a G-norm defined as $\|x\|_{G} = \sqrt {(x,x)_{G}}, \forall x\in \mathbb {R}^{n}$. Noth that, when G = I, then the GArnoldi process reduces to the standard Arnoldi process with the Euclidean norm. The aim of step 3 is to obtain the matrix V_m+ 1 and H_m+ 1,m, where $V_{m+1} = [v_{1},v_{2},\cdots ,v_{m+1}] \in \mathbb {R}^{n\times (m+1)}$ is a G-orthogonal matrix and $H_{m+1,m} = (h_{ij})\in \mathbb {R}^{(m+1)\times m}$ is an upper Hessenberg matrix. More details about the GArnoldi process can be found in [25].

• In the step 5, σ_m denotes the minimal singular value of the matrix H_m+ 1,m − [I;0]^T, s_m and u_m denotes the right and left singular vector associated with σ_m respectively. The matrix V_m consists of the first m columns of the matrix V_m+ 1.

• Since all SPD matrices are diagonalized, for simplicity, it is reasonable to set G as a diagonal matrix. As shown in the step 7, the matrix G is chosen as G = diag{|r|/∥r∥₁}, where r is the residual vector obtained from the step 5. It is worth mentioning that the residual vector r changes after every cycle of Algorithm 2, such that the matrix G, or the weights, is adaptively changed with the changing of the current residual vector.

3 The adaptive GArnoldi-MPIO method for computing PageRank

In this section, for accelerating the computations of PageRank problems, a new method is proposed by using the adaptive GArnoldi method as a preconditioner of the MPIO method. The new method is called as an adaptive GArnoldi-MPIO method. We first give its construction, and then discuss its convergence.

3.1 The adaptive GArnoldi-MPIO method

The construction of the adaptive GArnoldi-MPIO method is partially similar to the construction of these methods in [4, 11, 19, 26]. However, there are several obvious differences between our new method and the other methods. For example, comparing the adaptive GArnoldi-MPIO method with the Power-Arnoldi method [4], there are three main differences between them. The first one is that the aim of our new method is to accelerate the MPIO method, not the power method. The second one is that the former employs the adaptive GArnoldi method as a preconditioner, while the latter uses the thick restarted Arnoldi method. The last one is that our proposed method first runs the adaptive GArnoldi method for a few times such that an approximate vector is obtained, while the Power-Arnoldi method first runs the power method. Now we outline the steps of the adaptive GArnoldi-MPIO method for computing PageRank as follows.

According to Algorithm 3, the mechanism of the adaptive GArnoldi-MPIO method can be simply summarized as follows: given an unit initial vector v, we first run the adaptive GArnoldi method (Algorithm 2) for a few times (e.g., 2–3 times) to get an approximate PageRank vector. If the approximate PageRank vector is unsatisfactory, we use the resulting vector as the initial vector of the MPIO method to obtain another approximate PageRank vector. If this approximate PageRank vector is still below the prescribed tolerance, rerun the adaptive GArnoldi method. Repeating the above procedure analogously until the described accuracy is achieved.

In Algorithm 3, one problem is that when and how to control the conversion between the MPIO method and the adaptive GArnoldi method. To solve this problem, a simple and easily realized strategy as given in [19] is chosen. That is, the parameters α₁, α₂, restart, maxit are used to control the flip-flop between the MPIO method and the adaptive GArnoldi method. Specifically, let τ^curr and τ^pre be the residual norm of the current and the previous MPIO method, respectively. Denote ratio = τ^curr/τ^pre. If ratio > α₁, then let restart = restart + 1, terminate the MPIO method and run the adaptive GArnoldi method. Let d^curr and d^pre be the residual norm of the current and the previous inner iteration of the MPIO method, respectively. Denote ratio₁ = d^curr/d^pre. If ratio₁ > α₂, then keep on running the inner iteration. In order to make sure the stability of our new method, it is important to set the values of α₁ and α₂. Since the largest eigenvalue of the Google matrix A is λ₁ = 1, and its second largest eigenvalue satisfies |λ₂|≤ α [27], it is reasonable to choose α₁ = α − 0.1 or α₁ = α − 0.2, and α₂ = α − 0.1 or α₂ = α − 0.2.

Now we consider the memory and the computational costs of the adaptive GArnoldi-MPIO method. According to the steps 2 and 3 of Algorithm 3, we find the main storage requirements are the G-orthogonal matrix V_m+ 1, the upper Hessenberg matrix H_m+ 1,m, the approximate PageRank vector x, the residual vector r, as well as the intermediate vectors z (line 3.7) and f (line 3.9). Thus the total memory cost of Algorithm 3 is approximately $(m+5)n + \frac {m^{2}}{2} + 2m$ in each cycle. Since the matrix G is chosen as a diagonal matrix, i.e., G = diag{|r|/∥r∥₁}, the G-inner product and G-norm in the GArnoldi process can be implemented by elementwise multiplication. So the main computational cost of our proposed method consists of the matrix-vector multiplications. For each cycle, it needs m matrix-vector multiplications in the GArnoldi process phase, and in the MPIO iteration phase, it requires m₁ matrix-vector multiplications for the power iteration (lines 3.5–3.8), while we do not know how many matrix-vector multiplications will be implemented for the inner-outer iteration (lines 3.11–3.17) because of the existence of the parameters η, ratio₁ and α₂. Thus the main computational cost of Algorithm 3 is m matrix-vector multiplications or at lease m + m₁ matrix-vector multiplications in each cycle.

3.2 Convergence analysis of the adaptive GArnoldi-MPIO method

In this subsection, we discuss the convergence analysis of the adaptive GArnoldi-MPIO method. Particularly, our analysis focuses on the procedure when turning from the MPIO iteration to the adaptive GArnodli method.

Assume that eigenvalues of the Google matrix A are arranged in decreasing order $1 = \left | {{\lambda _{1}}} \right | > \left | {{\lambda _{2}}} \right | \ge {\cdots } \ge \left | {{\lambda _{n}}} \right |$. Let $\mathcal {L}_{m-1}$ represent the set of polynomials of degree not exceeding m − 1, σ(A) denote the set of eigenvalues of the matrix A, (λ_i,φ_i),i = 1,2,⋯ ,n and $(\widetilde {\lambda }_{j}, \widetilde {y}_{j}), j = 1, 2, \cdots , m$ denote the eigenpairs of A and H_m, respectively. The Arnoldi method usually uses $\widetilde {\lambda }_{j}$ to approximate λ_j, $\widetilde {\varphi }_{j} = V_{m} \widetilde {y}_{j}$ to approximate φ_j. However, for each $\widetilde {\lambda }_{j}$, instead of using $\widetilde {\varphi }_{j}$ to approximate φ_j, Jia [3] tried to seek a unit norm vector $\widetilde {u}_{j} \in \mathcal {K}_{m}(A,v_{1})$ satisfying the condition

$$ \|(A-\widetilde{\lambda}_{j} I)\widetilde{u}_{j}\|_{2} = \min_{u\in \mathcal {K}_{m}(A,v_{1})} \|(A-\widetilde{\lambda}_{j} I)u\|_{2} $$

(7)

and use it to approximate φ_j, where $\mathcal {K}_{m}(A,v_{1}) = span(v_{1},Av_{1},\cdots ,A^{m-1}v_{1})$ is a Krylov subspace, and $\widetilde {u}_{j}$ is called a refined approximate eigenvector corresponding to λ_j. Convergence of the refined Arnoldi method is given below.

Theorem 1

[3]. Under the above notations, assume that $v_{1} = {\sum }_{i = 1}^{n} \gamma _{i}\varphi _{i}$ with respect to the eigenbasis {φ_i}_{i= 1,2,⋯ ,n} in which ∥φ_i∥₂ = 1,i = 1,2,⋯ ,n and γ_i≠ 0, let S = [φ₁,φ₂,⋯ ,φ_n], and

$$ \xi_{j} = {\sum}_{i \ne j} {|\lambda_{i} - \widetilde{\lambda}_{j}| \cdot \frac{|\gamma_{i}|}{|\gamma_{j}|}}. $$

Then

$$ \|(A-\widetilde{\lambda}_{j} I)\widetilde{u}_{j} \|_{2} \leq \frac{\sigma_{max}(S)}{\sigma_{min}(S)}\left( |\lambda_{j}-\widetilde{\lambda}_{j}|+\xi_{j} \min_{p \in \mathcal {L}_{m-1},p(\lambda_{j}) = 1} \max_{i\neq j}| p(\lambda_{i} )|\right), $$

where σ_max(S) and σ_min(S) are the largest and smallest singular value of the matrix S, respectively.

Before we give the convergence of the adaptive GArnoldi-MPIO method, a few useful conclusions are shown as follows.

Lemma 1

[26]. Let G = diag{w₁,w₂,⋯ ,w_n}, w_i > 0 (1 ≤ i ≤ n), then for any vector $x\in \mathbb {R}^{n}$, we have

$$ \min_{1\leq i \leq n}w_{i}\cdot \|x\|_{2}^{2} \leq \|x\|_{G}^{2} \leq \max_{1\leq i \leq n}w_{i}\cdot \|x\|_{2}^{2}, $$

(8)

where ∥⋅∥₂ denotes the 2-norm and ∥⋅∥_G denotes the G-norm.

Theorem 2

[27]. Let P be an n × n column-stochastic matrix. Let α be a real number such that 0 < α < 1. Let E be an n × n rank-one column-stochastic matrix E = ve^T, where e is the n-vector whose elements are all ones and v is an n-vector whose elements are all nonnegative and sum to 1. Let A = αP + (1 − α)E be an n × n column-stochastic matrix, then its dominant eigenvalue λ₁ = 1, $\left | {{\lambda _{2}}} \right | \le \alpha$.

Theorem 3

[28]. Assume that the spectrum of the column-stochastic matrix P is {1,π₂,⋯ ,π_n}, then the spectrum of the matrix A = αP + (1 − α)ve^T is {1,απ₂,⋯ ,απ_n}, where α ∈ (0,1) and v is a vector with nonnegative elements such that e^Tv = 1.

Since our analysis focuses on the procedure when turning from the MPIO iteration to the adaptive GArnodli method, it is necessary to derive the iterative formula of the MPIO method in Algorithm 3.

Lemma 2

Let v₁ be the initial vector for the MPIO method, which is obtained from the previous adaptive GArnoldi method. Then, the MPIO method in Algorithm 3 produces the vector

$$ v^{new}_{1} = \omega T^{k}v_{1}, $$

(9)

where k ≥ maxit, ω is a normalizing factor, and the iterative matrix T is expressed as

$$ T= (I - \beta P)^{-1}\left[\alpha^{m_{1}-1}(\alpha-\beta)P^{m_{1}}A + (\alpha-\beta)PM_{m_{1}-2}(\alpha,P)(A-\alpha P) + (A-\alpha P)\right], $$

where

$$ M_{m_{1}-2}(\alpha,P) = \alpha^{m_{1}-2}P^{m_{1}-2} + \alpha^{m_{1}-3}P^{m_{1}-3} + {\cdots} + \alpha P + I $$

sand m₁ is a multiple iteration parameter for the power iteration in the MPIO method.

Proof 1

Let v₁ be the initial vector for the MPIO method, then it has x^(k) = v₁. According to (2), we have

$$ \begin{array}{@{}rcl@{}} x^{(k+1)} &=& \alpha^{m_{1}}(\alpha-\beta)(I - \beta P)^{-1}P^{m_{1}+1}x^{(k)} + (I - \beta P)^{-1} (1-\alpha)v \\ & & + (\alpha-\beta)(I - \beta P)^{-1}P[(\alpha^{m_{1}-1}P^{m_{1}-1} + \alpha^{m_{1}-2}P^{m_{1}-2} + {\cdots} + \alpha P + I) (1-\alpha)v] \\ &=& \alpha^{m_{1}-1}(\alpha-\beta)(I - \beta P)^{-1}P^{m_{1}} [ \alpha P x^{(k)}+(1-\alpha)v ] + (I - \beta P)^{-1} (1-\alpha)v \\ & & + (\alpha-\beta)(I - \beta P)^{-1}P[(\alpha^{m_{1}-2}P^{m_{1}-2} + {\cdots} + \alpha P + I) (1-\alpha)v] \\ &=& \alpha^{m_{1}-1}(\alpha-\beta)(I - \beta P)^{-1}P^{m_{1}} [ \alpha P +(1-\alpha)E ]x^{(k)} + (I - \beta P)^{-1} (1-\alpha)E x^{(k)} \\ & & + (\alpha-\beta)(I - \beta P)^{-1}P M_{m_{1}-2}(\alpha,P)(1-\alpha)E x^{(k)} \\ &=& (I - \beta P)^{-1}\left[\alpha^{m_{1}-1}(\alpha-\beta)P^{m_{1}}A + (\alpha-\beta)PM_{m_{1}-2}(\alpha,P)(A-\alpha P) + (A-\alpha P)\right] x^{(k)}, \end{array} $$

where we used the relationships separately A = αP + (1 − α)ve^T, E = ve^T and e^Tx^(k) = 1. Thus, the conclusion in Lemma 2 is proved.

Remark 1

We need to indicate that our iterative matrix T in Lemma 2 is different from that in Lemma 3 of [19], more details please refer to it.

In the next cycle of the adaptive GArnoldi-MPIO method, $v_{1}^{new}$ is used as an initial vector for an m-step GArnoldi process (step 2 in Algorithm 3), so that the new Krylov subspace

$$ \mathcal {K}_{m}(A,v_{1}^{new}) = span(v_{1}^{new},Av_{1}^{new},\cdots,A^{m-1}v_{1}^{new}) $$

will be constructed. The following theorem shows the convergence of the adaptive GArnoldi-MPIO method.

Theorem 4

Under the above notations, assume that $v_{1} = {\sum }_{i = 1}^{n} \gamma _{i}\varphi _{i}$ with respect to the eigenbasis {φ_i}_{i= 1,2,⋯ ,n} in which ∥φ_i∥₂ = 1,i = 1,2,⋯ ,n and γ₁≠ 0, let S = [φ₁,φ₂,⋯ ,φ_n], G = diag{w₁,w₂,⋯ ,w_n}, w_i > 0 (1 ≤ i ≤ n), and

$$ \xi = {\sum}_{i = 2}^{n} |\lambda_{i}-1|\cdot\frac{|\gamma_{i}|}{|\gamma_{1}|}, \quad \zeta = \sqrt{\frac{\max_{1\leq i \leq n}w_{i}} {\min_{1\leq i \leq n}w_{i}}}. $$

Then

$$ \|(A-I)u\|_{G} \leq \left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \frac{\xi\cdot\zeta}{\sigma_{min}(S)}\mathop {\min }\limits_{p \in {\mathcal {L}_{m-1}},p({\lambda_{1}}) = 1} \mathop {\max }\limits_{\lambda \in \sigma (A)/\left\{ {{\lambda_{1}}} \right\}} \left| {p(\lambda )} \right|, $$

where $u\in \mathcal {K}_{m}(A,v_{1}^{new})$, and σ_min(S) is the smallest singular value of the matrix S.

Proof 2

According to Theorem 3, let π₁ = 1,π₂,⋯ ,π_n be eigenvalues of the matrix P, then λ₁ = 1,λ₂ = απ₂,⋯ ,λ_n = απ_n are eigenvalues of the matrix A = αP + (1 − α)ve^T, and $\mu _{1}=\frac {1}{1-\beta },\mu _{2}=\frac {1}{1-\beta \pi _{2}},\cdots ,\mu _{n}=\frac {1}{1-\beta \pi _{n}}$ are eigenvalues of the matrix (I − βP)^− 1. Such that we have

$$ \begin{array}{@{}rcl@{}} T \varphi_{i} &=& (I - \beta P)^{-1}\left[\alpha^{m_{1}-1}(\alpha-\beta)P^{m_{1}}A + (\alpha-\beta)PM_{m_{1}-2}(\alpha,P)(A-\alpha P) + (A-\alpha P)\right] \varphi_{i} \\ &=& \frac{\alpha^{m_{1}-1}(\alpha-\beta)\pi_{i}^{m_{1}}\lambda_{i} + (\alpha-\beta)\pi_{i}M_{m_{1}-2}(\alpha,\pi_{i})(\lambda_{i}-\alpha \pi_{i}) + (\lambda_{i}-\alpha \pi_{i})}{1-\beta\pi_{i}} \varphi_{i}, \end{array} $$

where $M_{m_{1}-2}(\alpha ,\pi _{i})=\alpha ^{m_{1}-2}\pi _{i}^{m_{1}-2} + {\cdots } +\alpha \pi _{i} +1, i=1,2,\cdots ,n$.

Assume that

$$ \phi_{i} = \frac{\alpha^{m_{1}-1}(\alpha-\beta)\pi_{i}^{m_{1}}\lambda_{i} + (\alpha-\beta)\pi_{i}M_{m_{1}-2}(\alpha,\pi_{i})(\lambda_{i}-\alpha \pi_{i}) + (\lambda_{i}-\alpha \pi_{i})}{1-\beta\pi_{i}}, i =1,2,\cdots,n, $$

(10)

then, it has

$$ \phi_{1} = 1, T\varphi_{1} = \varphi_{1}, T^{k}\varphi_{1} = \varphi_{1}, T\varphi_{i}=\varphi_{i}, T^{k}\varphi_{i} = {\phi_{i}^{k}} \varphi_{i}, i=2,\cdots,n. $$

(11)

From the result in Theorem 2, we have |λ_i|≤ α,i = 2,⋯ ,n. For i = 2,⋯ ,n, substituting the relationship $\pi _{i}=\frac {\lambda _{i}}{\alpha }$ into (10), we get

$$ \begin{array}{@{}rcl@{}} |\phi_{i}| &=& \left| \frac{\alpha^{m_{1}-1}(\alpha-\beta)\pi_{i}^{m_{1}}\lambda_{i}}{1-\beta\pi_{i}} \right| = \left| \frac{(\alpha-\beta)\frac{1}{\alpha}\lambda_{i}^{m_{1}+1}}{1-\frac{\beta}{\alpha}\lambda_{i}} \right| \leq \frac{(\alpha-\beta)\frac{1}{\alpha}|\lambda_{i}|^{m_{1}+1}} {1-\frac{\beta}{\alpha}|\lambda_{i}|} \leq \frac{\alpha^{m_{1}}(\alpha-\beta)} {1-\beta}. \end{array} $$

(12)

Since for any $u \in \mathcal {K}_{m}(A,v_{1}^{new})$, there exists $q(x) \in \mathcal {L}_{m-1}$ such that

$$ \begin{array}{@{}rcl@{}} \|(A-I)u\|_{G} &=& \min_{q\in {\mathcal {L}_{m-1}}}\frac{\|(A-I)q(A)v_{1}^{new}\|_{G}}{\|q(A)v_{1}^{new}\|_{G}} = \min_{q\in {\mathcal {L}_{m-1}}}\frac{\|(A-I)q(A)\omega T^{k} v_{1}\|_{G}}{\|q(A)\omega T^{k} v_{1}\|_{G}} \\ &=& \min_{q\in {\mathcal {L}_{m-1}}}\frac{\|(A-I)q(A)T^{k}\gamma_{1} \varphi_{1} + {\sum}_{i=2}^{n}(A-I)q(A)T^{k}\gamma_{i} \varphi_{i}\|_{G}} {\|{\sum}_{i=1}^{n}q(A)T^{k}\gamma_{i} \varphi_{i}\|_{G}} \\ &=& \min_{q\in {\mathcal {L}_{m-1}}}\frac{\|{\sum}_{i=2}^{n}(\lambda_{i}-1)q(\lambda_{i}){\phi_{i}^{k}}\gamma_{i}\varphi_{i}\|_{G}} {\|{\sum}_{i=1}^{n}q(\lambda_{i}){\phi_{i}^{k}}\gamma_{i}\varphi_{i}\|_{G}}, \end{array} $$

(13)

where we used the conditions of the theorem, the relationships in (9) and (11). Using (8) and (12), for the numerator of (13), it has

$$ \begin{array}{@{}rcl@{}} \left\|{\sum}_{i=2}^{n}(\lambda_{i}-1)q(\lambda_{i}){\phi_{i}^{k}}\gamma_{i}\varphi_{i} \right\|_{G} &\leq & \sqrt{\max_{1\leq i \leq n}w_{i}} \cdot \left\|{\sum}_{i=2}^{n}(\lambda_{i}-1) q(\lambda_{i}) {\phi_{i}^{k}} \gamma_{i}\varphi_{i}\right \|_{2} \\ &\leq & \sqrt{\max_{1\leq i \leq n}w_{i}} \cdot {\sum}_{i=2}^{n} |\lambda_{i}-1| \cdot |\phi_{i}|^{k} \cdot |\gamma_{i}| \cdot |q(\lambda_{i})| \\ &\leq & \sqrt{\max_{1\leq i \leq n}w_{i}} \cdot {\sum}_{i=2}^{n}\left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \cdot|\lambda_{i}-1| \cdot |\gamma_{i}| \cdot |q(\lambda_{i})|. \end{array} $$

(14)

For the denominator of (13), it obtains

$$ \begin{array}{@{}rcl@{}} \left\|{\sum}_{i=1}^{n}q(\lambda_{i}){\phi_{i}^{k}}\gamma_{i}\varphi_{i}\right\|_{G}^{2} &\geq& \min_{1\leq i \leq n}w_{i} \cdot \left\|{\sum}_{i=1}^{n} q(\lambda_{i}){\phi_{i}^{k}} \gamma_{i}\varphi_{i}\right\|_{2}^{2} \\ &\geq& \min_{1\leq i \leq n}w_{i} \cdot \sigma_{min}^{2}(S)\cdot {\sum}_{i=1}^{n}|{\phi_{i}^{k}}|^{2} \cdot |\gamma_{i}|^{2} \cdot |q(\lambda_{i})|^{2}. \end{array} $$

(15)

Combining (14) and (15) into (13), we get

$$ \begin{array}{@{}rcl@{}} \|(A-I)u\|_{G} &\leq& \min_{q\in {\mathcal {L}_{m-1}}} \frac{\sqrt{\max_{1\leq i \leq n}w_{i}} \cdot {\sum}_{i=2}^{n} \left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \cdot|\lambda_{i}-1| \cdot |w_{i}| \cdot |q(\lambda_{i})|} {\sqrt{\min_{1\leq i \leq n}w_{i} \cdot \sigma_{min}^{2}(S)\cdot {\sum}_{i=1}^{n}|{\phi_{i}^{k}}|^{2} \cdot |\gamma_{i}|^{2} \cdot |q(\lambda_{i})|^{2}}} \\ &\leq& \frac{1}{\sigma_{min}(S)} \cdot \sqrt{\frac{\max_{1\leq i \leq n}w_{i}}{\min_{1\leq i \leq n}w_{i}}} \cdot \min_{q\in {\mathcal {L}_{m-1}}} \frac{{\sum}_{i=2}^{n}\left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \cdot |\lambda_{i}-1| \cdot |\gamma_{i}| \cdot |q(\lambda_{i})|} {|\gamma_{1}| \cdot |q(\lambda_{1})|}\\ &=& \frac{1}{\sigma_{min}(S)} \cdot \sqrt{\frac{\max_{1\leq i \leq n}w_{i}}{\min_{1\leq i \leq n}w_{i}}} \cdot \left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \cdot \min_{q\in {\mathcal {L}_{m-1}}} {\sum}_{i=2}^{n}|\lambda_{i}-1| \cdot \frac{|\gamma_{i}|}{|\gamma_{1}|} \cdot \frac{|q(\lambda_{i})|}{|q(\lambda_{1})|}. \end{array} $$

Let p(λ) = q(λ)/q(1), where p(1) = 1, then we have

$$ \|(A-I)u\|_{G} \leq \left( \frac{\alpha^{m_{1}}(\alpha-\beta)}{1-\beta}\right)^{k} \frac{\xi\cdot\zeta}{\sigma_{min}(S)}\mathop {\min }\limits_{p \in {\mathcal {L}_{m-1}},p({\lambda_{1}}) = 1} \mathop {\max }\limits_{\lambda \in \sigma (A)/\left\{ {{\lambda_{1}}} \right\}} \left| {p(\lambda )} \right|. $$

Therefore, we complete the proof of Theorem 4.

Remark 2

Comparing our result in Theorem 4 with the result in Theorem 3 of [26], it is easy to find that the adaptive GArnoldi-MPIO method can increase the convergence speed of the adaptive Power-GArnoldi method by a factor of $(\alpha ^{m_{1}-1})^{k} \cdot \left (\frac {\alpha -\beta }{1-\beta }\right )^{k}$ when turning from the MPIO method to the adaptive GArnoldi method. Therefore, from the view of theory, our proposed method will have a faster convergence than the adaptive Power-GArnoldi method.

4 Numerical experiments

In this section, we give some numerical examples to test the effectiveness of the adaptive GArnoldi-MPIO method (denoted as “GA-MPIO”), and compare it with the MPIO method [7], the Power-Arnoldi method (denoted as “PA”) [4], the adaptive Power-GArnoldi method (denoted as “PGA”) [26] and the Arnoldi-MSPI method (denoted as “AMS”) [19] in terms of the iteration counts (IT), the number of matrix-vector products (Mv) and the computing time (CPU) in seconds. All the numerical results are obtained by using MATLAB R2016a on the Windows 10 (64 bit) operating system with 2.40 GHz Intel(R) Core(TM) i7-5500U CPU and RAM 8.00 GB.

In Table 1, we list the characteristics of our test matrices, where n denotes the matrix size, nnz is the number of nonzero elements, and den is the density which is defined by $den = \frac {nnz}{n\times n} \times 100$. All the test matrices are available from https://sparse.tamu.edu/.

Table 1 The characteristic of test matrices

For the sake of justification, in all the methods we use the same initial vector x⁽⁰⁾ = e/n with e = [1,1,⋯ ,1]^T. Meanwhile, similar to [9, 11, 18, 19], we set the damping factor as α = 0.99, 0.993, 0.995 and 0.997, respectively. The 2-norm of residual vector is chosen as our stopping criterion in all experiments, and the prescribed tolerance is set as tol = 10^− 8.

Additionally, in the MPIO, AMS and GA-MPIO methods, we set the default multiple iteration parameter as m₁ = 3 and the inner tolerance η = 10^− 2, β = 0.5 because they can yield nearly optimal results for the inner-outer method [6]. However, it is hard to determine the optimal choices of the parameters m and maxit, because their optimal choices are different for different damping factors α and different PageRank problems. Hence, based on the discussions and advisable values from the related papers [9, 11, 15, 18, 19, 25, 26], we uniformly set m = 8 and maxit = 8 in our experiments for a fair comparison. The parameters chosen to flip-flop are set as α₁ = α − 0.1 and α₂ = α − 0.1 in the AMS and GA-MPIO methods. And the same choice is used for the PA and PGA methods. In the PA and AMS methods, we run the thick restarted Arnoldi procedure two times per cycle with the number of approximate eigenpairs g = 6. Similarly, in the PGA and GA-MPIO methods, we run the adaptive GArnoldi procedure two times per cycle. Moreover, in order to describe the efficiency of our proposed method, we define

$$ \text{Spt} = \frac{\text{CPU}_{\text{MPIO}} - \text{CPU}_{\text{GA-MPIO}}}{\text{CPU}_{\text{MPIO}}} \times 100\%. $$

to show the speedup of the GA-MPIO method with respect to the MPIO method.

Numerical results of the five methods for all the test matrices are provided in Tables 2, 3, and 4. From Tables 2, 3, and 4, we can see that

• For all the test matrices, the GA-MPIO method outperforms the MPIO method in terms of the iteration counts, the number of matrix-vector products and the computing time. Especially, the speedup of the GA-MPIO method with respect to the MPIO method is up to 86.35%. Hence, it shows that considering the adaptive GArnoldi method as a preconditioned technique for the MPIO method is meaningful.

• The GA-MPIO method works better than the PA and PGA methods in terms of the iteration counts and the computing time for all the test matrices, even though it needs a little more matrix-vector products in some cases. One possible reason is that the MPIO method needs more matrix-vector products than the power method in each iteration. Another possible reason is that, in the Arnoldi process, 1 matrix-vector product is accomplished with much more vector-operations than in the power method. As we know, for the power iteration, 1 matrix-vector product is mainly accomplished with 1 vector-scaling operation and 1 vector-addition operation, while in the Arnoldi process, 1 matrix-vector product is accomplished mainly with $\frac {m+1}{2}$ vector inner-product operations, $\frac {m+1}{2}+\frac {m+1}{m}$ vector-scaling operations, $\frac {m+1}{2}$ vector-addition operations and $\frac {m+1}{m}$ norm computations. From the results in Tables 2, 3, and 4, it observes that the GA-MPIO method gets the smallest iteration counts, thus a smallest number of the Arnoldi process is implemented compared with the PA and PGA methods. That is why the GA-MPIO method costs remarkably smaller computing time, although it gets similar number of matrix-vector products with the PA and GPA methods in some cases. For example, when α = 0.997, for the PA and PGA methods, we find that their computing time are reduced by 54.75% and 37.34% in Table 1, 41.46% and 23.76% in Table 3, 49.23% and 36.30% in Table 4, respectively. Therefore, these numerical performances suggest that our proposed method has a faster convergence than the PA and PGA methods, which verifies our theoretical analysis in Remark 2.

• The last two columns list the numerical results of the AMS and GA-MPIO methods. As mentioned in Section 1, the main difference between the AMS and GA-MPIO methods lies in that the former used the thick restarted Arnoldi algorithm to preprocess the multi-step splitting iteration, while the latter used the adaptive GArnoldi method. According to the results in Tables 2, 3, and 4, we can see that all the numerical performance of the GA-MPIO method is superior to the AMS method for all the test matrices, except the Stanford-Berkeley matrix with α = 0.99 where the number of matrix-vector products of the GA-MPIO method is inferior to the AMS method. The main reason is that the convergence performance of the Arnoldi method is improved by the adaptively accelerating technique. For instance, when α = 0.997, the computing time of the AMS method is reduced by 47.81% in Table 2. Hence, we can say that our proposed method outperforms the AMS method when α is high, which also indicates that introducing a weighted inner product into the Arnoldi process for computing PageRank problems is significant.

Table 2 Numerical results of the five methods for the wb-cs-stanford matrix

Table 3 Numerical results of the five methods for the web-Stanford matrix

Table 4 Numerical results of the five methods for the Stanford-Berkeley matrix

Figures 1, 2 and 3 plot the convergence behavior of the MPIO method, the PA method, the PGA method, the AMS method and the GA-MPIO method for α = 0.99,0.993,0.995 and 0.997, respectively. They show that our proposed method converges faster than its counterparts again.

Fig. 1

Convergence behavior of the five methods for the wb-cs-stanford matrix

Fig. 2

Convergence behavior of the five methods for the web-Stanford matrix

Fig. 3

Convergence behavior of the five methods for the Stanford-Berkeley matrix

5 Conclusions

In this paper, we present a new method by considering the adaptive GArnoldi method as a preconditioned technique to accelerate the MPIO method. The new method is called as the adaptive GArnoldi-MPIO method, whose construction and convergence analysis can be found in Section 3. Numerical experiments in Section 4 show that our proposed method is efficient and has a faster convergence than its counterparts.

In the future, we would like to discuss the choice of experimental parameters, e.g., how to determine the optimal m and maxit so that the new method can work more efficiently. In addition, the optimal choice of the weighted matrix G is also required to be further analyzed.