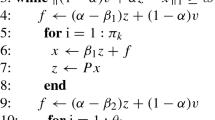1 Introduction

Many problems in scientific computing give rise to a system of linear equations

(1.1)

with A is a large sparse non-Hermitian matrix. Iterative methods play an important role for solving large sparse system of linear equations (1.1) as either solvers or preconditioners, in both theoretical studies and practical applications; for details, see [10, 31] and references therein.

Recently, with the booming development of the Internet, web search engines have become one of the most important Internet tools for information retrieval. One of the best-known algorithms in web search is Google’s PageRank algorithm [23]. PageRank is related to a link analysis algorithm for ranking Web pages whereby a page’s importance is determined according to the link structure of the Web. The core of the PageRank algorithm involves computing the principle eigenvector of the Google matrix representing the hyperlink structure of the web. The Google matrix is defined as a convex combination of matrices P and a certain rank-1 matrix:

(1.2)

where P is a column-stochastic matrix (i.e., the dangling nodes are already replaced by columns with 1/n), α (0≤α<1) is the damping factor, e is a column vector of all ones, and v is a personalization vector. It is common to set v=e/n in the PageRank model, see [14] for the details.

A key parameter in the model is the damping factor, a scalar that determines the weight given to the Web link graph in the model. Usually, the damping factor α is a real positive number close to 1. The question of the optimal choice of α is an interesting issue, one can see [4] for a recent study. It was argued in [18] that the PageRank vector derived from larger α such as 0.99 perhaps gives a ‘truer’ PageRank than α=0.85 does. In practice, it may therefore make sense to consider a large range of values [9]. Moreover, PageRank-type algorithms are used in application areas other than web search [22, 28], where the value of α often has a concrete meaning.

Usually, the Google matrix A is so extremely large and sparse that many algorithms for fast eigenvector computation in the field of the numerical linear algebra are unsuitable for this problem, because they require matrix inversions or matrix decompositions. For this reason, there are a variety of PageRank optimization methods which use the web link graph [13, 15, 21, 32]. Meanwhile, iterative methods based on matrix-vector products have been widely studied for this problem.

The original PageRank algorithm uses the power method to compute successive iterates that converge to the principal eigenvector of the Google matrix. However, the eigenvalues of A is the scaling of those of P, except for the dominant eigenvalue [6, 17]. Thus, when the largest eigenvalue of A is not well separated from other eigenvalues if the damping factor α is close to 1, then the power method converges very slowly. Many researchers proposed several methods to accelerate the convergence of the power method, such as the quadratic extrapolation method [14], the adaptive method [16], and the power extrapolation method [12]. And a number of iterative methods based on Krylov subspace were proposed for computing PageRank. For instance, Arnoldi-type method [9], power-Arnoldi method [25], Arnoldi-extrapolation method [26] and adaptively accelerated Arnoldi method [30]. For more theoretical analysis, we refer to [5, 27].

Generally speaking, these techniques can be classified into two groups: one is to reduce the total iterative steps, and the other is to reduce the computational cost per iteration. Unfortunately, these goals usually contradict each other. For a general review of these celebrated approaches, we refer the readers to [18–20].

On the other hand, some researchers focused their attention on the PageRank linear system [1, 7]. Iterative methods based on the linear system are good alternatives for computing the PageRank. We note that the smaller the damping factor is, the easier it is to solve the problem. Gleich et al. [8] proposed an inner-outer iteration method combined with Richardson iterations in which each iteration requires solving a linear system similar in its algebraic structure to the original one. This approach is very efficient as it can solve the PageRank problem with a lower damping factor β.

Recently, the idea of introducing iterative scheme based on splitting of the coefficient matrix into the linear systems has been successfully applied into the solution of linear equation (1.1) [2, 3, 29]. By taking the advantage of the inner-outer iteration algorithm in [8] and the idea of the splitting iterations, we propose a new algorithm for computing the PageRank vector in this paper.

This paper is organized as follows. In Sect. 2, we briefly introduce the PageRank linear system and the inner-outer iteration method for PageRank problem. In Sect. 3, we first study the multiplicative splitting iteration method, its theoretical properties, and then propose a multiplicative splitting iteration method for computing the PageRank. Numerical tests and comparisons are reported in Sect. 4. Finally, some brief concluding remarks are given in Sect. 5.

2 The inner-outer iteration method for computing PageRank

In this section, we briefly review the linear system formulation of PageRank problem and the inner-outer iteration method for computing PageRank.

2.1 PageRank linear system

By the Ergodic Theorem for Markov chains [11], the Markov chain defined by matrix A has a unique stationary probability distribution if A is aperiodic and irreducible. In the case of the PageRank model, the Google matrix A achieves these desirable properties.

Assuming that the probability distribution over the surfer’s location at time 0 is given by vector x (0), the probability distribution for the surfer’s location at time k is given by x (k)=A k x (0). The unique stationary distribution of the Markov chain is defined as lim k→∞ x (k), which is equivalent to lim k→∞ A k x (0), and is independent of the initial distribution x (0). This is simply the principal eigenvector of Google matrix A, which is exactly the PageRank vector we would like to compute. So the PageRank vector is defined as the vector satisfying x=Ax, with A is defined in (1.2).

Notice that A in (1.2) is dense because ve T is typically dense, but it never needs to be explicitly formed. In particular, the matrix-vector multiplication Ax can be efficiently computed by

(2.1)

where x is a probability vector, i.e., ∥x∥1=1. Obviously, if we give an initial vector with a unit 1-norm, then so do all the iterators x throughout the iteration, and the normalization is avoided.

Since e T x=1, the original PageRank problem can be recast from (2.1) as the linear system:

(2.2)

In what follows, we will refer to (2.2) as the PageRank linear system, and more details of the linear system formulation of PageRank problem can be found in [1, 7, 8].

2.2 The inner-outer iteration method for computing PageRank

By taking the fact that the original PageRank problem is easier to solve when the damping factor α is small, Gleich et al. [8] proposed an inner-outer iteration method for computing PageRank by using the linear system formulation of PageRank (2.2) and the stationary inner-outer iterations.

Instead of solving (2.2) directly, they consider the following stationary iteration:

(2.3)

defined as the outer iteration with a lower damping factor β, i.e., 0<β<α. Since solving the linear system with I−βP is still computationally difficult, they compute x k+1 using an inner Richardson iteration as follows. Setting the right-hand items of (2.3) as

(2.4)

then they define the inner linear system as

(2.5)

and apply the inner iteration

(2.6)

where, they take y 0=x k as the initial vector and assign the computed solution y l as the new x k+1.

To terminate the iterations, they apply the 1-norm of the residuals of the inner system (2.5) and the outer system (2.2) respectively as stopping criteria. For the inner iteration (2.6) they use

(2.7)

and for the outer iteration (2.3) they apply

(2.8)

the parameter η and τ are the inner and outer tolerances respectively.

The above algorithm is the core idea of the inner-outer iteration method for PageRank. More details and advantages of the inner-outer iteration method can be found in [8].

3 The multi-splitting iteration method for computing PageRank

In this part, we study the multiplicative splitting iterations and its theoretical properties, and then introduce our new algorithm based on the multiplicative splitting iterations. The motivation and implementation of our new algorithm are studied in details.

3.1 The multi-splitting iteration method for linear systems

The matrix splitting methods play an important role for solving large sparse system of linear equations (1.1). Let A=M i −N i  (i=1,2) be two splittings of the matrix \(A \in\mathcal {C}^{n\times n}\). The multiplicative splitting iteration method for solving the system of linear equations (1.1) is defined as follows (see [2]):

Given an initial guess x 0, for k=0,1,2,… , until {x k } converges, compute

(3.1)

If we introduce matrices

then the multiplicative splitting iteration method can be equivalently written in the form:

(3.2)

We note that (3.1) can be generalized to the two-step splitting iteration framework, and the following lemma describes a general convergence criterion for a two-step splitting iteration (see [3]).

Lemma 3.1

Let \(A \in\mathcal{C}^{n\times n}\), A=M i −N i  (i=1,2) be two splittings Footnote 1 of the matrix A, and let \(x_{0} \in\mathcal{C}^{n}\) be a given initial vector. If {x k } is a two-step iteration sequence defined by

then

Moreover, if the spectral radius \(\rho(M_{2}^{-1}N_{2}M_{1}^{-1}N_{1})\) is less than 1, then the iteration sequence {x k } converges to the unique solution \(x^{\ast}\in\mathcal{C}^{n\times n}\) of the system of linear equations (1.1) for all initial vectors \(x_{0}\in \mathcal{C}^{n} \).

Evidently, the multiplicative splitting iteration method for the original system of linear equations (1.1) is convergent if the spectral radius of the iteration matrix H msi is less than 1, i.e., ρ(H msi )<1.

3.2 The multi-splitting iteration method for computing PageRank

We now present our new algorithm for computing PageRank by using the PageRank linear system (2.2) and the multi-splitting iterations (3.1).

As is described in Sect. 2.1, the PageRank problem x=Ax can be reformulated as (2.2). Moreover, it is obvious that the smaller the damping factor is, the easier it is to solve the problem. In other words, the same PageRank problem with β as a damping factor, namely

is easier to solve than the original problem (2.2) if β is smaller than α.

Due to this consideration, we introduce two parameters β 1 and β 2 in the multiplicative splitting iterations for PageRank computation. This leads to the following multiplicative splitting iteration method for computing PageRank (or, simply denoted by MSI method).

Method 3.1

(MSI method)

Given an initial guess x 0, for k=0,1,2,… , until {x k } converges, compute

(3.3)

where α is the given damping factor, two parameters β 1 and β 2 satisfying 0≤β 1<α, 0≤β 2<α, as for the initial guess we may take x 0=e/∥e∥1, which is commonly used, see the following section.

The new method MSI is actually a two-parameter two-step iterative method and we will argue that there exists a reasonable convergent domain of two-parameters for MSI method.

Clearly, the multiplicative splitting iteration method for (2.2) is associated with the splitting of the coefficient matrix I−αP:

And the corresponding two-step iteration matrix of the multiplicative splitting iteration method (3.3) is given by

We now study the convergence properties of the multiplicative splitting iteration method for computing PageRank. For the convergence properties of the MSI method, we apply Lemma 3.1 to obtain the following main theorem.

Theorem 3.1

Let α be the damping factor in the PageRank linear system (2.2), and let M i =I−β i P, N i =(α−β i )P (i=1,2) are the two splittings of the matrix I−αP. Then the iterative matrix \(\widetilde{H}_{\mathit{msi}}(\beta_{1},\beta_{2})\) of the MSI method for PageRank computation is given by

(3.4)

and its spectral radius \(\rho(\widetilde{H}_{\mathit{msi}}(\beta _{1},\beta_{2}))\) is bounded by

therefore, it holds that

i.e., the multiplicative splitting iteration method for PageRank computation converges to the unique solution \(x^{\ast}\in\mathcal {C}^{n}\) of the linear system of equations (2.2).

Proof

By putting

in Lemma 3.1 and noting that M 1=I−β 1 P and M 2=I−β 2 P are diagonally dominant M-matrix for any positive constant β i <α (i=1,2) [24], we obtain Eq. (3.4).

By observing that if λ i is an eigenvalue of P, then

is an eigenvalue of \(\widetilde{H}_{\mathit{msi}}(\beta_{1},\beta _{2})\). Since |λ i |≤1, we get

with equality holding for λ 1=1, so \(\rho(\widetilde {H}_{\mathit{msi}}(\beta_{1},\beta_{2}))=\frac{(\alpha-\beta_{2}) (\alpha-\beta_{1})}{(1-\beta_{2})(1-\beta_{1})}<1\). □

Theorem 3.1 shows that the MSI method converges to the unique solution of the linear system (2.2), i.e., PageRank vector, for any given constant β 1 and β 2 satisfying 0≤β 1<α, 0≤β 2<α.

As an immediate consequence of Theorem 3.1, we have the following corollary.

Corollary 3.1

Let α, β 1, β 2 and |μ i | be defined in Theorem 3.1. If β 1 β 2<α, then |μ i |<α.

From Corollary 3.1, it can be concluded that the asymptotic convergence rate of the MSI method is faster than that of the power method with β 1 and β 2 satisfying some moderate conditions.

Next, we will discuss the implementation detail of MSI method for PageRank computation. Notice that each iteration of this method involves solving a two half-step linear system:

(3.5)

when 0<β 1<α, 0<β 2<α, but each of them is still computationally difficult, even when β i  (i=1,2) is small. In this case, the implementation of the half-step of MSI method in each iteration is similar to that of the inner-outer iteration method [8], i.e., instead of solving linear system with I−β i P (i=1,2) directly, we define the following inner linear systems as

(3.6)

where f 1=(α−β 1)Px k +(1−α)v or f 2=(α−β 2)Pu k+1+(1−α)v. Then we use the inner iteration (2.6) to get approximate solution u k+1 and x k+1 in (3.5), respectively. To terminate the inner iterations, we apply

(3.7)

as stopping criteria for (2.6).

For the original PageRank problem (2.2), the iterations of our algorithm is terminated, when the solution vector x k+1 satisfies the stopping criteria:

(3.8)

In particular, when at least one of the two parameters β 1 and β 2 in (3.3) equals to 0, we give some remarks about the proposed algorithm.

Remark 3.1

When β 1=β 2=0, the MSI method reduces to the power method [23]. That is, in each iteration of MSI method for PageRank computation, we need to apply the power method twice. Obviously, the convergence rate of the MSI method also reduces to the square of power method’s, i.e., α 2.

Remark 3.2

When β 1=0, β 2≠0, the MSI method reduces to a new special two-step method. That is, in each iteration of MSI method for PageRank computation, we first need to run power method only once in the half iteration step and then solve the remaining linear sub-system by inner iterations, the similar results hold for β 1≠0, β 2=0.

4 Numerical examples

In this section, we present the numerical experiments to illustrate the performance of the multiplicative splitting iteration method.

In our experiment, we test three methods for computing PageRank, i.e., the power method, the inner-outer iteration (called as ‘in-out’) method in [8] and the multiplicative splitting iteration (called as ‘MSI’) method, with damping factor α varying from 0.95 to 0.998. For the inner-outer method, it is observed in [8] that the algorithm is effective for a crude inner tolerance η and is not sensitive to the choice of the parameter β. Hence, our experiments use the choices η=10−2 and β=0.5. And for a fair comparison, just like in the inner-outer method, the inner tolerance in (3.7) is taken as η=10−2.

Because the 1-norm is a natural choice for the PageRank computation [14], in our comparisons we choose the 1-norm of the residual as stopping criterion. For the power method, the stopping criterion is

whereas for the inner-outer iteration method and the multiplicative splitting iteration method, the stopping criterion is

The test matrices are obtained from: http://www.cise.ufl.edu/research/sparse/matrices/groups.html. In Table 1, we list the characteristics of the test matrices including matrix size (n), number of nonzeros (nnz) and density (den), which is defined by

In our experiments, the largest test matrix is of size 683,446 and has 7,583,376 nonzeros.

Table 1 The characteristics of test matrices
Full size table

Numerical experiments were done on a computer with an Inter Corei3 2.27 GHz with 2G memory. For justification, we set the initial vector x (0)=e/∥e∥1, where e=(1,1,…,1) n , and n is the dimension of the Google matrix. When we state a speedup, we use relative percentage gain

(4.1)

where v r is a reference performance and v t is a test performance.

4.1 Choice of the number of β 1 and β 2

According to Theorem 3.1, the MSI method converges for any β 1 and β 2, satisfying 0≤β 1<α, 0≤β 2<α. Table 2 and Table 3 show the number of iterations of the MSI method for two matrices ‘Web-Stanford’ and ‘Stanford-Berkeley’ when α=0.99, β 1 grows from 0.1 to 0.9 and β 2 varies from 0.1 to 0.9, respectively.

Table 2 The number of iteration of MSI versus β 1 and β 2 for ‘Web-Stanford’ matrix
Full size table
Table 3 The number of iteration of MSI versus β 1 and β 2 for ‘Stanford-Berkeley’ matrix
Full size table

From Table 2 and Table 3, a rough conclusion is that with one of the parameters β 1 and β 2 determined, the iteration steps usually first decrease and then increase with the other parameter increasing; for instance, in Table 3, for β 2=0.1, the iteration steps first decrease for β 1 from 0.1 to 0.7, and then increase for β 1 from 0.8 to 0.9. However, to find an explicit relation between β 1 and β 2, or to find the optimal β 1 and β 2 appear very complicated for general PageRank matrices. Our extensive empirical experience shows that the choice with β 1=0.5 and β 2=0.85 generally yields good performance. That’s why we choose β 1=0.5 and β 2=0.85 for MSI method in our experiments.

4.2 Comparison of CPU time and the number of iteration

In Table 4, we list the number of iterations and CPU time for all the test matrices. In the MSI algorithm, according to the analysis of Sect. 4.1, we choose β 1=0.5 and β 2=0.85. The “Gain” in the last column of Table 4 denotes the efficiency of MSI over in-out in terms of CPU time calculated by (4.1). Numerical experiments indicate that our algorithm is better than the inner-outer iteration method.

Table 4 Comparison of various methods for test matrices
Full size table

In all examples, the multiplicative splitting iteration method converges with about half the iterative steps as that of the inner-outer iteration method. Obviously, our method requires less time than the inner-outer method for increasing value of α and n, where α and n denote respectively the damping factor and the size of the Google matrix. For the matrix “Stanford-Berkeley” with α=0.998, for example, the inner-outer iteration method and the multiplicative iteration method require 470.485 s, 426.671 s respectively to reach the desired accuracy; see Table 4. Thus the effectiveness of the proposed algorithm is verified. However, as for the matrix-vector products, they are approximately equal because each iteration of MSI method needs about two matrix-vector multiplications.

Before ending this section, we would like to discuss the complexity of the three methods. The computational cost of the power method per iteration is essentially a matrix-vector product. The in-out method is slightly more expensive than that of the power method per iteration but with much less total iteration steps. Since the MSI method per iteration consists of two in-out processes, then its cost per iteration approximates that of two steps of the in-out method; see, for instance, [8, 14].

5 Conclusions

In this paper, we proposed a generalized two-step iteration scheme for the computation of the PageRank vector and demonstrated that the iterative series produced by MSI method converge to the PageRank vector when the parameters β 1 and β 2 satisfy some moderate conditions. Our new algorithm is easy to be implemented. Numerical tests indicate that our new method works better than the inner-outer iteration method. In the future, the theory of the optimal choice for the two parameter β 1 and β 2 is still required to be further analyzed.