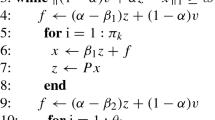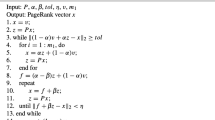1 Introduction

Consider the solution of the eigenvalue problem with the following form:

$$\begin{aligned} Ax=x,~~A=\alpha P+(1-\alpha )ve^T, \end{aligned}$$
(1.1)

where P is the column-stochastic matrix with appropriate dimension, i.e., its entries are nonnegative real numbers and all its columns sum to one. \(\alpha \in (0,1)\) denotes the damping factor which determines the weight given to the Web link graph. e is a column vector with all the ones, and v is a personalization vector or a teleportation vector. x is the eigenvector to be determined.

The above linear system (1.1), the so-call PageRank problem, occurs when one determines the importance of the Web pages based on the graph of the Web. PageRank can be viewed as a stationary distribution of a Markov chain (Langville and Meyer 2005). The PageRank has been widely exploited by Google as part of its search engine technology with the rapid development of the Internet. Although the exact ranking techniques and calculation approaches used by Google have been improved gradually, the PageRank method still receives great attention and becomes a hot issue in the field of science and engineering calculation in the last years.

At present, the method for solving the model (1.1) can be classified as a direct method and iterative method. The direct method often involves a lot of storage of the filling elements; especially when the coefficient matrix and the condition number are very large, the stability of the direct method is weak. In view of the sparsity of the matrix P, one can take advantage of the sparse structure to reduce the storage space and computation. The iterative method has become a popular approach for solving the eigenvalue problem. Sauer developed the Power method to compute PageRank, as it converges for every choice of a nonnegative starting vector (Sauer 2005). But, when the damping factor \(\alpha \) is large, the Power method easily causes a low efficiency in the convergence performance. An extrapolation method was proposed, which speeds up the convergence by calculating and then subtracting off estimates of the contributions of the second and third eigenvectors (Kamvar et al. 2003). Also, Kamvar et al. (2004) proposed the adaptive methods to improve the computation of PageRank, in which the PageRank of pages that have converged are not recomputed per iteration. PageRank-type algorithms are used in application areas other than Web search (Morrison et al. 2005). Capizzano considered the Jordan canonical form of the Google matrix, which is a potential contribution to the PageRank computation (Capizzano 2005). The Krylov subspace methods have also been considered recently. Jia presented the restarted refined Arnoldi method (Jia 1997) which can be regarded as the variant of the Arnoldi-type algorithm proposed by Golub et al. in (2006). A lot of approaches have been given; see the book (Langville and Meyer 2006), which provides a more comprehensive description of the PageRank problem, the papers (Bai et al. 2004, 1996; Bai 2012; Berkhin 2005; Gleich et al. 2010; Langville and Meyer 2005, 2006; Page et al. 1999; Yin et al. 2012; Golub and Van Loan 1996; Wu and Wei 2007; Kamvar et al. 2003; Huang and Ma 2015; Fan and Simpson 2015; Skardal et al. 2015), which contain many additional results and useful references, and the book (Stewart 1994), which includes overviews of the Markov chains.

Gu et al. (2015) developed a two-step matrix splitting iteration (TSS) for computing PageRank which is based on the inter–outer iteration (IOI) approach proposed by Gleich et al. in (2010) and Bai in (2012). Inspired by these works, in this paper, we construct a new relaxed two-step splitting iteration method (RTSS) for computing PageRank, which can be showed as a more efficient and flexible technique for this problem.

The remainder of the paper is organized as follows. In Sect. 2, we first give a brief review of the inter–outer iteration and two-step matrix splitting iteration methods. Also, consider a new relaxed two-step splitting iteration method for computing PageRank (1.1). In Sect. 3, we provide the convergence analysis in detail. Some numerical experiments are given to illustrate that the new method is efficient in Sect. 4. Finally, we end the paper with some conclusions in Sect. 5.

2 The RTSS method

In this section, we review the inner–outer iteration and two-step matrix splitting iteration approaches for computing the PageRank problem.

It is obvious that the eigenvector problem (1.1) is equivalent to solve the following linear system

$$\begin{aligned} (I-\alpha P)x=(1-\alpha )v, \end{aligned}$$
(2.1)

where I denotes the identity matrix with the corresponding dimension clear from the context.

By (2.1), it is known that the smaller the damping parameter \(\alpha \), the easier it is to solve the problem. In view of this consideration, Gleich et al. presented the inner–outer iteration approach for solving the system (2.1) (Gleich et al. 2010). Now, we give a brief review of this approach.

The coefficient matrix of (2.1) can be written as the following splitting:

$$\begin{aligned} \mathcal {A}:=(I-\alpha P)=M_1-N_1, \end{aligned}$$
(2.2)

where \(M_1=I-\beta P,~N_1=(\alpha -\beta )P.\) Then, the fixed point equation of (2.1) gives

$$\begin{aligned} (I-\beta P)x=(\alpha -\beta )Px+(1-\alpha )v. \end{aligned}$$

So the stationary outer iteration scheme

$$\begin{aligned} (I-\beta P)x^{k+1}=(\alpha -\beta )Px^k+(1-\alpha )v,~~~k=0,1,2\ldots , \end{aligned}$$

where \(0<\beta <\alpha .\) Moreover, the inner Richardson iteration

$$\begin{aligned} y^{j+1}=\beta Py^j+f \end{aligned}$$

is considered to speed up the outer iteration, where \(f=(\alpha -\beta )Px^k+(1-\alpha )v,~j=0,1,2\ldots ,l-1,~y^0=x^k.\) The l-th step inner solution \(y^l\) is assigned to be the next new \(x^{k+1}.\) The inner–outer iteration method is listed following Algorithm 2.1.

figure a

Based on the inner–outer iteration method, Gu et al. proposed a two-step splitting iteration (TSS) for PageRank which is closely related to the power method and Richardson iteration. It is shown in the following Algorithm 2.2

figure b

In fact, an iteration updating (2.3) was considered before the vector f can be computed in step 2 of the IOI method in Algorithm 2.1. It has been shown that the TSS method derived better performances than the IOI method. Inspired by Gleich et al. (2010), Gu et al. (2015), we further consider these methods by introducing a new relaxed parameter \(\gamma ,\) which can accelerate the TSS method to a certain extent. Specially, the TSS method only involves the stationary outer iteration scheme, namely, the inner iteration must be a precise iteration. In Algorithm 2.2, the inner loop is an inaccurate iteration. The convergence of the TSS method was shown by Theorem 2 in Gu et al. (2015); however, the inner loop that leads to Algorithm 2.2 is a non-stationary iteration, which has been ignored. So, in the paper, we will discuss the situation in detail.

Now, we consider the coefficient matrix \(\mathcal {A}\) in the following splitting:

$$\begin{aligned} \mathcal {A}=(I-\alpha P)=M_2-N_2, \end{aligned}$$
(2.3)

where \(M_2=\gamma I-\beta P, N_2=(\gamma -1)I+(\alpha -\beta )P,\) \(\gamma >0\). The relaxed two-step splitting iteration is described in the Algorithm 2.3.

figure c

Remark 2.1

In fact, if we set \(\gamma =1\), the RTSS is reduced to the TSS, so the RTSS approach is a generalized version of the TSS method. The flexible choice of the relaxation parameter \(\gamma \) of the RTSS generates excellent convergence performances than the TSS method, which can be seen in our numerical test parts.

Remark 2.2

Algorithm 2.3 is generated by the stationary iteration scheme, so it can be extended to study the absolute value equation (AVE) \(Ax+|x|=b\) (Mangasarian and Meyer 2006; Rohn 2012; Moosaei et al. 2015; Yong 2016; Yong et al. 2011), which can also be expressed in the form of a stationary equation. The importance of the AVE derives from the fact that quadratic programs, linear programs, bimatrix games and many other problems can all be reduced to a linear complementarity problem (LCP) (Cottle and Dantzig 1968; Cottle et al. 1992) which is equivalent to the AVE. Furthermore, we know that the AVE is NP-hard. It was testified in (Mangasarian 2007) by reducing the LCP corresponding to the NP-hard knapsack feasibility problem to an AVE. Under suitable hypotheses, such as when the singular values of the coefficient matrix A exceed 1, some efficient approaches can be utilized to solve the problem, for instance, generalized Newton method. In our future work, we will devote ourselves to investigate the AVE by the proposed method or its improved version.

3 The convergence properties

In this section, we discuss the convergence property of Algorithm 2.3 in detail. To this end, we rewrite Algorithm 2.3 as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x^{k+\frac{1}{2}}=\alpha Px^k+(1-\alpha )v, ~~x^{k,0}=x^{k+\frac{1}{2}},\\ x^{k,j+1}=\frac{\beta }{\gamma }Px^{k,j}+\frac{\gamma -1}{\gamma }x^{k+\frac{1}{2}}+\frac{\alpha -\beta }{\gamma }Px^{k+\frac{1}{2}}+\frac{1-\alpha }{\gamma }v, ~~j=0,1,2,\ldots ,m_k-1,\\ x^{k+1}=x^{k,m_k},~~ k=0,1,2,\ldots . \end{array} \right. \nonumber \\ \end{aligned}$$
(3.1)

Theorem 3.1

Let parameters \(0<\beta <\alpha <\gamma \le 1\) and \(1-\alpha <\gamma \), \(m_k\) be the inner loop numbers for the k-th outer iteration. Algorithm 2.3 generates the iteration scheme

$$\begin{aligned} x^{k+1}=T^kx^k+(1-\alpha )Q^kv,\quad k=0,1,2,\ldots , \end{aligned}$$
(3.2)

where

$$\begin{aligned} \left\{ \begin{array}{l} T^k=\frac{\alpha \gamma }{\beta }(\frac{\beta }{\gamma }P)^{m_k+1}+\frac{\alpha (\gamma -1)}{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j} +\frac{\alpha (\alpha -\beta )}{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j}P,\\ Q^k=(\frac{\beta }{\gamma }P)^{m_k}+\Sigma _{j=0}^{m_k-1}(\frac{\beta }{\gamma }P)^{j} +\frac{\alpha -\beta }{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j}. \end{array} \right. \end{aligned}$$
(3.3)

Then, the iteration solution \(x^k\) generated by Algorithm 2.3 converges to the exact solution \(x^*\) of the PageRank problem (1.1).

Proof

From (3.1), we obtain

$$\begin{aligned} x^{k+1}&=x^{k,m_k} \nonumber \\&=\frac{\beta }{\gamma }Px^{k,m_k-1}+\frac{(\gamma -1)I+(\alpha -\beta )P}{\gamma }\big (\alpha Px^k+(1-\alpha )v\big )+\frac{1-\alpha }{\gamma }v \nonumber \\&=\frac{\beta }{\gamma }P\left[ \frac{\beta }{\gamma }Px^{k,m_k-2}+\frac{(\gamma -1)I+(\alpha -\beta )P}{\gamma }\big (\alpha Px^k+(1-\alpha )v\big )+\frac{1-\alpha }{\gamma }v\right] \nonumber \\&\quad +\frac{(\gamma -1)I+(\alpha -\beta )P}{\gamma }\big (\alpha Px^k+(1-\alpha )v\big )+\frac{1-\alpha }{\gamma }v \nonumber \\&=\left( \frac{\beta }{\gamma }P\right) ^2x^{k,m_k-2}+\left[ \frac{\gamma -1}{\gamma }\left( \frac{\beta }{\gamma }P+I\right) +\frac{\alpha -\beta }{\gamma }\left( \frac{\beta }{\gamma }P+I\right) P\right] \alpha Px^k \nonumber \\&\quad +\big [\frac{\gamma -1}{\gamma }\left( \frac{\beta }{\gamma }P+I\right) +\frac{(\alpha -\beta ) P+I}{\gamma }(\frac{\beta }{\gamma }P+I)\big ](1-\alpha )v \nonumber \\&=\left( \frac{\beta }{\gamma }P\right) ^{m_k}x^{k,0}+\frac{\alpha (\gamma -1)}{\beta }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}x^k \quad +\frac{\alpha (\alpha -\beta )}{\beta }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}Px^k \nonumber \\&\quad +\frac{(1-\alpha )(\gamma -1)}{\gamma }\Sigma _{j=0}^{m_k-1}\left( \frac{\beta }{\gamma }P\right) ^{j}v +\frac{(1-\alpha )(\alpha -\beta )}{\beta }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}v\nonumber \\ {}&\quad +\frac{1-\alpha }{\gamma }\Sigma _{j=0}^{m_k-1}(\frac{\beta }{\gamma }P)^{j}v. \end{aligned}$$
(3.4)

Note that \(x^{k,0}=\alpha Px^k+(1-\alpha )v;\) moreover, we get

$$\begin{aligned} x^{k+1}&=\Big [\frac{\alpha \gamma }{\beta }(\frac{\beta }{\gamma }P)^{m_k+1}+\frac{\alpha (\gamma -1)}{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j} +\frac{\alpha (\alpha -\beta )}{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j}P\Big ]x^k\\&+\,\, (1-\alpha )\Big [(\frac{\beta }{\gamma }P)^{m_k}+\Sigma _{j=0}^{m_k-1}(\frac{\beta }{\gamma }P)^{j}+ \frac{\alpha -\beta }{\beta }\Sigma _{j=1}^{m_k}(\frac{\beta }{\gamma }P)^{j}\Big ]v, \end{aligned}$$

and therefore (3.2) holds.

It follows from (3.2)–(3.3) and the exact solution \(x^*\) that

$$\begin{aligned} x^*=T^kx^*+(1-\alpha )Q^kv, \end{aligned}$$
(3.5)

where \(T^k\) denotes the k-th step iteration matrix. Combined with (3.2) and (3.5), we have

$$\begin{aligned} x^{k+1}-x^*=T^k(x^{k}-x^*)=\cdots =T^kT^{k-1}\cdots T^0(x^0-x^*). \end{aligned}$$
(3.6)

Then, one gives

$$\begin{aligned} \lim _{k\rightarrow +\infty }x^k=x^* \end{aligned}$$

if and only if

$$\begin{aligned} \lim _{k\rightarrow +\infty }T^kT^{k-1}\cdots T^0=0. \end{aligned}$$

If \(\Vert T^k\Vert _1<\eta \) (\(0<\eta <1\)), then

$$\begin{aligned} \lim _{k\rightarrow +\infty }&\Vert T^kT^{k-1}\cdots T^0\Vert _1\\&\le \lim _{k\rightarrow +\infty }\Vert T^k\Vert _1\Vert T^{k-1}\Vert _1\cdots \Vert T^0\Vert _1 \nonumber \\&=\prod _{k=0}^{+\infty }\Vert T^k\Vert _1\le \prod _{k=0}^{+\infty }\eta =0. \nonumber \end{aligned}$$
(3.7)

Now, we will show the existence of the upper bound parameter \(\eta ^k\).

Table 1 Numerical results with \(\alpha =0.901\), \(\beta =0.9\) and \(\gamma =0.94\)
Full size table
Table 2 Numerical results with \(\alpha =0.45\), \(\beta =0.4\) and \(\gamma =0.8\)
Full size table

By (3.3), we get

$$\begin{aligned} T^k&=\frac{\alpha \gamma }{\beta }\left[ \left( \frac{\beta }{\gamma }P\right) ^{m_k+1}+\frac{\gamma -1}{\gamma }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j} +\frac{\alpha -\beta }{\gamma }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}P\right] \\&=\frac{\alpha \gamma }{\beta }\left[ \left( \frac{\beta }{\gamma }P\right) ^{m_k+1}+\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j} \left( \frac{\gamma -1}{\gamma }I+\frac{\alpha -\beta }{\gamma }P\right) \right] \\&=\frac{\alpha \gamma }{\beta }\left[ \left( \frac{\beta }{\gamma }P\right) ^{m_k+1}+\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j} \left( \left( I-\frac{\beta }{\gamma }P\right) -\left( \frac{1}{\gamma }I-\frac{\alpha }{\gamma }P\right) \right) \right] \\&=\frac{\alpha \gamma }{\beta }\left[ \left( \frac{\beta }{\gamma }P\right) ^{m_k+1}+\frac{\beta }{\gamma }P-\left( \frac{\beta }{\gamma }P\right) ^{m_k+1}- \Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}\left( \frac{1}{\gamma }I-\frac{\alpha }{\gamma }P\right) \right] \\&=\frac{\alpha \gamma }{\beta }\left[ \frac{\beta }{\gamma }P-\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}\left( \frac{1}{\gamma }I-\frac{\alpha }{\gamma }P\right) \right] . \end{aligned}$$

It follows from \(e^TP=e^T\) that

$$\begin{aligned} e^TT^k&=\frac{\alpha \gamma }{\beta }\bigg [ \frac{\beta }{\gamma }e^T-e^T\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }P\right) ^{j}\big (\frac{1}{\gamma }I-\frac{\alpha }{\gamma }P\big )\bigg ]\\&=\frac{\alpha \gamma }{\beta }\bigg [ \frac{\beta }{\gamma }e^T-\frac{1-\alpha }{\gamma }\Sigma _{j=1}^{m_k}\left( \frac{\beta }{\gamma }\right) ^{j}e^T\bigg ] \nonumber \\&=\frac{\alpha \gamma }{\beta }\bigg [\frac{\beta }{\gamma }-\frac{\beta }{\gamma }\frac{(1-\alpha )[1-(\frac{\beta }{\gamma })^{m_k}]}{\gamma -\beta }\bigg ]e^T \nonumber \\&=\frac{\alpha \gamma }{\beta }\bigg [\frac{\beta (\gamma -\beta )-\beta (1-\alpha )[1-(\frac{\beta }{\gamma })^{m_k}]}{\gamma (\gamma -\beta )}\bigg ]e^T \nonumber \\&=\eta ^ke^T\nonumber , \end{aligned}$$
(3.8)
Fig. 1
figure 1

The bfwa398 matrix with \(\alpha =0.901\), \(\beta =0.9\) and \(\gamma =0.94\)

Full size image
Fig. 2
figure 2

The rdb5000 matrix with \(\alpha =0.901\), \(\beta =0.9\) and \(\gamma =0.94\)

Full size image
Fig. 3
figure 3

The cryg10000 matrix with \(\alpha =0.901\), \(\beta =0.9\) and \(\gamma =0.94\)

Full size image
Fig. 4
figure 4

The bfwa398 matrix with \(\alpha =0.45\), \(\beta =0.4\) and \(\gamma =0.8\)

Full size image
Fig. 5
figure 5

The rdb5000 matrix with \(\alpha =0.45\), \(\beta =0.4\) and \(\gamma =0.8\)

Full size image
Fig. 6
figure 6

The cryg10000 matrix with \(\alpha =0.45\), \(\beta =0.4\) and \(\gamma =0.8\)

Full size image

where

$$\begin{aligned} \eta ^k:=\frac{\alpha \gamma }{\beta }\bigg [\frac{\beta (\gamma -\beta )-\beta (1-\alpha )[1-(\frac{\beta }{\gamma })^{m_k}]}{\gamma (\gamma -\beta )}\bigg ]. \end{aligned}$$

As

$$\begin{aligned} 0<\beta <\alpha <\gamma \le 1 ~~\text {and}~~0<1-\alpha <\gamma , \end{aligned}$$
(3.9)

it holds that

$$\begin{aligned} 0<\beta <\gamma ,~~0<\frac{\beta (1-\alpha )}{\gamma ^2}<1. \end{aligned}$$
(3.10)

Furthermore, we have

$$\begin{aligned} \frac{\beta (\gamma -\beta )-\beta (1-\alpha )[1-(\frac{\beta }{\gamma })^{m_k}]}{\gamma (\gamma -\beta )}&\le \frac{\beta (\gamma -\beta )-\beta (1-\alpha )[1-\frac{\beta }{\gamma })]}{\gamma (\gamma -\beta )} \nonumber \\&=\frac{\beta \gamma (\gamma -\beta )-\beta (1-\alpha )[\gamma -\beta ]}{\gamma ^2(\gamma -\beta )} \nonumber \\&=\frac{\beta }{\gamma }(1-\frac{1-\alpha }{\gamma })<1. \end{aligned}$$
(3.11)

So,

$$\begin{aligned} \eta ^k\le \alpha (1-\frac{1-\alpha }{\gamma })=:\eta <1. \end{aligned}$$

By (3.8)–(3.11), it means that

$$\begin{aligned} \Vert T^k\Vert _1\le \eta <1. \end{aligned}$$

Combining with (3.7), we immediately get the conclusion, that is, the iteration solution \(x^k\) generated by Algorithm 2.3 converges to the exact solution \(x^*\) of the PageRank problem (1.1). This completes the proof. \(\square \)

4 Numerical experiments

In this section, we report some numerical results to illustrate the effectiveness of the relaxed two-step iteration (RTSS) method for solving the linear system (1.1) arising from the Google PageRank problem. All examples have been carried out by MATLAB R2011b (7.13), Intel(R) Core(TM) i7-2670QM, CPU 2.20GHZ, RAM 8.GB PC Environment. We compare our algorithm to the IOI and TSS methods. We use the following examples to examine these approaches with different iteration performances from these aspects of the iteration numbers(denoted by ‘IT’), elapsed CPU time in seconds (denoted by ‘CPU’) and the residual (denoted as ’RES’) defined by

$$\begin{aligned} \mathrm {RES}:=\Vert \alpha z^k+(1-\alpha )v-x^k\Vert _1<10^{-14}. \end{aligned}$$

We compare three approaches by choosing different parameters \(\alpha \), \(\beta \), and \(\gamma \) in a reasonable interval. Three sparse matrices, bfwa398, rdb5000 and cryg10000, are selected from the University of Florida sparse matrix collection (available at http://www.cise.ufl.edu/research/sparse/mat/). All numerical tests are shown in Tables 1,2 and Figs. 1, 2, 3, 4, 5 and 6. These results illustrate that the convergence of the RTSS approach performs better than the TSS and IOI methods’ both CPU time and the numbers of the iteration step, which demonstrates that the introduced approach is efficient.

5 Conclusion

In this paper, we have furthermore improved the two-step splitting iteration by introducing an additional relaxation parameter \(\gamma \) and presented a relaxed two-step splitting iteration for solving the PageRank problem, which can be regarded as a type of generalization for the TSS method. If we choose \(\gamma =1\), the RTSS approach is reduced to the TSS method. It is readily seen that the selection of the proper parameters \(\gamma \) may generate better convergence performances than the TSS and IOI methods. Numerical experiments show the effectiveness of the proposed approach.