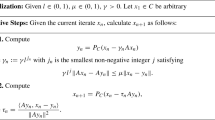New algorithms and convergence theorems for solving variational inequalities with non-Lipschitz mappings

Abstract

We propose and study new projection-type algorithms for solving pseudomonotone variational inequality problems in real Hilbert spaces without assuming Lipschitz continuity of the cost operators. We prove weak and strong convergence theorems for the sequences generated by these new methods. The numerical behavior of the proposed algorithms when applied to several test problems is compared with that of several previously known algorithms.

1 Introduction

We consider the variational inequality problem (VI) [10, 11] of finding a point x^∗∈ C such that

$$ \langle Fx^{*},x-x^{*}\rangle \geq 0 \ \ \ \forall x\in C, $$

(1)

where C is a nonempty, closed, and convex subset of a real Hilbert space H, F : H → H is a single-valued mapping, and 〈⋅,⋅〉 and ∥⋅∥ are the inner product and the induced norm on H, respectively. We denote by Sol(C,F) the solution set of problem (1). Variational inequality problems are fundamental in a broad range of mathematical and applied sciences; the theoretical and algorithmic foundations, as well as the applications of variational inequalities, have been extensively studied in the literature and continue to attract intensive research. For a detailed exposition of the field in the finite-dimensional setting, see, for instance, [9] and the extensive list of references therein.

Many authors have proposed and analyzed several iterative methods for solving the variational inequality (1). The simplest one is the following projection method, which can be considered an extension of the projected gradient method for optimization problems:

$$ x_{n+1}=P_{C}(x_{n}-\lambda Fx_{n}), $$

(2)

for each n ≥ 1, where P_C denotes the metric projection from H onto C. Convergence results for this method require some monotonicity properties of F. This method converges under quite strong hypotheses. If F is Lipschitz continuous with Lipschitz constant L and α-strongly monotone, then the sequence generated by (2) converges to an element of Sol(C,F) for $\lambda \in \left (0, \frac {2\alpha }{L^{2}}\right )$.

In order to find an element of Sol(C,F) under weaker hypotheses, Korpelevich [21] (and, independently, Antipin [1]) proposed to replace method (2) by the extragradient method in the finite-dimensional Euclidean space $\mathbb {R}^{m}$ for a monotone and L-Lipschitz continuous operator $F: \mathbb {R}^{m}\to \mathbb {R}^{m}$. Her algorithm is of the form

$$ x_{0}\in C,\ \ y_{n}=P_{C}(x_{n}-\lambda Fx_{n}),\ \ x_{n+1}=P_{C}(x_{n}-\lambda Fy_{n}), $$

(3)

where $\lambda \in \left (0,\frac {1}{L}\right )$. The sequence {x_n} generated by (3) converges to an element of Sol(C,F) provided that Sol(C,F) is nonempty.

In recent years, the extragradient method has been extended to infinite-dimensional spaces in various ways; see, for example, [3,4,5,6, 22, 25, 26, 30,31,32] and the references cited therein.

We may observe that, when F is not Lipschitz continuous or the constant L is very difficult to compute, Korpelevich’s method is not so practical because we cannot determine the step size λ. To overcome this difficulty, Iusem [16] proposed in the Euclidean space $\mathbb {R}^{m}$ the following iterative algorithm for solving Sol(C,F):

$$ y_{n}=P_{C}(x_{n}-\gamma_{n} Fx_{n}),\ \ x_{n+1}=P_{C}(x_{n}-\lambda_{n} Fy_{n}), $$

(4)

where γ_n > 0 is computed through an Armijo-type search and $\lambda _{n}=\frac {\langle Fy_{n},x_{n}-y_{n}\rangle }{\|Fy_{n}\|^{2}}$. This modification has allowed the author to establish convergence without assuming Lipschitz continuity of the operator F.

In order to determine the step size γ_n in (4), we need to use a line search procedure which contains one projection. So at iteration n, if this procedure requires m_n steps to arrive at the appropriate γ_n, then we need to evaluate m_n projections.

To overcome this difficulty, Iusem and Svaiter [19] proposed a modified extragradient method for solving monotone variational inequalities which only requires two projections onto C at each iteration. A few years later, this method was improved by Solodov and Svaiter [30]. They introduced an algorithm for solving (1) in finite-dimensional spaces. As a matter of fact, their method applies to a more general case, where F is merely continuous and satisfies the following condition:

$$ \langle Fx, x - x^{*} \rangle \geq 0 \ \ \forall x\in C \text{ and } x^{*}\in Sol(C,F). $$

(5)

Property (5) holds if F is monotone or, more generally, pseudomonotone on C in the sense of Karamardian [20]. More precisely, Solodov and Svaiter proposed the following algorithm:

Vuong and Shehu [36] have recently modified the result of Solodov and Svaiter in the spirit of Halpern [14], and obtained strong convergence in infinite-dimensional real Hilbert spaces. Their algorithm is of the following form:

Vuong and Shehu proved that if F : H → H is pseudomonotone, uniformly continuous, and weakly sequentially continuous on bounded subsets of C, and the sequence {α_n} satisfies the conditions $\lim _{n\to \infty }\alpha _{n}=0$ and ${\sum }_{n=1}^{\infty } \alpha _{n}=\infty$, then the sequence {x_n} generated by Algorithm 2 converges strongly to p ∈ Sol(C,F), where p = P_Cx₁.

Motivated and inspired by [30, 36], and by the ongoing research in these directions, in the present paper, we introduce new algorithms for solving variational inequalities with uniformly continuous pseudomonotone operators. In particular, we use a different Armijo-type line search in order to obtain a hyperplane which strictly separates the current iterate from the solutions of the variational inequality under consideration.

Our paper is organized as follows. We first recall in Section 2 some basic definitions and results. Our algorithms are presented and analyzed in Section 3. In Section 4, we present several numerical experiments which illustrate the performance of the algorithms. They also provide a preliminary computational overview by comparing it with the performance of several related algorithms.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty, closed, and convex subset of H. The weak convergence of a sequence $\{x_{n}\}_{n=1}^{\infty }$ to x as $n \to \infty$ is denoted by $x_{n}\rightharpoonup x$ while the strong convergence of $\{x_{n}\}_{n=1}^{\infty }$ to x as $n \to \infty$ is denoted by x_n → x. For each x,y ∈ H, we have

$$ \|x+y\|^{2}\le \|x\|^{2}+2\langle y,x+y\rangle. $$

Definition 2.1

Let F : H → H be an operator. Then,

• 1. The operator F is called L-Lipschitz continuous with Lipschitz constant L > 0 if

  $$ \|Fx-Fy\|\le L \|x-y\| \ \ \ \forall x,y \in H. $$

  If L = 1, then the operator F is called nonexpansive and if L ∈ (0,1), then F is called a strict contraction.

• 2. F is called monotone if

  $$ \langle Fx-Fy,x-y \rangle \geq 0 \ \ \ \forall x,y \in H. $$

• 3. F is called pseudomonotone if

  $$ \langle Fx,y-x \rangle \geq 0 \Longrightarrow \langle Fy,y-x \rangle \geq 0 \ \ \ \forall x,y \in H. $$

• 4. F is called α-strongly monotone if there exists a constant α > 0 such that

  $$ \langle Fx-Fy,x-y\rangle\geq \alpha \|x-y\|^{2} \ \ \forall x,y\in H. $$

• 5. The operator F is called sequentially weakly continuous if the weak convergence of a sequence {x_n} to x implies that the sequence {Fx_n} converges weakly to Fx.

It is easy to see that every monotone operator is pseudomonotone, but the converse is not true.

For each point x ∈ H, there exists a unique nearest point in C, denoted by P_Cx, which satisfies ∥x − P_Cx∥≤∥x − y∥ ∀y ∈ C. The mapping P_C is called the metric projection of H onto C. It is known that P_C is nonexpansive.

Lemma 2.1

([13]) Let C be a nonempty, closed, and convex subset of a real Hilbert space H. If x ∈ H and z ∈ C, then z = P_Cx⇔〈x − z,z − y〉≥ 0 ∀y ∈ C.

Lemma 2.2

([13]) Let C be a closed and convex subset of a real Hilbert space H and let x ∈ H. Then,

i) ∥P_Cx − P_Cy∥² ≤〈P_Cx − P_Cy,x − y〉 ∀y ∈ H;

ii) ∥P_Cx − y∥² ≤∥x − y∥² −∥x − P_Cx∥² ∀y ∈ C.

More properties of the metric projection can be found in Section 3 in [13].

The following lemmas are useful in the convergence analysis of our proposed methods.

Lemma 2.3

([17, 18]) Let H₁ and H₂ be two real Hilbert spaces. Suppose F : H₁ → H₂ is uniformly continuous on bounded subsets of H₁ and M is a bounded subset of H₁. Then, F(M) is bounded.

Lemma 2.4

([7], Lemma 2.1) Let C be a nonempty, closed, and convex subset of a real Hilbert space H, and let F : C → H be pseudomonotone and continuous. Then, x^∗ belongs to Sol(C,F) if and only if

$$ \langle Fx, x - x^{*}\rangle\geq 0 \ \ \forall x \in C. $$

The following lemma can be found in [15].

Lemma 2.5

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let h be a real-valued function on H and define K := {x ∈ C : h(x) ≤ 0}. If K is nonempty and h is Lipschitz continuous on C with modulus 𝜃 > 0, then

$$ dist(x, K) \geq \theta^{-1} \max\{h(x), 0\}\ \ \forall x \in C, $$

where dist(x,K) denotes the distance of x to K.

Lemma 2.6

([28]) Let C be a nonempty subset of H and let {x_n} be a sequence in H such that the following two conditions hold:

• i) For every x ∈ C, $\lim _{n\to \infty }\|x_{n}-x\|$ exists;

• ii) Every sequential weak cluster point of {x_n} is in C.

  Then, {x_n} converges weakly to a point in C.

The next technical lemma is very useful and has been used by many authors; see, for example, Liu [23] and Xu [37]. A variant of this lemma has already been used by Reich in [29].

Lemma 2.7

Let {a_n} be sequence of non-negative real numbers such that:

$$ a_{n+1}\le (1-\alpha_{n})a_{n}+\alpha_{n} b_{n}, $$

where {α_n}⊂ (0,1) and {b_n} is a real sequence such that

• a) ${\sum }_{n=0}^{\infty } \alpha _{n}=\infty$;

• b) $\limsup _{n\to \infty }b_{n}\le 0$.

  Then, $\lim _{n\to \infty }a_{n}=0$.

3 Main results

In this section, we introduce two new methods for solving (1). In the convergence analysis of these algorithms, the following three conditions are assumed.

Condition 3.1

The feasible set C is a nonempty, closed, and convex subset of the real Hilbert space H.

Condition 3.2

The operator F : C → H associated with the VI (1) is pseudomonotone and uniformly continuous on C.

Condition 3.3

The mapping F : H → H satisfies the following property:

$$ \text{ whenever } \{x_{n}\} \subset C, x_{n} \rightharpoonup z, \text{ one has } \|F(z)\| \le \liminf_{n\to\infty}\|Fx_{n}\|. $$

Condition 3.4

The solution set of the VI (1) is nonempty, that is, Sol(C,F)≠∅.

3.1 Weak convergence

We begin by introducing a new projection-type algorithm.

Lemma 3.1

Assume that Conditions 3.1–3.4 hold. Then, the Armijo-type search rule (3.1) is well defined.

Proof

Since l ∈ (0,1) and the operator F is continuous on C, the sequence {〈Fx_n − F(x_n − l^jr_λ(x_n)),r_λ(x_n)〉} converges to zero as j tends to infinity. On the other hand, as a consequence of Step 1, ∥r_λ(x_n)∥ > 0 (otherwise, the procedure would have stopped). Therefore, there exists a non-negative integer j_n satisfying (3.1). □

Lemma 3.2

Assume that the sequence {x_n} is generated by Algorithm 3. Then, we have

$$ \langle Fx_{n}, r_{\lambda} (x_{n})\rangle \geq \lambda^{-1}\|r_{\lambda} (x_{n})\|^{2}. $$

Proof

Since P_C is the metric projection, we know that ∥x − P_Cy∥² ≤〈x − y,x − P_Cy〉 for all x ∈ C and y ∈ H. Let y = x_n − λFx_n,x = x_n. Then,

$$ \|x_{n}-P_{C}(x_{n}-\lambda Fx_{n})\|^{2}\le \lambda \langle Fx_{n}, x_{n}-P_{C}(x_{n}-\lambda Fx_{n})\rangle $$

and so

$$ \langle Fx_{n}, r_{\lambda} (x_{n})\rangle \geq \lambda^{-1}\|r_{\lambda}(x_{n})\|^{2}. $$

□

Lemma 3.3

Assume that Conditions 3.1–3.4 hold. Let x^∗ be a solution of problem (1) and let the function h_n be defined by (3.1). Then, $h_{n} (x_{n}) =\frac {\tau _{n}}{2\lambda }\|r_{\lambda } (x_{n})\|^{2}$ and h_n(x^∗) ≤ 0. In particular, if r_λ(x_n)≠ 0, then h_n(x_n) > 0.

Proof

The first claim of Lemma 3.3 is obvious. In order to prove the second claim, Let x^∗ be a solution of problem (1) Then by Lemma 2.4, we have h_n(x^∗) = 〈Fy_n,y_n − x^∗〉≥ 0. We also have

$$ \begin{array}{@{}rcl@{}} h_{n}(x^{*})&=&\langle Fy_{n},x^{*}-x_{n}\rangle+\frac{\tau_{n}}{2\lambda}\|r_\lambda(x_n)\|^2\\ &=&-\langle Fy_{n},x_{n}-y_{n}\rangle- \langle Fy_{n},y_{n}-x^{*}\rangle+\frac{\tau_{n}}{2\lambda}\|r_\lambda(x_n)\|^2\\ &\le& -\tau_{n} \langle Fy_{n},r_{\lambda}(x_{n})\rangle+\frac{\tau_{n}}{2\lambda}\|r_\lambda(x_n)\|^2. \end{array} $$

(10)

On the other hand, by (3.1) we have

$$ \langle Fx_{n}-Fy_{n}, r_{\lambda} (x_{n})\rangle \le\frac{ \mu}{2} \|r_{\lambda} (x_{n})\|^{2}. $$

Thus,

$$ \langle Fy_{n}, r_{\lambda}(x_{n})\rangle \geq \langle Fx_{n}, r_{\lambda} (x_{n})\rangle -\frac{\mu}{2} \|r_{\lambda} (x_{n})\|^{2}. $$

Using Lemma 3.2, we get

$$ \langle Fy_{n}, r_{\lambda}(x_{n})\rangle\geq \left( \frac{1}{\lambda}-\frac{\mu}{2}\right) \|r_{\lambda} (x_{n})\|^{2}. $$

(11)

Combining (10) and (11), we now see that

$$ h_{n}(x^{*})\le -\frac{\tau_{n}}{2} \left( \frac{1}{\lambda}-\mu\right) \|r_{\lambda} (x_{n})\|^{2}. $$

Thus, h_n(x^∗) ≤ 0, as asserted. □

We adapt the technique developed in [35] to obtain the following result.

Lemma 3.4

Assume that Conditions 3.1–3.4 hold. Let {x_n} be a sequence generated by Algorithm 3. If there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges weakly to z ∈ C and $\lim _{k\to \infty }\|x_{n_{k}}-z_{n_{k}}\|=0$, then z ∈ Sol(C,F).

Proof

Since $z_{n_{k}}=P_{C}(x_{n_{k}}-\lambda F_{n_{k}})$, we have

$$ \langle x_{n_{k}}-\lambda Fx_{n_{k}}-z_{n_{k}},x-z_{n_{k}}\rangle \le 0 \ \ \forall x\in C $$

or equivalently,

$$ \langle x_{n_{k}}-z_{n_{k}},x-z_{n_{k}}\rangle \le \langle \lambda Fx_{n_{k}},x-z_{n_{k}}\rangle \ \ \forall x\in C. $$

This implies that

$$ \left\langle \frac{x_{n_{k}}-z_{n_{k}}}{\lambda},x-z_{n_{k}}\right\rangle +\langle Fx_{n_{k}},z_{n_{k}}-x_{n_{k}}\rangle \le \langle Fx_{n_{k}},x-x_{n_{k}}\rangle \ \ \forall x\in C. $$

(12)

Since $\|x_{n_{k}}-z_{n_{k}}\|\to 0$ as $k \to \infty$ and since the sequence $\{Fx_{n_{k}}\}$ is bounded, taking $k \to \infty$ in (12), we get

$$ \liminf_{k\to\infty}\langle Fx_{n_{k}},x-x_{n_{k}}\rangle \geq 0. $$

(13)

Next, to show that z ∈ Sol(C,F), we first choose a decreasing sequence {𝜖_k} of positive numbers which tends to 0. For each k, we denote by N_k the smallest positive integer such that

$$ \langle Fx_{n_{j}},x-x_{n_{j}}\rangle +\epsilon_{k} \geq 0 \ \ \forall j\geq N_{k}, $$

(14)

where the existence of N_k follows from (13). Since the sequence {𝜖_k} is decreasing, it is easy to see that the sequence {N_k} is increasing. Furthermore, for each k, since $\{x_{N_{k}}\}\subset C$, we have $Fx_{N_{k}}\ne 0$ and setting

$$ v_{N_{k}} = \frac{Fx_{N_{k}}}{\|Fx_{N_{k}}\|^{2} }, $$

we have $\langle Fx_{N_{k}}, x_{N_{k}}\rangle = 1$ for each k. Now, we can deduce from (14) that for each k,

$$ \langle Fx_{N_{k}}, x+\epsilon_{k} v_{N_{k}}-x_{N_{k}}\rangle \geq 0. $$

Since the operator F is pseudomonotone, it follows that

$$ \langle F(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-x_{N_{k}}\rangle \geq 0. $$

This implies that

$$ \langle Fx, x-x_{N_{k}}\rangle \geq \langle Fx-F(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-x_{N_{k}} \rangle-\epsilon_{k} \langle Fx, v_{N_{k}}\rangle. $$

(15)

Next, we show that $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Indeed, we have $x_{n_{k}}\rightharpoonup z\in C \text { as } k \to \infty$. Since F satisfies Condition 3.3, we have

$$ 0 < \|Fz\|\le \liminf_{k\to \infty}\|Fx_{n_{k}}\|. $$

Since $\{x_{N_{k}}\}\subset \{x_{n_{k}}\}$ and 𝜖_k → 0 as $k \to \infty$, we obtain

$$ \begin{array}{@{}rcl@{}} 0 \le \limsup_{k\to\infty} \|\epsilon_{k} v_{N_{k}} \| = \limsup_{k\to\infty} \left( \frac{\epsilon_{k}}{\|Fx_{n_{k}}\|}\right)\le \frac{\limsup_{k\to\infty}\epsilon_{k} } {\liminf_{k\to\infty}\|Fx_{n_{k}}\|}=0, \end{array} $$

which implies that $\lim _{k\to \infty } \epsilon _{k} v_{N_{k}} = 0$.

Now, letting $k\to \infty$, we see the right-hand side of (15) tends to zero because F is uniformly continuous, the sequences $\{x_{n_{k}}\}$ and $\{v_{N_{k}}\}$ are bounded, and $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Thus, we get

$$ \liminf_{k\to\infty}\langle Fx,x-x_{N_{k}}\rangle \geq 0. $$

Hence, for all x ∈ C, we have

$$ \langle Fx, x-z\rangle=\lim_{k\to\infty} \langle Fx, x-x_{N_{k}}\rangle =\liminf_{k\to\infty} \langle Fx, x-x_{N_{k}}\rangle \geq 0. $$

Appealing to Lemma 2.4, we obtain that z ∈ Sol(C,F) and the proof is complete. □

Lemma 3.5

Assume that Conditions 3.1–3.3 hold. Let {x_n} be a sequence generated by Algorithm 3. If $\lim _{n\to \infty }\tau _{n}\|r_{\lambda } (x_{n})\|^{2}=0$, then $\lim _{n\to \infty }\|x_{n}-z_{n}\|=0$.

Proof

First we consider the case where $\liminf _{n\to \infty }\tau _{n}>0$. In this case, there is a constant τ > 0 such that τ_n ≥ τ > 0 for all $n\in \mathbb {N}$. We then have

$$ \begin{array}{@{}rcl@{}} \|x_{n}-z_{n}\|^{2} = \frac{1}{\tau_{n}} \tau_{n}\|x_{n}-z_{n}\|^{2}\le \frac{1}{\tau}.\tau_{n}\|x_{n}-z_{n}\|^{2}=\frac{1}{\tau}\tau_{n}\|r_\lambda(x_n)\|^2. \end{array} $$

(16)

Combining the assumption and (16), we see that

$$ \lim_{n \to \infty}\|x_{n}-z_{n}\|=0. $$

Second, we consider the case where $\liminf _{n\to }\tau _{n}=0$. In this case, we take a subsequence {n_k} of {n} such that

$$ \lim_{k\to\infty}\tau_{n_{k}}=0 $$

and

$$ \lim_{k\to \infty}\|x_{n_{k}}-z_{n_{k}}\|=a>0. $$

(17)

Let $y_{n_{k}}=\frac {1}{l}\tau _{n_{k}} z_{n_{k}}+(1-\frac {1}{l}\tau _{n_{k}})x_{n_{k}}$. Since $\lim _{n\to \infty }\tau _{n}\|r_{\lambda } (x_{n})\|^{2}=0$, we have

$$ \lim_{k\to\infty}\|y_{n_{k}}-x_{n_{k}}\|^{2}=\lim_{k\to\infty}\frac{1}{l^{2}}\tau_{n_{k}}. \tau_{n_{k}}\|x_{n_{k}}-z_{n_{k}}\|^{2}=0. $$

(18)

From the step size rule (3.1) and the definition of y_k, it follows that

$$ \langle Fx_{n_{k}}-Fy_{n_{k}}, x_{n_{k}}-z_{n_{k}}\rangle >\frac{ \mu }{2}\|x_{n_{k}}-z_{n_{k}}\|^{2}. $$

(19)

Since F is uniformly continuous on bounded subsets of C, (18) implies that

$$ \lim_{k\to\infty} \|Fx_{n_{k}}-Fy_{n_{k}}\|=0. $$

(20)

Combining now (19) and (20), we obtain

$$ \lim_{k\to \infty}\|x_{n_{k}}-z_{n_{k}}\|=0. $$

This, however, is a contradiction to (17). It follows that $\lim _{n \to \infty } \|x_{n} - z_{n}\| = 0$ and this completes the proof of the lemma. □

Theorem 3.1

Assume that Conditions 3.1–3.4 hold. Then, any sequence {x_n} generated by Algorithm 3 converges weakly to an element of Sol(C,F).

Proof

Claim 1. We first prove that {x_n} is a bounded sequence. Indeed, for p ∈ Sol(C,F), we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}=\|P_{C_{n}}x_{n}-p\|^{2}&\le& \|x_{n}-p\|^{2}-\|P_{C_{n}}x_{n}-x_{n}\|^{2} \\ &=&\|x_{n}-p\|^{2}-dist^{2}(x_{n},C_{n}). \end{array} $$

(21)

This implies that

$$ \|x_{n+1}-p\|\le \|x_{n}-p\|. $$

and so $\lim _{n\to \infty }\|x_{n}-p\|$ exists. Thus, the sequence {x_n} is bounded, and it also follows that the sequences {y_n} and {Fy_n} are bounded too.

Claim 2. We claim that

$$ \left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda} (x_{n})\|^{2}\right]^{2}\le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2} $$

(22)

for some L > 0. Indeed, since the sequence {Fy_n} is bounded, there exists L > 0 such that ∥Fy_n∥≤ L for all n. Using this fact, we see that for all u,v ∈ C_n,

$$ \|h_{n}(u)-h_{n}(v)\|=\|\langle Fy_{n}, u-v\rangle\|\le \|Fy_{n}\|\|u-v\|\le L \|u-v\|. $$

This implies that h_n(⋅) is L-Lipschitz continuous on C_n. By Lemma 2.5, we obtain

$$ dist(x_{n}, C_{n})\geq \frac{1}{L} h_{n}(x_{n}), $$

which, when combined with Lemma 3.3, yields the inequality

$$ dist(x_{n}, C_{n})\geq \frac{\tau_{n}}{2\lambda L}\|r_{\lambda} (x_{n})\|^{2}. $$

(23)

Combining the proof of Claim 1 with (23), we obtain

$$ \|x_{n+1}-p\|^{2}\le \|x_{n}-z\|^{2}-\left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda} (x_{n})\|^{2}\right]^{2}, $$

which implies, in its turn, Claim 2.

Claim 3. We claim that {x_n} converges weakly to an element of Sol(C,F). Indeed, since {x_n} is a bounded sequence, there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges weakly to z ∈ C.

Appealing to Claim 2, we find that

$$ \lim_{n\to\infty}\frac{\tau_{n}}{2\lambda L}\|r_{\lambda} (x_{n})\|^{2}=0, \ \text{ that is }, \lim_{n\to\infty}\tau_{n}\|r_{\lambda} (x_{n})\|^{2}=0. $$

Thanks to Lemma 3.5 we also get

$$ \lim_{n\to\infty}\|x_{n}-z_{n}\|=0. $$

(24)

Using Lemma 3.4 and (24), we may infer that z ∈ Sol(C,F).

Thus, we have proved that

• i) For every p ∈ Sol(C,F), the limit $\lim _{n\to \infty }\|x_{n}-p\|$ exists;

• ii) Every sequential weak cluster point of the sequence {x_n} is in Sol(C,F).

  Lemma 2.6 now implies that the sequence {x_n} converges weakly to an element of Sol(C,F).

□

Remark 3.1

1. When the operator F is monotone, it is not necessary to assume Condition 3.3 (see, [8, 35]).

2. Note that in our work we use Condition 3.3, which is strictly weaker than the sequential weak continuity of the operator F, an assumption which has frequently been used in recent articles on pseudomonotone variaional inequality problems [12, 33,34,35,36]. Indeed, if F is sequentially weakly continuous, then Condition 3.3 is fulfilled because the norm is weakly lower semicontinuous. On the other hand, it is not difficult to see that the operator F : H → H, defined by F(x) := ∥x∥x,x ∈ H, satisfies condition 3.3, but is not sequentially weakly continuous.

3.2 Strong convergence

In this section, we introduce an algorithm for solving variational inequalities which is based on the viscosity method [27] and on Algorithm 3. We assume that f : C → C is a contractive mapping with a coefficient ρ ∈ [0,1) and that the following condition is satisfied:

Condition 3.5

The real sequence {α_n} is contained in (0,1) and satisfies

$$ \lim_{n\to\infty}\alpha_{n}=0, \sum\limits_{n=1}^{\infty}\alpha_{n}=\infty. $$

Theorem 3.2

Assume that Conditions 3.1–3.4 and 3.5 hold. Then, any sequence {x_n} generated by Algorithm 4 converges strongly to p ∈ Sol(C,F), where p = P_Sol(C,F) ∘ f(p).

Proof

Claim 1. We first prove that the sequence {x_n} is bounded. To this end, let $w_{n}=P_{C_{n}}x_{n}$. By (21) we have

$$ \begin{array}{@{}rcl@{}} \|w_{n}-p\|^{2}\le\|x_{n}-p\|^{2}-dist^{2}(x_{n},C_{n}). \end{array} $$

This implies that

$$ \|w_{n}-p\|\le \|x_{n}-p\|. $$

(25)

Using (25), we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|&=&\|\alpha_{n} f(x_{n})+(1-\alpha_{n})w_{n}-p\|\\ &=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(w_{n}-p)\|\\ &\le& \alpha_{n}\|f(x_{n})-p\|+(1-\alpha_{n})\|w_{n}-p\|\\ &\le& \alpha_{n}\|f(x_{n})-f(p)\|+\alpha_{n} \|f(p)-p\|+(1-\alpha_{n})\|w_{n}-p\|\\ &\le& \alpha_{n} \rho \|x_{n}-p\|+\alpha_{n}\|f(p)-p\|+(1-\alpha_{n})\|x_{n}-p\|\\ &\le& [1-\alpha_{n}(1-\rho)]\|x_{n}-p\|+\alpha_{n}(1-\rho)\frac{\|f(p)-p\|}{1-\rho}\\ &\le& \max\left\{\|x_{n}-p\|,\frac{\|f(p)-p\|}{1-\rho}\right\}\\ &\le& ...\le \max\left\{\|x_{1}-p\|,\frac{\|f(p)-p\|}{1-\rho}\right\}. \end{array} $$

Thus, the sequence {x_n} is indeed bounded. Consequently, the sequences {y_n}, {f(x_n)}, and {Fy_n} are bounded too.

Claim 2. We claim that

$$ \|w_{n}-x_{n}\|^{2}\le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p, x_{n+1}-p\rangle. $$

To prove this, we first note that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(w_{n}-p)\|^{2} \\ &\le&(1-\alpha_{n})\|w_{n}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle \\ &\le& \|w_{n}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. \end{array} $$

(26)

On the other hand, we have

$$ \|w_{n}-p\|^{2}=\|P_{C_{n}}x_{n}-p\|^{2}\le \|x_{n}-p\|^{2}-\|w_{n}-x_{n}\|^{2}. $$

(27)

Substituting (27) into (26), we get

$$ \|x_{n+1}-p\|^{2} \le \|x_{n}-p\|^{2}-\|w_{n}-x_{n}\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. $$

This implies that

$$ \|w_{n}-x_{n}\|^{2} \le \|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+2\alpha_{n} \langle f(x_{n})-p,x_{n+1}-p\rangle. $$

Claim 3. We claim that

$$ \left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda}(x_{n})\|^{2}\right]^{2}\le\|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+\alpha_{n}\|f(x_{n})-p\|^{2}. $$

Indeed, according to (22), we get

$$ \|w_{n}-p\|^{2}\le \|x_{n}-p\|^{2}-\left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda}(x_{n})\|^{2}\right]^{2}. $$

(28)

It follows from the definition of the sequence {x_n} and (28) that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}(f(x_{n})-p)+(1-\alpha_{n})(w_{n}-p)\|^{2}\\ &=&\alpha_{n}\|f(x_{n}) - p\|^{2}+(1 - \alpha_{n})\|w_{n} - p\|^{2} -\alpha_{n}(1-\alpha_{n})\|f(x_{n})-w_{n}\|^{2}\\ &\le& \alpha_{n}\|f(x_{n})-p\|^{2}+(1-\alpha_{n})\|w_{n}-p\|^{2}\\ &\le&\alpha_{n}\|f(x_{n}) - p\|^{2}+(1-\alpha_{n})\|x_{n} - p\|^{2} - (1 -\alpha_{n})\left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda}(x_{n})\|^{2}\right]^{2}\\ &\le&\alpha_{n}\|f(x_{n})-p\|^{2}+\|x_{n}-p\|^{2}-(1-\alpha_{n})\left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda}(x_{n})\|^{2}\right]^{2}. \end{array} $$

This implies that

$$ (1-\alpha_{n})\left[\frac{\tau_{n}}{2\lambda L}\|r_{\lambda}(x_{n})\|^{2}\right]^{2}\le\|x_{n}-p\|^{2}-\|x_{n+1}-p\|^{2}+\alpha_{n}\|f(x_{n})-p\|^{2}. $$

Claim 4. We prove that

$$ \|x_{n+1}-p\|^{2}\le (1-(1-\rho)\alpha_{n})\|x_{n}-p\|^{2}+(1-\rho)\alpha_{n}\frac{2}{1-\rho}\langle f(p)-p,x_{n+1}-p\rangle. $$

Indeed, we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p\|^{2}&=&\|\alpha_{n}f(x_{n})+(1-\alpha_{n})z_{n}-p\|^{2} \\ &=&\|\alpha_{n}(f(x_{n})-f(p))+(1-\alpha_{n})(z_{n}-p)+\alpha_{n}(f(p)-p)\|^{2} \\ &\le& \|\alpha_{n}(f(x_{n})-f(p))+(1-\alpha_{n})(z_{n}-p)\|^{2}+2\alpha_{n}\langle f(p)-p,x_{n+1}-p\rangle \\ &\le&\alpha_{n}\|f(x_{n})-f(p)\|^{2}+(1-\alpha_{n})\|z_{n}-p\|^{2}+2\alpha_{n}\langle f(p)-p,x_{n+1}-p\rangle \\ &\le&\alpha_{n}\rho\|x_{n}-p\|^{2}+(1-\alpha_{n})\|x_{n}-p\|^{2}+2\alpha_{n}\langle f(p)-p,x_{n+1}-p\rangle \\ &=&(1-(1-\rho)\alpha_{n})\|x_{n}-p\|^{2}+(1-\rho)\alpha_{n}\frac{2}{1-\rho}\langle f(p)-p,x_{n+1}-p\rangle. \end{array} $$

Claim 5. Now we intend to show that the sequence {∥x_n − p∥²} converges to zero by considering two possible cases.

Case 1: There exists an $N\in {\mathbb N}$ such that ∥x_n+ 1 − p∥² ≤∥x_n − p∥² for all n ≥ N. This implies that $\lim _{n\to \infty }\| x_{n}-p\|^{2}$ exists. It now follows from Claim 2 that

$$ \lim_{n\to\infty} \|x_{n}-w_{n}\|=0. $$

Since the sequence {x_n} is bounded, there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} that weakly converges to some point z ∈ C such that

$$ \limsup_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle =\lim_{k\to \infty}\langle f(p)-p,x_{n_{k}}-p\rangle=\langle f(p)-p,z-p\rangle. $$

Now, according to Claim 3, we see that

$$ \lim_{k \to \infty}\left[\frac{\tau_{n_{k}}}{2\lambda L}\|r_{\lambda}(x_{n_{k}})\|^{2}\right]^{2}=0. $$

It follows that

$$ \lim_{k\to \infty}\tau_{n_{k}}\|r_{\lambda}(x_{n_{k}})\|^{2}=\lim_{k\to \infty}\tau_{n_{k}}\|x_{n_{k}}-z_{n_{k}}\|^{2}=0. $$

Thanks to Lemma 3.5, we infer that

$$ \lim_{k\to \infty}\|x_{n_{k}}-z_{n_{k}}\|=0. $$

(29)

Using the fact that $x_{n_{k}}\rightharpoonup z$, (29), and Lemma 3.4, we now conclude that z ∈ Sol(C,F).

On the other hand,

$$ \|x_{n+1}-w_{n}\|=\alpha_{n}\|f(x_{n})-w_{n}\|\to 0 \text{ as } n\to \infty. $$

Thus,

$$ \|x_{n+1}-x_{n}\|=\|x_{n+1}-w_{n}\|+\|x_{n}-w_{n}\|\to 0 \text{ as } n\to \infty. $$

Since p = P_Sol(C,F)f(p) and $x_{n_{k}} \rightharpoonup z\in Sol(C,F)$, we get

$$ \limsup_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle =\langle f(p)-p,z-p\rangle\le 0. $$

This implies that

$$ \begin{array}{@{}rcl@{}} \limsup_{n\to \infty}\langle f(p)-p,x_{n+1}-p\rangle&\le& \limsup_{n\to \infty}\langle f(p)-p,x_{n+1}-x_{n}\rangle \\ &&+\limsup_{n\to \infty}\langle f(p)-p,x_{n}-p\rangle\le 0, \end{array} $$

which, when combined with Claim 4 and Lemma 2.7, implies that

$$ x_{n}\to p \text{ as } n\to \infty. $$

Case 2: Assume that there is no $n_{0} \in \mathbb {N}$ such that $\{\|x_{n}-p\|\}_{n=n_{0}}^{\infty }$ is monotonically decreasing. In this case, we adapt a technique of proof used in [24]. Set Γ_n = ∥x_n − p∥² for all n ≥ 1 and let $\eta : \mathbb {N} \to \mathbb {N}$ be a mapping defined for all n ≥ n₀ (for some n₀ large enough) by

$$ \eta (n) := \max\{k \in \mathbb{N} : k \le n, {\varGamma}_{k} \le {\varGamma}_{k+1}\}, $$

that is, η(n) is the largest number k in {1,...,n} such that Γ_k increases at k = η(n); note that, in view of Case 2, this η(n) is well defined for all sufficiently large n. Clearly, η is an increasing sequence such that $\eta (n)\to \infty$ as $n \to \infty$ and

$$ 0\le {\varGamma}_{\eta(n)}\le {\varGamma}_{\eta(n)+1} \ \ \forall n\geq n_{0}. $$

According to Claim 2, we have

$$ \begin{array}{@{}rcl@{}} \|w_{\eta(n)}-x_{\eta(n)}\|^{2}&\le& \|x_{\eta(n)} - p\|^{2} - \|x_{{\eta(n)}+1} - p\|^{2}+2\alpha_{\eta(n)} \langle f(x_{\eta(n)}) - p, x_{{\eta(n)}+1} - p\rangle.\\ &\le&\alpha_{\eta(n)} \langle f(x_{\eta(n)})-p, x_{{\eta(n)}+1}-p\rangle\\ &\le&\alpha_{\eta(n)}\| f(x_{\eta(n)})-p\| |x_{{\eta(n)}+1}-p\|\to 0 \text{ as } n \to \infty. \end{array} $$

From Claim 3, it follows that

$$ \begin{array}{@{}rcl@{}} (1 - \alpha_{\eta(n)})\left[ \frac{\tau_{\eta(n)}}{2 \lambda L}\|r_{\lambda}(x_{\eta(n)})\|^{2}\right]^{2}&\le&\|x_{\eta(n)} - p\|^{2} - \|x_{{\eta(n)}+1} - p\|^{2}+\alpha_{\eta(n)}\|f(x_{\eta(n)}) - p\|^{2}\\ &\le&\alpha_{\eta(n)}\|f(x_{\eta(n)})-p\|^{2} \to 0 \text{ as } n\to\infty. \end{array} $$

Using the same arguments as in the proof of Case 1, we obtain

$$ \lim_{k\to \infty}\|x_{\eta(n)}-z_{\eta(n)}\|=0, \lim_{k\to \infty}\|x_{\eta(n)+1}-x_{\eta(n)}\|\to 0 $$

and

$$ \limsup_{n\to \infty}\langle f(p)-p,x_{\eta(n)+1}-p\rangle\le 0. $$

(30)

Thanks to Claim 4 we get

$$ \begin{array}{@{}rcl@{}} \|x_{\eta(n)+1}-p\|^{2}&\le& (1-\alpha_{\eta(n)}(1 - \rho))\|x_{\eta(n)} - p\|^{2}+2\alpha_{\eta(n)}\langle f(p)-p,x_{\eta(n)+1}-p\rangle\\ &\le& (1 - \alpha_{\eta(n)}(1 - \rho))\|x_{\eta(n)+1} - p\|^{2}+ 2\alpha_{\eta(n)}\langle f(p) - p,x_{\eta(n)+1} - p\rangle. \end{array} $$

Thus,

$$ (1- \rho)\|x_{\eta(n)+1}-p\|^{2}\le 2\langle f(p)-p,x_{\eta(n)+1}-p\rangle, $$

which, when combined with (30), implies that $\limsup _{n\to \infty }\|x_{\eta (n)+1}-p\|^{2}\le 0$, that is, $\lim _{n\to \infty }\|x_{\eta (n)+1}-p\|=0$.

Next, we show that for all sufficiently large n, we have

$$ 0 \le {\varGamma}_{n} \le {\varGamma}_{\eta(n)+1}. $$

(31)

Indeed, for n ≥ n₀, it is not difficult to observe that η(n) ≤ n for n ≥ n₀. Now consider the following three cases: η(n) = n,η(n) = n − 1, and η(n) < n − 1. In the first and second cases, it is obvious that Γ_n ≤Γ_η(n)+ 1 for n ≥ n₀. In the third case, η(n) ≤ n − 2, we infer from the definition of η(n) that for any integer n ≥ n₀, Γ_j ≥Γ_j+ 1 for η(n) + 1 ≤ j ≤ n − 1. Thus, ${\varGamma }_{\eta (n)+1} \geq {\varGamma }_{\eta (n)+2} \geq {\dots } \geq {\varGamma }_{n-1} \geq {\varGamma }_{n}$. As a consequence, we obtain inequality (31). Now, using (31) and $\lim _{n\to \infty }\|x_{\eta (n)+1}-p\|=0$, we conclude that x_n → p as $n\to \infty$. □

Applying Algorithm 3 with f(x) := x₁ for all x ∈ C, we obtain the following corollary.

Corollary 3.1

Given μ > 0,l ∈ (0,1), and $\lambda \in (0,\frac {1}{\mu })$, let x₁ ∈ C be arbitrary. Compute

$$ z_{n}=P_{C}(x_{n}-\lambda Fx_{n}) $$

and r_λ(x_n) := x_n − z_n. If r_λ(x_n) = 0, then stop; x_n is a solution of Sol(C,F). Otherwise,

Compute

$$ y_{n}=x_{n}-\tau_{n} r_{\lambda} (x_{n}), $$

where $\tau _{n}:=l^{j_{n}}$ and j_n is the smallest non-negative integer j satisfying

$$ \langle Fx_{n}-F(x_{n}- l^{j} r_{\lambda} (x_{n})), r_{\lambda}(x_{n})\rangle \le \frac{\mu}{2} \|r_{\lambda}(x_{n})\|^{2}. $$

Compute

$$ x_{n+1}=\alpha_{n} x_{1}+(1-\alpha_{n}) P_{C_{n}} (x_{n}), $$

where

$$C_{n}:=\{x\in C: h_{n}(x_{n})\le 0\}\text{\ \ and \ \ } h_{n}(x)=\langle Fy_{n},x-x_{n}\rangle+\frac{\tau_{n}}{2\lambda}\|r(x_{n})\|^{2}.$$

Assume that Conditions 3.1–3.4 hold. Then, the sequence {x_n} converges strongly to a point p ∈ Sol(C,F), where p = P_Sol(C,F)x₁.

4 Numerical illustrations

In this section, we provide several numerical examples regarding our proposed algorithms. We compare Algorithm 3 (also called Proposed Alg. 3.3 or TD Agl) with Algorithm 1 (Solodov and Svaiter, Alg. 1.1) and Algorithm 2 (Vuong and Shehu, Alg. 1.2) in Examples 1 and 2. In Example 3, we compare Algorithm 4 (also called Algorithm 3.4) with Algorithm 2 (also called Algorithm 1.2). All the numerical experiments were performed on an HP laptop with Intel(R) Core(TM)i5-6200U CPU 2.3GHz with 4 GB RAM. All the programs were written in Matlab2015a.

Example 1

We first consider a classical example for which the usual gradient method does not converge to a solution of the variational inequality. The feasible set is $C := \mathbb {R}^{m}$ (for some positive even integer m) and F := (a_ij)_1≤i,j≤m is the m × m square matrix the terms of which are given by

$$ \begin{array}{@{}rcl@{}} a_{i j} = \begin{cases} -1&\text{ if } j = m + 1 -i > i,\\ 1 &\text{ if } j = m + 1- i < i,\\ 0 &\text{otherwise}. \end{cases} \end{array} $$

It is clear that the zero vector x^⋆ = (0,...,0) is the solution of this test example. We take $\alpha _{n}=\frac {1}{n}$ and the starting point is $x_{1} = (1, 1, . . . , 1)^{T} \in \mathbb {R}^{m}$. We terminate the iterations if ∥x_n − x^⋆∥≤ 𝜖 with 𝜖 = 10^− 4 or if the number of iterations ≥ 1000. The results are presented in Table 1 and in Figs. 1 and 2 below.

Table 1 Numerical results obtained by the algorithms with λ = 1.8, μ = 0.5, and l = 0.5

Fig. 1

Comparison of all the algorithms with m = 200

Fig. 2

Comparison of all the algorithms with m = 500

Example 2

Assume that $F:\mathbb {R}^{m} \to \mathbb {R}^{m}$ is defined by F(x) := Mx + q with M = NN^T + S + D, N is an m × m matrix, S is an m × m skew-symmetric matrix, D is an m × m diagonal matrix, whose diagonal entries are positive (so M is positive definite), q is a vector in $\mathbb {R}^{m}$, and

$$ C := \{x \in \mathbb{R}^{m}: -5 \leq x_{i} \leq 5, i=1,\cdots,m\}. $$

It is clear that F is monotone and Lipschitz continuous with a Lipschitz constant L = ∥M∥. Thus, F is a uniformly continuous pseudomonotone operator. For q = 0, the unique solution of the corresponding variational inequality is {0}.

In our experiments, all the entries of N, S, and D are generated randomly in the interval (− 2,2) and those of D are in the interval (0,1). The starting point is $x_{1} = (1, 1, . . . , 1)^{T} \in \mathbb {R}^{m}$ and $\alpha _{n}=\frac {1}{\sqrt {n}}$. We use the stopping rule ∥x_n − x^⋆∥≤ 10^− 4 and we also stop if the number of iteration ≥ 1000 for all the algorithms. The numerical results are presented in Table 2 and in Figs. 3 and 4.

Table 2 Numerical results obtained by the algorithms with λ = 1.8, μ = 0.5, and l = 0.5

Fig. 3

Comparison of all the algorithms with m = 50

Fig. 4

Comparison of all the algorithms with m = 100

Example 3

Consider C := {x ∈ H : ∥x∥≤ 2}. Let $g: C\rightarrow \mathbb {R}$ be defined by $g(u):=\frac {1}{1+\|u\|^{2}}$. Observe that g is L_g-Lipchitz continuous with $L_{g}=\frac {16}{25}$ and $\frac {1}{5}\leq g(u)\leq 1,~~\forall u \in C$. Define the Volterra integral operator $A :L^{2}([0,1]) \rightarrow L^{2}([0,1])$ by

$$ A(u)(t) := {{\int}_{0}^{t}} u(s)ds,~~\forall u \in L^{2}([0,1]), t \in [0,1]. $$

The operator A is bounded and linear monotone (see Exercise 20.12 of [2]) and $\|A\|=\frac {2}{\pi }$. Next, define $F:C\rightarrow L^{2}([0,1])$ by F(u)(t) := g(u)A(u)(t), ∀u ∈ C,t ∈ [0,1]. Then, F is pseudomonotone and L_F-Lipschitz-continuous with $L_{F} = \frac {82}{\pi }$.

Take μ = 0.3, l = 0.9, and $\alpha _{n}=\frac {1}{n}$ in Algorithm 4 and Algorithm 2. Choose $\lambda =\frac {0.9}{\mu }$ and f(x) := x₁ in Algorithm 4. Let the initial point be $x_{0}=\sin \limits (2\pi t^{2})$.

We compared Algorithm 4 with Algorithm 2. The numerical results are presented in Fig. 5. It shows that the performance of Algorithm 4 is better than that of Algorithm 2.

Fig. 5

Comparison of Algorithm 4 and Algorithm 2 in Example 3

5 Conclusions

In this paper, we have proposed new projection-type algorithms for solving variational inequalities in real Hilbert spaces. We have established weak and strong convergence theorems for these algorithms under a pseudomonotonicity assumption imposed on the cost operator, which is not assumed to be Lipschitz continuous. Moreover, our algorithms require the calculation of only two projections onto the feasible set per each iteration. These two properties bring out the advantages of our proposed algorithms over several existing algorithms which have recently been proposed in the literature. Numerical experiments in both finite- and infinite-dimensional spaces illustrate the good performance of our new schemes.