A new iterative method for solving pseudomonotone variational inequalities with non-Lipschitz operators

Abstract

The purpose of this paper is to study and analyze a new projection-type algorithm for solving pseudomonotone variational inequality problems in real Hilbert spaces. The advantage of the proposed algorithm is the strong convergence proved without assuming Lipschitz continuity of the associated mapping. In addition, the proposed algorithm uses only two projections onto the feasible set in each iteration. The numerical behaviors of the proposed algorithm on a test problem are illustrated and compared with several previously known algorithms.

1 Introduction

We consider the following variational inequality problem (VI) of finding a point $x^*\in C$ such that

$$\begin{aligned} \langle Ax^*,x-x^*\rangle \ge 0 \ \ \forall x\in C, \end{aligned}$$

(1)

where C is a nonempty closed convex subset in a real Hilbert space H,  $A: H\rightarrow H$ is a single-valued mapping, and $\langle \cdot ,\cdot \rangle$ and $\Vert \cdot \Vert$ are the inner product and the norm in H, respectively.

Let us denote the solution set of VI (1) by VI(C, A). Variational inequality problems are fundamental in a broad range of mathematical and applied sciences; the theoretical and algorithmic foundations as well as the applications of variational inequality problems have been extensively studied in the literature and continue to attract intensive research. For the current state of the art in the finite dimensional setting, see for instance (Facchinei and Pang 2003; Konnov 2001) and the extensive list of references therein.

Many authors have proposed and analyzed several iterative methods for solving the variational inequality (1). The simplest one is the following projection method, which can be seen as an extension of the projected gradient method for optimization problems:

$$\begin{aligned} x_{n+1}=P_C(x_n-\tau Ax_n), \end{aligned}$$

(2)

for each $n\ge 1$, where $P_C$ denotes the metric projection from H onto C. Convergence results for this method require some monotonicity properties of A. This method converges under quite strong hypotheses. If A is Lipschitz continuous with Lipschitz constant L and $\alpha$-strongly monotone, then the sequence generated by (2) converges to an element of VI(C, A), if $\tau \in \left( 0, \dfrac{2\alpha }{L^2}\right)$.

To deal with the weakness of the method defined by (2). Korpelevich 1976 (also independently by Antipin (1976)) proposed the extragradient method in the finite dimensional Euclidean space ${\mathbb {R}}^m$ for a monotone and L-Lipschitz continuous operator $A: {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$. The algorithm is of the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in C,\\ y_n=P_C(x_n-\tau _n Ax_n),\\ x_{n+1}=P_C(x_n-\tau _n Ay_n), \end{array}\right. } \end{aligned}$$

(3)

where $\tau _n \in \left( 0,\dfrac{1}{L}\right)$. The sequence $\{x_n\}$ generated by (3) converges to an element of VI(C, A) provided that VI(C, A) is nonempty.

In recent years, the extragradient method was further extended to infinite-dimensional spaces in various ways, see, e.g. (Censor et al. 2011a, b, c; Bello Cruz and Iusem 2009, 2010, 2012, 2015; Bello Cruz et al. 2019; Gibali et al. 2019; Kanzow and Shehu 2018; Konnov 1997, 1998; Maingé and Gobinddass 2016; Malitsky 2015; Thong and Hieu 2018, 2019; Thong et al. 2019c; Thong and Vuong 2019; Thong and Gibali 2019a, b; Thong et al. 2019a, b; Vuong 2018) and the references therein.

Note that, when A is not Lipschitz continuous or the constant L is very difficult to compute, the method of Korpelevich is not applicable (or possible to use) because we cannot determine the step-size $\tau _n$. To overcome this obstacle, Iusem (1994) proposed an iterative algorithm in the finite dimensional Euclidean space ${\mathbb {R}}^m$ for VI(C, A) as follows:

Algorithm 1.1

It is worth noting that this modification allows the author to prove convergence without Lipschitz continuity of the operator A.

Algorithm 1.1 may require many iterations in the iterative procedure used to select the stepsize $\gamma _n$ and each iterations uses a new projections. This may lead to a large computational effort that should be avoided.

Motivated by this idea, Iusem and Svaiter (1997) proposed a modified extragradient method for solving monotone variational inequalities which requires only two projections onto C at each iteration. Few years later, this method was improved by Solodov and Svaiter (1999). They introduced an algorithm for solving (1) in finite-dimensional spaces. In fact, the method in Solodov and Svaiter (1999) can solve a more general case where A is only continuous and satisfies the following condition:

$$\begin{aligned} \langle Ax, x - x^* \rangle \ge 0 \ \ \forall x\in C \text { and } x^*\in VI(C,A). \end{aligned}$$

(5)

The property (5) holds if A is monotone or more generally pseudomonotone on C in the sense of Karamardian (1976). Very recently, Vuong and Shehu (2019) modified result of Solodov and Svaiter to obtain strong convergence in infinite dimensional real Hilbert spaces. They constructed the algorithm based on Halpern method (Halpern 1967) and method of Solodov and Svaiter. The algorithm is of the following form:

Algorithm 1.2

They proved that if $A:H\rightarrow H$ is a pseudomonotone, uniformly continuous and sequentially weakly continuous on bounded subsets of C and the sequence $\{\alpha _n\}$ satisfies the conditions $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^\infty \alpha _n=\infty$, then the sequence $\{x_n\}$ generated by Algorithm 1.2 converges strongly to $p\in VI(C,A)$, where $p=P_{C}x_1.$ Note that when $\alpha _n=0 \ \forall n$ then Algorithm 1.2 reduces to the algorithm of Solodov and Svaiter.

Motivated and inspired by the works in Moudafi (2000), Solodov and Svaiter (1999) and Vuong and Shehu (2019), and by the ongoing research in these directions, in this paper we introduce a modification of the algorithm proposed by Solodov and Svaiter for solving variational inequalities with uniformly continuous pseudomonotone operator. The main modification is to use a different Armijo-type line search to obtain a hyperplane strictly separating current iterate from the solutions of the variational inequalities.

The paper is organized as follows: We first recall some basic definitions and results in Sect. 2. Our algorithm is presented and analyzed in Sect. 3. In Sect. 4 we present some numerical experiments which demonstrate the proposed algorithm performances as well as provide a preliminary computational overview by comparing it with some related algorithms.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty, closed and convex subset of H. The weak convergence of $\{x_n\}_{n=1}^{\infty }$ to x is denoted by $x_{n}\rightharpoonup x$ as $n\rightarrow \infty$, while the strong convergence of $\{x_n\}_{n=1}^{\infty }$ to x is written as $x_n\rightarrow x$ as $n\rightarrow \infty .$ For each $x,y\in H$, we have

$$\begin{aligned} \Vert x+y\Vert ^2\le \Vert x\Vert ^2+2\langle y,x+y\rangle . \end{aligned}$$

Definition 2.1

Let $T:H\rightarrow H$ be an operator. Then

• 1. The operator T is called L-Lipschitz continuous with $L>0$ if

  $$\begin{aligned} \Vert Tx-Ty\Vert \le L \Vert x-y\Vert \ \ \ \forall x,y \in H. \end{aligned}$$

  if $L=1$ then the operator T is called nonexpansive and if $L\in (0,1)$, T is called contraction.

• 2. T is called monotone if

  $$\begin{aligned} \langle Tx-Ty,x-y \rangle \ge 0 \ \ \ \forall x,y \in H. \end{aligned}$$

• 3. T is called pseudomonotone if

  $$\begin{aligned} \langle Tx,y-x \rangle \ge 0 \Longrightarrow \langle Ty,y-x \rangle \ge 0 \ \ \ \forall x,y \in H. \end{aligned}$$

• 4. T is called $\alpha$-strongly monotone if there exists a constant $\alpha >0$ such that

  $$\begin{aligned} \langle Tx-Ty,x-y\rangle \ge \alpha \Vert x-y\Vert ^2 \ \ \forall x,y\in H. \end{aligned}$$

• 5. The operator T is called sequentially weakly continuous if for each sequence $\{x_n\}$ we have: $x_n$ converges weakly to x implies ${Tx_n}$ converges weakly to Tx.

It is easy to see that every monotone operator is pseudomonotone but the converse is not true.

We next present an academic example of a variational inequality problem (VI) in infinite dimensional Hilbert spaces where the cost function A is pseudomonotone, uniformly continuous and sequentially weakly continuous, but A fails to be Lipschitz continuous on H.

Example 1

Consider the Hilbert space

$$\begin{aligned} H=l_2:=\left\{ u=(u_1,u_2,\ldots ,u_i,\ldots ) \mid \sum _{i=1}^\infty |u_i|^2<+\infty \right\} \end{aligned}$$

equipped with the inner product and induced norm on H:

$$\begin{aligned} \langle u,v\rangle =\sum _{i=1}^\infty u_i v_i \text { and } \Vert u\Vert =\sqrt{\langle u,u\rangle } \end{aligned}$$

for any $u=(u_1,u_2,\ldots ,u_i,\ldots ), v=(v_1,v_2,\ldots ,v_i,\ldots )\in H.$

Consider the set and the mapping:

$$\begin{aligned} C=\{u=(u_1,u_2,\ldots ,u_i,\ldots )\in H: |u_i|\le \dfrac{1}{i} \ \ \ \forall i=1,2,\ldots \},\ \ Au=\left( \Vert u\Vert +\dfrac{1}{\Vert u\Vert +1}\right) u. \end{aligned}$$

With this C and A, it is easy to see that $VI(C,A)\ne \emptyset$ since $0\in VI(C,A)$ and moreover, A is pseudomonotone, uniformly continuous and sequentially weakly continuous on C, but A fails to be Lipschitz continuous on H.

Now let $u,v\in C$ be such that $\langle Au,v-u\rangle \ge 0$. This implies that $\langle u,v-u\rangle \ge 0$. Consequently,

$$\begin{aligned} \langle Av,v-u\rangle&=\left( \Vert u\Vert +\dfrac{1}{\Vert u\Vert +1}\right) \langle v,v-u\rangle \\&\ge \left( \Vert u\Vert +\dfrac{1}{\Vert u\Vert +1}\right) \left( \langle v,v-u\rangle - \langle u,v-u\rangle \right) \\&=\left( \Vert u\Vert +\dfrac{1}{\Vert u\Vert +1}\right) \Vert v-u\Vert ^2\ge 0 \end{aligned}$$

meaning that A is pseudomonotone. Now, since C is compact, the mapping A is uniformly continuous on C and A is sequentially weakly continuous on C.

Finally, we show that A is not Lipschitz continuous on H. Assume to the contrary that A is Lipschitz continuous on H, i.e., there exists $L>0$ such that

$$\begin{aligned} \Vert Au-Av\Vert \le L\Vert u-v\Vert \ \ \forall u,v\in H. \end{aligned}$$

Let $u=(L,0,\ldots ,0,\ldots )$ and $v=(0,0,\ldots ,0,\ldots )$, then

$$\begin{aligned} \Vert Au-Av\Vert =\Vert Au\Vert =\left( \Vert u\Vert +\dfrac{1}{\Vert u\Vert +1}\right) \Vert u\Vert =\left( L+\dfrac{1}{L+1}\right) L. \end{aligned}$$

Thus, $\Vert Au-Av\Vert \le L\Vert u-v\Vert$ is equivalent to

$$\begin{aligned} \left( L+\dfrac{1}{L+1}\right) L\le L^2, \end{aligned}$$

equivalently

$$\begin{aligned} \dfrac{1}{L+1}\le 0, \end{aligned}$$

this leads to a contradiction and thus A is not Lipschitz continuous on H.

For every point $x\in H$, there exists a unique nearest point in C, denoted by $P_Cx$ such that $\Vert x-P_Cx\Vert \le \Vert x-y\Vert \ \forall y\in C$. $P_C$ is called the metric projection of H onto C. It is known that $P_C$ is nonexpansive.

Lemma 2.1

(Goebel and Reich 1984) Let C be a nonempty closed convex subset of a real Hilbert space H. Given $x\in H$ and $z\in C$. Then $z=P_Cx\Longleftrightarrow \langle x-z,z-y\rangle \ge 0 \ \ \forall y\in C.$

Lemma 2.2

(Goebel and Reich 1984) Let C be a closed and convex subset in a real Hilbert space H,  $x\in H$. Then

(i):

$\Vert P_Cx-P_Cy\Vert ^2\le \langle P_C x-P_C y,x-y\rangle \ \forall y\in H$;

(ii):

$\Vert P_C x-y\Vert ^2\le \Vert x-y\Vert ^2-\Vert x-P_Cx\Vert ^2 \ \forall y\in C;$

(iii):

$\langle (I-P_C)x-(I-P_C)y,x-y\rangle \ge \Vert (I-P_C)x-(I-P_C)y\Vert ^2 \ \forall y\in H.$

For properties of the metric projection, the interested reader could be referred to Sect. 3 in Goebel and Reich (1984) and Chapter 4 in Cegielski (2012).

The following Lemmas are useful for the convergence of our proposed method.

Lemma 2.3

(Iusem and Garciga 2001) Let $H_1$ and $H_2$ be two real Hilbert spaces. Suppose $A : H_1 \rightarrow H_2$ is uniformly continuous on bounded subsets of $H_1$ and M is a bounded subset of $H_1$. Then A(M) is bounded.

Lemma 2.4

(Cottle and Yao 1992, Lemma 2.1) Consider the problem VI(C, A) with C being a nonempty, closed, convex subset of a real Hilbert space H and $A : C \rightarrow H$ being pseudomonotone and continuous. Then, $x^*$ is a solution of VI(C, A) if and only if

$$\begin{aligned} \langle Ax, x - x^*\rangle \ge 0 \ \ \forall x \in C. \end{aligned}$$

Lemma 2.5

(He 2006) Let C be a nonempty closed and convex subset of a real Hilbert space H. Let h be a real-valued function on H and define $K := \{x \in C: h(x) \le 0\}$. If K is nonempty and h is Lipschitz continuous on C with modulus $\theta > 0$, then

$$\begin{aligned} {\mathrm{dist}}(x, K) \ge \theta ^{-1} \max \{h(x), 0\}\ \ \forall x \in C, \end{aligned}$$

where $\mathrm{dist}(x, K)$ denotes the distance function from x to K.

Lemma 2.6

(Maingé 2008) Let $\{a_n\}$ be a sequence of nonnegative real numbers such that there exists a subsequence $\{a_{n_i}\}$ of $\{a_n\}$ such that $a_{n_{i}}<a_{n_{i}+1}$ for all $i\in {\mathbb {N}}$. Then there exists a nondecreasing sequence $\{m_k\}$ of ${\mathbb {N}}$ such that $\lim _{k\rightarrow \infty }m_k=\infty$ and the following properties are satisfied by all (sufficiently large) number $k\in {\mathbb {N}}$:

$$\begin{aligned} a_{m_k}\le a_{m_{k}+1} \text { and } a_k\le a_{m_k+1}. \end{aligned}$$

In fact, $m_k$ is the largest number n in the set $\{1,2,\ldots ,k\}$ such that $a_n<a_{n+1}$.

Lemma 2.7

(Xu 2002) Let $\{a_n\}$ be a sequence of nonnegative real numbers such that:

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\alpha _n b_n, \end{aligned}$$

where $\{\alpha _n\}\subset (0,1)$ and $\{b_n\}$ is a sequence such that

a):

$\sum _{n=0}^\infty \alpha _n=\infty$;

b):

$\limsup _{n\rightarrow \infty }b_n\le 0.$

Then $\lim _{n\rightarrow \infty }a_n=0.$

3 Main results

In this section we introduce a new modified method of Solodov and Svaiter for solving (1), and the following conditions are assumed for the convergence of the proposed method:

Condition 1

The feasible set C is a nonempty, closed, and convex subset of the real Hilbert space H.

Condition 2

The VI (1) associated operator $A:H\rightarrow H$ is a pseudomonotone, uniformly continuous and sequentially weakly continuous on bounded subsets of C.

Condition 3

The solution set of the VI (1) is nonempty, that is $VI(C,A)\ne \emptyset$.

Condition 4

We assume that $f:C\rightarrow C$ is a contractive mapping with a coefficient $\rho \in [0,1)$, and we add the following condition

Condition 5

Let $\{\alpha _n\}$ be a real sequences in (0, 1) such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=0, \sum _{n=1}^\infty \alpha _n=\infty . \end{aligned}$$

Algorithm 3.3

Now let us compare the above algorithm with Algorithm 1.2. In the step of the Armijo-type linesearch, the above algorithm uses a different procedure which replaces the one described in (6) as follows:

$$\begin{aligned} \langle Ax_n-A(x_n- l^j r_\lambda (x_n)), r_\lambda (x_n)\rangle \le \mu \Vert r_\lambda (x_n)\Vert ^2, \end{aligned}$$

where $\mu >0$ and $\lambda \in \left( 0,\dfrac{1}{\mu }\right)$. Unlike (6), which requires $\mu \in (0,1)$ and $\lambda =1$. Such choices are crucial for the convergence analysis in Solodov and Svaiter (1999) and Vuong and Shehu (2019), while the parameter $\mu$ in our algorithm can take any positive scalar. In addition, we use viscosity techniques to solve this problem, which increases the speed of the proposed algorithm (see our numerical experiments). So our algorithm can be applied more conveniently in practice.

Remark 3.1

It is easy to see that $x_n,y_n,z_n$ in Algorithm 3.3 belong to C.

We start the analysis of the algorithm’s convergence by proving some Lemmas.

Lemma 3.8

Assume that Conditions 1–2 hold. The Armijo-line search rule (7) is well defined.

Proof

Since $l\in (0,1)$ and A is continuous on C hence $\langle Ax_n-A(x_n- l^j r_\lambda (x_n)), r_\lambda (x_n)\rangle$ converges to zero as j tends to infinite. On the other hand, as a consequence of Step 1, $\Vert r_\lambda (x_n)\Vert >0$ (otherwise, the procedure stops). Therefore, there exists a non-negative integer $j_n$ satisfying (7). $\square$

Lemma 3.9

Assume that $\{x_n\}$ is generated by Algorithm 3.3; then we have

$$\begin{aligned} \langle Ax_n, r_\lambda (x_n)\rangle \ge \lambda ^{-1}\Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

Proof

By the projection property we have $\Vert x-P_Cy\Vert ^2\le \langle x-y,x-P_Cy\rangle$ for all $x\in C$ and $y\in H$. Let $y=x_n-\lambda Ax_n, x=x_n$; then

$$\begin{aligned} \Vert x_n-P_C(x_n-\lambda Ax_n)\Vert ^2\le \lambda \langle Ax_n, x_n-P_C(x_n-\lambda Ax_n)\rangle ; \end{aligned}$$

thus

$$\begin{aligned} \langle Ax_n, r_\lambda (x_n)\rangle \ge \lambda ^{-1}\Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

$\square$

Lemma 3.10

Assume that Conditions 1–3 hold. Let $x^*$ be a solution of problem (1) and the function $h_n$ be defined by (8). Then $h_n (x^*)\le 0$ and $h_n (x_n)\ge \tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2$. In particular, if $r_\lambda (x_n)\ne 0$ then $h_n(x_n)>0.$

Proof

Since $x^*$ is a solution of problem (1), by Lemma 2.4 we have $h_n(x^*)=\langle Ay_n,x^*-y_n\rangle \le 0.$ The first claim of Lemma 3.10 is proved. Now, we prove the second claim. We have

$$\begin{aligned} h_n(x_n)=\langle Ay_n,x_n-y_n\rangle =\langle Ay_n, \tau _n r_\lambda (x_n)\rangle =\tau _n \langle Ay_n, r_\lambda (x_n)\rangle . \end{aligned}$$

(9)

On the other hand, from (7) we have

$$\begin{aligned} \langle Ax_n-Ay_n, r_\lambda (x_n)\rangle \le \mu \Vert r_\lambda (x_n)\Vert ^2, \end{aligned}$$

thus

$$\begin{aligned} \langle Ay_n, r_\lambda (x_n)\rangle \ge \langle Ax_n, r_\lambda (x_n)\rangle -\mu \Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

Using Lemma 3.9 we get

$$\begin{aligned} \langle Ay_n, r_\lambda (x_n)\rangle \ge \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

(10)

Combining (9) and (10) we get

$$\begin{aligned} h_n(x_n)\ge \tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

$\square$

Remark 3.2

From Lemma 3.10 we have $C_n\ne \emptyset$.

Lemma 3.11

Assume that Conditions 1–3 hold. Let $\{x_n\}$ be a sequence generated by Algorithm 3.3. If there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $\{x_{n_k}\}$ converges weakly to $z\in C$ and $\lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =0$ then $z\in VI(C,A).$

Proof

We have $z_{n_k}=P_C(x_{n_k}-Ax_{n_k})$ thus,

$$\begin{aligned} \langle x_{n_k}-Ax_{n_k}-z_{n_k},x-z_{n_k}\rangle \le 0 \ \ \forall x\in C. \end{aligned}$$

or equivalently

$$\begin{aligned} \langle x_{n_k}-z_{n_k},x-z_{n_k}\rangle \le \langle Ax_{n_k},x-z_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$

This implies that

$$\begin{aligned} \langle x_{n_k}-z_{n_k},x-z_{n_k}\rangle +\langle Ax_{n_k},z_{n_k}-x_{n_k}\rangle \le \langle Ax_{n_k},x-x_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$

(11)

Taking $k\rightarrow \infty$ in (11) since $\Vert x_{n_k}-z_{n_k}\Vert \rightarrow 0$ and $\{Ax_{n_k}\}$ is bounded, we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax_{n_k},x-x_{n_k}\rangle \ge 0. \end{aligned}$$

(12)

Let us choose a sequence $\{\epsilon _k\}_k$ of positive numbers decreasing and tending to 0. For each $\epsilon _k$, we denote by $N_k$ the smallest positive integer such that

$$\begin{aligned} \left\langle Ax_{n_j}, x- x_{n_j} \right\rangle + \epsilon _k \ge 0 \quad \forall j \ge N_k, \end{aligned}$$

(13)

where the existence of $N_k$ follows from (12). Since $\left\{ \epsilon _k \right\}$ is decreasing, it is clear that the sequence $\left\{ N_k \right\}$ is increasing. Furthermore, for each k, $Ax_{N_k} \not = 0$ and, setting

$$\begin{aligned} v_{N_k}=\frac{Ax_{N_k}}{\Vert Ax_{N_k}\Vert ^2}, \end{aligned}$$

we have $\left\langle Ax_{N_k},v_{N_k} \right\rangle =1$ for each k. Now we can deduce from (13) that for each k

$$\begin{aligned} \left\langle Ax_{N_k},x+\epsilon _k v_{N_k} -x_{N_k} \right\rangle \ge 0, \end{aligned}$$

and, since A is pseudomonotone on H, that

$$\begin{aligned} \left\langle A(x+\epsilon _k v_{N_k}),x+\epsilon _k v_{N_k} -x_{N_k} \right\rangle \ge 0. \end{aligned}$$

(14)

On the other hand, we have that $\left\{ x_{n_k} \right\}$ converges weakly to z when $k \rightarrow \infty$. By the fact that A is sequentially weakly continuous on C, we have that $\left\{ Ax_{n_k} \right\}$ converges weakly to Az. We assume that $Az \not = 0$ (otherwise, z is a solution). By the sequentially weakly lower semicontinuity of norm, we get

$$\begin{aligned} 0<\Vert Az \Vert \le \lim \inf _{k \rightarrow \infty } \Vert Ax_{n_k}\Vert . \end{aligned}$$

Since $\left\{ x_{N_k} \right\} \subset \left\{ x_{n_k} \right\}$ and $\epsilon _k \rightarrow 0$ as $k \rightarrow \infty$, we obtain

$$\begin{aligned} 0\le & {} \lim \sup _{k \rightarrow \infty } \Vert \epsilon _k v_{N_k}\Vert = \lim \sup _{k \rightarrow \infty } \Big (\frac{\epsilon _k}{\Vert Ax_{n_k}\Vert }\Big )\\\le & {} \frac{\lim \sup _{k \rightarrow \infty }\epsilon _k}{\lim \inf _{k \rightarrow \infty }\Vert Ax_{n_k}\Vert } \le \frac{0}{\Vert Az\Vert }=0, \end{aligned}$$

which implies that $\lim _{k \rightarrow \infty } \Vert \epsilon _k v_{N_k}\Vert =0$. Hence, taking the limit as $k \rightarrow \infty$ in (14), we obtain

$$\begin{aligned} \left\langle Ax,x-z \right\rangle \ge 0. \end{aligned}$$

By Lemma 2.4 we obtain $z\in VI(C,A).$$\square$

Theorem 3.1

Assume that Conditions 1–5 hold. Then any sequence $\{x_n\}$ generated by Algorithm 3.3 converges strongly to $p\in VI(C,A)$, where $p=P_{VI(C,A)}\circ f(p).$

Proof

Claim 1. The sequence $\{x_n\}$ is bounded. Indeed, let $w_n=P_{C_n}x_n$. Since $p\in C_n$ we have

$$\begin{aligned} \Vert w_n-p\Vert ^2=\Vert P_{C_n}x_n-p\Vert ^2&\le \Vert x_n-p\Vert ^2-\Vert P_{C_n}x_n-x_n\Vert ^2 \nonumber \\&=\Vert x_n-p\Vert ^2-\mathrm{dist}^2(x_n,C_n). \end{aligned}$$

(15)

This implies that

$$\begin{aligned} \Vert w_n-p\Vert \le \Vert x_n-p\Vert . \end{aligned}$$

(16)

Using (16) we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert \alpha _n f(x_n)+(1-\alpha _n)w_n-p\Vert \\&=\Vert \alpha _n(f(x_n)-p)+(1-\alpha _n)(w_n-p)\Vert \\&\le \alpha _n\Vert f(x_n)-p\Vert +(1-\alpha _n)\Vert w_n-p\Vert \\&\le \alpha _n\Vert f(x_n)-f(p)\Vert +\alpha _n \Vert f(p)-p\Vert +(1-\alpha _n)\Vert w_n-p\Vert \\&\le \alpha _n \rho \Vert x_n-p\Vert +\alpha _n\Vert f(p)-p\Vert +(1-\alpha _n)\Vert x_n-p\Vert \\&\le [1-\alpha _n(1-\rho )]\Vert x_n-p\Vert +\alpha _n(1-\rho )\dfrac{\Vert f(p)-p\Vert }{1-\rho }\\&\le \max \{\Vert x_n-p\Vert ,\dfrac{\Vert f(p)-p\Vert }{1-\rho }\}\\&\le \cdots \le \max \left\{ \Vert x_1-p\Vert ,\dfrac{\Vert f(p)-p\Vert }{1-\rho }\right\} . \end{aligned}$$

Thus, the sequence $\{x_n\}$ is bounded. Consequently, the sequences $\{y_n\}, \{f(x_n)\}, \{Ay_n\}$ are bounded.

Claim 2.

$$\begin{aligned} \Vert w_n-x_n\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+2\alpha _n \langle f(x_n)-p, x_{n+1}-p\rangle . \end{aligned}$$

We have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n(f(x_n)-p)+(1-\alpha _n)(w_n-p)\Vert ^2 \nonumber \\&\le (1-\alpha _n)\Vert w_n-p\Vert ^2+2\alpha _n \langle f(x_n)-p,x_{n+1}-p\rangle \nonumber \\&\le \Vert w_n-p\Vert ^2+2\alpha _n \langle f(x_n)-p,x_{n+1}-p\rangle . \end{aligned}$$

(17)

On the other hand, we have

$$\begin{aligned} \Vert w_n-p\Vert ^2=\Vert P_{C_n}x_n-p\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert w_n-x_n\Vert ^2. \end{aligned}$$

(18)

Substituting (18) into (17) we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2 \le \Vert x_n-p\Vert ^2-\Vert w_n-x_n\Vert ^2+2\alpha _n \langle f(x_n)-p,x_{n+1}-p\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert w_n-x_n\Vert ^2 \le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+2\alpha _n \langle f(x_n)-p,x_{n+1}-p\rangle . \end{aligned}$$

Claim 3.

$$\begin{aligned} (1-\alpha _n)\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1} -p\Vert ^2+\alpha _n\Vert f(x_n)-p\Vert ^2. \end{aligned}$$

We first prove that

$$\begin{aligned} \Vert w_n-p\Vert ^2\le \Vert x_n-p\Vert ^2-\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2. \end{aligned}$$

(19)

Since $\{Ay_n\}$ is bounded, there exists $L>0$ such that $\Vert Ay_n\Vert \le L$ for all n. Using this fact, we have for all $u, v\in C_n$ that

$$\begin{aligned} \Vert h_n(u)-h_n(v)\Vert =\Vert \langle Ay_n, u-v\rangle \Vert \le \Vert Ay_n\Vert \Vert u-v\Vert \le L \Vert u-v\Vert . \end{aligned}$$

This implies that $h_n (\cdot )$ is L-Lipschitz continuous on $C_n$. By Lemma 2.5 we obtain

$$\begin{aligned} \mathrm{dist}(x_n, C_n)\ge \dfrac{1}{L} h_n(x_n), \end{aligned}$$

which, together with Lemma 3.10 we get

$$\begin{aligned} {\mathrm{dist}}(x_n, C_n)\ge \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2. \end{aligned}$$

(20)

Combining (15) and (20) we obtain

$$\begin{aligned} \Vert w_n-p\Vert ^2\le \Vert x_n-p\Vert ^2-\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2. \end{aligned}$$

Now, we prove Claim 3. From the definition of the sequence $\{x_n\}$ and (19) we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n(f(x_n)-p)+(1-\alpha _n)(w_n-p)\Vert ^2\\&=\alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2-\alpha _n(1-\alpha _n)\Vert f(x_n)-w_n\Vert ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert x_n-p\Vert ^2\\&\quad -(1-\alpha _n)\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+\Vert x_n-p\Vert ^2-(1-\alpha _n)\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2. \end{aligned}$$

This implies that

$$\begin{aligned} (1-\alpha _n)\left[ \dfrac{1}{L}\tau _n \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_n)\Vert ^2\right] ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1} -p\Vert ^2+\alpha _n\Vert f(x_n)-p\Vert ^2. \end{aligned}$$

Claim 4.

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le (1-(1-\rho )\alpha _n)\Vert x_n-p\Vert ^2+(1-\rho )\alpha _n\dfrac{2}{1-\rho }\langle f(p)-p,x_{n+1}-p\rangle . \end{aligned}$$

We have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _nf(x_n)+(1-\alpha _n)z_n-p\Vert ^2 \nonumber \\&=\Vert \alpha _n(f(x_n)-f(p))+(1-\alpha _n)(z_n-p)+\alpha _n(f(p)-p)\Vert ^2 \nonumber \\&\le \Vert \alpha _n(f(x_n)-f(p))+(1-\alpha _n)(z_n-p)\Vert ^2+2\alpha _n\langle f(p)-p,x_{n+1}-p\rangle \nonumber \\&\le \alpha _n\Vert f(x_n)-f(p)\Vert ^2+(1-\alpha _n)\Vert z_n-p\Vert ^2+2\alpha _n\langle f(p)-p,x_{n+1}-p\rangle \nonumber \\&\le \alpha _n\rho \Vert x_n-p\Vert ^2+(1-\alpha _n)\Vert x_n-p\Vert ^2+2\alpha _n\langle f(p)-p,x_{n+1}-p\rangle \nonumber \\&=(1-(1-\rho )\alpha _n)\Vert x_n-p\Vert ^2+(1-\rho )\alpha _n\dfrac{2}{1-\rho }\langle f(p)-p,x_{n+1}-p\rangle . \end{aligned}$$

(21)

Claim 5. The sequence $\{\Vert x_n-p\Vert ^2\}$ converges to zero by considering two possible cases on the sequence $\{\Vert x_n-p\Vert ^2\}$.

Case 1: There exists an $N\in {\mathbb N}$ such that $\Vert x_{n+1}-p\Vert ^2\le \Vert x_n-p\Vert ^2$ for all $n\ge N.$ This implies that $\lim _{n\rightarrow \infty }\Vert x_n-p\Vert ^2$ exists. It implies from Claim 2 that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_n-w_n\Vert =0. \end{aligned}$$

Since the sequence $\{x_n\}$ is bounded, it implies that there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ that converges weakly to some $z\in C$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle =\lim _{k\rightarrow \infty }\langle f(p)-p,x_{n_k}-p\rangle =\langle f(p)-p,z-p\rangle . \end{aligned}$$

Now, according to Claim 3

$$\begin{aligned} \lim _{k\rightarrow \infty }(1-\alpha _{n_k})\left[ \dfrac{1}{L}\tau _{n_k} \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_{n_k})\Vert ^2\right] ^2=0. \end{aligned}$$

This follows that

$$\begin{aligned} \lim _{k\rightarrow \infty }\tau _{n_k}\Vert r_\lambda (x_{n_k})\Vert ^2=\lim _{k\rightarrow \infty }\tau _{n_k}\Vert x_{n_k}-z_{n_k}\Vert ^2=0. \end{aligned}$$

(22)

Now, we prove that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =0. \end{aligned}$$

(23)

We first consider the case $\liminf _{k\rightarrow \infty }\tau _{n_k}>0$. In this case, there is a constant $\tau >0$ such that $\tau _{n_k}\ge \tau >0$ for all $k\in {\mathbb {N}}$. We have

$$\begin{aligned} \Vert x_{n_k}-z_{n_k}\Vert ^2=\dfrac{1}{\tau _{n_k}} \tau _{n_k}\Vert x_{n_k}-z_{n_k}\Vert ^2\le \dfrac{1}{\tau }.\tau _{n_k}\Vert x_{n_k}-z_{n_k}\Vert ^2. \end{aligned}$$

(24)

Combining (22) and (24) we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =0. \end{aligned}$$

Second, we consider the case $\liminf _{k\rightarrow }\tau _{n_k}=0$. In this case, we take a subsequence $\{n_{k_j}\}$ of $\{n_k\}$ if necessary, we assume without loss of generality that

$$\begin{aligned} \lim _{k\rightarrow \infty }\tau _{n_k}=0, \end{aligned}$$

(25)

and

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =a>0. \end{aligned}$$

(26)

Let $y_k=\dfrac{1}{l}\tau _{n_k} z_{n_k}+\left( 1-\dfrac{1}{l}\tau _{n_k}\right) x_{n_k}$. Using (25), we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert y_k-x_{n_k}\Vert =\lim _{k\rightarrow \infty }\dfrac{1}{l} \tau _{n_k}\Vert x_{n_k}-z_{n_k}\Vert =0. \end{aligned}$$

(27)

From the step size rule (6) and the definition of $y_{k}$ we have

$$\begin{aligned} \langle Ax_{n_k}-Ay_k, x_{n_k}-z_{n_k}\rangle > \mu \Vert x_{n_k}-z_{n_k}\Vert ^2. \end{aligned}$$

(28)

Since A is uniformly continuous on bounded subsets of C and using (27) it implies that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert Ax_{n_k}-Ay_k\Vert =0. \end{aligned}$$

(29)

Combining (28) and (29) we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =0. \end{aligned}$$

This is a contraction to (26). Therefore, the limit (23) is proved.

Since $x_{n_k}\rightharpoonup z$ and (23), Lemma 3.11 shows that $z\in VI(C,A).$

On the other hand,

$$\begin{aligned} \Vert x_{n+1}-w_{n}\Vert =\alpha _{n}\Vert f(x_n)-w_{n}\Vert \rightarrow 0 \text { as } n\rightarrow \infty . \end{aligned}$$

Thus

$$\begin{aligned} \Vert x_{n+1}-x_{n}\Vert =\Vert x_{n+1}-w_{n}\Vert +\Vert x_{n}-w_{n}\Vert \rightarrow 0 \text { as } n\rightarrow \infty . \end{aligned}$$

Since $p=P_{VI(C,A)}f(p)$ and $x_{n_k} \rightharpoonup z\in VI(C,A)$ we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle =\langle f(p)-p,z-p\rangle \le 0. \end{aligned}$$

This implies that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n+1}-p\rangle&\le \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n+1}-x_n\rangle +\limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle \\&=\langle f(p)-p,z-p\rangle \le 0, \end{aligned}$$

which, together with Claim 4, implies from Lemma 2.7 that

$$\begin{aligned} x_n\rightarrow p \text { as } n\rightarrow \infty . \end{aligned}$$

Case 2: There exists a subsequence $\{\Vert x_{n_j}-p\Vert ^2\}$ of $\{\Vert x_{n}-p\Vert ^2\}$ such that $\Vert x_{n_j}-p\Vert ^2 < \Vert x_{n_j+1}-p\Vert ^2$ for all $j\in {\mathbb {N}}$. In this case, it follows from Lemma 2.6 that there exists a nondecreasing sequence $\{m_k\}$ of ${\mathbb {N}}$ such that $\lim _{k\rightarrow \infty }m_k=\infty$ and the following inequalities hold for all $k\in {\mathbb {N}}$:

$$\begin{aligned} \Vert x_{m_k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2 \text { and } \Vert x_{k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2. \end{aligned}$$

(30)

According to Claim 2 we have

$$\begin{aligned} \Vert w_{m_k}-x_{m_k}\Vert ^2&\le \Vert x_{m_k}-p\Vert ^2-\Vert x_{{m_k}+1}-p\Vert ^2+2\alpha _{m_k} \langle f(x_{m_k})-p, x_{{m_k}+1}-p\rangle .\\&\le \alpha _{m_k} \langle f(x_{m_k})-p, x_{{m_k}+1}-p\rangle \\&\le \alpha _{m_k}\Vert f(x_{m_k})-p\Vert |x_{{m_k}+1}-p\Vert \rightarrow 0 \text { as } k \rightarrow \infty . \end{aligned}$$

According to Claim 3 we have

$$\begin{aligned}&(1-\alpha _{m_k})\left[ \dfrac{1}{L}\tau _{m_k} \left( \dfrac{1}{\lambda }-\mu \right) \Vert r_\lambda (x_{m_k})\Vert ^2\right] ^2\\&\quad \le \Vert x_{m_k}-p\Vert ^2-\Vert x_{{m_k}+1}-p\Vert ^2+\alpha _{m_k}\Vert f(x_{m_k})-p\Vert ^2\\&\quad \le \alpha _{m_k}\Vert f(x_{m_k})-p\Vert ^2 \rightarrow 0 \text { as } k\rightarrow \infty . \end{aligned}$$

Using the same arguments as in the proof of Case 1, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{n_k}-z_{n_k}\Vert =0, \lim _{k\rightarrow \infty }\Vert x_{m_k+1}-x_{m_k}\Vert \rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle f(p)-p,x_{m_k+1}-p\rangle \le 0. \end{aligned}$$

Since (21) we get

$$\begin{aligned} \Vert x_{m_k+1}-p\Vert ^2&\le (1-\alpha _{m_k}(1- \rho ))\Vert x_{m_k}-p\Vert ^2+2\alpha _{m_k}\langle f(p)-p,x_{m_k+1}-p\rangle \\&\le (1-\alpha _{m_k}(1- \rho ))\Vert x_{m_k+1}-p\Vert ^2+2\alpha _{m_k}\langle f(p)-p,x_{m_k+1}-p\rangle , \end{aligned}$$

which, together with (30), implies that

$$\begin{aligned} \Vert x_k-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2\le 2\langle f(p)-p,x_{m_k+1}-p\rangle . \end{aligned}$$

Therefore, $\limsup _{k\rightarrow \infty }\Vert x_k-p\Vert \le 0$, that is $x_k \rightarrow p$. The proof is completed. $\square$

4 Numerical illustrations

In this section, we discuss the numerical behavior of our proposed Algorithm 3.3 using different test examples and compare our method with method (1.2). In all the examples, we take $\alpha _{n}=1/(n+1)$ and some choices of $\mu$, $\lambda$ and l.

Example 2

We take a classical example (see, e.g., Maingé and Gobinddass 2016) for which the usual gradient method does not converge to a solution of the variational inequality. Here, the feasible set is $C:={\mathbb {R}}^m$ (for some positive even integer m) and $A:=(a_{ij})_{1\le i,j\le m}$ is the square matrix $m \times m$ whose terms are given by

$$\begin{aligned} a_{ij}= \left\{ \begin{array}{llll} &{} -1,~~\mathrm{if} ~~j=m+1-i~~\mathrm{and}~~j>i\\ &{} 1,~~\mathrm{if} ~~j=m+1-i~~\mathrm{and}~~j<i\\ &{} 0~~\mathrm{otherwise} \end{array} \right. \end{aligned}$$

Table 1 Proposed Alg. 3.3 vs Vuong and Shehu Alg. 1.2 with $(\mu ,\lambda ,l)=(0.1,9,0.5)$

It is clear that the zero vector $z = (0,\ldots ,0)$ is the solution of this test example. Let $x_{1}$ be the initial point whose element is randomly chosen in the closed interval $[-1,1]$. We terminate the iterations if $\Vert x_{n}-z_n\Vert _2\le \varepsilon$ with $\varepsilon =10^{-4}$. The results are listed in Table 1 below. We consider different values of m.

We next consider some model in infinite dimensional Hilbert spaces in the following example:

Example 3

Consider $C:=\{x \in H:\Vert x\Vert \le 2\}$. Let $g: C\rightarrow {\mathbb {R}}$ be defined by $g(u):=\frac{1}{1+\Vert u\Vert ^2}$. Observe that g is $L_g$-Lipschitz continuous with $L_g=\frac{16}{25}$ and $\frac{1}{5}\le g(u)\le 1,~~\forall u \in C$. Define the Volterra integral operator $F:L^2([0,1])\rightarrow L^2([0,1])$ by $F(u)(t):=\int _0^t u(s)ds,~~\forall u \in L^2([0,1]), t \in [0,1].$ Then F is bounded linear monotone (see Exercise 20.12 of Bauschke and Combettes 2011) and $\Vert F\Vert =\frac{2}{\pi }$. Now, define $A:C\rightarrow L^2([0,1])$ by $A(u)(t):=g(u)F(u)(t),~~\forall u \in C, t \in [0,1].$ Suppose $\langle Au, v-u\rangle \ge 0,~~\forall u,v \in C$; then we have that $\langle Fu, v-u\rangle \ge 0$ (noting that $g(u)\ge \frac{1}{5}>0$). Hence,

$$\begin{aligned} \langle Av, v-u\rangle= & {} g(v) \langle F(v),v-u\rangle \\\ge & {} g(v)\Big [\langle F(v),v-u\rangle -\langle F(u),v-u\rangle \Big ]\\= & {} g(v)\langle F(v)-F(u),v-u\rangle \ge 0. \end{aligned}$$

Therefore, A is pseudomonotone. Observe that A is not monotone since $\langle Av-Au,v-u\rangle =-\frac{1}{20}<0$ with $v=1$ and $u=2$. Furthermore, for all $u, v \in C$, we have

$$\begin{aligned} \Vert Au-Av\Vert= & {} \Vert g(u)F(u)-g(v)F(v)\Vert \\= & {} \Vert g(u)F(u)-g(u)F(v)+g(u)F(v)-g(v)F(v)\Vert \\\le & {} \Vert g(u)F(u)-g(u)F(v)\Vert +\Vert g(u)F(v)-g(v)F(v)\Vert \\\le & {} |g(u)|\Vert F(u)-F(v)\Vert +\Vert F(v)\Vert |g(u)-g(v)|\\\le & {} |g(u)|\Vert F\Vert \Vert u-v\Vert +\Vert F\Vert \Vert v\Vert L_g\Vert u-v\Vert \\= & {} (|g(u)|\Vert F\Vert +\Vert F\Vert \Vert v\Vert L_g)\Vert u-v\Vert \\= & {} \frac{82}{\pi }\Vert u-v\Vert . \end{aligned}$$

Hence, A is $L_A$-Lipschitz-continuous with $L_A=\frac{82}{\pi }$. Therefore, A is uniformly continuous.

Observe that $VI(C,A) \ne \emptyset$ since $0 \in VI(C,A)$. We take $\frac{\Vert x_{n+1}-x_n\Vert _2}{\max \{1,\Vert x_n\Vert _2\}}\le \epsilon$ as stopping criterion, with $\epsilon =10^{-2}$. We consider different initial points $x_1=1$, $x_1=1+t^2$, $x_1=e^t$ and $x_1=sin(t)$ in the following cases:

Case I: $(\mu ,\lambda )=(0.3,3.2)$

Case II: $(\mu ,\lambda )=(3.0,0.3)$

We report the numerical behaviour of this example in Figs. 11, 12, 13 and 14 and Table 2.

Fig. 1

Comparison with $m=50$

Fig. 2

Comparison with $m=100$

Fig. 3

Comparison with $m=150$

Fig. 4

Comparison with $m=200$

Fig. 5

Proposed Alg. 3.3 with $m=500$

Fig. 6

Proposed Alg. 3.3 with $m=1000$

Fig. 7

Proposed Alg. 3.3 with $m=2000$

Fig. 8

Proposed Alg. 3.3 with $m=3000$

Fig. 9

Proposed Alg. 3.3 with $m=5000$

Fig. 10

Proposed Alg. 3.3 with $m=10000$

Fig. 11

Proposed Alg. 3.3 with $x_1=1$

Fig. 12

Proposed Alg. 3.3 with $x_1=1+t^2$

Fig. 13

Proposed Alg. 3.3 with $x_1=e^t$

Fig. 14

Proposed Alg. 3.3 with $x_1=\sin (t)$

Table 2 Proposed algorithm 3.3 with $l=0.2$

Remark 4.3

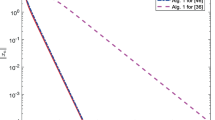
• 1. From the numerical results of Examples 2–3, we observe that our proposed Algorithm 3.3 is efficient and easy to implement. See Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 and Tables 1 and 2.

• 2. In Example 2, there is no significant change in the number of iterations required as we increase the dimension m. This is a significant improvement since the iteration number required to terminate the proposed Algorithm 3.3 does not depend on the size of the problem. See Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 and Table 1.

• 3. In Example 3, we observe also that both the choice of initial points and the parameters $\mu$ and $\lambda$ do not have significant effect on the number of iterations and the CPU time. See Figs. 11, 12, 13 and 14 and Table 2.

• 4. Clearly from the numerical Examples presented above, our proposed Algorithm 3.3 outperformed Algorithm 1.2 proposed by Vuong & Shehu. See Table 1 and Figs. 1 2, 3 and 4. We have omitted some of the comparison results (part in Example 2 and all in Example 3) due to large amount of time required by Vuong and Shehu Algorithm 1.2 to terminate.

Our preliminary examples in this section play a role in illustrating the rationality in studying pseudomonotone variational inequality. In future works, we shall give more interesting examples from applications.

5 Conclusions

In this paper we proposed a new algorithm for solving variational inequalities in real Hilbert spaces. The proposed algorithm shows the strongly convergence property under pseudomonotonicity and non-Lipschitz continuity of the mapping A. The algorithm requires the calculation of only two projections onto the feasible set C per iteration. These two properties pseudomonotonicity and non-Lipschitz continuity of the mapping A emphasize the applicability and advantages over several existing results in the literature. Numerical experiments in finite and infinite dimensional spaces illustrate the performance of the new scheme.