1 Introduction

Vaccination against COVID-19 infection started in the UK at the end of 2020 [33]. Presently, ten WHO-recommended vaccine candidates are in use throughout the globe [42]. A good proportion of the population is vaccinated in the one year of its application [7]. Though the COVID-19 pandemic has not been controlled, its morbidity and mortality have significantly reduced due to vaccination [35, 36]. Numerous mathematical models have been proposed and analysed to determine the course of the COVID-19 pandemic since the WHO announced the public health emergency of international concern (PHEIC) on 30 January 2020 [41] to restrict the spread of the novel coronavirus. These are mainly deterministic SEIR epidemic models or their variants [2, 17, 25, 26, 29, 30, 32, 38]. A few are stochastic models [1, 16, 19, 40, 45]. Obviously, these earlier models did not consider the effect of vaccination and can no longer be used for the epidemic course once the full-fledged COVID-19 vaccination has started. Any current time epidemic model should contain a vaccinated class. Recently, some researchers have proposed and analysed some COVID-19 vaccination models to find the effect of immunization on the disease dynamics [11, 12, 18, 27, 28, 34, 39, 44]. A case study of Japan shows that reduced vaccine efficacy and roll-out of COVID-19 restriction may lead to a surge of COVID-19 cases [11]. Ghostine et al. [12] have proposed an enhanced SEIR model, including a vaccination compartment to mimic the spread of the coronavirus epidemic in Saudi Arabia. It is shown that intensifying the vaccination campaign can significantly decrease the number of confirmed cases and deaths. Kurmi and Chouhan [18] analysed an eight-compartment COVID-19 vaccination model using optimal control theory. They investigated the impact of vaccination on the spread of the disease and demonstrated that a combination of community mitigation strategies and vaccination can effectively minimize this pandemic. The simulations, however, were done with a hypothetical parameter set. A COVID-19 vaccination model was studied in [27] to show that the waning of vaccine-induced immunity significantly impacts the disease dynamics. Rabiu and Iyaniwura [34] developed a COVID-19 model to assess the impact of vaccination and immunity waning on the dynamics of the disease. Without considering a precise vaccination class, De la Sen and Ibeas [39] analysed an SEIR-type epidemic model to observe the combined role of vaccination and antiviral drugs in controlling the COVID-19 pandemic. An SEIR-type epidemic model with time delay and vaccination control was considered by Zhai et al. [44]. They have considered the vaccination strategy based on feedback linearization techniques and showed that the disease would persist in the population if there is no vaccination control. All these models are deterministic types and do not consider any uncertainty in the rate parameters. None of these models studied the effect of vaccine-induced immunity loss on the persistence of the disease. However, understanding the dynamics of a novel virus is insufficient if the inherent noise in the rate parameters is not considered. It is reported that there is uncertainty in the COVID-19 infection rate [24]. Due to spatial heterogeneity and other physical factors, there is a significant variation in the COVID-19 recovery time and rate [8, 37]. Most importantly, the efficacy of vaccines produced in the shortest time is primarily unknown. It is also unclear how long these vaccines will provide protection against COVID-19 infection and to what extent. Even after taking a total dose of the vaccine, it is now recommended for a booster dose, implying the vaccine’s efficacy loss [6, 15]. This indicates the existence of many uncertainties in the COVID-19 disease dynamics, its recovery rate and vaccine efficacy. So the question is: Can the existing vaccination drive eradicate the disease? If it is, what should be the parametric condition, given that there are many uncertainties in COVID-19 disease and vaccine efficacy? We answered these questions by analysing a six-dimensional stochastic epidemic model and demonstrated the effect of vaccination in controlling the COVID-19 epidemic. We considered noise in these rate parameters due to the variability in the infection rate, recovery rate and vaccine efficacy and determined the disease persistence and eradication conditions. Using the Indian and Italian COVID-19 data, we estimated the best-fitted parameters and noise intensities for the considered model. We then observed the variational effects of the force of infection, vaccination and immunity waning rate parameters. Our analysis reveals that the COVID-19 disease will persist over the existing vaccine efficacy and transmissibility for a long time.

The remaining portion of this paper is organized in the following sequence. The stochastic COVID-19 vaccination model is proposed in Sect. 2. Analytical results, including disease extinction conditions and stationary distribution of the solutions, are prescribed in Sect. 3. Section 4 shows parameter estimation and two case studies. A discussion is presented in Sect. 5, and the paper ends with a conclusion in Sect. 6.

2 The model

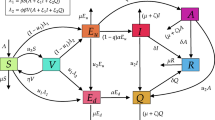
We propose an extended SEIR stochastic compartmental epidemic model to investigate the COVID-19 disease under vaccination. The total human population, N(t), of a region is divided into six mutually exclusive groups, viz. susceptible, exposed, detected infectives, undetected infectives, recovered and vaccinated, which are denoted by S, E, I, A, R and V, respectively. The susceptible individuals are recruited through birth at a rate \(\varLambda \). After effective contact with a detected or undetected COVID-19 infected individual, susceptible individuals become infected and join the E class, who carry the virus but are not yet infectious. The transmission probability of COVID-19 infection from the detected and undetected individuals may differ. Assume that \(\kappa \) is the transmission probability of disease due to the contact between susceptible and undetected infected individuals. The same is \((1-\kappa )\) for the contact between the susceptible and detected individuals. If \(\beta \) is the average per capita daily contact, then the susceptible individual that joins the E class is given by \(\beta (\frac{ (1-\kappa )SI}{N}+\frac{\kappa SA}{N}\)). The susceptible individuals are vaccinated at a rate q and join the V class. Since the vaccination of a susceptible individual does not give 100 % immunity against coronavirus, the vaccinated people may again be infected by the undetected and detected individuals, but possibly at a lower rate. Considering \(\eta \) as the vaccination-induced immunity loss, the portion of the vaccinated individuals who join the exposed class at time t is \(\eta (\frac{ (1-\kappa )SI}{N}+\frac{\kappa SA}{N})\). Observe that it gives the fraction of vaccinated individuals at time t losses immunity after effective interaction with the detected and undetected infected individuals. We call \(\eta \) the vaccine-induced immunity loss parameter or the vaccine efficacy parameter. If \(\eta =0\), then the vaccine will be \(100\%\) effective. An exposed class individual spends on an average \(\frac{1}{\omega }\) time in E class and then joins either the undetected class with probability \(\delta \) or the detected class with probability \((1-\delta )\). An average time of \(\frac{1}{\gamma _1}\) and \(\frac{1}{\gamma }\) are spent by the undetected and detected individuals, respectively, before moving to the recovered class. Recovered people can also lose immunity and join the susceptible class at a rate of g. Natural death at a rate m is incorporated in every compartment, and an additional disease-related death rate \(d_i\) is included in the detected class, I. We do not consider any disease-related death in the A class because critically ill individuals, if any, may be shifted to the I class at a rate \(\nu \). Since the coronavirus is a novel virus, there are substantial uncertainties in the rate constants, like infection rate [22], recovery rate [3] in A and I classes, and also in the rate of immunity loss [10]. To incorporate this uncertainty, we consider random perturbations to these parameters as follows: \({\mp } \beta \rightarrow {\mp } \beta +\sigma _1 \text {d}B_1(t),~\eta \rightarrow \eta +\sigma _2\text {d}B_2(t),~\gamma _1 \rightarrow \gamma _1 + \sigma _3\text {d}B_3(t),~\gamma \rightarrow \gamma +\sigma _4\text {d}B_4(t),\) where \(B_i (t)\) are standard mutually independent Brownian motions and \(\sigma _i ^2, i=1,2,3,4\), are the intensities of the white noises. Similar parametric perturbation has also been considered in other biological models [4, 20, 21, 43, 46]. Encapsulating all these assumptions, the stochastic compartmental model for COVID-19 reads

$$\begin{aligned} \text {d}S&=\left[ \varLambda -qS-\frac{\beta S}{N}\left( (1-\kappa )I+\kappa A\right) -mS+gR\right] \text {d}t\nonumber \\&\quad -\frac{\sigma _1 S}{N}\left[ (1-\kappa )I+\kappa A\right] \text {d}B_1(t),\nonumber \\ \text {d}E&=\bigg [\frac{\beta S}{N}\left( (1-\kappa )I+\kappa A\right) +\frac{\eta V}{N}\left( (1-\kappa )I+\kappa A\right) \nonumber \\&\quad -\omega E -mE\bigg ]\text {d}t+\frac{\left[ (1-\kappa )I+\kappa A\right] }{N} \nonumber \\&\quad (\sigma _1 S \text {d}B_1(t)+ \sigma _2 V \text {d}B_2(t)),\nonumber \\ \text {d}A&=\left[ \delta \omega E-(\gamma _1+\nu +m)A\right] \text {d}t-\sigma _3A\text {d}B_3(t),\nonumber \\ \text {d}I&=\left[ (1-\delta )\omega E-(\gamma +m+d_i)I+\nu A\right] \text {d}t\nonumber \\&\quad -\sigma _4I\text {d}B_4(t),\nonumber \\ \text {d}R&=\left[ \gamma _1A+\gamma I-gR-mR\right] \text {d}t\nonumber \\&\quad +\sigma _3A\text {d}B_3(t)+\sigma _4I\text {d}B_4(t),\nonumber \\ \text {d}V&=\left[ qS-\frac{\eta V}{N}\left[ (1-\kappa )I+\kappa A\right] -mV\right] \text {d}t\nonumber \\&\quad -\frac{ \sigma _2 V}{N}\left[ (1-\kappa )I+\kappa A\right] \text {d}B_2(t). \end{aligned}$$
(1)

In each equation, the expression multiplied with \(\text {d}t\) is called the drift coefficient and the expression multiplied with \(\text {d}B_i(t)\) is called the diffusion coefficient.

The initial values for the state variables are considered as

$$\begin{aligned}{} & {} S(0)\ge 0,~E(0)\ge 0,~A(0)\ge 0, ~I(0)\ge 0, ~R(0)= 0,\nonumber \\{} & {} V(0)= 0. \end{aligned}$$
(2)

3 Results

It is to be noted that the system (1) considers the human population as its variables which must be non-negative and bounded. Also, from a dynamical point of view, the solution of the system (1) should exist uniquely. The multiplicative noise considered in (1) may cause a population explosion. It is, therefore, imperative to show that the supposed system has a unique solution without any population explosion, i.e. the solution is global, and all the solutions are positive when starting with positive initial values. We have the following theorem for these results.

Theorem 1

For any initial value \((S(0),E(0),A(0),I(0), R(0),V(0))\in {\mathbb {R}}^6_+\), there exists a unique global solution of the system (1) such that (S(t), E(t), A(t), I(t), R(t),  \(V(t))\) \(\in {\mathbb {R}}^6_+\) for all \(t\ge 0\) and the solution remains in \({\mathbb {R}}^6_+\) with probability 1, i.e. almost surely (a.s).

Proof

See Appendix I for its proof. \(\square \)

It is worth mentioning that the stochastic system (1) has no equilibrium point. However, it may have some stationary distribution, meaning that no significant change will occur in the asymptotic solution of the system when the time is substantial. From an epidemic point of view, such distribution implies the long-term persistence of the disease. We show that the stationary distribution occurs if the following theorem holds good. We adopted the technique given in [13] to prove this result. The following lemma will be used in the sequel.

Lemma 1

[47] Let X(t) be a regular Markov process (time-homogeneous) in \({\mathbb {R}}_+^n\) whose dynamics is described by the stochastic equation

$$\begin{aligned} \text {d}X(t)=b(X) t+\varSigma _{r=1}^kh_r(X) \text {d}B_r(t). \end{aligned}$$
(3)

Then the corresponding diffusion matrix is defined as

$$\begin{aligned} A(x)=\left[ a_{\text {ij}}\right] , ~~ a_{\text {ij}}=\varSigma _{r=1}^kh_r^i(X) h_r^j(X) \end{aligned}$$

and the solution X(t) of (3) has a unique stationary distribution \(\pi (.)\) if there exist a bounded domain \(U \in R^n\) with regular boundary \(\varGamma \) and (a) there is a positive number \(M_2\) such that \(\varSigma _{i,j=1}^l a_{ij}(x)\xi _i \xi _j \ge M_2 |\xi |^2\), (b) there exist a non-negative \(C^2\)-function \(V_1\) such that \(LV_1\) is negative for any \({\mathbb {R}}_+^n\) for all \(x\in \) \({\mathbb {R}}_+^n\), where f(.) is a function integrable with respect to the measure \(\pi \).

Theorem 2

Assume that

$$\begin{aligned} \begin{aligned}&R_{0V}^S=\frac{ \omega (\beta m+\eta q)}{(q+m+\frac{1}{2}\sigma _1^2)(\gamma +m+d_i+\frac{1}{2}\sigma _4^2)} \\&\quad \times \frac{\{\kappa \delta (\gamma +m+d_i)+(1-\kappa )(\delta \nu +(1-\delta )(\nu +\gamma _1+m))\}}{(\nu +\gamma _1+m+\frac{1}{2}\sigma _3^2)(\omega +m+\frac{1}{2}(\sigma _1^2+\sigma _2^2))}. \end{aligned} \end{aligned}$$

Then, for any initial value (S(0), E(0), A(0), I(0), R(0), 

\( V(0)) \in {\mathbb {R}}_+^6\), a sufficient condition for existing a stationary distribution \(\pi (.)\) of the system (1) is \(R_{0V}^S>1\).

Proof

By Theorem 1, for any initial size of population \((S(0), E(0), A(0), I(0), R(0), V(0))\in {\mathbb {R}}_+^6\), there exists a unique non-local global solution \((S,E,A,I,R,V) \in {\mathbb {R}}^6_+\). Let us denote \(D=\frac{1 }{N}\left[ (1-\kappa )I+\kappa A\right] \). The diffusion matrix of the system (1) is given by

$$\begin{aligned}A'= \begin{pmatrix} \sigma _1^2 S^2 D^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} &{} \\ 0 &{} \sigma _1^2 S^2D^2+ &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} \sigma _2^2 V^2D^2 &{} &{} &{} &{} \\ 0 &{} 0 &{} \sigma _3^2 A^2 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \sigma _4^2 I^2 &{} 0 &{} 0\\ &{} &{} &{} &{} &{} \\ 0 &{} 0 &{} 0 &{} 0 &{} \sigma _3^2 A^2+ &{} 0\\ &{} &{} &{} &{} \sigma _4^2 I^2 &{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sigma _2^2 V^2D^2\\ \end{pmatrix}. \end{aligned}$$

Let \(\bar{D_\alpha }\) be a bounded domain in \({\mathbb {R}}^6_+\) which excludes the origin. Choose \(M_1=\text{ min } _{(S,E,A,I,R,V) \in \bar{D_\alpha }\in {\mathbb {R}}^6_+}\{\sigma _1^2\,S^2 D^2,\) \((\sigma _1^2\,S^2+\sigma _2^2 V^2)D^2, \sigma _3^2 A^2, \sigma _4^2 I^2, \sigma _3^2 A^2+\sigma _4^2 I^2, \sigma _2^2 V^2\)\(D^2\}\). For \({\bar{\zeta }}=(\bar{\zeta _1}, \bar{\zeta _2}, \bar{\zeta _3}, \bar{\zeta _4}, \bar{\zeta _5}, \bar{\zeta _6}) \in {\mathbb {R}}^6_+\), we obtain

$$\begin{aligned} \begin{aligned}&\varSigma _{i,j=1}^6a_{ij}(S,E,A,I,R,V) \bar{\zeta _i} \bar{\zeta _j}=\sigma _1^2 S^2 D^2 \bar{\zeta _1}^2\\&\quad +(\sigma _1^2 S^2+\sigma _2^2 V^2)D^2\bar{\zeta _2}^2+ \sigma _3^2 A^2\bar{\zeta _3}^2+ \sigma _4^2 I^2 \bar{\zeta _4}^2\\&\quad + (\sigma _3^2 A^2+\sigma _4^2 I^2)\bar{\zeta _5}^2+\sigma _2^2 V^2D^2\bar{\zeta _6}^2, \\&(S,E,A,I,R,V) \in \bar{D_\alpha }. \end{aligned} \end{aligned}$$

Thus, the condition (a) of Lemma 1 holds. In order to prove the second assertion of the lemma, define a non-negative \(C^2\) function \(H_1\), where \(H_1: {\mathbb {R}}^6_+ \rightarrow {\mathbb {R}}\) be such that \(H_1=(S+E+A+I+R+V)-B_1 \text{ ln }S -B_2\text{ ln }E- B_3 \text{ ln }A-B_4\text{ ln }I\), where \(B_1, B_2, B_3\) and \(B_4\) are positive constants to be determined later.

Applying Ito formula, one gets

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}(S+E+A+I+R+V) =\varLambda -m (S+E+A+I\\&\quad +R+V)-d_i I, \\&{\mathcal {L}}(-\text{ ln }S)=-\frac{\varLambda }{S}+\frac{\beta }{N}[\kappa A+(1-\kappa )I]+q+m-\frac{gR}{N}\\&\quad +\frac{1}{2N^2} \sigma _1^2 [\kappa A+(1-\kappa )I]^2, \\&{\mathcal {L}}(-\text{ ln }E)=-\frac{\eta V}{N E}[\kappa A+(1-\kappa )I]\\&\quad -\frac{\eta V}{N E}[\kappa A+(1-\kappa )I]\\&\quad +\omega +m +\frac{1}{2N^2E^2}(\sigma _1 ^2 S^2+\sigma _2 ^2 V^2) [\kappa A+(1-\kappa )I]^2, \\&{\mathcal {L}}(-\text{ ln }A)= -\frac{\delta \omega E}{A}+(\gamma _1+\nu +m)+\frac{1}{2}\sigma _3^2, \\&{\mathcal {L}}(-\text{ ln }I)= -\frac{(1-\delta )\omega E}{I}-\frac{\nu A}{I}+(\gamma +m+d_i)+\frac{1}{2}\sigma _4^2. \end{aligned} \end{aligned}$$

Therefore, we have

$$\begin{aligned}{} & {} {\mathcal {L}}H_1=\varLambda -m (S+E+A+I+R+V)-d_i I \nonumber \\{} & {} \qquad +B_1\bigg (-\frac{\varLambda }{S}+\frac{\beta }{N}[\kappa A+(1-\kappa )I]+q+m \nonumber \\{} & {} \qquad -\frac{gR}{N}+\frac{1}{2N^2} \sigma _1^2 [\kappa A+(1-\kappa )I]^2\bigg ) \nonumber \\{} & {} \qquad +B_2\bigg (-\frac{\beta S}{NE}[\kappa A+(1-\kappa )I]+\omega +m \nonumber \\{} & {} \qquad -\frac{\eta \beta V}{N E}[\kappa A+(1-\kappa )I] \nonumber \\{} & {} \qquad +\frac{1}{2N^2E^2}(\sigma _1 ^2 S^2+\sigma _2 ^2 V^2) [\kappa A+(1-\kappa )I]^2 \bigg ) \nonumber \\{} & {} \qquad + B_3\bigg (-\frac{\delta \omega E}{A}+(\gamma _1+\nu +m)+\frac{1}{2}\sigma _3^2\bigg )\nonumber \\{} & {} \qquad +B_4 \left( -\frac{(1-\delta )\omega E}{I}-\frac{\nu A}{I}+(\gamma +m+d_i)+\frac{1}{2}\sigma _4^2 \right) \nonumber \\{} & {} \quad \le -4\bigg (m(S+E+A+I+R+V)\frac{\varLambda B_1}{S} \frac{\beta S B_2 \kappa A}{NE}\bigg )^{\frac{1}{4}} \nonumber \\{} & {} \qquad \times \bigg (\frac{\delta \omega B_3 E}{A}\bigg )^{\frac{1}{4}} \nonumber \\{} & {} \qquad +\left( q+m+\frac{1}{2}\sigma _1^2\right) B_1 +\varLambda + \bigg (\omega +m \nonumber \\{} & {} \qquad +\frac{1}{2}(\sigma _1^2+\sigma _2^2)\bigg )B_2 +\left( \gamma _1+\nu +m+\frac{1}{2}\sigma _3^2\right) B_3 \nonumber \\{} & {} \qquad + \bigg (\gamma +m+d_i+\frac{1}{2}\sigma _4^2\bigg )B_4-d_i I\nonumber \\{} & {} \qquad +\frac{1}{N}\beta (\kappa A+(1-\kappa )I)B_1\nonumber \\{} & {} \qquad -\frac{\beta (1-\kappa )SI}{NE}B_2-\frac{gR}{N}B_1\nonumber \\{} & {} \qquad -\frac{ \beta V}{NE}(\kappa A+(1-\kappa )I)B_2-\frac{(1-\delta )\omega E}{I}B_4\nonumber \\{} & {} \qquad -\frac{\nu A}{I}B_4. \end{aligned}$$
(4)

Define \(B_1=\frac{(\beta m+\eta q) (\kappa \delta (\gamma +m+d_i)+(1-\kappa )\delta \nu +(1-\kappa )(1-\delta )(\gamma _1+\nu +m))}{\left( q+m+\frac{1}{2}\sigma _1^2\right) m \beta \kappa \delta \left( \gamma +m+d_i+\frac{1}{2}\sigma _4^2\right) }\) and let

$$\begin{aligned} \varLambda= & {} \left( \omega +m+\frac{1}{2}(\sigma _1^2+\sigma _2^2)\right) , \\ B_2= & {} \left( \gamma _1+\nu +m+\frac{1}{2}\sigma _3^2\right) , \\ B_3= & {} \left( \gamma +m+d_i+\frac{1}{2}\sigma _4^2\right) B_4. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}&B_2= \frac{\varLambda }{\left( \omega +m+\frac{1}{2}(\sigma _1^2+\sigma _2^2)\right) },\\&B_3= \frac{\varLambda }{\left( \gamma _1+\nu +m+\frac{1}{2}\sigma _3^2\right) }, \\&B_4= \frac{\varLambda }{\left( \gamma +m+d_i+\frac{1}{2}\sigma _4^2\right) }. \end{aligned} \end{aligned}$$

Define

$$\begin{aligned}{} & {} R_{0V}^S=\frac{ \omega (\beta m+\eta q)}{(q+m+\frac{1}{2}\sigma _1^2)(\gamma +m+d_i+\frac{1}{2}\sigma _4^2)}\nonumber \\{} & {} \quad \times \frac{\{\kappa \delta (\gamma +m+d_i)+(1-\kappa )(\delta \nu +(1-\delta )(\nu +\gamma _1+m))\}}{(\nu +\gamma _1+m+\frac{1}{2}\sigma _3^2)(\omega +m+\frac{1}{2}(\sigma _1^2+\sigma _2^2))} \nonumber \\ \end{aligned}$$
(5)

so that (4) becomes

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}H_1 \le -4\varLambda \left[ \left( R_{0V}^S\right) ^{\frac{1}{4}}- 1 \right] + \left( q+m+\frac{1}{2}\sigma _1^2\right) B_1-d_i I \\&\quad +\frac{1}{N}\beta (\kappa A+(1-\kappa )I)B_1 -\frac{\beta (1-\kappa )SI}{NE}B_2 -\frac{\nu A}{I}B_4\\&\quad -\frac{\beta V}{NE}(\kappa A+(1-\kappa )I)B_2-\frac{(1-\delta )\omega E}{I}B_4. \end{aligned}\nonumber \\ \end{aligned}$$
(6)

We further define

$$\begin{aligned} \begin{aligned}&H_2=B_5((S+E+A+I+R+V)-B_1 \text{ ln }S -B_2\text{ ln }E\\&\quad - B_3 \text{ ln }A-B_4\text{ ln }I)-\text{ ln } S -\text{ ln }R- \text{ ln }V+(S+E+A\\&\quad +I+R+V) =(B_5+1)(S+E+A+I+R+V)\\&\quad -(1+B_1B_5)\text{ ln }S-B_2B_5 \text{ ln } E-B_3B_5 \text{ ln }A -\text{ ln }R-\text{ ln }V. \end{aligned}\nonumber \\ \end{aligned}$$
(7)

Let \(W_{k_1}=\left( \frac{1}{{k_1}},{k_1}\right) \times \left( \frac{1}{{k_1}},{k_1}\right) \times \left( \frac{1}{{k_1}},{k_1}\right) \times \left( \frac{1}{{k_1}},{k_1}\right) \times \left( \frac{1}{{k_1}},{k_1}\right) \times \left( \frac{1}{{k_1}},{k_1}\right) \). As \({k_1} \rightarrow \infty \), it is evident that

$$\begin{aligned}{} & {} \text{ lim }~\text{ inf}_{(S,E,A,I,R,V) \in {\mathbb {R}}^6_+ \backslash W_{k_1}}\nonumber \\{} & {} \quad H_2(S,E,A,I,R,V)=+\infty . \end{aligned}$$
(8)

Now, we intend to prove that \(H_2(S,E,A,I,R,V)\) has the unique smallest value

$$\begin{aligned} H_2(S(0),E(0),A(0),I(0),R(0),V(0)). \end{aligned}$$

Taking partial derivatives of the function \(H_2(S,E,A,I,R, V)\) with respect to each state variable, we get

$$\begin{aligned} \frac{\partial H_2(S,E,A,I,R,V)}{\partial S}= & {} 1+B_5-\frac{1+B_1B_5}{S}, \nonumber \\ \frac{\partial H_2(S,E,A,I,R,V)}{\partial E}= & {} 1+B_5-\frac{B_2B_5}{E}, \nonumber \\ \frac{\partial H_2(S,E,A,I,R,V)}{\partial A}= & {} 1+B_5-\frac{B_3B_5}{A}, \nonumber \\ \frac{\partial H_2(S,E,A,I,R,V)}{\partial I}= & {} 1+B_5-\frac{B_4B_5}{I}, \nonumber \\ \frac{\partial H_2(S,E,A,I,R,V)}{\partial R}= & {} 1+B_5-\frac{1}{R}, \nonumber \\ \frac{\partial H_2(S,E,A,I,R,V)}{\partial V}= & {} 1+B_5-\frac{1}{V}. \end{aligned}$$
(9)

Making each of these partial derivatives equal to zero, one gets \(S=\frac{1+B_1B_5}{1+B_5}, E=\frac{B_2B_5}{1+B_5}, A= \frac{B_3B_5}{1+B_5}, I=\frac{B_4B_5}{1+B_5},\) \( R=\frac{1}{1+B_5}, V=\frac{1}{1+B_5}\) as the unique stagnation point of \(H_2\). Furthermore, the Hesse matrix of the function \(H_2(S,E,A,I,R,V)\) at the given initial population density reads

$$\begin{aligned} M_1=\left( \begin{array}{cccccc} \frac{1+B_1B_5}{S^2(0)} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{B_2B_5}{E^2(0)} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{B_3B_5}{A^2(0)} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \frac{B_4B_5}{I^2(0)} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{R^2(0)} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{V^2(0)}\\ \end{array} \right) . \end{aligned}$$

Clearly, the matrix \(M_1\) is positive definite. Hence, \(H_2\) attains the smallest value at \(\bigg (\frac{1+B_1B_5}{1+B_5},\frac{B_2B_5}{1+B_5},\frac{B_3B_5}{1+B_5},\frac{B_4B_5}{1+B_5},\) \(\frac{1}{1+B_5},\frac{1}{1+B_5}\bigg )\). From the continuity of \(H_2\) and using equation (8), the function \( H_2(S,E,A,I,R,V)\) has the unique smallest value \(H_2(S(0),E(0),A(0),I(0),R(0),V(0))\) inside \({\mathbb {R}}^6_+\).

We now define a non-negative \(C^2\) function \(H:{\mathbb {R}}^6_+ \rightarrow \mathbb {R_+}\) such that \(H(S,E,A,I,R,V)=H_2(S,E,A,I,R,V)-H_2(S(0),E(0),A(0),I(0),R(0),V(0)).\) Applying Ito formula on H and using the model (1), one obtains

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}(H) \le B_5\bigg \{-4\varLambda \left[ \left( R_{0V}^S\right) ^{\frac{1}{4}}- 1 \right] + \left( q+m+\frac{1}{2}\sigma _1^2\right) B_1\\&\quad -d_i I -\frac{gR}{N}B_1-\frac{\beta (1-\kappa )SI}{NE}B_2\\&\quad +\frac{1}{N}\beta (\kappa A+(1-\kappa )I)B_1\\&\quad -\frac{\nu A}{I}B_4-\frac{\beta V}{NE}(\kappa A+(1-\kappa )I)B_2 -\frac{(1-\delta )\omega E}{I}B_4 \bigg \}\\&\quad -\frac{\varLambda }{S} +\frac{\beta }{N}(\kappa A+(1-\kappa )I)+q\\&\quad +m-\frac{gR}{N}+\frac{1}{2}\sigma _1^2-\frac{\gamma _1A}{R}\\&\quad -\frac{\gamma I}{R}+g\\&\quad +m +\frac{1}{2}\sigma _3^2 \frac{A^2}{R^2}+\frac{1}{2} \sigma _4^2 \frac{I^2}{R^2}-\frac{qS}{V}+m+\frac{1}{2} \sigma _2^2+\varLambda \\&\quad +\frac{\beta }{V}[\kappa A+(1-\kappa )I]-d_i I \\&\quad -m(S+E+A+I+R+V). \end{aligned}\nonumber \\ \end{aligned}$$
(10)

Under the assumption \(B_6=4\varLambda \left[ \left( R_{0V}^S\right) ^{\frac{1}{4}}- 1 \right] >0\), (10) becomes

$$\begin{aligned}{} & {} {\mathcal {L}}(H) \le -B_5B_6-(B_5+1)d_iI+B_1B_5\left( q+m+\frac{1}{2}\sigma _1^2\right) \nonumber \\{} & {} \quad +(1+B_1B_5)\frac{\beta }{N}(\kappa A+(1-\kappa )I)-(1+B_1B_5)\frac{gR}{N} \nonumber \\{} & {} \quad -\frac{\beta (1-\kappa )\text {SI}}{\text {NE}}B_2B_5-\frac{B_4B_5\nu A}{I} \nonumber \\{} & {} \quad -\frac{\gamma _1A}{R}-\frac{\gamma I}{R}-\frac{\varLambda }{S}+g \nonumber \\{} & {} \quad -\frac{\beta V}{\text {NE}}(\kappa A+(1-\kappa )I)B_2B_5-\frac{(1-\delta )\omega E}{I}B_4B_5 \nonumber \\{} & {} \quad -\frac{qS}{V}+q+3m+\varLambda +\frac{1}{2}\sigma _1^2+\frac{1}{2} \sigma _2^2+\frac{1}{2}\sigma _3^2 \frac{A^2}{R^2}\nonumber \\{} & {} \quad +\frac{1}{2}\sigma _4^2 \frac{I^2}{R^2}-mN. \end{aligned}$$
(11)

Consider now the following bounded subset \(U=\bigg \{\delta _1<S<\frac{1}{\delta _2},~ \delta _1< E< \frac{1}{\delta _2},~ \delta _1< A < \frac{1}{\delta _2},\) \( ~\delta _1< I< \frac{1}{\delta _2}, ~\delta _1< R< \frac{1}{\delta _2},~\delta _1< V < \frac{1}{\delta _2} \bigg \},\) where \(\delta _i>0\), for \(i=1, 2\), are negligibly small constants to be chosen later on. Now, we divide the domain \({\mathbb {R}}^6_+\backslash U\) into the following sub-domains:

$$\begin{aligned} \begin{aligned}&U_1 =\left\{ (S,E,A,I,R,V): 0< S \le \delta _1 \right\} , \\&U_2 =\left\{ (S,E,A,I,R,V): 0< E \le \delta _1, S>\delta _2 \right\} ,\\&U_3 =\left\{ (S,E,A,I,R,V): 0< A \le \delta _1, E>\delta _2 \right\} ,\\&U_4 =\left\{ (S,E,A,I,R,V): 0< I \le \delta _1, A>\delta _2 \right\} ,\\&U_5 =\left\{ (S,E,A,I,R,V): 0< R \le \delta _2, I>\delta _1 \right\} ,\\&U_6 =\left\{ (S,E,A,I,R,V): 0< V \le \delta _1, R>\delta _2 \right\} , \\&U_7 =\left\{ (S,E,A,I,R,V): S \ge \frac{1}{\delta _2} \right\} , \\&U_8=\left\{ (S,E,A,I,R,V): E \ge \frac{1}{\delta _2} \right\} , \\&U_9 =\left\{ (S,E,A,I,R,V): A \ge \frac{1}{\delta _2} \right\} , \\&U_{10} =\left\{ (S,E,A,I,R,V): I \ge \frac{1}{\delta _2} \right\} , \\&U_{11} =\left\{ (S,E,A,I,R,V): R \ge \frac{1}{\delta _2} \right\} , \\&U_{12} =\left\{ (S,E,A,I,R,V): V \ge \frac{1}{\delta _2} \right\} . \end{aligned} \end{aligned}$$
(12)

We have to prove that \({\mathcal {L}}H(S,E,A,I,R,V)< 0\) on \({\mathbb {R}}^6_+\backslash U\), or equivalently, \({\mathcal {L}}H<0\) in all of the above twelve regions. We provide proofs of the first two cases. The other cases can be proved with a similar argument.

Case 1. Suppose \((S,E,A,I,R,V) \in U_1\), then (11) becomes

$$\begin{aligned}{} & {} {\mathcal {L}}(H) \le -B_5B_6-(B_5+1)d_iI\\{} & {} \quad +B_1B_5\left( q+m+\frac{1}{2}\sigma _1^2\right) \\{} & {} \quad +(1+B_1B_5)\frac{\beta }{N}(\kappa A+(1-\kappa )I) \\{} & {} \quad -(1+B_1B_5)\frac{gR}{N} \\{} & {} \quad -\frac{\beta (1-\kappa )SI}{NE}B_2B_5-\frac{B_4B_5\nu A}{I} -\frac{\varLambda }{\delta _1}\\{} & {} \quad -\frac{\gamma _1A}{R}-\frac{\gamma I}{R}+g\\{} & {} \quad -\frac{\beta V}{NE}(\kappa A+(1-\kappa )I)B_2B_5\\{} & {} \quad -\frac{(1-\delta )\omega E}{I}B_4B_5 -\frac{qS}{V} \\{} & {} \quad +q+3m+\varLambda +\frac{1}{2}\sigma _1^2+\frac{1}{2} \sigma _2^2\\{} & {} \quad +\frac{1}{2}\sigma _3^2 \frac{A^2}{R^2}+\frac{1}{2} \sigma _4^2 \frac{I^2}{R^2}-mN. \end{aligned}$$

Choosing \(\delta _1>0\) sufficiently small, one obtains \({\mathcal {L}}(H)<0\) for every \((S,E,A,I,R,V)\in U_1\).

Case 2. If \((S,E,A,I,R,V) \in U_2\), then from (11), we obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}(H) \le -B_5B_6-(B_5+1)d_iI\\&\quad +B_1B_5\left( q+m+\frac{1}{2}\sigma _1^2\right) \\&\quad +(1+B_1B_5)\frac{\beta }{N}(\kappa A+(1-\kappa )I) -(1+B_1B_5)\frac{gR}{N} \\&\quad -\frac{\beta (1-\kappa )\text {SI}}{\text {NE}}B_2B_5-\frac{B_4B_5\nu A}{I}\\&\quad -\frac{\varLambda }{S}-\frac{\gamma _1A}{R}-\frac{\gamma I}{R}+g\\&\quad -\frac{\beta V}{\text {NE}}(\kappa A+(1-\kappa )I)B_2B_5\\&\quad -\frac{(1-\delta )\omega E}{I}B_4B_5 -\frac{qS}{V} \\&\quad +q+3m+\varLambda +\frac{1}{2}\sigma _1^2+\frac{1}{2} \sigma _2^2+\frac{1}{2}\sigma _3^2 \frac{A^2}{R^2}\\&\quad +\frac{1}{2} \sigma _4^2 \frac{I^2}{R^2}-\frac{m \delta _2}{\delta _1}. \end{aligned} \end{aligned}$$

Letting \(\delta _2^2=\delta _1\) and choosing large positive value of \(B_5\) and sufficiently small value of \(\delta _2\), one have \({\mathcal {L}}(H)<0\) for every \((S,E,A,I,R,V)\in U_2\). Similarly, by selecting sufficiently small values of either \(\delta _1>0\) or \(\delta _2>0\), it can be easily shown that \({\mathcal {L}}(H)<0\) for the rest cases. Thus, \({\mathcal {L}}(H)<0\) can be attained for every \((S,E,A,I,R,V)\in U_{12}\). Therefore, condition (b) of Lemma 1 is satisfied, and hence, Theorem 2 is proved, following Lemma 1. \(\square \)

Remark 1

Here, \( R_{0V}^S\) defined in (5) may be called as the stochastic basic reproduction number (SBRN), which ensures the disease establishment in the stochastic system (1) when \(R_{0V}^S>1\).

Remark 2

One can easily obtain (see Appendix II) the deterministic basic reproduction number (DBRN) as \(R_{0V}^D\!=\!\frac{ \omega (\beta m\!+\!\eta q)\{\kappa \delta (\gamma +m+d_i)\!+\!(1-\kappa )\delta \nu +(1-\kappa )(1-\delta )(\nu +\gamma _1+m)\}}{(q+m)(\gamma +m+d_i)(\nu +\gamma _1+m)(\omega +m)}\). If \(R_{0V}^D>1\), then disease can be established in the corresponding deterministic system. Observe that the basic reproduction number of the stochastic system (\(R_{0V}^S\)) is smaller than that of the corresponding deterministic system (\(R_{0V}^D\)). Furthermore, if \(\sigma _i=0, i=1,..,4\), then \(R_{0V}^S\) coincides with \(R_{0V}^D\).

Observe that both the infected classes (symptomatic and asymptomatic) originate from the exposed class. Thus, the infection will eventually be eradicated if the individuals of the exposed class go extinct. For the system (1), the exposed class E(t) is said to be extinct (i.e. the system will be disease-free) if \(\lim _{t \rightarrow \infty } E(t)=0 ~a.s.\) [19]. We give here some sufficient conditions for which the exposed class dies out over time. In proving the extinction criterion, the result of the strong law of large number given in the following lemma will be used.

Lemma 2

[31] Let \(M=\{M\}_{t\ge 0}\) be a continuous valued local martingale and vanishing at \(t=0\), then

$$\begin{aligned} \text{ lim}_{t \rightarrow \infty }<M, M_t> < \infty \implies \lim _{t \rightarrow \infty }\frac{M_t}{<M,M>_t}=0, \end{aligned}$$

and

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{<M,M>_t}{t}<0 \implies \lim _{t \rightarrow \infty } \frac{M_t}{t}=0~~\text{ a.s. } \end{aligned}$$

Theorem 3

The exposed individuals of the system (1) tend to zero exponentially almost surely if \(R_{0V}^{ext}<1\), where \(R_{0V}^{ext}=\frac{1}{\omega +m}\left( \frac{\beta ^2}{2\sigma _1^2}+\frac{\eta ^2}{2 \sigma _2^2}\right) \).

Proof

Assume that \((S(t),E(t),A(t),I(t),R(t),V(t))\in {\mathbb {R}}^6_+\) is a solution of system (1) satisfying the initial value \((S(0),E(0),A(0),I(0),R(0),V(0))\in {\mathbb {R}}^6_+\). Following Ito’s formula, we have

$$\begin{aligned} \begin{aligned}&d(\ln E(t))=\bigg (\frac{\beta S(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N(\tau )E(\tau )}\\&\quad -\frac{\sigma _1^2S^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N^2(\tau )E^2(\tau )}\bigg )dt \\&\quad +\bigg (\frac{\eta V(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N(\tau )E(\tau )}\\&\quad -\frac{ \sigma _2^2V^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N^2(\tau )E^2(\tau )}\bigg )dt-\left( \omega +m\right) \\&\quad +\frac{\sigma _1 S}{NE}((1-\kappa )I+\kappa A)~dB_1(t)\\&\quad +\frac{\sigma _2 V}{NE}((1-\kappa )I+\kappa A)~dB_2(t). \end{aligned} \end{aligned}$$
(13)

Upon integration from 0 to t, we have

$$\begin{aligned} \begin{aligned}&\ln E(t)=\int ^{t}_{0}\bigg (\frac{\beta S(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N(\tau )E(\tau )}\\&\quad -\frac{\sigma _1^2S^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N(\tau )^2E^2(\tau )}\bigg )dt \\&\quad +\int ^{t}_{0}\bigg (\frac{\eta V(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N(\tau )E(\tau )}\\&\quad -\frac{ \sigma _2^2V^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N^2(\tau )E^2(\tau )}\bigg )dt \\&\quad -\left( \omega +m\right) t+ M_1(t)+M_2(t)+\ln E(0), \end{aligned} \end{aligned}$$
(14)

where \(M_1(t)=\int ^{t}_{0}\frac{\sigma _1 S}{NE}((1-\kappa )I+\kappa A)~dB_1(\tau ),~~~M_2(t)=\int ^{t}_{0}\frac{\sigma _2 V}{NE}((1-\kappa )I+\kappa A)~dB_2(\tau )\) are the local continuous martingale with \(M_1(0)=0, ~M_2(0)=0.\) We, then have \(<M_1,M_1>_t=\int ^{t}_{0}\frac{\sigma _1^2\,S^2}{N^2E^2}((1-\kappa )I+\kappa A)^2~dt<\sigma _1^2~~\text{ and }\) \(<M_2,M_2>_t=\int ^{t}_{0}\frac{\sigma _2^2 V^2}{N^2E^2}((1-\kappa )I+\kappa A)^2~dt<\sigma _2^2~.\) Using the fact \(\text{ max }~\Big (\frac{\beta S(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N}(\tau )E(\tau )-\frac{\sigma _1^2\,S^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N(\tau )^2E^2(\tau )}\Big )\)=\(\frac{\beta ^2}{2 \sigma _1^2}\) and \(\left( \frac{\eta V(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))}{N(\tau )E(\tau )}-\frac{ \sigma _2^2V^2(\tau )((1-\kappa )I(\tau )+\kappa A(\tau ))^2}{2N^2(\tau )E^2(\tau )}\right) \)=\(\frac{\eta ^2}{2 \sigma _2^2},\) (14) can be written as

$$\begin{aligned} \begin{aligned} \ln E(t)&\le \left( \frac{\beta ^2}{2\sigma _1^2}+\frac{\eta ^2}{2 \sigma _2^2}-\left( \omega +m\right) \right) t\\&\quad + M_1(t)+M_2(t)+\ln E(0). \end{aligned} \end{aligned}$$
(15)

Taking the limit superior as \(t \rightarrow \infty \), after dividing both sides of (15) by \(t~(>0)\) and using Lemma 2, we have

$$\begin{aligned} \lim _{t \rightarrow \infty } \sup {\frac{\ln E(t)}{t}} \le \left( \frac{\beta ^2}{2\sigma _1^2}+\frac{\eta ^2}{2 \sigma _2^2}-\left( \omega +m\right) \right) <0.\nonumber \\ \end{aligned}$$
(16)

If \(\frac{1}{\omega +m}\left( \frac{\beta ^2}{2\sigma _1^2}+\frac{\eta ^2}{2 \sigma _2^2}\right) <1\), then \(\lim _{t \rightarrow \infty }E(t)=0\) almost surely. Hence, the theorem is proved. \(\square \)

It is observable that \(R_{0V}^{ext}\) is an increasing function of \(\beta \) and \(\eta \). Thus, if the infection rate increases or the vaccine-induced immunity loss increases, the inequality \(R_{0V}^{ext}<1\) may not be held, and consequently, the disease eradication may not be possible.

4 Case study

For the case study, we considered the COVID-19 data from two countries, India and Italy. The parameters estimation and other detailed analysis were done using the Indian COVID-19 epidemic data available from the repositories Covid19India.Org (https://covid19india.org) and Worldometers.info (https://www.worldometers.info/coronavirus/country/india/). The daily and cumulative numbers of infected, recovered, deceased, and vaccinated cases are reported and updated daily in these depositories. The results of Italy were obtained following a similar analysis.

The per day birth rate of new susceptibles is assumed to be constant during the study period. So, we considered this rate \(\varLambda \) as a constant. However, the parameters, infection spreading rate \(\beta \), probability of joining from the exposed class to the undetected class \(\delta \), the recovery rates \(\gamma _1, \gamma \), the death rate \(d_i\), vaccination-induced immunity loss rate \(\eta \) and vaccination rate (q) are all subject to be different at different time. For example, \(\beta \) is different because the severity of the contagious nature of the COVID-19 virus is different due to the different infectivity of the virus strain. The parameter value of \(\delta \) may be different because of the different policies imposed by the government from time to time. The parameters \(\gamma _1, \gamma , d_i, \eta \) are also different as the different COVID-19 strains have different fatalities, and different individuals have different immunity levels, and the presence of comorbidities and other immunosuppression factors. The vaccination rate (q) is also not uniform throughout the period as it depends on the vaccine availability and the infrastructure level. It is unexpected to have a single data set for the long vaccination period of any country that will best fit the actual data. Instead, it will be more worthwhile to adopt the method of piecewise fitting the actual data with the vaccine model (1).

Table 1 Estimated parameter values of system (1) for Indian COVID-19 data for the periods: (1) 2 February 2021 to 6 May 2021; (2) 7 May 2021 to 27 December 2021; (3) 28 December 2021 to 20 January 2022; (4) from 21 January 2022 to 15 April 2022; (5) from 16 April 2022 to 7 July 2022
Full size table
Fig. 1
figure 1

COVID-19 data fitting with the parameter values and noise intensities as in Table 1. The first row provides the cumulative actual COVID-19 data (red-coloured curve) of the confirmed, recovered and vaccinated cases in India from 2 February 2021 to 5 May 2021. The solution (blue-coloured curve) of the stochastic model (1) is the fitted curve with the parameter values of the first row of Table 1. The other rows represent the same consecutive periods mentioned in Table 1

Full size image

We have considered India’s COVID-19 data for 2 February 2021 to 7 July 2022. Different variants of Covid-19 have different infectivity and virulence. Furthermore, the vaccination rate was low initially but increased subsequently. We, therefore, divided the data set of the study period into five intervals to obtain a good fit parameter set: (1) from 2 February 2021 to 6 May 2021 (the date when the peak is attained in the second wave); (2) from 7 May 2021 to 27 December 2021 (end of the second wave); (3) from 28 December 2021 to 20 January 2022 (the date when the peak of the third wave is attained); (4) from 21 January 2022 to 15 April 2022 (end of the third wave); and (5) from 16 April 2022 to 7 July 2022, where study period ends. We fitted (see Fig. 1) the actual COVID-19 data (in red colour) for the considered period with the stochastic model solution (in blue colour). Table 1 provides the best-fitted parameters and optimal noise intensities. The Italian COVID-19 data (available from the repository ourworldindata.org (https://ourworldindata.\(\backslash \backslash \)org/covid-cases), used for the study period 11 October 2021 to 7 July 2022, were divided into three time segments: (1) from 11 October 2021 to 18 January 2022 (the date when the peak is attained in the second wave); (2) from 18 January 2022 to 20 April 2022 (peak is attained in third wave); (3) from 21 April 2022 to 7 July 2022 (where the study period ends). As in the case of Indian COVID-19 data fitting, we fitted (see Fig. 7) the actual COVID-19 data (red colour) of Italy with the model generated data (blue colour). The best-fitted parameters and the optimal noise intensities are provided in Table 2. The parameters and noise estimation techniques are given in Appendix III.

Fig. 2
figure 2

Per day COVID-19 positive cases in India for the variation in the rate parameters \(\eta \) and q, representing the immunity loss and vaccination rate, respectively. The total disease cases (asymptotic plus symptomatic) are the end values of the solutions for 1000 time steps. Noise intensities and other parameter values remain fixed from 28 December 2021 to 20 January 2022 (see Table 1, third row), the increasing phase of COVID-19 cases of the last wave

Full size image
Fig. 3
figure 3

Per day COVID-19 positive cases with respect to \(\beta \) and q (up) and \(\beta \) and \(\eta \) (down). Noise intensities and other parameter values remain fixed for the period of 28 December 2021 to 20 January 2022, see Table 1

Full size image

Indian COVID-19 vaccination programme started on 16 January 2021 [5]. Though the initial vaccination rate was slow, it intensified later on. We demonstrated how the vaccination rate (q) and the immunity loss rate \((\eta )\) jointly influence the disease burden. We also explained why the COVID-19 positive cases increased during the third wave even after mass vaccination. To elucidate, we considered the parameter values of the third row (see Table 1), representing the increasing phase of the third wave, and plotted (Fig. 2) the per day COVID-19 positive cases \((A+I)\) from the solution of system (1) for simultaneous variation in q and \(\eta \). The parameters q and \(\eta \) were varied in the range 0\(-\)0.024 and 0.1\(-\)0.25, respectively. The lower range value of each parameter was considered smaller than all the estimated values of the said parameter (see Table 1), and the value at the higher range was considered larger than all the estimated values. It shows that daily COVID-19 positive cases increase with the increasing vaccination rate (q) when the vaccine-induced immunity loss (\(\eta \)) exceeds the value 0.23, i.e. if the vaccine efficacy is lower than \(77\%\). On the contrary, if vaccine efficacy is higher than \(77\%\) (or \(\eta <0.23\)), then daily COVID-19 positive cases decrease with increasing immunization. Observe that the per day cases become as high as 0.397 million when \(\eta =0.25\) and \(q=0.22\). It is to be mentioned that Indian COVID-19 positive cases during the peak (\(20^{th}\) January) of the third wave were reported as 0.34 million per day (https://www.worldometers.info/coronavirus/country/india/). Thus, increased vaccination cannot eradicate COVID-19 infection if the vaccine efficacy is low; instead, it increases the COVID-19 cases. However, infection eradication is possible with a higher vaccination rate if the vaccine immunity is more than \(77\%\). It is to be mentioned that \(R_{0V}^{S} <1\) holds for the lower values of q and \(\eta \); \( R_{0V}^S>1\) for its higher values.

Fig. 4
figure 4

Left: Per day COVID-19 positive cases in Italy for the variation in the rate parameters \(\eta \) and q, representing the immunity loss and vaccination rate, respectively. The total disease cases (asymptotic plus symptomatic) are the end values of the solutions for 1000 time steps. Right: same for the variation of \(\beta \) and \(\eta \). Noise intensities and other parameter values remain fixed in the period from 21\(^{st}\) April 2022 to 7\(^{th}\) July 2022 (see Table 2)

Full size image

A similar phenomenon is plotted in Fig. 3 (up) when the vaccination rate (q) and force of infection (\(\beta \)) are varied simultaneously. The COVID-19 positive cases gradually increase if \(\beta \) is high and q is low. The number of positive cases may be as high as 0.5 million per day at the low vaccination and high transmission rates (below figure). In the opposite case, the disease is eradicated. The lower figure represents the newly infected per day COVID-19 cases when the force of infection \((\beta )\) and the vaccine efficacy (\(\eta \)) parameters are jointly varied. The infection spreads rapidly when \(\beta >0.25\) and \(\eta >0.2\) (Fig. 3, below). The COVID-19 cases in this parametric range may be as high as 0.532 million per day. It is also to be noted that the number of COVID-19 cases will be few if \(\beta \) is high and \(\eta \) is low. It demonstrates that vaccine effectiveness is crucial in controlling the COVID-19 cases. The disease may be controlled even at a very high infection rate if the vaccine efficacy is close to \(100\%\) (i.e. \(\eta \) is close to zero). On the other hand, daily COVID-19 cases will remain under control if \(\beta \) is low and \(\eta \) is significantly high. Thus, a strain of coronavirus with low infectivity would not sustain at the present immunization rate.

Table 2 Estimated parameter values of system (21) for Italian COVID-19 data for the periods: (1) 11 October 2021 to 18 January 2022; (2) 19 January 2022 to 20 April 2022; and (3) 21 April 2022 to 7 July 2022
Full size table
Fig. 5
figure 5

Left: Predicted cumulative COVID-19 confirmed cases in India for the next 150 days starting 7 July 2022. The simulation results of the system (1) (blue line) predict that India may observe \(4.88 \times 10^7\) positive cases until the first week of November 2022. The confidence interval (\(95\%\)) is plotted with a yellow shed. Right: Predicted daily confirmed cases for the same period. The red curve in both figures indicates the actual cases, and the dotted vertical line indicates 7 July 2022. Parameters and noise intensities as in the last row of Table 1

Full size image

We plotted a similar figure as in the case study for India (Fig. 2) to explore how the number of disease cases in Italy would change under the variation of parameters q and \(\eta \). In the case of Italy, we observe (Fig. 4, left) that if the vaccination-induced immunity loss is higher than 12%, the epidemic will rapidly grow. In case of variation of \(\beta \) and \(\eta \), it is observed that when \(\beta \) is low (\(<0.1\)), number of confirmed cases is low (Fig. 4, right). However, confirmed cases increase rapidly for a higher transmission rate.

Fig. 6
figure 6

Left: Predicted cumulative COVID-19 confirmed cases in Italy for the next 150 days starting 7 July 2022. The simulation results of the system (1) (blue line) predict that Italy may observe \(2.49 \times 10^7\) positive cases until the first week of November 2022. The confidence interval (\(95\%\)) is plotted with a yellow shed. Right: Predicted daily confirmed cases for the same period. The red curve in both figures indicates the actual cases; the dotted vertical line means 7 July 2022. Parameters and noise intensities as in the last row of Table 2

Full size image

Indian COVID-19 cases are again in increasing mode. We predicted the cumulative confirmed COVID-19 positive cases for the next 150 days based on the current epidemiological status of India. To provide a forecast, we repeated the stochastic system’s solution 1000 times and then took the mean to get the estimated values with a 95 % confidence interval (blue line of Fig. 5, left). The curve is increasing and will continue till the first week of November 2022, indicating that the newly infected cases are surging gradually. The cumulative number of the predicted infected case till the first week of November 2022 might be between 4.82 \(\times 10^7\) to 5.01 \(\times 10^7\) in the 95% confidence interval. The predicted daily COVID-19 confirmed cases in India till the first week of November 2022 are presented in Fig. 5, right. The COVID-19 cases in Italy also exhibit an increasing trend. Figure 6 indicates that the daily case may be around 37,142 and the cumulative cases might be between \(2.41 \times 10^7\) to \(2.54 \times 10^7\) till the first week of November 2022. It is, however, to be mentioned that the accurate prediction for a significantly long period is quite impossible in the case of COVID-19 infection because this novel virus can mutate to some strains with high infectivity [14]. Also, a change in the control measure imposed by the authority can change the trend.

5 Discussion

The COVID-19 infection has put the world under pressure for more than two years. Most countries have experienced several waves of this infection at the cost of millions of lives. A massive vaccination programme started at the end of 2020, hoping the disease would be controlled. Though the morbidity and mortality of the COVID-19 disease reduced significantly, disease eradication, even of its control, is far from expected. In the second and third waves, many countries experienced higher positive cases than the previous peak values. Several European countries, the UK and the USA have fully vaccinated a significant proportion of their population but cannot resist further COVID-19 infection. This fact has put the efficacy of the vaccine under question. Recent studies show that vaccine-induced immunity is significantly reduced after six to eight months post-vaccination. The level of a COVID-19 antibody that persists after this period may not be sufficient to prevent reinfection. There is, however, uncertainty regarding the immunity loss rate among the vaccinated population. Uncertainty also exists in different rate parameters, e.g. the force of infection and recovery rates. It is undoubtedly true that the infectivity of the omicron variant is much higher than the previous strains. Also, the severity of the disease is relatively low, and the recovery rate is high in the current wave caused due to the omicron variant of coronavirus. Thus, there are many uncertainties in the COVID-19 disease dynamics, the force of infection, recovery rate, vaccine availability and administration. The efficacy of vaccines and their protection duration is unclear even after receiving the full vaccine dose. There is also uncertainty regarding the immunity loss rate among the vaccinated population. Therefore, we searched for the answer to whether existing vaccination drives eradicate the disease. What would be the parametric condition for disease eradication through vaccination in the presence of various uncertainties?

Considering such uncertainties in the rate parameters, we have proposed and analysed a six-dimensional stochastic COVID-19 epidemic model in the presence of vaccination to know whether the ongoing vaccination drive can eliminate the disease. We used the theories of the asymptotic behaviour of the nonlinear stochastic system to analyse this noise-induced dynamical system. We here prescribed both the disease persistence and eradication conditions. It is shown that the disease indeed persists for a long time if the stochastic basic reproduction number (SBRN) is greater than unity. It is noticed that this value of SBRN is smaller than the DBRN (deterministic basic reproduction number) of the corresponding deterministic model, which is usually considered a measure of disease establishment in the latter type of epidemic models. A sufficient condition (\(R_{0V}^{\text {ext}} <1\)) is established for the disease eradication from the system. Noticeably, this condition may not hold if the disease’s infectivity increases and/or the vaccine-induced immunity loss increases (i.e. if the vaccine efficacy is reduced). Both issues are probably real for many countries, where vaccination starts in the initial months of 2021, implying that vaccinated people will significantly lose their immunity from July/August onwards (seven to eight months post-vaccination). Furthermore, the new variant, omicron, is highly infectious. These two reasons are probably responsible for the second, third and subsequent waves in different countries. We used the Indian and Italian COVID-19 data to demonstrate the variational effects of the rate parameters \(q, \eta \) and \(\beta \). Noticeably, if the vaccine-induced immunity loss rate, \(\eta \), is higher than 0.23 for India, eradicating infection is practically impossible. The same value of \(\eta \) for Italy is 0.12. The COVID-19 positive cases will surge in India if the force of infection is high (\(>0.25\)) and vaccine-induced immunity loss is higher than 20%. For Italy, these values are 0.1 and \(12\%\), respectively. It implies that the disease will last long unless a long-lasting vaccine candidate appears or a low infectious variant replaces the highly contagious variant.

There are, however, some limitations of this model. For example, this model does not consider the population’s age structure. It is to be mentioned that a higher age group population is more prone to COVID-19 infection. Secondly, there are many variants of coronavirus with different infectivity and virulence. Therefore, a multi-strain epidemic model would be more appropriate to represent the ongoing pandemic. Despite such limitations, our theoretical and simulation results justify the reason for long-lasting disease persistence even when a large-scale immunization process has been implemented. To our knowledge, such effects have not been reported earlier using a dynamic mathematical model.

6 Conclusion

Nonlinear analysis of a six-dimensional stochastic epidemic model reveals that eradicating COVID-19 infection is challenging if the vaccine-induced immunity loss or the infectivity of the virus strain is high. Therefore, the disease will last long unless a long-lasting vaccine candidate appears or a low infectious variant replaces the highly contagious variant. Using the method described here, one can estimate the required vaccination rate when the vaccine-induced immunity loss or the infectivity of the disease is known, and vice versa. The authority may use it in the immunization and disease eradication process of COVID-19.