1 Introduction

Spreading the COVID-19 disease has become a very difficult global problem, and several international efforts have been proposed to control this disease. For July 19th, 2023, there were 768,237,788 confirmed cases, 6,951,677 deaths, and a total of 13,474,348,801 doses of vaccine have been administered around the world [1].

Therefore, there were many approaches to deal with this issue globally. Emergencies and preventive measures were declared in infected areas of the world, and at the global level, public health was seriously challenged. Consequently, it is very important to understand all critical parameters to control the spread of this disease through surveillance. Thus, mathematical models and computational simulations are also being performed at each level to inform the people and policy makers. There are some mathematical techniques to calculate the basic reproduction number depending on the characteristics of the disease and the population [2, 3]. Other measures proposed by governments throughout the world to prevent the spread of COVID-19 include social isolation, international travel restrictions, rapid-test, and even lockdown [4]. An effective way to control this disease is through lockdown because it can reduce this spreading more quickly among all the aforementioned control strategies [5] and decrease the mobility of the population  [6].

Many ecological interactions and biological processes are modeled by a system of differential equations with constant rates. Such systems may not have exact analytic solutions, therefore numerical methods and computational approaches can help in understanding such problems more widely. Recently, some numerical approaches and computational tools have been used to study some real-world problems, for sample, a fractional-order predator–prey system with consuming food resource was discussed for stability analysis given in [7], a predator–prey system with consuming resources and disease in prey species was studied for self-diffusion and cross-diffusion shown in [8], a fractional explicit-implicit numerical method was used for solving time-dependent partial differential equations in [9].

Recently, some models of COVID-19 have been proposed, which represent a good step forward in understanding the dynamics of this disease [10,11,12,13]. Accordingly, we have developed some models of COVID-19, we have also identified some important critical parameters with sensitivity analysis [14,15,16,17,18,19]. More recently, we improved the previous models and added the vaccination compartment. The vaccination parameters have been considered. The impact of vaccination strategies in controlling this disease has been discussed, the reader can see more details about the suggested model in [20].

Although some mathematical approaches have been suggested so far to understand this disease. Such models can be defined using the mass action law including reaction rate constants. Then, using local sensitivity methods to evaluate each model state in relation to model parameters, the results might be improved. Recently, we have applied three different techniques of local sensitivities on some suggested models of COVID-19, they are provided us a wide range for identifying the critical parameters of the model. In a complicated modeling case such as the new coronavirus, it is required to pay more attention to the impact of vaccination strategy on the spatiotemporal pattern dynamics more accurately and widely. The idea of the spatiotemporal pattern of diffusion-equation was generally suggested for epidemic models in [21], reaction–diffusion epidemic model [22], geographical analysis of vaccination efforts on COVID-19 [23]. Recently, this idea was further discussed for epidemiological landscapes vaccination allocation model, this model includes two main compartments: an age-structured deterministic compartmental model and a graph-based spatial model, more details about this model explained in [24]. Furthermore, the idea of spatial vaccine distribution strategy suggested to control the spreading of COVID-19 more effectively [25]. The study proposed a computational model with different transmission rates, the model is basically based on Brownian agents and allows deriving a (nonuniform) statistical mean-field model. The suggested studies discussed the idea of the spatiotemporal pattern of diffusion-equation in different views, but they have not studied the vaccination rate association with spatiotemporal distribution of COVID-19, this rate provides a great role in understanding this pandemics and it gives a wide range to minimize the total number of infected individuals.

In this work, we have further developed our previous models, we consider a system of diffusion equations for spreading COVID-19 with vaccinated individuals, all model equations can be solved numerically using MATLAB for different initial states and model transmission rates.

The main contribution of work is investigating the influence of COVID-19 vaccinations parameters as an alternate technique for COVID-19 suppression. Another contribution here is the identification of the critical model parameters using three techniques of local sensitivities, which allows biologists to work with less knowledge of mathematical modeling and also facilitate the improvement of the model for future developments. Furthermore, using a system of diffusion equations seems to be an attractive approach that provides an additional technique to properly and thoroughly comprehend the dynamics and transmission of the virus. This mathematical approach improves the ability to develop efficient control and prevention strategies by facilitating a more detailed investigation of the many connections and variables involved in the spread of COVID-19. As a consequence, using a system of diffusion equations can open another path to understand such issues more widely and accurately.

2 A mathematical model for COVID-19

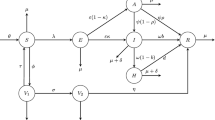
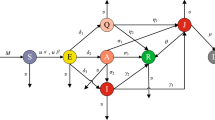
Infectious diseases spread may be effectively understood by using mathematical models with their transmission rates. The well-defined model to describe the spreading such diseases is “Susceptible–Exposed–Infectious–Recovered” model. This is how the SEIR model is sometimes referred [26]. The main design of this model is related to the clinical progression, epidemiological individuals and intervention measures. Accordingly, the SEIR model for infectious diseases can also be developed with the combination of intervention subjects, such as treatment, isolation (hospitalisation), vaccination, and quarantine. The basic models of epidemic diseases normally include components (individuals) and their transmissions among population components. In other words, for a given model network of infectious disease, nodes are individuals, and the edges represents transmission rates. In terms of a graphical network, this representation helps in understanding infectious disease models. Currently, the developed modes have been proposed to show all model compartments and transmission rates in spreading the COVID-19. Accordingly, the vaccination component is an effective variable, it plays an important role in controlling this disease. There are some challenging approaches in using COVID-19 vaccine. Firstly, we need to analyze the effects of a vaccination before it is actually put into practice. Using mathematical modelling can help forecast how the vaccination will affect the population. The model proposed here includes several key aspects: detected and undetected (unreported) cases, contact tracing and rapid testing, quarantined individuals, and vaccination strategy, we recently studied this model as a system of ordinary differential equations with constant rates all model equations with their initial states and parameters given in [20]. The suggested model network with all transmission rates are shown in Fig. 1 (Table 1).

Table 1 The model states and parameters with their biological definitions, the range of model parameters was previously shown based on the real data given in [20]
Full size table
Fig. 1
figure 1

COVID-19 model transmission diagram

Full size image

In addition, we focus on the system spatially and proceed to the dynamics of the spatial system Eqs. (1–8) which is described as follows:

$$\begin{aligned} \frac{\partial S}{\partial t}= & {} D_S \frac{\partial ^{2}{S}}{\partial {x^{2}}}+ \Lambda -\beta S(A+\xi _1 I + \xi _2 Q)-\mu S-u_3 S+\eta V, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial V}{\partial t}= & {} D_V \frac{\partial ^{2}{V}}{\partial {x^{2}}}+u_3 S-\eta V- \phi \beta V(A+\xi _1 I+\xi _2 Q)-\mu V, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial E_u}{\partial t}= & {} D_{E_u} \frac{\partial ^{2}{E_u}}{\partial {x^{2}}}+(1-u_1)\beta (S+\phi V)(A+\xi _1 I+\xi _2 Q)-\alpha E_u - \mu E_u -u_2 E_u, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial E_d}{\partial t}= & {} D_{E_d} \frac{\partial ^{2}{E_d}}{\partial {x^{2}}}+ u_1 \beta (S+\phi V)(A+\xi _1 I+\xi _2 Q)-\alpha E_d- \mu E_d +u_2 E_u, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial A}{\partial t}= & {} D_A \frac{\partial ^{2}{A}}{\partial {x^{2}}}+ q\alpha E_u - \delta A- u_2 A -(\mu +\zeta )A, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial I}{\partial t}= & {} D_I \frac{\partial ^{2}{I}}{\partial {x^{2}}}+ (1-q)\alpha E_u-\delta I-u_2 I - (\mu +\zeta )I, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial Q}{\partial t}= & {} D_Q \frac{\partial ^{2}{Q}}{\partial {x^{2}}}+ \alpha E_d+u_2(A+I)-\delta Q -(\mu +\zeta )Q, \end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial R}{\partial t}= & {} D_R \frac{\partial ^{2}{R}}{\partial {x^{2}}}+ \delta (A+I+Q)-\mu R. \end{aligned}$$
(8)

Here we divide the population into seven groups as follows: \(S=S(x,t)\) is the susceptible individuals, \(V=V(x,t)\) is the vaccinated individuals, \(E_u=E_u(x,t)\) and \(E_d=E_d(x,t)\) are undetected and detected individuals, \(A=A(x,t)\) and \(I=I(x,t)\) are the asymptomatic and symptomatic individuals and \(Q=Q(x,t)\) is quarantined and \(R=R(x,t)\) recovered individuals, respectively, at time t and position x.

3 An algorithm of model solution

The model transmission equations for the spreading COVID-19 given in Eqs. 1–8 can simplify and analyze their model dynamics using some steps. The following suggested steps help us to understand the model solutions and identify the model critical parameters. The suggested algorithm has the following steps:

  1. 1.

    Define the model transmission rates for the suggested model of COVID-19 as a system of reaction–diffusion equations with initial populations given below

    $$\begin{aligned} \frac{\partial C}{\partial t} = D_C \frac{\partial ^{2}{C}}{\partial {x^{2}}}+F(C,P), \quad C(0)=C_0, \end{aligned}$$
    (9)

    where \(C \in \mathbb {R}^{n}\) and it is the set of model compartments, \(P \in \mathbb {R}^{m}\) and it is set of model parameters, and a finite domain \(0<x<L\) where L is the domain length.

  2. 2.

    Use an appropriate random perturbation on the systems’ steady states given below:

    $$\begin{aligned} C = C_0 + \epsilon * \text {rand}, \end{aligned}$$
    (10)

    where \(\epsilon \) is a random perturbation coefficient, and “rand” is a one-dimensional array of random numbers uniformly distributed in the range of [0, 1]. The system of reaction–diffusion equations are solved numerically for disease compartments in 1D, 2D and 3D for their initial states and suggested parameter values using finite difference method for zero-flux boundary condition with different mesh steps \(\Delta x\) and \(\Delta t\).

  3. 3.

    Calculate the model local sensitivities using the following formula

    $$\begin{aligned} \mathcal {S}^{C_{i}}_{P_{j}}=\dfrac{\partial C_{i}}{\partial P_{j}}, \end{aligned}$$
    (11)

    where \(\mathcal {S}^{C_{i}}_{P_{j}}\) is measured as a sensitivity coefficients of each \(C_{i}\) respect to each parameter \(P_{j}\).

  4. 4.

    Identify a very sensitive set of model parameters called \(P^* \subseteq P\) from the computational simulations.

  5. 5.

    Excluding a set of parameters \(P^*\) from the model when they have a big effect on model solutions.

  6. 6.

    Repeat Step 3.

All suggested steps here of model analysis algorithm can be presented as a Flowchart given below:

figure a

The Flowchart shows all suggested steps of model analysis based on the numerical approaches and local sensitivities.

4 Computational simulations

Equations 1–8 are focused numerically in a finite domain \(0<x<L\) where L is the domain length by finite difference method with zero-flux boundary condition and the mesh steps are chosen as \(\Delta x=0.5\) and \(\Delta t=0.01\). Note that, further decrease on mesh steps are checked to prevent any significant artifacts numerically. The system’s initial value is a random perturbation of the coexistence state [21]. Note that, to generate appropriate random perturbation on the systems’ steady state, \(\epsilon \) is used as random perturbation coefficient, \(\epsilon =0.02\). For example, the initial condition for susceptible individuals is given by \(S=S_0 + \epsilon *rand\). The initial starting points for perturbation are as \(S_0=1046727\), \(V_0=400\), \(E_u{_0}=210\), \(E_d{_0}=0\), \(A_0=10\), \(I_0=40\), \(Q_0=20\), \(R_0=90\).

We previously discussed the range of parameters based on the real data shown in [20]. Since accurate evaluations of the relative infectivity levels of those with symptomatic and asymptomatic populations are unclear, \(D_S\) and \(D_ V\) are considered to be equal [27, 28]. The rest of the diffusion coefficients are consistent with the study on diffusion–reaction system application on COVID-19 [29], i.e., \(D_S=D_V=4,35.10^{-2}\), \(D_{Eu}=D_{Ed}=1,98.10^{-2}\), \(D_A=D_R=0,75.10^{-2}\), \(D_I=1.10^{-4}\) and assuming that quarantined individuals are immobile, i.e., \(D_Q=0\) [29].

Fig. 2
figure 2

Spatial distribution of individuals in 1D for \(t=300\) for \(u_3=0.01\) for given perturbed initial values

Full size image
Fig. 3
figure 3

Corresponding spatio-temporal distribution of individuals in 3D for \(t=300\) for \(u_3=0.01\) for given perturbed initial values

Full size image
Fig. 4
figure 4

Spatial distribution of individuals in 3D for \(t=300\) for \(u_3=0.01\) for given perturbed initial values

Full size image
Fig. 5
figure 5

Corresponding spatial distribution of individuals in 2D for \(t=300\) for \(u_3=0.01\) for given perturbed initial values

Full size image

Given that the primary motivation of this work is to demonstrate the influence of COVID-19 vaccination parameters suppression with the addition of local sensitivity analysis, we now proceed to numerical simulations for different values of vaccination rate, i.e., \(u_3\). Figures 2, 3, 4 and 5 show the spatial distributions obtained at \(t=300\) and \(u_3=0.01\). Figure 2 shows spatial distribution of individuals given in Eqs. 1–8 in 1D for different initial states and parameters. In addition, Figs. 3 and 4 show spatial distribution in 3D for some given parameters and initial states, however the axes are different. Accordingly, Figs. 4 and 5 are identical, they are presented in 3D and 2D, respectively. The evolution process in time is patchy and the density of infected individuals fluctuates across different locations.

Interestingly, Fig. 6 shows spatial distribution of the recovered individuals under the effect of increasing vaccination rates, i.e., \(u_3=0\), \(u_3=0.02\), \(u_3=0.4\) and \(u_3=0.6\) from top to bottom for given time \(t=300\) in both 2D and 3D, different vaccination rates are computed to simulate the dynamics of the recovered individuals. From the numerical results, it is clearly observed that the increase in vaccination rate, i.e. \(u_3\), the group of patches shrinks and no regular pattern formation observed.

Fig. 6
figure 6

Spatial distribution of recovered individuals under the effect of increasing vaccination rate in 3D with its corresponding distribution in 2D for \(t=300\) for \(u_3=0\), \(u_3=0.02\) \(u_3=0.4\) and \(u_3=0.6\), respectively from top to bottom, for given perturbed initial values

Full size image

5 Model sensitivity analysis

The idea of sensitivity can be used on infectious disease models to determine which variable or parameter is sensitive to a specific condition. Suppose that an infectious disease model has n compartments \(C_{i}\) for \(i=1,2,\ldots ,n\) and m parameters \(P_{j}\) for \(j=1,2,\ldots ,m\). The model balanced equations are assumed to be represented as a system of differential equations, the derivations of local sensitivities with more details are presented in [14, 16]:

$$\begin{aligned} \dfrac{d C_{i}}{dt}=F_{i}(C,P), \end{aligned}$$
(12)

where \(C \in \mathbb {R}^{n}\) and \(P \in \mathbb {R}^{m}\). The model sensitivities can be determined using three different techniques: non-normalizations, half-normalizations, and full-normalizations. The sensitivity to non-normalization are provided by

$$\begin{aligned} \mathcal {S}^{C_{i}}_{P_{j}}=\dfrac{\partial C_{i}}{\partial P_{j}}, \end{aligned}$$
(13)

where \(\mathcal {S}^{C_{i}}_{P_{j}}\) is measured as a sensitivity coefficients of each \(C_{i}\) respect to each parameter \(P_{j}\). The sensitivity to half-normalization are provided by

$$\begin{aligned} \mathcal {S}^{C_{i}}_{P_{j}}=\left( \dfrac{1}{C_{i}} \right) \left( \dfrac{\partial C_{i}}{\partial P_{j}}\right) . \end{aligned}$$
(14)

Furthermore, the sensitivity to full–normalization are defined by

$$\begin{aligned} \mathcal {S}^{C_{i}}_{P_{j}}=\left( \dfrac{P_{j}}{C_{i}} \right) \left( \dfrac{\partial C_{i}}{\partial P_{j}}\right) . \end{aligned}$$
(15)

Another key element that can be considered for the COVID–19 disease is called the model sensitive analysis. We recently applied this approach to some suggested models of this virus in [14,15,16,17,18]. The method can be used to calculate the local sensitivities for non-normalizations, half normalizations, and full normalizations in computational simulations. For the COVID–19 described model provided here, it is crucial to work more broadly and precisely in order to find the critical model parameters based on sensitivity analysis. In the computational simulations, we have used the model initial populations and parameters presented in [20]: \(S(0)=1046727, \;V(0)=400, \; E_{u}(0)=210, \;E_{d}(0)=0, \; A(0)=10, \; I(0)=40, \; Q(0)=20, \; R(0)=90\) and the model parameters \(\Lambda =607.7\), \(\mu =4.214 \times 10^{-5}\), \(\beta =4.743 \times 10^{-8}\), \(\xi _{1}=0.9\), \(\xi _{2}=0.3\), \(\alpha = 0.196\), \(\delta =0.1\), \(q=0.6\), \(\zeta =0.06\), \(u_{1}= 0.5\),\(u_{2}= 0.083\),\(u_{3}= 0.05\), \(\eta = 0.1\), \(\phi = 0.8\). In our computer simulations, we used such estimated values and initial variables. The results provided in this work represent a crucial step forward in understanding the model dynamics to a greater extent. This helps us in identifying critical model parameters as well as how each model individual is influenced by the other model individuals.

The model sensitivities are calculated using three distinct techniques: non-normalizations, half-normalizations and full-normalizations; see Figs. 7, 8 and 9. Interestingly, the results provide us with a deeper understanding of the model and help us identify the critical model parameters. For instance, it appears that the set \(\{ \beta , \mu , u_{3}, \eta \}\) is the most critical model parameters for the suggested model, whereas the set \(\{ \Lambda , \xi _1, \xi _2, \phi , u_{1} \}\) is the less critical model parameters according to non-normalization technique; see Fig. 7. Figure 8 indicates that parameters \( \Lambda , \xi _1, \xi _2, \phi , u_{1} \) are mainly the less critical model parameters whereas the other model parameters are often model sensitive. According to Fig. 9, the set of parameters \(\{ \Lambda , \mu , \xi _{2}, \phi \}\) is the less sensitive model parameters, but the rest of the model parameters become sensitive for the model variables. Identifying the critical model parameters based on local sensitivities using computational simulations can thus effectively work to further study the model practically and theoretically, and provide some suggestions for future improvements to the disease and its vaccination programs, interventions, and virus control.

Fig. 7
figure 7

Local sensitivity analysis with Non-normalizations in computational simulations for the suggested COVID–19 model using MATLAB, a the sensitivity of all variables to all parameters, b the sensitivity of all variables to all model parameters excluding \(\mu , \beta , u_3,\) and \(\eta \)

Full size image
Fig. 8
figure 8

Local sensitivity analysis with Half normalizations in computational simulations for the suggested COVID–19 model using MATLAB, a the sensitivity of all variables to all parameters, b the sensitivity of all variables to all model parameters excluding \(\beta \)

Full size image
Fig. 9
figure 9

Local sensitivity of all variables with respect to all parameters with full normalizations in computational simulations for the suggested COVID–19 model using MATLAB

Full size image

6 Conclusion and discussion

Only biological principles and healthcare preventions may not adequately explain how to deal with the COVID-19 pandemic. Mathematical models with computational simulations play a great role to widely understand such issues globally. Therefore, such models can help ones to identify the model critical parameters and their impacts in reducing this virus on the community.

It is worth noting that although the vaccination strategies are investigated, the influence of vaccination rate on spatiotemporal distribution of population with the local sensitivity analysis has remained unclear, that is the primary motivation for our paper. From a physical standpoint, our research attempts to bridge the gap between theoretical frameworks and real-world implications. We want to figure out the complicated processes that occur when looking at vaccination rates in the context of spatiotemporal distribution. We hope that by using a physical approach, we will be able to not only reveal the underlying mechanisms, but also give practical insights that will help to design more effective and centred programmes for community health. In the ongoing attempt to address the problems caused by infectious diseases such as COVID-19, this approach corresponds with an increasing requirement for comprehensive methods that account for both theoretical model and real-world data.

With this approach, the COVID-19 model that is provided in this work helps to effectively describe the dynamics of the model states. Thus, it can be summarized as prime results. Firstly, we have modeled the dynamics of all possible compartments, i.e., susceptible, vaccinated, undetected exposed infected, detected exposed infected, asymptomatic infected, symptomatic infected, quarantined and recovered individuals to analyze accurate transmission dynamics of the COVID-19 pandemics. Second, MATLAB has been used to approximation the numerical solutions of the model states for various parameters and initial values. Another important result here is that a system of diffusion equations was considered of the spreading COVID-19 with vaccinated individuals. These equations have been studied with different vaccination rates, they were simulated in 1D, 2D and 3D planes. Additionally, three different techniques non-normalizations, half-normalizations, and full-normalizations are used to compute the local sensitivities. The results based on the local sensitivities provide a good range to identify the models sensitive parameters in spreading this disease. In such case, identifying the critical parameters of the model will help to suggest further interventions and control strategies with lower budget.

Our model practical use extends to real-world scenarios, providing useful insights for optimising vaccination efforts in the context of infectious diseases. Health authorities may strategically supply vaccinations to regions most at risk by using our approach, which incorporates vaccination rates and performs local sensitivity analysis. The proposed model gives an in-depth knowledge of how vaccination rates impact the spatiotemporal dynamics of the population, this focused approach confirms a more effective use of resources. Finally, our model goes beyond theoretical constructions to provide real solutions to improve the precision and efficiency of public health initiatives in the vaccination strategy against infectious diseases.

In comparing our results with the other studies, it can be concluded some main points. First, the proposed model provides an essential range to understand this global issue theoretically, results can help international efforts to control this disease. In this work, we mainly focused on vaccination rates to minimize the total number of infected individuals, some possible strategies are highlighted. Second, identifying the most critical parameters in spreading this virus is another technique to control this pandemic in the community, we improved this work by calculating the local sensitivities between model compartments and parameters. Finally, using a system of diffusion equations for the COVID-19 pandemics instated of ordinary differential equations can help ones to study this issue more widely for different initial states, our results here are more improved compared to the previous studies because we suggest spatial distributions for model compartments for different initial states and parameters.