1 Introduction

Over the past decade, bistable structures have received significant attention due to their distinct advantages of effectively improving the low-frequency response, bandwidth, and large displacement transitions. The intrinsic features of bistability render them versatile and promising candidates in a wider range of applications, examples include energy harvesting [1, 2], vibration absorption [3, 4], smart sensors [5, 6], and morphing structures [7, 8]. The performance enhancement of these bistable systems is highly dependent on nonlinear restoring force design and characterization [9, 10]. However, robust nonlinear restoring force parameter identification is an open issue in practical applications due to the distinct characteristics of snap-through and disturbance of the high-level noise in dynamic responses.

For the purpose of characterizing the nonlinear restoring force in bistable structures. Stanton et al. deduced the dynamic model of the magnetic coupled bistable piezoelectric energy harvester using the energy principles and magnetic dipoles theory [11]. Zou et al. adopted the magnetic dipoles theory to calculate an underwater magnetically coupled bistable beam energy harvester [12]. Yan et al. [13, 14] introduced the equivalent magnetic current method to obtain nonlinear restoring force in a bistable vibration isolator and then fitted it with a higher-order polynomial function. Yang et al. [15] utilized Lagrange's equations to derive parameters of the nonlinear restoring force of a bistable electromagnetic actuator. The nonlinear restoring force analytical calculation and simplification methods are necessary for the initial bistable structures design. However, the characteristics of a bistable system are easily changed in experimental vibration conditions due to high sensitivity to structural parameters. Moreover, the quasi-static measurement and then polynomial fitting was also widely used to directly obtain the nonlinear restoring force of the bistable system. Shaw et al. [16] measured the nonlinear restoring force of a bistable composite plate in a high static low dynamic stiffness vibration isolator. Zou et al. [17] used force gauges and screw micrometers to measure the customized tristable nonlinear forces in a piezoelectric cantilever beam. However, the nonlinear restoring force is required to be measured repeatedly for reducing the measurement error due to snap-through characteristics.

System identification techniques can effectively estimate parameters of nonlinear vibrating structures under practical situations. Many identification methods have been successfully developed and applied to nonlinear restoring force identification of monostable structures. Yuan et al. [18] used the Hilbert transform method to identify hardening and softening nonlinearity in a circular piezoelectric laminated plate. Wang et al. [19] employed Hilbert vibration decomposition to estimate a nonlinear vibration absorber with quadratic and cubic stiffness. Noël et al. [20] identified piecewise nonlinear stiffness force in an aerospace structure using wavelet transform and the restoring force surface method. Xu et al. [21] developed a double Chebyshev polynomials-based approach to identify nonlinear restoring force in shape memory alloy dampers. In recent years, the identification of bistable systems has also attracted extensive attention. Zhou et al. [22] utilized a genetic algorithm to identify the damping and electromechanical coupling coefficient in a magnetic coupled bistable energy harvester. Feldman developed the method of the “FREEVIB” identification and Hilbert Vibration Decomposition to estimate the stiffness force curves of the Duffing-Holmes autonomous oscillator [23, 24]. Cohen et al. [25] presented the slow and fast decomposition method to identify the backbone curves of the two asymmetric potential wells and the linearized nonlinear stiffness force in a bistable electromagnetic energy harvester. Liu et al. [26] comparatively analyzed the displacement and acceleration measurement restoring force surface method for identifying bistable nonlinear restoring force. Anastasio combined restoring force surface and nonlinear subspace methods to estimate an asymmetric double-well Duffing system's nonlinear stiffness and damping characters [27, 28]. Liu et al. [29] developed a two-stage nonlinear subspace method to estimate the parameters of a nonlinear bistable piezoelectric energy harvesting structure. However, the traditional restoring force surface and Hilbert transform method always encounter the difficulty of numerical differentiation and dynamic response selection to identify bistable structures [26, 30]. Moreover, it is difficult to perform the model selection in the nonlinear subspace method because the prior knowledge of a nonlinear restoring force function should be obtained before identification.

Therefore, statistical and optimization methods were introduced to enhance the performance of classical parameter identification methods. Zhu et al. [31] employed the Bayesian probability method in nonlinear subspace identification to select the best model and improve the accuracy. Miguel et al. [32] introduced the Bayesian model identification through the harmonic balance method for predicting the nonlinear behavior of bolted structures. Tang et al. [33] proposed the technique of combining the Hilbert transform and the Bayesian approach to identify the stiffness and damping of a nonlinear absorber using free-response. Although these methods improve identification accuracy, there is still a lack of investigation into bistable structures combining nonparametric methods with modern statistical or optimization methods.

To enhance the identification performance of bistable structures, it is necessary to search for the optimal nonlinear restoring force from the estimated interval by nonparametric identification. Inspired by natural evolutionary optimization methods used in phenomenological model identification [34, 35], an optimal Hilbert transform method is proposed to identify bistable vibrating structures under the disturbance of high-level noise. The value range of mass, damping, and nonlinear restoring force coefficients are estimated through the Hilbert transform identification method. The optimal values can be searched based on evolutionary optimization. Numerical simulation of an asymmetric bistable equation under different noise levels and dynamic responses is carried out to investigate the identification accuracy. The numerical results indicate that the proposed method is preferable to the traditional one. Moreover, an experimental evaluation based on a magnetic coupled bistable cantilever beam verifies the effectiveness of the proposed method. The reconstructed dynamic response of the identified system equation is in good agreement with the measured response of the bistable structure.

The remainder of this paper is organized as follows. Section 2 introduces the modeling of a bistable vibrating structure. In Sect. 3, the optimal identification method is provided. Section 4 numerically investigates the dynamic response selection. Finally, experimental verification is conducted on a magnetic coupled bistable cantilever beam in Sect. 5.

2 Modeling and dynamic analysis of a bistable structure

2.1 Modeling of bistable vibrating structures

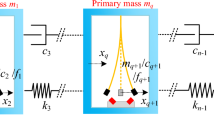
A bistable structure can be realized by coupling nonlinear negative stiffness force on the linear oscillator. The oblique spring, buckled beam and magnetic coupling are commonly used approaches to achieve negative stiffness. It should be noted that the identification method proposed in this paper is only suited for a single-degree-of-freedom system with constant mass, linear viscous damping and bistable nonlinear restoring force. Therefore, the mass and damping are assumed to be linear. Then, the governing equation of the single-degree-of-freedom nonlinear bistable vibrating structure, as shown in Fig. 1a, can be modeled as

$$ m\ddot{x} + c\dot{x} + kx + f_{n} (x) = f_{ext} $$
(1)

where m, c and k are the equivalent mass, linear viscous damping, and stiffness. And \(f_{n} (x) = \sum\nolimits_{i = 1}^{n} {\alpha_{i} x^{i} }\) is the external nonlinear restoring force, commonly described by a polynomial function.

Fig. 1
figure 1

a Schematic representation of lumped parameter model of a bistable vibrating structure; b the nonlinear restoring force characteristics

Full size image

Bistable systems with asymmetric nonlinear restoring force functions have received considerable interest due to fabrication imperfections and installation uncertainties [36, 37]. Therefore, asymmetric bistable structures are also employed in this paper to investigate the identification method. The most simple nonlinear restoring force equation [38] of an asymmetric bistable structure can be deduced as

$$ f_{n} (x) = (k + \alpha_{1} )x + \alpha_{2} x^{2} + \alpha_{3} x^{3} { = }\alpha_{3} (x - x_{1} )(x - x_{2} )(x - x_{3} ) $$
(2)

where \(k + \alpha_{1} = \alpha_{3} x_{1} x_{3}\) represents the first-order term of combined nonlinear restoring force;\(\alpha_{2} = - \alpha_{3} (x_{1} + x_{3} )\); x1 and x3 are stable equilibrium points; x2 is unstable equilibria and is often set as zero, as shown in Fig. 1b. It has been verified that only when \((k + \alpha_{1} ) \) is negative and \(\alpha_{3}\) is positive, the dynamic response of Eq. (1) can exhibit bistable characteristics. The parameter \(\alpha_{2}\) determines the degree of asymmetry of the bistable system.

2.2 Dynamic response selection and identification analysis

Dataset selection is essential in the nonlinear system identification procedure. The commonly used excitation approaches for obtaining identification datasets are frequency-swept, random and sine excitation, etc. For nonlinear monostable structures, such as piecewise linear and cubic nonlinear stiffness structures, the physical parameters and nonlinear restoring force functions can be identified by the ‘FORCEVIB’ algorithm [39] using frequency-swept excitation. However, the nonlinear restoring force of a bistable vibrating structure cannot be calculated straightforwardly by the frequency-swept response due to incapable to extract the envelope and instantaneous natural frequency characteristics while the large periodic inter-well oscillations occur across two potential energy wells.

Therefore, the identification process needs to be divided into two stages for all parameter identification in bistable structures. The coupled nonlinear stiffness force in bistable structures can be removed in many situations. The mass and damping coefficient can be identified using the traditional Hilbert transform-based method. Moreover, bistable vibrating structures can be regarded as two nonlinear monostable oscillators around their equilibrium points. The frequency-swept response can also identify the mass and damping. For nonlinear restoring force identification, the free vibration signal around two potential wells can be decomposed into slowly-varying components. Then, the congruent envelope and congruent natural frequency can be calculated. The nonlinear restoring force is equal to the product of the congruent envelope and congruent natural frequency [23].

It should be noted that the differentiator with a filtering procedure is necessary for modern Hilbert transform-based parameter identification [39, 40]. A higher quality of displacement signal acquisition is required. Moreover, the nonlinear restoring force to be identified is nonparametric, and curve fitting is essential for accurate characterization [18, 41]. Therefore, the noise levels will greatly affect the identification accuracy. To address these issues, the optimal Hilbert transform is introduced in the following section.

3 Optimal Hilbert transform method

In this section, the optimal Hilbert transform method is proposed to enhance the identification performance of bistable structures. The optimal method has the following characteristics: all parameters to be identified are set in a reasonable interval due to the effect of noise; all parameters to be identified are optimal values based on an evolutionary optimization algorithm. The specific process is as follows.

3.1 Linear parameter identification

The governing equation of a bistable vibrating structure becomes linear when the coupled nonlinear stiffness force is removed, and Eq. (1) can be rewritten as

$$ \ddot{x}(t) + h_{0} \dot{x}(t) + \omega_{0}^{2} x(t) = \frac{{f_{\rm ext} }}{m} $$
(3)

where h0 = c/m and \(\omega_{0}^{2} = k/m\).

In the Hilbert transform method, all signals need to be expressed in analytical signal form. The real-valued Eq. (3) is transformed into an analytical signal equation based on the balance of the real part and the imaginary part.

$$ \left\{ \begin{gathered} \frac{{\ddot{A}_{x} }}{{A_{x} }} - \omega_{x}^{2} + \omega_{0}^{2} + h_{0} \frac{{\dot{A}_{x} }}{{A_{x} }} = \frac{\alpha }{m} \hfill \\ \left( {2\frac{{\dot{A}_{x} }}{{A_{x} }}\omega_{x} + \dot{\omega }_{x} + h_{0} \omega_{x} } \right) = \frac{j\beta }{m} \hfill \\ \end{gathered} \right. $$
(4)

where

$$ \alpha = \frac{{xf + \tilde{x}\tilde{f}}}{{x^{2} + \tilde{x}^{2} }},{\kern 1pt} \;\beta = \frac{{\tilde{x}f - x\tilde{f}}}{{x^{2} + \tilde{x}^{2} }},\;{\kern 1pt} A_{x} = \sqrt {x^{2} + \tilde{x}^{2} } $$
(5)

The \(\tilde{x}\) and \(\tilde{f}\) are related to x and f by Hilbert transform, respectively. The envelope Ax and instantaneous frequency \(\omega_{x}\) are calculated from the displacement response.

The natural frequency and damping can be deduced from Eqs. (4). Moreover, the natural frequency \(\omega_{0}\) does not vary for a short period \(\Delta t\) because of the constant value of mass. Finally, the mass can also be solved from Eqs. (4). Therefore, linear parameters are derived as the following equations:

$$ \omega_{0}^{2} = \frac{\alpha }{m} + \omega_{x}^{2} - \frac{{\ddot{A}_{x} }}{{A_{x} }} + 2\frac{{\dot{A}_{x}^{2} }}{{A_{x}^{2} }} + \frac{{\dot{A}_{x} \dot{\omega }_{x} }}{{A_{x} \omega_{x} }} - \frac{{\dot{A}_{x} \beta }}{{A_{x} m\omega_{x} }} $$
(6)
$$ h_{0} = \frac{\beta }{{m\omega_{x} }} - 2\frac{{\dot{A}_{x} }}{{A_{x} }} - \frac{{\dot{\omega }_{x} }}{{\omega_{x} }} $$
(7)
$$ m = \frac{{\Delta \left( {\alpha - \frac{{\beta \dot{A}_{x} }}{{A_{x} \omega_{x} }}} \right)}}{{\Delta \left( { - \omega_{x}^{2} + \frac{{\ddot{A}_{x} }}{{A_{x} }} - 2\frac{{\dot{A}_{x}^{2} }}{{A_{x}^{2} }} - \frac{{\dot{A}_{x} \dot{\omega }_{x} }}{{A_{x} \omega_{x} }}} \right)}} $$
(8)

Thus, the underlying linear system's mass, damping coefficient and stiffness of Eq. (1) can be estimated by Eqs. (6)–(8). Due to the extraction of instantaneous natural frequency and instantaneous amplitude, the high-level noise will affect the identification results of these parameters. Therefore, each identified parameter in this stage is in a certain interval with upper and lower boundaries, not an exact value.

3.2 Nonlinear restoring force identification

For bistable vibrating structures, the Hilbert Vibration Decomposition [42,43,44] can be used for signal decomposition of free vibration responses. The congruent envelope Ac(t) and congruent natural frequency ωc(t) can be described by the sum of high-order synchronous components [23]. The deduced equations are as follows

$$ A_{c} (t) = \sum\limits_{n = 1}^{L} {A_{n} (t)\cos \psi_{n} (t)} ,\quad \omega_{c} \left( t \right) = \sum\limits_{n = 1}^{L} {\omega_{0n} (t)\cos \psi_{n} (t)} $$
(9)

where An and ω0n(t) represent the envelope and instantaneous natural frequency of the n-order harmonics, respectively. The \(\psi_{n}\) is the phase angle between the primary and the n-order harmonic components.

For asymmetrical bistable vibrating structures, congruent functions must be separated into four parts due to the two steady-state points and the asymmetric characteristics. Furthermore, the nonlinear restoring force per unit mass can be expressed as the product of four congruent envelopes and their congruent natural frequencies [23].

$$ f_{\rm non} = \left\{ \begin{gathered} \omega_{cn1}^{2} A_{cn1} \;(x < 0) \hfill \\ \omega_{cn2}^{2} A_{cn2} \;(x > 0) \hfill \\ \omega_{cp1}^{2} A_{cp1} \;(x < 0) \hfill \\ \omega_{cp2}^{2} A_{cp2} \;(x > 0) \hfill \\ \end{gathered} \right. $$
(10)

where subscript p stands for positive envelope and n represents negative envelope.

Due to the fact that the above procedure can only obtain the nonlinear restoring force trajectory, a fitting function is required to characterize nonlinear restoring force. However, the optimal Hilbert transform does not take the static fitting function as the final identification result. The proposed method attempts to search for the optimal nonlinear restoring force function from the dynamic response instead of the static fitting.

3.3 Evolutionary optimization

The prior knowledge of mass, damping and nonlinear restoring force coefficients is provided in Sects. 3.1 and 3.2. Therefore, each parameter can be assigned to a region with upper and lower boundaries. Assuming that m, c, k, and αi are subjected to side constraints as follows:

$$ m_{lb} \le m \le m_{ub} ;\;c_{lb} \le c \le c_{ub} ;\;k_{lb} \le k \le k_{ub} ;\;\alpha_{ilb} \le \alpha_{i} \le \alpha_{iub} $$
(11)

where subscripts lb and ub represent lower boundary and upper boundary, respectively.

In order to obtain the optimal value in the above intervals, a Normalized Mean-Square Error (NMSE) between the ‘measured’ dynamic response and that predicted by the identified system [45] is introduced to estimate the optimization performance. The fitness function of optimization is given by:

$$ J(m,c,k,\alpha_{i} ) = \frac{100}{{N\sigma_{x}^{2} }}\sum\limits_{i = 1}^{N} {(x_{i} - \hat{x}_{i} (m,c,k,\alpha_{i} ))^{2} } $$
(12)

where \(\sigma_{x}^{2}\) is the variance of the “measured” displacement xi, and \(\hat{x}_{i}\) is the reconstructed response by the identified parameters.

Particle swarm optimizer with passive congregation [46] is employed for the optimization of bistable second-order differential equations. It is assumed that the population consists of d individuals. Every individual has its position and velocity, corresponding to \({\mathbf{s}}_{t}\) and \({\mathbf{v}}_{t}\), respectively. The initial particles are randomly distributed in the designed vector space. The next position vector of individual d is iterated by the following equations

$$ \left\{ \begin{gathered} {\mathbf{s}}_{t + 1}^{d} = {\mathbf{s}}_{t}^{d} + {\mathbf{v}}_{t + 1}^{d} \hfill \\ {\mathbf{v}}_{t + 1}^{d} = w_{t} {\mathbf{v}}_{t}^{d} + c_{1} {\mathbf{r}}_{1} \otimes ({\mathbf{p}}_{t}^{d} - {\mathbf{s}}_{t}^{d} ) + c_{2} {\mathbf{r}}_{2} \otimes ({\mathbf{p}}_{g}^{d} - {\mathbf{s}}_{t}^{d} ) + c_{2} {\mathbf{r}}_{3} ({\mathbf{R}}_{t}^{d} - {\mathbf{s}}_{t}^{d} ) \hfill \\ \end{gathered} \right. $$
(13)

where \(w_{t} \) is the inertia factor at time instant t; the c1, c2, c3 represent the cognitive parameter, social parameter and passive congregation coefficient, respectively; the r1, r2, r3 are pseudo-random variables with uniform distribution in the value range [0, 1]. The best previous position vector of individual d is at time instant t and \({\mathbf{p}}_{{\text{g}}}\) is the best last position vector among all individuals at time instant t. The \({\mathbf{R}}_{t}^{d}\) is a particle selected randomly in the swarm. The symbol \(\otimes\) denotes the term-by-term product.

The optimal Hilbert transform method for the identification of bistable vibrating structures can be summarized in Fig. 2. The Hilbert transform interval estimation of mass, damping and nonlinear restoring force coefficients are conducted firstly for obtaining the reasonable range of identified parameters. Furthermore, an optimization fitness function is established to obtain the optimal value of nonlinear parameters in bistable vibrating structures.

Fig. 2
figure 2

Flowchart of the optimal Hilbert transform identification of bistable vibrating structures

Full size image

Due to that the whole identification process involves different excitations, the step to step identification data sets acquisition procedure are listed as follows:

  1. 1.

    Frequency-sweeping test is conducted on the underlying linear system if the external rotatable magnets are removed;

  2. 2.

    The two free-vibration responses are obtained by giving the bistable structure different impacts or large displacements. The two free-vibration responses need to contain both inter-well and intra-well motions. Besides, they must finally move into different stable equilibrium points.

  3. 3.

    Finally, the free-vibration response and sinusoidal vibration responses can be used for optimal identification procedure.

4 Numerical investigations

In this section, an asymmetric bistable system described by Eq. (1) is selected for the numerical investigation of the proposed identification method. System parameters of Eq. (1) is assumed that m = 0.01 kg, c = 0.01 N/(m/s), k = 150 N/m, the external nonlinear restoring force fn = − 250x + 2500x2 + 1250000x3. The bistable vibrator has an unstable equilibrium point of zero and two steady-state points − 0.01 m and 0.008 m. Due to the bistable characteristics, the mass, damping coefficient and nonlinear restoring force cannot be identified simultaneously [29]. Therefore, the linear parameters of m and c are firstly estimated by the frequency-swept response and then the nonlinear restoring force is identified by free attenuation responses.

4.1 Underlying linear parameter identification

Linearly increasing frequency excitation simulation is performed over the frequency range of 10–30 Hz and a constant base acceleration of 2.5 m/s2. The sampling frequency is 500 Hz and the sweeping frequency rate is 30 Hz/min. The dynamic displacement response is depicted in Fig. 3a and the envelope can be extracted by the Hilbert transform. The backbone curve with a blue line is calculated using Eq. (6), as shown in Fig. 3b. The result indicates that the instantaneous natural frequency is 19.35 Hz and does not change with the amplitude increases. Meanwhile, the damping coefficient per unit mass is plotted in Fig. 3c using Eq. (7). It can be estimated that the damping coefficient c = 1.014*0.01≈0.01 N·s/m. In Fig. 3d, the linear elastic force trajectory is plotted by the product of instantaneous natural frequency and envelope. The linear stiffness is obtained by the least-square fitting and the final k = 150 N/m. Finally, the mass is calculated by Eq. (8) and the value is 0.01 kg.

Fig. 3
figure 3

Identification of underlying linear parameters. a envelope extraction; b backbone curve calculation; c damping curve; d linear force trajectories

Full size image

The above identification results indicate that the relative error of each parameter is almost zero when there is no noise disturbance. However, the Hilbert transform identification involves differential procedures, and the noise level significantly influences the identification results. In this paper, the white Gaussian noise with Signal-to-Noise-Ratio (SNR) of 40 dB, 30 dB and 20 dB are added to the dynamic response to investigate the effect of noise levels. The relative error Re for each parameter is defined as the following equation:

$$ R_{e} = \left| {\frac{{R_{i} - R_{r} }}{{R_{r} }}} \right| \times 100\% $$
(14)

where Re and Rr represent identified and real value, respectively.

Table 1 summarizes the identification results under different noise level disturbances. It can be observed in Table 1 that m, c, k have the relative error of 5%, 17% and 6.7% under 40 dB noise level, respectively. When the noise level increases to 30 dB, the identified relative error raise to 21%, 18% and 20%. Moreover, the relative error of identified parameters under 20 dB noise are 26%, 46% and 27%, respectively. Therefore, the noise level has a great impact on the identification results.

Table 1 Estimated linear system parameters under different noise levels
Full size table

4.2 Nonlinear restoring force identification

To identify nonlinear restoring force, two corresponding free attenuation responses around two steady-state points should be obtained. In this simulation, two large values of the initial displacement × 0 =  ± 0.018 m with zero velocity are selected and two corresponding attenuation responses with 30 dB noise level are shown in Fig. 4a. It can be observed that the oscillator moves across two potential wells and then falls to different potential wells of − 0.01 m and 0.008 m. The free vibration response of nonlinear bistable structures is generally rich in harmonic contents with the major component having a primary natural frequency and other minor components containing higher frequencies. Therefore, two attenuation responses are decomposed into four slow-varying components by using the Hilbert Vibration Decomposition [23], as shown in Fig. 4b. The decomposed 8 components are employed for the congruent envelope and natural frequency calculation by using Eq. (9). The congruent envelopes around 0.008 m and − 0.01 m are plotted with blue, pink, red and green curves, as depicted in Fig. 4c. Finally, the blue, pink, red and green nonlinear restoring force trajectories corresponding to four congruent envelopes are calculated by Eq. (10), as shown in Fig. 4d. The identified trajectories have a good agreement with the theoretical nonlinear restoring force curve drawn with a black line.

Fig. 4
figure 4

Identification of nonlinear restoring force characteristics. a two free attenuation responses with 30 dB white noise; b four decomposed slow-varying components by Hilbert Vibration Decomposition; c four segments of congruent envelopes; d the estimated four segments of nonlinear restoring force trajectories

Full size image

Table 2 lists the estimated nonlinear restoring force functions with the different white noise levels. It can be observed that the nonlinear restoring force coefficients have little difference from the theoretical one under 40 dB noise. However, it becomes worse when the noise level increases to 30 dB and the relative error of α1, α2, α3 are 20%, 4% and 8.8%, respectively. When the noise level is increased to 20 dB, the identified accuracy of nonlinear restoring force distinctly reduces. It must be noted that the nonlinear restoring force function is governed by four parameters α0, α1, α2, α3. The identification accuracy may not be defined by simply comparing the relative error of each coefficient. Therefore, comparing the reconstructed dynamic response with the simulated one is more reasonable and will take considered in the following sections.

Table 2 Estimated nonlinear restoring force function and its relative error under different noise levels
Full size table

From the above Hilbert transform analysis, physical parameters m, c, k and the polynomial coefficients of the nonlinear restoring force fn can be estimated reasonably under weak noise conditions. However, the identification accuracy decreases dramatically with the noise level increases. In the following analysis, all simulations are under 20 dB noise level. Therefore, the interval of each parameter in the Hilbert transform identification is obtained. The mass, damping and nonlinear restoring force coefficients are assigned at an error of 50%, 50% and 20%, respectively. The specific values range is as follows:

$$ \begin{aligned} 0.005 \le & m \le 0.015;\;0.005 \le c \le 0.015;\; - 120 \le k + \alpha_{1} \le - 80; \\ 1920 \le & \alpha_{2} \le 2880;\;960000 \le \alpha_{2} \le 1440000. \\ \end{aligned} $$
(15)

Moreover, all optimal identification in the following procedure selects the following parameter conditions: (1) population size d = 100; (2) the cognitive parameter and passive parameter c2 = c2 = 0.6. (3) the passive congregation coefficient c3 = 0.6 + c3step*iteration; (4) the inertia factor w = 0.8.

4.3 Optimal identification under free vibration

In the optimal identification procedure, the datasets use free attenuation response as in Sect. 4.2 is considered. The displacement response does not need to include oscillations around two potential energy wells. Therefore, only the first six seconds of datasets with 20 dB noise level are selected for optimal identification. In Fig. 5a, the free attenuation response is plotted with a blue line. Then, the damping and nonlinear restoring force can be estimated by Eq. (15) and the evolutionary optimization algorithm. It can be viewed from Fig. 5b that the value of NMSE gradually converged to 2.52% after 1000 analyses. Finally, the optimized damping c is 0.0099 N s/m with a relative error of 1% and the nonlinear restoring function is fnon = − 98.98x + 2592x2 + 1.25 × 106x3. It is observed in Fig. 5c that the identified nonlinear restoring force has a good agreement with the theoretical curve. The reconstructed dynamic response is compared to the simulated one with the 20 dB noise level, as depicted in Fig. 5d. The results indicate that the reconstructed system identified by the proposed method has the same vibration response as the simulation system.

Fig. 5
figure 5

Optimal identification under free vibration response. a free attenuation response with 20 dB white noise; b NMSE changes with the analyses; c the identified nonlinear restoring force and the theoretical one; d reconstructed dynamic response versus simulated datasets under 20 dB noise

Full size image

4.4 Optimal identification under forced vibration

To verify the effectiveness of evolutionary optimization using forced vibration signals, periodic oscillation is adopted because of its easy acquisition. When the excitation acceleration is 50 m/s2 with the frequency of 19 Hz is adopted to excite the same bistable structure, inter-well periodic oscillations may be observed in the simulation. It can be viewed in Fig. 6a that the oscillator moves across two potential wells at high speed when the transient response of the system disappears in 0.5 s. The amplitude of the system fluctuates slightly due to the 20 dB noise level. Then, the optimization identification is carried out, and the NMSE finally converged to 1.64% after 2000 analyses, as shown in Fig. 6b. The identified mass and damping coefficients are 0.0098 kg and 0.0129 N·s/m with a relative error of 2% and 29%, respectively. Moreover, the optimal estimated nonlinear restoring force function is fnon = − 90.48x + 2423x2 + 1.17 × 106x3. It is observed in Fig. 6c that the identified nonlinear restoring force has an excellent fit with the theoretical curve. Moreover, the comparison between the reconstructed dynamic response and the simulated one is depicted in Fig. 6d. The results verify the effectiveness of the proposed method.

Fig. 6
figure 6

Optimal identification under large periodic oscillation. a forced response with 20 dB white noise and the oscillator exhibits large oscillations across two potential wells; b NMSE changes with the analyses; c comparison between the identification of nonlinear restoring force and theoretical one; d the reconstructed dynamic response versus simulated datasets under 20 dB noise

Full size image

From the numerical investigation of optimal identification under free and forced vibration, the results demonstrated that free vibration is more desirable for obtaining damping coefficient and nonlinear restoring force function. Moreover, forced vibration is suitable for mass estimation.

4.5 The influence of damping

The traditional Hilbert transform-based method and the optimal one are all based on the free vibration responses of bistable vibrators. Then, a question is raised here “If the damping ratio continues to increase and the free attenuation becomes faster and faster, then is the proposed method still effective?”. In this section, numerical simulations will be conducted to explore the damping ratio effects on identification results.

In these simulations, the equivalent damping ratios are set as 0.02, 0.06, 0.1 and 0.3, respectively. The two free vibration responses with different damping ratios are obtained under no noise disturbance, as shown in Fig. 7a–d. It can be observed that as the damping ratios increase, the bistable oscillator used less time moving to stable equilibrium points. The less free attenuation responses can be used for the calculation of nonlinear congruent envelopes and congruent natural frequencies. The identified nonlinear restoring force trajectory is obtained, as shown in Fig. 7e–h with black asterisk lines. The third-order polynomial function is used to fit the identified nonlinear restoring force trajectory. The fitted results are then compared with the theoretical ones. The results demonstrate that the identified nonlinear restoring forces all have good agreements with the theoretical ones. However, with the increasing of equivalent damping ratio, there will be fewer and less useful free attenuation responses for nonlinear restoring force calculation. The proposed method is applicable as long as there are sufficient attenuation trajectories.

Fig. 7
figure 7

The influence of damping ratios on identification results. a–d Two free vibration responses with damping ratios of 0.02, 0.06, 0.1 and 0.3, respectively. e–h The comparisons between the identified results with the theoretical ones(damping ratio of 0.02, 0.06, 0.1 and 0.3, respectively)

Full size image

5 Experimental validations

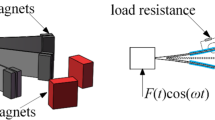
An experimental setup is established to verify the effectiveness of optimal Hilbert transform parameter identification for bistable structures. A magnetically coupled cantilever beam is designed to make a typical bistable structure for experimental investigation. Figure 8 shows the schematic of the whole experimental setup. A vibration exciter (JZK-50, Econ Technologies Co., Ltd), a power amplifier (YE5874A, Econ Technologies Co., Ltd), and a controller (VT-9002–1, Econ Technologies Co., Ltd)) are employed for generating acceleration generation and signal control. An acceleration sensor (CXL04GP3, MEMSIC., Inc) and a displacement sensor (HL-G112-A-C5, Keyence) are utilized to acquire excitation acceleration and displacement response, respectively. The datasets are synchronously recorded to the oscilloscope (TBS2000, Tektronix). The cantilever beam is made of spring steel with a size of 200 × 15 × 0.8mm3. The tip magnets have a dimension of 20 × 10 × 3.5mm3, and the external magnet has a diameter of 10 × 10 × 10mm3. Besides, the nonlinear restoring force around two stable equilibrium points can be repeatedly measured based on arranged measuring instruments. The force and displacement can be simultaneously obtained by reciprocating the ball screw structure. The final measurement force–displacement trajectory will be compared with the identified results.

Fig. 8
figure 8

Experimental setup for identifying a magnetically coupled bistable cantilever beam

Full size image

A forward and reverse sine sweep signal with an amplitude of 4 m/s2 ranging from 5 to 20 Hz is utilized to excite the cantilever beam for identification of the underlying linear system's mass, damping, and stiffness. The sampling time is 64 s with a sampling frequency of 312.5 Hz. The base excitation and displacement response are depicted in Fig. 9a and the resonance occurred at 23 s and 46 s. Then, the envelope is extracted with a black line, as shown in Fig. 9b. The instantaneous natural frequency is a straight line due to linear sweeping and will not be depicted here. Finally, the underlying linear system parameters of linear stiffness, damping coefficient and mass are calculated by Eq. (6) to Eq. (8). The estimated linear stiffness k = 93 N/m, damping coefficient c = 0.014 N/(m/s) and mass m = 0.012 kg.

Fig. 9
figure 9

Underlying linear system parameter identification. a the excitation and dynamic response of linear cantilever beam; b the calculated envelope based on Hilbert transform

Full size image

According to the numerical results in Sect. 4.2, it is more effective to utilize free attenuation response around two-steady points of the bistable system to identify nonlinear restoring force coefficients. Therefore, the end of the cantilever beam in the experimental setup is placed in large deformation and then released. The displacement response history of free attenuation with the sampling frequency of 312.5 Hz is recorded. The first and second attenuation responses started from 0.02311 m and 0.02005 m and moved to two different potential energy well locations, respectively, as depicted in Fig. 10a. Then, the Hilbert Vibration Decomposition is adopted here for signal decomposition. In Fig. 10b, the black, blue, red and green line depicts the decomposed signal components. The blue line shows the largest slow-varying component and the black line determines which potential energy well the oscillator will eventually move to. When four slowly-varying components are extracted from the attenuation response, the congruent envelope can be calculated by Eq. (9). As depicted in Fig. 10c, the blue and green lines represent the congruent envelopes around positive potential energy well. Meanwhile, the congruent envelopes around the negative potential energy well are drawn by blue and pink lines. The amplitude envelope far away from two bistable potential energy wells does not need to make further analysis because the above four congruent envelopes are enough for nonlinear restoring force characterization. Finally, the four segments of nonlinear restoring force corresponding to four congruent envelopes are calculated by Eq. (10), as shown in Fig. 10d. By taking least-square fitting, a seventh-order polynomial is used to characterize these nonlinear restoring force trajectories and the final function is fnon = 0.4 − 220x − 1.3 × 104x2 + 4.2 × 106x3 + 1.1 × 108x4 − 2.2 × 1010x5 − 2.7 × 1011x6 + 4.2 × 1013x7.

Fig. 10
figure 10

Experimental identification of nonlinear restoring force. a two free attenuation responses around two-steady points; b signal decomposition of two free attenuation responses using Hilbert Vibration Decomposition; c four segments of congruent envelopes; d the calculated four segments of nonlinear restoring force trajectories and a seventh-order polynomial fitting curve

Full size image

The numerical simulation in Sect. 4 shows that the traditional Hilbert transform-based method to identify bistable structures is not optimal or cannot estimate due to high noise levels. Therefore, the physical and nonlinear restoring force parameters identified above are assigned a value range. Assuming that there is a tolerance of ± 20% for each parameter in this experiment. Therefore, the value range of each parameter is assigned as

$$ \begin{aligned} & 0.0096 \le m \le 0.0144;\;0.0112 \le c \le 0.0168;\;0.32 \le \alpha_{0} \le 0.48; \\ & - 264 \le \alpha_{1} \le - 176;\; - 1.56 \times 10^{4} \le \alpha_{2} \le - 1.04 \times 10^{4} ;\;3.36 \times 10^{6} \le \alpha_{3} \le 5.04 \times 10^{6} ; \\ & \quad 8.8 \times 10^{7} \le \alpha_{4} \le 1.32 \times 10^{8} ;\; - 2.64 \times 10^{10} \le \alpha_{5} \le - 1.76 \times 10^{10} ; \\ & - 3.24 \times 10^{11} \le \alpha_{6} \le - 2.16 \times 10^{11} ;\;3.36 \times 10^{13} \le \alpha_{7} \le 5.04 \times 10^{13} . \\ \end{aligned} $$
(16)

The numerical simulations indicate that free attenuation and periodic oscillation under constant frequency excitation can obtain the optimal nonlinear restoring force parameters. Therefore, these two types of dynamic responses are performed under experimental conditions. It should be noted that the fitted nonlinear restoring force is effective in the deflection range of − 0.015 to 0.015 m because of the geometric nonlinearity of the cantilever beam. The measured responses need to be intercepted in the range of [− 0.015 0.015], and then the evolutionary optimization identification is conducted.

Firstly, the intercepted free attenuation response with an initial displacement of 0.01568 m is selected for optimal identification. In this case, the oscillator finally moved to the positive potential well. It is observed in Fig. 11a that after 1000 analyses, the NMSE converged to 6.63%. The comparison between reconstructed dynamic responses with measured datasets is shown in Fig. 11b. The results indicate that the reconstructed system identified by the proposed method has almost the same vibration response as the measured datasets. Secondly, the intercepted free attenuation response with an initial displacement of 0.01508 m is adopted for identification. The oscillator moved to negative potential well in this situation. The relationship between NMSE and analyses steps is depicted in Fig. 11c and the NMSE value finally converged to 9.83% after 1000 analyses. The reconstructed dynamic response has a good agreement with the measured datasets, as shown in Fig. 11d. Through the above analysis, the average NMSE of two free attenuation responses around two potential wells is 8.23%. The damping c = 0.015 N/(m/s) and nonlinear restoring force function fnon = 0.40–195.94x − 1.35 × 104x2 + 4.18 × 106x3 + 1.07 × 108x4 − 2.28 × 1010x5 − 2.60 × 1011x6 + 4.24 × 1013x7 are finally identified.

Fig. 11
figure 11

Optimal identification by two intercepted free attenuation datasets. a First intercepted free attenuation response with the initial displacement of 0.01568 m; b comparison between reconstructed response and experimental data; c second intercepted free attenuation response with the initial displacement of 0.01508 m; d comparison of reconstructed steady-state response and experimentally measured response

Full size image

Two intra-well periodic oscillations are selected for parameter optimization of mass value to improve the identification accuracy. The periodic response around the negative potential well is obtained under the level of 15 m/s2 and the frequency of 18 Hz. The evolutionary optimization is conducted and the NMSE converged to 4.13% after 1000 analyses, as shown in Fig. 12a. The reconstructed dynamic response has a good agreement with the measured datasets between − 0.012 and − 0.006 m, as depicted in Fig. 12b. The result indicates that the mass and nonlinear restoring characteristics in the range of − 0.012 to − 0.006 m can be estimated by the proposed method. Moreover, the periodic response around positive potential well under excitation of 5 m/s2 is also investigated. Figure 12c shows the NMSE of 8.65% is obtained after 1000 analyses. The comparison between the reconstructed dynamic response with the measured datasets is shown in Fig. 12d. The result demonstrates that the mass and nonlinear restoring characteristics in the range of 0.008 m to 0.011 m can also be identified. At this stage, the final identified mass value is equal to 0.0119 kg.

Fig. 12
figure 12

Optimal identification by two forced responses. a Forced response under base excitation of 15 m/s2 at 18 Hz; b comparison between reconstructed response and experimental data; c forced response under base excitation of 5 m/s2 at 18 Hz; d comparison of reconstructed response and experimentally measured response

Full size image

The proposed optimal Hilbert transform parameter identification shows that the bistable vibrating structures can be optimally identified under free and forced vibration. Moreover, free attenuation response and periodic oscillation under constant frequency excitation are easily collected datasets in practical situations, which is convenient for optimal identification.

To give a quantitative evaluation index of the proposed optimal method against the classic one. The NMSE between the identified nonlinear restoring force functions with the experimentally measured one is finally adopted. Due to that large deformation will increase the measurement error in quasi-static measurement, the nonlinear restoring force is measured in the range of − 0.01 m and 0.01 m with a step of 0.001 m. The classic Hilbert transform-based identified, the proposed optimal identified and experimentally measured one are plotted in Fig. 13, respectively. The final NMSE of the nonlinear restoring force of the optimal one and the classic one is 1.20% and 4.55%, respectively. The results demonstrate that the proposed method increases the accuracy by 3.35% for identification of nonlinear restoring force.

Fig. 13
figure 13

Nonlinear restoring force comparison between the classic Hilbert transform-based method, the proposed optimal method and the experimentally measured one

Full size image

6 Conclusions

This paper proposed an optimal Hilbert transform method for the accurate identification of bistable vibrating structures. The proposed method can identify bistable vibrating structures under high-level noise. Numerical investigation of an asymmetric bistable dynamic equation shows that the proposed method can effectively identify mass, damping and nonlinear restoring force under 20 dB noise level. The reconstructed dynamic response exhibits an NMSE of 2.52% for free vibration and 1.64% for forced vibration response. Moreover, the evolutionary optimization identification under free and forced vibration response shows that choosing free vibration to determine damping and nonlinear restoring force is more desirable. Meanwhile, the mass value can be identified by forced periodic oscillation. As all know, the decay time of free attenuation responses is highly dependent on the damping ratio. Thus, the investigation of the damping ratio from 0.04 to 0.3 on nonlinear restoring force identification results is conducted. The results show that the identification of nonlinear restoring force is not affected as long as there are sufficient attenuation trajectories around two steady-state points. Experimental measurements of a magnetic coupled bistable cantilever beam under different conditions are performed to identify the nonlinear system parameters. Experimental results indicate that the proposed method can effectively identify the nonlinear bistable structures with an average NMSE value of 8.23% for free vibration and 6.39% for forced vibration, respectively. Moreover, the optimal identified nonlinear restoring force can improve the NMSE of 4.55% to 1.20% compared to classic Hilbert transform-based identification method.