1 Introduction

In the past decade, bistable nonlinear energy sinks have received growing attention due to their wide applications in the fields of energy harvesting and vibration absorption [1, 2]. There are various types of bistable nonlinear energy sinks have been developed, e.g., well-designed bistable tracks [3], local bistable beams [4] and oblique springs integration [5]. The precise identification of local bistable nonlinear stiffness force plays an important role in designing and predicting the performance of vibration absorbers. However, the introduction of bistability poses a huge challenge to the identification of nonlinear stiffness forces in practical applications because of snap-through chaotic motions [6]. Many data-driven identification methods have been developed for parameter identification of structural dynamics. However, balancing the efficiency and accuracy of identification will be a difficulty when it comes to high-degrees-of-freedom systems.

For nonlinear restoring force identification of single-degree-of-freedom bistable vibrating oscillators, many approaches have been developed to address this issue. Liu et al. comparatively studied the displacement and acceleration measurement restoring force surface method to identify nonlinear bistable nonlinear stiffness force and linear damping force [7]. Feldman proposed the Hilbert Vibration Decomposition (HVD) combined with the “FREEVIB” algorithm for the identification of the nonlinear stiffness force of the Duffing-Holmes bistable oscillator [8, 9]. Anastasio combined restoring force surface and nonlinear subspace methods to identify the nonlinear stiffness force of an asymmetric double-well Duffing oscillator and its nonlinear damping characteristics [10, 11]. Liu et al. [12] developed a two-stage nonlinear subspace method to identify the parameters of the nonlinear bistable piezoelectric energy harvester. Zhu et al. [13] integrated the Bayesian probability method to select the best model in nonlinear subspace identification which can improve the model reliability and accuracy of bistable nonlinear identification.

For nonlinear stiffness force identification in nonlinear energy sink structures, Wang et al. [14] employed the restoring force surface method to identify the nonlinear stiffness and damping of a piecewise linear nonlinear energy sink and a hyperbolic tangent function is used for characterization. Lund et al. [15] adopted an unscented Kalman filter to identify geometrically nonlinear stiffness and Coulomb damping in a nonlinear energy sink device. Moore developed the characteristic nonlinear system identification method which is based on Hilbert transform and analytical approach to identify the dynamics of local piecewise linear attachments [16]. These methods have typically been found to be accurate and reliable for their designed nonlinear energy sinks.

Recently, with the rapid development of the data-driven regression method, sparse identification using the SINDy algorithm has become a hot topic due to its robustness. Brunton et al. originally proposed the nonlinear dynamic equation discovery method based on sparse regression and applied it to Lorenz and Navier Stokes’s equations [17]. Then, it has been developed in the multi-degree-of-freedom system with local polynomial and hysteretic nonlinear systems [18, 19]. The reason is it has high efficiency and strong anti-noise ability if proper basis function and numerical differentiation techniques are used [20]. However, compared with the traditional signal processing method, the selection of basis functions is unclear. If the assumed candidate model basis functions are inappropriate, the computing time will greatly increase and the accuracy will be influenced. As we all know, the identification time is very important in control. Therefore, it is necessary to investigate the accuracy and efficiency of sparse identification of high degrees of freedom nonlinear systems.

This paper proposed the concept of BNESC which is a strongly nonlinear multi-degree-of-freedom system with many local bistable attachments. The dynamic model and sparse identification using SINDy and the physics-informed SINDy method are presented. The numerical simulations of a two-degree-of-freedom and eight-degree-of-freedom BENSC will show the vibration suspension ability. Besides, the accuracy and efficiency of SINDy identification and physics-informed SINDy identification of BNESC will be illustrated on two to ten-degree-of-freedom BENSC under noise levels of 40 dB, 30 dB and 20 dB. Finally, some discussions are given.

2 Modeling of BNESC

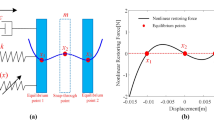
The system of Bistable Nonlinear Energy Sink Chains (BNESC) considered in this paper is schematically depicted in Fig. 1. It consists of n/2 linear primary structures with n/2 bistable nonlinear beams, where n represents the total degrees of freedom along the x-direction and also must be an even number. Every primary structure is connected to each other by a linear spring and linear damper. Besides, every primary structure has a bistable attachment with a linear damper and nonlinear magnetic coupled nonlinear stiffness force. When the BNESC is under impact or based excitation, the bistable nonlinear attachment will pump lots of energy from the primary mass and suppress the vibration of the main oscillator. Besides, the nonlinear bistable attachment can be used for energy harvesting.

Fig. 1
figure 1

Schematic view of BNESC system

Full size image

The equations of motion of BNESC can be modeled as:

$$ \left\{ \begin{gathered} m_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} + c_{2} (\dot{x}_{1} - \dot{x}_{2} ) + \alpha_{1} (x_{1} - x_{2} ) + \beta_{1} (x_{1} - x_{2} )^{3} \hfill \\ \quad + c_{3} (\dot{x}_{1} - \dot{x}_{3} ) + k_{3} (x_{1} - x_{3} ) = 0 \hfill \\ \quad m_{2} \ddot{x}_{2} + c_{2} (\dot{x}_{2} - \dot{x}_{1} ) + \alpha_{1} (x_{2} - x_{1} ) + \beta_{1} (x_{2} - x_{1} )^{3} = 0 \hfill \\ \ddots \hfill \\ m_{q} \ddot{x}_{q} + c_{q - 1} (\dot{x}_{q} - \dot{x}_{q - 2} ) + k_{q - 1} (x_{q} - x_{q - 2} ) + c_{q + 1} (\dot{x}_{q} - \dot{x}_{q + 1} ) \hfill \\ \quad + \alpha_{q} (x_{q} - x_{q + 1} ) + \beta_{q} (x_{q} - x_{q + 1} )^{3} + c_{q} (\dot{x}_{q} - \dot{x}_{q + 2} ) + k_{q} (x_{q} - x_{q + 2} ) = 0 \hfill \\ \quad m_{q + 1} \ddot{x}_{q + 1} + c_{q + 1} (\dot{x}_{q + 1} - \dot{x}_{q} ) + \alpha_{q} (x_{q + 1} - x_{q} ) + \beta_{q} (x_{q + 1} - x_{1} )^{3} = 0 \hfill \\ \ddots \hfill \\ m_{n - 1} \ddot{x}_{n - 1} + c_{n - 1} (\dot{x}_{n - 1} - \dot{x}_{n - 3} ) + k_{n - 1} (x_{n - 1} - x_{n - 3} ) + c_{n} (\dot{x}_{n - 1} - \dot{x}_{n} ) \hfill \\\quad + \alpha_{n - 1} (x_{n - 1} - x_{n} ) + \beta_{n - 1} (x_{n - 1} - x_{n} )^{3} = 0 \hfill \\\quad m_{n} \ddot{x}_{n} + c_{n} (\dot{x}_{n} - \dot{x}_{n - 1} ) + \alpha_{n - 1} (x_{n} - x_{n - 1} ) + \beta_{n - 1} (x_{n} - x_{n - 1} )^{3} = 0 \hfill \\ \end{gathered} \right. $$
(1)

where m is the equivalent mass of each primary structure and bistable nonlinear attachment. x is the displacement response of each oscillator. The subscript n represents where the mass is. The linear stiffness and damping are represented by k and c. The bistable nonlinear stiffness forces are all assumed third-order polynomials with coefficients of α, β with different subscripts.

3 SINDy and physics-informed SINDy of BNESC

When the BNESC is described by Eq. (1), the linear parameters of m, k, and c can be easily measured or identified by linear parameter identification methods. However, the bistable nonlinear stiffness force is always hard to measure or identify due to snap-through characteristics. Besides, the bistable nonlinear stiffness force is strongly sensitive to the installation parameters of two rotatable magnets.

For modern data-driven methods, the sparse identification of nonlinear dynamical systems has the following procedures [17, 21]. Firstly, Eq. (1) is rewritten as the following forms:

$$ \frac{{{\text{d}}y_{k} (t)}}{{{\text{d}}t}} = \Theta (y)\xi_{k} { + }\sigma Z_{k} $$
(2)

where Θ(y) is the candidate function and ξk contains the coefficients of the sparse vector. The \(\sigma\) here is defined as the Signal to Noise Ratio (SNR) and \(Z_{k}\) is the root mean square of the measured data yk(t).

It must be noted that numerical differentiation techniques and robust noise removal methods in Eq. (2) may play an important role in SINDy identification accuracy [22,23,24]. In this paper, these advanced techniques will not be compared in detail.

According to Eq. (2), the candidate function Θ(y) consists of polynomial terms, therefore:

$$ {{\varvec{\Theta}}}({\mathbf{Y}}) = \left[ {\begin{array}{*{20}c} {\theta_{1} ({\mathbf{Y}})} & {\theta_{2} ({\mathbf{Y}})} & \cdots & {\theta_{P} ({\mathbf{Y}})} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \vdots & \vdots & \vdots & \vdots \\ {{\mathbf{Y}}^{{P_{1} }} } & {{\mathbf{Y}}^{{P_{2} }} } & \cdots & {{\mathbf{Y}}^{{P_{n} }} } \\ \vdots & \vdots & \vdots & \vdots \\ \end{array} } \right] $$
(3)

where \({\mathbf{Y}}^{{P_{n} }}\) denotes the n-order polynomial nonlinearities in the state space Y.

To explain the importance of candidate function Θ(y) selection in SINDy, a two-degree-of-freedom BNES is taken as an example:

$$ \begin{aligned} & m_{1} \ddot{x}_{1} + c_{1} (\dot{x}_{1} - \dot{x}_{2} ) + k_{1} (x_{1} - x_{2} ) + c_{2} (\dot{x}_{1} - \dot{x}_{2} ) \\ &\qquad + \alpha (x_{1} - x_{2} ) + \beta (x_{1} - x_{2} )^{3} = 0 \hfill \\ & m_{2} \ddot{x}_{2} + c_{2} (\dot{x}_{2} - \dot{x}_{1} ) + \alpha (x_{2} - x_{1} ) + \beta (x_{2} - x_{1} )^{3} = 0 \hfill \\ \end{aligned} $$
(4)

Derive the first-order differential equation by reducing the order in Eq. (4):

$$ \left\{ \begin{array}{l} {\text{d}}y(1) = y(2) \hfill \\ {\text{d}}y(2) = - \frac{{c_{1} + c_{2} }}{{m_{1} }}\left[ {y(2) - y(4)} \right]\\ \qquad - \frac{{k_{1} + \alpha }}{{m_{1} }}\left[ {y(1) - y(3)} \right] - \frac{\beta }{{m_{1} }}\left[ {y(1) - y(3)} \right]^{3} \hfill \\ {\text{d}}y(3) = y(4) \hfill \\ {\text{d}}y(4) = - \frac{{c_{2} }}{{m_{2} }}\left[ {y(4) - y(2)} \right] - \frac{\alpha }{{m_{2} }}[y(3) - y(1)] \\ \qquad- \frac{\beta }{{m_{2} }}[y(3) - y(1)]^{3} \hfill \\ \end{array} \right. $$
(5)

where y(1) is equal to x1 and y(3) is equal to x2.

Based on Eq. (5), the basis function only has basis function terms of

$$ \begin{gathered} \Theta_{{{\text{prior}}}} = \left\{ {y(2)\;\;y(2) - y(4)\;\;y(1) - y(2)\;\;[y(1) - y(3)]^{3} } \right. \hfill \\ {\kern 1pt} \quad \quad \quad \,\left. {y(4)\,y(4) - y(2)\,y(3) - y(1)\,[y(3) - y(1)]^{3} } \right\} \hfill \\ \end{gathered} $$
(6)

where \(\Theta_{{{\text{prior}}}}\) represents physics-informed basis functions.

There are only 8 terms of basis functions in Eq. (6). However, the basis functions will contain 35 terms if a third-order polynomial is chosen for identification in SINDy. The nonlinear basis functions will greatly be increased with the increase in degrees of freedom or polynomial order. The identification efficiency will greatly decrease if the basis functions in Eq. (3) are not physically informed.

Once the basis function is established, the coefficients ξ can be obtained by performing a standard regression. The L1 regularization term needs to be added to the regression:

$$ {\varvec{\xi}}{ = }\mathop {{\text{argmin}}}\limits_{{{\varvec{\xi}}^{\prime } }} \left\| {\Theta {\varvec{\xi}}^{\prime } - {\mathbf{y}}} \right\|_{2} + \lambda \left\| {{\varvec{\xi}}^{\prime } } \right\|_{1} $$
(7)

where \(\lambda\) weights the sparsity constraint. The formula is related to compressed sensing, which allows sparse vectors to be determined from relatively few noncoherent random measurements [25].

The specific identification processes of SINDy and physics-informed SINDy for BNESC can be summarized as follows:

  1. 1.

    Give the BNESC an impact or initial displacement at any degree of freedom;

  2. 2.

    Collect the displacement responses of each-degree-of-freedom;

  3. 3.

    Obtain the velocity and acceleration by numerical differentiation;

  4. 4.

    Rearrange matrices of displacement, velocity and acceleration signals based on Eqs. (5) and (6);

  5. 5.

    Select an appropriate polynomial order based on Eqs. (3) or (6) of nonlinear stiffness force and then construct the candidate function matrix in sparse regression;

  6. 6.

    Use the sequential thresholded least-squares algorithm to achieve sparse regression and the coefficients ξ can be identified.

  7. 7.

    Select the identified parameters and then reconstruct the nonlinear stiffness for comparison.

4 Numerical analysis of vibration absorption

To give specific views of vibration suppression abilities of BNESC systems. Two numerical simulations on two-degree-of-freedom BNESC and eight-degree-of-freedom BNESC are illustrated. According to current studies of bistable nonlinear energy sink analysis, third-order polynomial functions are adopted for nonlinear stiffness force characterization [26,27,28,29,30,31]. In the following simulations, the four nonlinear bistable beams all have the same nonlinear stiffness force with a function of f = − 100x + 106x3. The selected parameters in Eq. (1) are all illustrated in Table 1.

Table 1 Illustration of parameters of BNESC
Full size table

For two-degree-of-freedom BNESC, the initial condition of Eq. (1) is set as [0; 1 m/s; 0; 0]. The sampling frequency of 1000 Hz in the time interval of t = 0 to t = 6 s is set. The displacement responses of mass m1 and m2 are obtained by conducting a Runge–Kutta ode45 simulation. Figure 2 shows the displacement responses of m1 and m2. It can be observed that the nonlinear energy sink mass moves across two potential wells in the first 2.5 s and finally moves into the positive equilibrium point of + 0.01 m. The primary structure’s vibration is suppressed and the amplitude quickly decays to zero.

Fig. 2
figure 2

The dynamic responses of two-degree-of-freedom BNESC. a primary mass response. b nonlinear energy sink mass response

Full size image

To give a specific view of vibration suppression ability, the dynamic response of the primary mass of BNESC is compared with no BNES primary structure, as shown in Fig. 3. The dynamic response of the primary structure without BENS is exponentially descending. However, the free attenuation response with BNES has faster attenuation and smaller amplitude characteristics.

Fig. 3
figure 3

Comparison of free vibration responses of primary structure with BNES and without BNES

Full size image

For eight-degree-of-freedom BNESC, the initial condition of Eq. (1) is set as [0; 3 m/s; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0]. The sampling frequency of 1000 Hz in the time interval of t = 0 to t = 6 s is set. The displacement responses of mass m1 to m8 are obtained by conducting a Runge–Kutta ode45 simulation. Figure 4 shows the displacement responses of m1 to m8. It can be observed that four BNES masses move across two potential energy wells at the beginning and then fall into any two equilibrium points. The primary structures of m1, m3, m5 and m7 exhibit irregular attenuation.

Fig. 4
figure 4

Free vibration responses of eight-degree-of-freedom BNESC

Full size image

Figure 5 shows the nonlinear vibration suppression ability of eight-degree-of-freedom BNESC. The amplitude of the primary structure in BENSC is always lower than the linear four-degree-of-freedom system without BNES. It must be noted that the BNESC is not optimized in this paper. Therefore, the vibration absorption is not as good enough. The optimization and design of a bistable nonlinear energy sink structure can refer to these references [32,33,34]. It must be noted that the selection of parameters in BNESC will not affect the identification results due to that third-order polynomial function was used to represent nonlinear stiffness force of BNESC. Theoretically, the identification procedure will not be affected if basis functions, noise interference and sparse regression algorithm were determined, as described in Eqs. (2), (3) and (7).

Fig. 5
figure 5

Comparison of vibration suppression ability with and without BNES

Full size image

5 Identification accuracy and efficiency of BNESC

The dynamic responses of a BNESC are sensitive to nonlinear stiffness force parameters and initial conditions due to the strongly nonlinear coupling characteristics. Therefore, the Normalized Mean Square Error (NMSE) of the nonlinear stiffness force is defined here to evaluate identification accuracy.

$$ J = \frac{100}{{N\sigma_{f}^{2} }}\sum\limits_{i = 1}^{N} {(f - \hat{f}_{i} )^{2} } $$
(8)

where N denotes the total sampling points of nonlinear stiffness force. The \(\sigma_{f}^{2}\) is the variance of theoretical nonlinear stiffness force. The \(\hat{f}\) is the identified nonlinear stiffness force sequence.

The sparse identification algorithm is conducted on two-degree-of-freedom to ten-degree-of-freedom systems. Besides, the 40 dB, 30 dB and 20 dB Gaussian White Noise are added to the displacement responses of each degree of freedom. Figure 6a shows the comparison between the identified nonlinear stiffness force and theory. It has a good agreement with the theory even under the noise level of 20 dB. Besides, it can be seen in Fig. 6b that with the increase in noise levels, the relative error between identified and theory greatly increased.

Fig. 6
figure 6

Identified nonlinear stiffness force and relative error of a two-degree-of-freedom BNESC. a comparison between the identified (20 dB) and theory. b relative error

Full size image

For eight-degree-of-freedom BNESC, the identified nonlinear stiffness force has a good agreement with the theory when the noise level is under 30 dB, as shown in Fig. 7a. There is an unreasonable error if the noise level increases to 20 dB. Figure 7b gives a comparison of identified relative errors under different noise levels. It demonstrates that with the increase in noise levels, a sharp increase in identification NMSE.

Fig. 7
figure 7

Identified nonlinear stiffness force and relative error of an eight-degree-of-freedom BNESC. a comparison between the identified (40 dB, 30 dB, 20 dB) and theory. b relative error

Full size image

Table 2 lists the identified NMSE error from two to ten-degree-of-freedom BNESC. With the increase in the degrees of freedom, the identified nonlinear stiffness force error is increased. The same is true for the influence of noise levels on the accuracy of nonlinear stiffness force identification. Under the noise level of 20 dB, the identified results in eight and ten-degree-of-freedom BNESC are 30.3485% and 63.0856%, respectively. The results demonstrate that if the noise level and degrees of freedom are simultaneously very high, the sparse identification may fail to identify the nonlinear stiffness force. However, under the noise level of 40 dB, the identified nonlinear stiffness has good accuracy with the highest NMSE of only 0.6450%. Even under the noise level of 30 dB, the identified results are also relatively good with NMSE of 0.0331% to 9.7115%.

Table 2 Identification results of BNESC under different noise levels
Full size table

To give a specific view of identification accuracy and efficiency of sparse identification with third-order polynomial basis functions for BNESC, 100 cycles on BNESC systems with different degrees of freedom are performed. Figure 8a–c show the relationship between NMSE and degrees of freedom under noise levels of 40 dB, 30 dB and 20 dB, respectively. The noise levels and degrees of freedom all have a great impact on identification accuracy. Figure 8d gives the relationship between computing time and degrees of freedom. It can be observed that the identification efficiency is greatly decreased with the increase in degrees of freedom.

Fig. 8
figure 8

Identification accuracy and computing time using the SINDy method with a third-order polynomial. a Identification accuracy versus degrees of freedom (40 dB). b Identification accuracy versus degrees of freedom (30 dB). c Identification accuracy versus degrees of freedom (20 dB). d the computing time versus degrees of freedom

Full size image

To give a comparison, 100 cycles using physics-informed SINDy on a BNESC system with different degrees of freedom are performed. The identified accuracy keeps around 0.5% even under the noise of 20 dB, as depicted in Fig. 9a. Besides, the computing times are 0.9 s, 1.7 s, 2.9 s, 5.1 s and 12.3 s for two degrees of freedom to ten degrees of freedom BNESC, respectively. The identification accuracy greatly improved compared to SINDy identification with third-order polynomial basis functions, as shown in Fig. 9b.

Fig. 9
figure 9

Identification accuracy and computing time using physics-informed SINDy. a Identification accuracy versus degrees of freedom (20 dB). b computing time versus degrees of freedom (20 dB)

Full size image

6 Conclusions

This paper gives a new investigation on the efficiency and accuracy of sparse identification and physics-informed sparse identification of bistable nonlinear energy sink chains (BNESC). The numerical simulations of a two-degree-of-freedom and eight-degree-of-freedom BNESC have shown the vibration suppression ability. The relationship between the identified NMSE of nonlinear stiffness force and degrees of freedom of BNESC is illustrated. Besides, the 40 dB, 30 dB and 20 dB noise are added to test the anti-noise robustness. With the increase in degrees of freedom and noise levels, the identification accuracy will be greatly decreased using SINDy with third-order polynomial functions. However, the identification accuracy remains around 0.5% if the prior basis function of BNESC is known. Besides, the identification efficiency will greatly improve compared with SINDy. The investigated results give special views of the significance of basis function information for the identification of BNESC system. However, the acquisition of prior information of basis functions in SINDy is still challenging in the future.