Stochastic vibration responses of the bistable electromagnetic actuator with elastic boundary controlled by the random signals

Abstract

This paper comprehensively investigates the stochastic vibration responses of a bistable electromagnetic actuator with elastic boundary (EB-bistable actuator) controlled by Gaussian white noise and low-pass filtered stochastic noise. The EB-bistable actuator uses an oblique spring and another linear spring to realize the bistability and the elastic boundary, respectively. The elastic boundary can dynamically vary the bistability to enhance the vibration outputs of the EB-bistable actuator under the stochastic control signals. The paper firstly presents the governing equations and numerical integration method of the EB-bistable actuator controlled by the Gaussian white noise and low-pass filtered stochastic noise, respectively. Secondly, experiments are performed to verify the numerical predictions. Thirdly, the performance improvement of the EB-bistable actuator is validated, by comparing its stochastic responses with a bistable actuator with a fixed boundary (the FB-bistable actuator) and a linear actuator. Compared with the FB-bistable actuator for some appropriate parameters, the displacement variance of the EB-bistable actuator can be increased by 27.1% under Gaussian white noise signal and by 26.2% under low-pass filtered stochastic noise owing to the enhancement of the stochastic inter-well response, respectively. Moreover, the displacement variance of the EB-bistable actuator can be 109 times and 1138 times higher than that of the linear actuator controlled by Gaussian white noise and low-pass filtered stochastic noise, respectively. Finally, this paper uncovers the influence of the actuator structure parameters and control signal features, which presents the useful guidelines of the EB-bistable actuator for stochastic vibration application.

1 Introduction

Electromagnetic vibration actuators are widely employed for vibration attenuation [1,2,3] and excitation [4,5,6], owing to their quick response when controlled. A conventional electromagnetic vibration actuator structure is a linear oscillator [7]. The linear spring that connects the moving part and fixed part of the actuator is used to reset the moving part when the actuator is free of load. Since the linear-spring restoring force is opposite to the actuation direction of the moving part, it always decelerates the moving part during the actuation, which degrades the vibration actuation efficiency, i.e., increasing the power consumption. Therefore, to improve the vibration actuation efficiency, an effective solution is to use a nonlinear-oscillator-based actuator structure by replacing the linear spring with a nonlinear spring.

In recent decades, researches have shown that nonlinear oscillators have higher efficiency of energy conversion than linear oscillators [8,9,10]. Among various types of nonlinear oscillators, bistable nonlinear oscillator draws great attention [11, 12]. Bistable nonlinear layout of the springs brings a ‘negative linear spring effect’, and thus bistable oscillator has an unstable equilibrium position between the two stable equilibrium positions [12, 13]. In a bistable nonlinear system, the oscillator mass can be accelerated when it crosses the unstable equilibrium position, which leads to the large amplitude vibration response, i.e., inter-well vibration between these two stable equilibria [14,15,16,17,18]. The displacement amplitude is one of the most important design parameters of an actuator. The large displacement amplitude actuators have great application potential for dynamic performance tests of the large deformable flexible space truss and control of the vibration-driven locomotion system. Thus, the outstanding physical feature of bistable nonlinear oscillators described above is widely utilized to design the vibration actuator [18,19,20,21]. For example, Gary et al. [20, 21] proposed the design space to modify a bistable magnetic actuation mechanism for having a large actuation distance and low switching energy. Additionally, the bistable nonlinear oscillators are also widely applied to the design of mechanical energy harvesters [12, 22,23,24,25], and fluid-induced energy harvesters [14, 26, 27], where a high-efficient energy conversion is required. For example, Gao et al. [24] conceived a bistable piezoelectric cantilever vibration energy harvester with an elastic support external magnet to keep the system in the state of bistable oscillation. Wu et al. [25] designed a novel bistable piezoelectric energy harvester dedicated to vibration energy harvesting in the direction of gravity. Zou et al. [26] presented a new magnetically coupled bistable piezoelectric energy harvesting system that possesses great potential for underwater application. In recent years, the applications of bistable structures in vibration isolation have also attracted a lot of attention [13, 16, 28]. For example, Yan et al. [28] used a specific model to provide a guideline for the design, analysis and optimization of the bistable vibration isolators.

It is discovered that having additional dynamic coupling terms can enhance the bistable oscillator responses. For example, Harne et al. [29] conducted the analysis and experiment of a flight mechanism able to adjust motor axial support stiffness and compression characteristics, and found that these additional elastic axial supporting terms can dramatically modulate the amplitude range and type of wing stroke dynamics achievable. The author’s group investigated robust optimization of a dual-stage bistable energy harvester considering parametric uncertainties [30]. Besides, apart from the measures of adding another independent degree of freedom along with the vibration direction of the bistable oscillator, the author’s group proposed a novel bistable electromagnetic actuator by adding a spring perpendicular to the vibration direction to form an elastic boundary, which can dynamically change the bistable spring during vibration actuation [18, 31,32,33]. The results have shown that the elastic boundary can help enhancing the large amplitude inter-well responses of the actuator under the harmonic inputs, significantly decreasing the power consumption of the actuator. Besides, the broadband active vibration isolation of this actuator has also been thoroughly investigated to provide useful guideline for the vibration isolation subjected to the base excitation [33].

However, the previous researchers were focused on the vibration responses of the advanced bistable actuator with the elastic boundary under the harmonic input signals only. The vibration responses of this actuator under stochastic control signals have not yet been investigated. Apart from the harmonic vibration response, a stochastic vibration response is an important performance index of an actuator, due to the demands of the random vibration tests and control in marine, aerospace and civil engineering [34, 35]. Therefore, it is very meaningful to develop a theory of the stochastic vibration responses of the new bistable actuator with the elastic boundary. Driven by this interest, this paper will thoroughly investigate the vibration responses of the bistable electromagnetic actuator with the elastic boundary (simply named EB-bistable actuator in the rest of this paper), when it is controlled by two classic stochastic signals: Gaussian white noise and low-pass filtered random noise. Through the experimental and numerical studies, the guidelines of the EB-bistable actuator under stochastic control signals will be developed.

The rest of this paper is presented as follows. Section 2 presents the modeling of the EB-bistable actuator under Gaussian white noise and low-pass filtered stochastic noise, respectively. Section 3 presents the numerical and experimental validation of the numerical solutions of the stochastic responses. Then, Sect. 4 compares the performance between the EB-bistable actuator, linear actuator and the fixed boundary bistable actuator, so as to show the stochastic response improvement of the proposed actuator. The parametric studies of the EB-bistable actuator under the two types of stochastic control signals are performed in Sects. 5 and 6, which will give the design guidelines. Finally, Sect. 7 concludes the key findings of this paper.

2 Modeling

2.1 Mathematical modeling of the EB-bistable actuator

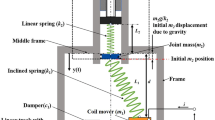
Figure 1 shows the schematic of the EB-bistable actuator controlled by the stochastic signals. The EB-bistable actuator has a mover mass $m_{1}$, an oblique spring with stiffness $k_{1}$, a joint mass $m_{2}$, a linear spring with stiffness $k_{2}$, a linear track embedded with permanent magnets, and an adjustable bolt. The elastic boundary is constituted by the joint mass, the linear spring, and the adjustable bolt. The original lengths of the oblique spring and the linear springs are $L_{1}$ and $L_{2}$, respectively. By tuning the adjustable bolt, $L_{1} > d$, where $d$ is the height between the connection point of the oblique spring on the mover and the bottom of the linear spring when the system is at its static equilibrium. As a result, the oblique spring’s compressing force will push the mover away from the centerline, leading to two stable static positions of the mover that are symmetric about the centerline, thereby creating bistability. The mover has coils, and therefore the mover can be driven by an electromagnetic force owing to the interaction between the coil current and the magnetic field of the permanent magnet. The electromagnetic coupling is a constant $\theta$. When the coil is input with stochastic current $i$, the electromagnetic force $F = \theta i$ will produce the random vibration of the mover.

Fig. 1

The schematic of the EB-bistable actuator controlled by stochastic current signals $i$

Define $x$ as the displacement of the mover deviating from the centerline, and $y$ is the displacement of the joint mass deviating from its zero-state described in Fig. 1. Assume that the linear damping coefficients $c_{1}$ and $c_{2}$ exist as shown in Fig. 1. The governing equations of this system can be obtained through the Lagrange equation as follows:

$$ \frac{d}{dt}\frac{\partial T}{{\partial \dot{x}_{k} }} - \frac{\partial T}{{\partial x_{k} }} + \frac{\partial V}{{\partial x_{k} }} + \frac{\partial D}{{\partial \dot{x}_{k} }} = F_{{x_{k} }} $$

(1)

where $T$ denotes the total kinetic energy of the system due to its motion and $V$ represents the total potential energy of the system (the sum of gravity potential energy and elastic potential energy in this case). $D$ is the Rayleigh dissipation function used to handle the effect of velocity-proportional friction force in Lagrange mechanics. $x_{k}$ is the kth position coordinate and $F_{{x_{k} }}$ is the generalized force corresponding to $x_{k}$.

The kinetic, potential energy and dissipation functions of this system are, respectively, expressed as follows,

$$ T = \frac{1}{2}m_{1} \dot{x}^{2} + \frac{1}{2}m_{2} \dot{y}^{2} $$

(2)

$$ V = \frac{1}{2}k_{1} \left( {\sqrt {\left( {d - y} \right)^{2} + x^{2} } - L_{1} } \right)^{2} - m_{2} gy + \frac{1}{2}k_{2} y^{2} $$

(3)

$$ D = \frac{1}{2}c_{1} \dot{x}^{2} + \frac{1}{2}c_{2} \dot{y}^{2} $$

(4)

The system’s governing equations are

$$ m_{1} \ddot{x} + c_{1} \dot{x} + k_{1} x\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {d - y} \right)^{2} + x^{2} } }}} \right) = \theta i $$

(5)

$$ m_{2} \ddot{y} + c_{2} \dot{y} + k_{2} y + k_{1} \left( {y - d} \right)\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {d - y} \right)^{2} + x^{2} } }}} \right) - m_{2} g = 0 $$

(6)

Defining the parameters in Table 1, the governing equations are normalized as

$$ \ddot{x} + \eta_{1} \omega_{1} \dot{x} + \omega_{1}^{2} x\left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - y} \right)^{2} + x^{2} } }}} \right) = \beta i $$

(7)

$$ \ddot{y} + \eta_{2} \omega_{2} \dot{y} + \omega_{2}^{2} y + \mu \omega_{1}^{2} \left( {y - d} \right)\left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - y} \right)^{2} + x^{2} } }}} \right) - g = 0 $$

(8)

Table 1 The definitions of the normalized parameters

The equilibria of the mover are calculated by Eqs. (7) and (8) by letting all the time derivative terms and the input signal $i$ be zero as

$$ x_{{{\text{eq}}}} = \pm \sqrt {\left( {\alpha^{2} d^{2} - \left( {d - \frac{g}{{\omega_{2}^{2} }}} \right)^{2} } \right)} $$

(9)

2.2 The SDEs under Gaussian white noise signals

When the control current signal is the Gaussian white noise $W\left(t\right)$, the stochastic differential equations (SDEs) of the actuator based on Eqs. (7) and (8) are obtained as follows,

$$ dQ_{1} = Q_{3} dt $$

(10)

$$ dQ_{2} = Q_{4} dt $$

(11)

$$ dQ_{3} = \beta \cdot dB\left( t \right) - \left[ {\eta_{1} \omega_{1} Q_{3} + \omega_{1}^{2} Q_{1} \left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - Q_{2} } \right)^{2} + Q_{1}^{2} } }}} \right)} \right]dt $$

(12)

$$ dQ_{4} = - \left[ {\eta_{2} \omega_{2} Q_{4} + \omega_{2}^{2} Q_{2} + \mu \omega_{1}^{2} \left( {Q_{2} - d} \right)\left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - Q_{2} } \right)^{2} + Q_{1}^{2} } }}} \right) - g} \right]dt $$

(13)

where $\left[{Q}_{1},{Q}_{2},{Q}_{3},{Q}_{4}\right]=[x,y,\dot{x},\dot{y}]$ are the random variables. · is Ito differential operation. $dB\left( t \right)/dt = W\left( t \right)$ and ${\text{E}}\left[ {W\left( t \right)W\left( {t + \tau } \right)} \right] = 2D\delta \left( \tau \right)$. $2D$ is the Gaussian white noise intensity, $\delta \left( \tau \right)$ is the Dirac function, and $E\left[ \cdot \right]$ represents the averaging.

2.3 The SDEs under low-pass filtered stochastic noise

When the Gaussian white noise $W\left( t \right)$ passes through a second-order low pass filter (e.g., the resistance-inductance-capacitance circuit), the low-pass filtered stochastic noise is produced. The low-pass filtered stochastic noise is usually used to test the stochastic response of an actuator in the low-frequency band. The second-order low pass filter after Laplace transformation is presented as follows,

$$ {\text{Filter}} = \frac{{G_{0} \omega_{0}^{2} }}{{s^{2} + \eta \omega_{0} s + \omega_{0}^{2} }} $$

(14)

where $s$ is the complex variable, $G_{0}$ is the filter gain, $\eta$ is the filter loss factor, and $\omega_{0}$ is the filter’s natural frequency. When $\eta = 1.414$, the value of $\omega_{0}$ is actually the bandwidth of the filter.

According to Eqs. (7), (8) and (14), the SDEs of the EB-bistable actuator under the low-pass filtered stochastic noise are

$$ dQ_{1} = Q_{3} dt $$

(15)

$$ dQ_{2} = Q_{4} dt $$

(16)

$$ dQ_{3} = \beta Q_{5} dt - \left[ {\eta_{1} \omega_{1} Q_{3} + \omega_{1}^{2} Q_{1} \left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - Q_{2} } \right)^{2} + Q_{1}^{2} } }}} \right)} \right]dt $$

(17)

$$ Q_{4} = - \left[ {\eta_{2} \omega_{2} Q_{4} + \omega_{2}^{2} Q_{2} + \mu \omega_{1}^{2} \left( {Q_{2} - d} \right)\left( {1 - \frac{\alpha d}{{\sqrt {\left( {d - Q_{2} } \right)^{2} + Q_{1}^{2} } }}} \right) - g} \right]dt $$

(18)

$$ dQ_{5} = Q_{6} dt $$

(19)

$$ dQ_{6} = G_{0} \omega_{0}^{2} { }\cdot dB\left( t \right) - \left( {\eta \omega_{0} Q_{6} + \omega_{0}^{2} Q_{5} } \right)dt $$

(20)

where $\left[ {Q_{1} ,Q_{2} ,Q_{3} ,Q_{4} } \right] = \left[ {x,y,\dot{x},\dot{y}} \right]$. $Q_{5}$ and $Q_{6}$ are the low-pass filtered stochastic noise and its derivative. $dB\left( t \right)/dt = W\left( t \right)$ and ${\text{E}}\left[ {W\left( t \right)W\left( {t + \tau } \right)} \right] = 2D\delta \left( \tau \right)$.

2.4 Numerical integration method

The improved Euler–Maruyama (IEM) method is used to numerically solve the SDEs, which can ensure both computation efficiency and precision [36]. Taking Eqs. (10)–(13) as an example, the SDEs can be rewritten as follows,

$$ {\text{d}}{\mathbf{Q}} = {\varvec{F}}\left( {{\varvec{Q}},t} \right){\text{dt}} + {\mathbf{G}}\left( {{\mathbf{Q}},{\text{t}}} \right){\text{dB}}\left( {\text{t}} \right) $$

(21)

where ${\mathbf{Q}} = \left[ {Q_{1} ,Q_{2} ,Q_{3} ,Q_{4} } \right]$, ${\varvec{F}}\left( {{\varvec{Q}},t} \right)$ is the drift coefficient vector, and ${\varvec{G}}\left( {{\varvec{Q}},t} \right)$ is the diffusion coefficient vector. Discretize the time t into $t_{1}$, $t_{2}$, …$t_{n}$, with the equal interval $\Delta t = t_{n} - t_{n - 1}$. The IEM’s iteration form is [36]

$$ {\varvec{Q}}_{{n + \frac{1}{2}}} = {\varvec{Q}}_{n} + \frac{1}{2}{\varvec{F}}\left( {{\varvec{Q}}_{n} ,t_{n} } \right)\Delta t $$

(22)

$$ {\varvec{Q}}_{n + 1} = {\varvec{Q}}_{n} + {\varvec{F}}\left( {{\varvec{Q}}_{{n + \frac{1}{2}}} ,t_{n} + \frac{1}{2}\Delta t} \right)\Delta t + {\varvec{G}}\left( {{\varvec{Q}}_{{n + \frac{1}{2}}} ,t_{n} + \frac{1}{2}\Delta t} \right)\Delta B_{n} $$

(23)

Since $dB\left( t \right)/dt = W\left( t \right)$ and ${\text{E}}\left[ {W\left( t \right)W\left( {t + \tau } \right)} \right] = 2D\delta \left( \tau \right)$, $\Delta B_{n} = \sqrt {2D{\Delta }t} N\left( {0,1} \right)$, where $N\left( {0,1} \right)$ is a random number satisfying the normal distribution. The IEM’s fidelity is also proved in this paper by using the finite difference method to solve the Fokker–Planck–Kolmogorov equation derived from Eq. (21), which can be seen in detail in Sect. 3.1.

Through this numerical integration method, the displacement $x$, speed $\dot{x}$ and acceleration $\ddot{x}$ of the mover mass $m_{1}$ can be derived and used for further discussion. To be specific, the displacement data will be used for the statistic of displacement probability density function and displacement variance. The acceleration data will be used for the statistic of acceleration power spectrum density and the calculation of acceleration average power. By definition, the acceleration average power is $P = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\mathop \smallint \limits_{{t_{0} - \frac{T}{2}}}^{{t_{0} + \frac{T}{2}}} \left| {\ddot{x}} \right|^{2} dt = \mathop \smallint \limits_{0}^{\infty } S\left( f \right)df$, where the period $T$ is centered about $t = t_{0}$ (when the transient component of the vibration response is too small and can be neglected) and $S\left( f \right)$ is the one-sided power spectral density of acceleration $\ddot{x}$ [37]. According to the definition, $P$ is the acceleration variance for the discrete data, which represents the summation of the acceleration power in the whole frequency band.

3 Numerical and experimental validation

Before developing the insights of the EB-bistable actuator’s stochastic vibrations, the IEM method is verified by the finite-difference method and experiments are also conducted to validate the mathematical model of the EB-bistable actuator and numerical solutions of the SDEs.

3.1 Numerical validation

Consider the excitation signal $i$ is the Gaussian white noise $W\left( t \right)$ satisfying ${\text{E}}\left[ {W\left( t \right)W\left( {t + \tau } \right)} \right] = 2D\delta \left( \tau \right)$, where $2D$ is the Gaussian white noise intensity. Define $\left[ {Q_{1} ,Q_{2} ,Q_{3} ,Q_{4} } \right]$ as the random variables satisfying $\left[ {Q_{1} ,Q_{2} ,Q_{3} ,Q_{4} } \right] = \left[ {x,y,\dot{x},\dot{y}} \right]$, and $\left[ {q_{1} , q_{2} , q_{3} , q_{4} } \right]$ are the relate state variables. According to the governing Eqs. (5) and (6), the FPK equations are obtained as follows:

$$ \frac{\partial p}{{\partial t}} + \frac{\partial }{{\partial q_{1} }}\left( {a_{1} p} \right) + \frac{\partial }{{\partial q_{2} }}\left( {a_{2} p} \right) + \frac{\partial }{{\partial q_{3} }}\left( {a_{3} p} \right) + \frac{\partial }{{\partial q_{4} }}\left( {a_{4} p} \right) - \frac{1}{2}\frac{{\partial^{2} }}{{\partial q_{3}^{2} }}\left( {b_{33} p} \right) = 0 $$

(24)

where $p = p\left( {q_{1} ,q_{2} ,q_{3} ,q_{4} ,t} \right)$ is the joint probability density function of the system and $t$ is the time.$a_{j} ,b_{jk} \left( {j,k = 1,2,3,4} \right)$ are called 1st derivative moment and 2nd derivative moment, respectively, which satisfy:

$$ a_{1} = q_{3} $$

(25)

$$ a_{2} = q_{4} $$

(26)

$$ a_{3} = - \frac{1}{{m_{1} }}\left( {c_{1} q_{3} + k_{1} q_{1} \left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {d - q_{2} } \right)^{2} + q_{1}^{2} } }}} \right)} \right) $$

(27)

$$ a_{4} = - \frac{1}{{m_{2} }}\left( {c_{2} q_{4} + k_{2} q_{2} + k_{1} \left( {q_{2} - d} \right)\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {d - q_{2} } \right)^{2} + q_{1}^{2} } }}} \right) - m_{2} g} \right) $$

(28)

$$ b_{33} = 2D\left( {\frac{\theta }{{m_{1} }}} \right)^{2} $$

(29)

The values of 2nd derivative moments are equal to zero except ${b}_{33}$. The definitions of all the characters are the same as those in Sect. 2.

Consider the system has reached a steady state, which indicates that the value of $\frac{\partial p}{{\partial t}}$ is 0. The FPK equation of the system Eq. (24) can be rewritten as:

$$ \frac{\partial }{{\partial q_{1} }}\left( {a_{1} p} \right) + \frac{\partial }{{\partial q_{2} }}\left( {a_{2} p} \right) + \frac{\partial }{{\partial q_{3} }}\left( {a_{3} p} \right) + \frac{\partial }{{\partial q_{4} }}\left( {a_{4} p} \right) - \frac{1}{2}\frac{{\partial^{2} }}{{\partial q_{3}^{2} }}\left( {b_{33} p} \right) = 0 $$

(30)

The finite difference method is used to solve Eq. (30) and the values of all the parameters are listed in Table 2. The difference area and the interval are as follows:

$$ \left\{ {\begin{array}{*{20}l} { - 0.08 \le q_{1} \le 0.08,} \hfill & {\Delta q_{1} = 0.001} \hfill \\ { - 0.003 \le q_{2} \le 0.004,} \hfill & {\Delta q_{2} = 0.001} \hfill \\ { - 1.5 \le q_{3} \le 1.5,} \hfill & {\Delta q_{3} = 0.1} \hfill \\ { - 0.15 \le q_{4} \le 0.15,} \hfill & {\Delta q_{4} = 0.01} \hfill \\ \end{array} } \right. $$

Table 2 Parameters for numerical validation

Use a 4th order precision scheme for the simulation:

$$ \left( {\frac{\partial f}{{\partial x_{i} }}} \right)_{n} = \frac{{8\left( {f_{n + 1} - f_{n - 1} } \right) - \left( {f_{n + 2} - f_{n - 2} } \right)}}{{12\Delta x_{i} }} $$

(31)

$$ \left( {\frac{{\partial^{2} f}}{{\partial x_{i}^{2} }}} \right)_{n} = \frac{{16\left( {f_{n + 1} + f_{n - 1} } \right) - \left( {f_{n + 2} + f_{n - 2} } \right) - 30f_{n} }}{{12\left( {\Delta x_{i} } \right)^{2} }} $$

(32)

where $f$ is the function to be solved, $x_{i}$ is the independent variable, and $\Delta x_{i}$ is the difference interval related to $x_{i}$. The solution region of $x_{i}$ is divided by $\Delta x_{i}$, and the value of function or parameters at the discrete point $\left( {x_{i} } \right)_{n}$ in n^th grid is written as $\left( \cdot \right)_{n}$.

Moreover, the SOR iterative method is also used for the update of discrete variables:

$$ p_{i,j,m,n}^{k + 1} = sp_{i,j,m,n}^{*} + \left( {1 - s} \right)p_{i,j,m,n}^{k} $$

(33)

The $\left[ {i,j,m,n} \right]$ in Eq. (33) are the discrete labels of $\left[ {q_{1} ,q_{2} ,q_{3} ,q_{4} } \right]$, respectively. $\left( \cdot \right)^{k}$ is the function/parameters value in the kth iteration. $\left( \cdot \right)^{*}$ represents the intermediate value between the kth iterative result and (k + 1)th iterative result, which is calculated by the fourth-order precision scheme above. $s$ is the relaxation factor, which is set as $2 \times 10^{ - 5}$ in the simulation.

The initial value of the iteration is a uniform distribution $p = 0.0001$. In the process of simulation, $p$ less than 0 is set to 0 and the iteration results are normalized every 10 steps for the purpose of improving the convergence rate. After about 10 million iterations, the numerical result of $p$ is obtained. By integrating the joint probability density function $p$ with respect to ${ }\left[ {q_{2} ,q_{3} ,q_{4} } \right]$, the displacement probability density function $p_{x}$ of the motion of $m_{1}$ on the x-axis can be obtained. Besides, using the IEM method described in Sect. 2.4 under the same parameters, the other simulation result for comparison is got. In order to possess the steady-state stochastic response of the actuators under IEM method, the simulation spans 2000s with interval 0.0002 s, and data of the later 1000 s is used for further analysis. Figure 2 shows the results under these two methods, it is easily found that the curves fit with each other well. Thus, the validity of IEM method is approved. Additionally, considering that the finite-difference method requires a large amount of computing resources and much time to achieve the required accuracy, it is not chosen for the simulation in this paper.

Fig. 2

The simulation results of the Finite Difference method and IEM method

3.2 Experimental validation

In this part, swept harmonic signals are used to experimentally validate the actuator mathematical model. Both the Gaussian white noise signals and low-pass filtered stochastic noise are utilized to verify the numerical solutions of the SDEs.

3.2.1 The experimental setup

The EB-bistable actuator prototype is shown in Fig. 3 and the whole experiment process is shown in Fig. 4. The foundation of the EB-bistable actuator prototype is mounted on a workshop table. A programmable function generator (NI PXIe-1082) is used to produce the control voltage signals, which are then transformed into the current signals by a digital power amplifier with a ratio 1 V: 0.42 A. The current signals are input into the EB-bistable actuator’s coil, leading to vibration actuation of the actuator. The accelerometer installed on the actuator mover acquires the vibration accelerations and passes the data to the NI equipment. Finally, the acceleration data is recorded in the computer.

Fig. 3

The EB-bistable actuator prototype

Fig. 4

The experiment process

The prototype parameters identified by experiments are shown in Table 3. For example, the parameters in Table 3 are obtained as follows: the mover mass and the joint mass are measured using an electronic balance; spring stiffness are obtained by measuring their static deformations when supporting a unit mass (1 kg). The electromechanical coupling is equal to the static input current divided by the force of the actuator mover. The static input current is produced by a direct current source, and force is measured by a force sensor. The damping ratios are estimated through parameter identification where only the linear vibration response has been activated using the small-amplitude excitation.

Table 3 The parameters of the EB-bistable actuator

3.2.2 The experiment validation of the mathematical model

This section uses the swept harmonic signals to experimentally validate the actuator mathematical model. The experimental parameters are listed in Table 3. Figure 5 shows both the experimental and numerical results of the EB-actuator under the forward and backward swept harmonic input current signals with different amplitudes [0.168, 0.210] A. The swept frequency range is from 0.1 to 12 Hz and the sweeping time is 200 s. The numerical results with respect to the swept harmonic signals are obtained by integrating Eqs. (7) and (8) directly with the fourth-order Runge–Kutta method. Results show that both the experimental and numerical results are in good agreement, which validates the mathematical model.

Fig. 5

Experimental and numerical results of the EB-actuator under the forward and backward swept harmonic input current signals

3.2.3 Experiment validation of numerical solutions of the SDEs

Figure 6 shows both the numerical and experimental results of the power spectrum density (PSD) of the EB-actuator under the Gaussian white noise signals with different strengths $2{\text{D}} = \left[ {{ }2.54, \,3.46, \,4.52{ }} \right]\, \times \,10^{ - 4}$ ${\text{A}}^{2} /{\text{Hz}}$. It is seen that, along with the increase of the strength $2{\text{D}}$, the numerically predicted PSD is increased, which agrees well with the experimental results. For the three strengths, the maxima of the PSD are around 4 Hz and the PSD curve decreases for the higher frequency, which also agrees well with the experimental findings.

Fig. 6

Numerical and experimental PSD results of the EB-bistable actuator under the Gaussian white noise signals with different strengths

As shown in Sect. 2.3, the low-pass filtered stochastic signal has another three filter parameters: filter gain $G_{0}$, filter loss factor $\eta$, and filter’s natural frequency $\omega_{0}$. In the experiment, $\eta = 1.414$, and strength $2{\text{D}} = 8.82 \times 10^{ - 5} \,{\text{A}}^{2} /{\text{Hz}}$.

Figure 7 shows both the numerical and experimental results of the EB-bistable actuator PSD under the low-pass filtered stochastic signals for different filter gains $G_{0} = \left[ {2.2, \,2.4, \,2.6} \right]$, where the filter’s natural frequency $\omega_{0} =$ 100 rad/s ($15.92$ Hz). It is also seen that both the numerical and experimental results are in good agreement in terms of the variation trends with respect to the $G_{0}$ in the wide frequency band. Additionally, Fig. 8 shows the EB-bistable actuator’s PSD under the low-pass filtered stochastic signals for different filter natural frequencies $\omega_{0} = \left[ {50, 100, 150} \right]$ rad/s $\left( {\left[ {7.96, 15.92, 23.89} \right]\, {\text{Hz}}} \right)$, where $G_{0} = 2.5$. Both the numerical and experimental results show that, in the lower frequency band (2–6 Hz), the three PSD curves are close. However, in the higher frequency (> 6 Hz), the PSD decreases more sharply for the $\omega_{0} = 50{\text{ rad}}/{\text{s}}$ ($7.96$ Hz) than the other two cases. This is because the low-pass filter with the smaller $\omega_{0}$ shortens the passing band of the input energy. Therefore, it attenuates more input energy in the higher frequency.

Fig. 7

Numerical and experimental PSD results of the EB-bistable actuator under low-pass filtered stochastic signals for $G_{0} = \left[ {2.2, 2.4, 2.6} \right]$, where $\omega_{0} = 100{\text{ rad}}/{\text{s}}$ ($15.92$ Hz)

Fig. 8

Numerical and experimental PSD results of the EB-bistable actuator under low-pass filtered stochastic signals for $\omega_{0} = \left[ {50, 100, 150} \right]{\text{ rad}}/{\text{s}}$ $(\left[ {7.96, 15.92, 23.89} \right] {\text{Hz}}$), where $G_{0} = 2.5$

Overall, both the above results in Fig. 2 and experimental results in Figs. 5, 6, 7 and 8 validate the numerical predictions of the stochastic responses and the mathematical model of the nonlinear actuator, despite some discrepancies. There are many possible sources of the discrepancies. For example, the bias between the experimental excitation and numerical analysis and the errors between the experimental prototype and the mathematical model will lead to the discrepancies between the numerical curves and experimental curves. Besides, the high-frequency component of the excitation from an open-loop exciter and the background noise of the accelerometer and acquisition system may cause the errors of the results in the higher frequency band.

4 Performance comparison

To show the advancement of the EB-bistable actuator under the stochastic control signals, in this section, performance comparisons between the proposed EB-bistable actuator, the bistable electromagnetic actuator with fixed boundary (the FB-bistable actuator), and the traditional linear actuator are presented.

4.1 Description of the counterparts

Figure 9a and b shows schematics of the FB-bistable actuator and the traditional linear actuator. The FB-bistable actuator has a mover mass $m_{1}$ on a linear track embedded with permanent magnets and an oblique string with stiffness $k_{1}$ which connects the mover mass and the frame. When a stochastic current $i$ is fed into the coil in the mover’s mass $m_{1}$, the electromagnetic force $F = \theta i$ will act on the mover. The difference between FB-bistable and EB-bistable actuators is that one end of the oblique spring of the FB-bistable actuator is fixed on the frame. For a meaningful comparison, the linear counterpart is modeled as follows. When the amplitude of input signal $i$ is very small, the mover of the FB-bistable actuator would oscillate around one of its stable equilibrium points, exhibiting small oscillations. In that case, the nonlinearity can be ignored and the FB-bistable will act nearly as a linear actuator. As a result, the linear actuator shown in Fig. 9b is defined as the linearization of the FB-bistable actuator around one of the stable equilibria. The mover mass $m_{1}$ is on a linear track embedded with permanent magnets, and the linear spring with stiffness $k_{l}$ connects the mover mass and the frame, which satisfies $k_{l} = k_{1} \left( {1 - \frac{{d^{2} }}{{L_{1}^{2} }}} \right).{ }$

Fig. 9

The schematics of a The FB-bistable actuator and b Linear actuator

Define $x$ as the displacement of the movers deviating from the centerline and assume the linear damping coefficient in $x$-direction is $c_{1}$. For the FB-bistable actuator, the system’s governing equation is:

$$ m_{1} \ddot{x} + c_{1} \dot{x} + k_{1} \left( {1 - \frac{{L_{1} }}{{\sqrt {d^{2} + x^{2} } }}} \right)x = \theta i $$

(34)

Using the same definition of the parameters shown in Table 1, the governing equation of the FB-bistable actuator is normalized as follows:

$$ \ddot{x} + \eta_{1} \omega_{1} \dot{x} + \omega_{1}^{2} \left( {1 - \frac{\alpha d}{{\sqrt {d^{2} + x^{2} } }}} \right)x = \beta i $$

(35)

The governing equation of the linear actuator is:

$$ m_{1} \ddot{x} + c_{1} \dot{x} + k_{1} \left( {1 - \frac{{d^{2} }}{{L_{1}^{2} }}} \right)x = \theta i $$

(36)

The normalized governing equation of the linear actuator is:

$$ \ddot{x} + \eta_{1} \omega_{1} \dot{x} + {\upomega }_{1}^{2} \left( {1 - \frac{1}{{\alpha^{2} }}} \right)x = \beta i $$

(37)

Firstly, consider the input current $i$ is the Gaussian white noise $W\left(t\right)$ described as Sect. 2.2, and define $\left[{Q}_{1},{Q}_{2}\right]=[x,\dot{x}]$ as the random variables. The SDEs of the FB-bistable actuator can be derived according to Eq. (35) as follows:

$$ dQ_{1} = Q_{2} dt $$

(38)

$$ dQ_{2} = \beta \cdot dB\left( t \right) - \left( {\eta_{1} \omega_{1} Q_{2} + \omega_{1}^{2} \left( {1 - \frac{\alpha d}{{\sqrt {d^{2} + Q_{1}^{2} } }}} \right)Q_{1} } \right)dt $$

(39)

According to Eq. (37), the SDEs of the linear actuator can be expressed as follows:

$$ dQ_{1} = Q_{2} dt $$

(40)

$$ dQ_{2} = \beta \cdot dB\left( t \right) - \left( {\eta_{1} \omega_{1} Q_{2} + \omega_{1}^{2} \left( {1 - \frac{1}{{\alpha^{2} }}} \right)Q_{1} } \right)dt $$

(41)

Besides, consider the input signal is a low-pass filtered stochastic noise shown as Sect. 2.3, and define $\left[{Q}_{1},{Q}_{2}\right]=[x,\dot{x}]$. ${Q}_{3}$ and ${Q}_{4}$ are the low-pass filtered stochastic noise and its differential. The SDEs of the FB-bistable actuator can be expressed as follows:

$$ dQ_{1} = Q_{2} dt $$

(42)

$$ dQ_{2} = \beta Q_{3} dt - \left( {\eta_{1} \omega_{1} Q_{2} + \omega_{1}^{2} \left( {1 - \frac{\alpha d}{{\sqrt {d^{2} + Q_{1}^{2} } }}} \right)Q_{1} } \right)dt $$

(43)

$$ dQ_{3} = Q_{4} dt $$

(44)

$$ dQ_{4} = G_{0} \omega_{0}^{2} \cdot d{\text{B}}\left( t \right) - \left( {\eta \omega_{0} Q_{4} + \omega_{0}^{2} Q_{3} } \right)dt $$

(45)

The SDEs of the linear actuator can be expressed as follows:

$$ dQ_{1} = Q_{2} dt $$

(46)

$$ dQ_{2} = \beta Q_{3} dt - \left( {\eta_{1} \omega_{1} Q_{2} + \omega_{1}^{2} \left( {1 - \frac{1}{{\alpha^{2} }}} \right)Q_{1} } \right)dt $$

(47)

$$ dQ_{3} = Q_{4} dt $$

(48)

$$ dQ_{4} = G_{0} \omega_{0}^{2} \cdot dB\left( t \right) - \left( {\eta \omega_{0} Q_{4} + \omega_{0}^{2} Q_{3} } \right)dt $$

(49)

4.2 Performance comparisons under Gaussian white noise signals

To prove the superiority of the EB-bistable actuator under Gaussian white noise, two sets of parameters listed in Table 4 are used for simulations and comparisons in this section. Parameters of set 1 are mostly the same as the experimental parameters listed in Table 3 and parameters of set 2 are partly different from set 1. In order to achieve the steady-state stochastic response of the actuators, the simulation spans 2000 s with interval 0.0002 s, and data of the later 1000 s is used for further analysis. Additionally, 30 independent simulations set as above are performed for each investigated case and the averaging of these results is used as the final outcome. Thus, by estimation, the equivalent simulation time is over 120 thousand times of the system period, which has reached the demand of random analysis.

Table 4 the values of parameters for the comparison under white-noise signals

Figures 10, 11 and 12 show the probability density function (PDF) curves of displacement $x$ and the PSD curves of acceleration $\ddot{x}$ under different values of $\beta$ for the parameters in set 1. The displacement–time plots in the case of $\beta =10$ have been demonstrated in Fig. 10c and d.

Fig. 10

Comparison results when $\beta =10.00$, a the PDF curves b the PSD curves c the time history plot for the EB-bistable actuator, the inter-well oscillation is obvious d the time history plot for the FB-bistable actuator, the mover just moves around one of the equilibrium points

Fig. 11

Comparison results when $\beta =16.09$ a the PDF curves b the PSD curves

Fig. 12

Comparison results when $\beta =22.00$ a the PDF curves b the PSD curves

When $\beta =10$, the PDF curves in Fig. 10a indicate that the FB-bistable actuator only oscillates around one of its equilibrium points (i.e., intra-well oscillation) because only a single peak in the PDF curve is observed. Therefore, the PSD of the FB-bistable actuator is really close to that of the linear actuator, as shown in Fig. 10b. As for the EB-bistable actuator, its PDF has two peaks, implying that the mover ${m}_{1}$ can stochastically jump between two equilibrium points (i.e., inter-well response). With the increase of $\beta$, the mover in the FB-bistable actuator starts to vibrate from one equilibrium position to another, as shown in Figs. 11a and 12a. For further analysis, it should be pointed out that the value of the PDF at $x=0$ (expressed as $p\left(0\right)$) can indicate how easy it is for ${m}_{1}$ to move back and forth between the equilibrium points, i.e., inter-well oscillation probability. The easier it for the mover ${m}_{1}$ to manifest the inter-well response, the larger the $p\left(0\right)$ will be. It can be found that $p\left(0\right)$ of the EB-bistable actuator is obviously larger than that of the FB-bistable actuator when $\beta$ = 16.09 and 22.00. Time history results in the case of $\beta =10$ are presented in Fig. 10c and d to validate the above prediction from the PDF curves. It is seen that the EB-bistable actuator exhibits inter-well oscillation while the FB-bistable actuator exhibits the small-amplitude intra-well oscillation, which agrees well with the prediction of the PDF results. Consequently, the results show that the inter-well oscillation of the EB-bistable actuator can be activated easier than that of the FB-bistable actuator.

As shown in the PSD curves of Figs. 10b, 11b, 12b, those three actuators all have a single peak within the lower frequency band (0–10 Hz), but the peak of the EB-bistable actuator is the lowest one. Thus, the lost power in the lower frequency band (0–10 Hz) for the EB-bistable actuator is distributed to the higher frequency band and forms a new peak in the frequency band of 50–60 Hz. Quantitatively, for $\beta =[\mathrm{10.00,16.09,22.00}]$, the acceleration average power of ${m}_{1}$ is $\left[2.027\times {10}^{2}, 5.236\times {10}^{2}, 9.785\times {10}^{2}\right]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ for the EB-bistable actuator, respectively. As for the FB-bistable actuator, the average power is $[2.086\times {10}^{2}, 5.393\times {10}^{2}, 1.005\times {10}^{3}]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. For the linear actuator, the values of acceleration average power are $[2.089\times {10}^{2}, 5.405\times {10}^{2}, 1.010\times {10}^{3}]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$. The EB-bistable actuator has relatively smaller average power in these situations, but the difference is small.

The displacement variances of each actuator have also been calculated. For $\beta = \left[ {10.00,16.09,22.00} \right]$, the displacement variances of $m_{1}$ are $\left[ {1.062 \times 10^{ - 3} , 1.044 \times 10^{ - 3} , 1.025 \times 10^{ - 3} } \right]\,{\text{m}}^{2}$ for the EB-bistable actuator, respectively. For the FB-bistable actuator, the displacement variances are $\left[ {1.025 \times 10^{ - 5} , 7.833 \times 10^{ - 4} , 1.086 \times 10^{ - 3} } \right]\,{\text{m}}^{2}$, respectively. As for the linear actuator, the values of displacement variances are $\left[ {9.744 \times 10^{ - 6} , 2.492 \times 10^{ - 5} , 4.731 \times 10^{ - 5} } \right]\,{\text{m}}^{2}$, respectively. For $\beta = 10.00$, since the mover $m_{1}$ of the FB-bistable actuator just moves around one of its equilibrium points, the displacement variances of the FB-bistable actuator and linear actuator are close to each other. The displacement variance of the EB-bistable actuator is 103.61 times higher than that of the FB-bistable actuator and 108.99 times higher than that of the linear actuator in this case. When $\beta = 16.09$, the displacement variance of the EB-bistable actuator is 33.3% greater than that of the FB-bistable actuator and is 41.89 times higher than that of the linear actuator. As for the case $\beta = 22.00$, the displacement variance of the EB-bistable actuator is close to that of the FB-bistable actuator and is 21.67 times of that of the linear actuator.

Based on the comparison, the EB-bistable actuator can easily exhibit the large-amplitude inter-well oscillation and its acceleration average power is close to that of the other two counterparts in the investigated cases.

The parameters of set 2 are used to further reveal the benefit of the EB-bistable actuator controlled by stochastic signals. Figures 13a, 14a, and 15a show the PDF curves of the investigated cases and Figs. 13b, 14b, and 15b show the PSD curves of acceleration $\ddot{x}$ under different $\beta$.

Fig. 13

Comparison results when $\beta =15.00$ a the PDF curves b the PSD curves

Fig. 14

Comparison results when $\beta =20.00$ a the PDF curves b the PSD density curves

Fig. 15

Comparison results when $\upbeta =25.00$ a the PDF curves b the PSD curves

From the PDF curves in Figs. 13a and 14a, it is seen that $p\left(0\right)$ of the EB-bistable actuator is larger than that of the FB-bistable actuator. This phenomenon indicates that the EB-bistable actuator can perform inter-well oscillation more easily than the FB-bistable actuator for both $\beta =15$ and 20. When $\beta$ is increased to 25, $p\left(0\right)$ of the EB-bistable actuator and the FB-bistable actuator are close. In this case, the PDF curve of EB-bistable shows smaller probability density in the region around $x=0$ and larger probability density in the edges of the curves, comparing with that of the FB-bistable actuator. This result indicates that the EB-bistable actuator vibrates with a larger amplitude than the FB-bistable actuator when $\beta =25$. For quantitative comparison, the displacement variances values in each case are listed following the order of EB-bistable actuator, the FB-bistable actuator and linear actuator. When $\beta =15$, the values are $[1.210\times {10}^{-3}, 1.064\times {10}^{-3}, 1.612\times {10}^{-4}]\,{\mathrm{m}}^{2}$, respectively. For the case $\beta =20$, the displacement variances are $[1.392\times {10}^{-3},1.138\times {10}^{-3}, 2.902\times {10}^{-4}]\,{\mathrm{m}}^{2}$, respectively. As for $\beta =25$, the values are $[1.605\times {10}^{-3}, 1.263\times {10}^{-3},4.466\times {10}^{-4}]\,{\mathrm{m}}^{2}$, respectively. In these cases, the displacement variance of EB-bistable actuator is increased by 13.7%, 22.3% and 27.1% than that of the FB-bistable actuator and is 7.51, 4.80 and 3.59 times higher than that of the linear actuator, respectively.

From the acceleration PSD curves in Figs. 13b, 14b, and 15b, it can be easily noticed that there is one peak in the lower frequency band (0–10 Hz) and one peak in the higher frequency band (30–40 Hz) with close height for the EB-bistable actuator, while other two counterparts just have one peak in the lower frequency band (0–10 Hz). Through calculation, the acceleration average power of these three actuators has been got, the results are listed in the order of $\beta =[15, 20, 25]$. For the EB-bistable actuator, the acceleration average power is $[2.2696\times {10}^{4}, 4.0433\times {10}^{4}, 6.3345\times {10}^{4}]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. As for the FB-bistable actuator, the values are $[2.2709\times {10}^{4}, 4.0399\times {10}^{4}, 6.3204\times {10}^{4}]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. The acceleration average power of the linear actuator is $[2.2824\times {10}^{4}, 4.0573\times {10}^{4}, 6.3391\times {10}^{4}]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. Although the peaks of the EB-bistable actuator are lower than that of the other two actuators in the frequency band of 0–10 Hz, its acceleration average power is close to that of the other two actuators, since the difference has been compensated in the higher frequency band (30–40 Hz).

For better understanding, the main results of the comparison above have been listed in Table 5. According to the results comparison, it is seen that it becomes easier for the EB-bistable actuator to perform the large-amplitude stochastic inter-well oscillation than the FB-bistable actuator for the investigated parameters; the acceleration average power of the EB-bistable actuator is close to that of the other two counterparts in the investigated cases as well. These conclusions are identical to the previous part of this section.

Table 5 The main results of the performance comparison under Gaussian white noise signals

4.3 Performance comparisons under low-pass filtered stochastic noise

In this section, two sets of parameters are used to compare the responses under low-pass filtered stochastic noise. In parameters of set 1, the value of $[\beta , {G}_{0}, \eta ]$ are fixed as $[16.09, 1.00, 1.414]$, and different values of ${\omega }_{0}=\left[10, 50, 300\right]\,\mathrm{rad}/\mathrm{s}$ ($[1.59, 7.96, 47.75]$ Hz) are investigated. Other parameters are the same as the parameters in set 1 of Table 4. In parameters of set 2, $[\beta , {G}_{0}, \eta ]$ are taken as $[25.00, 1.00, 1.414]$, and ${\omega }_{0}=\left[10, 50, 300\right]\,\mathrm{rad}/\mathrm{s}$ ($[1.59, 7.96, 47.75]$ Hz) are investigated as well. Other parameters in this group are equal to the parameters of set 2 in Table 4.

Figures 16, 17 and 18 show the PDF curves and acceleration PSD plots of these three actuators under low-pass filtered stochastic noise for set 1. The displacement-time plots of the EB-bistable actuator and the FB-bistable actuator in the case ${\upomega }_{0}=10.00\,\mathrm{ rad}/\mathrm{s}$ (1.59 Hz) have also been shown in Fig. 16c and d.

Fig. 16

Comparison results when ${\omega }_{0}=10.00\,\mathrm{ rad}/\mathrm{s}$ (1.59 Hz), a the PDF curves b the PSD curves c the time history plot for the EB-bistable actuator, the inter-well oscillation is existed d the time history plot for the FB-bistable actuator, the mover just moves around one of the equilibrium points

Fig. 17

Comparison results when ${\omega }_{0}=50.00\,\mathrm{ rad}/\mathrm{s}$ (7.96 Hz), a the PDF curves b the PSD curves

Fig. 18

Comparison results when ${\omega }_{0}=300.00\,\mathrm{ rad}/\mathrm{s}$ (47.75 Hz), a the PDF curves b PSD curves

In Fig. 16a, the PDF curve of the FB-bistable actuator just has a single peak, indicating that the mover of the FB-bistable actuator exhibits intra-well oscillation when ${\upomega }_{0}=10.00\,\mathrm{ rad}/\mathrm{s}$ (1.59 Hz). Thus, the PSD curve of the FB-bistable actuator is really close to that of the linear actuator in this case. As for the EB-bistable actuator, there are two peaks in its PDF curve, indicating the appearance of the inter-well response under the condition of ${\upomega }_{0}=10.00\,\mathrm{ rad}/\mathrm{s}$ (1.59 Hz). This fact can also be concluded from the time history results shown in Fig. 16c and d. In Figs. 17a and 18a, the fact that there are two peaks in the PDF curves of the FB-bistable actuator means that ${m}_{1}$ will move back and forth between two equilibrium points when ${\upomega }_{0}$ is increased up to 50 rad/s (7.96 Hz) and 300 rad/s (47.75 Hz). However, the $p\left(0\right)$ of the FB-bistable actuator is obviously smaller than that of the EB-bistable actuator in these two cases. Besides, it should be known that the value of ${\omega }_{0}$ is actually the bandwidth of the filter when $\eta =1.414$. Thus, it is seen that the EB-bistable actuator exhibits inter-well oscillation more easily than the FB-bistable actuator under different bandwidths of the investigated cases.

Figure 16b shows that the peak of the EB-bistable actuator in the lower frequency band (0–10 Hz) is higher than that of the other two counterparts when ${\omega }_{0}=10\, \mathrm{rad}/\mathrm{s}$ (1.59 Hz). However, the performance becomes adverse when ${\omega }_{0}$ is increased up to 50 rad/s (7.96 Hz) and 300 rad/s (47.75 Hz). Although one peak exists in the higher frequency band (50-60 Hz) in each PSD curve of EB-bistable actuator for these three cases, they are really small due to the attenuation of the excitation in the higher frequency caused by the low-pass filter feature. For quantitative comparison, the acceleration average power of each actuator under different ${\omega }_{0}$ is calculated. For ${\omega }_{0}=\left[10, 50, 300\right]\,\mathrm{rad}/\mathrm{s}$($[1.59, 7.96, 47.75]$ Hz), the average power of ${m}_{1}$ are $[0.899, 6.668, 16.361]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ for the EB-bistable actuator, respectively. As for the FB-bistable actuator, the average power is $[0.248, 19.659, 32.193] {\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. For the linear actuator, the values of acceleration average power are $[0.239, 20.307, 34.062]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$. It can be noticed that the acceleration average power of the EB-bistable actuator is the largest when ${\upomega }_{0}=10.00\, \mathrm{rad}/\mathrm{s}$ (1.59 Hz). However, the increase of ${\omega }_{0}$ broadens the excitation bandwidth and the attenuation of the peaks in the lower frequency band (0–10 Hz) of the FB-bistable actuator and linear actuator gradually recedes, which results in the higher acceleration average power of the FB-bistable actuator and linear actuator comparing with that of the EB-bistable actuator. Thus, the quantitative results are identical to the comparison results of PSD curves.

The displacement variances of each actuator have also been calculated. For ${\omega }_{0}=\left[10, 50, 300\right]\, \mathrm{rad}/\mathrm{s}$ ($[1.59, 7.96, 47.75]$ Hz), the displacement variances of ${m}_{1}$ are $\left[8.224\times {10}^{-4}, 1.048\times {10}^{-3}, 1.041\times {10}^{-3}\right]\,{\mathrm{m}}^{2}$ for the EB-bistable actuator, respectively. For the FB-bistable actuator, the displacement variances are $\left[7.317\times {10}^{-7}, 5.199\times {10}^{-4}, 8.348\times {10}^{-4}\right]\,{\mathrm{m}}^{2}$, respectively. As for the linear actuator, the values are $\left[7.241\times {10}^{-7}, 2.161\times {10}^{-5}, 2.495\times {10}^{-5}\right]\,{\mathrm{m}}^{2}$. When ${\omega }_{0}=10 \,\mathrm{rad}/\mathrm{s}$ (1.59 Hz), the displacement variance of the EB-bistable actuator is 1126.69 times higher than that of the FB-bistable actuator and is 1138.52 times of that of the linear actuator. Since the FB-bistable actuator does not show inter-well oscillation in this case, its displacement variance is close to that of the linear actuator. In the case ${\omega }_{0}=50 \,\mathrm{rad}/\mathrm{s}$ (7.96 Hz), the displacement variance of the EB-bistable actuator is twice of the FB-bistable actuator displacement variance and 48.50 times of that of the linear actuator. For the case ${\omega }_{0}=300\, \mathrm{rad}/\mathrm{s}$ (47.75 Hz), the displacement variance of EB-bistable actuator is increased by 24.7% compared to that of the FB-bistable actuator and is 41.72 times of the linear actuator displacement variance.

The above results indicate that the large-amplitude inter-well oscillation is more easily activated for the EB-bistable actuator in this set of parameters, comparing with the FB-bistable actuator. Besides, the acceleration average power of the EB-bistable actuator under a low-pass filtered stochastic noise with a small filter’s natural frequency ${\omega }_{0}$ is the largest among the three actuators in the investigated cases.

Figures 19, 20 and 21 exhibit the PDF curves and acceleration PSD curves of the EB-bistable actuator and other two counterparts for comparison based on parameters from set 2. From the PDF curves in Figs. 19a and 20a, $p\left(0\right)$ of the EB-bistable actuator is obviously higher than that of the FB-bistable actuator in the cases of ${\omega }_{0}=10 \,\mathrm{rad}/\mathrm{s}$ (1.59 Hz) and ${\omega }_{0}=50\, \mathrm{rad}/\mathrm{s}$ (7.96 Hz). This indicates that the mover ${m}_{1}$ of the EB-bistable actuator is more likely to exhibit the inter-well oscillation, comparing with the FB-bistable actuator. When ${\omega }_{0}$ rises up to 300 rad/s (47.75 Hz), the $p\left(0\right)$ of EB-bistable actuator and FB-bistable actuator are close to each other. That is, the PDF curve of EB-bistable exhibits smaller probability density in the region around $x=0$ and larger probability density in the edges of the curve than the FB-bistable actuator in this case, which indicates that the EB-bistable actuator performs an oscillation with larger displacement amplitude than the FB-bistable actuator.

Fig. 19

Comparison results when ${\omega }_{0}=10.00\,\mathrm{ rad}/\mathrm{s}$ (1.59 Hz), a the PDF curves b the PSD curves

Fig. 20

Comparison results when ${\omega }_{0}=50.00\,\mathrm{ rad}/\mathrm{s}$ (7.96 Hz), a the PDF curves b the PSD curves

Fig. 21

Comparison results when ${\upomega }_{0}=300.00\,\mathrm{ rad}/\mathrm{s}$ (47.75 Hz), a the PDF curves b the PSD curves

From the acceleration PSD curves in Fig. 19b, it is noticed that the peak of the EB-bistable actuator in the lower frequency band (0–10 Hz) is higher than that of the other two counterparts when ${\omega }_{0}=10\, \mathrm{rad}/\mathrm{s}$ (1.59 Hz). Due to the low-pass filter feature, the peak of the EB-bistable actuator in the higher frequency band (30–40 Hz) is much lower than the peak in the lower frequency band (0–10 Hz). In the cases of ${\omega }_{0}=50\, \mathrm{rad}/\mathrm{s}$ (7.96 Hz) and ${\omega }_{0}=300\, \mathrm{rad}/\mathrm{s}$ (47.75 Hz), the linear actuator has the highest peak in the frequency band of 0–10 Hz, and the peak of the EB-bistable actuator is the lowest in this region. However, with the increase of ${\omega }_{0}$, the peak value of the EB-bistable actuator in the higher frequency band (30–40 Hz) gradually becomes close to the peak in the lower frequency band (0–10 Hz).

For quantitative comparison, the values of displacement variances and acceleration average power in each case are calculated and listed as follow. When ${\omega }_{0}=10\,\mathrm{rad}/\mathrm{s}$ (1.59 Hz), the acceleration average power and displacement variance of the EB-bistable actuator are 52.7743 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $1.339\times {10}^{-3} \,{\mathrm{m}}^{2}$, respectively. The values for the FB-bistable actuator are 38.1035 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $1.180\times {10}^{-3} \,{\mathrm{m}}^{2}$, respectively. As for the linear actuator, the values are 4.2294 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $2.242\times {10}^{-5}\, {\mathrm{m}}^{2}$. So, the acceleration average power of the EB-bistable actuator is 1.39 times of that of the FB-bistable actuator and 12.48 times of that of linear actuator in this case. And the displacement variance of EB-bistable actuator is increased by 13.5% relative to the FB-bistable actuator and is 59.72 times higher than that of the linear actuator when ${\omega }_{0}=10\, \mathrm{rad}/\mathrm{s}$. For ${\omega }_{0}=50\, \mathrm{rad}/\mathrm{s}$ (7.96 Hz), the acceleration average power and displacement variance of the EB-bistable actuator are 535.9074 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $1.517\times {10}^{-3} \,{\mathrm{m}}^{2}$, respectively. As for the FB-bistable actuator, the values are 694.9413 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $1.213\times {10}^{-3} \,{\mathrm{m}}^{2}$, respectively. For the linear actuator, the acceleration average power and displacement variance are 716.5257 ${\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $3.3720\times {10}^{-4}\, {\mathrm{m}}^{2}$, respectively. In this case, the attenuation of peaks in PSD curves for the FB-bistable actuator and linear actuator in the lower frequency band (0–10 Hz) has receded due to the increase of the filter bandwidth. However, the peak in the higher frequency band (30–40 Hz) of the EB-bistable actuator still has a serious attenuation, which cannot compensate for the difference of acceleration average power in the lower frequency band. Thus, the acceleration average power of the EB-bistable actuator is less than the FB-bistable actuator and linear actuator. However, its displacement variance is still the largest among these three actuators, increased by 25.1% than the FB-bistable actuator and 4.50 times of that of the linear actuator. In the case of ${\omega }_{0}=300 \,\mathrm{rad}/\mathrm{s}$ (47.75 Hz), the acceleration average power and displacement variance of the EB-bistable actuator are $2.1256\times {10}^{3} \,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}, 1.598\times {10}^{-3}{\mathrm{m}}^{2}$, respectively. For the FB-bistable actuator, the numbers are $2.1063\times {10}^{3} \,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $1.266\times {10}^{-3} \,{\mathrm{m}}^{2}$, respectively. For the linear actuator, the values are $2.2909\times {10}^{3} \,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and $4.534\times {10}^{-4} \,{\mathrm{m}}^{2}$, respectively. It is noticed that the acceleration average power of the EB-bistable actuator is close to that of the other two actuators in this case, since the attenuation of its peak of PSD curve in the higher frequency band (30–40 Hz) has receded. Its displacement variance is still the biggest among these three actuators, increased by 26.2% relative to the FB-bistable actuator and 3.52 times of that of the linear actuator.

For better understanding, the main results of the comparison in this section have been shown in Table 6. Overall, when controlled by the low-pass filtered stochastic noise, the EB-bistable actuator can perform large-amplitude inter-well oscillation more easily than the FB-bistable actuator in this set of parameters and its acceleration average power is obviously larger than that of the other two counterparts when ${\omega }_{0}$ is small.

Table 6 The main comparison results under the low-pass filtered stochastic noise

5 Parametric studies under Gaussian white noise signals

In order to understand how the structural properties influence the performance of EB-bistable actuator under Gaussian white noise excitation, three parameters are selected for parametric study: the mass ratio $\mu$, the oblique spring natural frequency ${\omega }_{1}$, and the linear spring natural frequency ${\omega }_{2}$, where $\beta$ is fixed to 15 in the simulations. Other parameters’ values are kept the same as in set 2 listed in Table 4. The PDF curves of displacement $x$ and the PSD curves of acceleration $\ddot{x}$ under different cases are plotted for analysis.

5.1 The influence of mass ratio ${\varvec{\mu}}$

The mass ratio $\mu =[1, 5, 10]$ are investigated to uncover its effect, where the oblique spring natural frequency and the linear spring natural frequency are fixed as $\left[{\omega }_{1}, {\omega }_{2}\right]=\left[90, 140\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[14.32, 22.28\right]$ Hz). Figure 22a, b shows the PDF curves and the PSD results of the investigated cases, respectively. From Fig. 22a, it is noticed that the value of $p\left(0\right)$ is being raised with the increase of mass ratio $\mu$, which indicates that it becomes easier for the mover ${m}_{1}$ to perform inter-well oscillation. From the PSD curves in Fig. 22b, the rising of $\mu$ will cause the decrease of the peak in the lower frequency band, and the increase of peak and peak’s frequency in the higher frequency band. For $\mu =[1, 5, 10]$, the acceleration average power is $\left[2.269\times {10}^{4}, 2.270\times {10}^{4},2.271\times {10}^{4}\right]\, {\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively, and the displacement variances are $\left[1.124\times {10}^{-3},1.230\times {10}^{-3}, 1.322\times {10}^{-3}\right] \,{\mathrm{m}}^{2}$, respectively. It is seen that the increase of $\mu$ can raise up the displacement amplitude and improve the inter-well oscillation probability, but may bring little influence on acceleration average power.

Fig. 22

Simulation results when $\mu =[1, 5, 10]$ a the PDF curves b the PSD curves

5.2 The influence of oblique spring natural frequency ${{\varvec{\omega}}}_{1}$

The oblique spring natural frequency ${\omega }_{1}$ is set as $\left[80, 90, 100\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[12.73, 14.32, 15.91\right]$ Hz) for simulation, where the mass ratio $\mu =5$ and the linear spring natural frequency ${\omega }_{2}$ = 140 rad/s (22.28 Hz). Figure 23a, b shows the PDF curves and the PSD results of the investigated cases, respectively. From the PDF curves in Fig. 23a, it is found that the increase of ${\omega }_{1}$ will decrease the value of $p\left(0\right)$ and make it harder for the mover ${m}_{1}$ to exhibit inter-well oscillation. This is because the increase of ${\omega }_{1}$ hints the enlargement of the restoring force produced by the spring ${k}_{1}$ in the same displacement from the centerline, which would hinder the mover ${m}_{1}$ to move across $x=0$. Besides, the PSD curves in Fig. 23b indicate that the rising of ${\omega }_{1}$ can slightly decrease the peak in the lower frequency and increase the peak and peak’s frequency in higher frequency. Quantitatively, for ${\omega }_{1}=\left[80, 90, 100\right] \,\mathrm{rad}/\mathrm{s}$, the acceleration average power is $\left[2.268\times {10}^{4}, 2.270\times {10}^{4},2.272\times {10}^{4}\right] \,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. The displacement variances are $\left[1.276\times {10}^{-3},1.222\times {10}^{-3}, 1.152\times {10}^{-3}\right]\,{ \mathrm{m}}^{2}$, respectively. In general, the rising of ${\omega }_{1}$ would make it harder for ${m}_{1}$ to perform inter-well oscillation, and decrease the displacement amplitude at the same time. However, it may not bring a big difference in the value of acceleration average power.

Fig. 23

Simulation results when ${\omega }_{1}=\left[80, 90, 100\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[12.73, 14.32, 15.91\right]$ Hz) a the PDF curves b the PSD curves

5.3 The influence of linear spring natural frequency ${{\varvec{\omega}}}_{2}$

The linear spring natural frequencies ${\omega }_{2}=\left[140, 200, 260\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[22.28, 31.83, 41.38\right]$ Hz) are studied, where $\mu =5$ and ${\omega }_{1}=90 \,\mathrm{rad}/\mathrm{s}$ (14.32 Hz). Fig. 24a, b show the PDF curves and the PSD results of the investigated cases, respectively. According to Fig. 24a, it is easily found that the changing trend of PDF curves when raising ${\omega }_{2}$ is the same as that of ${\omega }_{1}$. In other words, the larger the ${\omega }_{2}$, the harder for ${m}_{1}$ to perform inter-well oscillation. From the PSD curves in Fig. 24b, it is seen that the peak grows higher in the lower frequency band (0–10 Hz) and the peak in the higher frequency band drops when ${\omega }_{2}$ becomes larger. The peak’s frequency in the higher frequency band also gets larger with the growth of ${\omega }_{2}$. The acceleration average power in these cases is $\left[2.270\times {10}^{4}, 2.265\times {10}^{4},2.265\times {10}^{4}\right] \,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. A slight increase is observed in the average power when ${\omega }_{2}$ getting larger. The displacement variances are $\left[1.199\times {10}^{-3},1.127\times {10}^{-3}, 1.081\times {10}^{-3}\right]\, {\mathrm{m}}^{2}$, respectively. That is, the increase of ${\omega }_{2}$ would decrease the displacement amplitude as well as the acceleration average power, and makes it harder for EB-bistable actuator to perform inter-well oscillation. The results may be relative to the fact that larger the ${\omega }_{2}$ is, more similar the EB-bistable actuator is to the FB-bistable actuator, since the FB-bistable actuator can be equivalent to the EB-bistable actuator with infinite ${\omega }_{2}$. More specifically, the equilibrium points of the FB-bistable actuator are calculated by Eq. (35) by letting all the time derivative terms and the input signal $i$ to be zero as $x_{{{\text{eq}}}}^{\prime } = \pm \sqrt {\left( {\alpha^{2} d^{2} - d^{2} } \right)}$. It is noticed that the equilibrium points $x_{{{\text{eq}}}}$ of the EB-bistable actuator described as Eq. (9) become the same as $x_{{{\text{eq}}}}^{\prime }$ when $\omega_{2}$ is set to infinite.

Fig. 24

Simulation results when ${\omega }_{2}=\left[140, 200, 260\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[22.28, 31.83, 41.38\right]$ Hz) a the PDF curves b the PSD curves

6 Parametric studies under low-pass filtered stochastic noise

To develop insights into the influence of filter property and structural property under low-pass filtered stochastic noise, two excitation parameters and three structural parameters are selected to performing the parametric study. The PDF curves of displacement $x$ and the PSD curves of acceleration $\ddot{x}$ under different situations are used for analysis as well.

6.1 Excitation parameters

The filter gain ${G}_{0}$ and filter’s natural frequency ${\omega }_{0}$ are chosen for further analysis in this part. The filter loss factor $\eta$ and the normalized electromagnetic couplings $\beta$ are set as $\left[\eta , \beta \right]=[1.414, 25]$. The values of other parameters are the same as parameters of set 2 in Table 4.

6.1.1 The influence of filter gain ${{\varvec{G}}}_{0}$

In this part, the filter gain ${G}_{0}$ is set as $[1.0, 1.5, 2.0]$ to explore its effect, where the filter’s natural frequency ${\omega }_{0}$ is fixed as 10 rad/s (1.59 Hz). Figure 25 a, b exhibits the PDF curves and the PSD results of the investigated cases, respectively.

Fig. 25

Simulation results when ${G}_{0}=[1.0, 1.5, 2.0]$ a the PDF curves b the PSD curves

From the PDF curves in Fig. 25a, it is observed that the value of $p\left(0\right)$ does not change a lot with the increase of ${G}_{0}$, which indicates that the value of ${G}_{0}$ may not influence the appearance probability of inter-well oscillation a lot in this set of parameters. This is probably because of the restrain of peaks in the PSD curves due to the small filter’s natural frequency ${\omega }_{0}$ in this case. The conjecture above will be verified in the next section. Besides, the distance between two peaks in the PDF curve becomes larger and the curve also gets ‘broader’ with the increase of ${G}_{0}$, hinting the increase of displacement amplitude. From the PSD curves in Fig. 25b, it is noticed that the increase of ${G}_{0}$ will raise the curves as a whole. Quantitatively, for ${G}_{0}=[1.0, 1.5, 2.0]$, the acceleration average power is $[52.882, 111.642, 182.554]\,\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and the displacement variances are $\left[1.337\times {10}^{-3},1.520\times {10}^{-3}, 1.683\times {10}^{-3}\right]\,{\mathrm{m}}^{2}$, respectively. Based on the results above, it is seen that the increase of ${G}_{0}$ can raise the acceleration average power and displacement amplitude, but it would not improve the inter-well oscillation probability under the investigated set of parameters.

6.1.2 The influence of filter’s natural frequency ${{\varvec{\omega}}}_{0}$

In this section, the filter’s natural frequency ${\omega }_{0}$ is set as $\left[10, 20, 50\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[1.59, 3.18, 7.96\right]$ Hz) to explore its effect, where the filter gain ${G}_{0}$ is fixed as 1. Figure 26a and b presents the PDF curves and the PSD results of the investigated cases, respectively.

Fig. 26

Simulation results when ${\omega }_{0}=\left[10, 20, 50\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[1.59, 3.18, 7.96\right]$ Hz) a the PDF curves b the PSD curves

The PDF curves in Fig. 26a indicating that the rising of ${\omega }_{0}$ will increase the value of $p\left(0\right)$ and make the curves flatter. Besides, as shown in Fig. 26b, the PSD curve would also rise up when ${\omega }_{0}$ getting larger. Quantitatively, the acceleration average power in the order of ${\omega }_{0}=\left[10, 20, 50\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[1.59, 3.18, 7.96\right]$ Hz) is $[52.882, 174.820, 533.691]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$, respectively. The displacement variances are $\left[1.337\times {10}^{-3},1.377\times {10}^{-3}, 1.511\times {10}^{-3}\right]\,{\mathrm{m}}^{2}$, respectively. Based on the results above, it is seen that the increase of ${\omega }_{0}$ can obviously enlarge the acceleration average power. It would also improve the inter-well oscillation probability and rise up the displacement amplitude of mover ${m}_{1}$.

6.2 Structural parameters

The mass ratio $\mu$, the oblique spring natural frequency ${\omega }_{1}$ and the linear spring natural frequency ${\omega }_{2}$ are selected for parametric study in this part. The values of $[ \beta , {G}_{0}, \eta , {\omega }_{0}]$ are fixed as $[25, 1, 1.414, 10]$. Other parameters are the same as parameters of set 2 in Table 4.

6.2.1 The influence of mass ratio ${\varvec{\mu}}$

Firstly, the mass ratio is set as $\mu =[1, 5, 10]$ to explore its influence on the actuator’s performance, where the oblique spring natural frequency and the linear spring natural frequency are fixed as $\left[{\omega }_{1}, {\omega }_{2}\right]=\left[90, 140\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[14.32, 22.28\right]$ Hz) in this section. Figure 27a, b presents the PDF curves and the PSD results of the investigated cases, respectively.

Fig. 27

Simulation results when $\mu =[1, 5, 10]$ a the PDF curves b the PSD curves

From the PDF curves in Fig. 27a, it is noticed that the value of $p\left(0\right)$ is rising with the increase of mass ratio $\mu$, which indicates that it becomes easier for the mover ${m}_{1}$ to perform inter-well oscillation. From the PSD curves in Fig. 27b, it is seen that the rising of $\mu$ will cause the increase of peak’s frequency in the higher frequency band. By calculation, the acceleration average power for $\mu =[1, 5, 10]$ is $[49.934, 52.882, 48.521]{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and the displacement variances are $\left[1.243\times {10}^{-3},1.337\times {10}^{-3}, 1.486\times {10}^{-3}\right]\,{\mathrm{m}}^{2}$, respectively. It is noticed that the increase of $\mu$ would raise the displacement amplitude and improve the inter-well oscillation probability, but may bring little influence on acceleration average power. These results are similar to the conclusion in Sect. 5.1.

6.2.2 The influence of oblique spring natural frequency ${{\varvec{\omega}}}_{1}$

In this section, the oblique spring natural frequency ${\omega }_{1}$ is set as $\left[80, 90, 100\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[12.73, 14.32, 15.91\right]$ Hz) to develop the insight of its effect, where the mass ratio $\mu$ is fixed as 5 and the linear spring natural frequency ${\omega }_{2}$ is set to 140 rad/s. Figure 28a, b exhibits the PDF curves and the PSD plots of the investigated cases, respectively.

Fig. 28

Simulation results when ${\omega }_{1}=\left[80, 90, 100\right] \,rad/s$ ($\left[12.73, 14.32, 15.91\right]$ Hz) a the PDF curves b the PSD curves

From the PDF curves in Fig. 28a, it is noticed that the growing of ${\omega }_{1}$ would slightly decrease the value of $p\left(0\right)$ and make it harder for the mover ${m}_{1}$ to vibrate from one equilibrium point to the other one. This is the same as the result in Sect. 5.2, which can be explained by the same reason. The PSD curves in Fig. 28b indicate that the increase of ${\omega }_{1}$ can slightly decrease the peak in the lower frequency and raise up the peak’s frequency in the higher frequency. Quantitatively, for ${\omega }_{1}=\left[\mathrm{80,90,100}\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[12.73, 14.32, 15.91\right]$ Hz), the acceleration average power is $[59.316, 52.882, 47.279]\,{\mathrm{m}}^{2}/{\mathrm{s}}^{4}$ and the displacement variances are $\left[1.371\times {10}^{-3},1.337\times {10}^{-3}, 1.307\times {10}^{-3}\right]\,{ \mathrm{m}}^{2}$, respectively. Based on the results above, the rising of ${\omega }_{1}$ can make it harder for ${m}_{1}$ to exhibit inter-well oscillation, and decrease the displacement amplitude. Besides, the acceleration average power will decrease when ${\omega }_{1}$ getting larger. This phenomenon may be caused by the severe attenuation of the peak in the higher frequency due to the small filter’s natural frequency in the simulation cases. Thus, the loss of average power in the lower frequency band cannot be compensated from the higher frequency band, and the acceleration average power will get less when ${\omega }_{1}$ becoming larger.

6.2.3 The influence of linear spring natural frequency ${{\varvec{\omega}}}_{2}$

In this section, the linear spring natural frequency is set as ${\omega }_{2}=\left[140, 200, 260\right]\, \mathrm{rad}/\mathrm{s}$ ($\left[22.28, 31.83, 41.38\right]$ Hz) to figure out its effect, where the mass ratio is fixed as $\mu =5$ and the oblique spring natural frequency is set to ${\omega }_{1}=90 \,\mathrm{rad}/\mathrm{s}$ (14.32 Hz). Figure 29a and b shows the PDF results and the PSD curves of the investigated cases, respectively.

Fig. 29

Simulation results when ${\omega }_{2}=\left[140, 200, 260\right] \,\mathrm{rad}/\mathrm{s}$ ($\left[22.28, 31.83, 41.38\right]$ Hz) a the PDF curves b the PSD curves

According to Fig. 29a, it is easily found that the changing trend of PDF curves when raising ${\omega }_{2}$ is the same as that of ${\omega }_{1}$ in Sect. 6.2.2. In other words, the larger the ${\omega }_{2}$ is, the harder it is for ${m}_{1}$ to perform inter-well oscillation. Besides, the distance between two peaks in the PDF curve seems to become slightly shorter when ${\omega }_{2}$ getting larger since the equilibrium points are described as ${x}_{\mathrm{eq}}=\pm \sqrt{\left({\alpha }^{2}{d}^{2}-{\left(d-\frac{g}{{\omega }_{2}^{2}}\right)}^{2}\right)}$. From Fig. 29b, it is seen that the peak in the lower frequency band (0–10 Hz) slightly grows higher while the peak in the higher frequency band falls down and even nearly disappears in the end when ${\omega }_{2}$ becomes larger. The peak’s frequency in the higher frequency band also gets larger with the growth of ${\omega }_{2}$. These facts all indicate that the EB-bistable actuator is converging to the FB-bistable actuator with the increase of ${\omega }_{2}$. Quantitatively, the acceleration average power in these cases is $[52.882, 56.068,54.866]{m}^{2}/{s}^{4}$ and the displacement variances are $\left[1.337\times {10}^{-3},1.243\times {10}^{-3}, 1.217\times {10}^{-3}\right]{\mathrm{m}}^{2}$, respectively. In all, the increase of ${\omega }_{2}$ will decrease the displacement amplitude and makes it harder for the EB-bistable actuator to perform inter-well oscillation. Its influence on acceleration average power is not evident in these cases.

7 Conclusion

This paper comprehensively investigates the stochastic responses of the bistable actuator with elastic boundary (EB-bistable actuator) under Gaussian white noise and low-pass filtered stochastic noise. To validate the advantages of the EB-bistable actuator for stochastic vibration actuation, the study performs the comparison of the EB-bistable actuator, the bistable actuator with the fixed boundary (the FB-bistable actuator) and the linear actuator. Through the experimental and numerical studies, the following key findings are demonstrated:

• (1) Under the Gaussian white noise, it is easier for the EB-bistable actuator to perform large-amplitude stochastic inter-well oscillation than for the FB-bistable actuator and the displacement amplitude of EB-bistable actuator is obviously larger than that of the linear actuator in the investigated cases. The acceleration average power of the EB-bistable actuator is close to that of other two actuators for some specific values of the parameters. When the low-pass filtered stochastic excitation is used, it is seen that it is still easier to activate the large-amplitude stochastic inter-well oscillation for the EB-bistable actuator than for the FB-bistable actuator and the displacement amplitude of the EB-bistable actuator is still obviously larger than that of the linear actuator in the investigated cases. Moreover, the acceleration average power of the EB-bistable actuator controlled by the low-pass filtered stochastic noise with a small filter’s natural frequency is the largest among these three actuators.

• (2) The parametric studies show that when controlled by the Gaussian white noise, for the considered set of parameters, the larger mass ratio $\mu$, the larger the inter-well oscillation probability and the response amplitude. Larger ${\omega }_{1}$ and ${\omega }_{2}$ degrades the dynamic performance of the EB-bistable actuator by hindering its inter-well oscillation and decreasing its response amplitude. All of the three parameters have little influence on the acceleration average power. The parametric study of the actuator controlled by the low-pass filtered stochastic noise has shown nearly the same trends of the actuation displacement as observed in the cases of the Gaussian-white-noise-signal cases in terms of the three structural parameters. However, the increase of ${\omega }_{1}$ will decrease the acceleration average power of the EB-bistable actuator under the low-pass filtered stochastic noise. Moreover, the increase of the filter gain ${G}_{0}$ improves the acceleration average power and displacement amplitude of the actuator, but may have limited influence on the inter-well oscillation probability. However, the increase of filter’s natural frequency ${\omega }_{0}$ will raise the acceleration average power, displacement amplitude, and enlarge the inter-well oscillation probability at the same time.