1 Introduction

In a companion paper [1], we developed two wave-based methods for predicting the nonlinear vibration response of jointed, continuous elastic bars. These methods consist of a nonlinear wave-based vibration approach (WBVA) informed by re-usable, perturbation-derived scattering functions, and a numerical plane wave expansion (PWE) approach exploiting wave solutions as expansion quantities. Both approaches were applied to finding periodic solutions in example systems in which continuous bars, connected by nonlinear joints, are constrained at their ends and harmonically excited. As documented in [1], the two approaches exhibit very good accuracy while significantly reducing the computation time required to obtain periodic solutions. They are also notable for having fixed problem size, independent of frequency. Arguably, stability of the periodic solutions predicted is as important as the solutions themselves. In [1] we report stability results for the examples studied using two new stability methods, which we deferred discussion of until the present paper.

Direct methods for assessing stability of wave-based solutions have not been presented in the literature, the necessity of which has been stated in recent studies (see, for instance [2, 3]). When stability has been treated, previous studies, owing to a lack of alternatives, have chosen to project the wave-based solution onto a finite element mesh and then use time-domain monodromy matrix calculations to estimate stability. Although this approach is very attractive owing to its simplicity, it leads to inaccuracies at larger amplitudes, which we document in Appendix A. In this paper, we assess stability of the multi-harmonic periodic solutions found in [1] using two new approaches: a strained parameter, analytical method applied to the governing partial differential equations based loosely on the technique as applied to parametrically excited ordinary differential equations [4], and a computational method employing the residue of the perturbed system’s eigenvalue problem. Both are informed by Floquet theory. Floquet theory (see [4]) provides the theoretical basis for the fact that stability transitions of a system perturbed around a periodic solution occur when the perturbed system has a purely imaginary eigenvalue with magnitude equaling an integer multiple of the frequency of the response (among other cases, see Sect. 3 below). Detection of such points along a forced response curve, as opposed to a complete spectral decomposition of the perturbed system for each response on the curve (such as the HBM perturbation approach in [5]), underpins both proposed approaches. In the strained parameter approach we find stability tongues in the parameter space distinguishing stable and unstable solutions, while in the perturbed eigenproblem residue approach we employ Floquet theory to find changes in the computed residues which indicate a stability transition.

The paper is organized as follows: we first develop an analytical, wave-based stability approach based on straining a single stiffness parameter in Sect. 2. This strained parameter approach yields stability curves (i.e., Arnold tongues) and surfaces associated with a parametrically excited continuous system. Next, in Sect. 3 we develop a computational approach termed the perturbation eigenproblem residue (PER) for predicting stability changes in the forced problem. In Sect. 4 we apply both methods to determine the stability of the two example systems studied in [1]. The paper concludes with discussions of the results and avenues for future work.

Fig. 1
figure 1

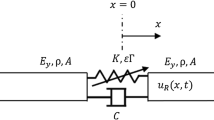
Two linearly elastic bars joined by a nonlinear spring and a linear dashpot. Each bar has one fixed end. Single-frequency plane waves are injected at the location of the forcing. Note that each wave coefficient includes itself plus its complex conjugate—this is only shown for \(\textbf{a}^+\), but assumed for all other coefficients. The global coordinate X denotes position starting from the left end. Periodic solutions to this problem have been found in [1]

Full size image

2 Stability via the strained parameter approach

We now formulate an analytical approach to determine stability of the multiple periodic solutions found in [1] for the single-jointed system shown in Fig. 1. The approach shares many similarities with the “strained parameter”, or Lindstedt-Poincaré, approach employed in the study of the damped Mathieu equation [4]. While the Mathieu equation is a single ordinary differential equation, the strained parameter approach developed herein assesses stability of continuous systems governed by partial differential equations. In addition, the motivating example studied consists of multiple continuous domains connected by a nonlinear joint.

The equations governing vibration response in the linearly elastic bars are given by,

$$\begin{aligned} \rho A\frac{\partial ^2u_L}{\partial t^2}-E_yA\frac{\partial ^2u_L}{\partial X^2}&=f_L(X,t), 0<X<(\alpha _1 + \alpha _2) l \end{aligned}$$
(1)
$$\begin{aligned} \rho A\frac{\partial ^2u_R}{\partial t^2}-E_yA\frac{\partial ^2u_R}{\partial X^2}&=f_R(X,t), (\alpha _1 + \alpha _2)<X<l \end{aligned}$$
(2)

where the left and right bars have displacement fields denoted by \( u_L\left( X,t\right) \) and \( u_R\left( X,t\right) \), while \(f_L\left( X,t\right) \) and \(f_R\left( X,t\right) \) denote forcing per unit length in the left and right subdomains, respectively. For simplicity of resulting expressions, the two bars considered share the same Young’s modulus \(E_y\), density per unit volume \(\rho \), and cross-sectional area A. The three values for \(\alpha _i, i=1,2,3\), form a partition of unity. Four boundary conditions are required to completely specify the vibration response of two jointed bars. The two clamped ends provide two boundary conditions, \(u_L(0,t)=0\) and \(u_R(l,t)=0\), while two others arise at the joint,

$$\begin{aligned} \left. E_yA\frac{\partial u_L}{\partial X}\right] _{X=X_J}&= \left. K\left( u_R{-u}_L\right) +\varepsilon \Gamma \left( u_R{-u}_L\right) ^3\right. \nonumber \\&\quad \left. +C\left( \frac{\partial u_R}{\partial t}-\frac{\partial u_L}{\partial t}\right) \right] _{X=X_J}, \end{aligned}$$
(3)
$$\begin{aligned} \left. E_yA\frac{\partial u_R}{\partial X}\right] _{X=X_J}&= \left. K\left( u_R{-u}_L\right) +\varepsilon \Gamma \left( u_R{-u}_L\right) ^3\right. \nonumber \\&\quad \left. +C\left( \frac{\partial u_R}{\partial t}-\frac{\partial u_L}{\partial t}\right) \right] _{X=X_J}, \end{aligned}$$
(4)

where \(X_J = (\alpha _1 + \alpha _2)l\). The joint considered has linear and cubic restoring stiffness characterized by coefficients K and \(\varepsilon \Gamma \), respectively, and linear damping characterized by C. Note that \(\varepsilon \) denotes a small book-keeping parameter later set to one [4].

We identify any periodic solution [1] with left and right displacement fields denoted by \(u_L^*(X,t)\) and \(u_R^*(X,t)\), respectively. Next, we assess the local stability of these solutions by introducing small perturbations \(\delta u_L(X,t)\) and \(\delta u_R(X,t)\) such that the total displacement fields are now given by,

$$\begin{aligned} u_L(X,t) =&u_L^*(X,t) + \delta u_L(X,t), 0<X<X_J, \end{aligned}$$
(5)
$$\begin{aligned} u_R(X,t) =&u_R^*(X,t) + \delta u_R(X,t), X_J<X<l. \end{aligned}$$
(6)

Substituting the above into the governing field equations, Eqs. (1), and (2), the joint conditions, Eqs. (3), and (4), and the zero displacement boundary conditions, we retain only linear terms in \(\delta u_L(X,t)\) and \(\delta u_R(X,t)\), yielding

$$\begin{aligned}&\rho A\frac{\partial ^2 \delta u_L}{\partial t^2}-E_yA\frac{\partial ^2 \delta u_L}{\partial X^2}=0, \qquad 0<X<X_J, \end{aligned}$$
(7)
$$\begin{aligned}&\rho A\frac{\partial ^2u_R}{\partial t^2}-E_yA\frac{\partial ^2u_R}{\partial X^2}=0, \qquad X_J<X<l, \end{aligned}$$
(8)
$$\begin{aligned}&\left. E_yA\frac{\partial \delta u_L}{\partial X}\right| _{X=X_J}=\left[ K + 3 \varepsilon \Gamma u^{*2}_J(t) \right] \left( \delta u_R(X_J,t) \right. \nonumber \\&\left. - \delta u_L(X_J,t) \right) + C \left( \delta \dot{u}_R(X_J,t)- \delta \dot{u}_L(X_J,t) \right) , \end{aligned}$$
(9)
$$\begin{aligned}&\left. E_yA\frac{\partial \delta u_R}{\partial X}\right| _{X=X_J}=\left[ K + 3 \varepsilon \Gamma u^{*2}_J(t) \right] \left( \delta u_R(X_J,t) \right. \nonumber \\&\left. - \delta u_L(X_J,t) \right) + C \left( \delta \dot{u}_R(X_J,t)- \delta \dot{u}_L(X_J,t) \right) , \end{aligned}$$
(10)
$$\begin{aligned}&\delta u_L(0,t) = 0, \end{aligned}$$
(11)
$$\begin{aligned}&\delta u_R(0,t) = 0, \end{aligned}$$
(12)

where \(u^{*}_J(t) \equiv u_R^*(X_J,t) - u_L^*(X_J,t) \) denotes the joint displacement. Retaining only terms up to and including \(\mathcal {O}(\varepsilon )\) in the stability analysis (i.e., only retaining the fundamental harmonic in \(u^*_J(t)\)), we rewrite the bracketed term on the right-hand side of Eqs. (9), and (10) as,

$$\begin{aligned} \left[ K + 3 \varepsilon \Gamma u^{*2}_J(t) \right] = K^{'} + \varepsilon P \cos (2\omega t), \end{aligned}$$
(13)

where we have used \(u^*_J(t) \equiv a^* \cos \left( \omega t + \phi ^* \right) \), \(\phi ^*\) denotes the joint displacement phase relative to the forcing, \(K^{'} \equiv K + \frac{3 \varepsilon \Gamma a^{*2}}{2}\), and \(P \equiv \frac{3 \Gamma a^{*2}}{2}\). We note that both the amplitude, \(a^*\), and phase, \(\phi ^*\), are known from the solutions obtained in [1], and these fully distinguish one solution from another.

Fig. 2
figure 2

a Damped, parametrically excited system arising from the local stability analysis of the corresponding forced system; solution approach at b zeroth-order, c first-order, and d second-order

Full size image

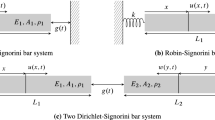
Using Eq. (13) in Eqs. (7–12), we recover a parametrically excited problem as illustrated in Fig. 2(a). While this problem arises from studying the stability of a directly excited system, it may be of general interest. For example, similar problems will arise when two domains are connected by time-varying stiffness, such as in parametrically driven micromechanical oscillators [6]. For the forced problem, of interest herein, stability of the solution is guaranteed when the parametrically excited problem is stable.

We next proceed to find wave-based solutions to the linear problem illustrated in Fig. 2(a). To do so, we employ a strained parameter approach. We first expand \(\delta u_L\) and \(\delta u_R\),

$$\begin{aligned} \delta u_L\left( X,t\right)&=u_{L}^{(0)}\left( X,t\right) + \varepsilon u_{L}^{(1)}\left( X,t\right) \nonumber \\&\quad + \varepsilon ^2 u_{L}^{(2)}\left( X,t\right) + \mathcal {O}\left( \varepsilon ^3\right) , \end{aligned}$$
(14)
$$\begin{aligned} \delta u_R\left( X,t\right)&=u_{R}^{(0)}\left( X,t\right) + \varepsilon u_{R}^{(1)}\left( X,t\right) \nonumber \\&\quad + \varepsilon ^2 u_{R}^{(2)}\left( X,t\right) + \mathcal {O}\left( \varepsilon ^3\right) , \end{aligned}$$
(15)

and subsequently expand the static component of the spring stiffness,

$$\begin{aligned} K^{'} = K_0 + \varepsilon K_1 + \varepsilon ^2 K_2 + \mathcal {O}\left( \varepsilon ^3\right) , \end{aligned}$$
(16)

which amounts to “straining” the stiffness in the problem. We also place the damping at first order to avoid decay in the ensuing zeroth-order problem: \(C \rightarrow \epsilon \hat{C}\). Substitution of the expanded and ordered quantities into Eqs. (7–13) results in three ordered problems, as illustrated in Fig. 2(b–d), governed by,

$$\begin{aligned}&\mathcal {O}\left( \varepsilon ^0\right) :\qquad \quad \nonumber \\&\rho A\frac{\partial ^2u_{L}^{(0)}}{\partial t^2}-E_yA\frac{\partial ^2u_{L}^{(0)}}{\partial X^2}=0, 0<X<X_J, \end{aligned}$$
(17)
$$\begin{aligned}&\rho A\frac{\partial ^2u_{R}^{(0)}}{\partial t^2}-E_yA\frac{\partial ^2u_{R}^{(0)}}{\partial X^2}=0, X_J<X<l, \end{aligned}$$
(18)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{L}^{(0)}}{\partial X}\right| _{X=X_J}=\left. K_0\left( u_{R}^{(0)}-{u}_{L}^{(0)}\right) \right| _{X=X_J}, \end{aligned}$$
(19)
$$\begin{aligned}&u_{L}^{(0)}(0,t) = 0, \end{aligned}$$
(20)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{R}^{(0)}}{\partial X}\right| _{X=X_J}=\left. K_0\left( u_{R}^{(0)}-{u}_{L}^{(0)}\right) \right| _{X=X_J}, \end{aligned}$$
(21)
$$\begin{aligned}&u_{R}^{(0)}(l,t) = 0, \end{aligned}$$
(22)
$$\begin{aligned}&\mathcal {O}\left( \varepsilon ^1\right) :\qquad \quad \nonumber \\&\rho A\frac{\partial ^2u_{L}^{(1)}}{\partial t^2}-E_yA\frac{\partial ^2u_{L}^{(1)}}{\partial X^2}=0, 0<X<X_J, \end{aligned}$$
(23)
$$\begin{aligned}&\rho A\frac{\partial ^2u_{R}^{(1)}}{\partial t^2}-E_yA\frac{\partial ^2u_{R}^{(1)}}{\partial X^2}=0, X_J<X<l, \end{aligned}$$
(24)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{L}^{(1)}}{\partial X}\right| _{X=X_J}\!\!=\!\left. K_0\left( u_{R}^{(1)}-{u}_{L}^{(1)}\right) \right| _{X=X_J} \!+\! F^{(1)}(t), \end{aligned}$$
(25)
$$\begin{aligned}&u_{L}^{(1)}(0,t) = 0, \end{aligned}$$
(26)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{R}^{(1)}}{\partial X}\right| _{X=X_J} = \left. K_0 \left( u_{R}^{(1)}-{u}_{L}^{(1)} \right) \right| _{X=X_J} \!+\! F^{(1)}(t), \end{aligned}$$
(27)
$$\begin{aligned}&u_{R}^{(1)}(l,t) = 0, \end{aligned}$$
(28)
$$\begin{aligned}&\mathcal {O}\left( \varepsilon ^2\right) :\qquad \quad \nonumber \\&\rho A\frac{\partial ^2u_{L}^{(2)}}{\partial t^2}-E_yA\frac{\partial ^2u_{L}^{(2)}}{\partial X^2}=0, 0<X<X_J, \end{aligned}$$
(29)
$$\begin{aligned}&\rho A\frac{\partial ^2u_{R}^{(2)}}{\partial t^2}-E_yA\frac{\partial ^2u_{R}^{(2)}}{\partial X^2}=0, X_J<X<l, \end{aligned}$$
(30)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{L}^{(2)}}{\partial X}\right| _{X=X_J}=\left. K_0\left( u_{R}^{(2)}-{u}_{L}^{(2)}\right) \right| _{X=X_J} \!+\! F^{(2)}(t), \end{aligned}$$
(31)
$$\begin{aligned}&u_{L}^{(2)}(0,t) = 0, \end{aligned}$$
(32)
$$\begin{aligned}&\left. E_yA\frac{\partial u_{R}^{(2)}}{\partial X}\right| _{X=X_J}=\left. K_0\left( u_{R}^{(2)}-{u}_{L}^{(2)}\right) \right| _{X=X_J} \!+\! F^{(2)}(t) \end{aligned}$$
(33)
$$\begin{aligned}&u_{R}^{(2)}(l,t) = 0, \end{aligned}$$
(34)

where the forcing arising at the joints at \(\mathcal {O}(\varepsilon ^1)\) and \(\mathcal {O}(\varepsilon ^2)\), respectively, is given by:

$$\begin{aligned} F^{(1)}(t)&= \left( K_1 + P \cos (2 \omega t) \right) \left( u_{R}^{(0)}\left( X_J,t\right) - u_{L}^{(0)}\left( X_J,t\right) \right) \nonumber \\&\quad + \hat{C}\left( \dot{u}_{R}^{(0)}\left( X_J,t\right) - \dot{u}_{L}^{(0)}\left( X_J,t\right) \right) , \end{aligned}$$
(35)
$$\begin{aligned} F^{(2)}(t)&= \left( K_1 + P \cos (2 \omega t) \right) \left( u_{R}^{(1)}\left( X_J,t\right) - u_{L}^{(1)}\left( X_J,t\right) \right) \nonumber \\&\quad + K_2 \left( u_{R}^{(0)}\left( X_J,t\right) - u_{L}^{(0)}\left( X_J,t\right) \right) \nonumber \\&\quad + \hat{C}\left( \dot{u}_{R}^{(1)}\left( X_J,t\right) - \dot{u}_{L}^{(1)}\left( X_J,t\right) \right) . \end{aligned}$$
(36)

Similar to the wave-based solution procedure for the nonlinear forced problem [1], we seek exact wave solutions for the three linear problems shown in Fig. 2(b–d). Starting with the zeroth-order problem in Fig. 2(b), we assign wave coefficients \(a_0^+\), \(a_0^-\), \(\ldots \), \(d_0^-\) and their complex conjugates. Note that the subscript notation here is different from that used in [1] where subscripts were used to denote the harmonic index while they are used here to denote the ordered wave components of the perturbation analysis. These coefficients are related by propagation relationships,

$$\begin{aligned}&b_0^+ = a_0^+ e^{ik \beta _1 l}, a_0^- = b_0^- e^{ik \beta _1 l}, d_0^+\nonumber \\&= c_0^+ e^{ik \beta _2 l}, c_0^- = d_0^- e^{ik \beta _2 l}, \end{aligned}$$
(37)

joint conditions,

$$\begin{aligned} c_0^+&= \frac{{iE}_yAk}{-2K_0+iE_yAk} c_0^- + \frac{-2K_0}{-2K_0+iE_yAk} b_0^+, \nonumber \\&b_0^- = \frac{{iE}_yAk}{-2K_0+iE_yAk} b_0^+ + \frac{-2K_0}{-2K_0+iE_yAk} c_0^-, \end{aligned}$$
(38)

and clamped boundary conditions,

$$\begin{aligned}&a_0^+ = - a_0^-, d_0^+ = - d_0^-, \end{aligned}$$
(39)

where k denotes the wavenumber associated with the system’s \(j^{th}\) natural frequency, \(\omega _j\). We point the reader to more details on wave-based approaches in [1], particularly as concerns joint conditions for the wave coefficients. Note that the zeroth-order stability problem is an eigenvalue problem. Next, we assemble the coefficient relationships into the form,

$$\begin{aligned} \mathbf {A^{(0)}_s}\left( \omega _j; K_0 \right) \mathbf {z_s^{(0)}} = \textbf{0}, \end{aligned}$$
(40)

where \(\mathbf {z_s^{(0)}}\) denotes an eigenvector holding the eight zeroth-order wave coefficients (see Fig. 2(b)) and \(\mathbf {A^{(0)}_s}\left( \omega _j; K_0 \right) \) denotes the zeroth-order stability coefficient matrix as a function of the \(j^{th}\) natural frequency \(\omega _j\) and parameterized by stiffness \(K_0\). Note that the dependence of \(\mathbf {A^{(0)}_s}\) on frequency is nonlinear, and as a result, there are an infinite number of natural frequencies satisfying Eq. (40) consistent with the fact that the jointed system is continuous. While it is not apparent until the next order analysis, we also note that \(K_0\) will be chosen based on requiring the eigenfrequency \(\omega _j\) to be equal to the forcing frequency \(\omega \). The zeroth-order problem is completed by finding the eigenvalues and eigenvectors associated with Eq. (40) [7].

Following completion of the zeroth-order problem, we turn our attention to the first-order problem. We note that the zeroth-order spring stretch required to evaluate Eq. (35) is now known and given by,

$$\begin{aligned}{} & {} u_{R}^{(0)}\left( X_J,t\right) - u_{L}^{(0)}\left( X_J,t\right) = a^{(0)} \cos \left( \omega _j(K_0) t \right) \nonumber \\{} & {} + b^{(0)} \sin \left( \omega _j(K_0) t \right) , \end{aligned}$$
(41)

where explicit dependence of \(\omega _j\) on \(K_0\) is noted. Since the zeroth-order solution is an eigenfunction, we can freely choose the harmonic amplitudes \(a^{(0)}\) and \(b^{(0)}\). Substitution of Eq. (41) into Eq. (35) yields an updated first-order forcing,

$$\begin{aligned} F^{(1)}(t)&= \underline{\underline{ \frac{P a^{(0)}}{2} \cos \left( (2 \omega - \omega _j(K_0)) t \right) }} \nonumber \\&\quad - \underline{\underline{ \frac{P b^{(0)}}{2} \sin \left( (2 \omega - \omega _j(K_0)) t \right) }} \nonumber \\&\quad + \frac{P a^{(0)}}{2} \cos \left( (2 \omega + \omega _j(K_0)) t \right) \nonumber \\&\quad + \frac{P b^{(0)}}{2} \sin \left( (2 \omega + \omega _j(K_0)) t \right) \nonumber \\&\quad + \underline{\left( K_1 a^{(0)} + \hat{C} \omega _j(K_0) b^{(0)} \right) \cos ( \omega _j(K_0) t ) } \nonumber \\&\quad + \underline{\left( K_1 b^{(0)} - \hat{C} \omega _j(K_0) a^{(0)} \right) \sin ( \omega _j(K_0) t )}. \end{aligned}$$
(42)

We note secular, or resonant, terms on the right-hand side of Eq. (42) having frequency dependence equal to one of the zeroth-order system’s eigenfrequencies; namely the underlined terms. These must be eliminated in order for the response to be bounded and to satisfy the assumed ordering of the asymptotic expansions. In addition, for particular choices of \(K_0\) such that \(2 \omega - \omega _j(K_0) = \omega _j(K_0)\), additional secular terms appear as indicated by the doubly underlined terms. In particular, the latter condition holds for a certain value of \(K_0\) close, but not equal, to K from the forced problem. When this occurs, the excitation frequency \(\omega \) equals the \(j^{th}\) eigenfrequency \(\omega _j(K_0)\), as remarked during the zeroth-order problem.

Proceeding with the choice of \(K_0\) such that \(\omega = \omega _j(K_0)\), we remove secular terms by requiring,

$$\begin{aligned} \begin{bmatrix} K_1 + \frac{P}{2} &{} \hat{C} \omega \\ -\hat{C} \omega &{} K_1 - \frac{P}{2} \end{bmatrix} \begin{Bmatrix} a^{(0)} \\ b^{(0)} \end{Bmatrix} = \begin{Bmatrix} 0 \\ 0 \end{Bmatrix}. \end{aligned}$$
(43)

Zeroing the determinant of the coefficient matrix in Eq. (43) yields \(K_1\),

$$\begin{aligned} K_1 = \pm \frac{1}{2} \sqrt{P^2 - 4 \hat{C}^2 \omega ^2}. \end{aligned}$$
(44)

We note that the two values of \(K_1\) in Eqs. (44) begin to form two sides of a stability tongue in the P versus \(K^{'}\) plane, as seen later. With known values for \(K_1\), it is also possible to find the eigenvectors, but these are not needed from this point forward.

With secular terms removed, we must still find the forced response associated with the non-secular terms in Eq. (42). As is the usual practice in perturbation approaches [4], we neglect the homogeneous (or unforced) solution in all orders above the zeroth-order without loss of generality. With the choice of \(K_0\) established, the non-secular forcing occurs at frequency \(3 \omega _j(K_0) \). We find the forced response of the \(\mathcal {O}(\varepsilon ^1)\) problem using another exact wave approach, as depicted by the wave coefficients in Fig. 2(c) and their complex conjugates. These first-order wave coefficients are related by propagation relationships,

$$\begin{aligned} b_1^+&= a_1^+ e^{i3k \beta _1 l}, a_1^- = b_1^- e^{i3k \beta _1 l}, \nonumber \\ d_1^+&= c_1^+ e^{i3k \beta _2 l}, c_1^- = d_1^- e^{i3k \beta _2 l}, \end{aligned}$$
(45)

joint conditions,

$$\begin{aligned} c_1^+&= \frac{{i3E}_yAk}{-2K_0+i3E_yAk} c_1^- + \frac{-2K_0}{-2K_0+i3E_yAk} b_3^+ \nonumber \\&\quad +\frac{\frac{P}{4} a^{(0)}}{-2K_0+i3E_yAk} +\frac{\frac{iP}{4} b^{(0)}}{-2K_0+i3E_yAk}, \nonumber \\ b_1^-&= \frac{{i3E}_yAk}{-2K_0+i3E_yAk} b_1^+ + \frac{-2K_0}{-2K_0+i3E_yAk} c_1^-\nonumber \\&\quad -\frac{\frac{P}{4} a^{(0)}}{-2K_0+i3E_yAk} -\frac{\frac{iP}{4} b^{(0)}}{-2K_0+i3E_yAk}, \end{aligned}$$
(46)

and clamped boundary conditions,

$$\begin{aligned} a_1^+&= - a_1^-, d_1^+ = - d_1^-, \end{aligned}$$
(47)

where the joint conditions have been developed similar to the discussion in [1] with the exclusion of damping and the inclusion of imposed forces \(\frac{P a^{(0)}}{4} e^{-3 \omega _j(K_0) t} + \frac{iP b^{(0)}}{4} e^{-3 \omega _j(K_0) t} + c.c.\). Similar to the zeroth-order problem, we assemble the coefficient relationships into matrix form,

$$\begin{aligned} \mathbf {A^{(1)}_s}\left( 3\omega _j(K_0) \right) \mathbf {z_s^{(1)}} = \mathbf {f_s^{(1)}}, \end{aligned}$$
(48)

where \(\mathbf {z_s^{(1)}}\) holds the eight first-order wave coefficients, \(\mathbf {A^{(1)}_s}\left( 3\omega _j(K_0) \right) \) denotes the first-order stability coefficient matrix, and \(\mathbf {f_s^{(1)}}\) holds forcing terms proportional to \(\frac{P}{4} a^{(0)}\) and \(\frac{iP}{4} b^{(0)}\). Unlike the eigenvalue problem at zeroth-order, Eq. (48) admits a single solution for the coefficients via inversion of \(\mathbf {A^{(1)}_s}\left( 3\omega _j(K_0) \right) \), when this inverse exists. For cases where this is not possible (see discussion of one such case in Sect. 4), it is implied that the strained system is resonant at \(3\omega _j(K_0)\) in addition to having \(\omega _j(K_0)\) as a resonance. We will, however, not dwell on this aspect presently and proceed with the general formulation of the method assuming that \(\mathbf {A^{(1)}_s}\left( 3\omega _j(K_0) \right) \) is non-singular.

Following the solution of Eq. (48), the spring displacement required in the second-order problem can be written as,

$$\begin{aligned} u_{R}^{(1)}\left( X_J,t\right) - u_{L}^{(1)}\left( X_J,t\right)= & {} a^{(1)} \cos \left( 3\omega _j(K_0) t \right) \nonumber \\{} & {} + b^{(1)} \sin \left( 3\omega _j(K_0) t \right) ,\nonumber \\ \end{aligned}$$
(49)

where we note that \(a^{(1)}\) depends only on \(a^{(0)}\) (and not \(b^{(0)}\)), and \(b^{(1)}\) depends only on \(b^{(0)}\) (and not \(a^{(0)}\)). In fact, \(\frac{a^{(1)}}{a^{(0)}}=\frac{b^{(1)}}{b^{(0)}}\). This results from the similarity in how \(a^{(0)}\) and \(b^{(0)}\) appear in the first-order joint relationships.

With the first-order problem complete, we turn final attention to the second-order problem. Substitution of \(\omega = \omega _j(K_0)\) and Eqs. (41), (49) into Eq. (36) yields an updated second-order forcing, of which only the secular portion is of interest,

$$\begin{aligned} F_{sec}^{(2)}(t)= & {} \left( \frac{P a^{(1)}}{2} + K_2 a^{(0)} \right) \cos (\omega _j(K_0) t) \nonumber \\{} & {} + \left( \frac{P b^{(1)}}{2} + K_2 b^{(0)} \right) \sin (\omega _j(K_0) t). \end{aligned}$$
(50)

Elimination of the two secular terms yields,

$$\begin{aligned} K_2 = - \frac{P}{2} \frac{a^{(1)}}{a^{(0)}} = - \frac{P}{2} \frac{b^{(1)}}{b^{(0)}} = - \frac{P}{2} r^{(1)/(0)}, \end{aligned}$$
(51)

where we introduce \(r^{(1)/(0)}\) to represent the ratio of first- to zeroth-order spring displacement components.

Lastly, we reconstitute the strained stiffness,

$$\begin{aligned} K^{'} \!=\! K_0 \pm \varepsilon \frac{1}{2} \sqrt{P^2 - 4 \hat{C}^2 \omega ^2} - \varepsilon ^2 \frac{P}{2} r^{(1)/(0)} \!+\! \mathcal {O}\left( \varepsilon ^3\right) ,\nonumber \\ \end{aligned}$$
(52)

recalling that \(K_0\) is found by enforcing that the excitation frequency \(\omega \) equals the \(j^{th}\) natural frequency of the zeroth-order stability problem, \(\omega = \omega _j(K_0)\). It is apparent from Eq. (52) that non-zero damping lifts the stability curves off of the \(K^\prime \) axis, and thus has a stabilizing effect. To return fully to assessing stability of the forced problem, we recall that \(K^{'} \equiv K + \frac{3 \varepsilon \Gamma a^{*2}}{2}\) and \(P \equiv \frac{3 \Gamma a^{*2}}{2}\), where \(a^*\) and \(\phi ^*\) denote the joint displacement’s amplitude and phase for the periodic solution under consideration. We also note that \(\hat{C}\) and \(\Gamma \) always appear with \(\varepsilon \), and thus, no generality is lost in setting \(\varepsilon \) to one. Inverting Eq. (52) yields two curves defining the stability tongue [8] separating stable and unstable solutions in the P versus \(K^{'}\) plane (depicted in Fig. 7 for the single-jointed case).

We note that the strained parameter approach may also be developed for the two-jointed system studied in [1], where it is only necessary to strain one of the two joint stiffnesses, regardless of the fact that these two joints have the same stiffness—i.e., if they differed, it would still be only necessary to strain one or the other, and not both. This is due to the fact that the stability problem has codimension-1, i.e., only one resonant condition must be met, and thus, only one parameter must be strained [9].

3 Stability via the perturbed eigenproblem residue approach

The second stability approach is based on a PWE formulation of the perturbed system of the original problem. We consider a generic single jointed-bar vibration problem of the form

$$\begin{aligned} \rho A \frac{\partial ^2 u_L}{\partial t^2} - E_y A \frac{\partial ^2 u_L}{\partial X^2}&= f_L(X, t),\quad 0<X<X_J \end{aligned}$$
(53)
$$\begin{aligned} \rho A \frac{\partial ^2 u_R}{\partial t^2} - E_y A \frac{\partial ^2 u_R}{\partial X^2}&= f_R(X, t),\quad X_J<X<l \end{aligned}$$
(54)
$$\begin{aligned} \left. E_yA \frac{\partial u_L}{\partial X}\right] _{X=X_J}&= f_{nl}(\Delta u, \Delta \dot{u}, \dots ) \end{aligned}$$
(55)
$$\begin{aligned} \left. E_yA \frac{\partial u_R}{\partial X}\right] _{X=X_J}&= f_{nl}(\Delta u, \Delta \dot{u}, \dots ), \end{aligned}$$
(56)
$$\begin{aligned} u_L(0,t)&= 0, \end{aligned}$$
(57)
$$\begin{aligned} u_R(l,t)&= 0, \end{aligned}$$
(58)

and formulate the approach using this case as an example. Application to cases with multiple joints is straightforward since the method does not make assumptions on the number or types of nonlinearities present. In the above, \(f_L(X,t)\) and \(f_R(X,t)\) denote general forcing functions (independent of the solution \(u_{L,R}\)). We note that this approach does not demand the presence of a small parameter, i.e., this approach is applicable for arbitrarily strong nonlinearities and not just weak nonlinearities (as was the case for the strained parameter approach presented in Sect. 2). Following the notation in Sect. 2, we use starred superscripts to denote the periodic solutions \(u^*_{L,R}\) of the original forced vibration problem and \(\delta u_{L,R}\) to denote infinitesimal perturbations of the

$$\begin{aligned} \text {left solution}\leftarrow u^*_L(X,t) + \delta u_L(X,t), \quad 0<X<X_J, \end{aligned}$$
(59)
$$\begin{aligned} \text {right solution}\leftarrow u^*_R(X,t) + \delta u_R(X,t),\quad X_J<X<l. \end{aligned}$$
(60)

Substituting these expressions into Eqs. (53–58) and dropping the higher-order terms yields a homogeneous set of governing equations for \(\delta u_{L,R}\). These can be expressed as

$$\begin{aligned} \rho A \frac{\partial ^2 \delta u_L}{\partial t^2} - E_y A \frac{\partial ^2 \delta u_L}{\partial X^2}&= 0,\quad 0<X<X_J \end{aligned}$$
(61)
$$\begin{aligned} \rho A \frac{\partial ^2 \delta u_R}{\partial t^2} - E_y A \frac{\partial ^2 \delta u_R}{\partial X^2}&= 0,\quad X_J<X<l \end{aligned}$$
(62)
$$\begin{aligned} \left. E_yA \frac{\partial \delta u_L}{\partial X}\right] _{X=X_J}&= \left. \frac{\partial f_{nl}}{\partial u}\right] _{\Delta u^*, \dots } \Delta \delta u \nonumber \\&\quad + \left. \frac{\partial f_{nl}}{\partial \dot{u}}\right] _{\Delta u^*, \dots } \Delta \dot{\delta u} \end{aligned}$$
(63)
$$\begin{aligned} \left. E_yA \frac{\partial \delta u_R}{\partial X}\right] _{X=X_J}&= \left. \frac{\partial f_{nl}}{\partial u}\right] _{\Delta u^*, \dots } \Delta \delta u \nonumber \\&\quad + \left. \frac{\partial f_{nl}}{\partial \dot{u}}\right] _{\Delta u^*, \dots } \Delta \dot{\delta u}. \end{aligned}$$
(64)
$$\begin{aligned} \delta u_L(0,t)&= 0, \end{aligned}$$
(65)
$$\begin{aligned} \delta u_R(l,t)&= 0. \end{aligned}$$
(66)

Since \(u^*_{L,R}(X,t)\) (and therefore \(\Delta u^*, \Delta \dot{u^*}, \dots \)) is fixed from the solution of Eqs. (53–58), the above is a linear homogeneous PDE with time-varying linear stiffness and damping acting at the joint, and the solution can be obtained using a wave-based approach. An important aspect in the homogeneous case, however, is that the frequency of the response is complex and unknown, unlike the inhomogeneous case where the frequency is real and fixed by the excitation. Resorting to a multi-harmonic wave-based representation of the solution, the solution \(\delta u_L\) can be represented, for instance, around the joint as

$$\begin{aligned} \delta u_L(X,t)&= \sum _j \left( d_j^+e^{jkX}e^{-j\lambda t} + d_j^-e^{-jkX}e^{-j\lambda t}\right) \nonumber \\&\quad + c.c.\quad \alpha _1l<X<(\alpha _1+\alpha _2)l, \end{aligned}$$
(67)

where k in the above comes from the dispersion relationship \(\lambda =\sqrt{E/\rho } k\). Here, \(\lambda \) denotes the unknown complex frequency that the perturbed system responds at. Assembling this system and using the FFT to obtain the wave-component stiffness coefficient contributions for the periodic stiffness terms in Eqs. (63) and (64) above (which are \(2\pi /\omega \)-periodic), we obtain a linear set of equations of the form

$$\begin{aligned} \textbf{A}(\lambda ; \textbf{P}, u^*, \omega ) \textbf{z} = \textbf{0} \end{aligned}$$
(68)

where \(\textbf{z}\in \mathbb {C}^{N_wN_h}\) is a complex vector consisting of the \(N_h\) complex harmonics of the \(N_w\) wave components; \(\textbf{A}\in \mathbb {C}^{N_rN_h\times N_rN_h}\) is a complex matrix that is a function of \(\lambda \) alone (but parameterized by the periodic solution \(u^*,\omega \)). Note that no AFT (Alternating Frequency -Time) procedure needs to be carried out in terms of the complex frequency \(\lambda \) here; we use the appropriate entries of the frequency-domain Jacobian of the PWE residue function (see [1]) to get the periodic stiffness components once. As expected from Floquet theory, this is a Nonlinear EigenProblem (NEP) in \(\lambda \). However, since \(\textbf{A}\) contains exponentials of \(\lambda \), it is not, in general, possible to spectrally decompose this problem quite easily and, furthermore, there exist an infinite set of eigenpairs. We unsuccessfully attempted the use of the Padé approximant and interpolatory Krylov techniquesFootnote 1 for partial spectral decomposition of this NEP, but still feel that such approaches must be explored in detail in the future to enable quantitative stability analysis.

Qualitative analysis of stability can, however, be carried out merely by seeking out the points along a given forced response curve where transitions of stability occur in a manner that completely avoids the challenges associated with spectral decomposition. Floquet theory asserts [4] that stability transitions occur when the perturbed system has as eigenvalue \(i m\xi \), a purely imaginary quantity with integer \(m>0\), with three possibilities for \(\xi \):

\(\xi =0\);:

Perturbation remains unchanging in time;

\(\xi =\omega \);:

Perturbation varies periodically with the same fundamental period as the solution; and

\(\xi =\omega /2\);:

Perturbation varies periodically with twice the fundamental period as the solution.

Choosing \(\xi =0\) gives rise to the trivial solution and need not be considered in the context of continuum dynamics with homogeneous essential boundary conditions. In a multi-harmonic approach such as the wave-based strategies considered presently, m can be set to 1 without loss of generality since the higher harmonics will be intrinsically included for each \(\xi \). In our context, therefore, the cases corresponding to \(\xi =\omega \) and \(\xi =\omega /2\) will have to be considered.

If \(\xi \) is an eigenvalue of the system in Eq. (68), the determinant of \(\textbf{A}\bigr ]_{\lambda =i\xi }\) will be exactly zero. Checking for points along any given forced response curve where this happens allows one to obtain the stability transition or critical points directly. Since \(\textbf{A}\) is complex, the determinant is, in general (for the cases when \(\xi \) is not an eigenvalue), also complex, making the task of detecting the zero point on a forced response curve challenging. We first therefore create a fully real counterpart of the Jacobian matrix (this process was previously alluded to in [1]). Denoting by \(\Re \{\textbf{z}\}\) and \(\Im \{\textbf{z}\}\) the real and imaginary parts of the vector of wave component harmonics z, Eq. (68) can be rewritten as

$$\begin{aligned} \textbf{A} \textbf{z}&= \textbf{A} \Re \{\textbf{z}\} + i \textbf{A} \Im \{\textbf{z}\}\nonumber \\&= \begin{bmatrix} \textbf{A}&i\textbf{A} \end{bmatrix} \begin{bmatrix} \Re \{\textbf{z}\}\\ \Im \{\textbf{z}\}\\ \end{bmatrix}. \end{aligned}$$
(69)

Symbols denoting the functional and parametric dependences of \(\textbf{A}\) are dropped in the above for brevity. Decomposing the complex quantity \({\textbf{A}}{\textbf{z}}\) into its real and imaginary parts denoted by \(\Re \{{\textbf{A}}{\textbf{z}}\}\) and \(\Im \{{\textbf{A}}{\textbf{z}}\}\), respectively, yields the following fully real form of Eq. (68):

$$\begin{aligned} \begin{bmatrix} \Re \{{\textbf{A}}{\textbf{z}}\}\\ \Im \{{\textbf{A}}{\textbf{z}}\} \end{bmatrix} = \begin{bmatrix} \Re \{\textbf{A}\} &{} \Re \{i\textbf{A}\}\\ \Im \{\textbf{A}\} &{} \Im \{i\textbf{A}\} \end{bmatrix} \begin{bmatrix} \Re \{\textbf{z}\}\\ \Im \{\textbf{z}\} \end{bmatrix} = \begin{bmatrix} \textbf{0}\\ \textbf{0} \end{bmatrix}. \end{aligned}$$
(70)

The Jacobian matrix of this system,

$$\begin{aligned} \hat{\textbf{A}} = \begin{bmatrix}\Re \{\textbf{A}\} &{} \Re \{i\textbf{A}\}\\ \Im \{\textbf{A}\} &{} \Im \{i\textbf{A}\} \end{bmatrix}, \end{aligned}$$
(71)

is fully real and its determinant will be real always.

Along a forced response curve, a zero-crossing of the determinant of \(\left. \textbf{A}\right] _{\lambda =i\xi }\) will be the same as a sign change in the determinant of \(\left. \hat{\textbf{A}}\right] _{\lambda =i\xi }\). The quantity \(\left. det(\hat{\textbf{A}})\right] _{\lambda =i\xi }\) will be referred to as the Perturbation Eigenproblem Residue (PER) henceforth. The sign-change property will be clear if elaborated upon in the following manner: suppose the true eigenvalues of Eq. (70) are denoted by \(\gamma _j\) with j being the index of the eigenvalue, we can write the PER as a characteristic polynomial in the following manner:

(72)

Here |(.)| and denote the absolute value and angle of their complex arguments respectively, and \(\alpha \) is some real constant. A sufficient condition for the existence and validity of such a polynomial representation is the analyticity of the PER for all points \(\lambda \) on the complex domain. The existence of a Taylor series representation is guaranteed in this case, justifying the use of the polynomial form above. This is clearly the case here since \(\lambda \) only appears as smooth functions in the matrix \(\textbf{A}(\lambda )\) (and therefore in its determinant). This analyticity condition could be violated in some problems with non-smooth nonlinearities (e.g., Filippov dynamical systems, see, for instance [10]). In these cases, classical Floquet theory is not strictly applicable and further considerations become necessary. We will presently not concern ourselves with such issues and proceed with the discussion making note of the fact that this framework is invalid for such cases. We also note here that there are no bounded values of \(\lambda \) for which the PER becomes unbounded; i.e., the characteristic polynomial does not have any poles on the complex plane. It, however, has an infinite number of zeros (despite the finite size of \(\hat{\textbf{A}}\)), referred interchangeably here as eigenvalues of the NEP, consistent with that expected in continuum dynamics.

Since the PER is always real, the effective phase is either \(0^\circ \) or \(180^\circ \). Consider two points right before and after a transition in stability such as shown in Fig. 3. Just before the critical point (point A in Fig. 3), the zero \(\gamma ^{(A)}_m\) closest to \(i\xi \) will lie just to its left (since the solution is known to be stable) such that the quantity equals \(0^\circ \). Equivalently, the vector in the complex plane joining \(\gamma ^{(A)}_m\) to \(i\xi \) points to the right since this solution is known to be stable. The total angle of the PER at this point can be expressed as the sum,

(73)

where the zero term is canceled in the final expression, which itself has to be either \(180^\circ \) or \(0^\circ \) since the PER is a real quantity.

Fig. 3
figure 3

A schematic forced response (stable: blue, solid lines; unstable: red, dashed lines) with insets showing the complex plane including the point \(i\xi \), the corresponding closest zero \(\gamma _m^{(A,B)}\), and the complex vector \((i\xi -\gamma _m^{(A,B)})\) denoted using a line segment and terminal arrow. A and B are two points on the response curve across the stability transition

Full size image

Looking at a point just after the transition (point B in Fig. 3), the zero \(\gamma ^{(B)}_m\) has crossed through \(i\xi \) and will now lie just to its right. Consequently, the quantity now takes a value of \(180^\circ \), and we can express the total angle of the PER at this point as the sum,

(74)

Around these transition points, due to the arbitrarily small change in the excitation frequency \(\omega \) and ensuing response amplitude, the zeros away from \(i\xi \) are assumed to undergo only negligible changes and therefore \(\gamma _j^{(A)}\approxeq \gamma _j^{(B)}\) is assumed for \(j\ne m\). The first term in Eq. (74) is approximated as (see Eq. (73) above) and can be simplified as

(75)

This shows that the difference in complex angle between the PER values across a critical point is exactly \(180^\circ \). Since the PER is always a real number, this amounts to a sign change as mentioned earlier. Similar reasoning can be employed to observe that a sign change will also happen at the other critical point in Fig. 3 where the solutions transition from unstable to stable.

One drawback of the method presented is the fact that it can only predict stability changes and it is not possible, in general, to determine the stability of a solution from just the sign or the value of the PER. Exact stability determination would instead require knowledge of the location in the left or right half-plane for all infinite number of \(\gamma _j\), of which little can be said at this point. An exploration of the necessary conditions for the PER sign change (stability transition is just a sufficient condition) is deferred for future research. But the efficacy of the approach is empirically demonstrated by the fact that it provides satisfactory estimates of the stable and unstable branches on the response curve for both the numerical examples considered in [1].

4 Stability results for an example system

In this section we present stability results for the single-jointed example problem illustrated in Fig. 1 and parameterized by quantities appearing in Table 1. Periodic solutions to this problem are presented in [1], which also contains stability results for a second example problem consisting of three bars connected by two nonlinear joints.

Table 1 Mechanical and geometric parameters used for the single-jointed bar example (see Fig. 1 for accompanying schematic)
Full size table

The stability boundary predicted by the strained parameter approach for a fixed excitation frequency \(\omega \) is a parabolic curve (known as a stability or Arnold tongue), in the \(P-K^\prime \) space, where P denotes the periodic stiffness and \(K^\prime \) the constant stiffness of the parametrically forced system (recall \(\epsilon \) set to 1)—such a curve will be presented later. If, in addition, we vary the frequency, a stability surface results separating regions of stable and unstable parametrically forced systems. We present this surface in the subplots of Fig. 4 near the second natural frequency of the single-jointed system shown in Fig. 1, and label it as the Stability Boundary—note that this boundary is the same surface in all six sub-figures. We provide a narrated video in the supplementary material which includes revolving views of the figures and further explanations. The stability analysis is carried-out up to, and including, first-order terms. When we return to the directly forced system, specifying values for the joint linear and nonlinear stiffness, K and \(\Gamma \), respectively, together with the excitation frequency \(\omega \) and response amplitude \(a^*\) for a given periodic solution, yields a point in the \(K^\prime -P-\omega \) space; see Eq. (13). If this point falls inside of the stability boundary, the solution is unstable, whereas as if it falls outside, the solution is stable. If in addition we sweep frequency, response curves result which lie in the same space - these appear in Fig. 4 as curves whose stable portions are indicated by solid black lines, and whose unstable portions by dashed green lines. A first-order WBVA approach is used to obtain the solutions (see [1] for details) and a first-order strained parameter approach is used to obtain the stability boundaries. We present solution curves at forcing levels of 7.5 MN, 15 MN, and 30 MN, and we provide two views for each forcing level to aid visualization. It is important to note that while K is fixed along these curves, \(K^{'}\) is not, and thus the curves bend towards increasing \(K^{'}\) as resonance is approached and the response amplitude \(a^{*}\) increases. If we also vary the linear stiffness K in the directly forced problem, we can generate a solution surface, shaded blue in Fig. 4 and labeled as the Solution Manifold. The solution curves and manifold occupy more space inside of the stability boundary as the forcing increases, as depicted in the progression of sub-figures. For example, at 7.5 MN forcing, the solution manifold never intersects the stability boundary, indicating all solutions are stable. In fact, the solutions for 7.5 MN forcing closely resemble the linear solutions such that no appreciable bending of the frequency response curve occurs, and thus multiple solutions near resonance have yet to appear. At 15 MN and 30 MN forcing, appreciable bending occurs together with multiple solutions and the solution manifolds intersect with the stability boundaries. For these forcing levels, the portions of the response curves associated with mid-amplitude response are now unstable. Lastly, we note that the intersection of the surface manifold with the stability boundary marks the Transition Boundary, as indicated by the solid magenta curves in the sub-figures.

Fig. 4
figure 4

Stability boundaries from the strained parameter approach and the solution manifolds (first-order perturbation for both) of the single-jointed system corresponding to excitation amplitudes of a 7.5 MN; b 15 MN; and c 30 MN. Two views of the surface are presented in each sub-figure for clarity

Full size image
Fig. 5
figure 5

Stability assessment of periodic solutions in the single-jointed system around the second resonance, undergoing a 45 MN amplitude periodic excitation: a first harmonic periodic response with three solutions indicated at 81.6 k rad/s, and b accompanying stability boundaries at 81.6 k rad/s using first- and second-order stability analysis. Also shown in (b) are the P and \(K^{\prime }\) pairs for the three periodic solutions where, in both sub-figures, a circle denotes the low-amplitude solution, squares the mid-amplitude solution, and hexagrams the high-amplitude solution

Full size image

We study the convergence of the stability tongues as the analysis order increases in Fig. 5. The sub-figure on the left presents the frequency response curve for the single-jointed system studied, evaluated with a forcing of 45 MN. At such a large forcing level, the ratio of nonlinear to linear restoring force at resonance is 0.25, well-above that which can be expected for solution accuracy. However, this forcing level yields three solutions whose stability can be used to test the accuracy of first-order versus second-order stability analyses. The three solutions are indicated in the left sub-figure at 81.6 k rad/s using three markers. Subsequently, values for P and \(K^{'}\) for each are computed and indicated with the same markers in the right sub-figure, together with the stability tongue corresponding to 81.6 k rad/s. We note from the right sub-figure that the stability tongues match closely at low values of P, and thus, only first-order stability is necessary to assess the stability of solutions at low forcing, justifying the use of first-order analysis in Fig. 4. At higher forcing amplitudes, the mid- and high-amplitude solutions correspond to larger values of P. If first-order stability analysis is employed, the stability determination can be inaccurate, and thus second-order stability must be employed. This is clearly documented in Fig. 5(b) where the high-amplitude solution appears inside of the first-order stability tongue, erroneously suggesting unstable response. However, using second-order stability analysis, this solution subsequently lies outside of the stability tongue as the tongue appears rotated away from the first-order tongue. In our investigations of solution response and stability using the WBVA and the strained parameter approach, focusing specifically on the resonance peak where issues in stability prediction might arise, we have found first-order analysis is always accurate for responses in which the ratio of nonlinear to linear restoring force is less than 0.1.

Fig. 6
figure 6

Frequency response (first harmonic amplitude) of the PWE solution of the single-jointed system undergoing harmonic excitation near the second resonance with amplitude 30 MN, along with the perturbation eigenproblem residue using a a linear scale and b a log scale. Stability transition points are denoted by red points, while the stable and unstable solutions are plotted in blue and red, respectively

Full size image
Fig. 7
figure 7

First- and second-order stability boundaries from the strained parameter approach for the single-jointed system

Full size image
Fig. 8
figure 8

Comparison of the forced response stability predictions for the single-jointed system a using the FE-HB approach with frequency domain Hill’s coefficients [5] for stability determination, and b using the PWE frequency response and the PER stability approach developed in Sect. 3. In all figures, the stable and unstable branches are plotted using solid and dashed lines, respectively

Full size image

Next we investigate the PER stability approach in the context of the single-jointed system. For all frequency responses considered, we set \(\xi \) equal to the excitation frequency \(\omega \) in detecting critical points for which the sign of the PER changes. No critical points were found by setting \(\xi \) to \(\omega /2\), implying that stability loss occurs only through the \(\xi =\omega \) case for the present system, consistent with the strained parameter approach. Figure  6 plots the frequency response and the perturbation eigenproblem residue corresponding to the PWE solution of the single-jointed system harmonically forced at an amplitude of 30 MN using both a linear and log scale. Specifically, we plot the PER, \(\left. det(\hat{\textbf{A}})\right] _{\lambda =i\xi }\), evaluated using \(\lambda = i\omega \). The left sub-figure shows the PER clearly changing signs at the two bifurcation points in the frequency response curve, correctly indicating stability transitions in agreement with the strained parameter approach. In the right sub-figure, the log value of the PER drops sharply at the bifurcation points, but interestingly, shows a drop and local minimum at approximately 79.8 k rad/s.

The PER approach does not provide insight into the mechanism for the log value exhibiting a local minimum at approximately 79.8 k rad/s. Revisiting the stability boundaries predicted by the strained parameter approach, however, provides the requisite insight. Figure 7 presents the stability boundaries when we carry-out the strained parameter approach to the first- and second-orders. At the second order, which also necessitates the inclusion of third harmonic terms, \(K_2\) (and thus \(K^\prime \)) goes unbounded at the same point in frequency where the PER exhibits a local minimum. Examining the coefficient matrix \(\textbf{A}(3\omega ; K_0)\) evaluated near the local minimum frequency, we find that it has a zero eigenvalue at 79.7636 k rad/s. Since the determinant of a matrix equals the product of its eigenvalues, it is apparent that \(3\omega \) at this frequency satisfies an internal resonance condition. Further investigation of the internal resonance mechanism lies beyond the scope of this paper, but may offer an interesting direction for follow-on efforts.

Lastly, Fig. 8 presents the finite element validation and PWE forced response solutions for the single-jointed system, where we assess stability of the PWE solutions using the PER approach. We note strong agreement between the two approaches in both the predicted response and accompanying stability. Notably, at a forcing level of 45 MN, the ratio of nonlinear to linear restoring force at resonance is over 0.7, which is well-beyond the validity region for the WBVA and the strained parameter stability approach. However, the PWE combined with the PER stability approach accurately captures both the frequency response and the multiple solution stability at all amplitudes considered. This can be further contrasted with the poor performance of the finite-element substitution approach discussed earlier and documented in Fig. 9(a).

5 Concluding remarks

As pointed out by previous researchers, a direct analysis of stability has been lacking in the literature for nonlinear wave-based solution approaches. We address this deficiency by developing two direct approaches, and then apply the methods to determine solution stability of an harmonically forced, example two-bar system connected by a nonlinear joint. The first stability approach expands (or strains) a stiffness parameter in the problem, which allows one to construct analytical stability boundaries in the parameter space of the perturbed problem using a wave-based method. Not only does this determine stability of periodic solutions arising from direct excitation of a continuous system, but it also directly governs the response and stability of parametrically forced continuous systems, which is a new development in and of itself. The second stability approach is primarily a computational tool which searches for sign changes in the residue of the perturbed eigenproblem. The strained parameter approach holds for only moderate nonlinear response due to its reliance on an asymptotic expansion; the PER avoids this limitation and in fact is used to determine stability of periodic solutions at large nonlinear response.

We now list some avenues for future research that were identified during the course of this study. One issue with the PER approach, as presented herein, is that it can only determine locations of stability change, and does not assess stability directly. Therefore, a PER approach that can assess the latter warrants investigation. Further, the PER method described in this paper only involves a sufficient condition for the sign change. An investigation of the necessary conditions could potentially yield greater insights. Both stability approaches (strained parameter as well as PER) rely on Floquet theory, whose applicability for non-smooth problems is not very clear at this point. This will have to be studied in detail (see [10], for instance) to understand the theoretical limitations of the methods more clearly. The internal resonance observed in the single-jointed problem (see Fig. 6 and related discussions) should also be given additional attention.