Nonsmooth modal analysis via the boundary element method for one-dimensional bar systems

Abstract

A numerical scheme grounded on the Boundary Element Method expressed in the Frequency Domain is proposed to perform Nonsmooth Modal Analysis of one-dimensional bar systems. The latter aims at finding continuous families of periodic orbits of mechanical components featuring unilateral contact constraints. The proposed formulation does not assume a semi-discretization in space of the governing Partial Differential Equations, as achieved in the Finite Element Method, and so mitigates a few associated numerical difficulties, such as chattering at the contact interface, or the questionable approximation of internal resonance conditions. The nonsmooth Signorini condition stemming from the unilateral contact constraint is enforced in a weighted residual sense via the Harmonic Balance Method. Periodic responses are investigated in the form of energy-frequency backbone curves along with the associated displacement fields. It is found that for the one-bar systems, the results compare well with existing works and the proposed methodology stands as a viable option in the field of interest. The two-bar system, for which no known results are reported in the literature, exhibits very rich nonsmooth modal dynamics with entangled nonsmooth modal motions combining hardening and softening effects via the intricate interaction of various, possibly subharmonic and internally resonant, nonsmooth modes of the two bars.

1 Introduction

Within the framework of structural dynamics and continuum mechanics, linear modal analysis is a daily used tool in industry, aiming at predicting vibratory resonances of periodically forced mechanical systems by searching for continuous families of periodic solutions exhibited by the underlying autonomous system. However, various challenges arise when possibly large-scale nonlinear dynamical systems are targeted and for which nonlinear modal analysis is needed instead. Nonlinear modal analysis focuses on the description of Nonlinear Normal Modes, which are commonly defined as periodic motions of conservative unforced systems [10, 17]. Readers could refer to [26, 27] for comprehensive reviews. The present work targets structural systems where the nonlinearity is a nonsmooth (possibly multi-valued) function of the state of the system, such as a unilateral contact. Nonsmooth Modal Analysis (NSA) is an incarnation of modal analysis dedicated to this latter class of systems.

There is a vast literature on the topic of impact oscillators. Most commonly, the investigated systems are of very small dimension with very few degrees-of-freedom and governed by impulsive dynamics: the acceleration involves Dirac $\delta$ distributions in time with chattering occurrences in the solution as a notable consequence. However, in the framework of continuum mechanics, it is now established that, at least for the bouncing bar example [4], neither impulsive dynamics nor chattering exist in the solution. Accordingly, it is crucial to develop solution methods capable of handling the above considerations, which discards the classical Finite Element Method (FEM) because of two major difficulties: the need of an impact law which generates chattering [24] or the implementation of a penalization technique with questionable residual penetrations and the difficulty to properly quantify the penalty parameter. The issue stems from the distribution of mass notably at the contact interface. Recent FEM formulations relying on Nitsche’s method [2] for the contact constraints might have interesting numerical properties yet to be tested for NSA purposes.

In light of this, a few numerical schemes have been proposed to perform NSA of continuous systems. For instance, the Wave Finite Element Method (WFEM) with a switch on boundary conditions [31] could partially solve the case of a one-dimensional bar system. The developed scheme preserves energy but excludes continuation techniques in time because time and space are discretized concurrently in order to preserve the geometry of the characteristic lines in the D’Alembert solution. Moreover, it cannot easily be extended to higher dimensions. A solution based on the Time-Domain Boundary Element Method (TD-BEM) was also proposed [28]. However, it requires various computations involving initial condition and attendant space semi-discretization of the domain of interest: this is not optimal since it heavily reduces the computational efficiency of TD-BEM. It has also been proven that higher dimensional TD-BEM might become unstable in time.

In order to perform NSA, the present work suggests a numerical scheme which combines the Frequency-Domain Boundary Element Method (FD-BEM) to the Harmonic Balance Method (HBM). The governing equation in the frequency domain is exactly solved, and the Signorini boundary condition of unilateral contact is satisfied in an weighted-residual sense. Modes of vibration are then computed.

2 Systems of interest

The systems explored in the remainder are academic systems yet not reduced to very few degrees-of-freedom as classically done in vibro-impact dynamics. The aim is to show that the investigation of vibro-impact responses is not necessarily limited to small scale systems with very few degrees-of-freedom. However, we recognize that the systems considered are of limited interest in the industrial sphere even though NSA was initially motivated by aerospace applications [13]. It also has ramifications in areas like music instruments [8], breathers [9] or applied mathematics [21] to cite a few. More generally, vibration analysis is commonly conducted during the design of a mechanical component and it is now recognized that unilaterally contact conditions, when unavoidable, strongly affect the dynamics and cannot be ignored [22].

2.1 Non-dimensional analysis

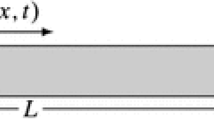
Three similar academic systems are considered in this work. They are depicted in Fig. 1a–c. The first two systems are simple one-dimensional bar with a Signorini condition at one of its boundaries and either a homogeneous Dirichlet or a Robin boundary condition otherwise. The third system embeds two one-dimensional bars facing each other through a common unilateral contact interface. The present works targets the periodic autonomous dynamics of such systems in the context of nonlinear and nonsmooth modal analysis. All systems of interest in this paper have space-independent Young’s modulus E, cross-sectional area A and density $\rho$.

Fig. 1

Unilaterally constrained mechanical vibratory systems of interest and corresponding physical quantities

The non-dimensional analysis is now introduced to later facilitate the exposition of the work and attendant analysis. The non-dimensional variables are introduced via an overbar notation which is then omitted: $\bar{\bullet }$ is the non-dimensional version of $\bullet$: $\bar{x}=x/L_1$, $\bar{y}=y/L_1$, $\bar{t}=t/\tau$, $\bar{u}=u/L_1$, and $\bar{w}=w/L_1$ with the characteristic time $\tau =L_1/c_1$ where $c_1=\sqrt{E_1/\rho _1}$. Derivatives of u are found using the chains rule: $u_{x}=L_1\bar{u}_{\bar{x}}\bar{x}_{x}=\bar{u}_{\bar{x}}$ and $u_{t}=L_1\bar{u}_{\bar{t}}\bar{t}_{t}=L_1\bar{u}_{\bar{t}}/\tau$. Higher derivatives can be found in a similar way: $u_{xx}=\bar{u}_{\bar{x}\bar{x}}/L_1$ and $u_{tt}=L_1\bar{u}_{\bar{t}\bar{t}}/\tau ^2$. For the second bar, when considered, we have $w_{t}=L_1\bar{w}_{\bar{t}}/\tau$ and $w_{tt}=L_1\bar{w}_{\bar{t}\bar{t}}/\tau ^2$. Meanwhile $\bar{c}=c_2/c_1$ and bar length $\bar{\ell }=L_2/L_1$ for the second bar are introduced. Non-dimensional boundary conditions are also applied. For the Robin boundary condition, non-dimensional spring stiffness $\bar{k}=k L_1/(E_1A_1)$ is introduced. Also, ratio $\alpha =E_1/E_2~A_1/A_2$ is introduced for two-bar contact condition.

In the remainder, the upper bar notation is dropped and all considered quantities are non-dimensional.

2.2 Governing equations

With the notations introduced above, the wave equation for the first bar reads

$$\begin{aligned} u_{tt}-u_{xx}=0,\quad x\in ]{0}\,;{1}[. \end{aligned}$$

(1)

Similarly, the governing equation of the second bar, when considered, is

$$\begin{aligned} w_{tt}-c^2w_{yy}=0,\quad y\in ]{0}\,;{\ell }[. \end{aligned}$$

(2)

2.3 Boundary conditions

2.3.1 Dirichlet–Signorini system

The first system of interest, in Fig. 1a, is clamped on the left so that a homogeneous Dirichlet boundary condition $u(0,t)=0$ applies. The condition $w(0,t)=0$ is also enforced for the two-bar system.

The nonsmooth periodic and autonomous dynamics of this system has already been investigated, numerically in [31] using WFEM and analytically in [25].

2.3.2 Robin–Signorini system

The second system of interest, in Fig. 1b, considers a Robin boundary condition at $x=0$, via a linear spring attaching the left tip of the bar to the rigid ground. This condition is expressed as follows:

$$\begin{aligned} -\,u_{x}(0,t)+k u(0,t)=0. \end{aligned}$$

(3)

The corresponding nonsmooth vibratory dynamics of this system has already been partially investigated using WFEM [30]. Compared to the previous Dirichlet–Signorini system, the Robin boundary condition annihilates the above full internal resonance condition featured by the first system in Fig. 1a, as aimed.

2.3.3 Signorini boundary condition

For the one bar case, unilateral contact on the right tip is a Signorini boundary condition. Defining $g(t)=g_0-u(1,t)$ as the gap and $g_0$ as the initial gap distance, it takes the form $g(t) \ge 0$, $u_{x}(1,t)\le 0$, and $g(t)u_{x}(1,t) = 0$ where the notation g(t) is a shortcut since g is not an explicit function of time t. By defining the Signorini residual $r(u(1,t),u_x(1,t))=u_{x}(1,t)+\max [a_{c}(u(1,t)-g_0)-u_{x}(1,t),0]$, where $a_{c}$ is an arbitrary strictly positive constant, they can equivalently be expressed as the equality [23]

$$\begin{aligned} r(u(1,t),u_x(1,t))=0. \end{aligned}$$

(4)

For the two-bar system, the Signorini residual comes with the equilibrium $u_{x}(1,t)=\alpha w_{y}(\ell ,t)$ at the contact interface and reads

$$\begin{aligned}&r(u(1,t),w(\ell ,t),u_x(1,t))\nonumber \\&\quad =u_{x}(1,t) \nonumber \\&\qquad +\max [a_{c}(u(1,t) \nonumber \\&\qquad +w(\ell ,t)-g_0)-u_{x}(1,t),0]. \end{aligned}$$

(5)

3 Solution method

A numerical scheme based on the Boundary Element Method is implemented. The BEM forms a family of methods for which the boundary of the domain of interest is the main ingredient of the formulation and full domain discretization is not required under the assumption of vanishing initial conditions and body forces [15]. It has the notable benefit of reducing the dimension of the formulation. Among the various incarnations of BEM, the FD-BEM combined with HBM is selected to perform nonsmooth modal analysis.

The FD-BEM, as its name implies, is a frequency-domain form of BEM which is appropriate when periodic solutions are targeted.

3.1 Fourier transform

The Fourier Transform along time of the displacement u(x, t) (an equivalent definition holds for w(y, t)) is

$$\begin{aligned} \hat{u}(x,\omega )=\frac{1}{2\pi }\int _{-\infty }^{\infty }u(x,t) \exp (-i\omega t)\mathrm{d}t \end{aligned}$$

(6)

and has two arguments, namely space x and frequency $\omega$. The wave Eqs. (1) and (2) accordingly transform into the well-known one-dimensional autonomous Helmholtz equations

$$\begin{aligned} \hat{u}_{xx}(x,\omega )+\omega ^{2} \hat{u}(x,\omega )&=0, \quad x\in ]{0}\,;{1}[ \end{aligned}$$

(7)

$$\begin{aligned} \hat{w}_{yy}(y,\omega )+\kappa ^{2} \hat{w}(y,\omega )&=0, \quad y\in ]{0}\,;{\ell }[ \end{aligned}$$

(8)

respectively, where $\kappa = \omega /c$ is the frequency number for the second bar.

3.2 BEM formulation

The methodology described below is provided for a single bar but can be adapted to the second bar in a straightforward fashion. It is very classical. FD-BEM is based on a weighted residual form of (7) where the weight function is the fundamental solution to the Helmholtz equation [11]. The formulations for the first bar will be derived at first for example. This fundamental solution is the distributional solution $\hat{u}^*_{xx}(x,\xi ,\omega )$ to

$$\begin{aligned} \hat{u}^*_{xx}(x,\xi ,\omega )+\omega ^{2} \hat{u}^*(x,\xi ,\omega ) =\delta (x-\xi ) \end{aligned}$$

(9)

which has a known closed-form solution

$$\begin{aligned} u^*(x,\xi ,\omega ) = \frac{1}{2 \omega } \sin (\omega |x-\xi |). \end{aligned}$$

(10)

The above Helmholtz equation is then transformed into an integral equation through the residual form [3]

$$\begin{aligned}&\int _{0}^{1}(\hat{u}_{xx}(x,\omega )+\omega ^2\hat{u}(x,\omega )) \hat{u}^{*}(x,\xi ,\omega ) \mathrm{d}x\nonumber \\&\qquad =0,\quad \forall \xi \in ]{0}\,;{1}[. \end{aligned}$$

(11)

Two integrations by parts with respect to x yield

$$\begin{aligned} \int _{0}^{1}\hat{u}_{xx}\hat{u}^{*}\mathrm{d}x =\hat{u}_{x}\hat{u}^{*}\Big |_{0}^{1}-\hat{u} \hat{u}^{*}_{x}\Big |_{0}^{1}+\int _{0}^{1} \hat{u}\hat{u}^{*}_{xx}\mathrm{d}x \end{aligned}$$

(12)

, and the residual form (11) becomes

$$\begin{aligned} \hat{u}_{x}\hat{u}^{*}\Big |_0^{1}-\hat{u}\hat{u}^{*}_{x} \Big |_{0}^{1}+\int _{0}^{1}(\hat{u}^{*}_{xx}+\omega ^{2} \hat{u}^{*})\hat{u}\mathrm{d}x=0. \end{aligned}$$

(13)

Recalling the definition of the Fundamental Solution (9), the integral part of Eq. (13) actually reads

$$\begin{aligned} \langle \hat{u}^{*}_{xx}+\omega ^{2} \hat{u}^{*},\hat{u}\rangle =\langle \delta _\xi ,\hat{u}\rangle =\hat{u}(\xi ,\omega ) \end{aligned}$$

(14)

in the distributional sense. In other words, the following equality holds:

$$\begin{aligned} \hat{u}(\xi ,\omega )&=\hat{u}_{x}(1,\omega )\hat{u}^{*}(1,\xi ,\omega ) -\hat{u}_{x}(0,\omega )\hat{u}^{*}(0,\xi ,\omega )\nonumber \\&\quad -\hat{u}(1,\omega ) \hat{u}^{*}_{x}(1,\xi ,\omega ) +\hat{u}(0,\omega ) \hat{u}^{*}_{x}(0,\xi ,\omega ). \end{aligned}$$

(15)

For the considered Helmholtz equation, substituting Identities (15) and (10) into Eq. (13) generates the targeted boundary integral equation (BIE)¹

$$\begin{aligned} 2\hat{u}(x,\omega&=\hat{u}(0,\omega )\cos \omega x+\hat{u}(1,\omega ) \cos (\omega (1-x)) \nonumber \\&\quad - \frac{1}{\omega }(\hat{p}(0,\omega )\sin \omega x\nonumber \\&\quad -\hat{p}(1,\omega )\sin (\omega (1-x))) \end{aligned}$$

(16)

where x and $\xi$ could be interchanged because they travel on the same domain. In Eq. (16), $\hat{p}(0,\omega )=-\hat{u}_{x}(0,\omega )$ and $\hat{p}(1,\omega )=\hat{u}_{x}(1,\omega )$ were used to follow the traditional notation in BEM, in the context of linear elasticity and small strains considered in the present work. The same time domain conventions are used in the remainder.

For the second bar, the BIE is

$$\begin{aligned} 2\hat{w}(y,\omega )&=\hat{w}(0,\omega )\cos \kappa y +\hat{w}(\ell ,\omega )\cos (\kappa (\ell -y))\nonumber \\&\quad - \frac{1}{\kappa }(\hat{q}(0,\omega )\sin \kappa y\nonumber \\&\quad -\hat{q}(\ell ,\omega )\sin (\kappa (\ell -y))) \end{aligned}$$

(17)

where $\hat{q}(\ell ,\omega )=\hat{w}_{y}(\ell ,\omega )$ and $\hat{q}(0,\omega )=-\hat{w}_{y}(0,\omega )$. Reading (16) on the boundary $\{0\}\cup \{1\}$ leads to the two linearly independent equations for the first bar

$$\begin{aligned}&\begin{bmatrix} \omega &{}\quad 0 &{}\quad -\omega \cos \omega &{}\quad \sin \omega \\ -\omega \cos \omega &{}\quad \sin \omega &{}\quad \omega &{}\quad 0 \end{bmatrix} \begin{pmatrix} \hat{u}(0,\omega ) \\ \hat{p}(0,\omega ) \\ \hat{u}(1,\omega ) \\ \hat{p}(1,\omega ) \end{pmatrix}\nonumber \\&\qquad =\begin{pmatrix} 0 \\ 0 \end{pmatrix}, \end{aligned}$$

(18)

and reading (17) on the boundary $\{0\}\cup \{\ell \}$ leads to the two linearly independent equations for the second bar

$$\begin{aligned}&\begin{bmatrix} \kappa &{}\quad 0 &{}\quad -\kappa \cos \kappa \ell &{}\quad \sin \kappa \ell \\ -\kappa \cos \kappa \ell &{}\quad \sin \kappa \ell &{}\quad \kappa &{}\quad 0 \end{bmatrix}\nonumber \\&\quad \begin{pmatrix} \hat{w}(0,\omega ) \\ \hat{q}(0,\omega ) \\ \hat{w}(\ell ,\omega ) \\ \hat{q}(\ell ,\omega ) \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{aligned}$$

(19)

Note that the above identities have been derived by solely transforming the wave equation, that is the local equation initially considered in our problem. They are exact and can be understood as a Frequency-Domain Boundary Element Method versions of D’Alembert’s solution to the wave equation, see Appendix 3. The boundary conditions at $x=0$ and $x=1$ (or $y=0$ and $y=\ell$) have yet to be used. The considered Dirichlet, Robin and Signorini boundary conditions will be inserted in the BEM formulation in the remainder.

It should be also understood that the identities (18) could be retrieved via the exact solution to Eq. (7) as briefly explained in Appendix 1. However, the above BEM format generalizes to higher dimensions in a more straightforward manner when the spatial domain of interest is not a simple geometric shape.

Also, identities (18) somewhat indicate the superiority of BEM formulations to FEM formulations in the context of unilateral contact dynamics, at least in the present one-dimensional framework. More precisely, and as already said in the introduction, a classical FEM formulation would transform the initially continuous nature of mass and inertia of the system into a discrete version, from which emerge difficult theoretical questions at the contact interface, and most notably the need of a possibly dissipative impact law. BEM does not suffer this drawback [6] and is capable of handling the Signorini conditions (4) without additional conditions, as explained in Appendix 2.

3.3 Periodicity in time

3.3.1 Fourier series

Periodicity in time of the sought solution is enforced by taking advantage of (18) showing that only quantities at the boundary are left as unknowns. Accordingly, let us seek the displacement u(1, t) and companion strain p(1, t), with a common frequency $\Omega$ in the forms of two distinct Fourier series

$$\begin{aligned} p(1,t)&= \frac{1}{2} a_{0}+\sum _{n=1}^{\infty }a_{n}\exp (j n\Omega t) \quad \text {and}\quad u(1,t) \nonumber \\&= \frac{1}{2} b_{0}+\sum _{n=1}^{\infty }b_{n} \exp (jn\Omega t) \end{aligned}$$

(20)

where the complex coefficients $a_n$ and $b_n$ are the new unknowns of the problem. The corresponding Fourier Transforms read

$$\begin{aligned} \hat{p}(1,\omega )&=\frac{1}{2}a_{0}\delta _0+\sum _{n=1}^{\infty }a_{n} \delta _{n\Omega }\quad \text {and}\quad \hat{u}(1,\omega )\nonumber \\&=\frac{1}{2}b_{0}\delta _0+\sum _{n=1}^{\infty }b_{n} \delta _{n\Omega }. \end{aligned}$$

(21)

Similar assumptions are made for the second bar in the bilateral contact case, yielding:

$$\begin{aligned} q(\ell ,t)&= \frac{1}{2} d_{0}+\sum _{n=1}^{\infty }d_{n} \exp (j n\Omega t)\quad \text {and}\quad w(\ell ,t)\nonumber \\&=\frac{1}{2} f_{0}+\sum _{n=1}^{\infty }f_{n}\exp (jn\Omega t)\nonumber \\ \hat{q}(\ell ,\omega )&= \frac{1}{2}d_{0}\delta _0 +\sum _{n=1}^{\infty }d_{n} \delta _{n\Omega }\quad \text {and} \quad \hat{w}(\ell ,\omega ) \nonumber \\&=\frac{1}{2}f_{0}\delta _0 +\sum _{n=1}^{\infty }f_{n} \delta _{n\Omega }. \end{aligned}$$

(22)

3.3.2 Boundary conditions

Here, the treatment of each boundary condition is discussed separately. Since the configurations of interest include different combinations of boundary conditions, the numerical solution procedure of each combination will be discussed later along with the discretization strategy.

3.3.3 Dirichlet boundary condition

Inserting the homogeneous Dirichlet boundary condition $u(0,t)=\hat{u}(0,\omega )=0$ into (18) implies

$$\begin{aligned} -\omega \cos \omega \,\hat{u}(1,\omega )+\sin \omega \hat{p}(1,\omega )=0. \end{aligned}$$

(23)

Equation (23) features infinitely many singularities when the $\omega \cos \omega$ or $\sin \omega$ terms vanish. Such singularities $\omega$ actually correspond to the natural frequencies of the Dirichlet–Neumann and Dirichlet–Dirichlet bar, respectively. Such frequencies are actually avoided in the remainder since the solutions of interest lie “between” these two extreme bar configurations where the contact gap is either always open or always closed. It is worth to state that Eq. (23), which dictates relationships between Fourier Transforms evaluated at $x=1$, stems from a boundary condition at $x=0$.

Inserting (21) into (23) leads to a system of linear equations in the coefficients $(a_n,b_n)$, $n=0,1,2,\ldots$ of the form

$$\begin{aligned} -\omega _{n}\cos \omega _{n}\,b_{n} +\sin \omega _{n}\,a_{n} =0\quad \text {with}\quad \omega _{n}=n\Omega . \end{aligned}$$

(24)

A counterpart obviously exists for the second bar in the form

$$\begin{aligned} -\kappa _n \cos \kappa _n \ell \,f_{n}+\sin \kappa _n \ell \,d_{n} =0\quad \text {with}\quad \kappa _{n}=n\Omega /c. \end{aligned}$$

(25)

3.3.4 Robin boundary condition

In the frequency domain, the Robin boundary condition becomes $k\hat{u}(0,\omega ) +\hat{p}(0,\omega )=0$. This condition is inserted in (18) to form the extended system

$$\begin{aligned}&\begin{bmatrix} \omega &{}\quad 0 &{}\quad -\omega \cos \omega &{}\quad \sin \omega \\ -\omega \cos \omega &{}\quad \sin \omega &{}\quad \omega &{}\quad 0\\ k &{}\quad 1&{}\quad 0&{}\quad 0 \end{bmatrix} \begin{pmatrix} \hat{u}(0,\omega ) \\ \hat{p}(0,\omega ) \\ \hat{u}(1,\omega ) \\ \hat{p}(1,\omega ) \end{pmatrix}\nonumber \\&\qquad =\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \end{aligned}$$

(26)

which simplifies to

$$\begin{aligned} \omega (\omega - k \cot \omega )\hat{u}(1,\omega ) +(k+\omega \cot \omega )\hat{p}(1,\omega ) =0. \end{aligned}$$

(27)

Again, the singularities in $\omega$, already mentioned for the Dirichlet boundary condition, correspond to the natural frequencies of the Robin–Neumann and Robin–Dirichlet bar, respectively [20] and are avoided in the remainder. Plugging (21) into (27) leads to a system of linear equations of the form

$$\begin{aligned} \omega _n(\omega _n - k \cot \omega _n)b_n+(k+\omega _n\cot \omega _n)a_n=0. \end{aligned}$$

(28)

It is important to mention here that the choice for the Fourier Series (20) is natural when periodic solutions are of interest but is also motivated by the Fourier Transform used in the formulation. This has the nice consequence that the Dirichlet and Robin boundary conditions above have simple forms and can be satisfied exactly in the frequency domain, at least up to the last considered harmonic in the computations. This Fourier choice has a drawback: the possibility to have Gibbs “spurious” oscillations in the approximated solutions, at least in the velocity fields and contact force. Instead, other periodic families could be implemented, within the theory of Wavelets for instance. However, combined to the chosen Fourier Transform formalism, identities like (25) or (28) cannot be readily derived and instead the boundary condition would have to be enforced in a Weighted Residual sense as done for the Signorini condition below.

3.3.5 Signorini boundary condition: unilateral contact

Unlike the above Dirichlet and Robin boundary conditions which can be explicitly expressed in terms of the unknown Fourier coefficients, the Signorini condition has no explicit form in the frequency domain. Instead, a numerical version of the Harmonic Balance Method is performed on (4) where expansions (20) are first inserted. This can be recast in the system of nonlinear implicit equations in the coefficients $(a_n,b_n)$, $n=0,1,2,\ldots$ (gathered in vectors $\mathbf {a}$ and $\mathbf {b}$)

$$\begin{aligned} g_n(\mathbf {a},\mathbf {b})&=\int _{0}^{T} \exp (jn\Omega t) \bigl (p(1,t)\nonumber \\&\quad +\max [a_{c}(u(1,t)-g_0)-p(1,t),0]\bigr )\nonumber \\&\qquad \mathrm{d}t = 0,\quad n=0,1,2,\ldots \end{aligned}$$

(29)

where $T=2\pi /\Omega$ is period of targeted periodic motion. In other words, the Signorini condition is satisfied in a weighted residual sense only, as achieved in any Galerkin-like strategy.

Fig. 2

One-bar system: HBM residuals $g_0$ (red) and $g_1$ (blue) with only one constant term (participation $a_0$) and one cosine term (participation $a_1$) in the Fourier series and Signorini residual projections (29). Participation $a_0=0$ in the right plot

A graphical example illustrates the nonsmoothness of Eq. (29). The Fourier series is limited to only one cosine term of magnitude $a_1$ and one constant term of magnitude $a_0$. The integrals in Eq. (29) are functions of the pair $(a_0,a_1)$. These two surfaces are plotted in Fig. 2. Their expected piecewise nature, induced by the $\max$ operator in the complementarity condition, shows lines where they do not seem to be differentiable in the classical sense, even though a thorough analysis would be needed here. They also intersect with the zero plane at the same point showing that a solution exists in this case. For the two-bar system, contact equilibrium reads

$$\begin{aligned} a_n=\alpha d_n,\quad \forall n \end{aligned}$$

(30)

Complementary enforced in a manner similar to Eq. (29) reads

$$\begin{aligned} g_n(\mathbf {a},\mathbf {b},\mathbf {f})&=\int _{0}^{T} \exp (jn\Omega t)\bigl (p(1,t)\nonumber \\&\quad +\max [a_{c}(u(1,t) +w(\ell ,t)-g_0)\nonumber \\&\quad -p(1,t),0]\bigr ) \nonumber \\&\qquad \mathrm{d}t = 0,\quad n=0,1,2,\ldots \end{aligned}$$

(31)

In Eq. (31), complementarity is enforced on p(1, t) and g(t). The complementarity between $q(\ell ,t)$ and g(t) is enforced through (30) along with (31).

As stated previously for the other boundary conditions, and to avoid the Gibbs phenomenon in the solution, other families of periodic functions could be considered for the test and trial functions in (29) and (31). The gain in how the Signorini conditions will be satisfied might be mitigated by the fact that other boundary conditions (Dirichlet or Robin) will not be exactly satisfied as with Fourier series: this has yet to be clarified.

3.4 Discretization and numerical approximation

Discretization comes into the proposed solution strategy when the Fourier expansions (20) are truncated to a finite number m of harmonics, such that we define ${u^{(m)}(1,t)}\approx u(1,t)$ and ${p^{(m)}}(1,t)\approx p(1,t)$. A second level of discretization lies in the computation of the integrals (29). It was found that the computed solutions were not sensitive to that numerical aspect. Accordingly, it was decided to compute the integrals (29) via a simple Riemann sum approximation with a subinterval $\Delta t=T/(n_h m)$ where T is targeted motion period, and $n_h$, a coefficient governing the accuracy of the approximation and chosen as $n_h = 30$ after a convergence check.

The system of nonlinear equations in $(\mathbf{a},b)$, and $(\mathbf{a},b,d,f)$ for the two-bar system, is then solved numerically using a trust-region dogleg [19] solver, a built-in numerical solver of Matlab®, even though the equations are not expected to be sufficiently smooth, due to (29). For the Dirichlet–Signorini case, the system is formed by Eqs. (24) and (29). For the Robin–Signorini case, the system is formed by Eqs. (28) and (29). The two-bar system involves Eqs. (24), (25), (30) and (31).

3.5 Continuation

Once discretization is achieved, the task of finding periodic solutions translates into an equivalent multidimensional root finding problem of the form $\mathbf {F}(\mathbf {a},\mathbf {b}, \Omega )=\mathbf {0}$, where $\Omega$ is the unknown fundamental frequency of the Fourier series. To search for continuous families of periodic solutions and construct the desired solution branches, continuation techniques shall be implemented.

In this work, the classical sequential continuation technique [16] is used where $\Omega$ is successively increased by a small given increment on a given interval of interest: the nonlinear system is solved for the Fourier coefficients only. This technique is not able to handle turning-points in the skeleton curve [17]. Even though turning-points were not found for the considered systems, the pseudo-arclength method [7, 17], where $\mathbf {a}(s)$, $\mathbf {b}(s)$ and $\Omega (s)$ are functions of the arclength s, was also attempted for comparison purposes. In both approaches, numerical difficulties are expected due to the lack of smoothness in the system.

It should be noted that the proposed FD-BEM/HBM formulation nicely transforms the initial problem into a set of, yet nonsmooth, nonlinear equations for which continuation can be performed, at least in a piecewise fashion for continuation branches bounded by grazing solutions. This is in contrast to the fully discrete WFEM technique [31] where integer quantities are searched for, thus prohibiting the use of continuation strategies. Furthermore, the developed solution technique is not sensitive to the number of contact occurrences in the solution whereas WFEM is.

4 Results

Vibratory responses generated by the proposed FD-BEM can be compared to existing results for the one-bar systems, see [14, 25, 28,29,30,31]. The initial gap $g_0 = 0.001$ is used for all cases in this section, along with $a_{c} = 4$ in the definition of the Signorini residual functions. The solutions were not found to be really sensitive to $a_{c}$. Also, in all Fourier expansions and projections, only the constant and cosine terms were considered. This has the detrimental consequence of removing all solutions which are not even in time, even though they are known to exist [25]. However, this choice advantageously reduces the number of unknowns to be handled by the solver and also mitigates the numerical issues induced by the solution non-uniqueness [25]. All quantities defined above in the Fourier series and HBM projections are thus real.

In the coming sections, displacement fields are first shown as 3D plots for the one-bar system. They later are shown as in-plane 2D plots for the two-bar system because their 3D counterparts become meaningless. Both views are indicated in Fig. 3 for a given displacement field.

Fig. 3

Proposed illustrations and displacement fields

Fig. 4

Signorini boundary condition (4): Exact solution  and FD-BEM with $m=20$  and $m = 80$ . Bar displacement at the contact interface [left] and complementarity condition [right]. (Color figure online)

The energy-frequency plots in the coming sections are normalized. For the one-bar systems, the energy of vibration is normalized with respect to the energy of the first linear grazing mode. For the two-bar systems, the energy of vibration is normalized with respect to the first linear grazing mode of bar 1 (on the left).

4.1 Accuracy and convergence analysis

The analysis is conducted on three main aspects: the accuracy of the contact force, the convergence of an energy residual and comparison with existing solutions, all with respect to m.

Compared to known results [28, 31] and as expected, FD-BEM exhibits residual penetration at the contact interface, as shown in Fig. 4. This is explained by the fact that FD-BEM enforces the Signorini boundary condition in weighted residual sense only, through (29), in contrast with the TD-BEM and WFEM formulations where the complementary condition is enforced at every time step of the scheme, in a quasi-exact fashion up to a chosen tolerance. Another factor of error is the already mentioned Gibbs phenomenon, also observed in Fig. 4. It is expected to emerge on discontinuous functions like the strain and velocity fields within the bar, or the contact force, known to be piecewise continuous functions with a countable number of discontinuities when contact closes and opens [32]. This is not necessarily an issue since the convergence of interest in the present work is on the computed backbone curves, which are less sensitive to the above concerns (Fig. 5).

Fig. 5

Convergence analysis of the FD-BEM formulation. Error $R^{(m)}$ defined in Eq. (32)

Figure 6 compares time histories of the displacement, contact force and Signorini residual defined in Eq. (4) to the exact solution on the first nonsmooth mode. Again, small discrepancies emerge in the contact force, and to a lesser degree, in the displacement. Bear in mind that the Gibbs phenomenon in the displacement field is negligible and barely visible in all plots provided in the sequel. The small amplitude and high frequency waves for instance in Figs. 9, 12 or 14 are generated by internally resonant mechanisms in the solutions.

Fig. 6

Boundary displacement u(1, t)  and strain $u_x(1,t)$  along with Signorini residual r  for a periodic solution with active contact: $m=20$ [left], $m=40$ [center] and exact solution [right]. $T = 3.5$. (Color figure online)

Finally, convergence analysis is also conducted on the $L^2$-norm of the Signorini residual

$$\begin{aligned} R^{(m)} = \sqrt{\int _0^T r(u^{(m)}(1,t),p^{(m)}(1,t))^2 \mathrm{d}t} \end{aligned}$$

(32)

which depends on m. The convergence plot is shown in Fig. 5 for one solution located on the branch of the first nonsmooth mode (NSM) along with the corresponding period T. As expected, the error decreases with increasing m, following the rate of convergence ${\mathcal {O}}(1/m)$ exhibited by the Fourier series of a square wave, which here emerges in the contact force, that is in the function $u_x(1,t)$. Overall, it seems fair to state that the FD-BEM results can be read with a sufficient level of confidence even though the authors are aware of convergence issues in the HBM, for discrete systems [1, 5] at least.

4.2 Dirichlet–Signorini bar system

The system in Fig. 1a is considered. Backbone curves and corresponding displacement fields of low frequency modes are shown in Fig. 7. The provided results agree well with existing ones [18, 31]. In the displacement field, the participation of minor spurious high-frequency waves is caused by the truncation in the Fourier series and reduces by increasing m. Instead, in the velocity field and contact force, the Gibbs phenomenon is non-negligible due to the contact-induced discontinuities in those functions.

Fig. 7

Nonsmooth modal analysis of the Dirichlet–Signorini bar via FD-BEM with $m=20$

In Fig. 7a, the three shown backbone curves, computed via sequential continuation, show small spikes at certain frequencies. This aspect was explored in more details for the first NSM continuation curve, recomputed via both sequential and arclength continuations in Fig. 8. The general look of the low energy solutions as a function of $\Omega$ is the same and converges with m. However, the number of the small spikes increases with m. This is caused by the occurrences of internal resonances, a classical phenomenon in nonlinear systems where two or more modes interact together [12]. The Dirichlet–Signorini bar system is known to exhibit a full internal resonance condition since all the eigenvalues $\omega _k$ (or natural frequencies) of its linear Dirichlet–Neumann counterpart are commensurate to the first eigenvalue $\omega _1$ [31, Section 6.3]. Three different instances of such resonances are shown in Figs. 9a–c. In Fig. 9a around $8/7\omega _1$, the first NSM interacts with the fourth NSM. In other words, the first NSM illustrated in Fig. 7b is modulated by another NSM of higher frequency. Such a phenomenon has already been observed numerically [31] and is investigated analytically in [25].

Fig. 8

First NSM backbone curve: sequential [] and arclength [] continuation. (Color figure online)

Fig. 9

First NSM internally resonant solutions of the Dirichlet–Signorini bar with $m=40$

The sequential continuation is incapable of following vertical branches with constant $\Omega$ while arclength continuation can and so is more adapted to internal resonance branches, at least in principle. However, there is an issue in the investigated system: the existence of infinitely many internal resonances located at every rational number in the considered frequency range [25]. Many of these branches are annihilated by the truncated number of Fourier harmonics m but still, this mechanical feature strongly affects the arclength continuation procedure which is systematically attracted by such internal resonance branches. This has the detrimental effect of causing systematic continuation stalls between internal resonance branches such that the arclength continuation is not even able to capture the main, i.e., low energy, backbone curve, without frequent and user-control restarts of the procedure. This obviously becomes more severe with increasing m. Arclength continuation was accordingly discarded.

4.2.1 Terminology for nonsmooth modes

It is now convenient to better define the terminology characterizing the computed nonsmooth modes (NSM) of vibration, as used in the remainder of the paper. A (main) NSMi, $i=1,2,\ldots$, is a low-energy solution along a computed backbone curve located in the vicinity of the natural frequencies $\omega _i$ of the underlying linear system such as the solutions in Fig. 7b for $i=1$, or 7d for $i=2$ with one noticeable vibration node in space. A subharmonic k of NSMi, $k=1,2,\ldots$, is a low energy solution along a backbone curve located in the vicinity of $\omega _i/k$². The terminology “NSMi subk” is used in the remainder. An instance is provided in Fig. 7c for $i=2$ and $k=2$. The other possible solutions involve internal resonances. In the frequency-energy plots, they are located above the low-energy skeleton curves, i.e., with higher energies of vibration. They are challenging to compute but commonly emanate from a main NSMi and are characterized by the participation of higher-frequency NSMj with $j>i$ or NSMj subk with $j/k>i$, such as illustrated in Figs. 9a–c.

4.3 Robin–Signorini bar system

In this section, the system shown in Fig. 1b is considered with the non-dimensional stiffness $k=0.5$ in the Robin boundary condition. The first three natural frequencies of the system are $\omega _1$, $\omega _2\approx 5.09\omega _1$, and $\omega _3\approx 9.74\omega _1$.

The backbone curves exposed in Fig. 10, for the NSM1, can be compared to the configuration $\alpha =1/2$ in [30]. Both methodologies generate very similar outputs. However, in [30], a gap exists in the frequency interval, before $\omega _2/4$, where no solution could be found. The developed FD-BEM scheme is able to find solution in that frequency interval, but it is too early to really firmly state which of the methodologies is correct. Coming back to FD-BEM, the low energy backbone curves for $m=20$ and $m=40$ agree well, even though more interval resonances are detected for $m=40$, as expected. Also, the motion in Fig. 11 [center] compares very well with the motion reported in [30, Figure 1.4 (left)].

Fig. 10

NSM1 backbone curve of the Robin–Signorini bar via sequential continuation

Fig. 11

NSM1 of the Robin–Signorini bar with $m=40$: points a [left], b [center] and c [right] in Fig. 10b

The backbone curve corresponding to the second NSM can also be found by FD-BEM and sequential continuation, see Fig. 12. It compares favorably with [29, Figure 5.9] for $\alpha =1/2$. Clearly, internally resonant mechanisms are expected again but tracking them numerically is not an easy task. Their number increases with m, but their magnitude is limited here.

Fig. 12

NSM2 of the Robin–Signorini bar via sequential continuation. Backbone curve [left] together with solutions at points e [center] (low energy) and d [right] (internal resonance)

A subharmonic backbone curve is reported in Fig. 13 and corresponds to NSM2 sub3. In order to maintain accuracy in the results, the number of Fourier harmonics in the solution is set to $m=60$. Such a motion exhibits three, possibly grazing, contact occurrences per period along with one vibration node in space, as shown in Fig. 13.

Fig. 13

NSM2 sub3 of the Robin–Signorini bar with $m=60$. Backbone curve [left], point g with one contact and two grazings per period [center] and point f with two contacts and one grazing per period [right]

4.4 Two-bar system

In this section, the modal response of the two-bar system in Fig. 1c is explored for three distinct configurations defined by the triplet ($\ell$, c, $\alpha$) with $m=20$. A magnification factor is indicated for every plotted displacement field. Bar 1 is the bar on the left, while bar 2 is the bar on the right, see Fig. 1c, and the Signorini boundary positions $x=1$ and $y=\ell$ are marked with dashed lines on the shown displacement fields.

It should be noted that the dynamics observed in the bar responses is very rich and a thorough examination is out-of-scope of this paper. This part of the work plays the role of a proof-of-concept of the developed methodology and the analysis is focused on the similarities shared with the one-bar systems.

4.4.1 Linear modal analysis

The linear modes of the two-bar system are essentially the linear modes of the Dirichlet–Neumann one-bar systems taken separately. More exactly, the first linear mode of the two-bar system considered as a whole is the first linear mode of one bar, while the other bar is at rest. The linear modes of the whole system can then be identified by separately ranking all natural frequencies $\omega _i^{(j)}$, i.e., natural mode i of bar j (i being any strictly positive integer and $j=1$ or 2), from low frequency to high frequency. In other words, it is possible to uniquely define a one-to-one sequence of natural frequencies for the whole two-bar system by properly ranking the natural frequencies of the one-bar subsystems $j=1,2$ as, for instance: $(\omega _1,\omega _2, \omega _3,\ldots )=(\omega _1^{(1)},\omega _1^{(2)},\omega _2^{(1)}, \omega _3^{(1)},\omega _2^{(2)},\ldots )$, ranking which depends on the mechanical properties of each bar. In this contribution, it was decided to keep the notation $\omega _{i}^{(j)}$. This is a bit questionable, and this affects the coming analysis as follows: by assuming that $\omega _1=\omega _1^{(1)}<\omega _1^{(2)}=\omega _2$, the sentence “the first mode of bar 1 interacts with the first mode of bar 2” could identically be rephrased as “the first mode of the two-bar system interacts with the second mode of the two-bar system” and the color scheme used in the first part of the paper (green for NSM1, red for NSM2 and yellow for subharmonic NSM) becomes obsolete.

4.4.2 First configuration

The triplet ($\ell = 0.95$, $c = 1$, $\alpha = 1$) is chosen so that $\omega _1^{(1)}\lessapprox \omega _1^{(2)}$. The corresponding backbone curves are shown in Fig. 14a keeping the already used color scheme. Displacement fields are selectively chosen in the considered frequency range. First, it should be noted that the first computed low-frequency backbone curve does not seem to exist in the vicinity of $\omega _1^{(1)}$ and $\omega _1^{(2)}$, in contrast with the one-bar systems. This should be confirmed by further investigations. Second, the main low-energy backbone curve has an hardening trend. All solutions found in the frequency range $[\omega _1^{(2)};\tfrac{4}{3}\omega _1^{(2)}]$ involve NSM1 and possibly internal resonances of each bar (Fig. 14b–e). In other words, only motions without any zero-displacement nodes in space, or node of vibration, are observed (even though internal resonances tend to hide this), hence the selected green color. For instance, the motion of the first bar in Fig. 14e exhibits an internal resonance between NSM6 and NSM1, while the motion of the second bar shows an internal resonance of NSM4 with NSM1, probably with the residual participation of a higher frequency mode which is not easy to distinguish.

Fig. 14

First and second NSMs, and internal resonances, for ($\ell =0.95$, $c = 1$, $\alpha =1$)

NSM2 is also captured by FD-BEM as shown in right handside of Fig. 14a. Associated modal motions feature one node of vibration, clearly distinguishable in Fig. 14f, g. This NSM2 branch includes two subbranches, both of the hardening type. The first one starts in the vicinity of $\omega _2^{(1)}$, and the displacement field is shown in Fig. 14f. Interestingly, the solutions depicted in Fig. 14f and, to a lesser degree in Fig. 14g feature one bar in extension while the other bar is in compression during contact. All other solutions involve two bars in extension during contact. In this configuration, the first bar exhibits hardening, while the second bar shows softening and involves an internal resonance. On the second skeleton curve, two NSM2 of the hardening type interact together as shown in Fig. 14g, with a minor internal resonance in the first bar.

In order to highlight the difference with the one-bar systems, the response at the contact interface is indicated in Fig. 15. The main conclusion, and this is obviously expected, is that the contact interface now moves and depends on the solution, while it is fixed by the rigid foundation for the one-bar systems. This is clear in Fig. 15b.

Fig. 15

Strain (dotted) and position (solid) at the contact interface: bar 1  and bar 2 . (Color figure online)

Finally, and in order to support the above statements, FD-BEM is compared to a time-marching scheme based on the Time-Domain BEM combined with the floating boundary method to handle unilateral contact conditions [28]. Solution 14b at $t=0$ is used as an initial condition in the time-marching procedure, and the final state at $t=T$ is compared to the initial state for periodicity. The time-step for the TD-BEM simulation is set to $\Delta t=0.01$ in such a way that bar 1 has 100 elements in space while bar 2 has 95 elements. The corresponding displacement field and contact force are shown in Fig. 16, in the same scale as results of FD-BEM in Fig. 15a. It should be indicated that the TD-BEM solution is almost but not exactly periodic. The maximum difference between the initial and final states is less than $2\%$. Overall, TD-BEM and FD-BEM generated responses that bear a very strong resemblance. Only the contact forces are slightly different in pattern but similar in scale. The difference is mainly caused by how the Signorini condition is enforced, in a time-step fashion in TD-BEM and in an integral sense in FD-BEM.

Fig. 16

TD-BEM results with initial conditions specified by FD-BEM solution

4.4.3 Second configuration

The triplet ($\ell =3.8$, $c=4$, $\alpha =4$) is chosen. Compared to the first configuration, the second bar has different mechanical properties but shares the same natural frequencies as in configuration 1. The goal of the chosen triplet is to observe how the nonsmooth modal response is affected by the design rather than the linear modal signature of the system. The contribution of internal resonance along the first NSM main backbone curve is much less dominant than that in the first case. A displacement field is shown in Fig. 17 similar to Fig. 14b. Overall, the energy-frequency skeleton curves for NSM1 and NSM2, shown in Fig. 17a, share obvious similarities with their counterparts for configuration 1, with stiffening as the driving feature. In other words, the linear modal signature seems to dominate the design features in how the nonlinear system behaves.

Fig. 17

First NSM for $\ell =3.8$, $c = 4$ and $\alpha =4$

4.4.4 Third configuration

The triplet ($\ell =0.95$, $c=2$, $\alpha =1$) is chosen such that the first natural frequencies $\omega _1^{(1)}$, $\omega _1^{(2)}$ and $\omega _2^{(1)}$ are not in vicinity of each other (actually $\omega _1^{(2)}\approx 2.11\omega _1^{(1)}$). In contrast to the two first configurations, this system is shown to exhibit NSMs which combine NSM1 of one bar, possibly with the participation of internal resonance (green) with NSMj subk of the second bar (yellow). Accordingly, the backbone curve, shown in black in Fig. 18a, can no longer be colored in terms of the NSM category (that is green, yellow and red) as done in the previous sections. However, the displacement field plots keep the original color scheme in order to identify the motion NSM category in each bar, separately.

Fig. 18

NSM for ($\ell = 0.95$, $c=2$, $\alpha =2$) where NSM1 of bar 2 [] interacts with various subharmonic NSM of bar 1 []. (Color figure online)

The first family of NSMs is found in the range $[\omega _1^{(1)};1.13 \omega _1^{(1)}]$. The corresponding motion consists of one period of the NSM1 in bar 1 and various motions in bar 2, as detailed below. In the frequency range $[\omega _1^{(1)};\tfrac{1}{2}\omega _1^{(2)}]$, bar 2 exhibits softening along NSM1 sub2 and mainly acts in compression during contact as shown in Fig. 18b. It should be noted that point a in Fig. 18a is almost located in the middle of the frequency interval $[\omega _1^{(1)}; \tfrac{1}{2}\omega _1^{(2)}]$ whose bounds are close to each other. The system seems to find a balance between hardening in bar 1 and softening in bar 2. In the frequency range $[\tfrac{1}{2} \omega _1^{(2)};1.13\omega _1^{(1)}]$, bar 2 exhibits NSM1 in compression during contact, as indicated in Fig. 18c. Point b in Fig. 18a is located in the interval $[\tfrac{1}{2}\omega _1^{(2)};1.13\omega _1^{(1)}]$ but quite far from the upper bound. This seems to imply that the hardening effect in bar 1 dominates the softening effect in bar 2 so that the motion exists at the given frequency. Also, the transition from point a to point b is smooth: the behavior in bar 1 is not really affected but bar 2 continuously morphs from NSM1 sub2 (yellow) to NSM1 (green).

The second family of NSMs is found to lie in the frequency range $[\omega _1^{(2)};1.25 \omega _1^{(2)}]$. The corresponding motion consists of NSM1 in bar 2 (green) along with various subharmonic NSM in bar 1 (yellow): for example, NSM6 sub5 ($\approx \tfrac{1}{5}\omega ^{(1)}_6$) with softening effect in Fig. 18d; NSM3 sub2 ($\approx \tfrac{1}{2}\omega ^{(1)}_3$) with softening effect in Fig. 18e; NSM3 sub2 with hardening effect in Fig. 18f. The transition between subharmonics leads to a discontinuous backbone curve as well as frequency intervals where periodic solutions could not be found. For example, discontinuities are clear around $\tfrac{1}{5}\omega _6^{(1)}$ or for frequencies slightly lower than $\tfrac{1}{2}\omega _3^{(1)}$.

5 Conclusion

In this paper, a solution methodology relying on a Frequency-Domain formulation of the Boundary Element Method (FD-BEM) combined to the Harmonic Balance Method (HBM) is introduced to perform Nonsmooth Modal Analysis of one-dimensional bar systems. It is shown to be computationally efficient at the cost of satisfying the Signorini boundary conditions in a weighted residual sense only.

Nonsmooth modes are computed for a single Dirichlet–Signorini bar, a single Robin–Signorini bar, both constrained at one end by a rigid foundation, and two Dirichlet–Signorini bars interacting through a common unilateral contact interface. Various modal responses are investigated, and the findings for the single-bar system compare well with existing solutions reported in the literature confirming the reliability of the proposed procedure.

The modal dynamics of the two-bar system is very rich. Only a very partial overview could be provided. However, it includes the intricate interaction of nonsmooth modal motions within each bar with entangled hardening and softening mechanisms which do not seem to arise in nonlinear yet smooth mechanical systems.

The proposed formulation is energy-preserving by construction and could be extended to higher dimensional elasticity systems. However, additional challenges are expected in tracking Nonsmooth Modes of Vibration for such systems:

• The boundary of 1D problems does not need discretization since it reduces to a set of points. However, 2D/3D problems require spatial discretization of their boundary, thus adding an additional level of approximation in the solution.

• In the proposed implementation, a homogeneous system is assumed and an exact fundamental solution exists, which is highly beneficial. For 1D/2D/3D non-homogeneous elasticity problems, the fundamental solution might not have an analytical expression or might not exist at all. Instead, a scheme extending the alternate frequency-domain formulation given in Appendix 1 could be implemented through the use of the Finite Element Method for instance to approximate the solution to the counterpart of the Helmholtz equation. This might affect the convergence of the proposed algorithm, and BEM might not be as beneficial as in the present study. Moreover, it is known that the Finite Element Method implemented in unilaterally constrained systems is not necessarily well-posed in dynamics and should be complemented with an impact law, in the form of Newton’s law for instance [4]. It is not clear whether this aspect could affect the proposed formulation. It is possible that searching for periodic solutions with constant energy is sufficient for the well-posedness and the above impact law could be discarded. More work is needed on this important topic.

• In 1D elasticity problems, only p-waves exist. In 2D/3D elasticity problems, the targeted solutions combine both p- and s-waves. This might also affect the convergence of the proposed methodology.

To summarize, 2D/3D systems involve additional challenges when it comes to Nonsmooth Modal Analysis. Such challenges will be investigated in a coming work.

Appendices

Appendix 1: Alternate equivalent frequency-domain formulation

It is possible to retrieve Expression (18) without relying on the developed FD-BEM formulation. The Fourier Transform (6) of the displacement and the resulting Helmholtz Eq. (7) are considered. The general solution to the Helmholtz Eq. (7) is $\hat{u}(x,\omega )=A\cos \omega x+B\sin \omega x$ which induces $\hat{u}_{x}(x,\omega )=-\omega A\sin \omega x+\omega B\cos \omega x$. Reading the two previous identities on the boundary $\{0\}\cup \{1\}$ leads to

$$\begin{aligned}&\hat{u}(0,\omega )=A\nonumber \\&\hat{u}(1,\omega )=A\cos \omega +B\sin \omega \nonumber \\&\hat{u}_{x}(0,\omega )=\omega B=-\hat{p}(0,\omega )\nonumber \\&\hat{u}_{x}(1,\omega )=-\omega A\sin \omega +\omega B\cos \omega =\hat{p}(1,\omega ) \end{aligned}$$

(33)

which is strictly equivalent to (18). The rest of the procedure follows. However, the extension of the FD-BEM to higher dimensions in space is more straightforward for the enforcement of the boundary conditions.

Appendix 2: Separation of variables

It seems appropriate to highlight a major difference between the proposed approach based on direct and inverse Fourier Transforms and the classical separation of variables sometimes used in solving the wave equation via the superposition principle. The technique can be summarized as follows:

• Consider an ansatz solution of the form $u(x,t)=\Phi (x)\exp (j\omega t)$ and plug it into the wave Eq. (1). This implies that the function $\Phi (x)$ is solution to the Helmholtz equation $\Phi _{xx}+\omega ^2\Phi =0$, identical to Eq. (7) stemming from a Fourier Transform.

• The general solution is $\Phi (x)=A\cos \omega x+B\sin \omega x$.

• Enforce the boundary conditions. Let us consider the Dirichlet–Signorini bar for simplicity. Accordingly, $\Phi (0)=0$, that is $A=0$.

• From the above, the solution now reads $u(x,t)=B\sin \omega x\exp (j\omega t)$. However, the Signorini condition cannot be properly enforced at this stage, as achieved in (29). The usual approach would be to consider an homogeneous Neumann condition at $x=1$ in order to generate a family of eigenfunctions $\Phi _k(x)=\sin (k\pi x/2)$, $k=1,3,\ldots$ so that the sought solution is now expressed as the infinite sum

  $$\begin{aligned} u(x,t)=\mathfrak {R}\Bigl (\sum _{k,\mathrm{odd}} B_k\sin (k\pi x/2) \exp (jk\pi t/2)\Bigr ) \end{aligned}$$

  (34)

  and then try to enforce the Signorini condition. However, this would require either a penalization or an impact law, with the corresponding questions on the values of the companion parameters (penalization coefficient or impact law restitution coefficient). Note that a finite-element-based approach in space would not help either.

The Frequency-Domain procedure exposed in the current work overcomes the above difficulties by handling the Signorini condition directly in the frequency domain and never assumes a solution in the form (34), or similar.

Appendix 3: D’Alembert solution and Fourier transform

The general solution to the wave Eq. (1) is D’Alembert solution $u(x,t)=f(x+t)+g(x-t)$. The Dirichlet condition at $x=0$ implies $f(t)+g(-t)=0$, that is $u(x,t)=f(x+t)-f(t-x)$. The corresponding strain field is $u_{x}(x,t)=f'(x+t)+f'(t-x)$. At $x=1$, both equations yield $u(1,t)=f(t+1)-f(t-1)$ and $u_{x}(1,t)=f'(t+1)+f'(t-1)$. Applying a Fourier Transform to each quantity along t leads to $\hat{u}(1,\omega )=2j\sin \omega \hat{f}(\omega )$ and $\hat{u}_{x}(1,\omega ) =2j\omega \cos \omega \hat{f}(\omega )$, expressions which agree with (23). The same procedure applies to the Robin–Signorini system and Expression (27) would be retrieved. Again, this shows that the proposed approach is a Frequency-Domain procedure based on a Fourier Transform of the D’Alembert solution.