Darboux transformation, exact solutions and conservation laws for the reverse space-time Fokas–Lenells equation

Abstract

In this paper, we firstly deduce a reverse space-time Fokas–Lenells equation which can be derived from a rather simple but extremely important symmetry reduction of corresponding local equation. Next, the determinant representations of one-fold Darboux transformation and N-fold Darboux transformation are expressed in detail by special eigenfunctions of spectral problem. Depending on zero seed solution and nonzero seed solution, exact solutions, including bright soliton solutions, kink solutions, periodic solutions, breather solutions, rogue wave solutions and several types of mixed soliton solutions, can be presented. Furthermore, the dynamical behaviors are discussed through some figures. It should be mentioned that the solutions of nonlocal Fokas–Lenells equation possess new characteristics different from the ones of local case. Besides, we also demonstrate the integrability by providing infinitely many conservation laws. The above results provide an alternative possibility to understand physical phenomena in the field of nonlinear optics and related fields.

1 Introduction

The completely integrable Fokas–Lenells (FL) equation [1,2,3,4]

$$\begin{aligned} i\,q_{xt}-i\,q_{xx}+2\,q_{x}-q_{x}\,q\,q^{*}+i\,q=0, \end{aligned}$$

(1.1)

plays an important role in the study of soliton theory and integrable system, where $q=q(x, t)$ represents complex field envelope, asterisk denotes complex conjugation, and subscript x and t appended to q denote partial derivative with respect to x and t. In optics, the FL equation has been derived as a model to describe femtosecond pulse propagation through single-mode optical silica fiber when suitable higher-order linear and nonlinear optical effects were taken into account [2]. Another remarkable feature of the FL system is that it corresponds to the first negative flow of the integrable hierarchy associated with the derivative nonlinear Schrödinger (NLS) equation in the same way that the Camassa–Holm equation is related to the Korteweg–de Vries equation [3]. Furthermore, Lenells and Fokas used the bi-Hamiltonian structure and inverse scattering transformation to analyze the first few conservation laws, its Lax pair, the initial value problem and soliton solutions [4]. The explicit formulas for the N-bright, dark soliton solutions, breathers and higher-order rogue waves of the FL equation were constructed by means of the dressing method, Hirota direct method, the complex envelope function method, Darboux transformation (DT) method and so on [4,5,6,7,8,9,10]. In addition, the long-time asymptotic behavior of the solution of the FL equation was also discussed by the nonlinear steepest descent method [11].

Nonlocal problems in integrable equations have recently been the subject of intensive investigation [12,13,14,15,16,17,18,19,20], where they occur due to parity-time (PT) symmetry. Bender and Boettcher showed that large amounts of non-Hermitian Hamiltonians, the so-called PT-symmetric Hamiltonians, possess entirely real and positive spectrum [21]. Furthermore, they also obtained that the non-Hermitian Hamiltonian $H=\partial _{xx}+V(x)$ is PT-symmetric if the complex potential V(x) holds for $V(x)=V^{*}(-x)$ [22]. Following these ideas and using a new symmetry reduction of the well-known Ablowitz–Kaup–Newell–Segur (AKNS) system, a nonlocal NLS equation

$$\begin{aligned} i\,q_{t}+\,q_{xx}+2\,\sigma \,q^{2}\,q^{*}(-x,t)=0, \end{aligned}$$

(1.2)

was first proposed by Ablowitz and Musslimani [23] in 2013. Since possessing new special properties which are different from its corresponding local model, the nonlocal NLS equation has drawn interest [24, 25]. Subsequently, many new reverse space-time and in some cases reverse time nonlinear integrable equations have been investigated by utilizing the classical methods, like inverse scattering method, bilinear approach, Bäcklund transformation and DT method [26,27,28,29]. Meanwhile, the potential applications of nonlocal systems were also studied from various physical branches, such as optics, Bose–Einstein condensation, magnetics, electric circuits, mechanical systems and so on [30,31,32,33,34]. It is worth noting that the aforementioned work related to nonlocal integrable equations is based on the ones of local integrable equations. At present, various studies have exhibited great richness of local integrable equations, such as the work of Zhang in Ref. [35,36,37] and the work of Tian in Ref. [38, 39]. These results might be helpful for understanding how to construct exact solutions of nonlocal integrable equations and analyze potential physical phenomena.

Here, considering the physical significance of the FL equation and the importance of the recent interesting developments in the analysis of PT-symmetric of the NLS and the derivative-type NLS equations, we propose a new reverse space-time nonlocal FL equation as follow

$$\begin{aligned} i\,q_{xt}-i\,q_{xx}+2\,q_{x}-q_{x}\,q\,q(-x,-t)+i\,q=0,\nonumber \\ \end{aligned}$$

(1.3)

which can be derived from a special reduction of the negative flow for the Kaup–Newell (KN) hierarchy. As we all know, the DT method is a powerful and effective mathematical tool to seek new exact soliton solutions [40,41,42,43,44,45,46,47]. Among the nonlinear waves, bright soliton, dark soliton, periodic soliton, rogue waves and lump waves have been studied for some local nonlinear evolution equations [48,49,50]. In Ref. [9, 10], construction of DT method reveals that there exists a difference between the FL system and other integrable system, like the AKNS system and the KN system. Moreover, the solutions of nonlocal systems possess the novelty in comparison with its corresponding local systems. However, the reverse space-time FL equation (1.3) admits PT-symmetric, so the DT for Eq. (1.3) is rather hard to find. For these reasons, it is the meaningful research work to investigate the DT, various types of soliton solutions and the integrability of the reverse space-time nonlocal FL equation (1.3) by making use of the FL spectral problem. It should be mentioned that the questions of bright solitons, dark solitons, kink solitons, periodic solitons and mixed solitons to a nonlocal FL equation addressed [51], results of DT proved, as well as style of analysis borrow heavily, but higher-order DT involved to cope with mixed-type solution of breather and two periodic line waves, mixed-type solution of bright soliton, dark soliton and two periodic line waves, and mixed-type solution of two-breather and periodic line waves for a reverse space-time nonlocal FL equation (1.3) is non-trivial. Additionally, we also present propagation and interaction characteristics of the soliton solutions through figures.

The organization of this paper is as follows. In Sect. 2, the one-fold DT, N-fold DT, and formulas $q^{[1]}, q^{[1]}(-x,-t), q^{[N]}, q^{[N]}(-x,-t)$ are given in detail by choosing appropriate eigenfunctions $(\varphi _{j}(x,t), \varphi _{j}(-x,-t))^{T}$ of the Lax pair. Starting from zero seed solution and periodic seed solution with constant amplitude, Sect. 3 presents the construction of bright soliton solutions, kink solutions, periodic solutions, breather solutions, rogue wave solutions and several types of mixed soliton solutions by DT. Moreover, infinitely many conservation laws of Eq. (1.3) are obtained in Sect. 4. Finally, the conclusion is addressed in Sect. 5.

2 Darboux transformation

For our analysis, we start from the non-trivial flow of the FL system in the following form

$$\begin{aligned}&i\,q_{xt}-i\,q_{xx}+2\,q_{x}-q_{x}\,q\,r+i\,q=0, \end{aligned}$$

(2.1a)

$$\begin{aligned}&i\,r_{xt}-i\,r_{xx}-2\,r_{x}+r_{x}\,r\,q+i\,r=0, \end{aligned}$$

(2.1b)

which are exactly reduced to Eq. (1.1) for $r(x, t)=q^{*}(x,t)$. Under the new symmetry reduction $r(x, t)=q(-x,-t)$, the compatible system (2.1) leads to the reverse space-time FL equation (1.3), which is different from previous classic FL equation (1.1). The following Lax pair of a completely integrable equation (1.3) can be given by the FL spectral problem

$$\begin{aligned} \varPsi _{x}=&U\,\varPsi =(J\,\lambda ^{2}+Q\,\lambda )\varPsi , \end{aligned}$$

(2.2a)

$$\begin{aligned} \varPsi _{t}=&V\,\varPsi =(J\,\lambda ^{2}+Q\,\lambda +V_{0}+V_{-1}\nonumber \\&\lambda ^{-1}+\frac{1}{4}\,J\,\lambda ^{-2})\varPsi , \end{aligned}$$

(2.2b)

with

$$\begin{aligned} \begin{aligned}&J=\left( \begin{array}{cc} -i &{}0\\ 0 &{}i\\ \end{array} \right) ,\,Q= \left( \begin{array}{cc} 0 &{}q_{x}\\ q_{x}(-x,-t) &{}0\\ \end{array} \right) ,\\&V_{0}= \left( \begin{array}{cc} i-\frac{1}{2}\,i\,q\,q(-x,-t) &{}0\\ 0 &{}-i+\frac{1}{2}\,i\,q\,q(-x,-t)\\ \end{array} \right) ,\\&V_{-1}= \left( \begin{array}{cc} 0 &{}\frac{1}{2}\,i\,q\\ -\frac{1}{2}\,i\,q(-x,-t) &{}0\\ \end{array} \right) , \end{aligned} \end{aligned}$$

where $\lambda$ is called spectral parameter, and $\varPsi$ is the vector eigenfunction associated with $\lambda$ of the nonlocal FL system. Through direct computation, it is shown that the compatibility condition $U_{t}-V_{x}+[U, V]=0$ can precisely yield Eq. (1.3).

In what follows, based on the DT of FL system and nonlocal system, we will study DT method for the reverse space-time FL equation (1.3).

2.1 One-fold Darboux transformation for the reverse space-time FL equation

Taking gauge transformation for spectral problem with following form

$$\begin{aligned} \varPsi ^{[1]}=T^{[1]}\,\varPsi , \end{aligned}$$

(2.3)

the new function $\varPsi ^{[1]}$ satisfies

$$\begin{aligned} \varPsi ^{[1]}_{x}=&U^{[1]}\,\varPsi ^{[1]}=(J\,\lambda ^{2}+Q^{[1]}\,\lambda )\varPsi ^{[1]}, \end{aligned}$$

(2.4a)

$$\begin{aligned} \varPsi ^{[1]}_{t}=&V^{[1]}\,\varPsi ^{[1]}=(J\,\lambda ^{2}+Q^{[1]}\nonumber \\&\lambda +V^{[1]}_{0}+V^{[1]}_{-1}\,\lambda ^{-1}+\frac{1}{4}\,J\,\lambda ^{-2})\varPsi ^{[1]}, \end{aligned}$$

(2.4b)

with

$$\begin{aligned} \begin{aligned}&Q^{[1]}= \left( \begin{array}{cc} 0 &{}q^{[1]}_{x}\\ q^{[1]}_{x}(-x,-t) &{}0\\ \end{array} \right) , V^{[1]}_{-1}= \left( \begin{array}{cc} 0 &{}\frac{1}{2}\,i\,q^{[1]}\\ -\frac{1}{2}\,i\,q^{[1]}(-x,-t) &{}0\\ \end{array} \right) ,\\&V^{[1]}_{0}= \left( \begin{array}{cc} i-\frac{1}{2}\,i\,q^{[1]}\,q^{[1]}(-x,-t) &{}0\\ 0 &{}-i+\frac{1}{2}\,i\,q^{[1]}\,q^{[1]}(-x,-t)\\ \end{array} \right) . \end{aligned} \end{aligned}$$

Moreover, substituting Eq. (2.3) into (2.4), $T^{[1]}$ satisfies the following relations

$$\begin{aligned}&U^{[1]}=(T^{[1]}_{x}+T^{[1]}\,U)(T^{[1]})^{-1}, \end{aligned}$$

(2.5a)

$$\begin{aligned}&V^{[1]}=(T^{[1]}_{t}+T^{[1]}\,V)(T^{[1]})^{-1}. \end{aligned}$$

(2.5b)

Next, we assume the trial one-fold Darboux matrix $T^{[1]}$ as

$$\begin{aligned} T^{[1]}= & {} T^{[1]}(\lambda ; \lambda _{1}, \lambda _{2})=\left( \begin{array}{cc} a_{1} &{}b_{1}\\ c_{1} &{}d_{1}\\ \end{array} \right) \,\lambda +\left( \begin{array}{cc} a_{0} &{}b_{0}\\ c_{0} &{}d_{0}\\ \end{array} \right) \nonumber \\&+\left( \begin{array}{cc} a_{-1} &{}b_{-1}\\ c_{-1} &{}d_{-1}\\ \end{array} \right) \,\lambda ^{-1}, \end{aligned}$$

(2.6)

where $a_{-1}, b_{-1}, c_{-1}, d_{-1}, a_{0}, b_{0}, c_{0}, d_{0}, a_{1}, b_{1}, c_{1}, d_{1}$ are functions of x and t. According to Eq. (2.5), it is directly deduced that $b_{-1}=c_{-1}=b_{1}=c_{1}=0$ and $a_{-1}, d_{-1}$ are functions of t only (see Appendix A). In order to facilitate the subsequent calculations and analysis, under an assumption that $a_{-1}=d_{-1}=1, a_{0}=d_{0}=0$, let universality matrix $T^{[1]}$ be the form of

$$\begin{aligned} T^{[1]}= & {} T^{[1]}(\lambda ; \lambda _{1}, \lambda _{2})=\left( \begin{array}{cc} T^{[1]}_{11} &{}T^{[1]}_{12}\\ T^{[1]}_{21} &{}T^{[1]}_{22}\\ \end{array} \right) =\left( \begin{array}{cc} a_{1} &{}0\\ 0 &{}d_{1}\\ \end{array} \right) \,\lambda \nonumber \\&\quad +\left( \begin{array}{cc} 0 &{}b_{0}\\ c_{0} &{}0\\ \end{array} \right) +\left( \begin{array}{cc} 1 &{}0\\ 0 &{}1\\ \end{array} \right) \,\lambda ^{-1}. \end{aligned}$$

(2.7)

From the coefficient of $\lambda ^{-2}$ in Eq. (2.5b), the relationships between the new potential functions $q^{[1]}, q^{[1]}(-x,-t)$ and the old potential functions $q, q(-x,-t)$ are given by

$$\begin{aligned} q^{[1]}=q+b_{0},\,\,\,\,\,q^{[1]}(-x,-t)=q(-x,-t)+c_{0}. \end{aligned}$$

(2.8)

To obtain the exact form of $T^{[1]}$, we consider special eigenfunctions $\varPsi _{j}$ of the Lax pair as

$$\begin{aligned} \varPsi _{j}=\left( \begin{array}{c} \varphi _{j}(x,t)\\ \varphi _{j}(-x,-t)\\ \end{array}\right) ,\,\,\,\,\,j=1,\,2. \end{aligned}$$

(2.9)

Specially, from algebraic equations

$$\begin{aligned} T^{[1]}(\lambda )|_{\lambda =\lambda _{j}}\varPsi _{j}=0,\,\,\,\,\,j=1,\,2, \end{aligned}$$

(2.10)

coefficients $a_{1}, d_{1}, b_{0}, c_{0}$ are acquired by Cramer’s rule (see Appendix B). Then, $T^{[1]}$ with eigenfunctions $(\varphi _{j}(x,t), \varphi _{j}(-x,-t))^{T}, j=1, 2$ associated with $\lambda _{j}$ guarantees the validity of the reduction condition, that is, $b_{0}(-x,-t)=c_{0}$. Thus, it is the one-fold DT for the reverse space-time FL equation (1.3).

2.2 N-fold Darboux transformation for the reverse space-time FL equation

Considering the N-fold Darboux matrix $T^{[N]}$ with the following form

$$\begin{aligned} \varPsi ^{[N]}=T^{[N]}\,\varPsi , \end{aligned}$$

(2.11)

the spectral problem (2.2) turns to

$$\begin{aligned}&\varPsi ^{[N]}_{x}=U^{[N]}\,\varPsi ^{[N]}=(J\,\lambda ^{2}+Q^{[N]}\,\lambda )\varPsi ^{[N]}, \end{aligned}$$

(2.12a)

$$\begin{aligned}&\varPsi ^{[N]}_{t}=V^{[N]}\,\varPsi ^{[N]}=(J\,\lambda ^{2}+Q^{[N]}\nonumber \\&\lambda +V^{[N]}_{0}+V^{[N]}_{-1}\,\lambda ^{-1}+\frac{1}{4}\,J\,\lambda ^{-2})\varPsi ^{[N]}, \end{aligned}$$

(2.12b)

with

$$\begin{aligned} \begin{aligned}&Q^{[N]}= \left( \begin{array}{cc} 0 &{}q^{[N]}_{x}\\ q^{[N]}_{x}(-x,-t) &{}0\\ \end{array} \right) ,\,V^{[N]}_{-1}= \left( \begin{array}{cc} 0 &{}\frac{1}{2}\,i\,q^{[N]}\\ -\frac{1}{2}\,i\,q^{[N]}(-x,-t) &{}0\\ \end{array} \right) ,\\&V^{[N]}_{0}= \left( \begin{array}{cc} i-\frac{1}{2}\,i\,q^{[N]}\,q^{[N]}(-x,-t) &{}0\\ 0 &{}-i+\frac{1}{2}\,i\,q^{[N]}\,q^{[N]}(-x,-t)\\ \end{array} \right) , \end{aligned} \end{aligned}$$

where $\varPsi ^{[N]}$ is the eigenfunction of the Lax pair (2.12). In addition, $T^{[N]}$ satisfies the following equalities

$$\begin{aligned}&U^{[N]}=(T^{[N]}_{x}+T^{[N]}\,U)(T^{[N]})^{-1}, \end{aligned}$$

(2.13a)

$$\begin{aligned}&V^{[N]}=(T^{[N]}_{t}+T^{[N]}\,V)(T^{[N]})^{-1}. \end{aligned}$$

(2.13b)

Now, our aim is to propose the determinant representation of the N-fold Darboux matrix for the reverse space-time FL equation (1.3) in this subsection. For this purpose, we set

$$\begin{aligned} D= & {} \left\{ \left( \begin{array}{cc} a &{}0\\ 0 &{}d\\ \end{array} \right) |\,a,\,d\,are\,complex\,functions\,of\,x\,and\,t\right\} ,\\ A= & {} \left\{ \left( \begin{array}{cc} 0 &{}b\\ c &{}0\\ \end{array} \right) |\,b,\,c\,are\,complex\,functions\,of\,x\,and\,t\right\} , \end{aligned}$$

as in Ref. [52]. According to the form of $T^{[1]}$ in Eq. (2.7), we assume the matrix $T^{[N]}$ as following expression

$$\begin{aligned} T^{[N]}= & {} T^{[N]}(\lambda ; \lambda _{1}, \lambda _{2}, \ldots , \lambda _{2N})=\left( \begin{array}{cc} T^{[N]}_{11} &{}T^{[N]}_{12}\\ T^{[N]}_{21} &{}T^{[N]}_{22}\\ \end{array} \right) \nonumber \\= & {} \sum ^{N}_{k=-N}S_{k}\,\lambda ^{k}, \end{aligned}$$

(2.14)

with

$$\begin{aligned} S_{N}= & {} \left( \begin{array}{cc} a_{N} &{}0\\ 0 &{}d_{N}\\ \end{array} \right) \in D,\,\,S_{N-1}\\= & {} \left( \begin{array}{cc} 0 &{}b_{N-1}\\ c_{N-1} &{}0\\ \end{array} \right) \in A, \end{aligned}$$

$S_{k}\in D$ (if k-N is even), $S_{k}\in A$ (if k-N is odd).

Here, $S_{-N}$ is a constant matrix with $a_{-N}=d_{-N}=1,$ every member of the matrix $S_{k}(-(N-1)\le k \le N)$ is the function of x and t. Specifically, from algebraic equations

$$\begin{aligned}&\varPsi ^{[N]}_{j}=T^{[N]}(\lambda ; \lambda _{1}, \lambda _{2}, \ldots , \lambda _{2N})|_{\lambda =\lambda _{j}}\,\varPsi _{j}\nonumber \\&\quad =\sum ^{N}_{k=-N}S_{k}\,\lambda ^{k}_{j}\,\varPsi _{j}=0,\,\,j=1, 2, \ldots , 2N, \end{aligned}$$

(2.15)

the values of all unknown coefficients $S_{k}$ are solved by means of Cramer’s rule. Similarly, in order to investigate the exact form of $T^{[N]}$, we need to set eigenfunctions $\varPsi _{j}$ of the Lax pair

$$\begin{aligned} \varPsi _{j}=\left( \begin{array}{c} \varphi _{j}(x,t)\\ \varphi _{j}(-x,-t)\\ \end{array}\right) ,\,\,\,\,\,j=1,\,2,\ldots ,\,2N. \end{aligned}$$

(2.16)

After tedious but straightforward calculations, we can get the N-fold Darboux matrix $T^{[N]}$ (see Appendix C) as

$$\begin{aligned}&T^{[N]}(\lambda ; \lambda _{1}, \lambda _{2}, \ldots , \lambda _{2N})=\left( \begin{array}{cc} T^{[N]}_{11} &{}T^{[N]}_{12}\\ T^{[N]}_{21} &{}T^{[N]}_{22}\\ \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{cc} \frac{\widetilde{T^{[N]}_{11}}}{W^{[N]}} &{}\frac{\widetilde{T^{[N]}_{12}}}{W^{[N]}}\\ \frac{\widetilde{T^{[N]}_{21}}}{\widetilde{W^{[N]}}} &{}\frac{\widetilde{T^{[N]}_{22}}}{\widetilde{W^{[N]}}}\\ \end{array} \right) . \end{aligned}$$

(2.17)

Next, we consider the transformed new solutions $(q^{[N]}, q^{[N]}(-x,-t))$ corresponding to the N-fold DT for the reverse space-time FL equation (1.3). Substituting $T^{[N]}$ given by Eq. (2.14) into Eq. (2.13b) and then comparing the coefficients of $\lambda ^{-(N+1)}$, we can get the relationships between the new solutions $q^{[N]}, q^{[N]}(-x,-t)$ and the old solutions $q, q(-x,-t)$

$$\begin{aligned}&q^{[N]}=q+b_{-(N-1)},\,\,q^{[N]}(-x,-t)\nonumber \\&\quad =q(-x,-t)+c_{-(N-1)}. \end{aligned}$$

(2.18)

Furthermore, taking $b_{-(N-1)}, c_{-(N-1)}$, which are obtained from Eq. (2.15), new solutions $(q^{[N]}, q^{[N]}(-x,-t))$ can be rewritten (see Appendix D) as

$$\begin{aligned}&q^{[N]}=q+\frac{\varOmega _{-(N-1)}}{W^{[N]}},\,\,q^{[N]}(-x,-t)\nonumber \\&\quad \quad =q(-x,-t)+\frac{\widetilde{\varOmega _{-(N-1)}}}{\widetilde{W^{[N]}}}. \end{aligned}$$

(2.19)

It is easy to check the resulting $T^{[N]}$ with the help of following choice eigenfunctions $(\varphi _{j}(x,t), \varphi _{j}(-x,-t))^{T}, j=1, 2,\cdots , 2N$ associated with $\lambda _{j}$ can be called as N-fold Darboux matrix for the reverse space-time FL equation (1.3). In other words, $T^{[N]}$ shares the invariance, that is, $b_{-(N-1)}(-x,-t)=c_{-(N-1)}$.

3 Exact solutions

In this section, from zero seed solution and nonzero seed solution, we will combine N-fold DT to seek various types of exact solutions for the reverse space-time FL equation (1.3).

3.1 Exact solutions from zero seed solution for the reverse space-time FL equation

First of all, choosing zero seed solution $q=0, q(-x,-t)=0$, the eigenfunctions of Lax pair can be expressed as

$$\begin{aligned} \varPsi _{j}= & {} \left( \begin{array}{c} \varphi _{j}(x,t)\\ \varphi _{j}(-x,-t)\\ \end{array} \right) \nonumber \\= & {} \left( \begin{array}{c} \mathrm {e}^{-i(\lambda ^{2}_{j}\,x+(\lambda ^{2}_{j}-1+\frac{1}{4}\,\lambda ^{-2}_{j})t)}\\ \mathrm {e}^{i(\lambda ^{2}_{j}\,x+(\lambda ^{2}_{j}-1+\frac{1}{4}\,\lambda ^{-2}_{j})t)}\\ \end{array} \right) ,\,\,\,\,\,\nonumber \\&j=1,\,2,\ldots ,\,2N. \end{aligned}$$

(3.1)

Moreover, N-fold soliton solutions can be derived by direct calculation for the reverse space-time FL equation (1.3), which are omitted here.

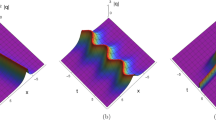
When $N=2$, substituting Eq. (3.1) and the seed solution into Eq. (2.19), we can obtain second-order soliton solutions. Setting $\lambda _{1}=\lambda ^{*}_{2}, \lambda _{3}=\lambda ^{*}_{4}$, the typical two-bright soliton is displayed with appropriate parameters in Fig. 1(a). Taking spectral parameters as $\lambda _{2R}=0, \lambda _{1I}=-\lambda _{2I}, \lambda _{3}=\lambda ^{*}_{4}$, mixed-type solution of kink and bright soliton can be seen in Fig. 1(b). Meanwhile, the heights of soliton wave are different under different planes background. Furthermore, with the help of parameters $\lambda _{1I}=\lambda _{3I}=\lambda _{4I}=0, \lambda _{2R}=0$, mixed-type solution of soliton and periodic waves is shown in Fig. 1(c).

Fig. 1

Two-bright soliton solution with $\lambda _{1}=1+i, \lambda _{2}=1-i, \lambda _{3}=0.6-0.5\,i, \lambda _{4}=0.6+0.5\,i$; (b) Mixed-type solution of kink and bright soliton with $\lambda _{1}=1+1.8\,i, \lambda _{2}=-1.8\,i, \lambda _{3}=0.57-0.01\,i,$ $\lambda _{4}=0.57+0.01\,i$; (c) Mixed-type solution of soliton and periodic waves with $\lambda _{1}=1, \lambda _{2}=3\,i,$ $\lambda _{3}=0.2, \lambda _{4}=0.8$

3.2 Exact solutions from nonzero seed solution for the reverse space-time FL equation

In the following, using the results of N-fold DT, we construct exact solutions from nonzero seed solution. Let a be real number and c be complex number, then assuming seed solution $q=c\,\mathrm {e}^{i(a\,x+(\frac{(a+1)^{2}}{a}-c^{2})t)}, q(-x,-t)=c\,\mathrm {e}^{-i(a\,x+(\frac{(a+1)^{2}}{a}-c^{2})t)}$ and substituting the above of form $q, q(-x,-t)$ into the Lax pair, the eigenfunctions $\varPsi _{j}$ associated with $\lambda _{j}$ are given by

$$\begin{aligned} \varPsi _{j}= & {} \left( \begin{array}{c} \varphi _{j}(x,t)\\ \varphi _{j}(-x,-t)\\ \end{array} \right) \nonumber \\= & {} \left( \begin{array}{c} (C_{1,j}\,\mathrm {e}^{A_{j}}-C_{2,j}\,\mathrm {e}^{-A_{j}})\mathrm {e}^{\frac{i}{2}(a\,x+(\frac{(a+1)^{2}}{a}-c^{2})t)}\\ (C_{1,j}\,\mathrm {e}^{-A_{j}}-C_{2,j}\,\mathrm {e}^{A_{j}})\mathrm {e}^{-\frac{i}{2}(a\,x+(\frac{(a+1)^{2}}{a}-c^{2})t)}\\ \end{array} \right) ,\,\,\,\,\,\nonumber \\&j=1,\,2,\ldots ,\,2N, \end{aligned}$$

(3.2)

where

$$\begin{aligned}&P_{j}=-a^{2}+4\,a(a\,c^{2}-1)\lambda ^{2}_{j}-4\,\lambda ^{4}_{j},\\&A_{j}=\frac{1}{2}\,\sqrt{P_{j}}(x+\frac{2\,a\,\lambda ^{2}_{j}+1}{2\,a\,\lambda ^{2}_{j}}\,t),\\&C_{1,j}=\frac{a+2\,\lambda ^{2}_{j}+i\,\sqrt{P_{j}}-2\,a\,c\,\lambda _{j}}{2\,a\,c\,\lambda _{j}\,\sqrt{P_{j}}},\\&C_{2,j}=\frac{a+2\,\lambda ^{2}_{j}-i\,\sqrt{P_{j}}-2\,a\,c\,\lambda _{j}}{2\,a\,c\,\lambda _{j}\,\sqrt{P_{j}}}. \end{aligned}$$

Through direct calculation, substituting Eq. (3.2) and the periodic seed solution into Eq. (2.19), we focus on various types of solutions for the reverse space-time FL equation (1.3). Here, we omit their analytic expressions to avoid the complicated formula.

Fig. 2

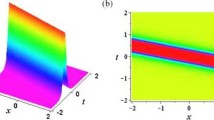
(a) Mixed-type solution of breather and periodic line waves with $\lambda _{1}=i, \lambda _{2}=1.0001\,i, a=0.1,$ $c=0.1$; (b) Mixed-type solution of two periodic line waves with $\lambda _{1}=2\,i, \lambda _{2}=1-2\,i, a=2, c=$ 1; (c) Ma breather with $\lambda _{1}=1+0.5\,i, \lambda _{2}=1-0.5\,i, a=-0.24, c=4.68$

Fig. 3

(a) General breather with $\lambda _{1}=0.5+0.67\,i, \lambda _{2}=0.5-0.67\,i, a=1, c=1$; (b) Akhmediev breather with $\lambda _{1}=0.5+0.2\,i, \lambda _{2}=0.5-0.2\,i, a=1.35, c=1$; (c) First-order rogue wave with $\alpha _{1}$ $=0.34, \beta _{1}=0.5$

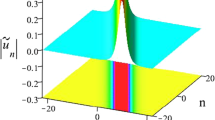
When $N=1$, according to Eq. (3.2), we can obtain one-order soliton solutions. Choosing $\lambda _{1R}=\lambda _{2R}=0, \lambda _{2I}\rightarrow \lambda _{1I}$ and appropriate parameters a and c, special breather, which appears both in space and time, is derived under periodic line waves background, see Fig. 2(a). Setting $\lambda _{1R}=0, \lambda _{1I}=-\lambda _{2I}$ with appropriate a and c, a composition of two periodic line waves with different background heights is illustrated in Fig. 2(b). In addition, we can easily get all kinds of breathers, including Ma breather [53], general breather [54], Akhmediev breather [55]. The dynamical evolution of $q^{[1]}$ is plotted in Figs. 2(c) and 3(a), (b). Under the choice in Eq. (3.2) with one-paired eigenvalue $\lambda _{1}=\alpha _{1}+i\,\beta _{1}$ and $\lambda _{2}=\alpha _{1}-i\,\beta _{1}$, combining with the limit $a\rightarrow 2\,(\alpha _{1}^{2}+\beta _{1}^{2})$ for the condition $c=-\frac{\sqrt{a+2\,(\alpha _{1}^{2}-\beta _{1}^{2})}}{a}$, then we obtain new eigenfunctions which are the product of plane wave and rational function as form

$$\begin{aligned}&\varPsi _{1}=\left( \begin{array}{c} \varphi _{1}(x,t)\\ \varphi _{1}(-x,-t)\\ \end{array} \right) \nonumber \\&\qquad =\left( \begin{array}{c} -\frac{\eta _{1}}{2\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}+i\,\beta _{1})^{2}}\,\mathrm {e}^{\frac{i}{4}\,\theta }\\ \frac{\eta _{1}'}{2\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}+i\,\beta _{1})^{2}}\,\mathrm {e}^{-\frac{i}{4}\,\theta }\\ \end{array} \right) , \end{aligned}$$

(3.3a)

$$\begin{aligned}&\varPsi _{2}=\left( \begin{array}{c} \varphi _{2}(x,t)\\ \varphi _{2}(-x,-t)\\ \end{array} \right) \nonumber \\&\qquad =\left( \begin{array}{c} -\frac{\eta _{2}}{2\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}-i\,\beta _{1})^{2}}\,\mathrm {e}^{\frac{i}{4}\,\theta }\\ \frac{\eta _{2}'}{2\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}-i\,\beta _{1})^{2}}\,\mathrm {e}^{-\frac{i}{4}\,\theta }\\ \end{array} \right) , \end{aligned}$$

(3.3b)

where

$$\begin{aligned} \theta= & {} 4\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(x+t)+4\,t-\frac{(\alpha _{1}^{2}-\beta _{1}^{2})\,t}{(\alpha _{1}^{2}+\beta _{1}^{2})^{2}},\\ \eta _{1}= & {} 4\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}+i\,\beta _{1})^{2}\,(x+t)+(\alpha _{1}^{2}\\&+\beta _{1}^{2})\,(i\,\alpha _{1}-\beta _{1})+\alpha _{1}\,t,\\ \eta _{1}'= & {} 4\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}+i\,\beta _{1})^{2}\,(x+t)-(\alpha _{1}^{2}\\&+\beta _{1}^{2})\,(i\,\alpha _{1}-\beta _{1})+\alpha _{1}\,t,\\ \eta _{2}= & {} 4\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}-i\,\beta _{1})^{2}\,(x+t)\\&+(\alpha _{1}^{2}+\beta _{1}^{2})\,(i\,\alpha _{1}+\beta _{1})+\alpha _{1}\,t,\\ \eta _{2}'= & {} 4\,\alpha _{1}\,(\alpha _{1}^{2}+\beta _{1}^{2})\,(\alpha _{1}-i\,\beta _{1})^{2}\,(x+t)\\&-(\alpha _{1}^{2}+\beta _{1}^{2})\,(i\,\alpha _{1}+\beta _{1})+\alpha _{1}\,t. \end{aligned}$$

Next, substituting Eq. (3.3) into Eq. (2.19), the first-order rogue wave solution can be derived. Through Fig. 3(c), the main features, such as one peak and two depressions [56], of the first-order rogue wave are clearly shown.

When $N=2$, using Eq. (3.2), we can obtain second-order soliton solutions under periodic waves background. Taking $\lambda _{1}=\lambda ^{*}_{2}, \lambda _{3I}=-\lambda _{4I}, \lambda _{4R}=0$ and appropriate parameters a and c, mixed-type solution of breather and two periodic line waves and mixed-type solution of bright soliton, dark soliton and two periodic line waves are plotted in Figs. 4(a), (b), respectively. Fig. 4(c) shows mixed-type structure of two-breather and periodic line waves with $\lambda _{1}=\lambda ^{*}_{2}, \lambda _{3}=\lambda ^{*}_{4}$.

Fig. 4

(a) Mixed-type solution of breather and two periodic line waves with $\lambda _{1}=0.5-0.01\,i, \lambda _{2}=0.5+$ $0.01\,i, \lambda _{3}=0.7+1.5\,i, \lambda _{4}=-1.5\,i, a=1, c=1$; (b) Mixed-type solution of bright soliton, dark soliton and two periodic line waves with $\lambda _{1}=0.5-0.01\,i, \lambda _{2}=0.5+0.01\,i, \lambda _{3}=1+1.8\,i, \lambda _{4}=$ $-1.8\,i, a=1, c=2$; (c) Mixed-type solution of two-breather and periodic line waves with $\lambda _{1}=0.7+0.05i, \lambda _{2}=0.7-0.05\,i, \lambda _{3}=0.7+0.3\,i, \lambda _{4}=0.7-0.3\,i, a=1, c=1$

4 Conservation laws

In this section, we will seek the infinitely many conservation laws to discuss the integrability for the reverse space-time FL equation (1.3).

From Lax pair (2.2), we can deduce that

$$\begin{aligned}&\frac{\varphi _{x}(x,t)}{\varphi (x,t)}=-i\,\lambda ^{2}+\lambda \,q_{x}\,\varGamma ,\nonumber \\&\quad \frac{\varphi _{x}(-x,-t)}{\varphi (-x,-t)}=\lambda \,q_{x}(-x,-t)\,\varGamma ^{-1}+i\,\lambda ^{2}, \end{aligned}$$

(4.1)

where $\varGamma =\varphi (-x,-t)/\varphi (x,t)$. According to $\omega =q\,\varGamma$, we can derive the following Riccati-type equation

$$\begin{aligned} \omega _{x}=\frac{q_{x}}{q}\,\omega +\lambda \,q\,q_{x}(-x,-t)+2\,i\,\lambda ^{2}\,\omega -\lambda \,\frac{q_{x}}{q}\,\omega ^{2}. \end{aligned}$$

(4.2)

Assuming that

$$\begin{aligned} \omega =\sum _{j=0}^{\infty }\omega _{j}\frac{1}{\lambda ^{2j+1}}, \end{aligned}$$

(4.3)

and substituting Eq. (4.3) into Eq. (4.2), the recursion formulas can be obtained as

$$\begin{aligned} \omega _{0}= & {} -\frac{q\,q_{x}(-x,-t)}{2\,i},\quad \omega _{1}\nonumber \\= & {} \frac{1}{4}(q\,q_{xx}(-x,-t)-\frac{1}{2\,i}\,q\,q_{x}\,q_{x}^{2}(-x,-t)),\nonumber \\ \omega _{2}= & {} \frac{1}{16}(4\,q\,q_{x}\,q_{x}(-x,-t)\,q_{xx}(-x,-t)\nonumber \\&+q\,q_{xx}\,q_{x}^{2}(-x,-t)+i\,q\,q_{x}^{2}\,q_{x}^{3}\nonumber \\&(-x,-t)-2\,i\,q\,q_{xxx}(-x,-t)),\nonumber \\&\cdot \cdot \cdot \nonumber \\ \omega _{m}= & {} \frac{1}{2\,i}(\omega _{(m-1)x}-\frac{q_{x}}{q}\omega _{m-1}\nonumber \\&+\frac{q_{x}}{q}\,\sum _{j=0}^{m}\omega _{j}\,\omega _{m-1-j}), (m\ge 1). \end{aligned}$$

(4.4)

From the compatibility condition $(\frac{\varphi _{x}(x,t)}{\varphi (x,t)})_{t}=(\frac{\varphi _{t}(x,t)}{\varphi (x,t)})_{x}$, direct calculations lead to

$$\begin{aligned} (-i\,\lambda ^{2}+\lambda \,q_{x}\,\varGamma )_{t}=(A+B\frac{\omega }{q})_{x}, \end{aligned}$$

(4.5)

with

$$\begin{aligned} A= & {} -i\,\lambda ^{2}+i-\frac{1}{2}\,i\,q\,q(-x,-t)-\frac{1}{4}\,i\,\lambda ^{-2},\\ B= & {} \lambda \,q_{x}+\frac{1}{2}\,i\,q\,\lambda ^{-1}. \end{aligned}$$

Equating the terms with the same power series of $\lambda$ in Eq. (4.5), we can get the infinite number of conservation laws for Eq. (1.3). The first few conserved densities are expressed explicitly as follows:

$$\begin{aligned}&(q_{x}\,q_{x}(-x,-t))_{t}=(q_{x}\,q_{x}(-x,-t)-q\,q(-x,-t))_{x},\nonumber \\&\qquad (q_{x}\,q_{xx}(-x,-t)-\frac{1}{2\,i}\,q_{x}^{2}\,q_{x}^{2}(-x,-t))_{t}\nonumber \\&\quad =(q_{x}\,q_{xx}(-x,-t)-q\,q_{x}(-x,-t)\nonumber \\&\qquad -\frac{1}{2\,i}\,q_{x}^{2}\,q_{x}^{2}(-x,-t))_{x},\nonumber \\&(4\,q_{x}^{2}\,q_{x}(-x,-t)\,q_{xx}(-x,-t)+q_{x}\,q_{xx}\,q_{x}^{2}(-x,-t)\nonumber \\&\qquad +i\,q_{x}^{3}\,q_{x}^{3}(-x,-t)-2\,i\,q_{x}\,q_{xxx}(-x,-t))_{t}\nonumber \\&\quad =(q_{x}\,q_{xx}\,q_{x}^{2}(-x,-t)+4\,q_{x}^{2}\,q_{x}(-x,-t)\nonumber \\&\qquad q_{xx}(-x,-t)+i\,q_{x}^{3}\,q_{x}^{3}(-x,-t)\nonumber \\&\qquad -2\,i\,q_{x}\,q_{xxx}(-x,-t)\nonumber \\&\qquad +2\,i\,q\,q_{xx}(-x,-t)-q\,q_{x}\,q_{x}^{2}(-x,-t))_{x}. \end{aligned}$$

(4.6)

5 Conclusion

The reverse space-time FL equation has been systematically investigated in this paper. With the help of its Lax pair and infinitely many conservation laws, the integrability has been demonstrated. Under vanishing and non-vanishing backgrounds, we have given some soliton solutions with DT. Based on the obtained solutions, the dynamic characteristics of these solitons, including bright solitons, kink, periodic waves, breather, rogue wave and several types of mixed solitons, have been shown through figures. It’s easy to find that the nonlocal FL equation exhibits some novel results in comparison with local case. For instance, mixed-type solution of kink and bright soliton, mixed-type solution of soliton and periodic waves, mixed-type solution of breather and periodic line waves, mixed-type solution of two periodic line waves, mixed-type solution of breather and two periodic line waves, mixed-type solution of bright soliton, dark soliton and two periodic line waves, and mixed-type solution of two-breather and periodic line waves, which do not occur in the classic FL equation (1.1), exist in the reverse space-time FL equation (1.3). These results can be used to enrich solitary wave phenomena in the field of nonlinear wave. Therefore, the potential applications of solitary wave solutions obtained will be an interesting issue to be studied in future. In addition, N-fold rogue wave in this equation will be desirable, too.

Appendices

Appendix A

From Eq. (2.5a), comparing the coefficients of $\lambda ^{j}, j=3, 2, 1, 0, -1$, we can get

$$\begin{aligned}&\lambda ^{3}: b_{1}=0, c_{1}=0,\\&\quad \lambda ^{2}: 2\,i\,b_{0}+a_{1}\,q_{x}-d_{1}\\&\quad q^{[1]}_{x}=0, -2\,i\,c_{0}+d_{1}\\&\quad q_{x}(-x,-t)-a_{1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{1}: a_{1x}+b_{0}\,q_{x}(-x,-t)-c_{0}\\&\quad q^{[1]}_{x}=0, 2\,i\,b_{-1}+a_{0}\,q_{x}-d_{0}\,q^{[1]}_{x}=0,\\&\quad -2\,i\,c_{-1}+d_{0}\,q_{x}(-x,-t)-a_{0}\\&\quad q^{[1]}_{x}(-x,-t)=0, d_{1x}+c_{0}\,q_{x}\\&\quad -b_{0}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{0}: a_{0x}+b_{-1}\,q_{x}(-x,-t)-c_{-1}\,q^{[1]}_{x}=0, \\&\quad b_{0x}+a_{-1}\,q_{x}-d_{-1}\,q^{[1]}_{x}=0,\\&\quad c_{0x}+d_{-1}\,q_{x}(-x,-t)-a_{-1}\,q^{[1]}_{x}(-x,-t)=0, \\&\quad d_{0x}+c_{-1}\,q_{x}-b_{-1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{-1}: a_{-1x}=0, b_{-1x}=0, c_{-1x}=0, d_{-1x}=0. \end{aligned}$$

Similarly, from Eq. (2.5b), comparing the coefficients of $\lambda ^{j}, j=2, 1, 0, -1, -2, -3$ under the condition $b_{1}=0, c_{1}=0$, we can get

$$\begin{aligned}&\lambda ^{2}: 2\,i\,b_{0}+a_{1}\,q_{x}-d_{1}\,q^{[1]}_{x}=0, \\&\quad -2\,i\,c_{0}+d_{1}\,q_{x}(-x,-t)\\&\quad -a_{1}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{1}: d_{0}\,q_{x}(-x,-t)-a_{0}\,q^{[1]}_{x}(-x,-t)=0, \\&\quad a_{0}\,q_{x}-d_{0}\,q^{[1]}_{x}=0,\\&\quad -\frac{1}{2}\,i\,a_{1}\,q(-x,-t)\,q+\frac{1}{2}\,i\,a_{1}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+a_{1t}+b_{0}\,q_{x}(-x,-t)\\&\quad -c_{0}\,q^{[1]}_{x}=0,\\&\quad \frac{1}{2}\,i\,d_{1}\,q(-x,-t)\,q-\frac{1}{2}\,i\,d_{1}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+d_{1t}+c_{0}\,q_{x}\\&\quad -b_{0}\,q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{0}: -\frac{1}{2}\,i\,a_{0}\,q(-x,-t)\,q+\frac{1}{2}\,i\,a_{0}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+a_{0t}=0,\\&\quad \frac{1}{2}\,i\,d_{0}\,q(-x,-t)\,q-\frac{1}{2}\,i\,d_{0}\\&\quad q^{[1]}(-x,-t)\,q^{[1]}+d_{0t}=0,\\&\quad -2ib_{0}+\frac{1}{2}ia_{1}\,q+\frac{1}{2}ib_{0}q(-x,-t)q\\&\quad -\frac{1}{2}id_{1}q^{[1]}+\frac{1}{2}ib_{0}q^{[1]}(-x,-t)q^{[1]}+b_{0t}\\&\quad +a_{-1}q_{x} -d_{-1}q^{[1]}_{x}=0,\\&\quad 2\,i\,c_{0}-\frac{1}{2}\,i\,d_{1}\,q(-x,-t)\\&\quad -\frac{1}{2}\,i\,c_{0}\,q(-x,-t)\\&\quad q+\frac{1}{2}\,i\,a_{1}\,q^{[1]}(-x,-t)\\&\quad -\frac{1}{2}\,i\,c_{0}\,q^{[1]}(-x,-t)\,q^{[1]}\\&\quad +c_{0t}+d_{-1}\,q_{x}(-x,-t)-a_{-1}\\&\quad q^{[1]}_{x}(-x,-t)=0,\\&\quad \lambda ^{-1}: a_{0}\,q-d_{0}\,q^{[1]}=0, \\&\quad -d_{0}\,q(-x,-t)+a_{0}\,q^{[1]}(-x,-t)=0,\\&\quad -\frac{1}{2}\,i\,b_{0}\,q(-x,-t)-\frac{1}{2}\,i\,a_{-1}\\&\quad q(-x,-t)\,q-\frac{1}{2}\,i\,c_{0}\,q^{[1]}\\&\quad +\frac{1}{2}\,i\,a_{-1}\,q^{[1]}(-x,-t)\,q^{[1]}+a_{-1t}=0,\\&\quad \frac{1}{2}\,i\,c_{0}\,q+\frac{1}{2}\,i\,d_{-1}\,q(-x,-t)\,q\\&\quad +\frac{1}{2}\,i\,b_{0}\,q^{[1]}(-x,-t)-\frac{1}{2}\,i\,d_{-1}\,q^{[1]}(-x,-t)\,q^{[1]}\\&\quad +d_{-1t}=0,\\&\quad \lambda ^{-2}: b_{0}+a_{-1}\,q-d_{-1}\,q^{[1]}=0, \\&\quad c_{0}+d_{-1}\,q(-x,-t)-a_{-1}\,q^{[1]}(-x,-t)=0,\\&\quad \lambda ^{-3}: b_{-1}=0, c_{-1}=0. \end{aligned}$$

Appendix B

The $a_{1}, d_{1}, b_{0}, c_{0}$ for one-fold Darboux matrix $T^{[1]}$ yield

$$\begin{aligned} a_{1}= & {} \frac{\left| \begin{array}{cc} -\lambda _{1}^{-1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ -\lambda _{2}^{-1}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ d_{1}= & {} \frac{\left| \begin{array}{cc} -\lambda _{1}^{-1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ -\lambda _{2}^{-1}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| },\\ b_{0}= & {} \frac{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}-\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}-\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ c_{0}= & {} \frac{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}-\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}-\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }. \end{aligned}$$

In other words, we can deduce

$$\begin{aligned} T^{[1]}_{11}= & {} \frac{\left| \begin{array}{ccc} \lambda &{}0 &{}\lambda ^{-1}\\ \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t) &{}\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t) &{}\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ T^{[1]}_{12}= & {} \frac{\left| \begin{array}{ccc} 0 &{}1 &{}0\\ \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t) &{}\lambda _{1}^{-1}\,\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t) &{}\lambda _{2}^{-1}\,\varphi _{2}(x,t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(x,t) &{}\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(x,t) &{}\varphi _{2}(-x,-t)\\ \end{array} \right| },\\ T^{[1]}_{21}= & {} \frac{\left| \begin{array}{ccc} 0 &{}1 &{}0\\ \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t) &{}\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t) &{}\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| },\\ T^{[1]}_{22}= & {} \frac{\left| \begin{array}{ccc} \lambda &{}0 &{}\lambda ^{-1}\\ \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t) &{}\lambda _{1}^{-1}\,\varphi _{1}(-x,-t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t) &{}\lambda _{2}^{-1}\,\varphi _{2}(-x,-t)\\ \end{array} \right| }{\left| \begin{array}{cc} \lambda _{1}\,\varphi _{1}(-x,-t) &{}\varphi _{1}(x,t)\\ \lambda _{2}\,\varphi _{2}(-x,-t) &{}\varphi _{2}(x,t)\\ \end{array} \right| }. \end{aligned}$$

Appendix C

The $W^{[N]}, \widetilde{T^{[N]}_{11}}, \widetilde{T^{[N]}_{12}}, \widetilde{W^{[N]}}, \widetilde{T^{[N]}_{21}}, \widetilde{T^{[N]}_{22}}$ for N-fold Darboux matrix $T^{[N]}$ read

$$\begin{aligned}&W^{[N]}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{11}}=\left| \begin{array}{cccccccc} \lambda ^{N} &{}0 &{}\cdots &{}0 &{}\lambda ^{-N}\\ \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{12}}=\left| \begin{array}{cccccccc} 0 &{}\lambda ^{N-1} &{}\cdots &{}\lambda ^{-(N-1)} &{}0\\ \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{W^{[N]}}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\ {}&\widetilde{T^{[N]}_{21}}=\left| \begin{array}{ccccccc} 0 &{}\lambda ^{N-1} &{}\cdots &{}\lambda ^{-(N-1)} &{}0\\ \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| ,\\&\widetilde{T^{[N]}_{22}}=\left| \begin{array}{ccccccc} \lambda ^{N} &{}0 &{}\cdots &{}0 &{}\lambda ^{-N}\\ \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-1)}\,\varphi _{1}(x,t) &{}\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-1)}\,\varphi _{2}(x,t) &{}\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-1)}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-1)}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| . \end{aligned}$$

Appendix D

The $\varOmega _{-(N-1)}, \widetilde{\varOmega _{-(N-1)}}$ for N-soliton solutions ($q^{[N]}, q^{[N]}(-x, -t)$) arrive at

$$\begin{aligned}&\varOmega _{-(N-1)}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(x,t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(-x,-t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(x,t) &{}-\lambda _{1}^{-N}\,\varphi _{1}(x,t)\\ \lambda _{2}^{N}\,\varphi _{2}(x,t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(-x,-t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(x,t) &{}-\lambda _{2}^{-N}\,\varphi _{2}(x,t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(x,t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(-x,-t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(x,t) &{}-\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(x,t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(x,t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(-x,-t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(x,t) &{}-\lambda _{2N}^{-N}\,\varphi _{2N}(x,t)\\ \end{array} \right| ,\\&\widetilde{\varOmega _{-(N-1)}}=\left| \begin{array}{ccccccc} \lambda _{1}^{N}\,\varphi _{1}(-x,-t) &{}\lambda _{1}^{N-1}\,\varphi _{1}(x,t) &{}\cdots &{}\lambda _{1}^{-(N-2)}\,\varphi _{1}(-x,-t) &{}-\lambda _{1}^{-N}\,\varphi _{1}(-x,-t)\\ \lambda _{2}^{N}\,\varphi _{2}(-x,-t) &{}\lambda _{2}^{N-1}\,\varphi _{2}(x,t) &{}\cdots &{}\lambda _{2}^{-(N-2)}\,\varphi _{2}(-x,-t) &{}-\lambda _{2}^{-N}\,\varphi _{2}(-x,-t)\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ \lambda _{2N-1}^{N}\,\varphi _{2N-1}(-x,-t) &{}\lambda _{2N-1}^{N-1}\,\varphi _{2N-1}(x,t) &{}\cdots &{}\lambda _{2N-1}^{-(N-2)}\,\varphi _{2N-1}(-x,-t) &{}-\lambda _{2N-1}^{-N}\,\varphi _{2N-1}(-x,-t)\\ \lambda _{2N}^{N}\,\varphi _{2N}(-x,-t) &{}\lambda _{2N}^{N-1}\,\varphi _{2N}(x,t) &{}\cdots &{}\lambda _{2N}^{-(N-2)}\,\varphi _{2N}(-x,-t) &{}-\lambda _{2N}^{-N}\,\varphi _{2N}(-x,-t)\\ \end{array} \right| . \end{aligned}$$