Soliton, breather, rogue wave and continuum limit for the spatial discrete Hirota equation by Darboux–Bäcklund transformation

Abstract

In this paper, the spatial discrete Hirota equation is investigated by Darboux–Bäcklund transformation. Firstly, the pseudopotential of the spatial discrete Hirota equation is proposed for the first time, from which a Darboux–Bäcklund transformation is constructed. Comparing it with the corresponding onefold Darboux transformation, we find that they are equivalent because there is no difference except for a constant times. We believe that this equivalence may hold universal if these two transformations are all derived from the same discrete spectral problem and using the similar technique in the references. Secondly, starting from vanishing and plane wave backgrounds, a variety of nonlinear wave solutions, including bell-shaped one-soliton, three types of breathers, W-shaped soliton, periodic solution and rogue wave are given, and the relevant dynamical properties and evolutions are illustrated by plotting figures. The relationship between parameters and solutions’ structures is studied in detail, and the related method and technique can also be extended to other nonlinear integrable equations. Finally, we show that the continuum limit of breather and rogue wave solutions of the spatial discrete Hirota equation yields the counterparts of the Hirota equation. The results in this paper might be useful for understanding some physical phenomena in nonlinear optics.

1 Introduction

The Hirota equation introduced in [1] has the form:

$$\begin{aligned} {{i}} \nu _\tau = \gamma (\nu _{\textit{xx}} + 2 |\nu |^2 \nu ) + \mathrm{{i}} \alpha (\nu _{\textit{xxx}} + 6 |\nu |^2\nu _{\textit{x}}), \end{aligned}$$

(1)

where the complex function $\nu =\nu (x,\tau )$ denotes the wave envelopes, the subscripts represent partial differentiation to $\tau$ and x, the parameters $\gamma$ and $\alpha$ are real positive constants and ${i}=\sqrt{-1}$ stands for imaginary unit. Equation (1) is a typical integrable system in soliton theory and it has attracted a great deal of attention because of its physical applications in the vortex motion and the nonlinear optics [2]. For Eq. (1), the inverse scattering transform and Darboux transformation were performed and N-soliton solutions, rogue wave solutions and gauge equivalence were generated and systematically studied [3,4,5,6,7]. By means of the Ablowitz–Ladik’s formulation, Porsezian and Lakshmanan [8] constructed the integrable semi-discrete Hirota equation

$$\begin{aligned} \mathrm{{i}} u_{n,t}= & {} \gamma (u_{n+1}-2 u_n + u_{n-1} + |u_n|^2(u_{n+1}+u_{n-1}))\nonumber \\{} & {} +\mathrm{{i}} \alpha ((1+|u_n|^2)(u_{n+1}-u_{n-1})), \end{aligned}$$

(2)

which yields to the Hirota equation (1) in the continuum limit and can be regarded as an integrable semi-discretizations of Eq. (1). Many excellent and meaningful results related to Eq. (2) have been obtained. For instance, bright and dark soliton solutions were generated based on the Hirota bilinear method [9, 10] and Darboux transformation [11], and rogue waves were given in [12, 13]. However, one can check that these discrete solutions of the semi-discrete Hirota equation (2) does not converge to the solutions of the Hirota equation (1). Because of this reason, the following spatial discrete Hirota equation was proposed and investigated [14]

$$\begin{aligned} \begin{aligned} u_{n,t}&=\alpha (1+{\vert u_n \vert }^2)[u_{n+2}-u_{n-2}+2u_{n-1}-2u_{n+1}\\&\quad +u_{n}^*(u^2_{n+1}-u^2_{n-1})-{\vert u_{n-1} \vert }^2u_{n-2}+{\vert u_{n+1} \vert }^2u_{n+2}\\&\quad +u_n(u^*_{n-1}u_{n+1}-u^*_{n+1}u_{n-1})]\\&\quad -\beta {i} (1+{\vert u_n \vert }^2)(u_{n+1}+u_{n-1})+2 \beta {i} u_n, \end{aligned} \end{aligned}$$

(3)

where $u_n=u(n,t)$ is a complex-valued function of discrete space variable n and time variable t, $u_{n,t}=\frac{\textrm{d}}{\textrm{d}t}u_n$ and $*$ denotes the complex conjugate. In [14], the authors showed that the Lax pair, Darboux transformation and soliton solutions for the spatial discrete Hirota equation (3) yield to the corresponding results for the Hirota equation (1). The higher-order rogue wave solutions, which display triangular patterns and pentagons with different peaks, were investigated in [15]. By the Darboux transformation method, the positon solutions and breather solutions of equation (3) were constructed in [16]. Interestingly, the new Lax pair of the spatial discrete Hirota equation (3) was proposed in [17], from which the Darboux transformation, soliton solution, rogue wave solution, breather solution, the continuous limits and gauge equivalent structure were studied.

To describe and understand the physical phenomena simulated by the discrete integrable equations, it is significant to obtain and investigate their explicit exact solutions, especially soliton, breather and rogue wave solutions. Several effective and skillful methods for constructing explicit solutions have been proposed and developed, such as the inverse scattering method [18], the Hirota method [19,20,21], the algebra-geometric method [22], the discrete Jacobi sub-equation method [23], the Darboux transformation [24,25,26,27,28,29,30,31,32] and the Darboux–Bäcklund transformation [33,34,35]. Among these existing methods, the Darboux–Bäcklund transformation has turned out to be one of efficient skills to obtain soliton solutions. Recently, the pseudopotential of the Ablowitz–Ladik lattice and semi-discrete Hirota equation (2) were proposed, from which the Darboux–Bäcklund transformation of the equations were established and various localized nonlinear wave solutions were given [36, 37]. Pseudopotential is an another effective technique to construct the Darboux–Bäcklund transformation, compared with the Darboux transformation, it can avoid complex matrix calculations for us.

To the best of our knowledge, the Darboux–Bäcklund transformation based on the pseudopotential for the spatial discrete Hirota equation (3) has not been reported before; the relationship between parameters and solutions’ structures in Eq. (3) has not been investigated due to its complexity; the continuum limit of breather solution and rogue wave solution of equation (3) corresponding to the Lax pair (4) have not been studied. These three aspects are what we focus in this paper. The rest of this paper is organized as follows. In Sect. 2, the Darboux–Bäcklund transformation is constructed by using the pseudopotential, and the comparison between it and the one-fold Darboux transformation is performed. In Sect. 3, various types of nonlinear wave solutions are given and the relationship between parameters and solutions’ structures is discussed in detail. In Sect. 4, the continuum limit of breather solution and rogue wave solution related to the Lax pair (4) is investigated. Some remarks and summary are presented in the last section.

2 Darboux–Bäcklund transformation of the spatial discrete Hirota equation

In this section, we will focus on the Darboux–Bäcklund transformation for the spatial discrete Hirota equation (3). From Ref. [14], we know the Lax pair of the spatial discrete Hirota equation (3) is given by

$$\begin{aligned} E\phi _n=U_n \phi _n,~~~~~~~~~~\phi _{n,t}=V_n \phi _n, \end{aligned}$$

(4)

where E is the shift operator defined by $E\phi _n=\phi _{n+1}$, $\phi _n=(\phi _{n,1}, \phi _{n,2})^\texttt {T}$ is vector eigenfunction, $\texttt {T}$ denotes the transpose of the vector or matrix and $\lambda \in {\mathbb {C}}$ stands for the spectral parameter which is independent on the time t. The matrices $U_n$ and $V_n$ have the following forms:

$$\begin{aligned} U_n= & {} \left( \begin{array}{cc} \lambda &{} u_n \\ -u_n^* &{} \lambda ^{-1} \end{array} \right) ,~~~~\\ V_n= & {} \alpha \left( \begin{array}{cc} ~A_n(\lambda , \lambda ^{-1}, u_n) &{} B_n(\lambda , \lambda ^{-1}, u_n)\\ -B_n(\lambda ^{-1}, \lambda , u_n^*) &{} A_n(\lambda ^{-1}, \lambda , u_n^*) \end{array} \right) \\{} & {} \quad +\beta {i} \left( \begin{array}{cc} C_n(\lambda , \lambda ^{-1}, u_n) &{} ~D_n(\lambda , \lambda ^{-1}, u_n)\\ D_n(\lambda ^{-1}, \lambda , u_n^*) &{}-C_n(\lambda ^{-1}, \lambda , u_n^*) \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&A_n(\lambda , \lambda ^{-1},u_n)=\frac{1}{2}(\lambda ^4-\lambda ^{-4})\\&\quad -\lambda ^2+\lambda ^{-2}+\lambda ^2u_nu^*_{n-1}\\&\quad -\lambda ^{-2}u_{n-1}u_{n}^*-2u_{n}u^*_{n-1}+(u_nu_{n-1}^*)^2\\&\quad +(1+{\vert u_{n-1} \vert }^2)u_n u^*_{n-2}+(1+{\vert u_n \vert }^2)u_{n+1}u_{n-1}^*,\\&B_n(\lambda , \lambda ^{-1}, u_n)=\lambda ^3 u_n +\lambda ^{-3} u_{n-1}\\&\quad +\lambda ^{-1}[(1+{\vert u_{n-1} \vert }^2)u_{n-2}+u_{n-1}^2u_n^*-2u_{n-1}],\\&C_n(\lambda , \lambda ^{-1}, u_n)=-u_nu^*_{n-1}-\frac{1}{2} (\lambda -\lambda ^{-1})^2,~~\\&D_n(\lambda , \lambda ^{-1}, u_n)=-u_n\lambda +u_{n-1}\lambda ^{-1}. \end{aligned} \end{aligned}$$

One can directly verify that the discrete zero curvature condition $U_{n,t}=V_{n+1}U_n-U_nV_n$ of the Lax pair (4) gives rise to the spatial discrete Hirota equation (3).

To construct the Darboux–Bäcklund transformation for the spatial discrete Hirota equation (3), we introduce the variable

$$\begin{aligned} \Gamma _n=\frac{\phi _{n,1}}{\phi _{n,2}}, \end{aligned}$$

(5)

which is called as the pseudopotential of equation (3). Using (4), we obtain

$$\begin{aligned}{} & {} \Gamma _{n+1}=\frac{\lambda (u_n+\lambda \Gamma _n)}{1-\lambda {u}^*_n\Gamma _n},\nonumber \\{} & {} \quad \Gamma _{n,t}=-A_n\Gamma _n^2+B_n \Gamma _n+C_n, \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned}&A_n=-\alpha B_n(\lambda ^{-1}, \lambda , u_n^*) + \beta {i} D_n(\lambda ^{-1}, \lambda , u_n^*),~~\\&C_n=\alpha B_n(\lambda ,\lambda ^{-1}, u_n) + \beta {i} D_n(\lambda , \lambda ^{-1},u_n),\\&B_n=\alpha \left( A_n(\lambda , \lambda ^{-1}, u_n)-A_n(\lambda ^{-1}, \lambda , u_n^*)\right) \\&\qquad \quad + \beta {i} \left( C_n(\lambda , \lambda ^{-1}, u_n)+C_n(\lambda ^{-1}, \lambda , u_n^*)\right) . \end{aligned} \end{aligned}$$

Taking the conjugate of both sides of the first equation in (6) and solving the equations related to $u_n$ and $u^*_n$, we get

$$\begin{aligned} u_n=\frac{\lambda {\lambda }^{*2}\Gamma _n{\Gamma }^*_n\Gamma _{n+1}-\lambda \Gamma _n\Gamma _{n+1}{\Gamma }^*_{n+1} +{\lambda }^*\Gamma _{n+1}-\lambda ^2{\lambda ^*}\Gamma _n}{\lambda {\lambda ^*}(1-\Gamma _n{\Gamma }^*_n\Gamma _{n+1}{\Gamma }^*_{n+1})}.\nonumber \\ \end{aligned}$$

(7)

Inserting (7) into the second equation of (6), through a complicated computation, we derive a equation which is made up of $\Gamma _{n-2}$, $\Gamma _{n-1}$, $\Gamma _n$, $\Gamma _{n+1}$, $\Gamma _{n+2}$ and $\lambda$ without variables $u_{n-2}, u_{n-1}, u_n, u_{n+1}$, this equation is so tedious that we omit it for brevity. With the help of Maple, we can verify that this equation is invariant under the transformations of $\Gamma _{n-2}\rightarrow \Gamma _{n-2}$, $\Gamma _{n-1}\rightarrow \Gamma _{n-1}$, $\Gamma _n\rightarrow \Gamma _{n}$, $\Gamma _{n+1}\rightarrow \Gamma _{n+1}$, $\Gamma _{n+2}\rightarrow \Gamma _{n+2}$, $\lambda \rightarrow {\lambda }^{*-1}$. In other words, there exists new variable ${\tilde{u}}_n$ satisfying the same form of Eqs. (6) when $\lambda \rightarrow {\lambda }^{*-1}$, in which ${\tilde{u}}_n$ is considered as the new solution of equation (3). From the first equation of (6) and (7), using the transformation $\lambda \rightarrow {\lambda }^{*-1}$, the relation between the old solution $u_n$ and new solution ${\tilde{u}}_n$ can be derived as

$$\begin{aligned} {\tilde{u}}_n=\frac{\lambda {\lambda }^{*}+\Gamma _n{\Gamma }^*_n}{1+\lambda {\lambda ^*}\Gamma _n{\Gamma }^*_n}u_n +\frac{(\lambda ^2{\lambda }^{*2}-1)\Gamma _n}{{\lambda ^*}(1+\lambda {\lambda ^*}\Gamma _n{\Gamma }^*_n)}. \end{aligned}$$

(8)

which is called as the Darboux–Bäcklund transformation of Eq. (3). Based on (8), we can iterate the old solutions $u_n$ to get new ones ${\tilde{u}}_n$. It should be remarked that if the resulting solution is taken as the new starting point, and use the Darboux–Bäcklund transformation (8) once again, then another new solutions of equation (3) can be obtained. This process can be done continuously. Therefore, we can generate a sequence of explicit solutions for the spatial discrete Hirota equation (3).

In [14], by means of the Lax pair (4), the one-fold Darboux transformation related to Eq. (3) was given

$$\begin{aligned} {\tilde{u}}_n=\frac{\lambda }{\lambda ^*}\left( \frac{\lambda {\lambda }^{*} +\Gamma _n{\Gamma }^*_n}{1+\lambda {\lambda ^*}\Gamma _n{\Gamma }^*_n}u_n +\frac{(\lambda ^2{\lambda }^{*2}-1)\Gamma _n}{{\lambda ^*}(1+\lambda {\lambda ^*}\Gamma _n{\Gamma }^*_n)}\right) .\nonumber \\ \end{aligned}$$

(9)

Comparing the transformation (8) with (9), we find there is no difference except for a constant times. Noticing $\big |\frac{\lambda }{\lambda ^*}\big |=1$, so we consider these two transformations are equivalent. Moreover, we believe the equivalence may hold universal if the two transformations are all derived from the same discrete spectral problem and using the similar methods and techniques employed in literatures [36, 37] and [14, 38], respectively. To illustrate this fact, we establish the Darboux–Bäcklund transformation of the generalized discrete Hirota equation studied in [13] and the discrete complex mKdV equation proposed in [39]. Comparing with the one-fold Darboux transformations obtained in [13, 39], we observe that they remain equivalent.

In [17], by using the other new Lax pair, the one-fold Darboux transformation related to Eq. (3) was derived

$$\begin{aligned} {\tilde{u}}_n=\frac{\lambda ^2(1+\Gamma _n{\Gamma }^*_n)}{1+\lambda ^2{\lambda }^{*2}\Gamma _n{\Gamma }^*_n}u_n +\frac{\lambda ^2(\lambda ^2{\lambda }^{*2}-1)\Gamma _n}{{\lambda }^{*2}(1+\lambda ^2{\lambda }^{*2}\Gamma _n{\Gamma }^*_n)}, \end{aligned}$$

which is not equivalent with the transformation (8). Therefore, the explicit solutions we obtain in this paper may be different from the ones given in [17].

Although the transformations (8) and (9) are equivalent, the relationship between parameters and solutions’ structures in Eq. (3) has not been studied due to its complexity. On the other hand, the continuum limit of the breather and rogue wave solutions of Eq. (3) corresponding to the Lax pair (4) has not been reported before. These two parts are what we focus on in the following two sections.

3 Soliton, breather and rogue wave of the spatial discrete Hirota equation

In this section, we are going to give soliton, breather and rogue wave for the spatial discrete Hirota equation (3) by using the obtained Darboux–Bäcklund transformation (8) from vanishing and plane wave backgrounds, respectively. To figure out the different collision process of solitary waves and the corresponding dynamical properties, we assume that n is a continuous variable from $-\infty$ to $+\infty$ when we plot figures.

3.1 Soliton

Substituting the trivial solution $u_n=0$ into the Lax pair (4) and solving the related spectral equation, we obtain

$$\begin{aligned} \phi _{n,1}=\lambda ^n e^{\chi (\lambda )t},~~~~~~~~\phi _{n,2}=\lambda ^{-n} e^{- \chi (\lambda )t}, \end{aligned}$$

(10)

where $\chi (\lambda )=\alpha (\frac{1}{2}(\lambda ^4-\lambda ^{-4})+\lambda ^{-2}-\lambda ^2)-\frac{1}{2}\beta \textrm{i} (\lambda -\lambda ^{-1})^2.$ Let $\lambda =e^{a + {{i}} b}$, where a, b are real constants. Then we rewrite (10) as

$$\begin{aligned} \phi _{n,1}=e^{Z_R + \mathrm{{i}} Z_I },~~~~~~~~\phi _{n,2}=e^{-Z_R - \mathrm{{i}} Z_I }, \end{aligned}$$

(11)

where $Z_R$ and $Z_I$ are the associate real and imaginary parts and given by

$$\begin{aligned} Z_R&=a n + \{\alpha [\cos (4b)\sinh (4a)-2\cos (2b)\sinh (2a)]\\&\quad +\beta [\sin (2b)\sinh (2a)] \} t,\\ Z_I&=b n + \{\alpha [\sin (4b)\cosh (4a)-2\sin (2b)\cosh (2a)]\\&\quad -\beta [\cos (2b)\cosh (2a)] + \beta \} t. \end{aligned}$$

From (11), the pseudopotential (5) of the spatial discrete Hirota equation (3) is derived as

$$\begin{aligned} \Gamma _n=e^{2Z_R + 2 \mathrm{{i}} Z_I }. \end{aligned}$$

(12)

Thus, by using the Darboux–Bäcklund transformation (8) with (12), a one-soliton solution of the spatial discrete Hirota equation (3) is obtained

$$\begin{aligned} {\tilde{u}}_n=\frac{\lambda (|\lambda |^2-|\lambda |^{-2})e^{2 \mathrm{{i}} Z_I}}{2|\lambda |}\textrm{sech}(2Z_R+\ln |\lambda |). \end{aligned}$$

(13)

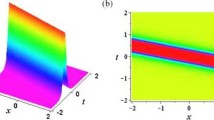
The solution (13) is the same as one obtained in [14], except for the amplitude. However, we mainly pay attention to some physical quantities related to solution (13) and investigate the relationship between the structure of solution (13) and the parameters $\alpha$, $\beta$, $\lambda$. From (13), some important physical quantities such as amplitude, width, wave number, velocity, primary phase and energy are listed in Table 1, in which the energy of $|{\tilde{u}}_n|$ is defined by $E_{|{\tilde{u}}_n|}=\int _{-\infty }^{+\infty }|{\tilde{u}}_n|^2dn$. Based on the Table 1, we find these physical quantities are invariant once the parameters are determined, which means the shape, amplitude, wave-length and direction of the solution $|{\tilde{u}}_n|$ don’t change during the propagation and it is much stable. It is easily seen that this one-soliton solution $|{\tilde{u}}_n|$ of (13) is nonsingular and displays the evolution structure of bell-shaped one-soliton for arbitrary parameters $\alpha$, $\beta$, $\lambda$ ($\lambda \ne 0,\pm 1,\pm \textrm{i}$). When the parameters $\alpha =0.3$, $\beta =0.2$, $\lambda =0.2+0.8 \mathrm{{i}}$, the corresponding evolution plots are shown in Fig. 1, from which we know that $|{\tilde{u}}_n|$ admits bell-shaped one-soliton structure and its shape and amplitude keep invariant during the propagation.

Table 1 Physical quantities of one-soliton solution $|{\tilde{u}}_n|$ in (13)

Fig. 1

a Bell-shaped one-soliton $|{\tilde{u}}_n|$ in (13) with parameters $\alpha =0.3$, $\beta =0.2$, $\lambda =0.2+ 0.8 \textrm{i}$

3.2 Breather

Three types of breathers, W-shaped soliton and periodic solution to the spatial discrete Hirota equation (3) based on the Darboux–Bäcklund transformation (8) will be presented in this subsection. For this purpose, take a nonzero seed solution-plane wave solution

$$\begin{aligned} u_n=c e^{\mathrm{{i}} z_n}, \end{aligned}$$

(14)

where c is a real-valued constant and called as the amplitude of the plane wave, $z_n=k n+\omega t$, k is wave number and $\omega$ is dispersion relation read as $\omega =2\beta -2\beta (1+c^2)\cos (k)+4 \alpha (1+c^2)[(3c^2+1)\cos (k)-1]\sin (k)$. For the plane wave solution (14) related to the Lax pair (4), breather and rogue wave solutions and their continuum limits for the spatial discrete Hirota equation (3) have not been studied, which is the main content of our study in the following.

For the sake of brevity, we introduce a gauge transformation related to the initial solution (14)

$$\begin{aligned} {\tilde{\phi }}_n=T \phi _n =\left( \begin{array}{cc} e^{-\frac{\mathrm{{i}}}{2} z_n} &{} 0 \\[2mm] 0 &{} e^{\frac{\mathrm{{i}}}{2} z_n} \end{array} \right) \phi _n, \end{aligned}$$

under this gauge transformation, we map the variable coefficient Lax pair (4) to the constant coefficient Lax pair,

$$\begin{aligned} E{\tilde{\phi }}_n={\tilde{U}}_n {\tilde{\phi }}_n,~~~~~~~~~~{\tilde{\phi }}_{n,t}={\tilde{V}}_n {\tilde{\phi }}_n, \end{aligned}$$

(15)

where

$$\begin{aligned} {\tilde{U}}_n= & {} \left( \begin{array}{cc} \lambda &{} c \\ -c &{}~~ \lambda ^{-1} \end{array} \right) ,~~~~~~~~\\ {\tilde{V}}_n= & {} \left( \begin{array}{cc} - \frac{\mathrm{{i}}}{2}\omega +\alpha A_1 +\beta \mathrm{{i}} A_2 &{} \alpha c A_3+\beta \mathrm{{i}} c A_4\\ - \alpha c B_3+\beta \mathrm{{i}} c B_4 &{} \frac{\mathrm{{i}}}{2}\omega +\alpha B_1-\beta \mathrm{{i}} B_2 \end{array} \right) , \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} A_1&=\frac{1}{2}(\lambda ^4-\lambda ^{-4})-\lambda ^2+\lambda ^{-2}+(\lambda ^2-2)c^2e^{\mathrm{{i}}k}\\&\quad -\lambda ^{-2} c^2 e^{-\mathrm{{i}}k}+(3 c^2+2) c^2 e^{2 \mathrm{{i}} k},~~~\\ A_2&=-c^2e^{\mathrm{{i}}k}-\frac{1}{2}(\lambda -\lambda ^{-1})^2,\\ A_3&=\lambda ^3+\lambda ^{-3}e^{- \mathrm{{i}} k}+\lambda [(1+2 c^2)e^{\mathrm{{i}} k}-2]\\&\quad +\lambda ^{-1}[(1+2c^2)e^{-2 \mathrm{{i}} k}-2 e^{-\mathrm{{i}} k}],~~~~~~~~~~~\\ A_4&=-\lambda +\lambda ^{-1}e^{-\mathrm{{i}}k},\\ B_1&=\frac{1}{2}(\lambda ^{-4}-\lambda ^{4})-\lambda ^{-2}+\lambda ^{2}\\&\quad +(\lambda ^{-2}-2)c^2e^{-\mathrm{{i}}k}-\lambda ^{2} c^2 e^{\mathrm{{i}}k}+(3 c^2+2) c^2 e^{-2 \mathrm{{i}} k},~\\ B_2&=-c^2 e^{-\mathrm{{i}}k}-\frac{1}{2}(\lambda -\lambda ^{-1})^2,\\ B_3&=\lambda ^{-3}+\lambda ^{3}e^{\mathrm{{i}} k}+\lambda ^{-1} [(1+2 c^2)e^{-\mathrm{{i}} k}-2]\\&\quad +\lambda [(1+2c^2)e^{2 \mathrm{{i}} k}-2 e^{\mathrm{{i}} k}],\quad B_4=-\lambda ^{-1}+\lambda e^{\mathrm{{i}}k}. \end{aligned} \end{aligned}$$

Solving the corresponding spectral equation related to the Lax pair (15), we obtain

$$\begin{aligned} {\tilde{\phi }}_n= \left( \begin{array}{c} {\tilde{\phi }}_{n,1}\\ {\tilde{\phi }}_{n,2} \end{array} \right) = \left( \begin{array}{c} C_1 \tau _1^ne^{\rho _1 t}+C_2 \tau _2^ne^{\rho _2 t}\\ C_1 \frac{\tau _1-\lambda }{c}\tau _1^ne^{\rho _1 t}+C_2 \frac{\tau _2-\lambda }{c} \tau _2^ne^{\rho _2 t} \end{array} \right) , \end{aligned}$$

where $C_1$, $C_2$ are arbitrary constants and

$$\begin{aligned} \begin{aligned}&\tau _1=\frac{1}{2}(\lambda +\lambda ^{-1}+\sqrt{\lambda ^2+\lambda ^{-2}-4c^2-2}),~~~~~~~~\\&\quad \rho _1=-\frac{\mathrm{{i}}}{2}\omega +\alpha A_1 +\beta \mathrm{{i}} A_2+(\alpha A_3+\beta \mathrm{{i}} A_4) (\tau _1-\lambda ),\\&\tau _2=\frac{1}{2}(\lambda +\lambda ^{-1}-\sqrt{\lambda ^2+\lambda ^{-2}-4c^2-2}),~~~~~~~~\\&\quad \rho _2=-\frac{\mathrm{{i}}}{2}\omega +\alpha A_1 +\beta \mathrm{{i}} A_2+(\alpha A_3+\beta \mathrm{{i}} A_4) (\tau _2-\lambda ). \end{aligned} \end{aligned}$$

Then, the general solution of the Lax pair (4) associated with the initial solution (14) can be given by

$$\begin{aligned}{} & {} \phi _n=T^{-1}{\tilde{\phi }}_n\nonumber \\{} & {} = \left( \begin{array}{c} (C_1 \tau _1^ne^{\rho _1 t}+C_2 \tau _2^ne^{\rho _2 t})e^{\frac{\mathrm{{i}}}{2} z_n}\\ (C_1 \frac{\tau _1-\lambda }{c}\tau _1^ne^{\rho _1 t}+C_2 \frac{\tau _2-\lambda }{c} \tau _2^ne^{\rho _2 t})e^{-\frac{\mathrm{{i}}}{2} z_n} \end{array} \right) . \end{aligned}$$

(16)

With the help of (16), the pseudopotential (5) of the spatial discrete Hirota equation (3) is derived as

$$\begin{aligned} \Gamma _n=\frac{C_1 \tau _1^ne^{\rho _1 t} + C_2 \tau _2^ne^{\rho _2 t}}{C_1\frac{\tau _1-\lambda }{c} \tau _1^ne^{\rho _1 t} + C_2 \frac{\tau _2-\lambda }{c} \tau _2^ne^{\rho _2 t}} e^{\mathrm{{i}}z_n}. \end{aligned}$$

(17)

Let

$$\begin{aligned} \mu _1= & {} \frac{\tau _1}{\sqrt{c^2+1}},~~\mu _2=\frac{\tau _2}{\sqrt{c^2+1}}, \eta _1=\frac{\tau _1-\lambda }{c},~~\\ \eta _2= & {} \frac{\tau _2-\lambda }{c},~~ \varrho =(\alpha A_3+\beta \mathrm{{i}} A_4)\\ {}{} & {} \sqrt{\lambda ^2+\lambda ^{-2}-4c^2-2}. \end{aligned}$$

Then, we can equivalently denote (17) as

$$\begin{aligned} \Gamma _n=\frac{C_1 \mu _1^ne^{\varrho t} + C_2 \mu _2^ne^{-\varrho t}}{C_1 \eta _1 \mu _1^ne^{\varrho t} + C_2 \eta _2 \mu _2^n e^{-\varrho t}} e^{\mathrm{{i}}z_n}. \end{aligned}$$

(18)

Since $\mu _1\mu _2=1$, $\eta _1\eta _2=1$, we rewrite

$$\begin{aligned} \mu _1= & {} e^{\kappa _1+ \mathrm{{i}} \kappa _2},~~~~~~ \mu _2=e^{-(\kappa _1+ \mathrm{{i}} \kappa _2)},~~~~~~\nonumber \\ \eta _1= & {} e^{\alpha _1+ \mathrm{{i}} \alpha _2},~~~~~~\eta _2=e^{-(\alpha _1+ \mathrm{{i}} \alpha _2)},~~~~~~ \varrho =\omega _1+ \mathrm{{i}} \omega _2,\nonumber \\ \end{aligned}$$

(19)

where $\kappa _i$, $\alpha _i$ and $\omega _i$ ($i=1,2$) are the corresponding real and imaginary parts, respectively. Noticing that $C_1$, $C_2$ in (18) are arbitrary constants, whose roles are only to change the phase of the nonlinear wave. For the sake of simplicity, we choose $C_1=1$, $C_2=-1$. Thus, by (18) and (19), the pseudopotential of the spatial discrete Hirota equation (3) is constructed as

$$\begin{aligned} \Gamma _n=\frac{e^{\theta _1+\mathrm{{i}}\theta _2} - e^{-(\theta _1+\mathrm{{i}}\theta _2)} }{e^{\theta _1+\mathrm{{i}}\theta _2+\alpha _1+ \mathrm{{i}} \alpha _2} - e^{-(\theta _1+\mathrm{{i}}\theta _2+\alpha _1+ \mathrm{{i}} \alpha _2)}} e^{\mathrm{{i}}z_n}, \end{aligned}$$

(20)

where

$$\begin{aligned} \theta _1=\kappa _1 n + \omega _1 t,\quad \theta _2=\kappa _2 n + \omega _2 t. \end{aligned}$$

From (20), we have

$$\begin{aligned} \Gamma _n=\frac{\sinh (\theta _1)\cos (\theta _2) + \textrm{i} \cosh (\theta _1)\sin (\theta _2)}{\sinh (\theta _1+\alpha _1)\cos (\theta _2+\alpha _2) + \textrm{i} \cosh (\theta _1+\alpha _1)\sin (\theta _2+\alpha _2) } e^{\mathrm{{i}}z_n}, \end{aligned}$$

(21)

and

$$\begin{aligned} \Gamma _n\Gamma _n^*=\frac{\cosh (2\theta _1)-\cos (2\theta _2)}{\cosh (2\theta _1+2\alpha _1)-\cos (2\theta _2+2\alpha _2)}. \end{aligned}$$

(22)

Therefore, by using the Darboux–Bäcklund transformation (8) with (21) and (22), the nonlinear wave solution of the spatial discrete Hirota equation (3) is given by

$$\begin{aligned} {\tilde{u}}_n=\frac{|\lambda |^2+\frac{\cosh (2\theta _1)-\cos (2\theta _2)}{\cosh (2\theta _1+2\alpha _1) -\cos (2\theta _2+2\alpha _2)}+\frac{|\lambda |^4-1}{c\lambda ^*} \frac{\sinh (\theta _1)\cos (\theta _2) + \mathrm{{i}} \cosh (\theta _1)\sin (\theta _2)}{\sinh (\theta _1+\alpha _1)\cos (\theta _2+\alpha _2) + \mathrm{{i}} \cosh (\theta _1+\alpha _1)\sin (\theta _2+\alpha _2) }}{1+|\lambda |^2\frac{\cosh (2\theta _1)-\cos (2\theta _2)}{\cosh (2\theta _1+2\alpha _1)-\cos (2\theta _2+2\alpha _2)}}c e^{\mathrm{{i}}z_n}. \end{aligned}$$

(23)

Obviously, the periodicity of the nonlinear wave solution (23) is mainly affected by $\theta _2$. When $\kappa _1=0$, $\kappa _2\ne 0$, $\theta _1$ is independent of space variable n and $\theta _2$ is periodic with respect to n, so solution (23) is periodic in the n direction; while $\omega _1=0$, $\omega _2\ne 0$, $\theta _1$ is independent of time variable t and $\theta _2$ is periodic with respect to t, then solution (23) becomes periodic in the t direction.

By choosing different parameters $\lambda$, c, $\alpha$, $\beta$ and k, the distinct wave structures can be obtained from (23). In what follows, we proceed to give three types of breather solutions, W-shaped soliton solution and periodic solution for the spatial discrete Hirota equation (3) and illustrate their dynamical properties and propagation process by plotting figures. Meanwhile, the relationship between parameters and breathers’ structures will be studied in detail.

Firstly, we will investigate the case where $\lambda$ is real. We are going to discuss solution (23) for two cases under the condition $\lambda ^2+\lambda ^{-2}-4c^2-2\ne 0$, the case of $\lambda ^2+\lambda ^{-2}-4c^2-2=0$ will be discussed in the next subsection. For the sake of convenience, we define the four sets related to the real parameters c, $\alpha$, $\beta$ and k:

$$\begin{aligned} \begin{aligned}&\Theta _1=\Big \{\lambda \in {\mathbb {R}}:\lambda<-c-\sqrt{c^2+1},\\&\qquad c-\sqrt{c^2+1}<\lambda<-c+\sqrt{c^2+1}, \lambda >c+\sqrt{c^2+1}\Big \},\\&\Delta _1=\Big \{\lambda \in {\mathbb {R}}:\alpha [\lambda (\lambda ^2-2)+\lambda ^{-1}\cos (k)(\lambda ^{-2}-2)\\&\qquad +(1{+}2c^2)(\lambda \cos (k){+}\lambda ^{-1}\cos (2k))]{+}\beta \lambda ^{-1}\sin (k){=}0\Big \},\\&\Theta _2=\Big \{\lambda \in {\mathbb {R}}:-c-\sqrt{c^2+1}<\lambda<c-\sqrt{c^2+1},\\&\qquad \quad -c+\sqrt{c^2+1}<\lambda <c+\sqrt{c^2+1}\Big \},\\&\Delta _2=\Big \{\lambda \in {\mathbb {R}}:\alpha [-\lambda ^{-1}\sin (k)(\lambda ^{-2}-2)\\&\qquad \quad +(1+2c^2)(\lambda \sin (k)-\lambda ^{-1}\sin (2k))]\\&\qquad \quad +\beta (-\lambda +\lambda ^{-1}\cos (k)) =0\Big \}. \end{aligned} \end{aligned}$$

Fig. 2

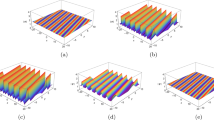
a Time-periodic Kuznetsov–Ma breather $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =2.8950$, $c=0.5$, $\alpha =0.1$, $\beta =5.0$, $k=4.0$; b W-shaped soliton $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =0.3552$, $c=0.5$, $\alpha =0.1$, $\beta =0.01$, $k=0.01$; c Spatiotemporally periodic breather $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =2.8$, $c=1.0$, $\alpha =0.01$, $\beta =0.2$, $k=2.8$

Table 2 The relationship between parameter $\lambda$ and solutions’ structures in (23)

Case 1: $\lambda \in \Theta _1$. For real parameters c, $\alpha$, $\beta$ and k, we know that $\mu _1$, $\mu _2$ in (19) are real when $\lambda \in \Theta _1$. Meanwhile, we notice that the expression $\Gamma _n$ in (18) are the same whether $\mu _1>0$, $\mu _2>0$ or $\mu _1<0$, $\mu _2<0$. Without loss of generality, we suppose that $\mu _1>0$, $\mu _2>0$. Then, we conclude that $\kappa _1\ne 0$, $\kappa _2=0$ when $\lambda \in \Theta _1$. In this case, each component of $\varrho$ in (18) can be split into real and imaginary parts as

$$\begin{aligned} \varrho =\omega _1+ \mathrm{{i}} \omega _2, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\omega _1=\{\alpha [\lambda (\lambda ^2-2)+\lambda ^{-1}\cos (k)(\lambda ^{-2}-2)\\&\qquad +(1+2c^2)(\lambda \cos (k)+\lambda ^{-1}\cos (2k))]\\&\qquad +\beta \lambda ^{-1}\sin (k)\}\sqrt{\lambda ^2+\lambda ^{-2}-4c^2-2},\\&\omega _2=\{\alpha [-\lambda ^{-1}\sin (k)(\lambda ^{-2}-2)+(1+2c^2)(\lambda \sin (k)\\&\qquad -\lambda ^{-1}\sin (2k))]+\beta (-\lambda +\lambda ^{-1}\cos (k))\}\\&\sqrt{\lambda ^2+\lambda ^{-2}-4c^2-2}. \end{aligned} \end{aligned}$$

Fig. 3

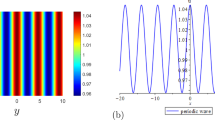
a Space-periodic Akhmediev breather $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =1.7238$, $c=1.0$, $\alpha =0.1$, $\beta =1.0$, $k=3.0$; b Periodic solution $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =0.9928$, $c=1.0$, $\alpha =0.1$, $\beta =2.0$, $k=6.0$; c Space-periodic Akhmediev breather $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =1.4$, $c=1.0$, $\alpha =0.1$, $\beta =1.5$, $k=1.0$

When $\lambda \in \Theta _1\bigcap \Delta _1$, we can verify that $\kappa _1\ne 0$, $\kappa _2=0$, $\omega _1=0$, $\omega _2\ne 0$, that is $\theta _{1}=\kappa _1 n$ and $\theta _{2}= \omega _{2} t$, the nonlinear wave solution (23) is localized in the n direction and periodic in the t direction, which can be considered as the time-periodic Kuznetsov–Ma breather, the amplitude distribution and evolution states corresponding different n under the condition of $\lambda =2.8950$, $c=0.5$, $\alpha =0.1$, $\beta =5.0$, $k=4.0$ are illustrated in Fig. 2a. When $\lambda \in \Theta _1\bigcap \Delta _2$, it is easy to verify that $\kappa _1\ne 0$, $\kappa _2=0$, $\omega _1\ne 0$, $\omega _2=0$, that is $\theta _{1}=\kappa _1 n+\omega _1t$ and $\theta _{2}=0$, the nonlinear wave solution (23) is localized both in the n and t direction, the W-shaped soliton solution can be obtained from (23), the evolution and density contour of this type by choosing parameters $\lambda =0.3552$, $c=0.5$, $\alpha =0.1$, $\beta =0.01$, $k=0.01$ are showed in Fig. 2b. When $\lambda \in \Theta _1\bigcap C_R(\Delta _1\bigcup \Delta _2)$, we have $\kappa _1\ne 0$, $\kappa _2=0$, $\omega _1\ne 0$, $\omega _2\ne 0$, that is $\theta _{1}=\kappa _1 n+\omega _1 t$ and $\theta _{2}= \omega _2 t$, the nonlinear wave solution (23) is localized both in the n and t direction, we can get the spatiotemporally periodic breather solution from (23), which is displayed in Fig. 2c by choosing parameters $\lambda =2.8$, $c=1.0$, $\alpha =0.01$, $\beta =0.2$, $k=2.8$. Comparing with Fig. 2a and c, we can observe the effect of $\omega _{1}$ to the structure of breather. From Fig. 2b and c, we can show the effect of $\omega _{2}$ to the structure of solution. Based on the above facts, we conclude the relationship between parameter $\lambda$ and solutions’ structures as presented in Table 2.

Table 3 The relationship between parameter $\lambda$ and solutions’ structures in (23)

Case 2: $\lambda \in \Theta _2$. For real parameters c, $\alpha$, $\beta$ and k, we find that $\mu _1$, $\mu _2$ are imaginary and $|\mu _1|=|\mu _2|=1$ when $\lambda \in \Theta _2$, so $\kappa _1=0$, $\kappa _2\ne 0$. Meanwhile, each component of $\varrho$ in (18) can be split into real and imaginary parts as

$$\begin{aligned} \varrho =\omega _1+ \mathrm{{i}} \omega _2, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\omega _1=-\{\alpha [-\lambda ^{-1}\sin (k)(\lambda ^{-2}-2)\\&\qquad +(1+2c^2)(\lambda \sin (k)-\lambda ^{-1}\sin (2k))]\\&\qquad +\beta (-\lambda +\lambda ^{-1}\cos (k)) \}\sqrt{-\lambda ^2-\lambda ^{-2}+4c^2+2},\\&\omega _2=\{\alpha [\lambda (\lambda ^2-2)+\lambda ^{-1}\cos (k)(\lambda ^{-2}-2)\\&\qquad +(1+2c^2)(\lambda \cos (k)+\lambda ^{-1}\cos (2k))]\\&\qquad +\beta \lambda ^{-1}\sin (k)\}\sqrt{-\lambda ^2-\lambda ^{-2}+4c^2+2}. \end{aligned} \end{aligned}$$

When $\lambda \in \Theta _2\bigcap \Delta _1$, it is easy to verify that $\kappa _1=0$, $\kappa _2\ne 0$, $\omega _1\ne 0$, $\omega _2=0$, that is $\theta _{1}=\omega _{1} t$ and $\theta _{2}= \kappa _2 n$, the nonlinear wave solution (23) is localized in the t direction and periodic in the n direction, which can be regarded as the space-periodic Akhmediev breather, the amplitude distribution and evolution states corresponding different n under the condition of $\lambda =1.7238$, $c=1.0$, $\alpha =0.1$, $\beta =1.0$, $k=3.0$ are displayed in Fig. 3a. When $\lambda \in \Theta _2\bigcap \Delta _2$, we have $\kappa _1=0$, $\kappa _2\ne 0$, $\omega _1=0$, $\omega _2\ne 0$, then $\theta _{1}=0$ and $\theta _{2}= \kappa _2 n + \omega _2 t$, the nonlinear wave solution (23) is periodic both in the n and t direction, from (23) we can obtain the periodic solution, which is illustrated in Fig. 3b by choosing parameters $\lambda =0.9928$, $c=1.0$, $\alpha =0.1$, $\beta =2.0$, $k=6.0$. When $\lambda \in \Theta _2\bigcap C_R(\Delta _1\bigcup \Delta _2)$, we can verify that $\kappa _1=0$, $\kappa _2\ne 0$, $\omega _1\ne 0$, $\omega _2\ne 0$, that is $\theta _{1}=\omega _1 t$ and $\theta _{2}= \kappa _2 n + \omega _2 t$, the nonlinear wave solution (23) is localized in the t direction and periodic in the n direction, the space-periodic Akhmediev breather solution can be obtained from (23), which is displayed in Fig. 3c by choosing parameters $\lambda =1.4$, $c=1.0$, $\alpha =0.1$, $\beta =1.5$, $k=1.0$. In this case, we obtain two types of the space-periodic Akhmediev breathers as showed in Fig. 3a and c, respectively, from which we can understand the effect of $\omega _{2}$ to the structure of breathers. Comparing with Fig. 3b and c, we can show the effect of $\omega _{1}$ to the structure of solution. Based on the above facts, we conclude the relationship between parameter $\lambda$ and structures of solutions given in Table 3.

Secondly, we investigate the case where $\lambda$ is imaginary. In this case, for real parameters c, $\alpha$, $\beta$ and k, we are hard to choose appropriate parameters $\lambda$ so that $\mu _{1}$, $\mu _{2}$ and $\varrho$ in (18) can be split into real and imaginary parts as above, which makes it challenging for us to accurately analyse the relationship between parameters and breathers’ structures. By experimenting with a large number of parameters, we find that we can only obtain the spatiotemporally periodic breather solutions when $\lambda$ is imaginary. For instance, when choosing $\lambda =1.5 \mathrm{{i}}$, $c=1.0$, $\alpha =0.4$, $\beta =0.01$, $k=0.1$ and $\lambda =2.0-1.2 \mathrm{{i}}$, $c=1.0$, $\alpha =0.01$, $\beta =0.1$, $k=0.1$, the corresponding spatiotemporally periodic breather solutions are showed in Fig. 4a and b, respectively.

3.3 Rogue wave

The rogue wave solution has the peculiarity of being localized both in the n and t directions and can be constructed from the breather by considering the limit technique in the mathematical point of view. To establish the rogue wave solution for the spatial discrete Hirota equation (3), we take $\lambda ^2+\lambda ^{-2}-4c^2-2 = 0$, i.e., $\lambda = \sigma _1c+\sigma _2\sqrt{c^2+1}$ ($\sigma _1=\pm 1$, $\sigma _2=\pm 1$), and choose $C_1=1$, $C_2=-1$ in (17). In this special case, the pseudopotential of the spatial discrete Hirota equation (3) can be derived as

$$\begin{aligned}{} & {} \Gamma _n=-\sigma _1\nonumber \\{} & {} \left( 1+\frac{\sigma _2\sqrt{c^2+1}}{\sigma _1 c n + 2 \sigma _1\sigma _2 c \sqrt{c^2+1} \chi t-\sigma _2 \sqrt{c^2+1}}\right) e^{{{i}}z_n},\quad \end{aligned}$$

(24)

where $\chi$ is given by replacing $\lambda$ in $\alpha A_3+\beta \mathrm{{i}} A_4$ with $\sigma _1c+\sigma _2\sqrt{c^2+1}$. For the sake of greater clarity, choosing parameters $\alpha =\frac{1}{10}$, $\beta =5$, $c=\frac{3}{4}$, $k=0$, $\sigma _1=1$, $\sigma _2=1$ and substituting (24) into the Darboux–Bäcklund transformation (8), the discrete rogue wave solution of the spatial discrete Hirota equation (3) is derived as

$$\begin{aligned} {\tilde{u}}_n=-\frac{3}{4}\left( 1+{\frac{4608000 \textrm{i}t-409600}{147456 n^{2}+311040 n t+13124025 t^{2}-98304 n-103680 t+81920}} \right) { e^{-{\frac{45 {i}}{8}}t}}, \end{aligned}$$

(25)

from which we know the maximum value of $|{\tilde{u}}_n|$ is $\frac{63}{16}$ at the point $(n,t)=(\frac{1}{3},0)$, the minimum of $|{\tilde{u}}_n|$ is always zero and $|{\tilde{u}}_n|\rightarrow \frac{3}{4}$ (background) as $n, t\rightarrow \infty$. Thus, we obtain $|{\tilde{u}}_n|_{max}$=5.25$|{\tilde{u}}_n|_{n,t\rightarrow \infty }$. The profile of the rogue wave solution (25) is showed in Fig. 4c, from which we find it crowds around the point $(n,t)=(\frac{1}{3},0)$ and holds one peakon and two depression points, the peak amplitude is at least five times the background. Through a direct calculation, we generate the conservation result $\int _{-\infty }^{+\infty }\left( |{\tilde{u}}_n|^2-\frac{9}{16}\right) dn=0,$ which means that the rogue wave is formed from the flat background.

Fig. 4

a The spatiotemporally periodic breather $|{\tilde{u}}_n|$ in (23) with parameters $\lambda =1.5 \mathrm{{i}}$, $c=1.0$, $\alpha =0.4$, $\beta =0.01$, $k=0.1$; b The spatiotemporally periodic breather $|{\tilde{u}}_n|$ in (23) with parameters and $\lambda =2.0-1.2 \mathrm{{i}}$, $c=1.0$, $\alpha =0.01$, $\beta =0.1$, $k=0.1$; c The rogue wave $|{\tilde{u}}_n|$ in (25) with parameters $\alpha =\frac{1}{10}$, $\beta =5$, $c=\frac{3}{4}$, $k=0$, $\sigma _1=1$, $\sigma _2=1$

Based on the facts in the Sects. 3.2 and 3.3, we conclude that when $\lambda ^2+\lambda ^{-2}-4c^2-2\ne 0$, we are able to obtain the time-periodic Kuznetsov–Ma breather, pace-periodic Akhmediev breather, spatiotemporally periodic breather, W-shaped soliton solution and periodic solution for the spatial discrete Hirota equation (3), while $\lambda ^2+\lambda ^{-2}-4c^2-2=0$, we can construct the rogue wave solution.

4 Continuum limit of the breather and rogue wave solutions

As we know, the relationship between discrete integrable systems and its relevant continuous counterparts is always quite significant. In [14], the authors showed that the Lax pair, Darboux transformation and soliton solutions of the spatial discrete Hirota equation (3) converge to the corresponding results of the Hirota equation (1). However, the continuum limit of the breather solution and rogue wave solution of Eq. (3) related to the Lax pair (4) has not been investigated, which is what we focus on in this section.

Based on the results in [14], we know the spatial discrete Hirota equation (3) leads to the Hirota equation (1) under the transformation

$$\begin{aligned} u_n=\delta v(x,\tau ),\quad x=n \delta ,\quad \tau =2 \delta ^3 t,\quad \beta = 2 \gamma \delta .\nonumber \\ \end{aligned}$$

(26)

For the sake of constructing the continuum limit of the breather solution and rogue wave solution, we define

$$\begin{aligned} \lambda =e^{\mu \delta }=1+\delta \mu + \frac{1}{2} \delta ^2 \mu ^2 + \frac{1}{6} \delta ^3 \mu ^3 + o(\delta ^3), \end{aligned}$$

(27)

where $\mu$ is a constant spectral parameter. We suppose that the continuum limit of $\Gamma _n$ is $\Gamma$. Then, by a direct analysis of the Darboux–Bäcklund transformation (8), we obtain the relation between ${\tilde{u}}_n$ and ${\tilde{v}}$:

$$\begin{aligned} {\tilde{u}}_n=\delta {\tilde{v}} + o(\delta ), \end{aligned}$$

(28)

where

$$\begin{aligned} {\tilde{v}}=v+\frac{2 (\mu + \mu ^* ) \Gamma }{1+\Gamma \Gamma ^*}, \end{aligned}$$

which is nothing but the one-fold Darboux transformation of the Hirota equation (1) given in [40].

In what follows, we are going to construct the continuum limit of the breather solution (23). Setting

$$\begin{aligned} c={\mathfrak {c}}\delta ,~~~~k={\mathfrak {k}}\delta , \end{aligned}$$

(29)

where ${\mathfrak {c}}$ and ${\mathfrak {k}}$ are real constants. Then, the leading term of the plane wave solution (14) is given

$$\begin{aligned} v={\mathfrak {c}}e^{\mathrm{{i}} ( {\mathfrak {k}} x + \mathfrak {\omega } \tau )},~~~~\mathfrak {\omega }=\gamma ({\mathfrak {k}}^2-2 {\mathfrak {c}}^2)+\alpha {\mathfrak {k}} (6{\mathfrak {c}}^2-{\mathfrak {k}}^2), \end{aligned}$$

(30)

which is just a plane wave solution of the Hirota equation (1). Notice that $\tau _j$ ($j=1,2$) in (16) admits the equation

$$\begin{aligned} \tau _j^2-(\lambda +\lambda ^{-1})\tau _j+c^2+1=0. \end{aligned}$$

(31)

Let $\tau _j=e^{r_j \delta }$ and using (27) and (29), the leading term of characteristic Eq. (31) yields continuous counterpart

$$\begin{aligned} r_j^2-\mu ^2+{\mathfrak {c}}^2=0. \end{aligned}$$

(32)

Choosing $C_1=1$, $C_2=-1$ in (17) and using (26), (27) and (29), we construct the continuum limit of $\Gamma _n$ as

$$\begin{aligned} \Gamma =\frac{e^{r_1 x+[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_1\tau } - e^{r_2 x+[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_2\tau }}{\frac{r_1-\mu }{{\mathfrak {c}}}e^{r_1 x+[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_1\tau } - \frac{r_2-\mu }{{\mathfrak {c}}}e^{r_2 x+[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_2\tau }}e^{\mathrm{{i}} ( {\mathfrak {k}} x + \mathfrak {\omega } \tau )}, \end{aligned}$$

(33)

Table 4 The relationship between parameter $\mu$ and solutions’ structures in (35)

where $r_1$, $r_2$ are obtained from (32), i.e. $r_1=\sqrt{\mu ^2-{\mathfrak {c}}^2}$ and $r_2=-\sqrt{\mu ^2-{\mathfrak {c}}^2}$. We can verify $\frac{r_1-\mu }{{\mathfrak {c}}}\frac{r_2-\mu }{{\mathfrak {c}}}=1$, so we define $\frac{r_1-\mu }{{\mathfrak {c}}}=e^{\mathfrak {\alpha _2} + \mathrm{{i}} \mathfrak {\beta _2}}$, $\frac{r_2-\mu }{{\mathfrak {c}}}=e^{-(\mathfrak {\alpha _2} + \mathrm{{i}} \mathfrak {\beta _2})}$. Let $r_1=\mathfrak {\kappa _1}+\mathrm{{i}}\mathfrak {\kappa _2}$, $[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_1=\mathfrak {\omega _1}+\mathrm{{i}}\mathfrak {\omega _2}$, then $r_2=-(\mathfrak {\kappa _1}+\mathrm{{i}}\mathfrak {\kappa _2})$, $[(\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}})+2\mathrm{{i}}\mu (\alpha {\mathfrak {k}}-\gamma )]r_2=-(\mathfrak {\omega _1}+\mathrm{{i}}\mathfrak {\omega _2})$. Here, $\mathfrak {\alpha _i}$, $\mathfrak {\kappa _i}$ and $\mathfrak {\omega _i}$ ($i=1,2$) are the corresponding real and imaginary parts, respectively. Based on these facts, we can write (33) as

$$\begin{aligned} \Gamma =\frac{e^{\mathfrak {\theta _1}+\mathrm{{i}}\mathfrak {\theta _2}}-e^{-(\mathfrak {\theta _1}+\mathrm{{i}}\mathfrak {\theta _2})}}{e^{\mathfrak {\theta _1}+\mathrm{{i}}\mathfrak {\theta _2}+\mathfrak {\alpha _1}+\mathrm{{i}}\mathfrak {\alpha _2}} -e^{-(\mathfrak {\theta _1}+\mathrm{{i}}\mathfrak {\theta _2}+\mathfrak {\alpha _1}+\mathrm{{i}}\mathfrak {\alpha _2})}}e^{\mathrm{{i}} ( {\mathfrak {k}} x + \mathfrak {\omega })} \end{aligned}$$

(34)

where

$$\begin{aligned} \mathfrak {\theta _1}=\mathfrak {\kappa _1} x + \mathfrak {\omega _1} \tau ,~~~~~~~~~~~~~~\mathfrak {\theta _2}=\mathfrak {\kappa _2} x + \mathfrak {\omega _2} \tau . \end{aligned}$$

Substituting (34) into (28), by a complicated computation, the breather solution of the Hirota equation (1) is derived

$$\begin{aligned} {\tilde{v}}=\left( 1+\frac{\frac{2(\mu +\mu ^*)}{\mathfrak {c}}\frac{\sinh (\mathfrak {\theta _1})\cos (\mathfrak {\theta _2}) + \textrm{i} \cosh (\mathfrak {\theta _1})\sin (\mathfrak {\theta _2})}{\sinh (\mathfrak {\theta _1+\alpha _1})\cos (\mathfrak {\theta _2+\alpha _2}) + \textrm{i} \cosh (\mathfrak {\theta _1+\alpha _1})\sin (\mathfrak {\theta _2+\alpha _2})}}{1+\frac{\cosh (2\mathfrak {\theta _1})-\cos (2\mathfrak {\theta _2})}{\cosh (2\mathfrak {\theta _1} +2\mathfrak {\alpha _1})-\cos (2\mathfrak {\theta _2}+2\mathfrak {\alpha _2})}}\right) \mathfrak {c}e^{\mathrm{{i}} ( {\mathfrak {k}} x + \mathfrak {\omega })}. \end{aligned}$$

(35)

Obviously, the periodicity of solution (35) is mainly effected by $\mathfrak {\theta _2}$. In a similar way as in the Sect. 3.2, we can get the time-periodic Kuznetsov–Ma breather, space-periodic Akhmediev breather, spatiotemporally periodic breather, W-shaped soliton and periodic solution for the Hirota equation (1). For the real parameters $\alpha$, $\gamma$, ${\mathfrak {c}}$ and ${\mathfrak {k}}$, we define the following four sets:

$$\begin{aligned} \begin{aligned}&\mathfrak {\Theta _1}=\left\{ \mu \in {\mathbb {R}}:\mu<-|{\mathfrak {c}}|,\mu >|{\mathfrak {c}}|\right\} ,~~~~\\&\mathfrak {\Delta _1}=\left\{ \mu \in {\mathbb {R}}:\alpha (4 \mu ^2-{\mathfrak {k}}^2+2{\mathfrak {c}}^2)+\gamma {\mathfrak {k}}=0\right\} ,\\&\mathfrak {\Theta _2}=\left\{ \mu \in {\mathbb {R}}:-|{\mathfrak {c}}|<\mu <|{\mathfrak {c}}|\right\} ,~~~~~~~\\&\mathfrak {\Delta _2}=\left\{ \mu \in {\mathbb {R}}: \mu (\alpha {\mathfrak {k}}-\gamma )=0\right\} . \end{aligned} \end{aligned}$$

Then, the relationship between parameters and solutions’ structures in (35) for Eq. (1) is provided in Table 4.

Next, we are going to construct the continuum limit of the rogue wave solution from (24) with $k=0$. By virtue of (26), (27) and (29), we obtain the corresponding continuum limit of $\Gamma _n$ in (24) as

$$\begin{aligned} \Gamma =-\sigma _1 \left( 1+ \frac{\sigma _2}{\sigma _1 \mathfrak {c} x + 4 \sigma _1\sigma _2 \mathfrak {c}^2 (3 \alpha \sigma _2 \mathfrak {c}- \mathrm{{i}} \gamma \sigma _1)\tau -\sigma _2 }\right) e^{-2 \textrm{i} \gamma {\mathfrak {c}}^2 \tau }.\nonumber \\ \end{aligned}$$

(36)

Inserting (36) into (28), through a tedious calculation, the rogue wave solution of the Hirota equation (1) is obtained

$$\begin{aligned} {\tilde{v}}=-\left( 1+\frac{16 c^2 \gamma \mathrm{{i}} \tau -2}{32c^4(9\alpha ^2c^2+\gamma ^{2})\tau ^{2}+2 c^2 x^2+48\alpha c^4\tau x-2 \sigma _1 c x-24 \alpha \sigma _1 c^3 \tau +1}\right) \mathfrak {c}e^{-2 \textrm{i} \gamma {\mathfrak {c}}^2 \tau }. \end{aligned}$$

(37)

As well known, different seed solutions to the same equation may lead to different new ones. Notice that the seed solution (30) is different from one in [40], so the breather solution (35) and the rogue wave solution (37) of Eq. (1) may be different from the ones given in [40]. Further, we can conclude that when $\mu ^2-\mathfrak {c}^2\ne 0$, we are able to obtain the breather solutions for the Hirota equation (1), while $\mu ^2-\mathfrak {c}^2=0$, we can construct the rogue wave solution.

5 Conclusions

In this paper, the pseudopotential of the spatial discrete Hirota equation (3) is proposed for the first time, from which a Darboux–Bäcklund transformation (8) is constructed. Comparing it with the one-fold Darboux transformation obtained in [14], we find they are equivalent because there is no difference except for a constant times. And we believe this equivalence may hold universal if these two transformations are all derived from the same discrete spectral problem and using the similar technique in literatures [14] and [36, 37], respectively. Various types of nonlinear wave solutions of Eq. (3), including bell-shaped one-soliton, three types of breathers, W-shaped soliton, periodic solution and rogue wave are given by using the obtained transformation (8), their evolutions and dynamical properties are illustrated graphically. Some important physical quantities such as amplitude, width, wave number, velocity, primary phase and energy of the bell-shaped one-soliton $|{\tilde{u}}_n|$ in (13) are listed in Table 1. Based on the nonlinear wave solution (23), the relationship between parameter $\lambda$ and solutions’ structures is presented in Tables 2 and 3. Finally, we show the continuum limit of breather and rogue wave solutions of the spatial discrete Hirota equation (3) yields the counterparts of the Hirota equation (1), and the relationship between parameter $\mu$ and solutions’ structures is provided in Table 4. The method and technique used in this paper can also be applied to some other nonlinear integrable equations. The results in this paper might be useful for understanding some physical phenomena in nonlinear optics.