1 Introduction

Nonlinear Schrödinger (NLS) equation

$$\begin{aligned} iq_{t}+q_{xx}+\mid q\mid ^{2}q=0, \end{aligned}$$
(1.1)

known as a prototypical completely integrable equation, possesses fundamental characters of integrable models. It can describe many nonlinear wave phenomena in Kerr media, plasma physics and optical pulses [1,2,3,4,5,6,7,8,9,10]. Later in order to achieve in the high intensity and short pulse subpicosecond, Kodama and Hasegawa considered higher order NLS equation (1.2) with higher-order terms describing linear and nonlinear dispersion as well as dissipation effects [11]

$$\begin{aligned}&iq_{t}+\frac{1}{2}q_{xx}-\mid q\mid ^{2}q\nonumber \\&\quad +\,i\epsilon (\alpha q_{xxx}-\beta \mid q\mid ^{2}q_{x}+\gamma q\mid q\mid ^{2}_{x})=0. \end{aligned}$$
(1.2)

Besides, derivative and discrete NLS equations are also studied to apply in physical fields [12,13,14,15,16]. However, we are supposed to obtain multiple equations with the help of variable transformation and parameters control, such as KdV equation, mKdV equation, Hirota equation, Sasa–Satsuma equation etc. [17,18,19]. Here, we take the proportion \(\alpha {:}\beta {:}\gamma =1{:}6{:}0\) to obtain Hirota equation (1.3) [17]. It was found to apply in the study of vortex motion [20], homoclinic orbit of laser [21].

$$\begin{aligned} iq_{t}+\alpha q_{xx}-2\alpha |q|^{2}q-i\beta (q_{xxx}-6|q|^{2}q_{x})=0. \end{aligned}$$
(1.3)

On the other hand, nonlocality was introduced by Ablowitz and Musslimani to study NLS equation (1.4) which provided a PT symmetric structure with nonlinear self-regulation in 2013 [22]

$$\begin{aligned} iq_{t}-q_{xx}-2\sigma q q^{*}(-x,t) q=0,~~~\sigma =\pm 1. \end{aligned}$$
(1.4)

PT symmetry, firstly proposed by Wadati [23], is an important reason for the emergence of nonlocal models which leads to real spectrum of non-Hamiltonian operator [24,25,26]. So it keeps system invariant under parity and time inversion transformation: \(x\rightarrow -x\), \(t\rightarrow -t\), \(i\rightarrow -i\), where P: \(x\rightarrow -x\) and T: \(t\rightarrow -t\) and \(i\rightarrow -i\) [27, 28, 31]. Solutions q(x, t) and \(q^{*}(-x,t)\) is determined both by the positions x and \(-x\), and self-induced potential \(V(x,t)=q(x,t)q^{*}(-x,t)\) meets PT symmetry condition \(V(x,t)=V^{*}(-x,t)\). In this case, soliton structure exists a stable state under certain conditions and propagation process is almost lossless. Then, the nice property became so popular in soliton theory that many nonlocal integrable equations [29,30,31,32,33,34,35,36,37,38] were presented and differences between local and nonlocal equations [38] were studied recently years. For instance, nonlocal reverse space-time NLS equation [29], semi-discrete NLS equation [30], vector NLS equation [31, 32], derivative NLS equation [33, 34], Hirota equation [18], modified Korteweg–de Vries equation [35, 36], Sine-Gordon equation [37]. In 2017, Stalin et al. discussed Eq. (1.4) and its parity transformation complex conjugate form (1.5) in a combined manner [39]

$$\begin{aligned}&iq^{*}_{t}(-x,t)+q^{*}_{xx}(x,t)+2\sigma q^{*}(-x,t) q q^{*}(-x,t)=0,\nonumber \\&\quad \sigma =\pm 1. \end{aligned}$$
(1.5)

In Eqs. (1.4) and (1.5), more general bright soliton solutions, including symmetry broken and unbroken soliton solutions, have been solved using bilinearization method and dynamic behaviors have been formed. For symmetry broken solutions, q(x, t) and \(q^{*}(-x,t)\) unstable and V(x, t) is complex spectrum. For symmetry unbroken solutions, they are stable and V(x, t) is completely real spectrum. Based on the works, we combined nonlocal version of Eq. (1.3) with parity transformation complex conjugate form to present nonlocal continuous Hirota system (1.6) as the subject of this paper

$$\begin{aligned} \begin{aligned} iq_{t}&=2\alpha q^{2}q^{*}(-x,t)+6i\beta q q^{*}(-x,t)q_{x}\\&\quad -\,\alpha q_{xx}-i\beta q_{xxx},\\ iq^{*}_{t}(-x,t)&=-2\alpha q (q^{*}(-x,t))^{2}\\&\quad +\,6i\beta q q^{*}(-x,t)q^{*}_{x}(-x,t)\\&\quad +\,\alpha q^{*}_{xx}(-x,t)-i\beta q^{*}_{xxx}(-x,t), \end{aligned} \end{aligned}$$
(1.6)

where \(*\) means complex conjugate, q(x, t), \(q^{*}(-x,t)\) are complex functions, and \(\alpha ,\beta \) are real constants. Subscripts x, t denote partial derivatives with respect to variables.

At present, only bright soliton solutions are obtained in Eqs. (1.4) and (1.5) and there are no dark and antidark soliton solutions [38]. For studied system (1.6), bright soliton solution can be derived by DT. Here, regarding \(q^{*}(-x,t)\) as a separate function is achieved through setting two independent solutions. Independence means that two eigenvalues, determining the solution form, do not satisfy any conditions. So we can get generalized solutions using independent eigenvalues, compared to the parallel solving methods. That is, the eigenvalues are very significant to enrich soliton models. From this perspective, more general dark and antidark soliton solutions are developed, and different collision combinations of potentials are obtained. Besides, some figures show that q(x, t) describes dark (or antidark) solitons, while \(q^{*}(-x,t)\) exhibits antidark (or dark) solitons with particular parameters. The reason is exactly that q(x, t) and \(q^{*}(-x,t)\) are mutually independent.

The paper is organized as follows. According to given Lax pair, N-fold DT and bright soliton, dark and antidark soliton solutions of system (1.6) are solved in Sect. 2. In Sect. 3, one and two bright solitons are plotted under zero background and relevant dynamic behaviors are discussed. Then, we plot the dark and antidark solitons and analyze asymptotic behaviors in Sect. 4. Finally, our conclusions will be drawn in Sect. 5.

2 Darboux transformation

As an effective method to solve solutions, DT connects the solutions of linear system skillfully [40,41,42]. In this section, we are ready to construct DT for system (1.6) by invariant \(2\times 2\) Lax pair, which is given by

$$\begin{aligned} \begin{aligned} \varPsi _{x}&=A \varPsi =J \varPsi \varLambda +P \varPsi ,\\ \varPsi _{t}&=B \varPsi =V_{3} \varPsi \varLambda ^{3}+V_{2} \varPsi \varLambda ^{2}\\&\quad +\,V_{1} \varPsi \varLambda +V_{0} \varPsi , \end{aligned} \end{aligned}$$
(2.1)

where

$$\begin{aligned} \begin{aligned} A&=J \varPsi \varLambda \varPsi ^{-1}+P,\\ B&=V_{3} \varPsi \varLambda ^{3} \varPsi ^{-1}+V_{2} \varPsi \varLambda ^{2} \varPsi ^{-1}\\&\quad +\,V_{1} \varPsi \varLambda \varPsi ^{-1}+V_{0}, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} J= & {} \left( \begin{array}{cc} i &{}\quad 0\\ 0 &{}\quad -i\\ \end{array} \right) ,\quad P=\left( \begin{array}{cc} 0 &{}\quad q\\ q^{*}(-x,t) &{}\quad 0\\ \end{array} \right) ,\\ V_{3}= & {} \left( \begin{array}{cc} -4 i \beta &{}\quad 0\\ 0 &{}\quad 4 i \beta \\ \end{array} \right) ,\quad V_{2}=\left( \begin{array}{cc} -2 i \alpha &{}\quad 4 \beta q\\ 4 \beta q^{*}(-x,t) &{}\quad 2 i \alpha \\ \end{array}\right) ,\\ V_{1}= & {} \left( \begin{array}{cc} -2 i \beta q q^{*}(-x,t) &{}\quad 2 \alpha q + 2 i \beta q_{x}\\ 2 \alpha q^{*}(-x,t) + 2 i \beta q^{*}_{x}(-x,t) &{}\quad 2 i \beta q q^{*}(-x,t)\\ \end{array} \right) ,\\ V_{0}= & {} \left( \begin{array}{cccc} -i \alpha q q^{*}(-x,t) + \beta &{}\quad i \alpha q_{x} + \beta \\ (q^{*}(-x,t) q_{x} + q q^{*}_{x}(-x,t)) &{}\quad (2 q^{2} q^{*}(-x,t) -q_{xx})\\ \\ i \alpha q^{*}_{x}(-x,t) + \beta &{}\quad i \alpha q q^{*}(-x,t) - \beta \\ (2 q q^{*}(-x,t)^{2}- q^{*}_{xx}(-x,t)) &{}\quad (q^{*}(-x,t) q_{x} + q q^{*}_{x}(-x,t))\\ \end{array} \right) . \end{aligned}$$

\(\varPsi =\left( \begin{array}{cc} \phi (x,t) &{}\phi ^{*}(-x,t)\\ \psi (x,t) &{}\psi ^{*}(-x,t)\\ \end{array} \right) \) is vector eigenfunction of spectral problem (2.1), and \(\varLambda =\left( \begin{array}{cc} \lambda &{}\quad 0\\ 0 &{}\quad \overline{\lambda }\\ \end{array} \right) \) is spectral parameter. In order to derive soliton wave solutions for system (2.1), \(\varPsi \) must to meet compatibility condition \(\varPsi _{xt}=\varPsi _{tx}\). Then, from (2.1), we derive zero curvature equation \(A_{t}-B_{x}+[A,B]=0~([A,B]=AB-BA)\) and easily yield Eq. (1.6).

Here, we assume that \(\varPsi _{j}\) are N linear independent solutions of system (2.1) at different \(\varLambda _{j}\) (\(1\le j\le N\)), where \((\phi _{j}(x,t), \psi _{j}(x,t))^{T}\) are the solutions of (2.1) at \(\lambda =\lambda _{j}\) and \((\phi ^{*}_{j}(-x,t), \psi ^{*}_{j}(-x,t))^{T}\) are the solutions of (2.1) at \(\lambda =\overline{\lambda _{j}}\) (superscript T refers to vector transpose). Moreover, \(\lambda _{j}\) and \(\overline{\lambda _{j}}\) cannot take real number to avoid trivial iteration of DT.

It is simple to transform system (2.1) into

$$\begin{aligned} \begin{aligned} \varPsi _{x}^{[N]}&=A^{[N]} \varPsi ^{[N]},~~~A^{[N]}=(T_{Nx} + T_{N} A) T_{N}^{-1},\\ \varPsi _{t}^{[N]}&=B^{[N]} \varPsi ^{[N]},~~~B^{[N]}=(T_{Nt} + T_{N} B) T_{N}^{-1} \end{aligned} \end{aligned}$$
(2.2)

by taking a generalized gauge transformation

$$\begin{aligned} \begin{aligned} \varPsi ^{[N]}&= T_{N} \varPsi \\&= \varPsi \varLambda ^{N} \\&\quad + t_{1}^{[N]} \varPsi \varLambda ^{N-1} + t_{2}^{[N]} \varPsi \varLambda ^{N-2} +\cdots + t_{N}^{[N]} \varPsi , \end{aligned} \end{aligned}$$
(2.3)

where \(t_{1}^{[N]}=-\sum \nolimits _{i=1}^{N}S_{i}\), \(t_{2}^{[N]}=\sum \nolimits _{i=1,i<j}^{N-1}S_{i}S_{j}\), \(t_{N}^{[N]} =\prod \nolimits _{i=1}^{N}S_{i}\), \(S_{j}=\varLambda -\varPsi _{j}\varLambda _{j}\varPsi _{j}^{-1}\), \(j=1,2,\ldots ,N\). According to Eqs. (2.2) and (2.3), we research that

$$\begin{aligned} A^{[N]}_{t}-B^{[N]}_{x}+[A^{[N]},B^{[N]}]=T_{N}(A_{t}-B_{x}+[A,B])T_{N}^{-1} \end{aligned}$$
(2.4)

and know that \(A^{[N]}\) and \(B^{[N]}\) have same matrix forms as A and B. If we would like to make the above equal to zero, \(T_{N}\) is so needed that to achieve N-iterated basic solutions and N-fold DT transformation. Assume that \(\varPsi _{j}\) is solutions of (2.1) at \(\varLambda =\varLambda _{j}\) (\(1\le j\le N\)). With the help of generalized relations \(\varPsi _{j}[N]=0\), we can derive

$$\begin{aligned} \begin{aligned} \varPsi _{j}^{[N]}=T_{N}\mid _{\lambda =\lambda _{j}} \varPsi _{j}=0. \end{aligned} \end{aligned}$$
(2.5)

this is

$$\begin{aligned} \varPsi _{j} \varLambda _{j}^{N}+t_{1}^{[N]} \varPsi _{j} \varLambda _{j}^{N-1}+t_{2}^{[N]} \varPsi _{j} \varLambda _{j}^{N-2}+\cdots +t_{N}^{[N]} \varPsi _{j}=0 \end{aligned}$$
(2.6)

Substituting (2.1) and (2.3) to (2.2) and using Cramer’s rule, N-fold DT appears that

$$\begin{aligned} \begin{aligned}&q^{[N]}(x,t)=q(x,t)+2i\frac{\varDelta _{2}^{[N]}}{\varDelta ^{[N]}},\\&q^{[N]*}(-x,t)=q^{*}(-x,t)-2i\frac{\varDelta _{3}^{[N]}}{\varDelta ^{[N]}}, \end{aligned} \end{aligned}$$
(2.7)

where

$$\begin{aligned} \begin{aligned}&\varDelta ^{[N]}= \left| \begin{array}{cccccc} \lambda ^{N-1}_{1} \phi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N-1}_{N} \phi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N-1} \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N-1} \phi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \phi _{1}(x,t) &{}\quad \cdots &{}\quad \phi _{N}(x,t) &{}\quad \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \phi ^{*}_{N}(-x,t)\\ \lambda ^{N-1}_{1} \psi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N-1}_{N} \psi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N-1} \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N-1} \psi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \psi _{1}(x,t) &{}\quad \cdots &{}\quad \psi _{N}(x,t) &{}\quad \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \psi ^{*}_{N}(-x,t)\\ \end{array} \right| ,\\&\varDelta _{2}^{[N]}= \left| \begin{array}{cccccc} \lambda ^{N}_{1} \phi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N}_{N} \phi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N} \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N} \phi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \phi _{1}(x,t) &{}\quad \cdots &{}\quad \phi _{N}(x,t) &{}\quad \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \phi ^{*}_{N}(-x,t)\\ \lambda ^{N-2}_{1} \psi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N-2}_{N} \psi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N-2} \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N-2} \psi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \psi _{1}(x,t) &{}\quad \cdots &{}\quad \psi _{N}(x,t) &{}\quad \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \psi ^{*}_{N}(-x,t)\\ \end{array} \right| ,\\&\varDelta _{3}^{[N]}= \left| \begin{array}{cccccc} \lambda ^{N}_{1} \psi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N}_{N} \psi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N} \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N} \psi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \psi _{1}(x,t) &{}\quad \cdots &{}\quad \psi _{N}(x,t) &{}\quad \psi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \psi ^{*}_{N}(-x,t)\\ \lambda ^{N-2}_{1} \phi _{1}(x,t) &{}\quad \cdots &{}\quad \lambda ^{N-2}_{N} \phi _{N}(x,t) &{}\quad \overline{\lambda _{1}}^{N-2} \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \overline{\lambda _{N}}^{N-2} \phi ^{*}_{N}(-x,t)\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ \phi _{1}(x,t) &{}\quad \cdots &{}\quad \phi _{N}(x,t) &{}\quad \phi ^{*}_{1}(-x,t) &{}\quad \cdots &{}\quad \phi ^{*}_{N}(-x,t)\\ \end{array} \right| . \end{aligned} \end{aligned}$$

3 Bright soliton

After having explicit form of DT, we consider constructing exact solutions of system (1.6). In this section, we choose seed solutions \(q(x,t)=q^{*}(-x,t)=0\) to obtain bright soliton solutions, which satisfy system

$$\begin{aligned} \varPsi _{x}= & {} J \varPsi \varLambda ,\nonumber \\ \varPsi _{t}= & {} \left( \begin{array}{cc} -4i\beta &{}\quad 0\\ 0 &{}\quad 4i\beta \\ \end{array} \right) \varPsi \varLambda ^{3}\nonumber \\&+\left( \begin{array}{cc} -2i\alpha &{}\quad 0\\ 0 &{}\quad 2i\alpha \\ \end{array} \right) \varPsi \varLambda ^{2}. \end{aligned}$$
(3.1)

Let \([\varPsi _{1}]_{\varLambda =\varLambda _{1}}\) is a solution of the system (3.1). Substituting \(\varPsi _{1}\) to (3.1) and using separation of variables, we have

$$\begin{aligned} \begin{aligned}&\phi _{1}(x,t)=c_{11} e^{K_{1}},~~~\psi _{1}(x,t)=c_{21} e^{-K_{1}},\\&\phi ^{*}_{1}(-x,t)=\overline{c_{11}} e^{\overline{K_{1}}},~~~\psi ^{*}_{1}(-x,t)=\overline{c_{21}} e^{-\overline{K_{1}}}, \end{aligned} \end{aligned}$$
(3.2)

with \(K_{1}=-i\lambda _{1}x-2i(\alpha \lambda ^{2}_{1}+2\beta \lambda ^{3}_{1})t\), \(\overline{K_{1}}=-i\overline{\lambda _{1}}x-2i(\alpha \overline{\lambda _{1}}^{2}+2\beta \overline{\lambda _{1}}^{3})t\), \(\alpha \), \(\beta \) are real value and \(c_{11}\), \(c_{21}\), \(\overline{c_{11}}\), \(\overline{c_{21}}\) are integration constants. Based on obtained basic solution of system (3.1), two parameter symmetry broken one-bright-soliton solution of system (1.6) stands clearly out

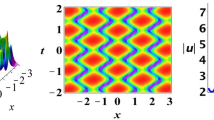
$$\begin{aligned} \begin{aligned} q^{[1]}(x,t)&=\frac{2i(\lambda _{1}-\overline{\lambda _{1}})\kappa _{11} e^{2K_{1}}}{e^{2(K_{1}-\overline{K_{1}})+ln(\frac{\kappa _{11}}{\kappa _{21}})}-1},\\ q^{[1]*}(-x,t)&=\frac{2i(\lambda _{1}-\overline{\lambda _{1}})\kappa _{21} e^{-2\overline{K_{1}}}}{e^{2(K_{1}-\overline{K_{1}})+ln(\frac{\kappa _{11}}{\kappa _{21}})}-1}, \end{aligned} \end{aligned}$$
(3.3)

with \(\kappa _{11}=\frac{c_{11}}{c_{21}}\), \(\kappa _{21}=\frac{\overline{c_{11}}}{\overline{c_{21}}}\). Figures of one bright soliton are shown in Fig. 1 with parameter values.

Fig. 1
figure 1

One-bright-soliton evolution of system (1.6), when \(\lambda _{1}=0.1-0.5i\), \(\overline{\lambda _{1}}=1+0.5i\), \(c_{11}=0.5+i\), \(\overline{c_{11}}=1-i\), \(c_{21}=-1-i\), \(\overline{c_{21}}=0.5-i\), \(\alpha =0.05\), \(\beta =0\)

Full size image
Fig. 2
figure 2

Two-bright-soliton evolution of system (1.6), when \(\lambda _{1}=-0.3+0.5i\), \(\overline{\lambda _{1}}=-0.6-0.5i\), \(\lambda _{2}=0.2-0.5i\), \(\overline{\lambda _{2}}=0.5+0.5i\), \(c_{11}=0.5+i\), \(\overline{c_{11}}=1-i\), \(c_{21}=-1-i\), \(\overline{c_{21}}=0.5-i\), \(c_{12}=0.5+i\), \(\overline{c_{12}}=1-i\), \(c_{22}=-1-i\), \(\overline{c_{22}}=0.5-i\), \(\alpha =0.05\), \(\beta =0\)

Full size image

If \([\varPsi _{1}]_{\varLambda =\varLambda _{1}}\) and \([\varPsi _{2}]_{\varLambda =\varLambda _{2}}\) are particular solutions of system (3.1), then we get basic solutions

$$\begin{aligned} \begin{aligned}&\phi _{j}(x,t)=c_{1j} e^{K_{j}},~~~\psi _{j}(x,t)=c_{2j} e^{-K_{j}},\\&\phi ^{*}_{1}(-x,t)=\overline{c_{1j}} e^{\overline{K_{j}}},~~~\psi ^{*}_{j}(-x,t)=\overline{c_{2j}} e^{-\overline{K_{j}}}, \end{aligned} \end{aligned}$$
(3.4)

with \(K_{j}=-i\lambda _{j}x-2i(\alpha \lambda ^{2}_{j}+2\beta \lambda ^{3}_{j})t\), \(\overline{K_{j}}=-i\overline{\lambda _{j}}x-2i(\alpha \overline{\lambda _{j}}^{2}+2\beta \overline{\lambda _{j}}^{3})t\), \(\alpha \), \(\beta \) are real value and \(c_{1j}\), \(c_{2j}\), \(\overline{c_{1j}}\), \(\overline{c_{2j}}\) (\(j=1,2\)) are integration constant. Substituting basic solutions to twofold DT formulas, we get two-bright-soliton solution which is observed in Fig. 2 with parameter values.

Similarly, let \([\varPsi _{j}]_{\varLambda =\varLambda _{j}}\) (\(j=1,2,\ldots ,N\)) are the solutions of system (3.1), we get basic solutions

$$\begin{aligned} \begin{aligned}&\phi _{j}(x,t)=c_{1j} e^{K_{j}},~~~\psi _{j}(x,t)=c_{2j} e^{-K_{j}},\\&\phi ^{*}_{1}(-x,t)=\overline{c_{1j}} e^{\overline{K_{j}}},~~~\psi ^{*}_{j}(-x,t)=\overline{c_{2j}} e^{-\overline{K_{j}}}, \end{aligned} \end{aligned}$$
(3.5)

with \(K_{j}=-i\lambda _{j}x-2i(\alpha \lambda ^{2}_{j}+2\beta \lambda ^{3}_{j})t\), \(\overline{K_{j}}=-i\overline{\lambda _{j}}x-2i(\alpha \overline{\lambda _{j}}^{2}+2\beta \overline{\lambda _{j}}^{3})t\), \(\alpha \), \(\beta \) are real value and \(c_{1j}\), \(c_{2j}\), \(\overline{c_{1j}}\), \(\overline{c_{2j}}\) (\(j=1,2,\ldots ,N\)) are integration constant. Substituting obtained basic solutions to N-fold DT formulas (2.7), we get concentrate N-order bright soliton expression.

Figure 1 shows one-bright-soliton solution by first DT, while Fig. 2 describes counterpart by second DT. Two sets of pictures possess similar evolution mechanism and we take Fig. 1 as an example. Interestingly, potentials \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) exist a huge density difference in Fig. 1. In other words, as \(t\rightarrow \infty \) in x direction, \(q^{[1]}(x,t)\) increases (or decreases) exponentially in amplitude, \(q^{[1]*}(-x,t)\) decreases (or increases) exponentially in amplitude. In this sense, nonlocal symmetry of potential is broken and the propagations are PT symmetric broken. More interestingly, product \(Q^{[1]}\) of \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) remains unchanged under regular changes of \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\). That is to say, interaction of \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) achieve a stable state and it has certain practical physical application.

4 Dark and antidark soliton

In this section, we assume that \(\alpha =-1\), \(\beta =0\) and take continuous waves (CW) \(q(x,t)=m e^{2imnt}\), \(q^{*}(-x,t)=n e^{-2imnt}\) as initial solutions to gain dark and antidark solitons, which should satisfy

$$\begin{aligned} \begin{aligned} \varPsi _{x}&= J \varPsi \varLambda +\left( \begin{array}{cc} 0 &{}\quad m e^{2imnt}\\ n e^{-2imnt} &{}\quad 0\\ \end{array} \right) \varPsi ,\\ \varPsi _{t}&= \left( \begin{array}{cc} 2i &{}\quad 0\\ 0 &{}\quad -2i\\ \end{array} \right) \varPsi \varLambda ^{2}\\&\quad +\left( \begin{array}{cc} 0 &{}\quad -2m e^{2imnt}\\ -2n e^{-2imnt} &{}\quad 0\\ \end{array} \right) \varPsi \varLambda \\&\quad +\left( \begin{array}{cc} imn &{}\quad 0\\ 0 &{}\quad -imn\\ \end{array} \right) \varPsi .\\ \end{aligned} \end{aligned}$$
(4.1)

4.1 One dark and antidark soliton

Let \(\varPsi _{1}\) is corresponding eigenfunction at \(\varLambda =\varLambda _{1}\). We substitute \(\varPsi _{1}\) to system (4.1) and derive the solution of obtained differential equations

$$\begin{aligned} \begin{aligned} \phi _{1}(x,t)&=e^{imnt} (c_{1} e^{\varrho _{1} \sigma _{1}}+c_{2} e^{-\varrho _{1} \sigma _{1}}),\\ \psi _{1}(x,t)&=e^{-imnt} \left( \frac{c_{1}}{m}p_{2} e^{\varrho _{1} \sigma _{1}}+\frac{c_{2}}{m}p_{1} e^{-\varrho _{1} \sigma _{1}}\right) ,\\ \phi ^{*}_{1}(-x,t)&=e^{imnt} (\overline{c_{1}} e^{\varrho _{2} \sigma _{2}}+\overline{c_{2}} e^{-\varrho _{2} \sigma _{2}}),\\ \psi ^{*}_{1}(-x,t)&=e^{-imnt} \left( \frac{\overline{c_{1}}}{m}p_{4} e^{\varrho _{2} \sigma _{2}}+\frac{\overline{c_{2}}}{m}p_{3} e^{-\varrho _{2} \sigma _{2}}\right) , \end{aligned} \end{aligned}$$
(4.2)

with \(\varrho _{1}=x-2\lambda _{1}t\), \(\varrho _{2}=x-2\overline{\lambda _{1}}t\), \(\sigma _{1}=\sqrt{mn-\lambda ^{2}_{1}}\), \(\sigma _{2}=\sqrt{mn-\overline{\lambda _{1}}^{2}}\), \(p_{1}=i\lambda _{1}-\sigma _{1}\), \(p_{2}=i\lambda _{1}+\sigma _{1}\), \(p_{3}=i\overline{\lambda _{1}}-\sigma _{2}\), \(p_{4}=i\overline{\lambda _{1}}+\sigma _{2}\), and \(c_{1}\), \(c_{2}\), \(\overline{c_{1}}\), \(\overline{c_{2}}\) are integration constants. Substituting (4.2) into (2.7), we arrive at dark and antidark soliton solution

$$\begin{aligned} \begin{aligned}&q^{[1]}(x,t)=e^{2imnt}(m+\frac{2i n (\overline{\lambda _{1}}-\lambda _{1})\chi _{1}\chi _{2}}{\chi _{1}\chi _{4}-\chi _{2}\chi _{3}},\\&q^{[1]*}(-x,t)= e^{-2imnt}\left( n+\frac{2i(\overline{\lambda _{1}}-\lambda _{1})}{n}\frac{\chi _{3}\chi _{4}}{\chi _{1}\chi _{4}-\chi _{2}\chi _{3}}\right) , \end{aligned} \end{aligned}$$
(4.3)

where

$$\begin{aligned} \begin{aligned}&\chi _{1}=\kappa _{1}e^{\varrho _{1}\sigma _{1}}+e^{-\varrho _{1}\sigma _{1}},~~~\chi _{2}=\kappa _{2}e^{\varrho _{2}\sigma _{2}}+e^{-\varrho _{2}\sigma _{2}},\\&\chi _{3}=\kappa _{1}p_{1}e^{\varrho _{1}\sigma _{1}}+p_{2}e^{-\varrho _{1}\sigma _{1}},\\&\chi _{4}=\kappa _{2}p_{3}e^{\varrho _{2}\sigma _{2}}+p_{4}e^{-\varrho _{2}\sigma _{2}}, \end{aligned} \end{aligned}$$

with \(\kappa _{1}=\frac{c_{1}}{c_{2}}\), \(\kappa _{2}=\frac{\overline{c_{1}}}{\overline{c_{2}}}\).

Fig. 3
figure 3

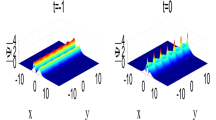
a Two-dark-soliton collision of \(|q^{[1]}(x,t)|\), b two-bright-soliton collision of \(|q^{[1]*}(-x,t)|\), c two-dark-soliton collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=-1.5\), \(\overline{\lambda _{1}}=1.2\), \(c_{1}=-1-0.5i\), \(\overline{c_{1}}=-0.5+0.5i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image

By controlling proper parameters, profile maps of onefold dark and antidark solitons are shown when \(t=1\) in Fig. 3, 4, 5, 6, 7, 8, 9, 10 and 11. Based on introduction part, we know that potentials \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) both exhibit two solitons and each soliton presents two possible shapes (namely dark or antidark solitons) by first DT. From this, \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) both have four possible collision combinations. Under CW background, two potentials have sixteen stable collision combinations and stably propagate when we choose an appropriate eigenvalue \(\lambda \). Because of the similarity of figure types, nine different combinations are summarized. According to the shape of self-induced potential V(x, t) , combinations can be classified as follows: (1) When  V(x, t) is two dark solitons, there are five possible combinations including Figs. 3, 4, 5, 7 and 10; (2) When V(x, t) is dark and antidark solitons, four combinations are supposed to observed as Figs. 8, 9 and 11; (3) When V(x, t) is two light solitons, only there are one combinations such as Fig.6. Besides, We see that \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) in Fig. 3, 4, 5, 6, 7, 8, 9, 10 and 11 exhibit noninteracting characteristics due to independence of eigenvalues and solution vectors, and show greater stability than in Figs. 1 and 2. In this sense, the propagations are PT symmetric unbroken. In addition, stable value of the self-induced potential is also the product of potentials’ stable values, which is an external manifestation of the definition. The internal manifestation is V(x, t)’s change in energy that resulting from the potentials.

Fig. 4
figure 4

a Two-bright-soliton collision of \(|q^{[1]}(x,t)|\), b two-dark-soliton collision of \(|q^{[1]*}(-x,t)|\), c two-dark-soliton collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=-1.5\), \(\overline{\lambda _{1}}=1.2\), \(c_{1}=1+0.5i\), \(\overline{c_{1}}=0.5-0.5i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 5
figure 5

a Two-dark-soliton collision of \(|q^{[1]}(x,t)|\) and b \(|q^{[1]*}(-x,t)|\), (c) two-dark-soliton collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=1\), \(\overline{\lambda _{1}}=-0.5\), \(c_{1}=1+i\), \(\overline{c_{1}}=1.5-3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 6
figure 6

a Two-bright-soliton collision of \(|q^{[1]}(x,t)|\) and b \(|q^{[1]*}(-x,t)|\), c two-bright-soliton collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\) when \(\lambda _{1}=0.01\), \(\overline{\lambda _{1}}=0.5\), \(c_{11}=1+0.7i\), \(\overline{c_{1}}=-1.5-0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 7
figure 7

a Two-dark-soliton collision of \(|q^{[1]}(x,t)|\), b dark and antidark solitons collision of \(|q^{[1]*}(-x,t)|\), c two-dark-soliton collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=0.5\), \(\overline{\lambda _{1}}=1\), \(c_{1}=-1-0.7i\), \(\overline{c_{1}}=-0.5+0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 8
figure 8

a Two-bright-soliton collision of \(|q^{[1]}(x,t)|\), b dark and antidark solitons collision of \(|q^{[1]*}(-x,t)|\), c dark and antidark solitons collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=1\), \(\overline{\lambda _{1}}=-0.5\), \(c_{1}=1-0.7i\), \(\overline{c_{1}}=-0.5+0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image

4.2 Asymptotic analysis

In this subsection, asymptotic analysis can be used to better understand evolution process of soliton. It turns out that (4.3) and (4.4) have four different asymptotic behaviors when \(t\rightarrow \pm \infty \).

Fig. 9
figure 9

a Dark and antidark solitons collision of \(|q^{[1]}(x,t)|\), b two-bright-soliton collision of \(|q^{[1]*}(-x,t)|\), c dark and antidark solitons collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=1\), \(\overline{\lambda _{1}}=-0.5\), \(c_{1}=-1+0.7i\), \(\overline{c_{1}}=-1+0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 10
figure 10

a Dark and antidark solitons collision of \(|q^{[1]}(x,t)|\), b two-dark-soliton collision of \(|q^{[1]*}(-x,t)|\), c dark and antidark solitons collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=1\), \(\overline{\lambda _{1}}=0.5\), \(c_{1}=1+0.7i\), \(\overline{c_{1}}=-0.5+0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image
Fig. 11
figure 11

a Dark and antidark solitons collision of \(|q^{[1]}(x,t)|\) and b \(|q^{[1]*}(-x,t)|\), c dark and antidark solitons collision of \(|q^{[1]}(x,t)q^{[1]*}(-x,t)|\), when \(\lambda _{1}=0.2\), \(\overline{\lambda _{1}}=0.5\), \(c_{1}=-1-0.7i\), \(\overline{c_{1}}=-1.5-0.3i\), \(c_{2}=1\), \(\overline{c_{2}}=1\), \(m=2\), \(n=1.5\)

Full size image

(1) Assume that Soliton 1 is in the vicinity of line \(x=2\lambda _{1}t\) (\(\varrho _{1}\approx 0\)) . Then, we let \(\xi _{1}=x-2\lambda _{1}t\) to change the frame co-moving. From \(\varrho _{2}=x-2\overline{\lambda _{1}}t=\xi _{1}-2(\overline{\lambda _{1}}-\lambda _{1})t\), we have \(\varrho _{2}\rightarrow \mp \infty \) as \(t\rightarrow \pm \infty \). So we have asymptotic formulas of \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\)

$$\begin{aligned}&q^{[1]}(x,t)\rightarrow \left\{ \begin{aligned}&e^{2imnt}\left( m+2i n (\overline{\lambda _{1}}-\lambda _{1})\frac{\chi _{1}}{\vartheta _{1}}\right) ,~~~t \rightarrow -\infty ,\\&e^{2imnt}\left( m+2i n (\overline{\lambda _{1}}-\lambda _{1})\frac{\chi _{1}}{\vartheta _{2}}\right) ,~~~t \rightarrow +\infty ,\\ \end{aligned} \right. \nonumber \\&q^{[1]*}(-x,t)\rightarrow \left\{ \begin{aligned}&e^{-2imnt}\left( n+\frac{2i(\overline{\lambda _{1}}-\lambda _{1})}{n}\frac{p_{3}\chi _{3}}{\vartheta _{1}}\right) ,~~~t \rightarrow -\infty ,\\&e^{-2imnt}\left( n+\frac{2i(\overline{\lambda _{1}}-\lambda _{1})}{n}\frac{p_{4}\chi _{3}}{\vartheta _{2}}\right) ,~~~t \rightarrow +\infty ,\\ \end{aligned} \right. \end{aligned}$$
(4.4)

with

$$\begin{aligned} \begin{aligned}&\vartheta _{1}=\kappa _{1}(p_{3}-p_{1})e^{\varrho _{1}\sigma _{1}}+(p_{3}-p_{2})e^{-\varrho _{1}\sigma _{1}},\\&\vartheta _{2}=\kappa _{1}(p_{4}-p_{1})e^{\varrho _{1}\sigma _{1}}+(p_{4}-p_{2})e^{-\varrho _{1}\sigma _{1}},\\&\chi _{1}=\kappa _{1}e^{\varrho _{1}\sigma _{1}}+e^{-\varrho _{1}\sigma _{1}},\\&\chi _{3}=\kappa _{1}p_{1}e^{\varrho _{1}\sigma _{1}}+p_{2}e^{-\varrho _{1}\sigma _{1}}. \end{aligned} \end{aligned}$$

(2) On the other hand, Soliton 2 will stably propagate near the line \(x=2\overline{\lambda _{1}}t\) if we assume that \(\varrho _{2}\approx 0\). Taking an indefinitely small \(\xi _{2}=x-2\overline{\lambda _{1}}t\), we get \(\varrho _{1}=x-2\lambda _{1}t=\xi _{2}+2(\overline{\lambda _{1}}-\lambda _{1})t\). Therefore, \(\varrho _{1}\rightarrow \pm \infty \) as \(t\rightarrow \pm \infty \) and we obtain that asymptotic expressions

$$\begin{aligned}&q^{[1]}(x,t)\rightarrow \left\{ \begin{aligned}&e^{2imnt}\left( m+2i n (\overline{\lambda _{1}}-\lambda _{1})\frac{\chi _{2}}{\vartheta _{3}}\right) ,~~~t \rightarrow -\infty ,\\&e^{2imnt}\left( m+2i n (\overline{\lambda _{1}}-\lambda _{1})\frac{\chi _{2}}{\vartheta _{4}}\right) ,~~~t \rightarrow +\infty ,\\ \end{aligned} \right. \nonumber \\&q^{[1]*}(-x,t)\rightarrow \left\{ \begin{aligned}&e^{-2imnt}\left( n+\frac{2i(\overline{\lambda _{1}}-\lambda _{1})}{n}\frac{p_{2}\chi _{4}}{\vartheta _{3}}\right) ,~~~t \rightarrow -\infty ,\\&e^{-2imnt}\left( n+\frac{2i(\overline{\lambda _{1}}-\lambda _{1})}{n}\frac{p_{1}\chi _{4}}{\vartheta _{4}}\right) ,~~~t \rightarrow +\infty ,\\ \end{aligned} \right. \end{aligned}$$
(4.5)

with

$$\begin{aligned} \begin{aligned}&\vartheta _{3}=\kappa _{2}(p_{3}-p_{2})e^{\varrho _{2}\sigma _{2}}+(p_{4}-p_{2})e^{-\varrho _{2}\sigma _{2}},\\&\vartheta _{4}=\kappa _{2}(p_{3}-p_{1})e^{\varrho _{2}\sigma _{2}}+(p_{4}-p_{1})e^{-\varrho _{2}\sigma _{2}},\\&\chi _{2}=\kappa _{2}e^{\varrho _{2}\sigma _{2}}+e^{-\varrho _{2}\sigma _{2}},\\&\chi _{4}=\kappa _{2}p_{3}e^{\varrho _{2}\sigma _{2}}+p_{4}e^{-\varrho _{2}\sigma _{2}}. \end{aligned} \end{aligned}$$

4.3 N dark and antidark soliton

Now we consider basic solutions

$$\begin{aligned} \phi _{j}(x,t)&=e^{imnt} (c_{1j} e^{\varrho _{1j} \sigma _{1j}}+c_{2j} e^{-\varrho _{1j} \sigma _{1j}}),\nonumber \\ \psi _{j}(x,t)&=e^{-imnt} \left( \frac{c_{1j}}{m}p_{2j} e^{\varrho _{1j} \sigma _{1j}}+\frac{c_{2j}}{m}p_{1j} e^{-\varrho _{1j} \sigma _{1j}}\right) ,\nonumber \\ \phi ^{*}_{j}(-x,t)&=e^{imnt} (\overline{c_{1j}} e^{\varrho _{2j} \sigma _{2j}}+\overline{c_{2j}} e^{-\varrho _{2j} \sigma _{2j}}),\nonumber \\ \psi ^{*}_{j}(-x,t)&=e^{-imnt} \left( \frac{\overline{c_{1j}}}{m}p_{4j} e^{\varrho _{2j} \sigma _{2j}}+\frac{\overline{c_{2j}}}{m}p_{3j} e^{-\varrho _{2j} \sigma _{2j}}\right) ,\nonumber \\ \end{aligned}$$
(4.6)

with \(\chi _{1j}=x-2\lambda _{j}t\), \(\overline{\varrho }_{2j}=x-2\overline{\lambda _{j}}t\), \(\sigma _{1j}=\sqrt{mn-\lambda ^{2}_{j}}\), \(\sigma _{2j}=\sqrt{mn-\overline{\lambda _{j}}^{2}}\), and \(p_{1j}=i\lambda _{j}-\sigma _{1j}\), \(p_{2j}=i\lambda _{j}+\sigma _{1j}\), \(p_{3j}=i\overline{\lambda _{j}}-\sigma _{2j}\), \(p_{4j}=i\overline{\lambda _{j}}+\sigma _{2j}\), \(j=1,2,\ldots ,N\). Substituting solutions (5.5) to N-fold formula (2.7), we can obtain N-order dark and antidark solitons and \(2^{2N}\times 2^{2N}\) collision combinations of potentials \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\). Because of the overlap between collision types, the number of collision combinations available is less than \(2^{2N}\times 2^{2N}\).

5 Conclusions

In this paper, system (1.6) is studied in the field and parity transformed complex conjugate field. To begin with, nonlinear system is converted to linear system and solutions of nonlinear system are converted to that of linear system. Further, N-fold DT is constructed by Lax pair. Moreover, we obtain bright soliton solutions under zero background and dark and antidark soliton solutions under CW background with the help of DT. Those soliton solutions include two kinds of types: symmetry broken solutions and symmetry unbroken solutions. For dark and antidark soliton solutions, we choose proper parameters for \(q^{[1]}(x,t)\) and \(q^{[1]*}(-x,t)\) and clarify evolution behaviors of each soliton in asymptotic analysis. The corresponding pictures are plotted, and they are useful as a nonlocal wave model in physical practical application, such as nonlinear optical fibers, plasmas and fluids [43, 44]. The contribution of this paper is as follows: (1) Two independent spatial solutions are used to obtain more general solitons; (2) all figure combinations between potentials are observed completely under CW background. Next, we will study physical meaning of explicit solutions, determine eigenvalue conditions and choose the range. In this way, different stable solitons can be found through symbolic calculation.