1 Introduction

In 2016, Ablowitz and Musslimani proposed some novel nonlocal nonlinear integrable equations, such as nonlocal integrable nonlinear Schrödinger (NNLS) equation, modified Korteweg–de Vries (mKdV) equation, sine-Gordon equation, three-wave interaction equations and so on [1, 2]. Some nonlocal nonlinear equations have new types of soliton solutions and are broadly applied in many fields of physics. Some works investigate the nonlocal nonlinear equations with a finite distance; the 3-dimensional spatiotemporal solitary waves have been investigated frequently in strongly nonlocal media [3], and some specific Hermite–Gaussian vector solitons are obtained in nonlocal optical media [4].

From an experimental viewpoint, the controlling of the complex refractive index distribution is realized with the PT-symmetric potential, the PT-symmetry breaking within the realm of optics has been observed in experiment, and some unusual characteristics of the unidirectional invisibility and nonlinear switching effect in the PT-symmetric waveguides have been revealed [5, 6]. In the nonlinear optics, the Kerr nonlinearity and PT-symmetric linear potentials of the nonlinear Schrödinger (NLS) equations have been intensively studied in [7, 8], including the interactions of bright and dark solitons with a PT-symmetric dipole and dynamical behaviors in the oligomers, and so on. Thus, the new nonlocal equation is PT-symmetric and has self-induced potential in the case of classical optics [9]; the wave propagation in PT-symmetric coupled waveguides or photonics lattices has been experimentally observed in classical optics [10].

A class of NNLS equations can describe the collapse arrest and the soliton stabilization in many nonlocal nonlinear medias [11]. Especially, the integrable NNLS equations with ‘parity-time symmetry’ [12] have some important characters [12]. Some exact solutions and numerical simulations of NNLS equation with self-induced PT-symmetric potential have been considered experimentally [13]. The PT-symmetric integrable local and nonlocal vector NLS equations are formulated with matrix Lax pairs in [14]. An improved Hirota bilinear method is achieved by bilinearization both the NNLS equation and its associated parity transformed complex conjugate equation in a novel way; one and two soliton solutions are invariant under combined space and time reversal transformations and are more general than the known ones [15]. The inverse scattering theory is developed by using a novel left–right Riemann–Hilbert problem, and the Cauchy problem for the NNLS equation is formulated, which can lead to explicit time-periodic one and two soliton solutions in [1]. A general integrable nonlocal coupled NLS system with the PT-symmetry is investigated in [16], which contains not only the nonlocal self-phase modulation and the nonlocal cross-phase modulation, but also the nonlocal four-wave mixing terms. Some novel soliton solutions of the 2-dimensional NLS equation with a PT-symmetric potential can be extended to the equations with two or more spatial variables [17]. The discrete and coupled NNLS equations are solved via the Darboux transformation in [18], and some dynamics of higher-order rational solitons of the NNLS equation are explained with generalized Darboux transformation in [19,20,21]. Some discrete rogue wave solutions with PT-symmetric potential of Ablowitz–Musslimani equation are derived by Yu in [22]. The generalized three coupled Gross–Pitaevskii equations are worked by means of the Darboux transformation and Hirota’s method; several non-autonomous matter-wave solitons including dark–dark–dark and bright–bright–bright shapes are obtained in [23]. The NNLS equation with nonzero boundary conditions is investigated with inverse scattering transform in [24]. An algebraic iterative algorithm is provided to obtain a series of analytic solutions for the discrete PT-symmetric NNLS equation in [25]. Zhou considers the Darboux transformations and global solutions for an nonlocal derivative NLS equation, which can be globally defined and bounded for all (x, t) in [26]. Integrability of a general integrable nonlocal coupled NLS equation is confirmed; some dynamics and interactions of different kinds of solitons are discussed by Zhu in [27]. Yan presents a method to construct some novel two-family-parameter equations, including the local, nonlocal and mixed-local–nonlocal vector NLS equations [28].

Recently, how to solve a class of NNLS equations is a focus problem. In this paper, we extend the ideas of the previous works and use the similarity transformation, Hirota method and Darboux transformation to study the generalized nonlocal nonlinear Hirota (GNNH) equation and nonlocal Gross–Pitaevskii (NGP) equation with the self-induced PT-symmetric potential. We can find that some novel results are different from the local nonlinear Hirota equation and Gross–Pitaevskii equation. Then, we obtain some non-autonomous breather (NB) solutions and non-autonomous rogue waves (NRWs) of GNNH equation, and non-autonomous rational (NR) waves of NGP equation. Some properties of the NR waves are investigated analytically for the nonlocal nonlinear equation, which are different from the solutions of the local nonlinear equation. The trajectories of peaks and depressions of the non-autonomous rogue waves are produced by means of analytical method, and the dynamical stabilities of the NR solutions are derived through the numerical method. The obtained different results can be useful to explain the corresponding wave phenomena in some nonlocal wave models.

The rest of this paper is organized as follows. In Sect. 2, we consider a generalized nonlocal nonlinear Hirota equation with PT-symmetric potential. In Sect. 3, some novel non-autonomous breather and rogue wave solutions are explicitly found, and the trajectories of motion of peaks and depressions of the derived DRWs are explicitly considered. In Sect. 4, the non-autonomous rational solutions of the NGP equation are obtained; then, the numerical simulations of rational wave solutions are performed. Finally, we give some conclusions.

2 A generalized nonlocal nonlinear Hirota equation with the PT-symmetric potential

We consider the variable coefficient GNNH equation with PT-symmetric potential, which is given rise to as following:

$$\begin{aligned}&i \frac{\partial \varPsi }{\partial t}+i c(x,t) \frac{\partial \varPsi }{\partial x }+b(t) \frac{\partial ^2\varPsi }{\partial x^2 }+g(t)\varPsi \varPsi ^{*}(-x,t)\varPsi \nonumber \\&\quad +\,id(t)\frac{\partial ^3\varPsi }{\partial x^3 }+ie(t) \varPsi \varPsi ^{*}(-x,t) \frac{\partial \varPsi }{\partial x}\nonumber \\&\quad +\,v(x,t) \varPsi +i\gamma (t)\varPsi =0, \end{aligned}$$
(1)

where \(\varPsi =\varPsi (x,t)\) is a complex valued function, x is the propagation variable, t is the transverse variable, and the \(i=\sqrt{-1}\). The \(\varPsi \varPsi ^{*}(-x,t)\) is a PT-symmetric potential; the b(t), c(x, t) and d(t) represent the group-velocity dispersion, first-order and third-order dispersion, respectively. The \(\gamma (t)\) is gain/loss time coefficient, and an external potential v(x, t) is real-valued function, and the g(t), e(t) are the nonlinearities of time functions. This variable coefficient GNNH equation arises in many fields such as nonlinear optics and BECs.

The variable coefficient GNNH (1) is an important nonlocal wave model and can explain the corresponding wave phenomena. We can derive an nonlocal Gross–Pitaevskii (NGP) equation with PT-symmetric external potential in some special reducing cases \(c(x,t)=d(t)=e(t)=0\)

$$\begin{aligned}&i \frac{\partial \varPsi }{\partial t}+b(t) \frac{\partial ^2\varPsi }{\partial x^2 }+g(t)\varPsi \varPsi ^{*}(-x,t)\varPsi \nonumber \\&\quad +\,v(x,t) \varPsi +i\gamma (t)\varPsi =0, \end{aligned}$$
(2)

which has an important application of soliton dispersion management experiment in nonlinear optics, where \(\varPsi (x ,t )\) is the complex envelope of the electric field. In the case of temporal solitons in optical fibers, x and t represent the propagation distance and the retarded time, respectively. The b(t) is real-valued function of time coordinate and represents the group-velocity dispersion, the nonlinearity g(t) is real-valued function of time coordinate, the nonlinearity can be modulated by a Feshbach resonance, the v(x, t) is the external potential, and \(\gamma (t)\) is the gain or loss function.

Recently, some integrable continuous and discrete NNLS equations describing wave propagation in nonlinear PT-symmetric media are also found [9, 29]. This Eq. (2) can describe the PT-symmetric optics with v(x, t), for which v(x, t) represents a ‘waveguide.’

We search for a similar transformation connecting nonlocal solutions of Eq. (1) with the solutions of NNH equation [30]. The NNH equation is given as following

$$\begin{aligned}&i \frac{\partial \varPhi }{\partial \tau }+i \epsilon \frac{\partial \varPhi }{\partial \eta } + \delta \frac{\partial ^2\varPhi }{\partial \eta ^2}+ \sigma \varPhi [\varPhi (-\eta , \tau )]^*\varPhi \nonumber \\&\quad +\,i \lambda \frac{\partial ^3\varPhi }{\partial \eta ^3}+3 i\lambda \sigma \varPhi [\varPhi (-\eta , \tau )]^* \frac{\partial \varPhi }{\partial \eta } =0, \end{aligned}$$
(3)

where the \(\sigma \) is an arbitrary constant, \(\eta \) and \(\tau \) are two variables.

When \(\epsilon =\lambda =0\), we can derive an NNLS equation with PT external potential [19] as following

$$\begin{aligned} i \frac{\partial \varPhi }{\partial \tau } + \delta \frac{\partial ^2\varPhi }{\partial \eta ^2}+ \sigma \varPhi [\varPhi (-\eta , \tau )]^*\varPhi =0, \end{aligned}$$
(4)

the \(\varPhi =\varPhi (\eta ,\tau )\) is a function of \(\eta =\eta (x,t)\) and \(\tau =\tau (t)\).

We consider a kind of similarity of the nonlocal equation, which is different from the method in [31], and search for the novel solutions of the nonlocal physical fields \(\varPsi (x,t)\) and \(\varPsi ^*(-x,t)\)

$$\begin{aligned} \varPsi (x,t)= & {} \rho (t)\hbox {e}^{i\varphi (x,t)}\varPhi (\eta (x,t),\tau (t)), \end{aligned}$$
(5)
$$\begin{aligned} \varPsi ^*(-x,t)= & {} \rho (t)\hbox {e}^{i\varphi ^*(-x,t)}\varPhi ^*(\eta (-x,t),\tau (t)), \end{aligned}$$
(6)

which must satisfy the following condition

$$\begin{aligned} \eta (-x,t)=-\eta (x,t), \end{aligned}$$
(7)

with \(\rho (t)\) and \(\varphi (x,t)\) are the indicated variables. And, we substitute transformations (5) and (6) into Eq. (1) and have the following system:

$$\begin{aligned} { \left\{ \begin{array}{llllll} \eta _{xx}=0,\quad \varphi _{xx}=0,\quad \rho \gamma (t)+\rho _t=0, \\ v(x,t)=\varphi _t+b(t) {\varphi _{{x}}}^{2}+c(x,t) {\varphi _{{x}}}-d(t) {\varphi _{{x}}}^{3}, \\ \tau _t=\frac{d(t) \eta ^3_{x}}{\lambda }, \quad b(t)=\left( 3\varphi _{{x}}+ \frac{\delta \eta _{x}}{\lambda }\right) d(t) ,\\ e(t)=\frac{3 \sigma \eta ^2_{x}}{ \rho ^2 \hbox {e}^{i(\varphi -\varphi ^*)}}d(t),\quad g(t)=\frac{3 \sigma \eta ^2_{x}}{ \rho ^2 \hbox {e}^{i(\varphi -\varphi ^*)}}\left( \frac{ \eta _{x}}{3 \lambda }+\varphi _{{x}}\right) d(t),\\ c(x,t)=\left( \frac{\epsilon \eta ^2_{x}}{ \lambda }-3\varphi ^2_{{x}}-\frac{ 2 \delta \varphi _{{x}} \eta ^2_{x}}{ \lambda }\right) d(t)- \frac{ \eta _{t}}{\eta _{x}} .\end{array} \right. } \end{aligned}$$
(8)

We consider the conditions \(\eta _{xx}=0\) and \(\varphi _{xx}=0\), can obtain the functions \(\eta (x, t), \tau (t), \rho (t)\) and \(\varphi (x,t)\). The other functions c(x, t), g(t), e(t) and b(t) can be expressed through the given function d(t). Thus, we can derive the novel non-autonomous soliton wave solutions of Eq. (1). And, the similarity variables \(\eta (x,t), \tau (t)\) and the \(\rho (t)\) are derived in the forms

$$\begin{aligned} \eta (x,t)= & {} \alpha (t) x,\quad \rho (t)=\rho _0 \hbox {e}^{-\int _0^t \gamma (s)\mathrm{d}s} ,\nonumber \\ \tau (t)= & {} \frac{1}{\lambda }\int _0^t \!d \left( s \right) \left( \alpha \left( s \right) \right) ^{3 }\,\mathrm{d}s. \end{aligned}$$
(9)

3 Novel non-autonomous solutions and trajectories of extreme points of GNNH Eq. (1)

Some various types of exact breather solutions of NNH Eq. (3) are presented in [28]. However, the non-autonomous breather (NB) solutions of the GNNH equation are not considered. In this section, we derive the NB solution of GNNH equation as following

$$\begin{aligned} \varPsi (x,t)= \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau -\varphi (x,t))}} {\frac{g}{f}}, \end{aligned}$$
(10)

with

$$\begin{aligned} g= & {} 1+{ a_1}\,{\mathrm{e}^{ip\eta -\varOmega \,\tau +\zeta { _1}}}+{ a_2}\, {\mathrm{e}^{-ip\eta -\varOmega \,\tau +\zeta { _1}}}\nonumber \\&+\,M{ a_1}\,{ a_2}\, {\mathrm{e}^{-2\,\varOmega \,\tau +\zeta { _1}+\zeta { _2}}}, \end{aligned}$$

and

$$\begin{aligned} f= & {} 1+{\mathrm{e}^{ip\eta -\varOmega \,\tau +\zeta { _1}}}+{\mathrm{e}^{-ip\eta - \varOmega \,\tau +\zeta { _2}}}\\&+M{\mathrm{e}^{-2\,\varOmega \,\tau +\zeta { _1}+\zeta { _2}}} \end{aligned}$$

where \( M=2\,{\frac{\sigma \,{\rho }^{2}}{2\,\sigma \,{\rho }^{2}-{p}^{2}}}, a_1=a_2=-{\frac{{p}^{2}-i\varOmega }{{p}^{2}+i\varOmega }}, c=\lambda \, \left( -3\,\sigma \,{\rho }^{2}+{p}^{2} \right) , \varOmega =\sqrt{{p}^{2} \left( 2\,\sigma \,{\rho }^{2}-{p}^{2} \right) }\), \(\eta \left( x,t \right) =a \left( t \right) x, \tau \left( t \right) ={\frac{\int _{0}^{t}\!d \left( s \right) \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}{\lambda }}.\)

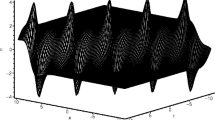
Some wave propagations of NB solution of GNNH Eq. (1) can be controlled via time-management functions a(t), d(t) and \(\gamma (t)\). Figure 1a describes the propagation of NB solution with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=1\). Figure 1b presents a novel ‘The-two-teams’-shape NB solution with \(\gamma (t)=0.1 \sin (t)\), \(a(t)=t^2\) and \(d(t)=1/t^2\). It is interesting to note that NB solution has the shape of Bi-opposite-parabola-liking on the hill in Fig. 1c.

Fig. 1
figure 1

(Color online) a NB solution \(|\varPsi |\) of (10) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=1\). b NB solution \(|\varPsi |\) of (10) with \(\gamma (t)=0.1 \sin (t)\), \(a(t)=t^2\) and \(d(t)=1/t^2\). c NB solution \(|\varPsi |\) of (10) with \(\gamma (t)=0.1 \hbox {Jacobi}SN(2t, 1)\), \(a(t)=t\) and \(d(t)=1/t^2\)

Full size image

The non-autonomous hyperbolic function solution of the GNNH equation is derived as following

$$\begin{aligned} \varPsi (x,t)= \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau -\varphi (x,t))}} {\frac{g}{f}}, \end{aligned}$$
(11)

with

$$\begin{aligned} g= & {} \sqrt{M} \left( \left( \cos \left( \beta \right) \right) ^{2}\cosh \left( \varTheta \right) + \left( \sin \left( \beta \right) \right) ^{2 }\sinh \left( \varTheta \right) \right. \nonumber \\&\left. +\,i\cos \left( \beta \right) \sin \left( \beta \right) \left( \cosh \left( \varTheta \right) -\sinh \left( \varTheta \right) \right) \right) \nonumber \\&+\,\cos \left( px \right) \left( \cos \left( \beta \right) +i\sin \left( \beta \right) \right) , \end{aligned}$$

and \(f= \sqrt{M}\cosh \left( \varTheta \right) +\cos \left( px \right) \), \( { a_1}={\mathrm{e}^{i\beta }}, c=\lambda \, \left( -3\,\sigma \,{\rho }^{2}+{p}^{2} \right) , \varTheta =\varOmega \, \left( t-{ t_0} \right) , \varOmega =\sqrt{{p}^{2} \left( 2\,\sigma \,{\rho }^{2}-{p}^{2} \right) }\), \(\eta \left( x,t \right) =a \left( t \right) x, \tau \left( t \right) ={\frac{\int _{0}^{t}\!d \left( s \right) \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}{\lambda }}. \) From the non-autonomous hyperbolic function solution (11), we can obtain the novel non-autonomous rogue wave (NRW) solution

$$\begin{aligned} \varPsi (x,t)= & {} \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i\left( \omega \,\tau -i\sigma \,{\rho }^{2}\tau \right) }}\nonumber \\&\times \left[ 1-2\,\frac{1+2\,i\sigma \,{\rho }^{2}\tau }{\sigma \,{\rho }^{2}}\right. \nonumber \\&\left. \times \,\left( 2\,\sigma \,{\rho }^{2}{\tau }^{2}+{\eta }^{2}+1/2\,{\frac{1}{\sigma \,{ \rho }^{2}}} \right) ^{-1}\right] . \end{aligned}$$
(12)
Fig. 2
figure 2

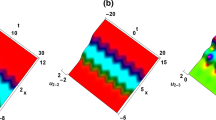
(Color online) a NRW solution \(|\varPsi |\) of (12) with \(\gamma (t)=0\), \(a(t)=1\), \(d(t)=1\) and \(\sigma =1\), \(\rho =1\). b NRW solution \(|\varPsi |\) of (12) with \(\gamma (t)=0\), \(a(t)=1\), \(d(t)=1\) and \(\sigma =1\), \(\rho =1.5\). c NRW solution \(|\varPsi |\) of (12) with \(\gamma (t)=0\), \(a(t)=1\), \(d(t)=0.2 \cos (t)\) and \(\sigma =1\), \(\rho =1\). d NRW solution \(|\varPsi |\) of (12) with \(\gamma (t)=\sin (t)\), \(a(t)=t^2\), \(d(t)=1/t^4\) and \(\sigma =1\), \(\rho =1\)

Full size image

Rogue waves (alias as freak waves, monster waves, killer waves, giant waves or extreme waves), as an important physical phenomenon, are localized both in space and time. From the study of the phenomenon, which depict a unique event that appears from nowhere and disappears without a trace. Consequently, RW has been studied extensively in other fields such as optics, thunderstorms, earthquakes and hurricanes. A standard RW is given in Fig. 2a, which has the all characters of rogue wave and is localized both in time and in space. From Fig. 2b, we can find that the parameter \(\rho \) has an important effecting to the rogue wave. The RW can change into a dark rogue wave when the \(\rho \) increases in Fig. 2b.

We hope that find a way to catch RW for a long time after their abrupt appearance through managing the nonlinear function d(t). If we choose the free function as the d(t) of time t, Fig. 2c depicts the dynamical behavior of the RW solution for a long time. A ‘long-life’ NRW is obtained in Fig. 2c, which means that we can catch the rogue wave in a larger time range. We find a long-lived RW, which still seems to appear from nowhere, but does not disappear like NLSE RW without a trace. And, there is a novel phenomenon appearing in Fig. 2d; one rogue wave and two bright soliton waves appear in a plane wave at the same time.

We consider the NRW solution \(\varPsi (x,t)\) in Eq. (12) and some trajectories of extreme points in the cases \(\gamma (t)=0\), \(a(t)=1\), \(d(t)=1\) and \(\sigma =1\), \(\rho =1\). We note that the NRW solution \(\varPsi (x,t)\) is localized both in time and in space, so we can derive some trajectories of extreme points:

$$\begin{aligned} \{\partial \left( |\varPsi (x,t)|^2\right) /\partial t=0,\quad \{\partial \left( |\varPsi (x,t)|^2\right) /\partial x=0. \end{aligned}$$
(13)

It is easy to see that expressions (13) have some critical points

$$\begin{aligned} (x_1,t_1)=(0,0),(x_{2,3},t_{2,3})=\left( \pm \frac{1}{2}\,{\frac{\sqrt{6}}{\sqrt{\sigma }\rho }},0\right) , \end{aligned}$$

and

$$\begin{aligned} (x_{4,5},t_{4,5})=\left( 0,\pm \frac{1}{2} {\frac{\sqrt{ \left( {\rho }^{4}-2 \right) \left( 3\,{\rho }^{4}-2 \right) }}{ \left( {\rho }^{4}-2 \right) \sigma \,{\rho }^{2}}}\right) , \end{aligned}$$
(14)

which are five real roots of system \(\{\partial \left( |\varPsi (x,t)|^2\right) /\partial t=0,\{\partial \left( |\varPsi (x,t)|^2\right) /\partial x=0\}\).

The trajectories of extreme points (x, t) are maximum or minima, as

$$\begin{aligned} \frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}=32^{*} \end{aligned}$$
(15)
$$\begin{aligned} {\frac{{\rho }^{2}\sigma \, \left( 16\,{\rho }^{8}{\sigma }^{4}{t}^{4 }-16\,{\rho }^{6}{\sigma }^{3}{t}^{2}{x}^{2}-64\,{\rho }^{4}{\sigma }^{4}{ t}^{4}-12\,{\rho }^{4}{\sigma }^{2}{x}^{4}+160\,{\rho }^{2}{\sigma }^{3}{t }^{2}{x}^{2}-8\,{\rho }^{4}{\sigma }^{2}{t}^{2}+36\,{\rho }^{2}\sigma \,{x }^{2}-16\,{\sigma }^{2}{t}^{2}-3 \right) }{ \left( 4\,{\rho }^{4}{\sigma }^{2}{t}^{2}+2\,{\rho }^{2}\sigma \,{x}^{2}+1 \right) ^{4}}}, \end{aligned}$$

and

$$\begin{aligned}&\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t^2}\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}\nonumber \\&\quad -\left( \frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t \partial x}\right) ^2= A \end{aligned}$$
(16)

\(A=2048\,{\rho }^{2}{\sigma }^{3} ( 192\,{\rho }^{16}{\sigma }^{6}{t}^{6 }+288\,{\rho }^{14}{\sigma }^{5}{t}^{4}{x}^{2}-1152\,{\rho }^{12}{\sigma } ^{6}{t}^{6}+144\,{\rho }^{12}{\sigma }^{4}{t}^{2}{x}^{4}-960\,{\rho }^{10 }{\sigma }^{5}{t}^{4}{x}^{2}-432\,{\rho }^{12}{\sigma }^{4}{t}^{4}+1536\, {\rho }^{8}{\sigma }^{6}{t}^{6}+24\,{\rho }^{10}{\sigma }^{3}{x}^{6}-96\,{ \rho }^{8}{\sigma }^{4}{t}^{2}{x}^{4}-432\,{\rho }^{10}{\sigma }^{3}{t}^{2 }{x}^{2}+1536\,{\rho }^{6}{\sigma }^{5}{t}^{4}{x}^{2}+1696\,{\rho }^{8}{ \sigma }^{4}{t}^{4}+48\,{\rho }^{6}{\sigma }^{3}{x}^{6}-108\,{\rho }^{8}{ \sigma }^{2}{x}^{4}+384\,{\rho }^{4}{\sigma }^{4}{t}^{2}{x}^{4}+608\,{ \rho }^{6}{\sigma }^{3}{t}^{2}{x}^{2}+228\,{\rho }^{8}{\sigma }^{2}{t}^{2} -1024\,{\rho }^{4}{\sigma }^{4}{t}^{4}-120\,{\rho }^{4}{\sigma }^{2}{x}^{4 }+114\,{\rho }^{6}\sigma \,{x}^{2}+256\,{\rho }^{2}{\sigma }^{3}{t}^{2}{x} ^{2}-248\,{\rho }^{4}{\sigma }^{2}{t}^{2}-60\,{\rho }^{2}\sigma \,{x}^{2}- 9\,{\rho }^{4}+32\,{\sigma }^{2}{t}^{2}+6) /-( \left( 4\,{\rho }^{4}{\sigma }^{2}{t}^{2}+2\,{\rho }^{2}\sigma \,{x}^{2}+ 1 \right) ^{7} )\), which make the meaning of condition with the parameters.

The critical point (x, t) is maximum (peak), as

$$\begin{aligned} \frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}=-96\,{\rho }^{2}\sigma , \quad \hbox {for}\quad \sigma >0, \end{aligned}$$
(17)

and

$$\begin{aligned}&\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t^2}\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}-\left( \frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t \partial x}\right) ^2\nonumber \\&\quad = -\,2048\,{\rho }^{2}{\sigma }^{3} \left( -\,9\,{\rho }^{4}+6 \right) ,\nonumber \\&\qquad \hbox {for}\quad \sigma>0, {\rho }^{4}> \frac{2}{3} \end{aligned}$$
(18)

at point (0, 0). Similarly, two critical points \(\varPsi (x,t)\) are minima (depressions), as

$$\begin{aligned}&\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}=3\,{\rho }^{2}\sigma , \quad \hbox {for} \sigma>0\\&\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t^2}\frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial x^2}-\left( \frac{\partial ^2\left( |\varPsi (x,t)|^2\right) }{\partial t \partial x}\right) ^2\\&\quad =24\rho ^2\sigma ^3,\quad \hbox {for} \quad \sigma >0 \end{aligned}$$

at points \(\left( \pm \frac{1}{2}\,{\frac{\sqrt{6}}{\sqrt{\sigma }\rho }},0\right) \).

Fig. 3
figure 3

(Color online) a 1-order NR solution \(|\varPsi |\) of (19) with \(\gamma (t)=\sin (t)\), \(a(t)=\cos (t)\) and \(d(t)=0.2 \cos (t)\). b\(|\varPsi |\) of (19) with \(\gamma (t)=0.1 \sin (1.5 t)\), \(a(t)=t\) and \(d(t)=5/t\). c\(|\varPsi |\) of (19) with \(\gamma (t)=\sin (t)\), \(a(t)=t\) and \(d(t)=1/t^2\). d\(|\varPsi |\) of (19) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=0.1 \cos (t)\)

Full size image
Fig. 4
figure 4

(Color online) The 1-order NR solution (19) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=0.1 \cos (t)\). a The exact 1-order NR solution (19), b the time evolution of 1-order NR solution without the perturbation, c the time evolution of 1-order NR solution with the small noise perturbation 0.2

Full size image

4 Non-autonomous rational solutions and dynamical behaviors of NGP Eq. (2)

Some dynamics of higher-order rational solitons of the NNLS equation are explained in [19]. However, the non-autonomous rational (NR) solutions of the NGP equation with PT-external potential are not considered. In this section, we derive the non-autonomous 1-order and 2-order rational solutions via similarity method. Based on the similarity method and the solutions of NNLS equation, we obtain the 1-order NR solution of NGP Eq. (2) as following

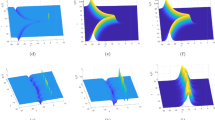
$$\begin{aligned}&\varPsi (x,t)=\rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau - \rho ^2\tau )}}\nonumber \\&\quad \times {\frac{2\,{\rho }^{3} \left( -{\rho }^{2}{\tau }^{2}+ \left( a \left( t \right) \right) ^{2}{x}^{2} \right) +\rho +2\,i{\rho }^{2} \left( 2\,\rho \,\tau +a \left( t \right) x \right) }{2\,{\rho }^{2} \left( -{\rho }^{2}{\tau }^{2}+ \left( a \left( t \right) \right) ^{2}{x}^{2} \right) -1+2\,i\rho \,a \left( t \right) x }}, \nonumber \\&\tau \left( t \right) ={{\int _{0}^{t} \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}}. \end{aligned}$$
(19)

The 1-order NR solution of NGP Eq. (2) exists the multi-peaks in Fig. 3. Furthermore, we study the dynamics of the 1-order NR solution and find that there are two peaks in local field through managing the nonlinear functions in Fig. 3b.

In this section, we consider some dynamical behaviors of the 1-order NR solution (19) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=0.1 \cos (t)\) in Fig. 4. Figure 4a describes the exact 1-order NR solution (19), Fig. 4b illustrates the time evolution of 1-order NR solution without the perturbation, and Fig. 4c illustrates the time evolution of 1-order NR solution with the small noise perturbation 0.2. We can note that the 1-order NR solution is almost stable in the time propagation in Fig. 4c.

In particular, we next will consider three kinds of 2-order NR solutions of NGP Eq. (2) in the different cases.

Case I The first 2-order NR solution of NGP Eq. (2) is given rise to

$$\begin{aligned} \varPsi (x,t)= \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau - \rho ^2\tau )}}\left( -\frac{G_1}{F_1}\right) , \end{aligned}$$
(20)

with \(G_1=16\,{\eta }^{6}-24\,{\eta }^{4}-144\,{\eta }^{2}-16\,{\tau }^{6}+48\,{\tau }^{3}+120\,{\tau }^{4}+144\,{\tau }^{2}-9+72\,i+48\,i{\eta }^{5}+72\,i{ \eta }^{3}-180\,i \left( \eta \right) -144\,i{\eta }^{2}+96\,i{\tau }^{5} +96\,i{\tau }^{3}-144\,i{\tau }^{2}+144\,{\eta }^{2} \left( \tau \right) -48\,{\eta }^{4}{\tau }^{2}+48\,{\tau }^{4}{\eta }^{2}-192\,{\eta }^{3} \left( \tau \right) -288\,{\eta }^{2}{\tau }^{2}+192\, \left( \eta \right) \,{\tau }^{3}+144\, \left( \eta \right) \, \left( \tau \right) +144\,i \left( \eta \right) \, \left( \tau \right) +48\,i \left( \eta \right) \,{\tau }^{4}-192\,i{\eta }^{2}{\tau }^{3}+96\,i{ \eta }^{4} \left( \tau \right) -\,216\,i \left( \eta \right) \,{\tau }^{2} -\,96\,i{\eta }^{3}{\tau }^{2}-72\,\tau +144\,\eta ,\) and \(F_1=144\,i \left( \eta \right) \,{\tau }^{2}+36\,i \left( \eta \right) +48 \,i \left( \eta \right) \,{\tau }^{4}-81+48\,i-96\,i{\eta }^{3}{\tau }^{2 }+144\,i \left( \eta \right) \, \left( \tau \right) -72\,i{\tau }^{3} \left( \eta \right) +144\,{\eta }^{2} \left( \tau \right) +48\,{\tau }^ {3}-48\,{\eta }^{4}{\tau }^{2}+48\,{\tau }^{4}{\eta }^{2}-144\,{\tau }^{2}+ 72\,\tau -24\,i{\eta }^{3}+{\eta }^{5}-16\,{\tau }^{6}+16\,{\eta }^{6}-72\, {\eta }^{4}-120\,{\tau }^{4}\), \( \eta (x,t)=a(t) x, \tau \left( t \right) ={{\int _{0}^{t} \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}}.\)

Case II The second 2-order NR solution of NGP Eq. (2) is obtained as following

$$\begin{aligned} \varPsi (x,t)= \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau - \rho ^2\tau )}}\left( -\frac{G_2}{F_2}\right) , \end{aligned}$$
(21)

with \(G_2= -16\,{\tau }^{6}+48\,{\tau }^{3}+120\,{\tau }^{4}+216\,{\tau }^{2}+16\,{ \eta }^{6}-24\,{\eta }^{4}-72\,{\eta }^{2}+96\,i{\eta }^{4} \left( \tau \right) +144\,i \left( \eta \right) \, \left( \tau \right) -360\,i{ \tau }^{2} \left( \eta \right) -45+72\,i+24\,i{\eta }^{3}+48\,i{\eta }^{5 }-144\,i{\eta }^{2}-36\,i \left( \eta \right) +96\,i{\tau }^{5}+96\,i{ \tau }^{3}-144\,i{\tau }^{2}-144\,i \left( \tau \right) +144\,{\eta }^{2} \left( \tau \right) -48\,{\eta }^{4}{\tau }^{2}+48\,{\tau }^{4}{\eta }^{2 }-192\,{\eta }^{3} \left( \tau \right) -288\,{\eta }^{2}{\tau }^{2}+192\, \left( \eta \right) \,{\tau }^{3}-144\, \left( \eta \right) \, \left( \tau \right) -192\,i{\eta }^{2}{\tau }^{3}+48\,i \left( \eta \right) \,{ \tau }^{4}-96\,i{\eta }^{3}{\tau }^{2}-72\,\tau +144\,\eta \), and \(F_2=-45+48\,i+48\,i \left( \eta \right) \,{\tau }^{4}-72\,i{\eta }^{3}+36\,i \left( \eta \right) -96\,i{\eta }^{3}{\tau }^{2}-72\,i{\tau }^{3} \left( \eta \right) +144\,{\eta }^{2} \left( \tau \right) +48\,{\tau }^ {3}-48\,{\eta }^{4}{\tau }^{2}+48\,{\tau }^{4}{\eta }^{2}+72\,\tau +144\,i \left( \eta \right) \, \left( \tau \right) +{\eta }^{5}-16\,{\tau }^{6} +16\,{\eta }^{6}-72\,{\eta }^{4}-120\,{\tau }^{4}+72\,{\eta }^{2}-72\,{ \tau }^{2} \), \( \eta (x,t)=a(t) x, \tau \left( t \right) ={{\int _{0}^{t} \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}}.\)

Case III The third 2-order NR solution of NGP Eq. (2) is derived as following

$$\begin{aligned} \varPsi (x,t)= \rho \,{\mathrm{e}^{-\int _{0}^{t}\!r \left( s \right) \,\mathrm{d}s}} {\mathrm{e}^{-i(\omega \,\tau - \rho ^2\tau )}}\left( -\frac{G_3}{F_3}\right) \end{aligned}$$
(22)

with \(G_3= 27+72\,i{\eta }^{3}+48\,i \left( \eta \right) \,{\tau }^{4}-192\,i{\eta } ^{2}{\tau }^{3}+48\,i{\eta }^{5}+96\,i{\tau }^{5}-216\,i \left( \eta \right) \,{\tau }^{2}+96\,i{\tau }^{3}+96\,i{\eta }^{4} \left( \tau \right) -96\,i{\eta }^{3}{\tau }^{2}-180\,i \left( \eta \right) -48\,{ \eta }^{4}{\tau }^{2}+48\,{\tau }^{4}{\eta }^{2}-192\,{\eta }^{3} \left( \tau \right) -288\,{\eta }^{2}{\tau }^{2}+192\, \left( \eta \right) \,{ \tau }^{3}+144\, \left( \eta \right) \, \left( \tau \right) -16\,{\tau } ^{6}+16\,{\eta }^{6}-24\,{\eta }^{4}+120\,{\tau }^{4}-144\,{\eta }^{2}+144 \,{\tau }^{2}\), and \(F_3=36\,i \left( \eta \right) -72\,i{\tau }^{3} \left( \eta \right) -24\,i{ \eta }^{3}-45+48\,i+144\,i \left( \eta \right) \,{\tau }^{2}-96\,i{\eta } ^{3}{\tau }^{2}+48\,i \left( \eta \right) \,{\tau }^{4}-48\,{\eta }^{4}{ \tau }^{2}+48\,{\tau }^{4}{\eta }^{2}-144\,{\tau }^{2}+{\eta }^{5}-16\,{ \tau }^{6}+16\,{\eta }^{6}-72\,{\eta }^{4}-120\,{\tau }^{4}\), \( \eta (x,t)=a(t) x, \tau \left( t \right) ={{\int _{0}^{t} \left( a \left( s \right) \right) ^{3}\,\mathrm{d}s}}.\)

Fig. 5
figure 5

(Color online) a 2-order NR solution \(|\varPsi |\) of (20) with \(\gamma (t)=0.1 \sin (t)\), \(a(t)=t^2\) and \(d(t)=1/t^4\). b\(|\varPsi |\) of (21) with \(\gamma (t)=0.1 \sin (t)\), \(a(t)=t^2\) and \(d(t)=1/t^4\). c\(|\varPsi |\) of (22) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=1\). d\(|\varPsi |\) of (22) with \(\gamma (t)=0.1 \hbox {Jacobi}SN(2t, 1)\), \(a(t)=t\) and \(d(t)=1/t^2\)

Full size image

The 2-order NR solutions (20)–(22) of NGP Eq. (2) are shown in Fig. 5. The 2-order NR soliton exhibits the strong interaction in Fig. 5a. And, the 2-order NR soliton is split into the interactions of multi-bright solitons and two dark solitons in Fig. 5b, which are multi-bright solitons and multi-dark solitons happened at the same time. It is interesting to note that the 2-order NR solution has the strong interaction on the hill in Fig. 5d.

Fig. 6
figure 6

(Color online) The 2-order NR solution (20) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=0.1 \cos (t)\). a The exact 2-order NR solution (20), b the time evolution of 2-order NR solution without the perturbation, c the time evolution of 2-order NR solution with the noise perturbation 0.2

Full size image

We also consider the dynamical behaviors of the 2-order NR solution (20) with \(\gamma (t)=0\), \(a(t)=1\) and \(d(t)=0.1 \cos (t)\) in Fig. 6. Figure 6a describes the exact 2-order NR solution (20), Fig. 6b illustrates the time evolution of 2-order NR solution without the perturbation, and Fig. 6c illustrates the time evolution of 2-order NR solution with the small noise perturbation 0.2. We can find that the 2-order NR solution is almost unstable in the time propagation in Fig. 6c.

A ‘mild’ modulation instability (MI) can permit a readily observable NR solution, while a ‘strong’ MI can ‘overwhelm’ or ‘mask’ the development. When the MI effect is weak, a NR solution can be readily observed (Figs. 4c, 6c). We have presented a bright soliton solution of NGP equation with external potential in Fig. 3d. Moreover, the stability of the obtained analytical soliton solution is investigated by using numerical simulations and the stable solution is found in a broad range of parameter. The evolution of the amplitude Fig. 4c with the background noise of 0.2 is shown, we can find that the formation of a NR solution with almost no influence from the background of modulation instability. It is observed from Fig. 4c that the bright exact solution (19) is dynamically stable with the choosing parameters. In addition, we can find that the phase noise regime of the stable solution is larger than the usual soliton solution through appropriately adjusting the free parameters and analyzing the phase noise, respectively.

5 Conclusions

We studied the GNNH equation with variable coefficients and NGP equation with the self-induced PT-symmetric potential by using similarity reduction, Hirota method and Darboux transformation. Furthermore, we obtained some NB solutions, NRW solutions and NR solutions of GNNH equation, which are different from the solutions of some local nonlinear equations. The trajectories of peaks and depressions of the non-autonomous rogue waves were produced by means of analytical method, and the dynamical stabilities of the NR solution were derived through the numerical method. We derived the multi-bright solitons and multi-dark solitons happened at the same time, which is interesting to note that a 2-order NR solution with the strong interaction on the hill. In particular, some trajectories of motion of peaks and depressions of the 1- and 2-order NRWs were produced through the analytical and numerical methods. The obtained different results might be useful to explain the corresponding wave phenomena in nonlocal wave models. In the next research work, we will further consider the coupled soliton equation with the self-induced PT-symmetric potential and derive some novel rational solutions. Furthermore, the stabilities and dynamics of the solutions will be tested through the numerical method.