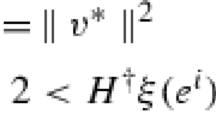1 Introduction

The study of fractional calculus allows considering a wider class of dynamical systems with more varied memory properties [1,2,3]. Fractional-order tools have been considered for designing flexible and precise control tools [4, 5].

In recent years, the study of dynamical systems with distributed-order dynamics has been considered as a natural generalisation of integer- and fractional-order systems, providing novel methodologies for preciser modelling and understanding of complex physical and engineering phenomena [6, 7], such as complex dynamics with multi-scale and non-local memory effects [8]. Inspiring studies on distributed-order systems consider the modelling of diffusion processes with slow [9,10,11,12] and ultra slow [13, 14] dynamics. Distributed-order models have been also employed in describing the dynamics of rheological materials [15, 16], viscoelastic effects [17], among other outstanding applications [18,19,20,21,22].

Distributed-order derivatives can be related to physical properties of dynamical systems that are composed of differential elements with different orders [9]. Dynamical systems with distributed-order dynamics are considerably more complicated than their integer- or fractional-order counterparts, and only few techniques are available for analysing a limited class of distributed-order systems [19, 20, 23, 24]. Thus, the stability analysis of a more general class of distributed-order systems remains as a major interest. Lyapunov-like methods for analysing stability in distributed-order systems is studied in the pioneer works [25, 26].

Even if outstanding contributions have been made in the field of distributed-order systems, at the present day, predefined-time convergence in distributed-order systems, such that, the solution of a distributed-order differential equation converges before a time that is predefined in advance, remains as an open problem. The predefined-time stability concept was proposed in [27, 28], studying a class of dynamical systems whose solutions converge within an arbitrary fixed-time, which is independent of the system initial conditions [29, 30]. In addition, the time of convergence is prescribed during the controller design. Fixed-time controllers for fractional-order systems have been proposed in [31,32,33]; and through the dynamic extension method of [34,35,36], first- and second-order predefined-time controllers for some general classes of fractional-order systems were proposed in [37, 38].

In contrast to the discussed pioneer works, the contributions of this paper can be stated as follows: Contribution A robust controller that enforces predefined-time convergence in distributed-order system. In addition, a predefined-time sliding mode design for the control of uncertain distributed-order system is also proposed.

The main difficulty in the control of distributed-order systems is that these systems can be recognised by their slow and ultra slow dynamics. Thereby, a way to induce fast convergence constitutes a major challenge. By extending the method of [34,35,36] to the case of distributed-order systems, exponential, finite- and fixed-time, and even predefined-time techniques can be deemed to obtain faster responses, in the latter case, imposing a convergence time with a prescribed upper bound, which provides a greater certainty about the dynamics of the closed-loop system.

The rest of this paper is organised as follows. Next Section presents the fundamentals on conventional fractional- and distributed-order calculus. Section 3 presents the design of the distributed-order nonlinear controller. Section 4 presents numerical results based on simulations. Finally, Section 5 discusses the main conclusion.

2 Fundamentals

2.1 On predefined-time stability

For the sake of completeness, some useful results on predefined-time stability of integer-order systems are presented below.

Consider the integer-order dynamical system

$$\begin{aligned} \dot{{{\varvec{x}}}}(t) = {\varvec{f}}(t, {\varvec{x}}(t)) \end{aligned}$$
(1)

where \({\varvec{x}}\in {\mathbb {R}}^n\) is the state, and \(t\in {\mathbb {R}}_{\ge 0} [0,\infty )\) is the time. The function \({\varvec{f}}:{\mathbb {R}}_{\ge 0} \times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) can be nonlinear, with \({\varvec{f}}(t,{\varvec{0}})={{\varvec{0}}}\). The following definitions are of interest.

Definition 1

(Finite-time stability [39]): The origin of (1) is finite-time stable if it is asymptotically stable, and any solution \({\varvec{x}}(t)\) of (1) reaches the origin at some finite time, this is, \({\varvec{x}}(t)={0} ~ \forall t\ge T({\varvec{x}}(0))\), where \(T:{\mathbb {R}}^n\rightarrow {\mathbb {R}}_{\ge 0}\) is the settling-time function.

Definition 2

(Fixed-time stability [29]): The origin of system (1) is fixed-time stable if it is finite-time stable and the settling-time function is bounded, i.e., \(\exists T_{\text {max}}>0~:~T({\varvec{x}}(0))\le T_{\text {max}}, ~\forall {\varvec{x}}(0)\in {\mathbb {R}}^n\).

Definition 3

(Predefined-time stability [27]): For a predefined-time constant \(T_c>0\), the origin of system (1) is predefined-time stable if it is fixed-time stable and the settling-time function fulfils

$$\begin{aligned}T({\varvec{x}}(0))\le T_c, \quad \forall {\varvec{x}}(0)\in {\mathbb {R}}^n,\end{aligned}$$

where \(T_c\) is called a predefined time.

2.2 On fractional-order calculus

Fractional calculus studies differentiation and integration of fractional order. For the real-valued vector function \({{\varvec{x}}}:\varOmega _t\rightarrow {\mathbb {R}}^n\), with \(\varOmega _t\subset {\mathbb {R}}\) a closed and bounded time-interval, the following operators are defined [40]:

  • Riemann-Liouville integral

    $$\begin{aligned} {\mathscr {I}}^{\alpha }{{\varvec{x}}}(t) = \frac{1}{\varGamma (\alpha )}\int _{0}^{t} (t-\tau )^{\alpha -1} {{\varvec{x}}}(\tau )d\tau \end{aligned}$$

  • Caputo derivative

    $$\begin{aligned} {\mathscr {D}}^{\alpha }{{\varvec{x}}}(t)= & {} {\mathscr {I}}^{\alpha }\frac{d}{dt}{{\varvec{x}}}(t) \end{aligned}$$

for \(\alpha \in (0,1)\) the fractional-order, where \(\varGamma (x)=\int _{0}^{\infty }z^{x-1}e^{-z}dz\) is the Gamma function.

The two-parameters Mittag–Leffler function is considered [40],

$$\begin{aligned} E_{\alpha ,\beta }(z) = \sum _{k=0}^\infty \frac{z^k}{\varGamma (\alpha k +\beta )} \end{aligned}$$

for \(\alpha ,\beta \in {\mathbb {R}}\). Note that, for the case of \(\beta =1\), one recovers the one-parameter Mittag–Leffler function, this is, \(E_{\alpha ,1}(z) = E_{\alpha }(z)\), and for \(\alpha = \beta = 1\), one has that \(e^z = E_{1,1}(z)\).

The following definition of [41, 42] is of interest.

Definition 4

The solution of \({\mathscr {D}}^\alpha {{\varvec{x}}}(t) = {{\varvec{f}}}(t,{{\varvec{x}}}(t))\) is Mittag–Leffler stable if \(\left\| {{\varvec{x}}}(t)\right\| \le \left\{ m({{\varvec{x}}}(0)) E_\beta (-\gamma t^\beta ) \right\} ^b\) for all \(t\ge 0\), where \(m({{\varvec{x}}})\ge 0\) is a locally Lipschitz continuous function on \({{\varvec{x}}}\) with \(m({{\varvec{0}}}) = 0\), \(\gamma>0,~b>0\) and \(\beta \in (0,1)\) some constants.

Remark 1

In [43], it is demonstrated that, for a continuous function x(t), with \(x(0) \ne 0\), which complies to \(x(t) = 0\) for all \(t\ge t_f\), for some finite time \(t_f>0\), the invariant \({\mathscr {D}}^\alpha x(t) = 0\), for arbitrary \(\alpha \in (0,1)\), cannot be enforced in finite-time. The above implies that, it is not possible for system \({\mathscr {D}}^\alpha x(t) = f(t,x(t))\) to possess finite-time stable equilibria. Therefore, on the one hand, as demonstrated in [44], for a continuous function f(t, x(t)), with \(f(t,0) = 0\) for all \(t\ge 0\), the invariant \(x(t) = 0\) cannot be enforced in finite-time. On the other hand, if the invariant \(x(t)=0\) is enforced in finite-time, the origin \(x^* = 0\) is not an equilibrium of \({\mathscr {D}}^\alpha x(t) = f(t,x(t))\). Thus, it is not possible to induce finite-time stable equilibria in fractional-order systems, rather to induce finite-time convergence of their solutions.

2.3 On distributed-order calculus

The distributed-order derivative in the Caputo sense of an integer-order differentiable function f(t), with respect to an order density function (weight function) \(c(\alpha ) \ge 0\), and \(\alpha \in [0,1]\), is defined as

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} f(t) = \int _0^1 c(\alpha ) {\mathscr {D}}^{\alpha } f(t) d\alpha , \end{aligned}$$
(3)

where \(c(\alpha )\) is the distribution function. In this paper one considers only distributed functions that satisfy \(c(\alpha )>0\) for some values of \(\alpha \in [0,1]\) and zero otherwise.

The Laplace transform of (3) is determined in [25].

Proposition 1

Let f(t) be an integer-order differentiable function such that \({\mathscr {D}}^{c(\alpha )} f(t)\) exists for all \(\alpha \in (0,1)\) at which \(c(\alpha )>0\). Then

$$\begin{aligned} {\mathscr {L}}\bigg \{{\mathscr {D}}^{c(\alpha )} f(t) \bigg \} = C_\alpha (s) F(s) - \frac{1}{s} C_\alpha (s) f(0) \end{aligned}$$

with \(C_\alpha (s) = \int _0^1 c(\alpha ) s^{\alpha } d\alpha \).

A generalisation of the Mittag-Leffler function to the distributed-order case is considered as follows to allow a cleaner presentation [25, 26]:

Definition 5

Consider the following function

$$\begin{aligned} {\mathcal {G}}_{\beta }^\gamma (t;c(\alpha )) = {\mathscr {L}}^{-1}\bigg \{ \frac{C_\alpha (s)}{s^\beta [C_\alpha (s) + \gamma ]} \bigg \} \end{aligned}$$

for \(\alpha \in [0,1]\) and \(\beta ,\gamma \in {\mathbb {C}}\); and \({\mathcal {G}}^\gamma (t;c(\alpha )) = {\mathcal {G}}_{1}^\gamma (t;c(\alpha ))\).

Note that, for the special case of \(c(\alpha ) = \delta (\alpha -\alpha _1)\) with \(\alpha _1\in (0,1)\), and \(\delta (\cdot )\) the Dirac’s delta function, one has that \(C_\alpha (s) = \int _0^1\delta (\alpha -\alpha _1)s^\alpha d\alpha = s^{\alpha _1}\), and one has that \( {\mathcal {G}}_{\beta }^\gamma (t;c(\alpha )) = {\mathscr {L}}^{-1}\bigg \{ \frac{ s^{\alpha _1-\beta }}{s^{\alpha _1} + \gamma } \bigg \} = t^{\beta -1}E_{\alpha _1,\beta }(-\gamma t^{\alpha _1})\). An interesting property of \({\mathcal {G}}_{\beta }^\gamma (t;c(\alpha ))\) is discussed below.

Proposition 2

Consider the generalised function \({\mathcal {G}}^\gamma (t;c(\alpha ))\), with \(c(\alpha )> 0\) for some values \(\alpha \in [0,1]\) and zero otherwise, such that \(C_\alpha (s)+\gamma = 0\) has all its roots in the open left-half complex plane for all \(\gamma > 0\), and \(C_\alpha (s)\rightarrow 0\) when \(s\rightarrow 0\). Then \({\mathcal {G}}^\gamma (t;c(\alpha ))\rightarrow 0\) when \(t\rightarrow \infty \)

Proof

Using the Final Value Theorem [23, 24], one has that

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty } {\mathcal {G}}^\gamma (t;c(\alpha ))&= \lim _{s\rightarrow 0} s \frac{C_\alpha (s)}{s[C_\alpha (s) + \gamma ]}\\&= \lim _{s\rightarrow 0} \frac{C_\alpha (s)}{C_\alpha (s) + \gamma } = 0 \end{aligned} \end{aligned}$$

and the proof is complete. \(\square \)

The Comparison Lemma of [25] is considered for the case of the extended distributed-order operator (3).

Lemma 1

Let x(t) and y(t) be two integer-order differentiable functions. If \({\mathscr {D}}^{c(\alpha )} x(t) \ge {\mathscr {D}}^{c(\alpha )} y(t) \), with \(\alpha \in [0, 1]\) and \(x(0) = y(0)\), and \(c(\alpha )\) such that \({\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha } d\alpha } \right\} \) is a nonnegative function. Then \(x(t) \ge y(t)\) for all \(t\ge 0\).

2.4 On distributed-order systems

Consider the distributed-order system

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{x}}}(t) = {{\varvec{f}}}(t,{{\varvec{x}}}(t)) \end{aligned}$$
(4)

with \({{\varvec{x}}}\) and integer-order differentiable function, \({{\varvec{f}}}(t,{{\varvec{x}}}(t))\) a Lipschitz continuous function in t and \({\varvec{x}}\), and \(C_\alpha (s) = \int _0^1 c(\alpha )s^\alpha d\alpha \ne 0\).

Definition 6

The solution of the distributed-order system (4) is \({\mathcal {G}}\)–stable if \(\left\| {{\varvec{x}}}(t)\right\| \le \left\{ m({{\varvec{x}}}(0)) {\mathcal {G}}^\gamma (t;c(\alpha )) \right\} ^b\) for all \(t\ge 0\), where \(m({{\varvec{x}}})\ge 0\) is a locally Lipschitz continuous function on \({{\varvec{x}}}\), with \(m({{\varvec{0}}}) = 0\), \(\gamma >0\), \(b>0\), and \(c(\alpha )> 0\) for some values \(\alpha \in [0,1]\) and zero otherwise, such that \({\mathcal {G}}^\gamma (t;c(\alpha ))\rightarrow 0\) as \(t\rightarrow \infty \).

The stability conditions for the distributed-order system (4) are analysed below.

The stability of fractional-order systems is analysed in [45] by means of proximal subdifferentials and subgradients of convex functions, [46, 47]. Thus, the following definitions are needed:

Definition 7

The function \(V:\varOmega \subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is convex if \(\varOmega \) is convex and \(\forall {{\varvec{x}}},{{\varvec{y}}}\in \varOmega \), the following inequality holds for all \(\lambda \in [0,1]\):

$$\begin{aligned} V(\lambda {{\varvec{x}}} + (1-\lambda ){{\varvec{y}}}) \le \lambda V({{\varvec{x}}}) + (1-\lambda )V({{\varvec{y}}}). \end{aligned}$$

In addition, function V is concave if \(-V\) is convex.

In contrast to smooth convex functions, consider the following [46, 47]:

Definition 8

Let \(V:\varOmega \subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}\) be a convex function. For any \({{\varvec{y}}}\in \varOmega \), the set-valued map

$$\begin{aligned} \partial V({{\varvec{x}}}) = \left\{ {{\varvec{\zeta }}}\in {\mathbb {R}}^n:~ V({{\varvec{y}}}) - V({{\varvec{x}}}) - {{\varvec{\zeta }}}^{T} ({{\varvec{y}}} - {{\varvec{x}}}) \ge 0 \right\} \nonumber \\ \end{aligned}$$
(5)

is the proximal subdifferential of V at \({{\varvec{x}}}\in \varOmega \), and \({{\varvec{\zeta }}}({{\varvec{x}}})\in \partial V({{\varvec{x}}})\) is a proximal subgradient of V at \({{\varvec{x}}}\).

If V is differentiable at \({{\varvec{x}}}\), then \(\partial V({{\varvec{x}}}) = \{\nabla V({{\varvec{x}}})\}\), thus, (5) becomes

$$\begin{aligned} V({{\varvec{y}}}) - V({{\varvec{x}}}) - \nabla V({{\varvec{x}}})^{T} ({{\varvec{y}}} - {{\varvec{x}}}) \ge 0. \end{aligned}$$

Lemma 2

Let \(V({{\varvec{x}}}(t))\) be a real-valued function that is Lipschitz continuous on \({{\varvec{x}}}\), with convex domain \(\varOmega \subseteq \mathbb R^n\), and let \({{\varvec{x}}}\in \varOmega \) be a real-valued-vector function and integer-order differentiable function, with \(c(\alpha )\ge 0\) for all \(\alpha \in [0,1]\). If \(V({{\varvec{x}}}(t))\) is convex, then the following holds:

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) \le \inf _{{{\varvec{\zeta }}}({{\varvec{x}}})\in \partial V({{\varvec{x}}})} {{\varvec{\zeta }}}({{\varvec{x}}}(t))^{T} \ {\mathscr {D}}^{c(\alpha )}{{\varvec{x}}}(t). \end{aligned}$$
(6)

Proof

From Lemma 10 of [45], one has that

$$\begin{aligned} {\mathscr {D}}^\alpha V({{\varvec{x}}}(t)) \le \inf _{{{\varvec{\zeta }}}({{\varvec{x}}})\in \partial V({{\varvec{x}}})} {{\varvec{\zeta }}}({{\varvec{x}}}(t))^{T} ~{\mathscr {D}}^\alpha {{\varvec{x}}}(t). \end{aligned}$$

Then, multiplying both sides by the nonnegative function \(c(\alpha )\), and integrating from 0 to 1 one has that

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) \le \inf _{{{\varvec{\zeta }}}({{\varvec{x}}})\in \partial V({{\varvec{x}}})} {{\varvec{\zeta }}}({{\varvec{x}}}(t))^{T} ~{\mathscr {D}}^{c(\alpha )}{{\varvec{x}}}(t) \end{aligned}$$

since the integration is conducted with respect to \(\alpha \). \(\square \)

Theorem 1

Consider the dynamical system

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{x}}}(t) = {{\varvec{f}}}(t,{{\varvec{x}}}(t)), \end{aligned}$$

with \(c(\alpha )> 0\) for some values \(\alpha \in [0,1]\) and zero otherwise, such that \(C_\alpha (s) = \int _0^1 c(\alpha ) s^{\alpha } d\alpha \ne 0\), \({\mathscr {L}}^{-1} \left\{ \frac{1}{C_\alpha (s)+\gamma } \right\} \ge 0\) for arbitrary \(\gamma \ge 0\), the roots of \(C_\alpha (s) + \gamma = 0\) are located in the open left-half complex plane for arbitrary \(\gamma > 0\), and \(C_\alpha (s)\rightarrow 0\) when \(s\rightarrow 0\). If

$$\begin{aligned} {{\varvec{\zeta }}}({{\varvec{x}}}(t))^{T} \ {\mathscr {D}}^{c(\alpha )}{{\varvec{x}}}(t) \le -\gamma \left\| {{\varvec{x}}}(t) \right\| ^{qb} \end{aligned}$$

for arbitrary \(b\ge 1\), almost all \(t\ge 0\), some \(\gamma >0\) and \(q\in (0,1]\), and \({{\varvec{\zeta }}}({{\varvec{x}}})\in \partial \left\| {{\varvec{x}}}(t) \right\| ^{b}\), then \({{\varvec{x}}}(t)\) is \({\mathcal {G}}\)-stable.

Proof

Let \(V({{\varvec{x}}}(t)) = \left\| {{\varvec{x}}}(t) \right\| ^b\). The case of \({\varvec{x}}(0) = {{\varvec{0}}}\) is straightforward; then, without loss of generality consider \({\varvec{x}}(0) \ne {{\varvec{0}}}\). The inequality (6) implies that

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) \le -\gamma V({{\varvec{x}}}(t))^q \le 0 \end{aligned}$$

Then \({\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) \le 0 = {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(0))\) since \(V({{\varvec{x}}}(0))\) is a constant. Thus, one has that

$$\begin{aligned} V({{\varvec{x}}}(t)) \le V({{\varvec{x}}}(0)) \quad \text{ for } \text{ all } \quad t\ge 0 \end{aligned}$$

by virtue of the distributed-order comparison principle. Therefore, it results that \(0\le [{V({{\varvec{x}}}(t))}/{V({{\varvec{x}}}(0))}] \le 1\), whereby

$$\begin{aligned} \frac{V({{\varvec{x}}}(t))^q}{V({{\varvec{x}}}(0))^q} \ge \frac{V({{\varvec{x}}}(t))}{V({{\varvec{x}}}(0))}, \end{aligned}$$

or equivalently \(V({{\varvec{x}}}(t))^q \ge V({{\varvec{x}}}(0))^{q-1} V({{\varvec{x}}}(t))\), which leads to

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) \le -{\bar{\gamma }} V({{\varvec{x}}}(t)), \end{aligned}$$

for \({\bar{\gamma }} = \gamma V({{\varvec{x}}}(0))^{q-1}\).

Considering the function \(m(t)\ge 0\), such that

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V({{\varvec{x}}}(t)) = -{\bar{\gamma }} V({{\varvec{x}}}(t)) - m(t), \end{aligned}$$

by taking the Laplace transform, one has that

$$\begin{aligned} C_\alpha (s) {{\hat{V}}}(s) - \frac{1}{s} C_\alpha (s) V({{\varvec{x}}}(0)) = -{\bar{\gamma }} {{\hat{V}}}(s) - M(s) \end{aligned}$$

for \({{\hat{V}}}(s) = {\mathscr {L}}\{V({{\varvec{x}}}(t))\}\) and \(M(s) = {\mathscr {L}}\{ m(t) \}\), or equivalently

$$\begin{aligned} {{\hat{V}}}(s)= \frac{C_\alpha (s)V({{\varvec{x}}}(0))}{s\left[ C_\alpha (s) + {\bar{\gamma }}\right] } - \frac{M(s)}{C_\alpha (s) + {\bar{\gamma }}}. \end{aligned}$$

Then, taking the inverse Laplace transform, one gets

$$\begin{aligned} \begin{aligned}&V(t) = {\mathscr {L}}^{-1}\bigg \{\frac{C_\alpha (s)}{s\left[ C_\alpha (s) + {\bar{\gamma }}\right] }\bigg \}V({{\varvec{x}}}(0)\\&\qquad + {\mathscr {L}}^{-1}\bigg \{\frac{M(s)}{C_\alpha (s) + {\bar{\gamma }}}\bigg \} \\&\quad = V({{\varvec{x}}}(0)) {\mathcal {G}}^{{\bar{\gamma }}}(t;c(\alpha ))- m(t) *{\mathscr {L}}^{-1}\bigg \{\frac{1}{C_\alpha (s) + {\bar{\gamma }}}\bigg \}\\&\quad \le V({{\varvec{x}}}(0)) {\mathcal {G}}^{{\bar{\gamma }}}(t;c(\alpha )). \end{aligned} \end{aligned}$$

Therefore \( \left\| {{\varvec{x}}}(t) \right\| = \bigg [ \left\| {{\varvec{x}}}(0) \right\| ^b {\mathcal {G}}^{{\bar{\gamma }}}(t;c(\alpha )) \bigg ]^{1/b}\). \(\square \)

The integer-order dynamics of the distributed-order system (4) can be inferred by means of the following result.

Theorem 2

For system (4) one has that

$$\begin{aligned} \dot{{{\varvec{x}}}}(t) = {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *f(t,{{\varvec{x}}}(t)) \end{aligned}$$

for \(*\) the convolution operator.

Proof

Taking the Laplace transform of (4) one has that

$$\begin{aligned} C_\alpha (s) {{\varvec{X}}}(s) - \frac{1}{s} C_\alpha (s) {{\varvec{x}}}(0) = {\mathscr {L}}\{ {{\varvec{f}}}(t,{{\varvec{x}}}(t)) \} \end{aligned}$$

or equivalently

$$\begin{aligned} s{{\varvec{X}}}(s) - {{\varvec{x}}}(0) = \frac{s}{C_\alpha (s)} {\mathscr {L}}\{ {{\varvec{f}}}(t,{{\varvec{x}}}(t)) \}, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} {\mathscr {L}}\{ \dot{{\varvec{x}}}(t) \} = \frac{s}{C_\alpha (s)} {\mathscr {L}}\{ {{\varvec{f}}}(t,{{\varvec{x}}}(t)) \}. \end{aligned}$$

Thus, taking the inverse Laplace transform of the above expression, it results

$$\begin{aligned} \dot{{{\varvec{x}}}}(t) = {\mathscr {L}}^{-1} \left\{ \frac{s}{\int _0^1 c(\alpha ) s^{\alpha } d\alpha } \right\} *f(t,{{\varvec{x}}}(t)) \end{aligned}$$

completing the proof. \(\square \)

3 Predefined-time control of distributed-order systems

3.1 Predefined-time robust control of distributed-order systems

Consider the distributed-order dynamical system

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{x}}}(t) = {{\varvec{u}}}(t) + {{\varvec{d}}}(t,{\varvec{x}}(t)) \end{aligned}$$
(7)

where \({\varvec{x}}\in {\mathbb {R}}^n\) is the pseudo-state, \({\varvec{d}}\) is a vector that condenses the effect of disturbances and uncertainties, with \(c(\alpha )> 0\) for some \(\alpha \in [0,1]\) and zero otherwise, such that \({\mathscr {L}}^{-1} \left\{ \frac{1}{C_\alpha (s)+\gamma } \right\} \ge 0\) for all \(\gamma \ge 0\), the roots of \(C_\alpha (s) + \gamma = 0\) are located on the open left-half of the complex plane for arbitrary \(\gamma > 0\), and \(C_\alpha (s)\rightarrow 0\) when \(s\rightarrow 0\). The predefined-time control of (7) is discussed in the following main result.

Theorem 3

Consider the distributed-order dynamical system (7), such that \({{\varvec{x}}}(t)\) is a real-valued vector and integer-order time differentiable function, and the controller

$$\begin{aligned} \begin{aligned} {{\varvec{u}}}(t)&= {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *{{\varvec{v}}}(t) \\ {{\varvec{v}}}(t)&= - \frac{\pi }{2 q T_c} \left( \lfloor {{\varvec{x}}}(t) \rceil ^{1-q} + \lfloor {{\varvec{x}}}(t) \rceil ^{1+q}\right) - \kappa \lfloor {{\varvec{x}}}(t) \rceil ^0 \end{aligned} \end{aligned}$$
(8)

with \(q\in (0,1)\), \(T_c > 0\), \(\lfloor {{\varvec{x}}} \rceil ^r = \bigg [ \lfloor x_1\rceil ^r, \ldots , \lfloor x_n \rceil ^r \bigg ]^{T}\), for \(\lfloor x_i \rceil ^{r} = |x_i|^r \mathrm {sign}(x_i)\) and \(r\in {\mathbb {R}}\), the extended power function; and \(\kappa \ge ||{{\varvec{\psi }}}||\), for

$$\begin{aligned} {{\varvec{\psi }}}(t,{\varvec{x}}(t)) = {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *{{\varvec{d}}}(t,{\varvec{x}}(t)). \end{aligned}$$

Then, the invariant sliding mode \({\varvec{x}}(t)={\varvec{0}}\) is enforced \(\forall t\ge T_c\).

Proof

Using the result of Theorem 2, one has that

$$\begin{aligned} \dot{{\varvec{x}}}(t) = {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *\left[ {{\varvec{u}}}(t) + {{\varvec{d}}}(t,{\varvec{x}}(t)) \right] . \end{aligned}$$

Then, substituting the definition of \({\varvec{u}}\) in (8), the above becomes

$$\begin{aligned} \begin{aligned}&\dot{{\varvec{x}}} = \\&\quad {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *{\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *{{\varvec{v}}}\\&\quad + {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *{{\varvec{d}}}(t,{\varvec{x}}), \end{aligned} \end{aligned}$$

or equivalently, \( \dot{{\varvec{x}}}(t) = {{\varvec{v}}}(t) + {{\varvec{\psi }}}(t,{\varvec{x}}(t)). \) Now, using the definitions of \({{\varvec{v}}}\) and \({{\varvec{\psi }}}\), one has that

$$\begin{aligned} \dot{{\varvec{x}}} = - \frac{\pi }{2 q T_c} \left( \lfloor {{\varvec{x}}} \rceil ^{1-q} + \lfloor {{\varvec{x}}} \rceil ^{1+q}\right) - \kappa \lfloor {{\varvec{x}}} \rceil ^0 + {{\varvec{\psi }}}. \end{aligned}$$

Therefore, considering the i-th component of the above dynamics, one has that

$$\begin{aligned} \dot{{x}}_i(t) = - \frac{\pi }{2 q T_c} \left( \lfloor x_i \rceil ^{1-q} + \lfloor x_i \rceil ^{1+q}\right) - \kappa \lfloor x_i \rceil ^0 + \psi _i. \end{aligned}$$

Besides, consider the candidate Lyapunov function \(V_i = |x_i|\); whereby, one has that

$$\begin{aligned} \begin{aligned} {\dot{V}}_i&= \lfloor x_i \rceil ^0 {\dot{x}}_i\\&= - \frac{\pi }{2 q T_c} \left( |x_i|^{1-q} + |x_i|^{1+q}\right) - \kappa + \lfloor x_i \rceil ^0 \psi _i\\&\le - \frac{\pi }{2 q T_c} \left( {V}_i^{1-q} + {V}_i^{1+q}\right) - \kappa + |\psi _i|\\&\le - \frac{\pi }{2 q T_c} \left( {V}_i^{1-q} + {V}_i^{1+q}\right) . \end{aligned} \end{aligned}$$

Then, using the integer-order Comparison Lemma, one has that \(V_i(t)\le z(t)\), where \(z(0) = V_i(0)\) and

$$\begin{aligned} \dot{z} = - \frac{\pi }{2 q T_c} \left( z^{1-q} + z^{1+q}\right) , \end{aligned}$$

whereby, using \(dz = \dot{z} dt\), one has that

$$\begin{aligned} dt = - \frac{2 q T_c}{\pi }\frac{dz}{z^{1-q} + z^{1+q}}. \end{aligned}$$
(9)

Therefore, the time T(z(0)) (at which \(z(t) = 0\) is enforced) is greater than \(T(x_i(0))\) (the time at which \(V(t) = 0\)), this is, \(T(x_i(0))\le T(z(0))\), which can be computed by integrating (9) from 0 to T(z(0)). Then,

$$\begin{aligned} \begin{aligned} T(z(0))&= \frac{2 q T_c}{\pi }\int _{0}^{z(0)}\frac{dz}{z^{1-q} + z^{1+q}}\\&= \frac{2 q T_c}{\pi }\int _{0}^{z(0)}\frac{z^{q-1} dz}{1 + z^{2q}}.\\ \end{aligned} \end{aligned}$$

Thus, using the change of variable \(\varsigma = z^q\), one has that \(d\varsigma = qz^{q-1}dz\). Hence,

$$\begin{aligned} \begin{aligned} T(z(0))&= \frac{2 T_c}{\pi }\int _{0}^{z^q(0)}\frac{d\varsigma }{1 + \varsigma ^2}\\&= \frac{2 T_c}{\pi }\arctan (z^q(0)) \le T_c \end{aligned} \end{aligned}$$

Therefore \(T(x_i(0))\le T_c\), and since \(x_i\) was an arbitrary component of \({\varvec{x}}\), one has that \({\varvec{x}}(t)={{\varvec{0}}}~\forall t\ge T_c\). \(\square \)

Remark 2

The term \({{\varvec{v}}}(t)\) in (8) admits a more general design [48]. However, for the sake of clarity, this paper only presents a representative case.

3.2 On predefined-time sliding mode control

Consider the distributed-order system

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{x}}}(t) = A {{\varvec{x}}}(t) + B [{{\varvec{u}}}(t) + {{\varvec{d}}} (t,{{\varvec{x}}}(t))] \end{aligned}$$
(10)

where \({{\varvec{x}}} \in {\mathbb {R}}^n\) is the system pseudo-state, \(A \in {\mathbb {R}}^{n \times n}\) and \(B \in {\mathbb {R}}^{n \times m}\) are constant known matrices, with \(m \le n\), \({{\varvec{u}}} \in {\mathbb {R}}^m\) is the control input, \({{\varvec{d}}} \in {\mathbb {R}}^m\) is an unknown matched disturbance, and \(c(\alpha )> 0\) for some \(\alpha \in [0,1]\) and zero otherwise, such that \({\mathscr {L}}^{-1} \left\{ \frac{1}{C_\alpha (s)+\gamma } \right\} \ge 0\) for all \(\gamma \ge 0\), the roots of \(C_\alpha (s) + \gamma = 0\) are located on the open left-half of the complex plane for arbitrary \(\gamma > 0\), and \(C_\alpha (s)\rightarrow 0\) when \(s\rightarrow 0\).

The following additional assumption are considered on system (10).

Assumption 1

The pair (A, B) is controllable.

Assumption 2

The matrix B is full column rank.

Similarly to the integer case [49], the above assumptions imply that there exits an invertible linear transformation \({{\varvec{x}}} \mapsto {{\varvec{z}}}\), defined as \({{\varvec{z}}} = T{{\varvec{x}}}\), where T is an invertible matrix, with

$$\begin{aligned} {{\bar{B}}} = TB = \begin{bmatrix} 0 \\ I \end{bmatrix}. \end{aligned}$$

Therefore, (10) becomes

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{z}}} = {{\bar{A}}} {{\varvec{z}}} + {{\bar{B}}} [ {{\varvec{u}}} + {{\varvec{d}}} ], \end{aligned}$$
(11)

with \({{\bar{A}}} = TAT^{-1}\). In addition, one can rewrite (11) as

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{z}}}_1&= A_{11} {{\varvec{z}}}_1 + A_{12} {{\varvec{z}}}_2 \in {\mathbb {R}}^{n-m}\\ {\mathscr {D}}^{c(\alpha )} {{\varvec{z}}}_2&= A_{21} {{\varvec{z}}}_1 + A_{22} {{\varvec{z}}}_2 + {{\varvec{u}}} + {{\varvec{d}}} ~~~~ \in {\mathbb {R}}^{m}\\ \end{aligned} \end{aligned}$$
(12)

for \({\varvec{z}} = [{\varvec{z}}_1^{T}~~{\varvec{z}}_2^{T}]^{T}\), and \(A_{ij}\) matrices of appropriate dimensions.

It is worth noticing that, since (A, B) is assumed to be controllable, the pair \((A_{11},A_{12})\) is controllable. Therefore, there is some matrix \(\varLambda \in {\mathbb {R}}^{m,n-m}\) such that \({\bar{\varLambda }} = A_{11} - A_{12}\varLambda \) is a Hurwitz matrix.

The problem is the design of \({{\varvec{u}}}\) such that \({{\varvec{x}}} \rightarrow {{\varvec{0}}}\) as \(t\rightarrow \infty \), even in the presence of the matched disturbance \({\varvec{d}}\). Thus, the proposed controller and the closed-loop stability analysis are discussed in the following second main result.

Fig. 1
figure 1

Simulation results: Disturbance-free case, and predefined-time control

Full size image
Fig. 2
figure 2

Simulation results: \({\mathscr {D}}^{c(\alpha )} x(t) = u(t) + d(t)\), with \(x(0)=10\)

Full size image

Theorem 4

Consider the distributed-order dynamical system (12), and the controller

$$\begin{aligned} \begin{aligned} {{\varvec{u}}}(t)&= - (\varLambda A_{11} + A_{21}) {{\varvec{z}}}_1(t) - (\varLambda A_{12} + A_{22}) {{\varvec{z}}}_2(t) \\&\quad \ + {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *{{\varvec{v}}}(t) \\ {{\varvec{v}}}(t)&= - \frac{\pi }{2 q T_c} \left( \lfloor {{\varvec{\sigma }}}(t) \rceil ^{1-q} + \lfloor {{\varvec{\sigma }}}(t) \rceil ^{1+q}\right) - \kappa \lfloor {{\varvec{\sigma }}}(t) \rceil ^0\\ {{\varvec{\sigma }}}(t)&= \varLambda {\varvec{z}}_1(t) + {\varvec{z}}_2(t) \end{aligned} \end{aligned}$$
(13)

with \(\varLambda \in {\mathbb {R}}^{m,n-m}\) a constant feedback matrix gain, such that \({{\bar{\varLambda }}} = A_{11} - A_{12}\varLambda \) is a Hurwitz matrix, \(q\in (0,1)\), \(T_c > 0\), and \(\kappa \ge ||{{\varvec{\psi }}}||\), for \({{\varvec{\psi }}} = {\mathscr {L}}^{-1} \left\{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1} d\alpha } \right\} *{{\varvec{d}}}.\) Then, the invariant sliding mode \({\varvec{\sigma }}(t)={\varvec{0}}\) is enforced \(\forall t\ge T_c\), and consequently \({\varvec{x}}(t)\rightarrow {\varvec{0}}\) as \(t\rightarrow \infty \).

Proof

The dynamics of the sliding variable \({{\varvec{\sigma }}}\) is given by the distributed-order differential equation

$$\begin{aligned} \begin{aligned}&{\mathscr {D}}^{c(\alpha )} {{\varvec{\sigma }}} = \varLambda \ {\mathscr {D}}^{c(\alpha )}{\varvec{z}}_1 + {\mathscr {D}}^{c(\alpha )}{\varvec{z}}_2\\&\quad = \varLambda (A_{11} {{\varvec{z}}}_1 + A_{12} {{\varvec{z}}}_2) + A_{21} {{\varvec{z}}}_1 + A_{22} {{\varvec{z}}}_2 + {{\varvec{u}}} + {{\varvec{d}}}\\&\quad = (\varLambda A_{11} + A_{21}){{\varvec{z}}}_1 + (\varLambda A_{12} + A_{22}){{\varvec{z}}}_2 + {{\varvec{u}}} + {{\varvec{d}}}.\\ \end{aligned} \end{aligned}$$

By substituting the definition of \({\varvec{u}}\), one gets

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{\sigma }}} = {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *{{\varvec{v}}} + {{\varvec{d}}}. \end{aligned}$$

Furthermore, using Theorem 2, the integer-order derivative of \({{\varvec{\sigma }}}\) yields

$$\begin{aligned} \begin{aligned} \dot{{{\varvec{\sigma }}}}&= {\mathscr {L}}^{-1}\bigg \{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1}d\alpha }\bigg \} *{\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} \\&\quad *{{\varvec{v}}} + {\mathscr {L}}^{-1}\bigg \{ \frac{1}{\int _0^1 c(\alpha ) s^{\alpha -1}d\alpha }\bigg \} *{{\varvec{d}}}\\&= {{\varvec{v}}} + {{\varvec{\psi }}}\\&= - \frac{\pi }{2 q T_c} \left( \lfloor {{\varvec{\sigma }}} \rceil ^{1-q} + \lfloor {{\varvec{\sigma }}} \rceil ^{1+q}\right) - \kappa \lfloor {{\varvec{\sigma }}} \rceil ^0+ {{\varvec{\psi }}}. \end{aligned} \end{aligned}$$

Therefore, in a very similar fashion as in the proof of Theorem 3, one has that \({\varvec{\sigma }}(t)={\varvec{0}}\) is enforced \(\forall t\ge T_c\).

The second part of the proof can be demonstrated as follows. The substitution of \({\varvec{z}}_2 = - \varLambda {\varvec{z}}_1 + {{\varvec{\sigma }}}\) into \({\mathscr {D}}^{c(\alpha )} {{\varvec{z}}}_1 = A_{11} {{\varvec{z}}}_1 + A_{12} {{\varvec{z}}}_2\) renders

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} {{\varvec{z}}}_1 = \bar{\varLambda } {{\varvec{z}}}_1 + A_{12} {{\varvec{\sigma }}}. \end{aligned}$$

Consider the candidate Lyapunov function \(V_1 = \sqrt{{{\varvec{z}}}_1^{T} P {{\varvec{z}}}_1}\), with P a symmetric and positive definite matrix that fulfils \(P\bar{\varLambda } + \bar{\varLambda }^{T}P + Q = 0\), where Q is a symmetric and positive definite matrix. Then

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{c(\alpha )} V_1&\le \frac{{{\varvec{z}}}_1^{T} P}{\sqrt{{{\varvec{z}}}_1^{T} P {{\varvec{z}}}_1}} \ {\mathscr {D}}^{c(\alpha )} {{\varvec{z}}}_1 \\&= \frac{{{\varvec{z}}}_1^{T} P \bar{\varLambda } {{\varvec{z}}}_1 }{\sqrt{{{\varvec{z}}}_1^{T} P {{\varvec{z}}}_1}} + \frac{{{\varvec{z}}}_1^{T} P A_{12} {{\varvec{\sigma }}}}{\sqrt{{{\varvec{z}}}_1^{T} P {{\varvec{z}}}_1}}\\&\le - \gamma V_1 + ||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}||, \end{aligned} \end{aligned}$$

where \(\gamma > 0\) is a constant that depends on the proper values of P and Q, and \(P = {{\bar{P}}}^{T}{{\bar{P}}}\). Then,

$$\begin{aligned} {\mathscr {D}}^{c(\alpha )} V_1(t) = - \gamma V_1(t) + ||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}(t)|| - m(t) \end{aligned}$$

for some function \(m(t)\ge 0\). Then, using the Laplace transform, one has that

$$\begin{aligned}&C_\alpha (s){\hat{V}}(s) - \frac{C_\alpha (s)}{s}V(0) \\&\quad = - \gamma {\hat{V}}(s) + ||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}|| - M(s), \end{aligned}$$

or equivalently,

$$\begin{aligned} {\hat{V}}_1(s)&= \frac{C_\alpha (s)}{s[C_\alpha (s)+\gamma ]} V_1(0)\\&\quad + \frac{1}{C_\alpha (s)+\gamma } {\mathscr {L}}\bigg \{||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}||\bigg \}\\&\quad - \frac{M(s)}{C_\alpha (s)+\gamma } \end{aligned}$$

Taking the inverse Laplace transform produces

$$\begin{aligned} \begin{aligned} V_1(t)&= {\mathcal {G}}^\gamma (t;c(\alpha ))V_1(0)\\&\quad + {\mathscr {L}}^{-1}\bigg \{[C_\alpha (s) +\gamma ]^{-1}\bigg \}*||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}(t)||\\&\quad - {\mathscr {L}}^{-1}\bigg \{[C_\alpha (s) +\gamma ]^{-1}\bigg \}*m(t)\\&\le {\mathcal {G}}^\gamma (t;c(\alpha ))V_1(0)\\&\quad + {\mathscr {L}}^{-1}\bigg \{[C_\alpha (s) +\gamma ]^{-1}\bigg \}*||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}(t)||. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned}&\lim _{t\rightarrow \infty } V_1(t)\\&\quad \le \lim _{t\rightarrow \infty }{\mathscr {L}}^{-1}\bigg \{[C_\alpha (s) +\gamma ]^{-1}\bigg \}*||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}(t)||\\&\quad = \lim _{s\rightarrow 0}\frac{s}{C_\alpha (s)+\gamma } {\mathscr {L}}\bigg \{||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}||\bigg \}\\&\quad = \frac{1}{\gamma } \lim _{s\rightarrow 0} s {\mathscr {L}}\bigg \{||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}||\bigg \}\\&\quad = \frac{1}{\gamma } \lim _{t\rightarrow \infty } ||{{\bar{P}}} A_{12} {{\varvec{\sigma }}}(t)|| = 0. \end{aligned}$$

Furthermore, note that \({\varvec{z_2}}(t) = \varLambda {{\varvec{z}}}_1(t) \rightarrow {{\varvec{0}}}\) as \(t\rightarrow \infty \), whereby \({\varvec{x}}(t) = T^{-1}{{\varvec{z}}}(t) \rightarrow {{\varvec{0}}}\) as \(t\rightarrow \infty \).

\(\square \)

Fig. 3
figure 3

Simulation results: \({\mathscr {D}}^{c(\alpha )} {{\varvec{x}}} = A {{\varvec{x}}} + B[u + d]\), with \({\varvec{x}}(0)=[5~~-2]^{T}\)

Full size image

4 Simulations

The simulations run in Simulink in Matlab, at 0.01 ms of sampling time. Besides, since the distribution functions in the following examples are of the form of comb functions, the distributed-order derivatives are computed as linear combinations of fractional-order ones, and the CRONE method is considered for approximating those fractional-order derivatives [50].

The suggested tuning for the control parameters \(T_c\), q and \(\kappa \) is considered as follows: The predefined time \(T_c\) is a realistic upper bound for the convergence time, and should be given in accordance to the system constraints and tasks specifications. The parameter q is in (0, 1) to fulfil the requirements of Theorem 3, thus, \(q=0.5\) is suggested but can be adjusted to improve the closed-loop response. The feedback gain \(\kappa \) is related to the robustness properties of the controller, such that, a larger \(\kappa \) can face a wider class of disturbances, nonetheless, at the price of a more aggressive control signal, thus, it is suggested to set \(\kappa \) at a small value, and gradually increase it to improve the system behaviour.

4.1 Disturbance-free scalar system

The first simulation considers the scalar system

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{c(\alpha )} x&= u,\\ u&= {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *v,\\ v&= -\frac{\pi }{2qT_c}(\lfloor x \rceil ^{1-q} + \lfloor x \rceil ^{1+q}),\\ \end{aligned} \end{aligned}$$

with \(q=0.5\) and \(T_c = 1\). The density function is \(c(\alpha ) = \sum _{l=1}^4\delta (\alpha - 0.2l)\).

Figure 1 shows the response of x(t) for different initial conditions

$$\begin{aligned} x(0) \in \{-10^4,-10^3,-10^2,-10,-1,1,10,10^2,10^3,10^4\}. \end{aligned}$$

In the same Fig. one can appreciate that the convergence time has the least upper bound \(T_c = 1\) s, such that \(x(t) = 0~\forall t\ge T_c\) and \(\lim _{|x(0)|\rightarrow \infty } T(x(0)) = T_c\). The response of the closed-loop system constitutes an evidence that the proposed controller induces a fast response, even in the case of dynamical systems with naturally slow and ultra slow responses. It can be appreciated in addition, that an upper bound for the convergence time exists, is independent of the initial conditions, and can be predefined as an adjustable control parameter.

4.2 Uncertain scalar system

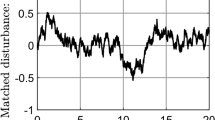
The second simulation considers the scalar system

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{c(\alpha )} x&= u + d,\\ u&= {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *v, \\ v&= - \frac{\pi }{2 q T_c} \left( \lfloor x(t) \rceil ^{1-q} + \lfloor x \rceil ^{1+q}\right) - \kappa \lfloor x \rceil ^0,\\ \end{aligned} \end{aligned}$$

with \(d = 0.1\cos (2t) + 0.1\sin (t) + \vartheta \), \(\vartheta = \frac{1}{2}\int _0^t (\mathrm {rand} - \vartheta )d\tau \), for \(\mathrm {rand}\) a random valued function in \([-10,10]\). The density function is \(c(\alpha ) = \sum _{l=1}^4\delta (\alpha - 0.2l)\), and the control parameters \(q=0.5\), \(T_c = 1\) and \(\kappa = 0.2\). Fig. 2 shows the convergence of x(t) before \(T_c\), even in the case of the unknown disturbance d. In this case, the least upper bound for the settling-time T(x(0)) is unknown due to \(d\ne 0\); nonetheless, it is possible to guarantee that \(x(t) = 0~\forall t\ge T_c\) and that \(\lim _{|x(0)|\rightarrow \infty } T(x(0)) \le T_c\), this is, \(T_c\) is a predefined upper bound, but not the least upper bound. It is worth to comment that \(\kappa \) only depends on an estimated upper bound for the apparent disturbance to the induced integer-order reaching phase, and not on the predefined time nor on the initial conditions, while the convergence time is upper bounded by the predefined constant \(T_c\), for arbitrary x(0).

4.3 Linear time invariant system subject to a matched disturbance

For this case of study consider system (10) with

$$\begin{aligned} A = \begin{bmatrix} 0 &{}&{} 2 \\ -1 &{}&{} 0 \end{bmatrix} \text{ and } B = \begin{bmatrix} 1 \\ 1 \end{bmatrix}. \end{aligned}$$

subject to \(d = 0.5\cos (2t) + 0.5\sin (t) + \vartheta \), with \(\vartheta = \frac{1}{2}\int _0^t (\mathrm {rand} - \vartheta )d\tau \), for \(\mathrm {rand}\) a random valued function in \([-10,10]\). The density function is \(c(\alpha ) = 0.5\delta (\alpha - 0.3) + 0.5\delta (\alpha - 0.5) + \delta (\alpha - 0.7)\), Therefore the transformation matrix

$$\begin{aligned} T = \frac{1}{2} \begin{bmatrix} 1 &{}&{} -1 \\ 1 &{}&{} 1 \end{bmatrix} \end{aligned}$$

produces

$$\begin{aligned} \begin{aligned} {\mathscr {D}}^{c(\alpha )} z_1&= -0.5 z_1 + 1.5 z_2\\ {\mathscr {D}}^{c(\alpha )} z_1&= -1.5 z_1 + 0.5z_2 + u + d. \end{aligned} \end{aligned}$$

Thus, it can be realised that \(z_2 = - \lambda z_1\) implies that \( {\mathscr {D}}^{c(\alpha )} z_1 = -(0.5+1.5 \lambda ) z_1\), and consequently \(z_1 \rightarrow 0\) as \(t\rightarrow \infty ~\forall \lambda > 0\). In this case, \( \lambda = 1\) is considered. Then, the sliding variable becomes

$$\begin{aligned} \sigma = z_1 + z_2 = x_1, \end{aligned}$$

and consequently, \({\mathscr {D}}^{c(\alpha )} \sigma = -2 z_1 + 2 z_2 + u + d\). The controller is proposed as

$$\begin{aligned} \begin{aligned} u&= 2 z_1 - 2 z_2 + {\mathscr {L}}^{-1}\bigg \{ \int _0^1 c(\alpha ) s^{\alpha -1}d\alpha \bigg \} *v\\ v&= - \frac{\pi }{2 q T_c} \left( \lfloor \sigma \rceil ^{1-q} + \lfloor \sigma \rceil ^{1+q}\right) - \kappa \lfloor \sigma \rceil ^0 \end{aligned} \end{aligned}$$

with \(q=0.5\), \(T_c = 1\) and \(\kappa = 1\).

Fig. 3 highlights the response of the system closed by the proposed controller. It can be noticed that, the pseudo-state \({\varvec{x}}\) and the auxiliary vector function \({\varvec{z}}\) converge asymptotically. In addition, the sliding variable \(\sigma \) converges before \(T_c\) and remains invariant afterwards, despite the effect of the unknown disturbance d. The controller u stays continuous and with admissible bounds. In this particular case, the system structure allowed to establish the invariant \(\sigma =x_1=0\) in predefined-time. However, in a more general case, \(\sigma =0\) is enforced in predefined-time, but \({{\varvec{x}}}\) converges asymptotically.

5 Conclusions

This paper proposed a predefined-time controller for a class of distributed-order systems, which relies on a dynamical extension to compensate the inherent memory characteristics of distributed-order systems. In addition, a robust sliding mode controller for linear time invariant systems subject to matched disturbances was proposed, such that, a stable sliding mode is enforced within a prescribed fixed-time. The simulation study highlights the reliability of the proposed methodology, in which, a fast convergence is induced for inherently slow dynamical systems. The proposed approach can be applied to predefined-time robust control of diffusion processes with slow dynamics; dynamical systems with multiple fractional devices of different orders, such as viscoelastic materials in mechanical system or biological tissues, or super-capacitor elements in electrical systems; as well as in the synchronisation of distributed-order chaotic systems.